磨削加工广泛应用于高精度、低表面粗糙度工件的加工,但砂轮表面大量无规则分布磨粒对工件所造成划擦、耕犁、切削的去除行为,导致磨削温度过高,使工件表面产生烧伤、软化、破裂等热损伤[1–3]。近年来,许多学者对磨削区的温度场分布预测进行了大量研究,建立了各类热源模型,并将热源模型假设为多项式曲线、椭圆等形状[4–5],但是这种热简化源模型不能准确反映复杂的磨削过程,因此,单颗磨粒磨削方法在磨削机理研究中得到了广泛的应用[6–8]。周雯雯等[9]采用不同形状的磨粒磨削SiCf /SiC,得到了磨粒形状对材料的影响规律。张红哲等[10]以SiCp /Al 复合材料为样本,进行了单颗磨粒在不同切削深度下对工件影响的仿真分析和试验验证。唐进元等[11]通过有限元软件计算了单颗磨粒作用下超声磨削温度场分布及磨削的最高温度,研究了各项磨削参数对单颗磨粒磨削区最高温度的影响。杨理钧等[12]建立了单颗刚玉磨粒切削齿轮钢的ABAQUS仿真模型和磨粒–工件的热传导模型,分析了不同的磨粒特性和工艺参数下工件最高温度的变化规律。刘寅等[13]建立了单颗磨粒微磨削的正交切削模型和玻璃金属的本构关系方程,采用有限元工艺仿真系统对块体金属玻璃进行了微磨削加工的温度场仿真。
上述研究只是针对单颗磨粒对工件的作用进行分析,并未考虑多个磨粒之间的影响,但在实际磨削过程中,磨削接触面温度是由无数个磨粒共同作用,互相影响产生。因此,针对多磨粒磨削,本文将磨粒简化为点热源,开展了磨粒间距对工件表面温度变化规律有限元仿真研究,并进行了材料的导热率、比热容和密度对工件表面温度变化影响规律仿真研究。
1 仿真建模
为研究点热源间距及材料特性对磨削温度的影响,运用ANSYS Workbench对磨削过程进行仿真。当砂轮磨削工件表面时,把磨粒作用在工件表面的痕迹简化为点热源,并假设热量均匀分布在点热源上,通过离散化的方式对磨削热量在工件表面传递进行仿真,以模拟磨削过程中磨粒对工件做功而产生的热量并相互干涉的效果。点热源间距对工件表面温度影响的仿真参数如表1所示;材料特性对工件表面温度影响的仿真参数如表2所示。
表1 点热源间距对工件表面温度的影响仿真参数
Table 1 Simulation parameters of influence of point heat source spacing on workpiece surface temperature
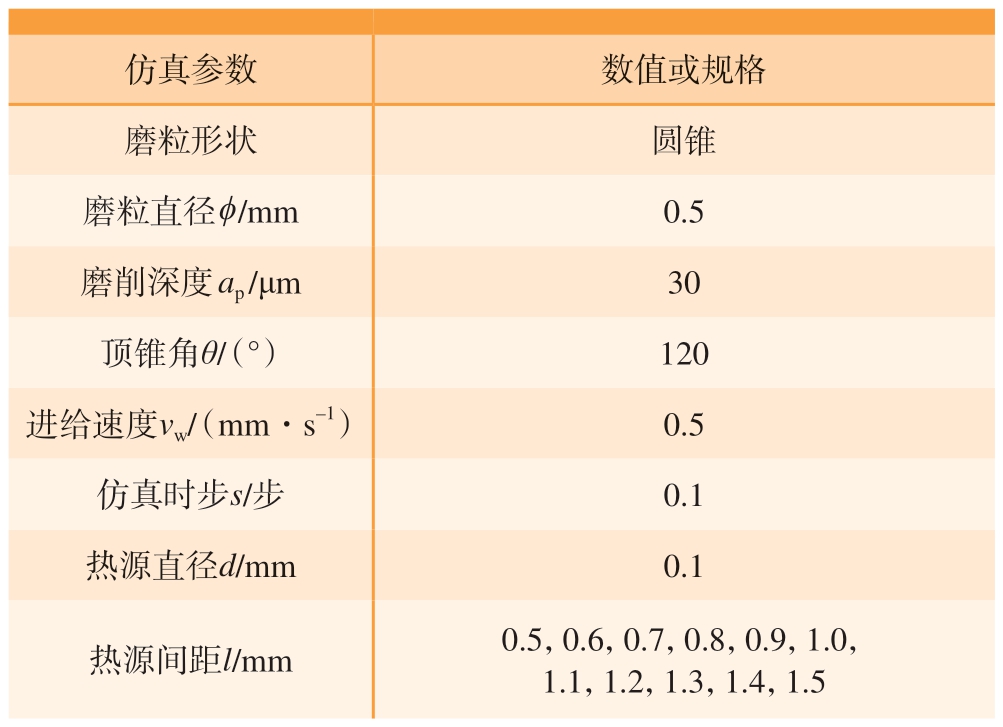
仿真参数数值或规格磨粒形状圆锥磨粒直径 ϕ/mm0.5磨削深度 ap /μm30顶锥角θ/(°)120进给速度vw/(mm·s–1)0.5仿真时步s/步0.1热源直径d/mm0.1热源间距l/mm0.5,0.6,0.7,0.8,0.9,1.0,1.1,1.2,1.3,1.4,1.5
表2 材料特性对工件表面温度的影响仿真参数
Table 2 Simulation parameters of influence of material properties on workpiece surface temperature
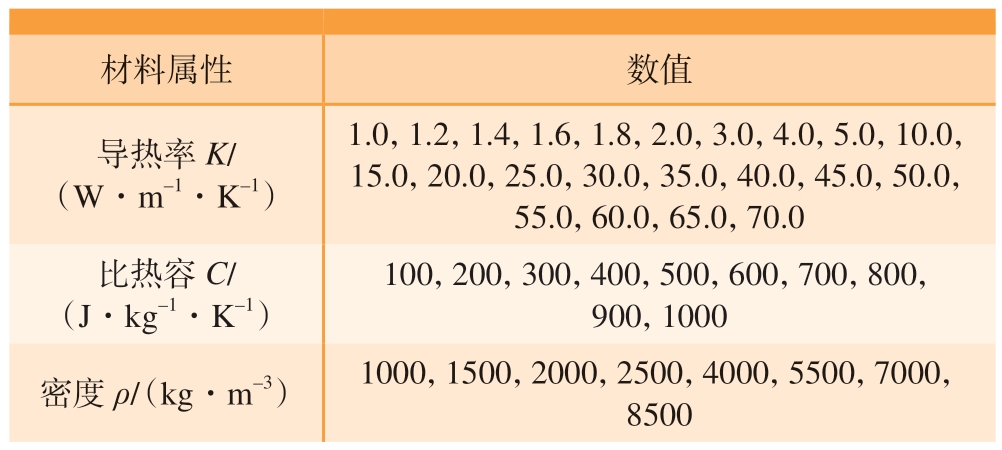
材料属性数值导热率K/(W·m–1·K–1)1.0,1.2,1.4,1.6,1.8,2.0,3.0,4.0,5.0,10.0,15.0,20.0,25.0,30.0,35.0,40.0,45.0,50.0,55.0,60.0,65.0,70.0比热容C/(J·kg–1·K–1)100,200,300,400,500,600,700,800,900,1000密度ρ/(kg·m–3)1000,1500,2000,2500,4000,5500,7000,8500
用UG画出工件并导入ANSYS Workbench,进行点热源间距及材料参数对温度影响的仿真研究。点热源间距对温度影响的几何建模工件尺寸为10 mm×20 mm×3 mm,将点热源间距0.5阵列于工件表面,按照此类方式增大点热源的横向间距至1.5 mm,并分别排列到材料(45#钢、玻璃、陶瓷、大理石、钛和不锈钢)工件的表面,分析点热间距在不同材料中对温度的影响,如图1(a)所示;材料特性对工件表面温度影响的工件尺寸为10 mm×10 mm×4 mm,点热源间距固定为0.5 mm,如图1(b)所示。对工件划分网格并细化热源面,通过离散化的方式完成模拟;对干磨进行仿真研究,设定环境温度为22 ℃,工件表面换热系数为0。
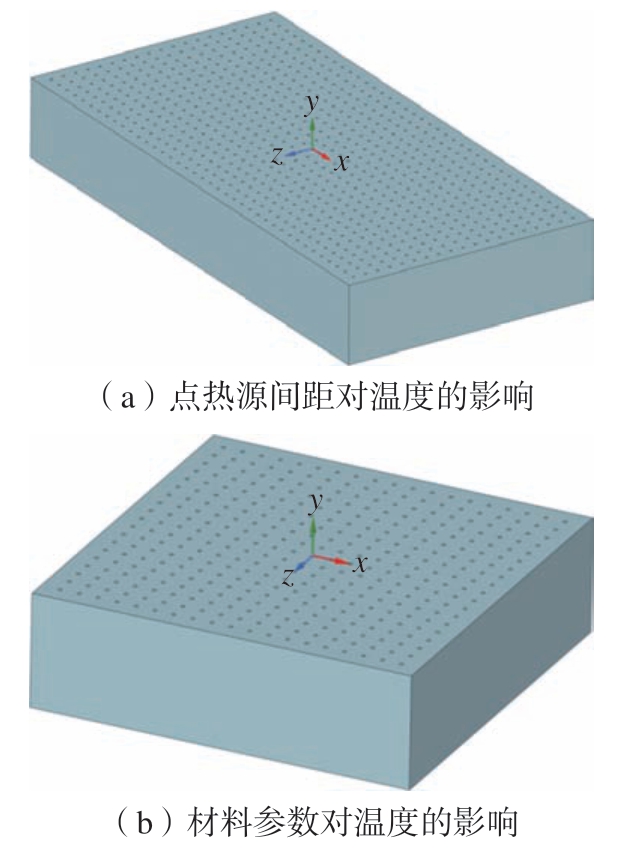
图1 几何建模
Fig.1 Geometric modeling
2 磨削温度场模型
2.1 磨削区热量分配
磨削加工中,要了解磨削区温度的分布情况,就必须确定流入工件的热量。工件磨削区所产生的总热流密度qtotal为[14]
式中,Ft表示切向磨削力;Vs表示砂轮的圆周速度;lc表示工件与砂轮的接触弧长;B表示磨削宽度。
为了减少外界因素的干扰,忽略磨削液带走的热量。磨屑带走的热量占比很少,因此可以视为0,只需考虑流入砂轮和工件的热量,则
式中,qw为流入工件的热流密度;qs为流入砂轮的热流密度。磨削过程中,工件自身占的热量比为[15]
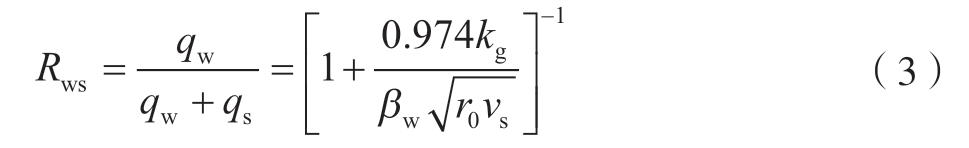
式中,kg为磨粒导热率;r0为磨粒接触半径;![]() 为工件材料的接触系数,其中kw为工件的导热系数,ρw为工件密度,cw为工件比热容。
为工件材料的接触系数,其中kw为工件的导热系数,ρw为工件密度,cw为工件比热容。
2.2 热传递模型
本文将点热源分布在工件表面,并赋予热流密度,在仿真过程中,点热源之间的热量相互作用,并假设工件与外界无热交换,因此,磨削温度场可视为二维传热,根据傅里叶传热定律及热力学第一定律,建立二维瞬态温度场的热平衡微分方程[16]。
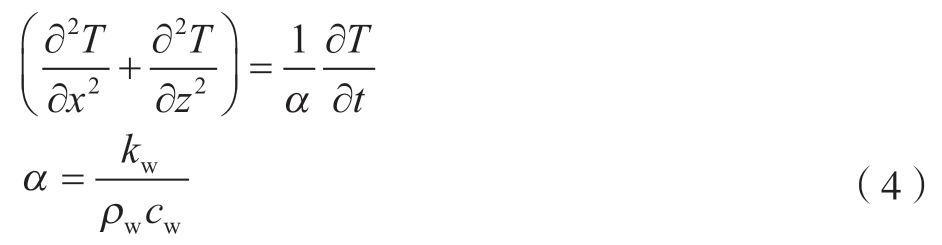
式中,T表示工件瞬时温度;t表示时间;α表示热扩散系数。
2.3 差分方程的建立
利用有限差分法建立二维矩形工件离散图,如图2所示,其横向点间距为x = 0.5 mm,纵向间距从z = 0.5 mm依照仿真过程依次扩大至z = 1.5 mm。任意选取一点(i,j),根据热力学第一定律,该点热源会与其他点热源相互作用。方程组为
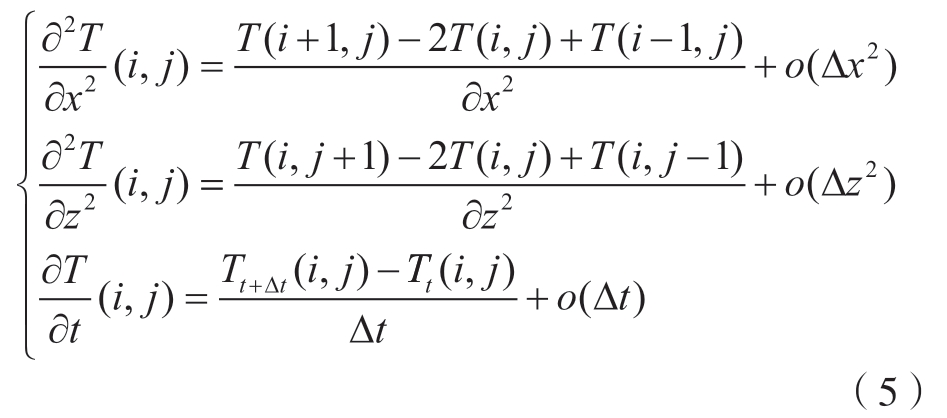
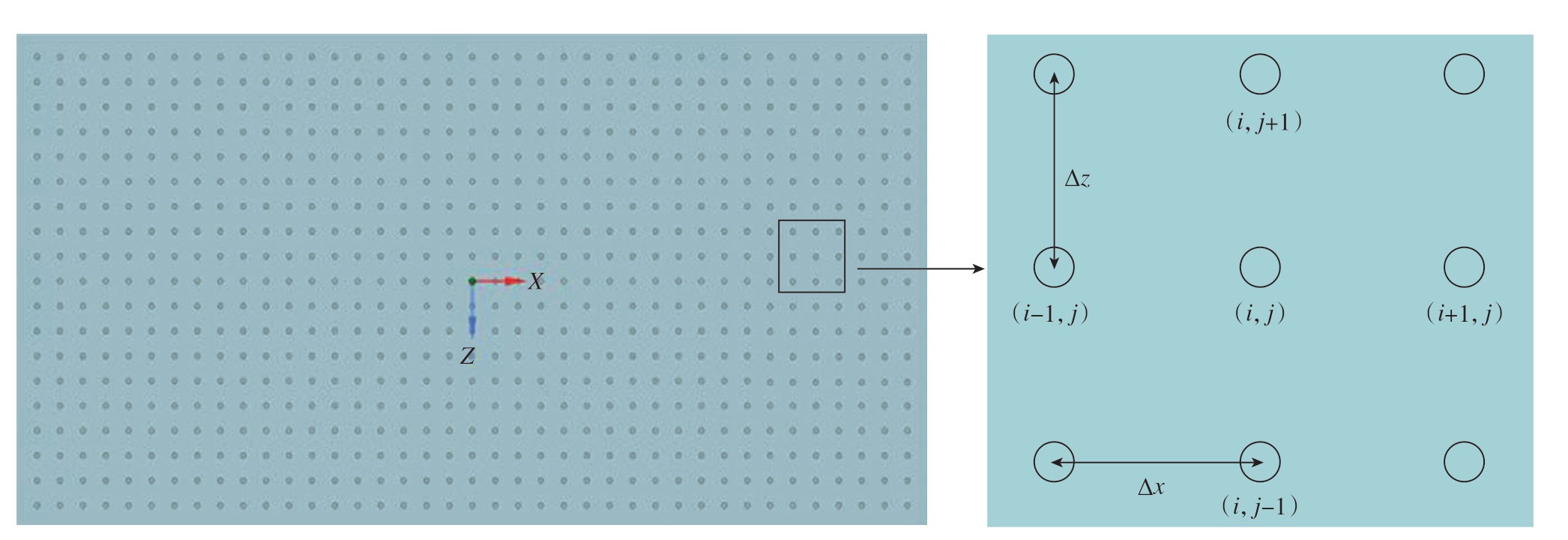
图2 工件表面温度传导
Fig.2 Workpiece surface temperature conduction
式中, T(i,j)表示坐标(i,j)点的温度;Tt+Δt(i,j)表示坐标(i,j)点在t +Δt时刻的温度值;Δt表示时间增量;o表示无穷小量。
将式(2)代入二维传导方程(式(5))中,得到各点热源处的差分方程,即
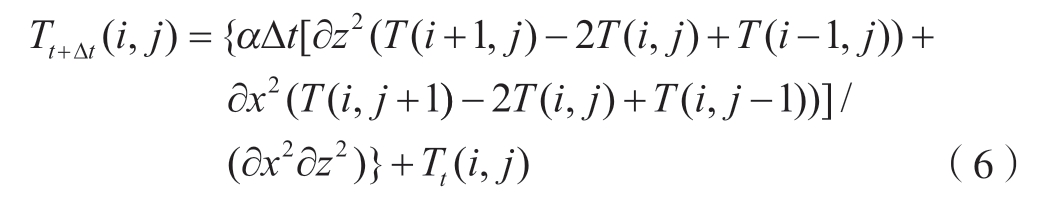
3 仿真及其分析
本文针对磨粒间距和材料特性对温度的影响做了仿真研究。
(1)将磨粒作用在工件表面的痕迹简化为点热源,对单列点热源分别施加热通量并设定时长以模拟单颗磨粒划擦整个工件表面时的温度,依次对多排点热源施加与单列点热源仿真相同的热通量条件,来模拟磨削过程中多个磨粒划擦整个工件表面时的温度,将点热源横向间距从0.5 mm依次增大到1.5 mm来模拟点热源间距对工件表面温度的影响,针对不同的材料重复上述模拟过程,并进行分析。
(2)在ANSYS Workbench中设置材料的导热率为1~70 W/(m·K),比热容为100~1000 J/(kg·℃),密度为1000~8500 kg/m3,模拟材料特性对磨削温度的影响。
3.1 磨粒间距对温度的影响有限元分析
图3为不同材料磨粒间距(点热源间距)对温度传导影响的仿真,将点热源横向间距依次从0.5 mm扩大至1.5 mm直至单颗磨粒。可以看出,在多磨粒仿真磨削过程中,热量随时间输入至每排点热源,使得点热源之间相互作用,导致磨削区温度逐渐升高。在仿真刚开始的前几秒,热量开始作用于第1排点热源,并于下一阶段点热源相互作用,从而导致磨削区温度迅速上升;几秒之后磨削区的温度上升逐渐平滑,直至磨削后期;由于在绝热的条件下,热量不能向空气中传播,而向上一阶段传递的热量又很少,导致在后期阶段的热量聚集,温度急剧上升,并且这种现象在图3(b)~(d)中更为明显。单颗磨粒在磨削不同材料时,由于单列点热源的热量可以迅速扩散至点热源周围,其温度最低,且随时间变化最小;当点热源间距在 0.5 mm、0.6 mm、0.7 mm、0.8 mm,以及0.9~1.5 mm 时,磨削区温度相差并不明显,这种情况在不同材料中都有表现。其原因:随着点热源间距不断扩大,热量在点热源之间的相互作用减弱,导致工件表面温度逐渐下降,且随时间变化幅度降低;由于工件表面的点热源相互作用和所给定的热流密度随时间变化及网格划分的关系,曲线具有一定的波动,这种波动在大理石和玻璃材料中尤为明显,所以针对这一现象,进行材料特性对温度影响的研究。
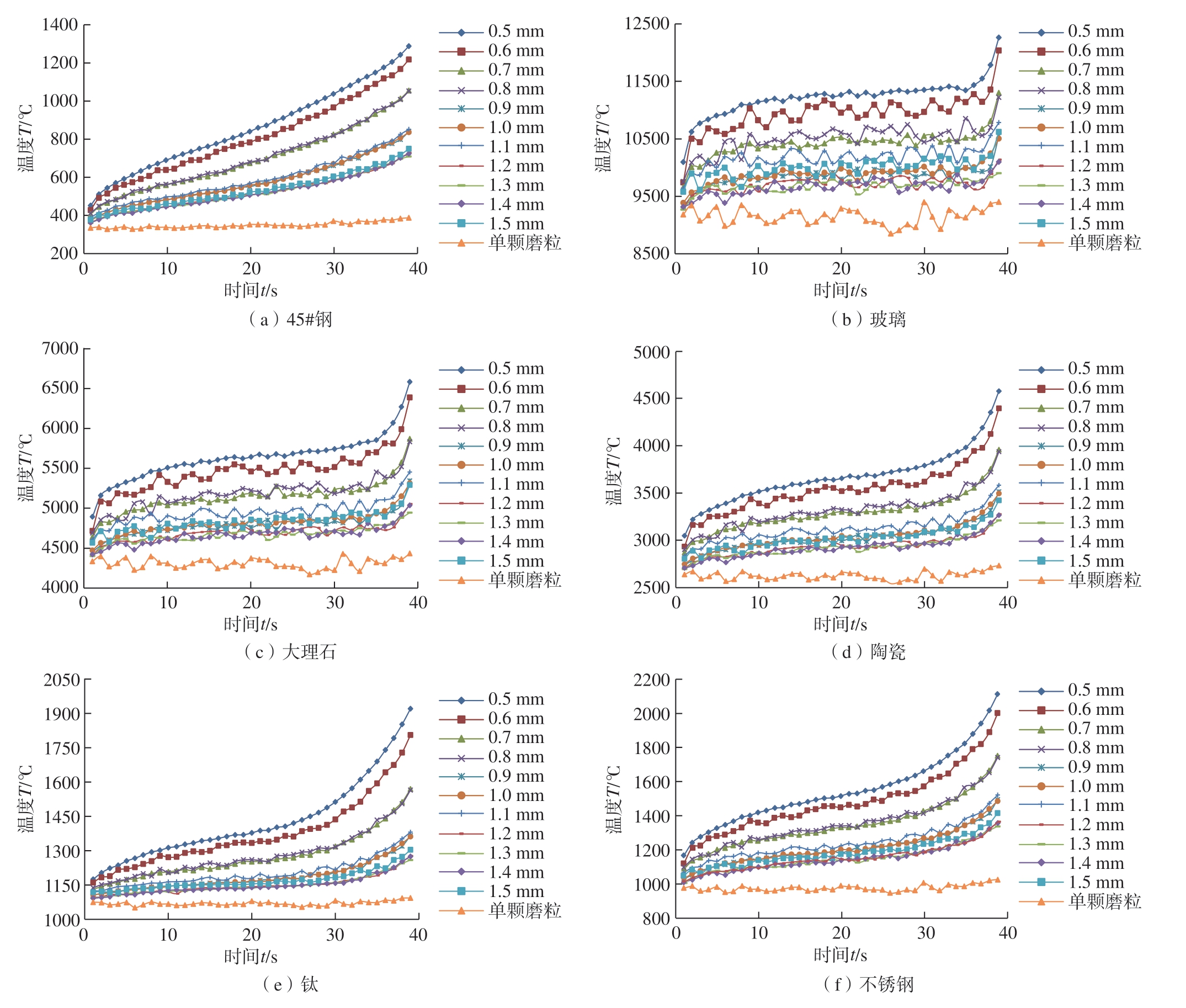
图3 不同材料磨粒间距对温度传导影响的仿真
Fig.3 Simulation of the influence of point heat source distance of different materials on temperature conduction
3.2 材料特性对温度影响的有限元分析
针对材料特性对磨削温度影响的仿真,将点热源间距定为0.5 mm,分别设置材料的导热率、比热容及密度,对温度曲线进行仿真和分析,如图4所示。
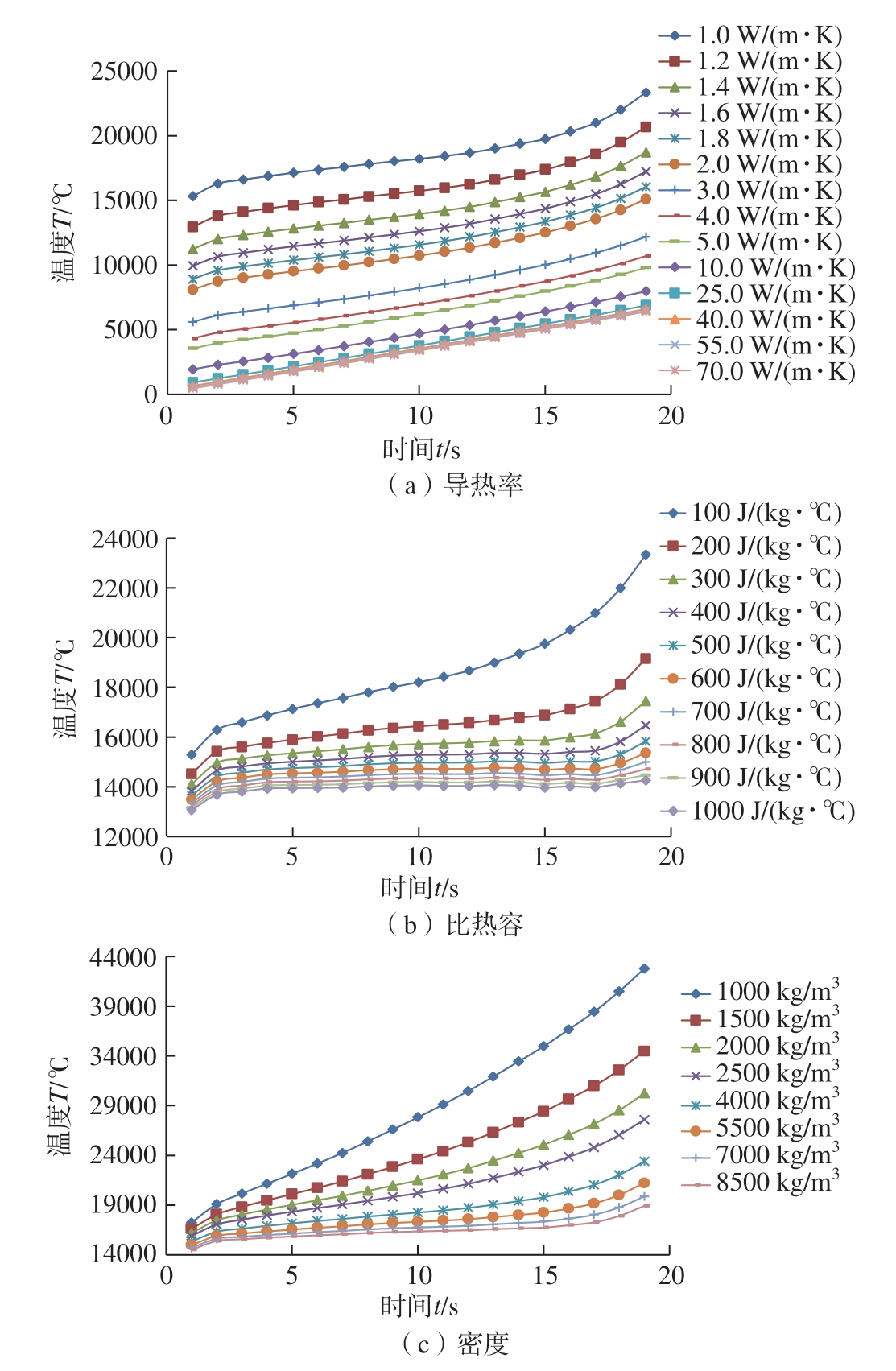
图4 不同材料特性对温度的影响
Fig.4 Influence of different material properties on temperature
由图4(a)可知,导热率从1 W/(m·K)升到70 W/(m·K),工件表面温度随时间变化呈相似趋势且逐渐升高,但随导热率增大而降低;当导热率从1 W/(m·K)升到10 W/(m·K)时,最高温度从23300 ℃左右降到7900 ℃左右;导热率从10 W/(m·K)升到70 W/(m·K)时,温度几乎不随导热率增大而变化。这主要是因为材料导热率小,热量聚集在点热源上,导致温度相对较高且热量不易扩散;当材料导热率较大时,热量在材料内快速传递,不会聚集在点热源,从而使工件温度较低。
由图4(b)可知,随着比热容从100 J/(kg·℃)升到1000 J/(kg·℃),工件表面温度随时间增加而升高,且随比热容的增大而减小;比热容从100 J/(kg·℃)升到400 J/(kg·℃),工件最高温度从23300 ℃左右降到16400 ℃左右;比热容从400 J/(kg·℃)升到1000 J/(kg·℃),最高温度从16400 ℃左右降到14200℃左右,而且当比热容较大时,温度随时间变化较缓慢,这种趋势是比热容的物理意义所决定的。
由图4(c)可知,材料密度对温度的影响规律和比热容类似,当材料密度从1000 kg/m3增大到4000 kg/m3时,工件表面最高温度从42600 ℃左右降到23300 ℃左右;材料密度从4000 kg/m3增大到8500 kg/m3时,最高温度从23300 ℃左右降到18800 ℃左右,其温度变化范围要比从1000 kg/m3增大到4000 kg/m3时小很多,这是因为当材料密度较小时,材料孔隙率太高,而孔隙中的气体又会阻碍热量传递,导致热量聚集,温度过高。
4 结论
利用ANSYS Workbench进行了磨削点热源的仿真,仿真结果曲线一致且规律明显,结论如下。
(1)随着仿真磨削过程的进行,工件表面温度因为热量不断地输入和点热源之间的干涉而不断升高。后期,由于工件与周围绝热,热量向下一级传递的很少,热量聚集,温度迅速升高。此结论有助于指导解决磨削后期温度突然升高的问题,改善工件表面因温度过高而产生热损伤、热变形等危害。
(2)当点热源间距从0.5 mm增大到1.5 mm时,温度逐渐降低,且温度随时间推移,上升的速度逐渐降低,但点热源间距分别在0.5 mm、0.6 mm、0.7 mm、0.8 mm、0.9 mm、1.5 mm时温度差距不大,直至单个点热源时达到最低值,其原因为随着点热源间距逐渐增大,热量干涉逐渐减弱导致温度降低。此结论用于指导砂轮制造时磨粒间距的选择,在确保加工质量的同时,防止因热量过于聚集导致工件出现烧伤、软化等问题。
(3)随着导热率增大,工件表面温度随时间呈相似升高趋势,但总体温度呈下降趋势。当导热率从1 W/(m·K)增大到10 W/(m·K)时,工件温度随着导热率增大而减小的趋势明显;当导热率大于10 W/(m·K)时,工件表面温度基本不随导热率的增大而减小。这是因为导热率小时,热量聚集在点热源,导致温度过高;当导热率较大时,热量不发生聚集而扩散至工件其他位置上,使得工件温度较低。
(4) 比热容从100 J/(kg·℃)增大到200 J/(kg·℃)时,工件温度随比热容增大有明显的下降,且随时间增大的趋势明显;比热容从200 J/(kg·℃)增大到1000 J/(kg·℃)时,工件温度随比热容增大而下降的趋势降低,且基本不随时间变化,这是由比热容的物理意义决定的。
(5)密度从1000 kg/m3增大到4000 kg/m3时,工件温度随密度的增大逐渐下降且随时间变化明显;密度从4000 kg/m3增大到8500 kg/m3时,磨削温度虽然也随密度增大而下降,但差距很小且随时间变化的速度很慢,其原因是低密度的材料孔隙率过高,热量易聚集从而导致局部温度过高。
(6)材料特性对磨削温度影响的结论有助于通过对比材料特性选择适合的磨削加工参数和砂轮,以减少磨削时因高能量的输入而产生的高温,从而改善工件因残余应力而导致的变形等问题。
[1] TIAN L, FU Y C, XU J H, et al. The influence of speed on material removal mechanism in high speed grinding with single grit[J].International Journal of Machine Tools and Manufacture, 2015, 89: 192–201.
[2] 何玉辉, 徐彦斌, 唐进元, 等. 磨削弧区高阶函数热源分布模型研究[J]. 机械工程学报, 2019, 55(7): 199–206.
HE Yuhui, XU Yanbin, TANG Jinyuan, et al. Study on heat source distribution model of high-order function in grinding arc area[J]. Journal of Mechanical Engineering, 2019, 55(7): 199–206.
[3] WANG L, TIAN X, LU Q, et al. Material removal characteristics of 20CrMnTi steel in single grit cutting[J]. Materials and Manufacturing Processes, 2017, 32(13): 1528–1536.
[4] LI B Z, ZHU D H, PANG J Z, et al. Quadratic curve heat flux distribution model in the grinding zone[J]. The International Journal of Advanced Manufacturing Technology, 2011, 54(9): 931–940.
[5] SHAH S M, NÉLIAS D, CORET M, et al.Numerical simulation of grinding induced phase transformation and residual stresses in AISI–52100 steel[J]. Finite Elements in Analysis & Design, 2012, 61: 1–11.
[6] BARGE M, RECH J, HAMDI H, et al. Experimental study of abrasive process[J]. Wear, 2008, 264(5–6): 382–388.
[7] 霍文国, 丁元法, 蔡兰蓉, 等. 基于单颗磨粒切削的钛合金磨削过程仿真研究[J]. 金刚石与磨料磨具工程, 2015, 35(3): 17–22.
HUO Wenguo, DING Yuanfa, CAI Lanrong, et al. Simulation of single grain grinding TC4 alloy[J]. Diamond & Abrasives Engineering, 2015, 35(3):17–22.
[8] SIEBRECHT T, BIERMANN D, LUDWIG H, et al. Simulation of grinding processes using finite element analysis and geometric simulation of individual grains[J]. Production Engineering, 2014, 8(3): 345–353.
[9] 周雯雯, 王建青, 赵晶, 等. 单颗磨粒划擦SiCf /SiC陶瓷基复合材料的试验研究[J]. 金刚石与磨料磨具工程, 2021, 41(1): 51–57.
ZHOU Wenwen, WANG Jianqing, ZHAO Jing, et al. Experimental research on single abrasive grain scratch SiCf /SiC ceramic matrix composites[J]. Diamond and Abrasives Engineering, 2021, 41(1): 51–57.
[10] 张红哲, 张旭, 朱晓春, 等. 基于单颗磨粒划切试验的SiCp /Al复合材料表面去除机理研究[J]. 浙江大学学报(工学版), 2022,56(2): 388–397.
ZHANG Hongzhe, ZHANG Xu, ZHU Xiaochun, et al. Surface removal mechanism study of SiCp /Al composites based on single-point cutting test[J].Journal of Zhejiang University (Engineering Science), 2022, 56(2): 388–397.
[11] 唐进元, 朱锦涛, 郑金超, 等. 超声磨削单颗磨粒磨削温度预测与试验研究[J]. 华中科技大学学报(自然科学版), 2018, 46(10): 63–68.
TANG Jinyuan, ZHU Jintao, ZHENG Jinchao, et al. Prediction and experimental study on temperature of ultrasonic-assisted grinding with single grit[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2018, 46(10): 63–68.
[12] 杨理钧, 刘谦, 田欣利, 等. 单颗刚玉磨粒切削齿轮钢温度场仿真研究[J]. 组合机床与自动化加工技术, 2017(4): 52–55.
YANG Lijun, LIU Qian, TIAN Xinli, et al. Simulation researh of cutting temperature in cuting gear steel by single alumina grit[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2017(4): 52–55.
[13] 刘寅, 巩亚东, 孙瑶, 等. 块体金属玻璃微磨削加工的温度场仿真[J]. 东北大学学报(自然科学版), 2018, 39(6): 828–833.
LIU Yin, GONG Yadong, SUN Yao, et al. Simulation of temperature field for bulk metallic glass in micro-scale grinding[J]. Journal of Northeastern University (Natural Science), 2018, 39(6): 828–833.
[14] 李伯民, 赵波. 现代磨削技术[M]. 北京: 机械工业出版社,2003.
LI Bomin, ZHAO Bo. Modern grinding technology[M]. Beijing: China Machine Press, 2003.
[15] RAMANATH S, SHAW M C. Abrasive grain temperature at the beginning of a cut in fine grinding[J]. Journal of Engineering for Industry,1988, 110(1): 15–18.
[16] SHEN B. Minimum quantity lubrication grinding using nanofluids[D]. Michigan: University of Michigan, 2008.