球头铣刀广泛应用于航空航天、汽车和模具等关键零部件的铣削加工,其铣削力学行为直接影响工件加工速度和加工精度,是加工参数选择和优化的依据,对其进行研究可为现代制造业提供重要的理论和技术支撑。同时,球头铣削力与铣削接触区几何特性之间联系紧密,故精准表征该接触区是分析球头铣削力的关键。
针对球头铣刀–工件接触区(Cutter–workpiece engagement,CWE)的精确求解方法,国内外学者进行了大量的研究。目前,CWE的求解方法主要有实体建模法、离散求解法和解析法等。Lazoglu等[1]基于边界表示的实体建模法开发了一个B-Rep模型来模拟复杂五轴球端铣削自由曲面中的CWE。张立强等[2]采用实体建模法分析刀具与工件的接触区,提出了面向五轴侧铣的球头铣削力学模型。Yang等[3]通过布尔运算提出了一种实体修剪法来分析CWE,有效地提高了实体建模方法的计算效率。倪其民等[4]通过实体建模建立了复杂曲面球头铣刀三轴铣削加工的铣削力。此外,Taner等[5]创建了一个有组织的点云,将刀具包络线分为轴向和径向段,并使用Z-Map离散方法提取了CWE边界。董永亨等[6]在考虑刀具姿态调整的情况下,使用微元积分方法建立了瞬时切削力的计算模型,改进了识别CWE的Z-Map算法。魏兆成等[7]通过Z-Map方法识别CWE,提出了一种考虑进给方向和刀具切除区域任意面的切削力预报方法。在解析法的计算当中,Ozturk等[8–9]提出了一个计算球端铣削单调曲面的CWE边界和切削厚度的分析模型。Guo等[10]通过解析法确定切除区域,并建立了考虑刀具跳动的五轴切削力系数求解模型。在一些研究中,利用计算机辅助制造(CAM)软件生成切削位置文件,从而获取加工条件和表面数据[11–13],分析CWE边界。魏兆成等[14]通过半解析法求得切除区域,将复杂曲面离散为小斜面以实现CWE建模分析。王亮[15]通过解析法建立了立铣工况球头铣刀与参数化斜面的CWE解析式。
以上解析法在考虑刀具姿态变化时,具有较高的计算效率和精度,但目前刀具姿态变化对铣削力的影响研究较少。为此,本文以球头铣刀为研究对象,提出基于齐次变换的CWE求解方法,并以此建立了刀具一般姿态的接触区域表达式,进而从接触区域视角分析了刀具姿态变化对铣削力的影响机制。
1 球头CWE求解与铣削力建模
1.1 球头铣刀铣削几何学特性
为更好地描述球头铣刀的铣削过程,建立工件坐标系o–xw ywzw、刀具坐标系ot–xt ytzt和过渡坐标系oc–xc yczc(图1);过渡坐标系原点位于球头铣刀球心,zc轴垂直于工件表面,xc轴负方向为刀具进给方向,yc轴指向未加工表面;在刀具坐标系ot–xt ytzt中,zt为刀具轴线,与过渡坐标系在无倾角时保持平行且坐标原点重合。同时,工件坐标系位于工件左下方顶点处,实际生产中视加工要求而定,通过平移与过渡坐标系重合。
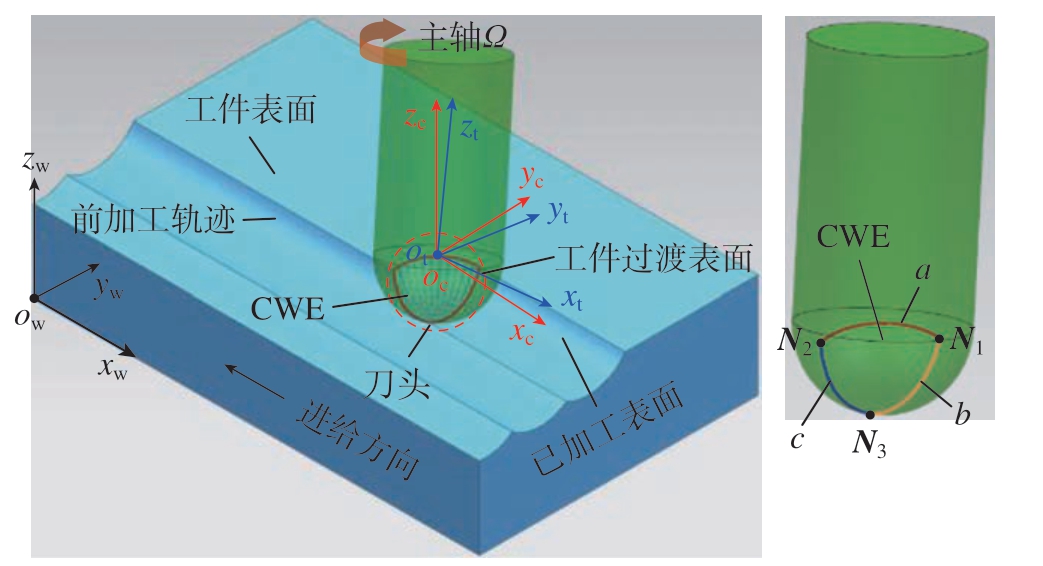
图1 球头铣刀铣削几何特性
Fig.1 Geometric characteristics of ball-end milling
1.2 基于齐次变换的多轴球头CWE求解
1.2.1 立铣工况下球头CWE求解
为求解刀具一般姿态的接触区,首先建立无倾角姿态的接触区,如图2所示。然后通过齐次坐标变换,求得任意姿态下的接触区。在过渡坐标系oc–xc yczc下,设球头铣刀的半径为R,轴向切削深度为ap,相邻刀轨行距为s,mm,刀具倾角λ = 0,γ = 0,且本次球头铣刀走刀的轮廓方程为xc2+yc2+zc2=R2,前一相邻走刀轨迹为轴线平行于xc轴的圆柱面一部分,在ycozc平面该圆柱面的轴线投影坐标为(–s,0),则前加工表面的公式为(yc+s)2+ zc2 = R2,进而可得到在过渡坐标系中无倾角状态下接触区曲线a、b、c的方程式及其交点坐标。
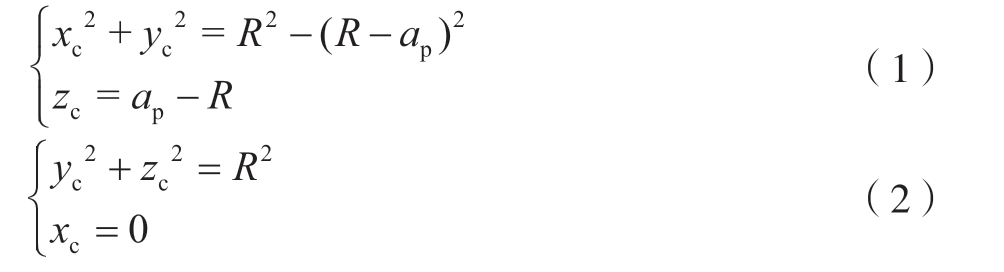
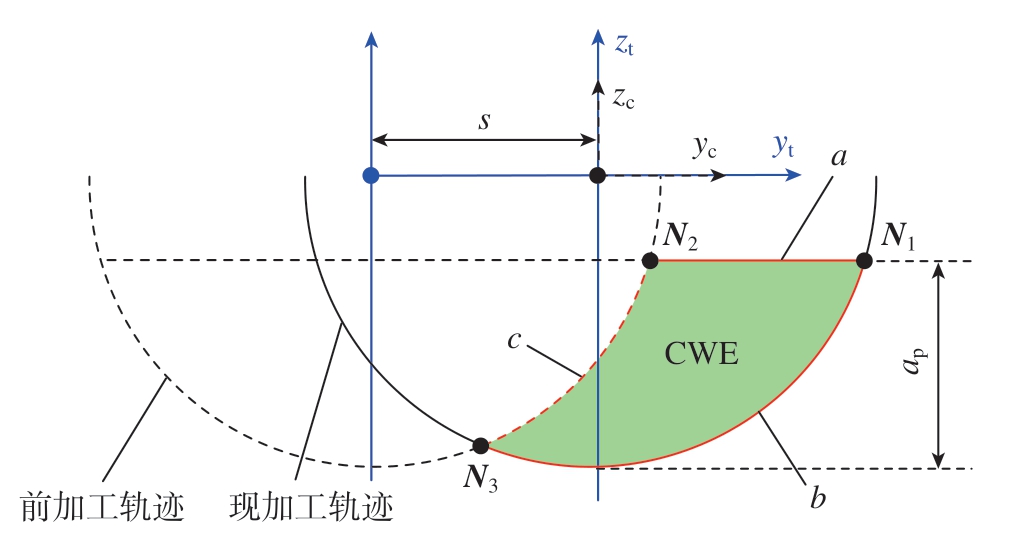
图2 立铣工况下接触区示意图
Fig.2 Schematic diagram of CWE under vertical milling condition
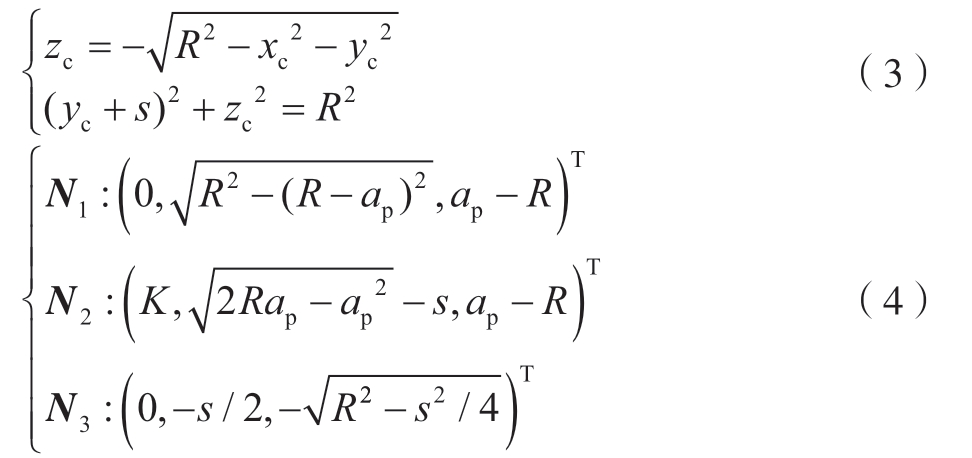
其中,![]() ,K为式(4)中N2的坐标x。式(1)~(3)分别为图1中接触区曲线a、b、c的方程;式(4)为接触曲线的交点坐标矩阵表达式。
,K为式(4)中N2的坐标x。式(1)~(3)分别为图1中接触区曲线a、b、c的方程;式(4)为接触曲线的交点坐标矩阵表达式。
1.2.2 一般姿态的球头CWE求解
在数控机床多轴系统中,可通过齐次坐标变换矩阵描述刀轴与机床本体之间的相对运动[16]。任意刀具坐标系都可以通过过渡坐标系旋转变换得到,如图3所示。首先过渡坐标系o – xc yczc绕yc轴旋转λ角,获得中间坐标系o – xg ygzg,然后绕中间坐标系的xg轴旋转γ角,得到刀具坐标系o – xt yt zt。
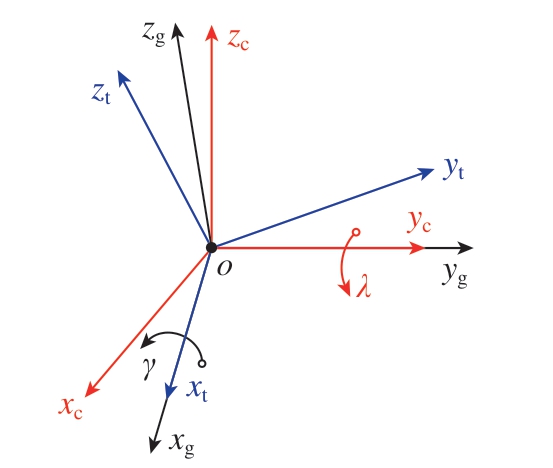
图3 齐次坐标旋转变换
Fig.3 Homogeneous coordinate rotation transformation
以上坐标旋转变换过程中,定义坐标系旋转角度λ为前倾角,γ为侧倾角,分析以上变换过程,得到过渡坐标系到刀具坐标系的变换矩阵Uλ和Uγ,坐标变换关系为
其中,
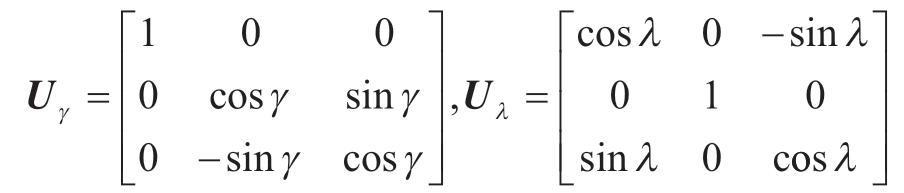
根据以上齐次坐标旋转变换关系,由式(5)得到接触区的边界曲线a、b、c,经坐标变换后在刀具坐标系下的一般姿态方程为
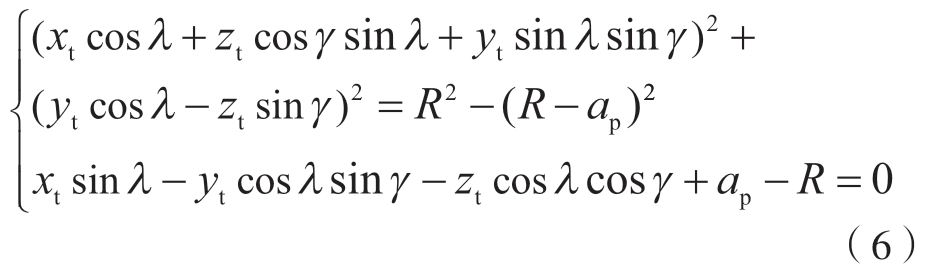
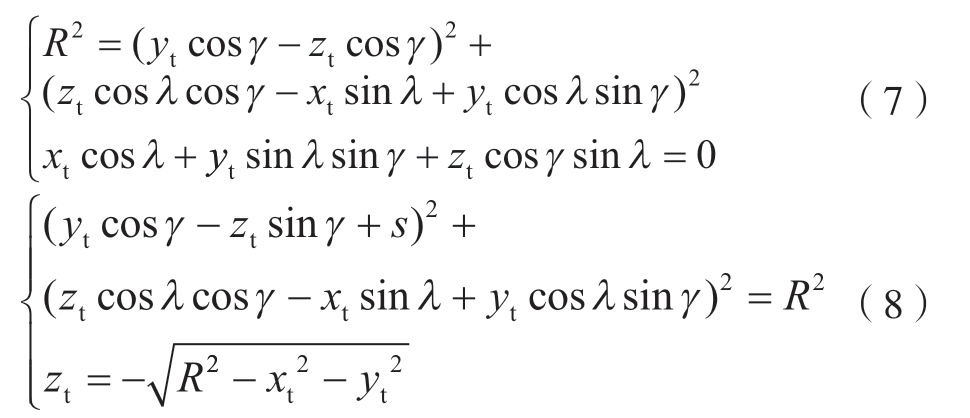
此外,坐标矩阵N1、N2和N3变换后在刀具坐标下的坐标矩阵Nt1、Nt2和Nt3为
基于上述研究,可构建工件表面相对刀具轴向任意姿态下的CWE边界方程及其交点,求解流程如图4所示。
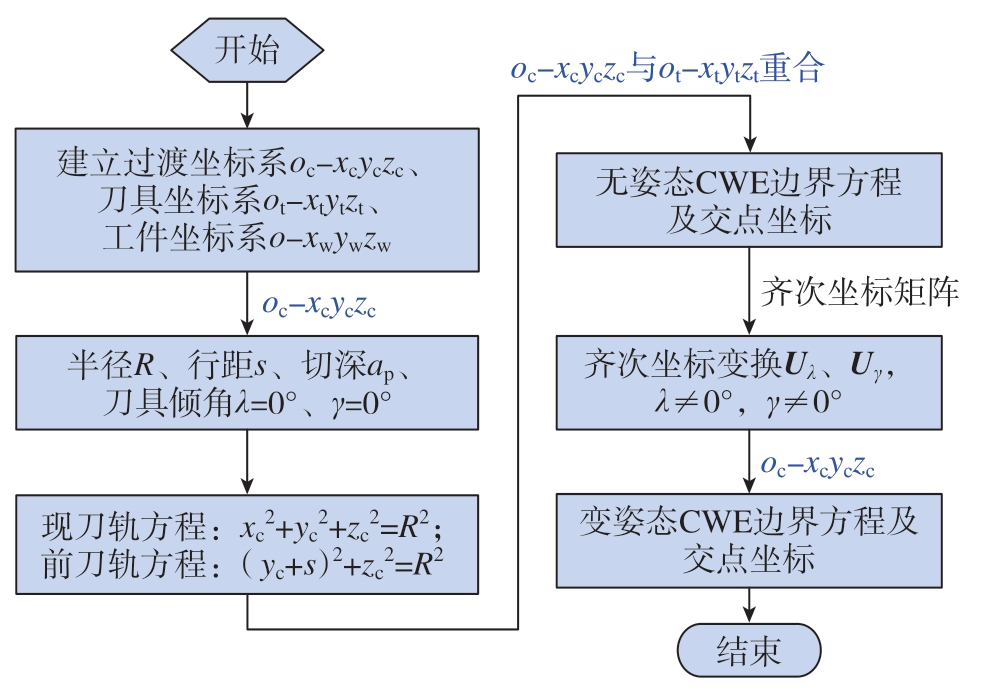
图4 基于齐次变换CWE求解流程图
Fig.4 Flow chart of CWE solution based on homogeneous transformation
1.3 基于CWE的球头铣削力建模
1.3.1 球头铣刀切削刃建模
在球头铣刀切削刃的几何建模中,将球头切削刃离散为微元,每一个切削微元对应唯一的轴向角σ,可以用轴向角来表示切削刃微元的坐标,刀具切削刃曲线方程[17]为
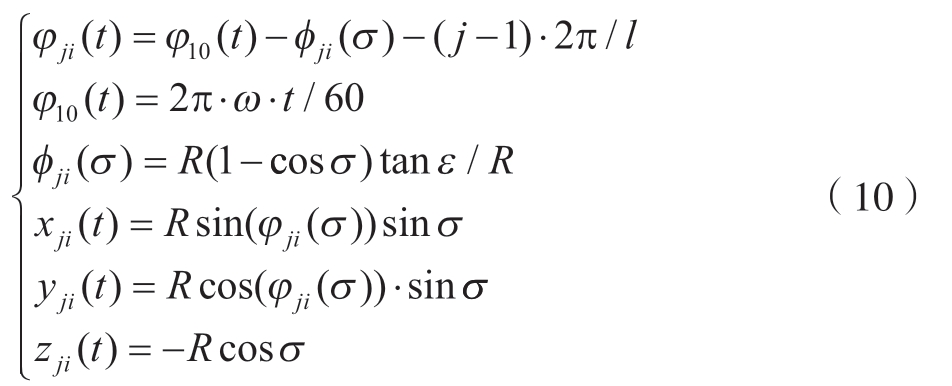
式中,ω为刀具旋转角速度;l为刀具的总刀齿数;j和i表示第j个切削刃上第i个切削微元;ε为切削刃螺旋角;t(s)为切削时间;σ为切削刃上的微元轴向角;φji(σ)为切削微元径向滞后角;φ10(t)为第一切削刃端点转过的角度;φji(t)为切削微元径向接触角。建立的球头铣刀模型如图5所示。
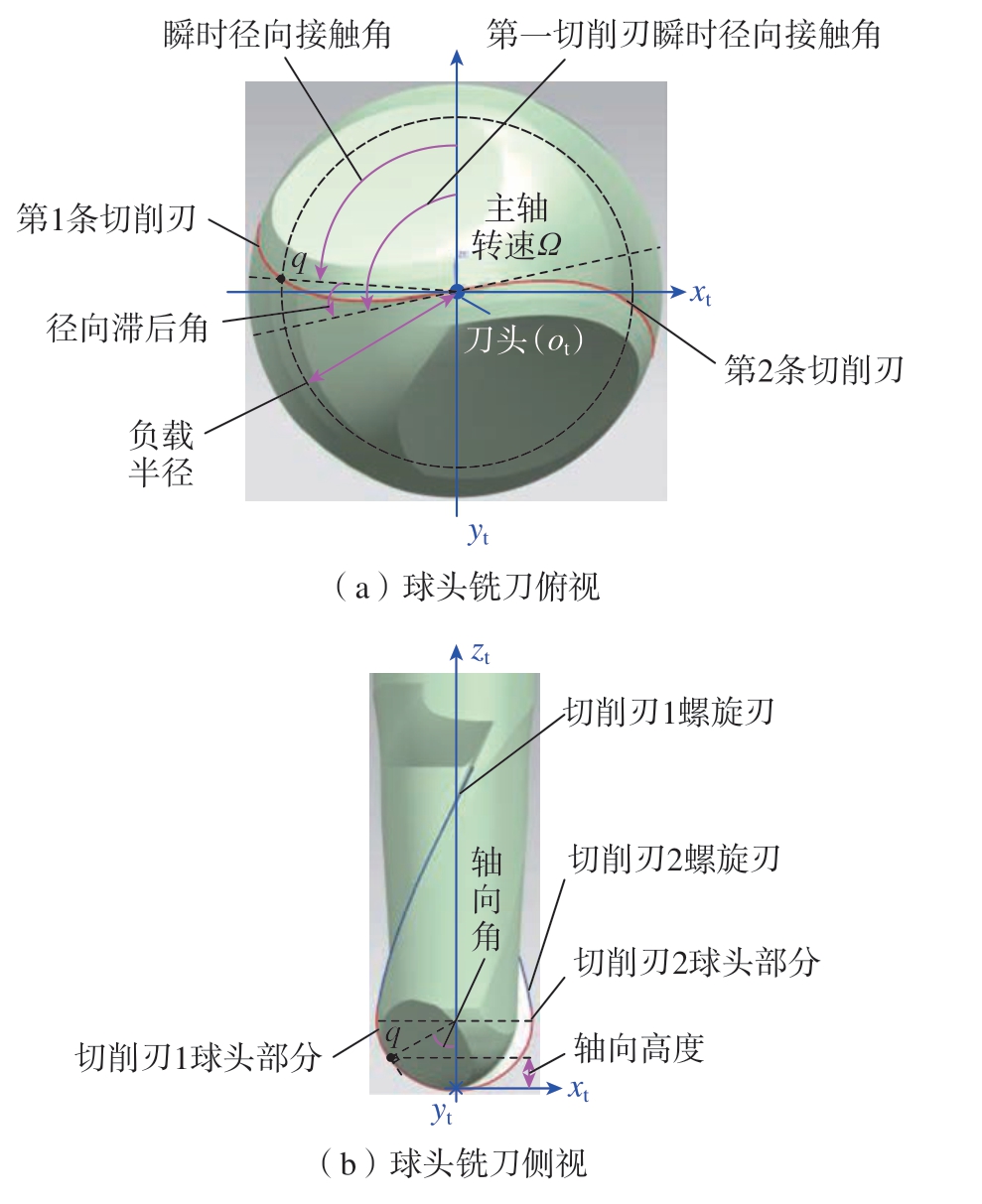
图5 球头铣刀铣削刃建模
Fig.5 Geometric modeling of cutting edge of ball-end milling cutter
1.3.2 有效切削刃辨识
上文描述了得到完整球头切削刃曲线方程的过程,在实际的铣削加工中,只有在接触区内部的切削刃参与了切削,因此,精确辨识CWE内实际参与切削的有效切削刃将成为求解铣削力的重点。为了提高计算效率,将图1中CWE边界曲线a、b、c和切削刃曲线投影到刀具坐标的xt ot yt平面来模拟切削过程,并以图5中球头铣刀的轴向角σ为度量进行有效切削刃计算。
球头铣刀的切削刃按图6所示方向旋转,其中有效切削刃为刀刃在接触区域内的部分。同时,在一个铣削周期T中,将周期离散为m个时间点,τ为一个离散时间段,即T = mτ。

图6 有效切削刃的辨识
Fig.6 Identification of effective cutting edges
如图6所示,刀具从tk = 0时开始,当刀具旋转时间tk = t0时,切削刃投影到达坐标nt3,此时切削刃以该点作为切削起点,刀具随之转动,且铣削力随着有效切削刃的增大而增加;此外,当tk = t2时,切削刃到达坐标nt2,此时有效切削刃达到最大值,即此刻的切削力最大;然后,刀具继续转动,有效切削刃和铣削力逐渐减小,且当tk = t4时,切削刃到达坐标nt1处,铣削结束。
当tk∈(t0,t2)时,定义刀刃与曲线b的轴向角为σmin,与曲线c的轴向角为σmax,并可通过数值计算方法得到此时两个轴向角的具体数值,同理可得tk∈(t2,t4)时段的轴向角数值,进而,获取铣削周期内任意t时刻的轴向角参数σ =(σmin,σmax)。
1.3.3 球头铣削力模型
根据Altintas的切削力模型[18],将有效切削刃离散为微分单元,从而计算微分单元上径向dFr、切向dFt和轴向dFa的微分力,其表达式为
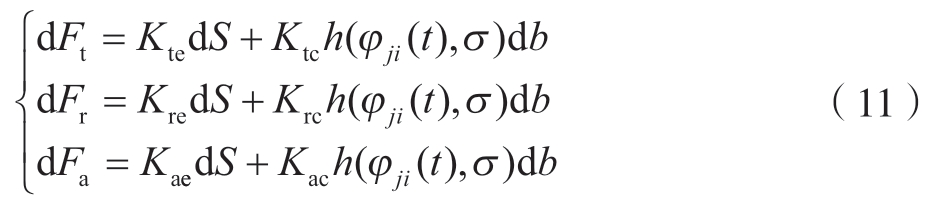
式中,Kte、Kre、Kae、Ktc、Krc和Kac为切削力系数;db为切削宽度,db = Rdσ;h(φji(t),σ)为切削厚度。切削刃长度dS为
由于存在前倾角λ和侧倾角γ,经过坐标旋转变换后,瞬时切削厚度h(φji(t),σ)变为
其中,
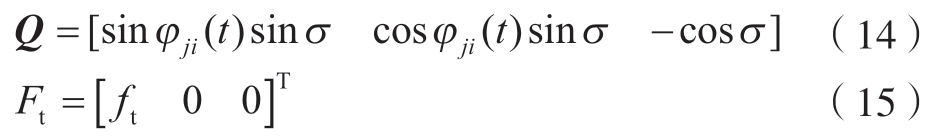
式中,ft为每齿进给量;Q为切削刃微元上的切削力转换矩阵。通过坐标变换,可获得切削微元在刀具坐标系的铣削力为
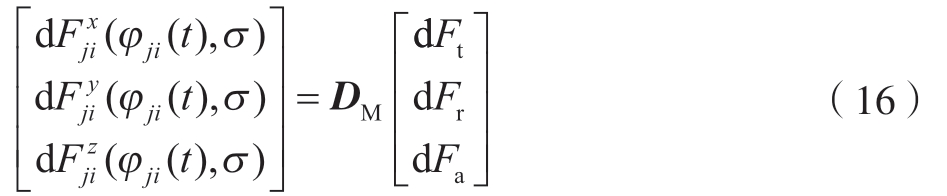
其中,
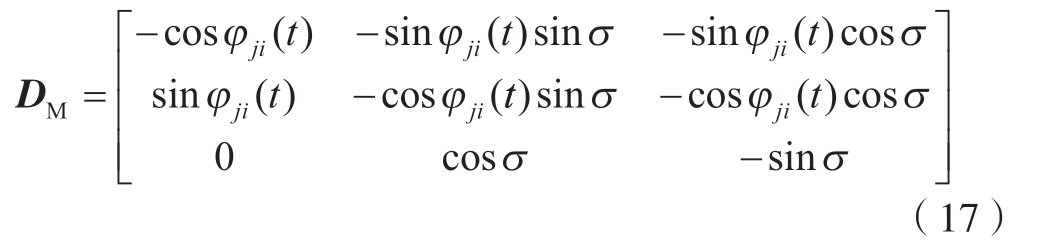
通过求解可得到轴向角参数σ,并将切削刃上的微分力进行积分,得到刀具坐标系下的铣削力,工件坐标系下的铣削力可具体表示为
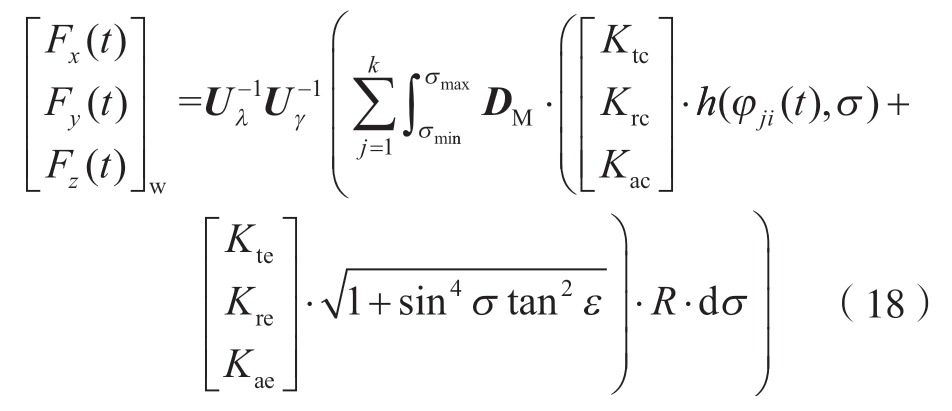
2 数值计算与试验验证
2.1 可变姿态球头的CWE
为准确预报不同刀具姿态的铣削力,精确辨识不同姿态的CWE是关键。故此,将不同姿态的CWE进行对比以深入分析变姿态CWE对铣削力的影响。故此,依据式(6)~(9)对变姿态CWE进行计算,采用刀具半径R = 5 mm,切深ap = 1 mm,行距s = 1.5 mm,并对有效切削刃进行辨识,可得图7所示不同姿态下CWE投影。如图7(a)所示,当前倾角λ确定,侧倾角γ不断增大时,接触区向y轴正向移动并逐渐减小,进而导致切入与切出角变大,切削刃参与铣削时间缩短。类似地,在图7(b)中,当侧倾角γ不变,前倾角λ增大时,接触区向x负向移动,导致切入角变大,切出角变小,且实际铣削时间减少、平均铣削力降低,同时接触区内有效切削刃减少,铣削力峰值降低。
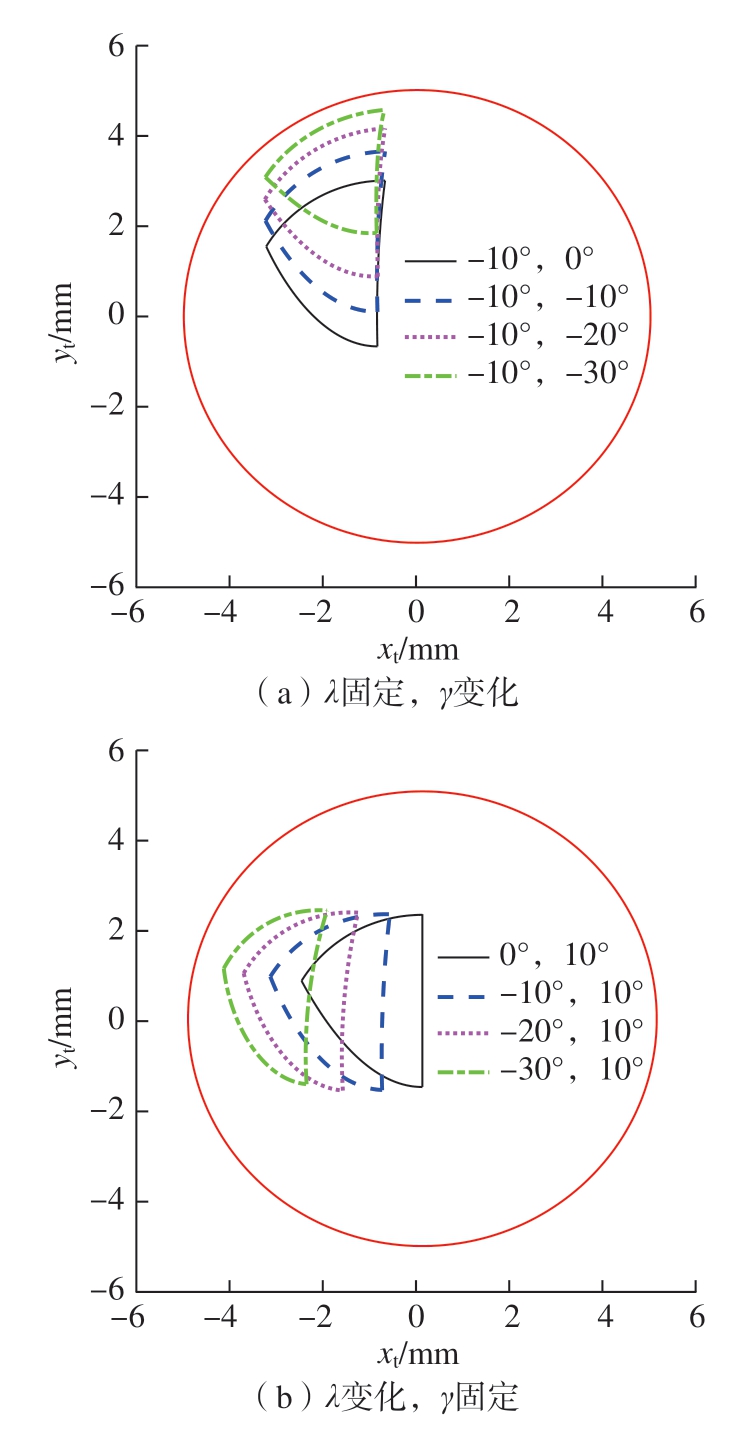
图7 不同姿态下CWE投影
Fig.7 CWE projection in different poses
2.2 试验验证与分析
试验平台搭建如图8所示,试验中,采用的机床型号为五轴联动加工中心DMG MORI – DMU100,结构为单转台单摆头,摆头与旋转轴B连接,其在zox平面内进行旋转运动。转台位于旋转轴C上,其旋转面为xoy平面。球头铣刀的刀齿数l = 2,刀具直径R' = 5 mm,螺旋角ε = 30°,刀具材质为钨钢,采用AiTiNPt涂层,工件材料为铝合金7075T6。同时,采用的测力仪器为Kistler 9257B测力仪,采样频率为10 kHz。

图8 五轴球头铣削力测试试验平台
Fig.8 Test platform of five-axis ball-end milling force testing
首先进行切削力系数辨识试验:主轴转速Ω = 4500 r/min,被吃刀量1 mm,每齿进给量分别在0.1 mm/r、0.15 mm/r、…、0.35 mm/r的条件下共进行6组槽切铣削试验,得到x、y和z向的平均切削力,并对实测平均铣削力进行线性回归分析[19],辨识得到平均切削力系数如表1所示。
表1 切削力系数
Table 1 Cutting force coefficient

Ktc/(N·mm–2)Krc/(N·mm–2)Kac/(N·mm–2)Kte/(N·mm–1)Kre/(N·mm–1)Kae/(N·mm–1)796.1168.822227.730.81.4
为验证球头铣刀切削力模型有效性,分别在两组刀具姿态下展开了切削力验证试验,试验与仿真参数:主轴转速Ω = 4500 r/min,背吃刀量为1 mm,径向切深s = 1.5 mm、每齿进给量为0.1 mm/r;刀具姿态分别为λ = –20°,γ = –10°和λ = –20°,γ = 10°。将上述切削力系数代入式(18)中,并进行仿真计算,同时,根据上述参数开展试验,仿真与试验结果如图9所示。可以看出,在不同刀具姿态下,试验过程中由于测试系统中的电荷漂移和切削振动,切削力信号存在小的波动现象,但切削力仿真结果与试验数据仍吻合良好。因此,本文所提基于CWE齐次变换的铣削力预报方法是可靠的,且准确性较高。
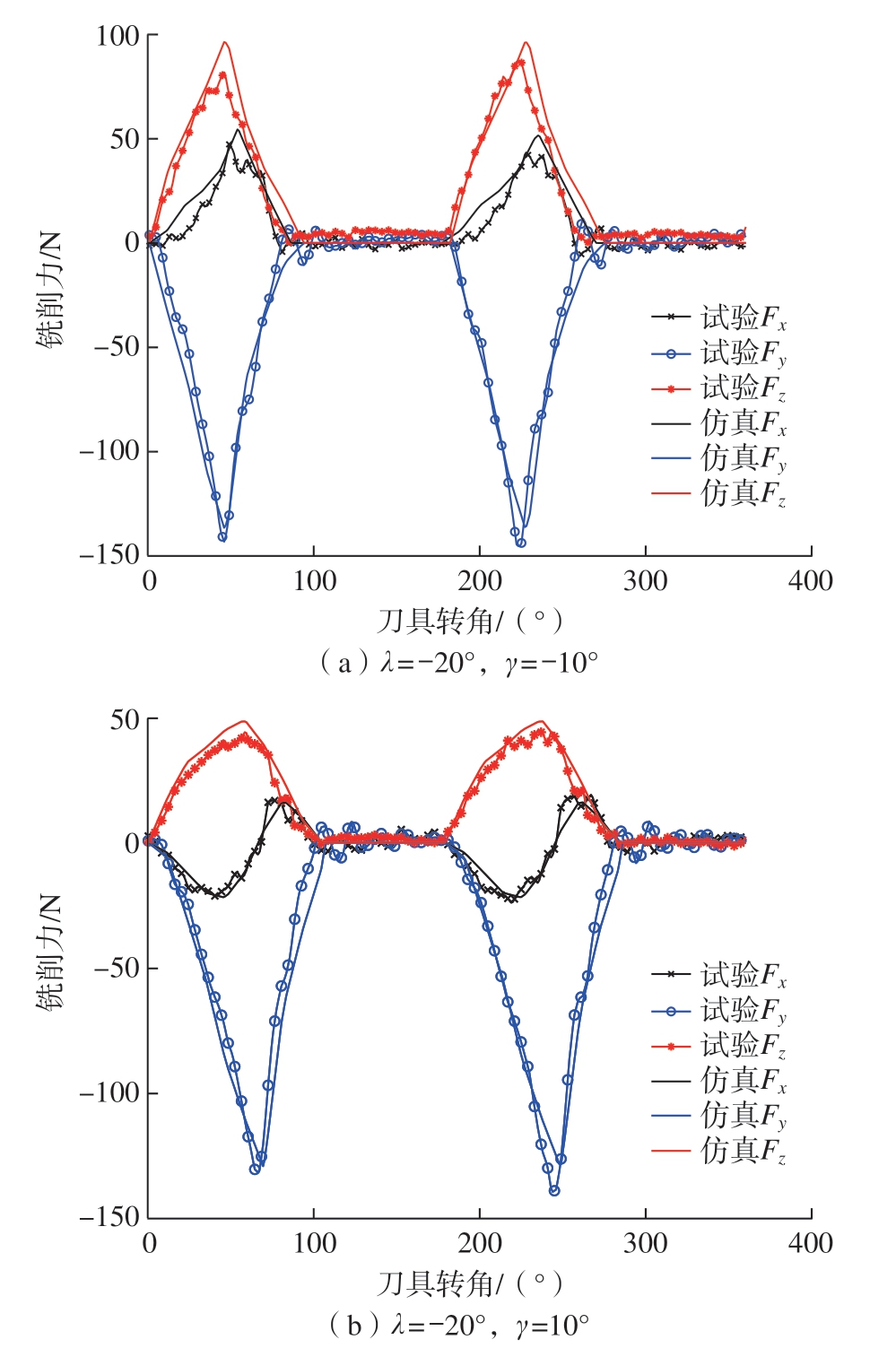
图9 球头铣削力试验与仿真对比
Fig.9 Comparison of ball-end milling force experiment and simulation verification
3 可变姿态对平均铣削力的影响
在铣削过程中,刀具磨损速度、接触区域的切削温度和刀具与工件的变形程度与平均铣削力密切相关[20]。在建立一般姿态球头铣刀切削力模型后,探究刀具姿态对平均铣削力变化规律的影响,其平均铣削力的计算方法为
式中,T为铣削周期。
对不同姿态下的铣削力进行仿真,前倾角λ和侧倾角γ的取值范围分别为– 40° ~ 0°和– 40° ~ 40°,其余参数与验证试验保持一致。通过对各种姿态下刀具切削力进行计算后,得到x、y和z方向的平均铣削力数据,如图10所示。可以看出,当侧倾角都向0°靠拢时,x方向平均铣削力呈现逐渐减小的趋势,且在前倾角为– 21°,侧倾角为0°时平均铣削力最小;同时,如图10(b)所示,当前倾角不变,侧倾角向0°靠拢时,y方向铣削力逐渐增大,且在前倾角为– 20°,侧倾角为40°时平均铣削力最小;此外,在图10(c)中,前倾角从– 20°向– 40°变化时,z方向铣削力变化趋势平缓,且当前倾角为– 40°,侧倾角为25°时取得最小值。
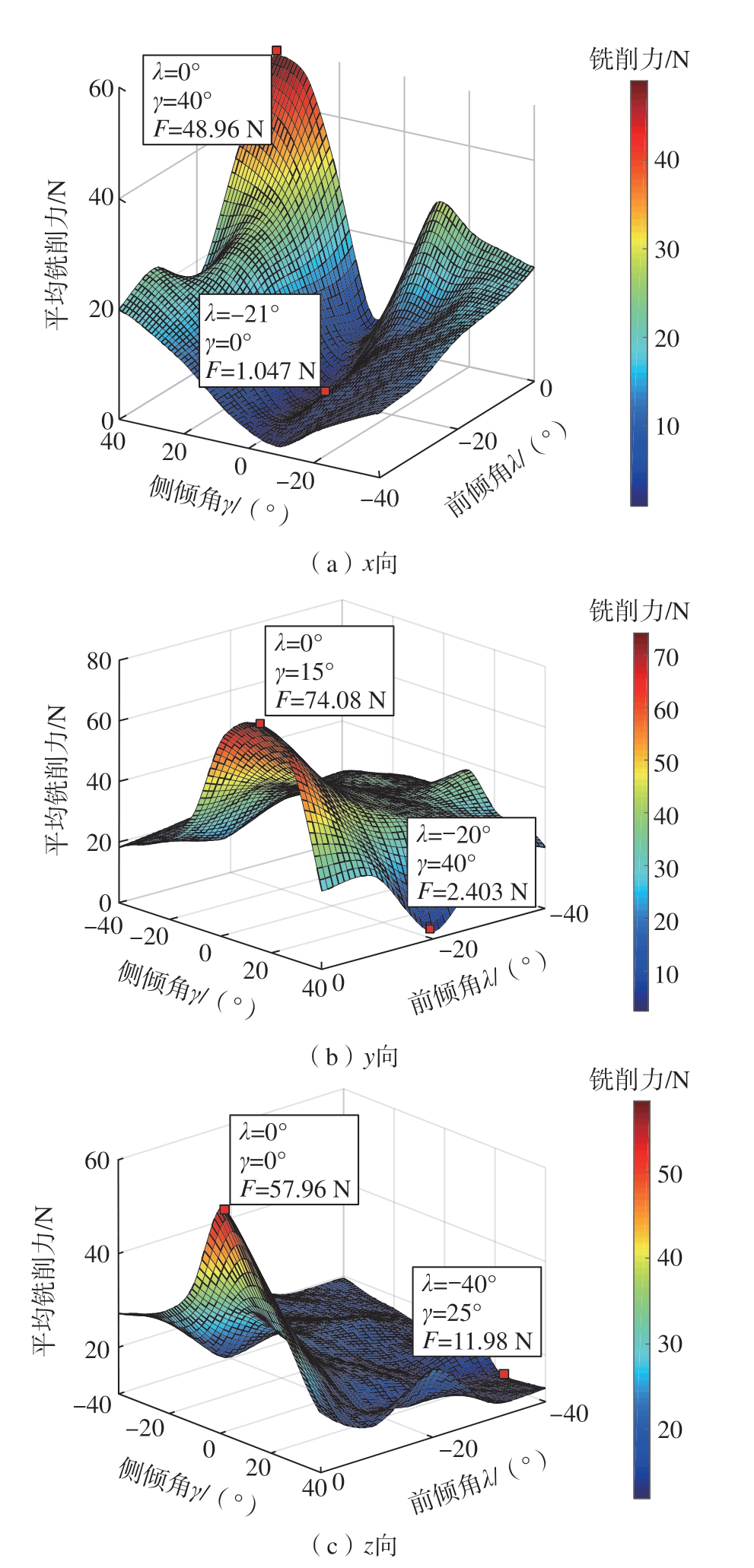
图10 可变姿态的各向平均铣削力
Fig.10 Average milling forces at different poses
对图10进行分析可知,不同刀具姿态对刀具铣削力的影响具有显著影响,且球头铣刀在前倾角和侧倾角分别为0°和40°时,x方向的平均铣削力最大;在前倾角和侧倾角分别为0°和15°时,y方向的平均铣削力最大;在前倾角和侧倾角均为0°时,z向平均铣削力最大。因此,实际生产中,为保证大的铣削力,应采用较小的前倾角。
为直观地观察刀具倾角变化对平均铣削力合力的影响,对图10中所示的3向平均铣削力进行矢量计算,并以此获取刀具姿态与平均铣削合力的对应关系,如图11所示。可知,平均铣削合力随着前倾角或侧倾角的增大呈减小趋势,且侧倾角增大对平均铣削合力的影响更为剧烈。
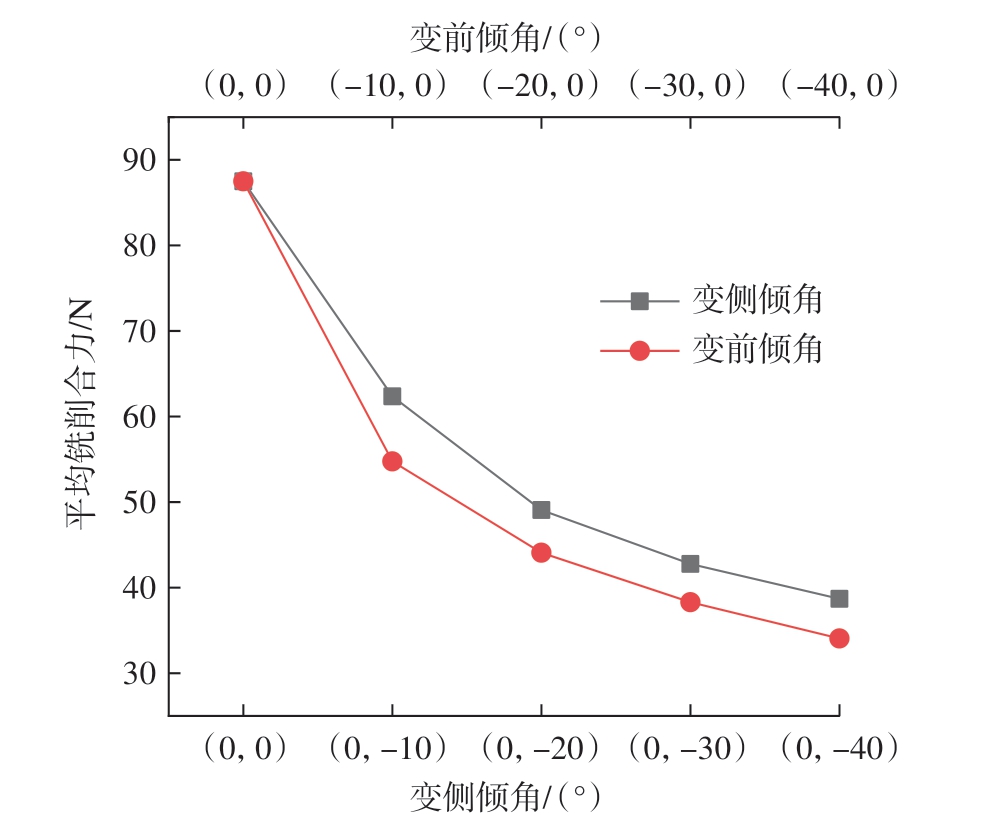
图11 刀具姿态对平均铣削合力的影响
Fig.11 Influence of tool attitude on average milling resultant force
4 结论
(1)借助齐次变换矩阵构建过渡坐标系到刀具坐标系的运动变换方程,推导出多轴球头铣刀任意姿态的通用CWE边界方程;并通过试验测试方法验证了在任意姿态下该方法预测刀具铣削力可靠性。
(2)前倾角不变,侧倾角增大使得切入角和切出角变大、切削刃铣削时间减少;侧倾角不变,前倾角增大导致切入角变大、切出角变小、切削刃参与铣削时间降低,且接触区内有效切削刃变短,铣削力峰值降低。
(3)在刀具的前倾角逐渐减小时,x、y和z方向的平均铣削力均呈增大趋势,且前倾角或侧倾角增大均使得平均铣削合力减小。同时,在实际生产中,切削力过大易导致加工工件的变形,因此,在满足加工质量和加工条件下可以采用较大的倾角以减小刀具铣削力。
[1] LAZOGLU I, BOZ Y, ERDIM H. Five-axis milling mechanics for complex free form surfaces[J]. CIRP Annals–Manufacturing Technology, 2011, 60(1): 117–120.
[2] 张立强, 王宇晗. 虚拟五轴侧铣加工过程建模与仿真分析[J]. 工程设计学报, 2011, 18(2): 98–102.
ZHANG Liqiang, WANG Yuhan. Modeling and analysis for virtual five-axis flank milling process[J]. Journal of Engineering Design, 2011,18(2): 98–102.
[3] YANG Y, ZHANG W H, WAN M, et al. A solid trimming method to extract cutter–workpiece engagement maps for multi-axis milling[J]. The International Journal of Advanced Manufacturing Technology, 2013, 68(9): 2801–2813.
[4] 倪其民, 李从心, 阮雪榆. 基于实体造型的球头铣刀三维铣削力仿真[J]. 上海交通大学学报, 2001, 35(7): 1003–1007.
NI Qimin, LI Congxin, RUAN Xueyu. Cutting forces simulation of ball-end milling based on solid modeling[J]. Journal of Shanghai Jiao Tong University, 2001, 35(7): 1003–1007.
[5] TANER T L, ÖMER Ö, ERHAN B. Generalized cutting force model in multi-axis milling using a new engagement boundary determination approach[J]. The International Journal of Advanced Manufacturing Technology, 2015, 77(1): 341–355.
[6] 董永亨, 李淑娟, 洪贤涛, 等. 基于Z-MAP方法的球头铣刀铣削力的建模[J]. 机械工程学报, 2019, 55(19): 201–212.
DONG Yongheng, LI Shujuan, HONG Xiantao, et al. Modeling on the milling force of ball-end milling cutter based on Z-MAP method[J].Journal of Mechanical Engineering, 2019, 55(19): 201–212.
[7] 魏兆成, 王敏杰, 蔡玉俊, 等. 球头铣刀三维曲面加工的铣削力预报[J]. 机械工程学报, 2013, 49(1): 178–184.
WEI Zhaocheng, WANG Minjie, CAI Yujun, et al. Prediction of milling force for machining three-dimensional curved surface of ball-end milling cutter[J]. Journal of Mechanical Engineering, 2013, 49(1): 178–184.
[8] OZTURK B, LAZOGLU I. Machining of free-form surfaces.Part I: Analytical chip load[J]. International Journal of Machine Tools and Manufacture, 2006, 46(7–8): 728–735.
[9] OZTURK B, LAZOGLU I, ERDIM H. Machining of freeform surfaces. Part II: Calibration and forces[J]. International Journal of Machine Tools and Manufacture, 2006, 46(7–8): 736–746.
[10] GUO M L, WEI Z C, WANG M J, et al. An identification model of cutting force coefficients for five-axis ball-end milling[J]. The International Journal of Advanced Manufacturing Technology, 2018,99(1–4): 937–949.
[11] CAO Q Y, XUE D Y, ZHAO J, et al. A cutting force model considering influence of radius of curvature for sculptured surface machining[J]. The International Journal of Advanced Manufacturing Technology, 2011, 54(5–8): 821–835.
[12] ZEROUDI N, FONTAINE M, NECIB K. Prediction of cutting forces in 3-axes milling of sculptured surfaces directly from CAM tool path[J]. Journal of Intelligent Manufacturing, 2012, 23(5): 1573–1587.
[13] TUNC L T. Rapid extraction of machined surface data through inverse geometrical solution of tool path information[J]. The International Journal of Advanced Manufacturing Technology, 2016,87(1–4): 353–362.
[14] 魏兆成, 王敏杰, 王学文, 等. 球头铣刀曲面多轴加工的刀具接触区半解析建模[J]. 机械工程学报, 2017, 53(1): 198–205.
WEI Zhaocheng, WANG Minjie, WANG Xuewen, et al. A semianalytical cutter workpiece engagement model for ball end milling of sculptured surface[J]. Journal of Mechanical Engineering, 2017, 53(1):198–205.
[15] 王亮. 基于CWE半解析模型的曲面加工铣削力预报[D].大连: 大连理工大学, 2013.
WANG Liang. Prediction of milling force in surface machining based on CWE semi-analytical model[D]. Dalian: Dalian University of Technology,2013.
[16] 黄强, 张根保, 张新玉. 机床位姿误差的敏感性分析[J]. 机械工程学报, 2009, 45(6): 141–146.
HUANG Qiang, ZHANG Genbao, ZHANG Xinyu. Sensitivity analysis of the pose error of machine tool[J]. Journal of Mechanical Engineering,2009, 45(6): 141–146.
[17] 代月帮. 铣削动力学高效分析方法及其在五轴加工中的应用研究[D]. 大连: 大连理工大学, 2019.
DAI Yuebang. Efficient analysis method of milling dynamics and its application in five-axis machining[D]. Dalian: Dalian University of Technology, 2019.
[18] LEE P, ALTINTAŞ Y. Prediction of ball-end milling forces from orthogonal cutting data[J]. International Journal of Machine Tools and Manufacture, 1996, 36(9): 1059–1072.
[19] 张孝峰. 球头铣削动力学建模及仿真[D]. 济南: 山东大学,2009.
ZHANG Xiaofeng. Dynamic modeling and simulation of ball milling[D]. Jinan: Shandong University, 2009.
[20] 王启东. 整体立铣刀瞬态切削力理论预报及应用研究[D].济南: 山东大学, 2012.
WANG Qidong. Theoretical prediction and application of instantaneous cutting force of integral end mill[D]. Jinan: Shandong University, 2012.