近年来,复合材料因具有比强度高、比刚度大和可设计性好等优点,已成为航空航天等领域最主要的结构材料之一[1]。复合材料由增强纤维编织的预成型体和各类基体材料进行复合制造形成[2],其中编织预成型体编织角、覆盖率等编织误差直接影响复合材料的力学性能[3]。目前,在使用机器人牵引具有变截面、大曲率弯曲等特征芯模进行编织的过程中,解决局部纱线堆积、牵引轨迹不流畅等工艺缺陷,保障编织角和覆盖率稳定是亟须解决的问题之一。
异形结构芯模的编织过程中,芯模的牵引过程不仅需要不断调整位姿以满足约束条件,还需要精准控制芯模进给速度。工业机器人因其灵活性、精准性、高效性的特点,在复合材料编织领域得到广泛的应用。但在预成型实际编织过程中,机器人末端的运行轨迹多数为人工示教得出,难以精确满足复杂芯模的位姿变换约束要求。
部分研究采用计算的方式求出编织过程中牵引轨迹的离散点,再根据编织过程的工艺特点进行离线轨迹规划。在进行异形结构芯模的编织时,针对芯模中轴线出现弯曲或转折情况,机器人夹持芯模根据规划好的牵引轨迹,先调整芯模姿态使芯模待编织段垂直导向环平面且编织起点与理论编织点重合,之后再进行垂直于编织点平面的进给运动。编织点和编织环平面之间存在一段收敛距离,收敛距离是影响预成型体编织角的重要因素[4]。吴修可等[5]考虑了收敛距离变化带来的编织误差,根据编织点静态模型在芯模进给方向对求解出的牵引轨迹进行偏移量补偿。Chi等[6]则不考虑收敛长度变化,提出建立编织点动态补偿模型,通过控制牵引速度来补偿芯模截面变化带来的编织角误差。Meng等[7]考虑了纱线张力扰动产生的芯模偏移,提出一种偏置补偿的三维芯棒轨迹生成方法。
以上机器人牵引芯模调整位姿的方式,芯模在调整姿态垂直编织环平面的过程中,编织机仍旧在运行,导致预成型体的编织角不稳定,且编织过程明显不流畅,很大程度影响了编织质量和效率。特别是针对大曲率弯曲特征的芯模,芯模弯曲内侧纱线堆积的特征更为明显,编织角波动范围过大,因此,针对大曲率复杂芯模,必须要优化当前机器人牵引芯模的轨迹。
编织过程中,编织点平面到导向环平面的距离随着芯模截面半径的变化而改变。多数研究以芯模轴线垂直于导向环为约束条件,无法保证弯曲芯模轴线达成垂直于编织点平面的约束条件,这大大增加了优化芯模牵引轨迹的难度。
本文提出一种基于偏移补偿模型的大曲率复杂芯模编织牵引轨迹优化控制方法,这种控制方法在计算机器人牵引轨迹时考虑收敛长度的变化,采用动态编织点平面,以每一段离散芯模的轴线垂直于稳态编织时的编织点平面为空间约束条件,利用编织过程中起始编织点迁移到稳定编织点这段过渡编织长度进行芯模的姿态调整,使得芯模在实现空间约束条件的前提下进行编织进给运动,进而避免预成型体弯曲段出现大的覆盖率波动,同时控制牵引速度使编织尽快进入稳定阶段。该方法能有效降低大曲率复杂结构芯模编织过程中的误差,提升预成型体的力学性能。
1 编织点预测模型
预成型体编织系统主要由编织机和牵引机器人组成。编织机控制工艺参数为携纱器在沿编织环圆周方向呈“∞”形运动的转速ω,机器人则控制芯模的牵引轨迹和牵引速度V。机器人通过控制牵引轨迹来实现芯模满足垂直于编织点平面的空间约束条件,同时完成芯模在编织过程中的进给运动。预成型体上的编织角θ,即纱线与芯模轴线的夹角,由转速ω、牵引速度V、芯模结构特征及芯模半径r决定。编织工艺如图1所示。
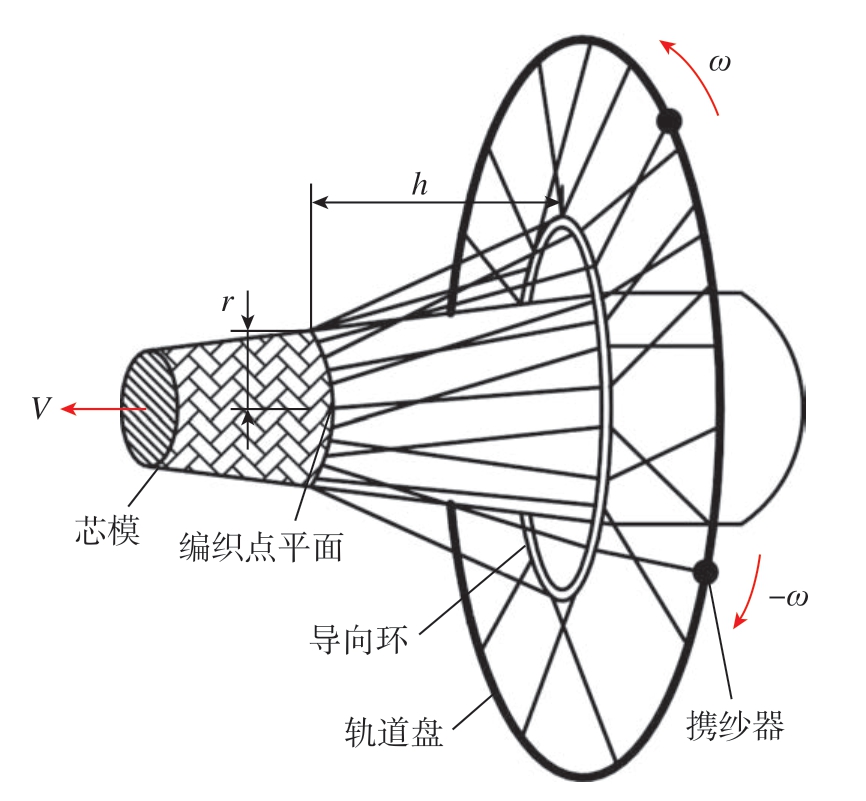
图1 编织工艺示意图
Fig.1 Schematic diagram of weaving process
预成型体编织过程中,收敛长度h表示编织点平面到导向环平面的距离;R为导向环半径。
预成型体编织过程中芯模半径r、牵引速度V、转速ω的变化均会导致收敛长度h发生变化,使得编织进入不稳定阶段,此时编织点平面相对于芯模轴线产生移动。
式中,Vr为相对运动速度;Va为纱线编织速度;芯模的牵引速度V是两者的合成速度。
针对不稳定编织阶段,王晓明等[8]提出了编织点和收敛距离h的预测模型,可以求得从不稳定编织状态起始时刻t = 0,h = h0过渡到稳定编织状态之间任意时刻的收敛距离h(t)。
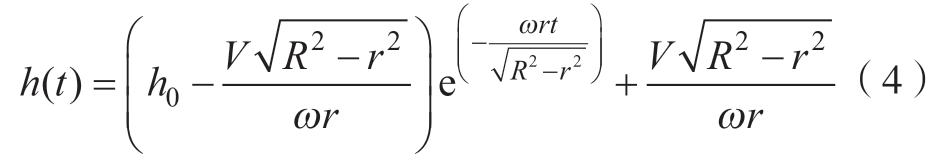
式中,e为欧拉数,约为2.718。
本文主要分析讨论由芯模半径突变导致编织进入不稳定阶段的情况。基于编织的连续性,芯模半径突变,起始编织收敛长度h却无法跟随进行突变,仍然保持在h0。由于编织点移动的长度反映收敛距离的长度变化,通过求解式(4)对时间t的导数,编织点移动速度Vr与时间之间的关系和纱线编织速度Va与时间关系为
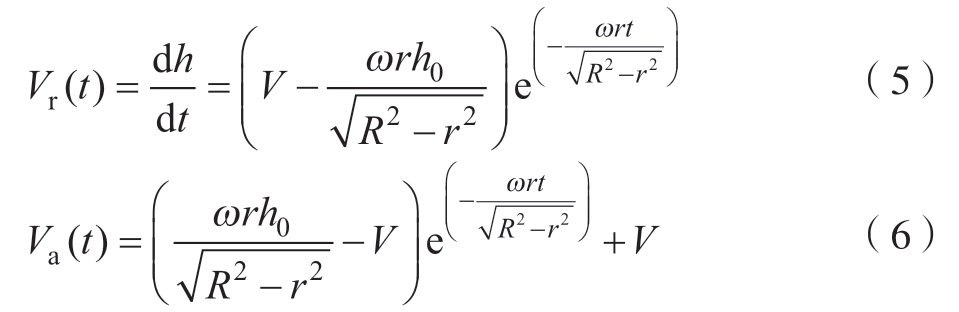
在编织稳定阶段,编织点不再发生移动,Vr = 0,V = Va。本文设定当|Vr|趋近于|kV|时,认定达到稳定编织阶段,即收敛距离稳定h = h1,其中判定是否到达稳定编织阶段的系数k取决于芯模半径的变化率,与芯模半径的变化率成正比。由此可以通过式(7)求得不稳定编织阶段经历的时间T。
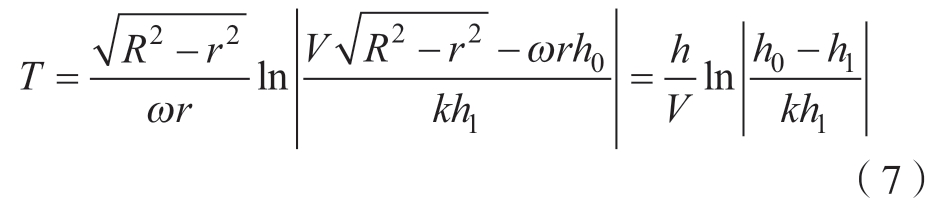
编织不稳定阶段过渡到稳定编织阶段的编织长度L的关系式为
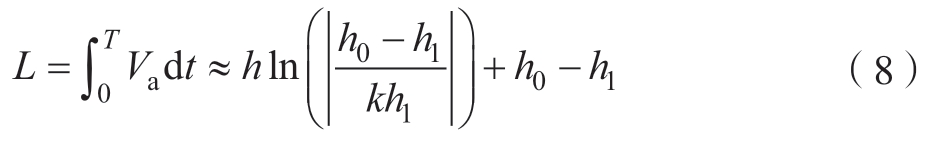
2 芯模牵引轨迹
2.1 坐标系设定
机器人辅助编织系统结构如图2所示,以芯模夹持点为原点建立工具坐标系并构建芯模几何模型,再将芯模的几何模型转化到基坐标系下描述。工具坐标系垂直于法兰中心点朝外的方向为z轴正方向。在计算得到工具中心点的位姿后通过指令库编写机器人的运行轨迹。工具中心点(TCP)包括x、y、z、a、b、c 6个值,其中x、y、z为工具坐标系原点在基坐标系中的位置信息;a、b、c表示工具坐标系绕z轴、y轴和x轴旋转的角度。

图2 机器人辅助编织系统
Fig.2 Robot aided knitting system
2.2 编织模型
芯模用沿中心线的n个离散点O(i)(i = 0,1,…,n–1)来表示。如图3所示,任取一小段芯模,将O(i)与O(i–1)之间的芯模形状近似为圆柱体,圆柱体的长度固定为d,圆柱体的半径为
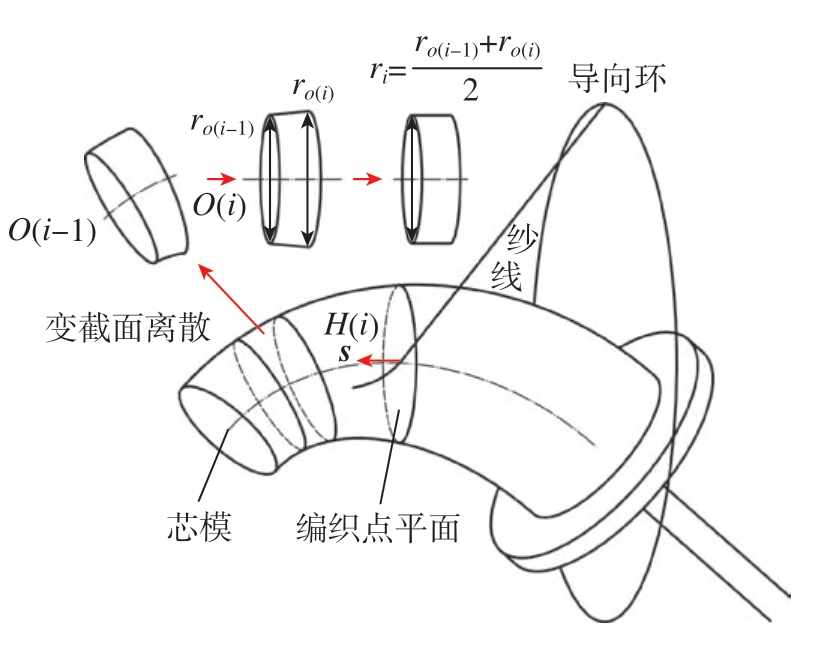
图3 芯模离散化
Fig.3 Mandrel discretization
式中,ro(i–1)和ro(i)分别表示在O(i–1)与O(i)点处芯模截面的半径。单位轴向向量o(i)(i=1,…,n–1)由O(i–1)指向O(i)。后续计算在以下基础上进行研究:
(1)近似圆柱体长度d能够满足机器人响应各段芯模牵引调整的需求;
(2)离散点数目n有足够的精度定义芯模形状。
图3为牵引大曲率复杂芯模的编织过程,机器人的牵引轨迹需要保证芯模垂直通过编织点所在平面。设基坐标系下导向环中点坐标S = [xs,ys,zs],考虑到编织过程中收敛长度h的变换,则实际动态编织点坐标为H(i)=[xs + h(i),ys,zs]。编织点平面平行于导向环平面,两者垂直向量均设为s。
根据式(2)得

2.3 芯模牵引轨迹求解
目前已知的机器人辅助编织预成型体过程中,最理想的轨迹是机器人夹持芯模时刻垂直穿过编织点平面,这样的轨迹对于直线型芯模来说容易实现,但是对于大曲率复杂芯模来说,由于导向环与实际编织点平面间存在一段变化的收敛距离h,且收敛距离h达到稳定阶段还存在一段不稳定编织距离,这导致芯模的中心线时刻垂直于编织点平面是不可能实现的,造成了芯模各段编织角不相等的问题。目前机器人牵引芯模过程中,均是先调整芯模姿态满足空间约束条件,再实现进给运动,这不可避免地产生纱线堆积,最终影响复合材料综合性能。故本文对轨迹进行求解时采用动态编织点进行轨迹补偿,每一段轨迹不稳定编织阶段采用KUKA机器人自带的LIN指令进行姿态调整,维持编织角稳定。
大曲率复杂芯模每段近似成圆柱体,每一段离散芯模呈台阶状连接。编织完成一段芯模进行下一段编织时,收敛距离进行过渡调整,这会导致实际编织长度与机器人夹持芯模通过编织点沿向量s方向的进给长度不相等。为保证编织过程中每段离散芯模的编织起点与理论上的动态编织点重合,每段芯模的实际进给长度di都需要进行补偿调整,求解公式为
机器人末端的轨迹根据TCP的数据确定,本文芯模被分为n个离散的点,设定每两个离散的点之间存在2次TCP的变换。TCP1(i)(i=1,2,…,n–1)为机器人工具中心点以恒速V1运行直线轨迹,同时以等角速度ωT绕自身旋转变换后的数据。芯模调整角速度ωT受限于机器人电机转速,角速度ωT的调整系数q由机械人自身参数决定,求解公式为
每当连续的两段离散芯模之间存在半径变化时,必然会因为编织点的调整出现不稳定编织长度Li。
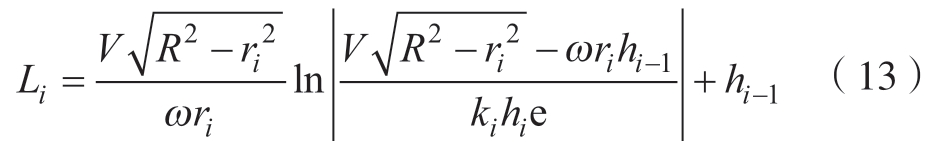
式中,ki为第i段离散芯模到达稳定编织阶段的判定系数。既然不稳定编织阶段不可避免,本文利用该段编织长度进行芯模姿态调整以减少纱线堆积状况。TCP2(i)(i = 0,1,…,n–1)为以速度V2平移变化后的数据,平移距离为di – Li。
记录编织起始位置,需将第1段芯模调整姿态垂直于编织点平面且起点与理论编织点重合,设定此时工具中心点数据为TCP2(0),然后逐段计算各段离散芯模的TCP1、TCP2。轨迹求解具体算法如图4所示。
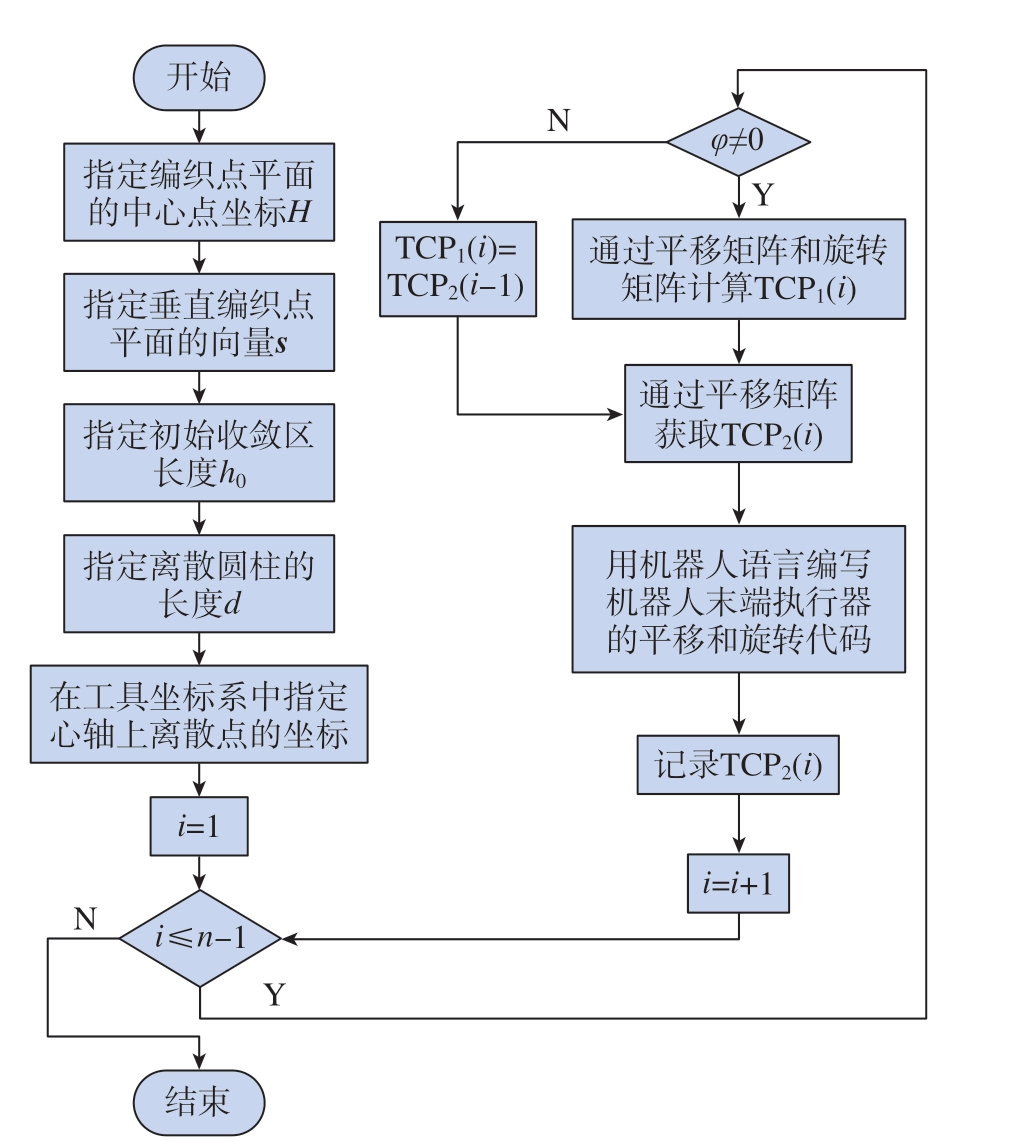
图4 机器人轨迹计算流程图
Fig.4 Flow chart of robot trajectory calculation
编织工艺描述如图5所示,在TCP1(i)计算过程中,需要使用TCP2(i–1)中的数据xi–1、yi–1、zi–1、ai–1、bi–1、ci–1,首先通过式(14)将工具坐标系下的向量o(i)转化为基坐标下的向量op(i),基坐标系下编织工艺描述如图5(a)所示。

图5 编织工艺描述
Fig.5 Description of weaving process
式中,Rot表示旋转变换;Rot(z,ai–1)为绕z轴逆时针旋转角度ai–1;Rot(y,bi–1)为绕y轴逆时针旋转角度bi–1;Rot(x,ci–1)为绕x轴逆时针旋转角度ci–1。对于中心线在同一平面内的芯模,装夹芯模时将中心线调整到x–z平面内,通过式(15)求得op(i)与s的夹角φ后,绕y轴旋转φ使op(i)与s方向一致,旋转矩阵如式(16)所示。
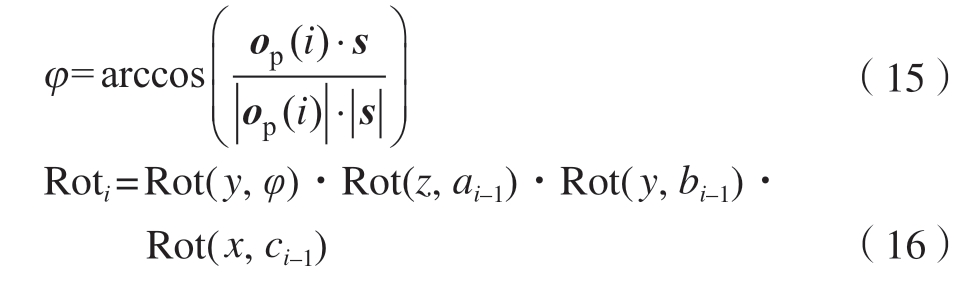
绕工具中心点旋转后,仅完成了离散段芯模垂直于编织点平面的要求,还需沿z轴与x轴方向平移,使得O(i–1)与编织点H重合后,再进给不稳定编织长度L(i)到达的目标点位P(i)=[xs + h(i)+ L(i),ys,zs],通过式(17)得到芯模上的离散点O(i–1)旋转后的坐标点与目标点组成的向量OP(i–1)。
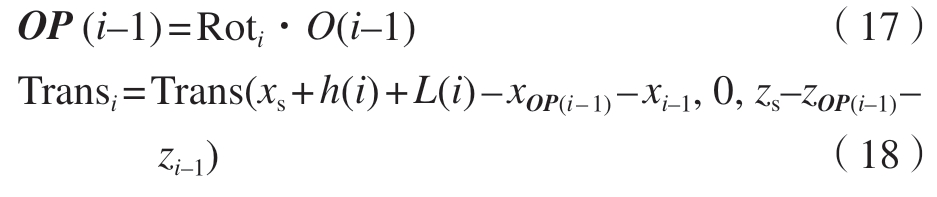
式中,xOP(i – 1)、yOP(i – 1)、zOP(i – 1)表示OP(i–1)在基坐标的x轴、y轴与z轴上的投影长度。故变换矩阵Ti为
为了定位变换后的的工具中心点,需要求出在本次变换过程中工具中心点在基坐标系下绕x轴、y轴、z轴旋转的角度αi、βi、γi,以及中心点在基坐标系下的坐标xi、yi、zi。齐次变换矩阵展开后为
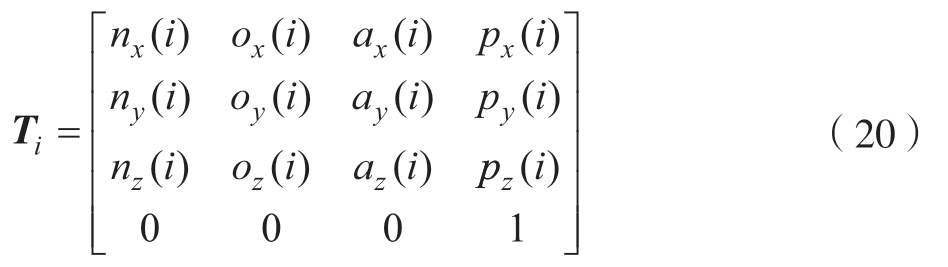
根据式(20)的齐次变换矩阵,可以直接在矩阵中读取到变换后的位置信息px(i)、 py(i)、 pz(i),与第i–1次的位置坐标相加,得到第i次的位置信息。对于求解角度时,使用滚、仰、翻变换解(RPY)进行求解[9]。在旋转的过程中先将工具坐标系绕基坐标系的x轴进行旋转γ,然后再绕基坐标系的y轴旋转β,最后绕基坐标系的z轴旋转α,经过上述旋转,工具坐标系就可以得到当前姿态,即
根据式(20)可以计算出编织第i段芯模所需要的机器人末端工具中心点在基坐标系下的位置与方向信息,TCP1(i) 、TCP2(i) 为
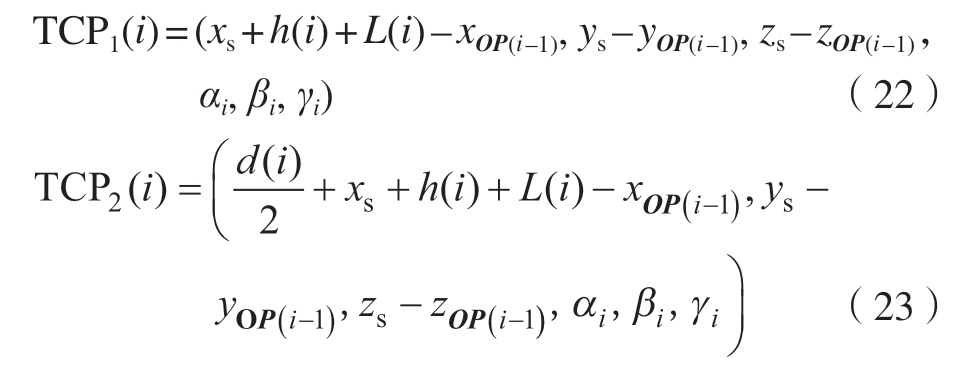
在得到二次变换后的工具中心点坐标后,依次输入到机器人指令中,并记录下本次移动停止点的位置与方位数据TCP2(i)=(xi,yi,zi,ai,bi,ci)并代入下一次计算中,其中不同编织阶段的结束姿势如图5(b)所示。根据本文所提出的计算过程,可以实现对机器人牵引芯模轨迹的精确控制,有效提高预成型体编织角稳定性。
2.4 芯模牵引速度
在机器人末端夹持芯模进行分段编织的过程中,第1阶段为机器人执行LIN指令,使得芯模第i段保持进给的同时,逐渐调整姿态最终垂直于编织点平面;第2阶段为机器人工具坐标系沿基座系x方向的平移进给运动。
第1阶段,机器人的牵引速度为V1,LIN指令执行过程中,工具中心点直线轨迹与编织点平面法向量s之间存在夹角φ,工具中心点到理论编织点向量TH实时长度为RT(t),向量TH与向量s实时夹角为δ(t),则机器人执行第1阶段牵引动作时,芯模编织点处的合成牵引速度为V。该速度的方向垂直于编织点平面,求解公式见式(24)。第1段编织过程中,δ(t)单调递增,RT(t)单调递减,因此V(t)为减函数;第2段编织过程中,机器人牵引速度V2为定值。ti(i=1,…,n)为编织第i段离散芯模机械人执行第1阶段LIN指令的时间。
对式(6)的牵引速度V求导可得式(25),dVa/dV恒大于0,由此可知,在t时刻,Va(V)为增函数。

为了使得第1阶段编织速度Va尽快接近期望编织速度Vs,机器人牵引速度V1需要满足的约束条件为
第2阶段机器人牵引速度V2 = Vs。
3 试验论证
为了验证本文提出的基于偏移补偿模型的大曲率复杂芯模编织牵引轨迹优化控制方法,以90°牛角弯管芯模为例,图6为芯模在机器人工具坐标系下的模型,细杆为增长杆,不对其进行编织。芯模首端截面直径为108 mm,尾端截面直径为159 mm,芯模轴线按长度进行10等分,等分点即是离散点,离散切面通过离散点O(i)垂直于向量o(i)将本芯模离散成10段,离散点和各段芯模等效为圆柱的方法如图6所示,各段芯模等效半径及离散点在工具坐标系下坐标如表1所示。试验使用云路复材176锭径向编织机,库卡KR250 R2700 – 2型机器人。在编织过程中,锭子运动的角速度ω为0.031 rad/s,振动电机频率为46 Hz,芯模编织过程中,机器人的牵引轨迹和牵引速度需要根据芯模的截面半径和弯曲程度进行调整。机器人牵引速度如图7所示,利用本文算法求解出的机器人牵引轨迹如表2所示。
表1 离散芯模各段几何信息
Table 1 Geometric information of each segment of discrete core mold mm

参数第1段第2段第3段第4段第5段第6段第7段第8段第9段第10段半径ri55.0056.8560.3764.7969.1472.5675.0077.4979.3079.62 O(i–1)坐标x方向– 435.63– 449.80– 456.96– 457.24– 451.19– 439.59– 423.19– 402.72– 378.78– 321.57 O(i–1)坐标z方向636.19610.39576.07541.00506.44473.33442.31413.80388.13355.54
表2 机器人程序中的工具中心点坐标
Table 2 Coordinates of tool center point in robot program
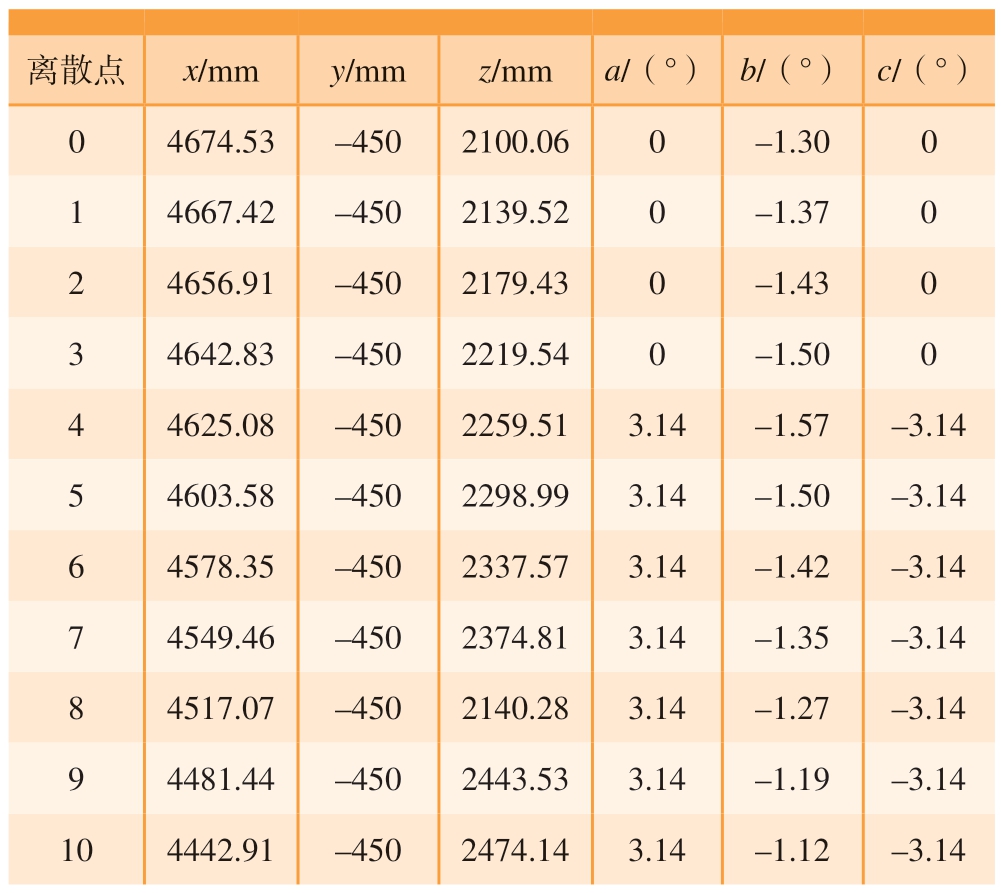
离散点x/mmy/mmz/mma/(°)b/(°)c/(°)04674.53–4502100.06 0–1.30 0 14667.42 –4502139.52 0–1.37 0 24656.91 –4502179.43 0–1.430 34642.83–4502219.540–1.500 44625.08–4502259.513.14–1.57–3.14 54603.58–4502298.993.14–1.50–3.14 64578.35–4502337.573.14–1.42–3.14 74549.46–4502374.813.14–1.35–3.14 84517.07–4502140.283.14–1.27–3.14 94481.44–4502443.533.14–1.19–3.14 104442.91–4502474.143.14–1.12–3.14
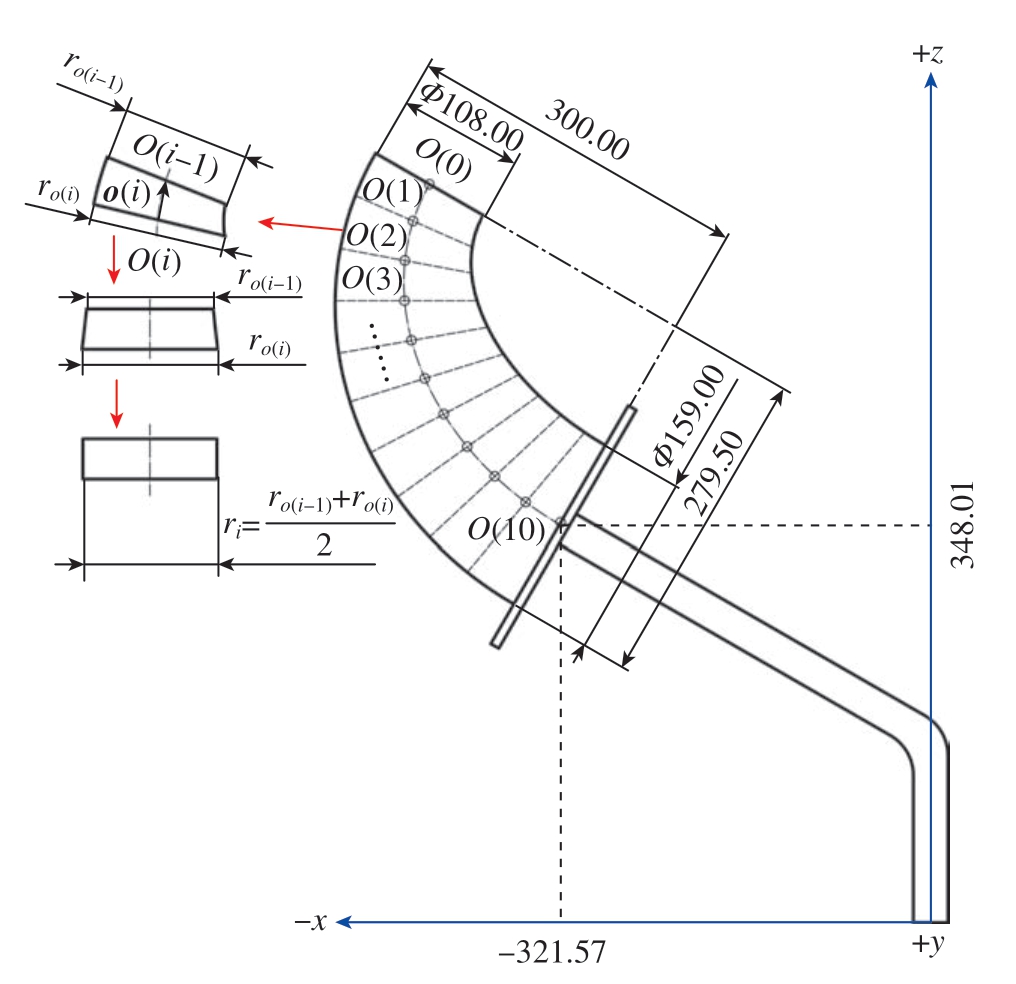
图6 芯模几何形状(mm)
Fig.6 Mandrel geometry (mm)
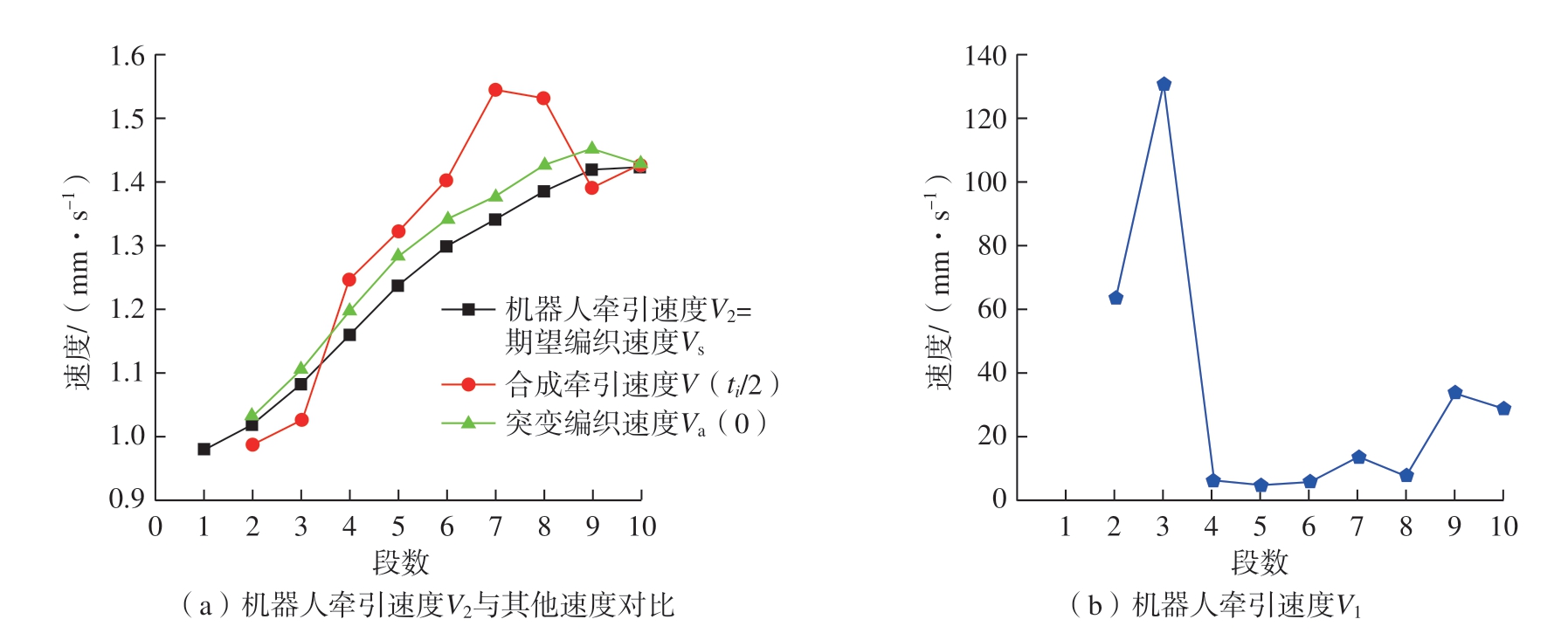
图7 编织过程中各段速度(θ=60°)
Fig.7 Speed of each segment in the knitting process (θ=60°)
图7为编织角60°时,对图6所示芯模进行编织的机器人牵引速度。机器人牵引速度分两段变化,执行第1段速度过程中,芯模姿态调整到垂直编织点平面,同时进行编织进给运动。针对此芯模结构,调整芯模姿态的前半段轨迹执行过程中合成牵引速度V(t)恒大于期望编织速度Vs,使得织物的编织速度尽快迫近期望编织速度,以保证编织角稳定。由于编织第2段芯模时是第1次调整芯模姿态,且第2、3段芯模截面突变半径和姿态调整角都远大于其他段芯模,这导致第3段芯模的机器人牵引速度V1远大于其他段芯模。
图8(a)为传统控制方法织造的预成型体。可以看出,传统控制方法编织过程中由于机器人轨迹没有考虑芯模姿态,调整过程中编织点处芯模需要进给运动,造成编织角波动过大、芯模弯曲内侧纱线堆积等问题。同时,传统方法的机器人牵引速度没有考虑截面的变化,导致无法保持预成型体编织角恒定。使用本文提出牵引轨迹优化控制方法进行编织预成型体,得到的成品如图8(b)所示,可以看出预成型体上纱线较为紧密,编织角波动小。

图8 两种编织控制方法生成的预成型体编织效果对比
Fig.8 Comparison of knitting effects of preforms generated by two knitting control methods
由于弯曲芯模表面的轴向长度在圆周方向上是不相等的,相同的时间内芯模弯曲外侧的编织长度大于内侧,而芯模弯曲内外侧的落纱量相同,这导致芯模弯曲内侧覆盖率高于外侧。
图9对比了两种控制方法编织的预成型体的编织角和弯曲外侧纱线覆盖率。在机器人进行辅助编织时,传统方法所得到的编织角与期望编织角最大相差7°以上,芯模弯曲内侧纱线覆盖率除首末两端有波动外,均已达到1,部分出现纱线堆积现象。本文提出的牵引轨迹优化控制方法进行机器人的位置姿态和牵引速度调整,将实际编织角控制在期望编织角的3.5°以内波动,可以实现大曲率弯曲变截面芯模的精确编织。应用本文控制方法编织芯模,芯模弯曲内侧覆盖率恒低于1,并且芯模内外侧覆盖率整体低于传统控制方法,有效避免纱线堆积情况。
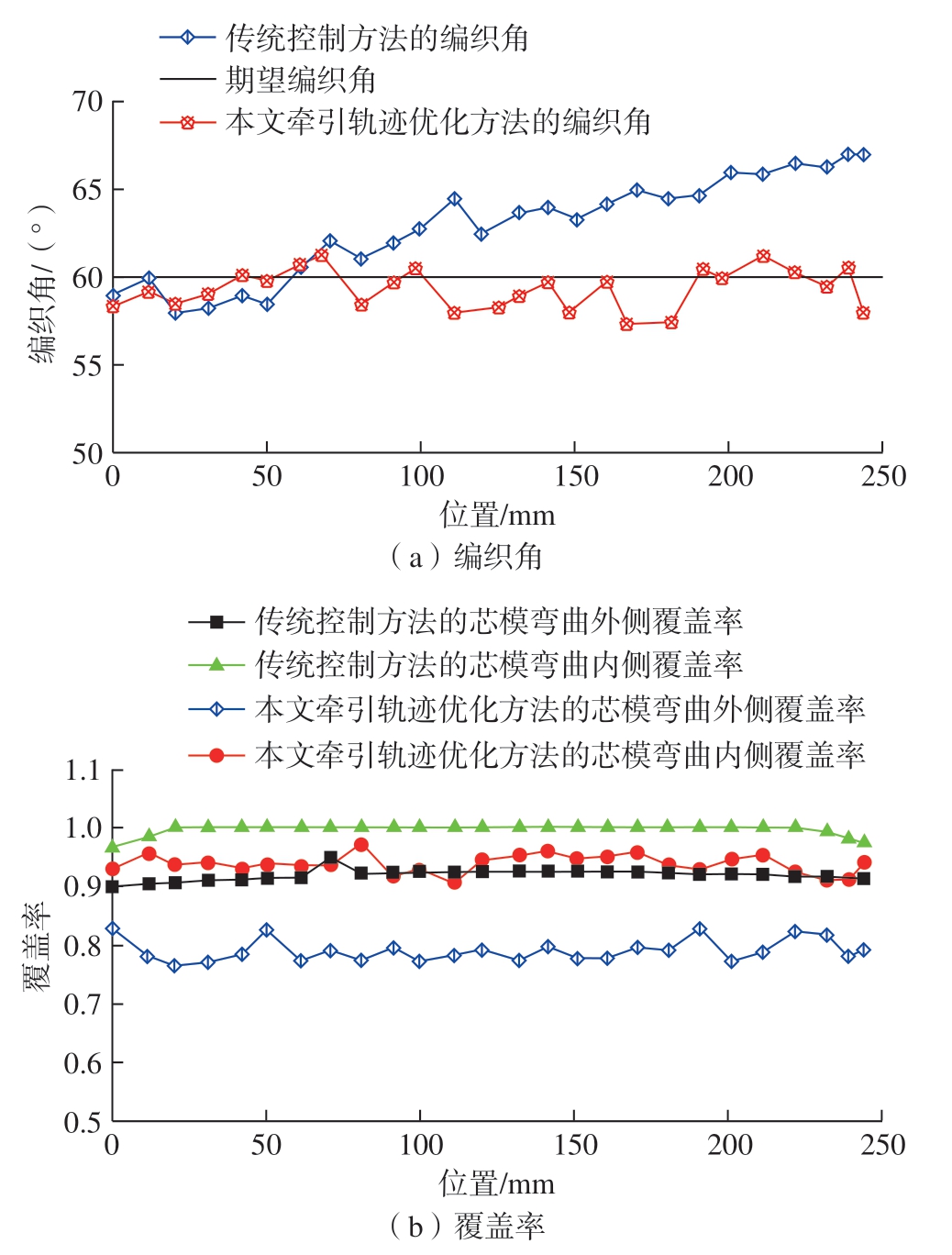
图9 两种编织控制方法的预成型体编织角和覆盖率
Fig.9 Braid angle and coverage of preform braided by two knitting control methods
4 结论
本文提出一种基于偏移补偿模型的大曲率复杂芯模编织牵引轨迹优化控制方法。
(1)该方法在将芯模离散成多段圆柱体的前提下,建立编织点预测模型,求解出芯模截面半径突变导致的不稳定编织长度,并补偿变截面导致的编织点移动距离。
(2)针对芯模大曲率弯曲这一特征,利用不稳定的编织长度调整芯模姿态,保障芯模姿态调整和编织进给运动同步进行,并对该段牵引速度进行调整使编织角尽快迫近设定值,控制编织角误差在3.5°以内,有效避免芯模弯曲内侧纱线堆积情况。
结果表明,本文提出的牵引轨迹优化控制方法符合实际生产精度。
[1] 高艳秋, 赵龙, 刘强, 等. 面向航空结构的高性能VARI复合材料技术[J]. 航空制造技术, 2013, 56(15): 66–69.
GAO Yanqiu, ZHAO Long, LIU Qiang, et al. High performance VARI composite technology for aviation structure[J]. Aeronautical Manufacturing Technology, 2013, 56(15): 66–69.
[2] 韩振宇, 梅海洋, 付云忠, 等. 三维编织预成型体的织造及三维编织复合材料细观结构研究进展[J]. 材料工程, 2018, 46(11): 25–36.
HAN Zhenyu, MEI Haiyang, FU Yunzhong, et al. Research progress on preform forming and microstructure of 3D braided composites[J].Journal of Materials Engineering, 2018, 46(11): 25–36.
[3] 卢子兴, 刘振国, 麦汉超, 等. 三维编织复合材料强度的数值预报[J]. 北京航空航天大学学报, 2002, 28(5): 563–565.
LU Zixing, LIU Zhenguo, MAI Hanchao, et al. Numerical prediction of strength for 3D braided composites[J]. Journal of Beijing University of Aeronautics and Astronautics, 2002, 28(5): 563–565.
[4] FOULADI A, JAFARI NEDOUSHAN R. Prediction and optimization of yarn path in braiding of mandrels with flat faces[J]. Journal of Composite Materials, 2018, 52(5): 581–592.
[5] 吴修可, 孟婥, 姚灵灵, 等. 基于齐次坐标变换的编织工艺及芯模牵引轨迹分析[J]. 东华大学学报(自然科学版), 2019, 45(3):425–430.
WU Xiuke, MENG Chuo, YAO Lingling, et al. Analysis of braiding process and mandrel’s traction trajectory based on homogeneous coordinate transformation[J]. Journal of Donghua University (Natural Science), 2019,45(3): 425–430.
[6] CHI X F, LI Q Y, YAN H X, et al. Robot trajectory optimization control of braiding for three-dimensional complex preforms[J]. Journal of Engineered Fibers and Fabrics, 2021, 16: 155892502110432.
[7] MENG Z, YAO L L, BU J Q, et al. Prediction method for offset compensation on three-dimensional mandrel with spatial irregular shape[J].Journal of Industrial Textiles, 2021, 50(8): 1205–1224.
[8] 王晓明, 邹婷, 李超婧, 等. 基于编织点起始位置及牵拉速度变化的编织角预测模型[J]. 纺织学报, 2015, 36(9): 28–33.
WANG Xiaoming, ZOU Ting, LI Chaojing, et al. Predicting model for braiding angle based on initial braiding height and take-up speed[J]. Journal of Textile Research, 2015, 36(9): 28–33.
[9] SCIAVICCO, SICILIANO L. Modelling and control of robot manipulators[J]. Measurement Science and Technology, 2000, 11(12): 1828–1829.