磨削加工通常作为机械加工的最后一道工序，直接影响零件的加工精度和表面质量。近年来，高效精密磨削技术在国防、航空航天、冶金、汽车工业等领域得到广泛应用[1–2]。随着磨削精度和磨削速度的提高，机床磨削加工稳定性的要求也不断提高。
磨削颤振及稳定性研究一直是国内外关注的热点问题[3–4]，Li等[5]提出了一种时域仿真方法来预测外圆磨削系统的颤振边界条件和颤振增长率，该时域仿真方法通过考虑砂轮与工件之间的几何干涉作用提高了颤振预测的精准性。蒋永翔等[6]对外圆磨削系统的稳定性进行研究，以磨削稳定性图为动态优化依据，优化了磨削加工工艺参数。Yan等[7]通过建立并分析切入式磨削的四自由度动力学模型，得到了磨削稳定性图，并利用该图确定了再生颤振和摩擦颤振的稳定性边界。Chen等[8]研究了磨削颤振和砂轮偏心对平面磨削动态性能的影响，并对磨削力和砂轮偏心变动下的磨削稳定性做了定性和定量研究。张氢等[9]基于再生激励效应，建立了包含凸轮轴和砂轮的磨削动力学模型并绘制了稳定性图。刘涛等[10]推导了非圆轮廓动态磨削深度计算方法，建立了多因素耦合的非圆轮廓磨削动力学模型，揭示了非圆轮廓磨削的颤振机理。
近年来，以碳纤维增强复合材料（Carbon fiber reinorced plastics，CFRP）为基体的新型砂轮在高速、超高速磨削中得到了广泛关注和应用，但关于CFRP砂轮磨削稳定性的研究还较少有人涉及。本课题组前期针对CFRP砂轮与钢基体砂轮的高速磨削过程进行了动力学特性的研究和对比[11]，本文将进一步以CFRP砂轮的外圆磨削过程为研究对象，结合工件的几何特征研究磨削过程的稳定性。其中，针对阶梯工件的动力学分析方法可以为磨削加工动力学研究提供参考，所得到的稳定性分析结果可以为磨削加工参数的选择提供帮助。
1 外圆磨削动力学建模与分析
1.1 外圆磨削动力学模型
切入式外圆磨削的加工过程如图1所示，为描述该磨削过程的动力学行为，Xg和Xw分别为砂轮和工件的位移；f为加工过程中砂轮的进给量。其中，砂轮被视为一个阻尼弹簧振子，mg为模态质量；cg为阻尼；kg为刚度；Ng为转速。砂轮的动力学方程为
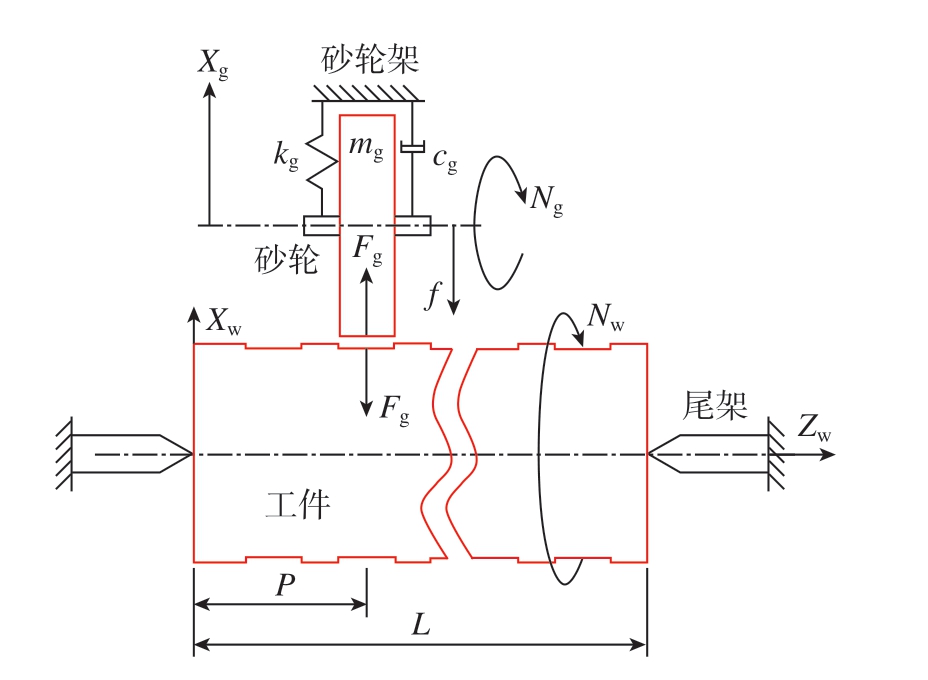
图1 切入式外圆磨削加工的动力学模型
Fig.1 Dynamic model of plunge cylindrical grinding
式中，Fg为砂轮和工件之间的法向磨削力，其与磨削深度Dg成正比，因此可写为Fg = KgDg，Kg为磨削力系数。结合再生颤振效应，实际磨削深度不仅与进给量相关，还需考虑当前砂轮和工件的相对位置Xg（t）– Xw（t）以及时滞项，则最终的动态磨削深度可写为
式中，Tg和Tw分别为砂轮和工件转一周所需的时间。结合式（1）和（2），由于进给量f在本研究中是一个恒定而与时间t无关的参数，因此较大的进给量虽然会增加实际磨削深度，进而提高强迫振动的幅值，但并不会对磨削过程的稳定性产生影响。
此外，工件可看作一个简支于两端尾架上的梁结构，其转速为Nw；轴向的坐标记为Zw；总长度为L，第i个阶梯特征的位置由Li表示，定义为该段阶梯梁的右边界到工件左端面之间的距离；磨削中砂轮所在的磨削位置由砂轮中心到工件左端面的距离P表示。
1.2 基于铁木辛柯梁理论的工件模态分析
在对回转轴类工件的横向振动进行动力学分析时，通常有3种梁理论可供选择，即欧拉–伯努利梁理论[12]、瑞利梁理论[13]和铁木辛柯梁理论[14]，3者的差异主要在于是否考虑梁在振动变形中的转动惯量和剪切变形，具体如表1所示。其中，欧拉–伯努利梁理论是一种线弹性理论的简化，只考虑横向弯曲，可看作铁木辛柯梁的特例。由于欧拉梁理论建模简单、计算速度快，经常被应用于长径比大于5的细长轴零件的动力学分析中。铁木辛柯梁理论则同时考虑了转动惯量和剪切变形对梁振动变形的影响，因此被认为是最复杂也最精确的梁变形理论。结合图2（a）所示的实际磨削用金属工件，长径比较小，仅为4.5，且在磨削过程中具有阶梯特征，因此使用铁木辛柯梁理论进行动力学分析，所建立的铁木辛柯梁模型如图2（b）所示，阶梯工件的材料及尺寸参数如表2所示。
表1 针对梁横向振动的3种梁理论
Table 1 Three beam theories of beam lateral vibration
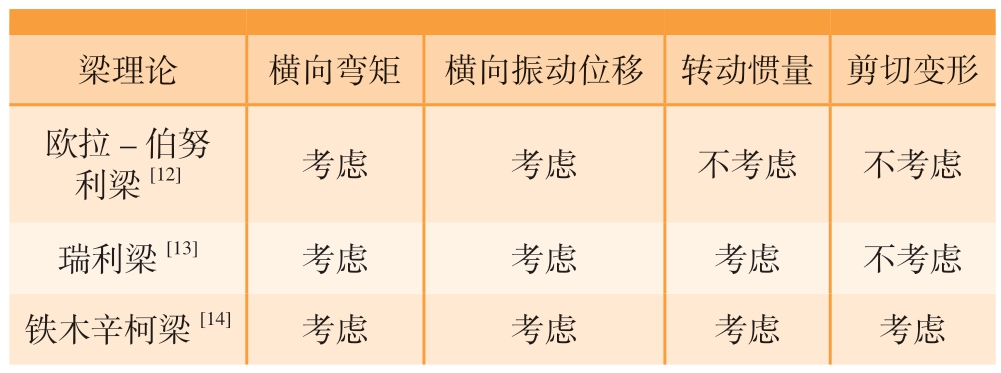
梁理论横向弯矩横向振动位移转动惯量剪切变形欧拉–伯努利梁[12]考虑考虑不考虑不考虑瑞利梁[13]考虑考虑考虑不考虑铁木辛柯梁[14]考虑考虑考虑考虑
表2 阶梯工件的GCr15材料及尺寸参数
Table 2 GCr15 material and dimension parameters of stepped workpiece
直径/m槽深/m密度ρ/（kg·m–3）测试点P3位置/m 0.060.00178102070.0150.03050.04050.270.150250.201250.25225弹性模量E/GPa长度L1/m长度L2/m长度L3/m总长度L/m测试点P1位置/m测试点P2位置/m
图2 针对阶梯工件的铁木辛柯梁模型
Fig.2 Timoshenko beam model based on stepped workpiece
从图2可知，工件在磨削过程中一共被砂轮从不同位置切入10次，形成与砂轮等宽的10个深度为1 mm的槽。为了提高计算和对比效率，从这10处工件磨削位置中选取3处进行具体的动力学分析和稳定性分析。选取过程首先考虑了工件在轴向的对称性，由于工件两端均为顶尖简支，所以仅考虑右侧一半的5个磨削位置，从中选择3处均匀分布的位置并标记为P1、P2和P3，如图2（b）所示。其中，Xw和Zw方向分别为梁的横向振动方向和回转轴方向。由哈密顿原理可以得到梁自由振动的方程为[15]
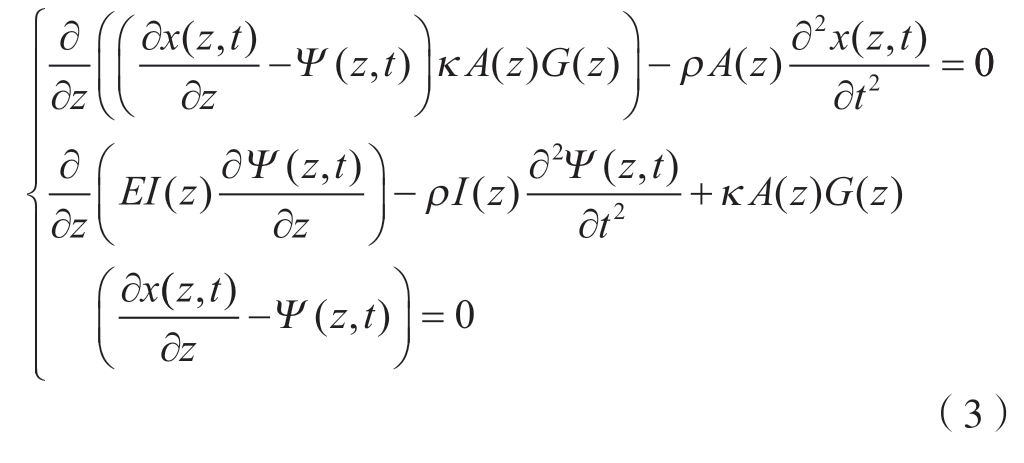
式中，x（z，t）是横向挠度函数；Ψ（z，t）是横向挠曲线转角函数；变量κA（z）、G（z）、ρA（z）、EI（z） 和ρI（z）分别为有效剪切面积、剪切模量、线密度、弯曲刚度和转动惯量，且都是沿轴向Zw方向连续或不连续变化的函数。通过整理可将式（3）中的横向位移和转角进行分离[16]，得到通解为
式中，T（t） = sin（ωnt + φ），ωn是梁横向振动的固有圆频率；φ为相位角，由振动初始条件决定。进一步，地将第i段梁的横向振动位移和转角利用三角函数来表示，即
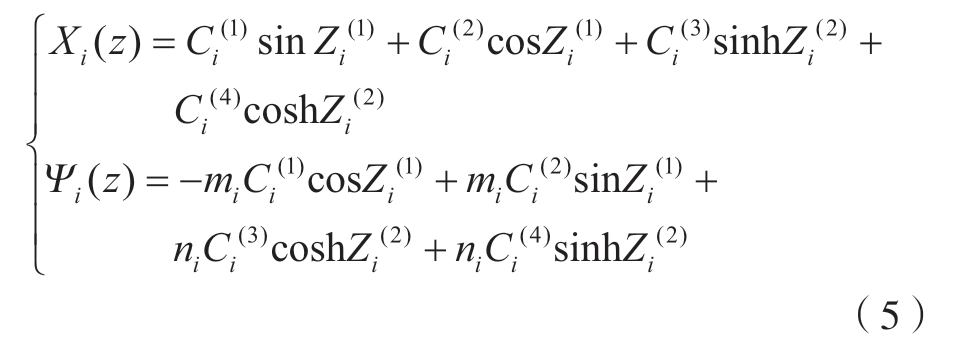
式中，
分别是由第i段梁的左右两端边界条件决定的待定系数。此外，
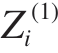= βi（z – zi–1），
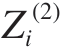= γi（z – zi–1），
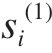= ω2（ρA）i /（EI）i，
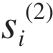=（ I）i /（A）i，
=（E）i /（κA）i，ai =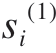 
（
+ 
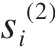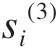）/2，
根据铁木辛柯梁理论，阶梯工件中相邻分段梁之间的连续条件为相邻的第i段梁和第i + 1段梁在连接点处的位移、转角、弯矩、剪力均相同，则可以用以下矩阵形式表示4组等式关系。
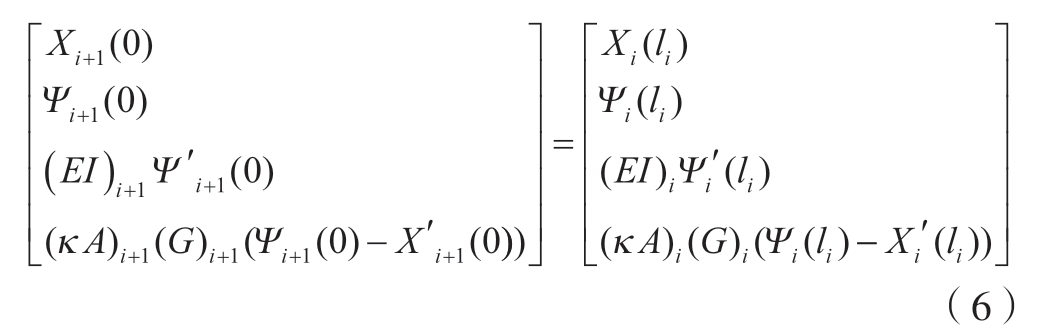
式中，li表示第i段梁的长度，和图2（b）中标识的对应关系为li = Li – Li–1（i>1）。
将第i段梁的待定系数表示为
，则式（6）可写为
其中，
考虑到式（7）中i的取值范围为[1，N – 1]，N为工件被切入后所具有的阶梯特征总数目，则可以得到首段梁待定系数C(1)和末段梁待定系数C(N)之间的关系为
其中，Z = Z(N–1)Z(N–2)…Z(2)Z(1)，矩阵Z中各元素均为固有圆频率ωn的函数，故可采用边界条件，用求解特征值的方式来求解固有频率和首段梁待定系数C(1)，进而得到每一阶模态下整个阶梯工件的模态振型函数。
对于外圆磨削的加工过程，工件的两端顶尖固定方式可以等效为两端简单支撑，边界条件为：两端的振动位移和弯矩为0，进一步得到下列4组等式。
根据该阶梯工件左端的边界条件，可以得到
根据该阶梯工件右端的边界条件，可以得到
其中，
将式（8）代入式（11），可以得到
将式（10）代入到式（12）得
为使式（13）有非零解，其待定系数前面的矩阵行列式必为0，得到阶梯简支工件的特征方程为
为了便于进行对比分析，将阶梯工件的振型函数进行质量归一化，则阶梯工件的模态质量为
阶梯梁质量归一化后阶梯工件第i段梁的横向振型函数为
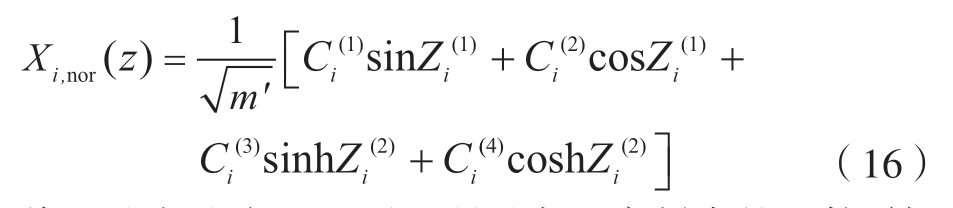
将上述方法应用于图2所示实际磨削中的工件，结合表2所提供的工件材料及尺寸参数，可以计算得到该阶梯工件的前3阶固有频率和振型，结果分别如表3和图3所示。
表3 阶梯工件的固有频率计算结果
Table 3 Calculated results of natural frequency of stepped workpiece
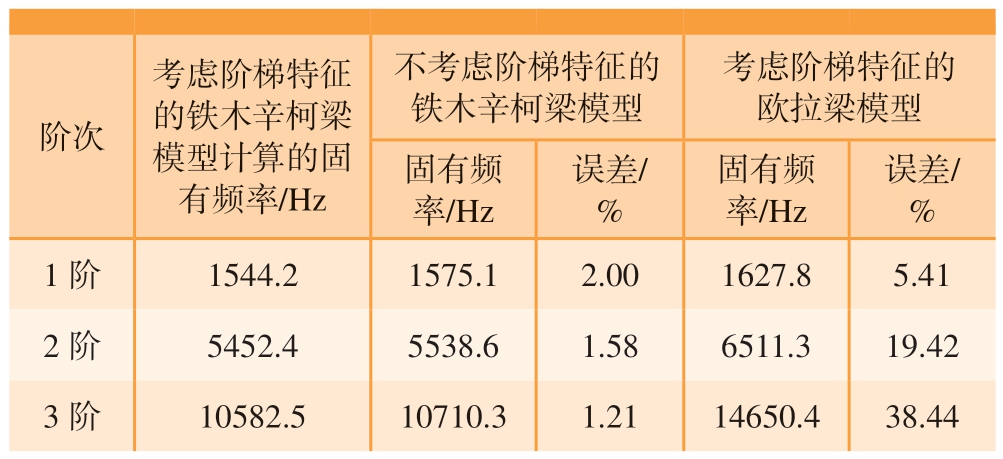
阶次不考虑阶梯特征的铁木辛柯梁模型考虑阶梯特征的铁木辛柯梁模型计算的固有频率/Hz考虑阶梯特征的欧拉梁模型固有频率/Hz误差/%1阶1544.21575.12.00 1627.85.41 2阶5452.45538.61.586511.319.42 3阶10582.510710.31.2114650.438.44误差/%固有频率/Hz
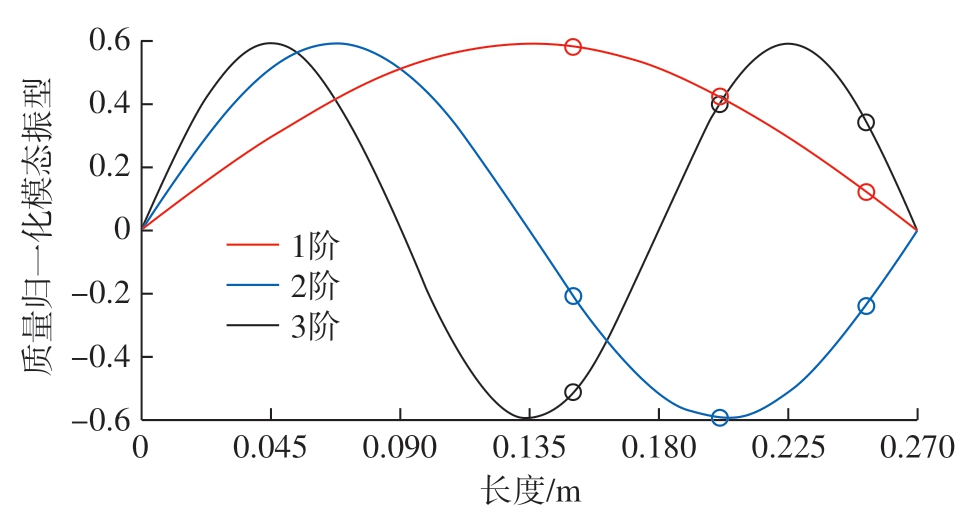
图3 阶梯工件的前3阶模态振型
Fig.3 First, second and third mode shapes of the stepped workpiece
在对具有阶梯特征的工件进行动力学分析的同时，还额外采用了不考虑阶梯特征的铁木辛柯梁模型和考虑阶梯特征的欧拉梁模型，所得到的固有频率也在表3中给出。通过对比可知，考虑工件阶梯特征和不考虑工件阶梯特征的铁木辛柯梁模型的固有频率计算结果误差非常小，1阶固有频率的误差仅为2.00%，并且该计算误差随着模态阶次的升高还在进一步缩小，3阶固有频率的误差已经降至1.21%，几乎可以忽略不计。这是由于造成工件阶梯特征的砂轮切入槽深度仅有1 mm，该深度仅为工件半径的3.33%。此外，从表3中还可以看出，采用欧拉梁模型计算出的固有频率误差较大，工件1阶固有频率误差达到5.41%，并且随着模态阶次的升高该误差仍在增大。这说明在分析短粗梁时，铁木辛柯梁模型具有更好的准确性。此外，从图3所示的前3阶模态振型可以看出，由于阶梯工件的阶梯特征并不明显，其模态振型呈现出典型的梁横向振动特征。第1阶模态振型没有节点，最大振动位移出现在工件的中间位置；而该位置恰好为第2阶模态振型的唯一节点位置，第2阶模态振型的最大振动出现在工件的1/4和3/4位置；第3阶模态振型的两个节点和3个最大振动位置也几乎是均匀分布在整个工件上，没有受到阶梯特征的影响。
1.3 不同工件位置的动力学分析
利用计算得到的阶梯工件前3阶模态振型，通过使用Wang等[17]提出的频响函数动力学分析方法，假定工件所受激励位置和响应位置均为zR，在Xw方向的位移响应函数可以表示为H（ω，zR）。
式中，mnum为所考虑的模态阶次数量；ξi和ωi分别为第i阶模态的阻尼比和固有频率。
利用式（17）并假定各阶模态的阻尼比均为0.01，可以得到图4所示的仿真频响函数的幅值和实部。图4中频响函数的激励位置和响应位置对应砂轮切入的位置，即图2（b）中的磨削位置P1、P2和P3，这3处亦在图3中进行了标识以便于对比其在各阶模态振型中的位置和振动幅值。根据图4所示的频响函数可知，第1阶模态为该工件的主要模态，其所呈现的振动能量远大于其他模态。此外，第1阶模态在位置1处的振动能量最大，说明此处的工件刚度最弱，与图3所示的第1阶模态振型相对应。当磨削位置逐渐向尾架顶尖方向移动时，第1阶模态的振动能量逐渐降低。对于第2阶模态，其在位置2处的振动能量最大，具体变化规律仍可从图3所示的第2阶模态振型相对应。
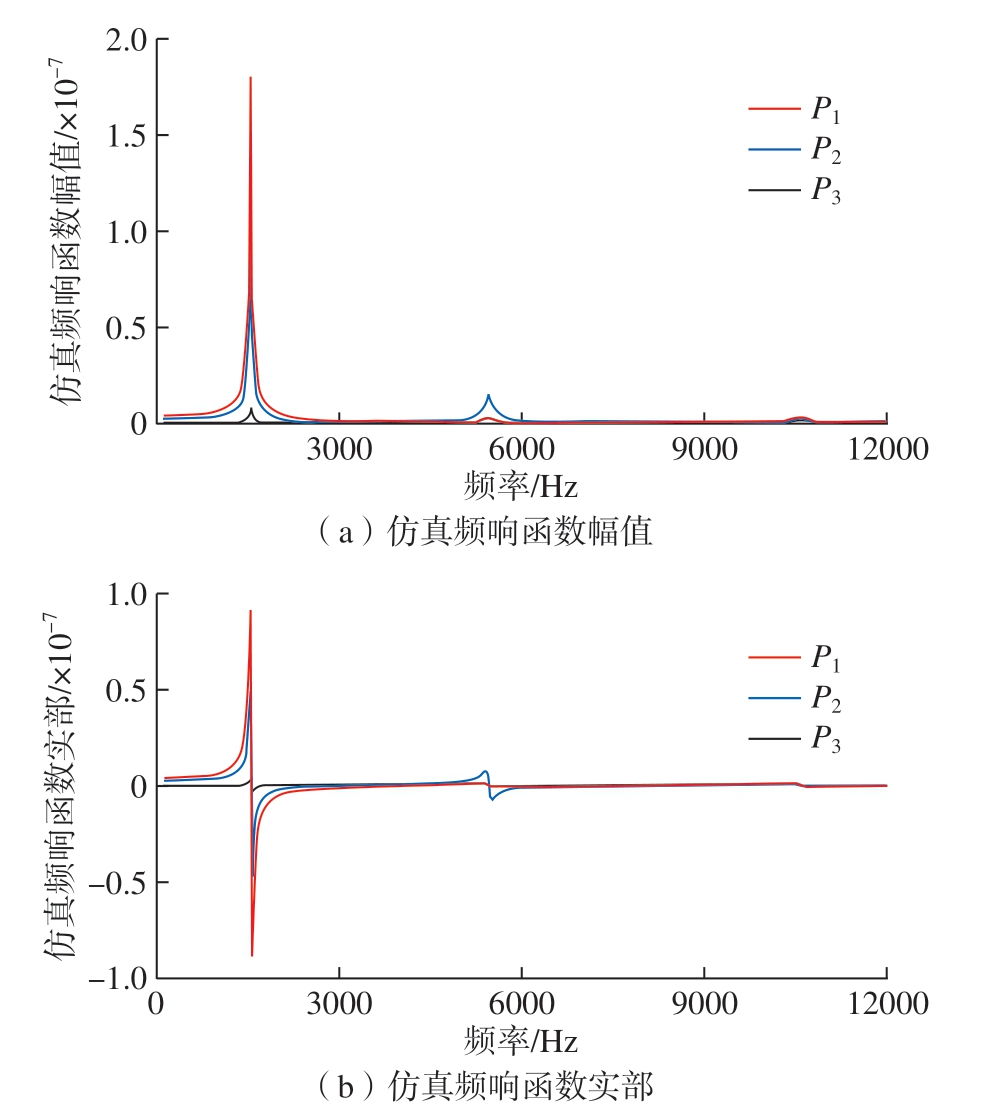
图4 阶梯工件不同位置处的仿真频响函数
Fig.4 Simulated frequency response function at different positions of stepped workpiece
1.4 砂轮的试验动态特性分析
根据图1所建立的切入式外圆磨削加工的动力学模型，针对一个砂轮–工件两自由度系统，不仅需要对工件进行动力学分析，还需要明确砂轮的动力学特性，才能进一步对整个磨削过程进行动力学和稳定性分析。考虑到砂轮所在的磨床主轴系统上轴承和主轴的型号及几何参数未知，此处通过锤击试验法[18]来获取其动力学特性。以力锤作为激振源在CFRP砂轮竖直方向进行单点施振，在砂轮中心位置布置一个三向加速度计以获取力锤施振时的振动响应信号，锤击试验过程如图5（a）所示。将采样频率设置为10000 Hz，同时采集并处理力信号和加速度信号，得到的位移频响函数如图5（b）和（c）所示。根据频响函数识别出的砂轮前3阶模态固有频率和阻尼比如表4所示。
表4 CFRP砂轮的前3阶固有频率和阻尼比
Table 4 First, second and third natural frequencies and damping ratios of CFRP based grinding wheel
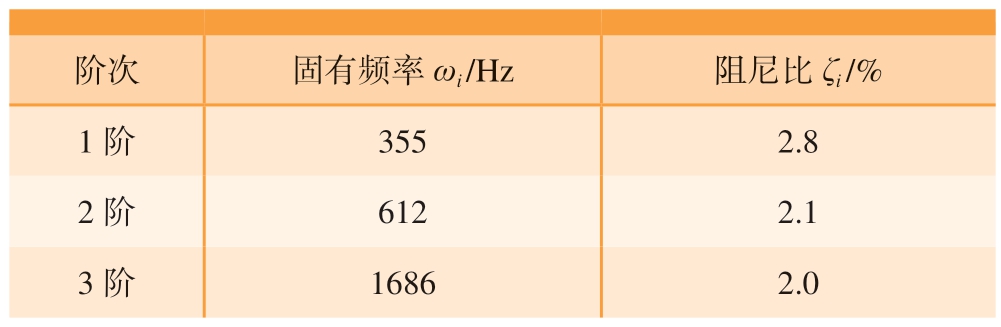
阶次固有频率ωi /Hz阻尼比ζi /%1阶3552.8 2阶6122.1 3阶16862.0
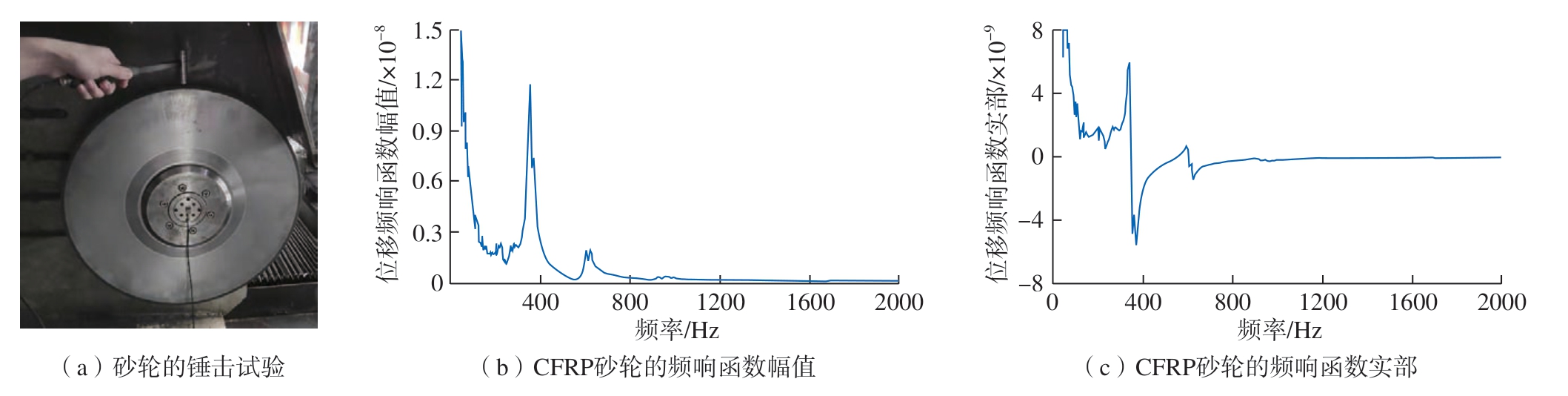
图5 CFRP砂轮的锤击试验及所测得的频响函数
Fig.5 Impact test of CFRP based grinding wheel and obtained frequency response function
根据图5中的位移频响函数和表4中所识别出的模态参数可知，CFRP砂轮以前两阶模态为主，高阶模态的固有频率在1000 Hz以后的频带中并不明显。将CFRP砂轮的频响函数和工件相对比，可知在磨削位置P1和P2处，工件的动刚度较差并作为薄弱环节决定着磨削过程的稳定性；在磨削位置P3处，工件和砂轮的动刚度相接近，两者将分别影响不同的转速区域并共同影响着磨削过程的稳定性。
2 外圆磨削稳定性分析
2.1 稳定性分析方法
机械加工不稳定是指在金属切削过程中由于刀具或工件的弱刚性而造成加工过程的系统性失稳并产生剧烈自激振动，也称为颤振现象。根据Munoa[19]和Quintana[20]等的研究，影响切削稳定性的主要因素是再生颤振效应，而稳定性图是反映切削稳定性与加工参数之间关系的重要且有效的工具。基于零阶傅里叶变换来模拟切削力，由Altintas[21]提出的单频法在实际场合中得到了广泛的应用并嵌入到许多商业软件中。然而，考虑到所研究的外圆磨削加工所具有的两自由度双再生颤振特征，此处采用钟建琳等[22]提出的改进的稳定性分析方法，计算方法为
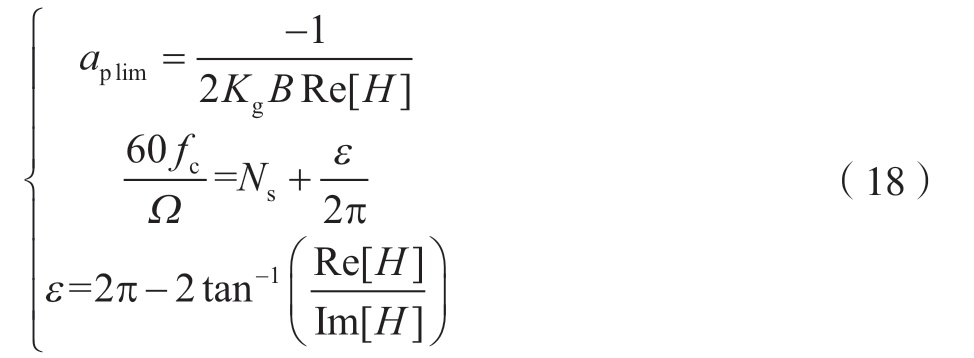
式中，ap lim为避免颤振所需的临界切削深度；fc为颤振频率；Ns为工件表面在一次旋转中所产生的振动波的整数；ε为当前转和前一转所产生振动的相位差；B为砂轮的宽度。需要注意的是，式（18）中的Ω表示引起再生效应的实际磨削转速，由于砂轮和工件均在旋转并且方向相反，因此该处的Ω是砂轮和工件的转速之和。
根据式（18）可知，保证稳定磨削的极限切削深度与磨削力系数、砂轮宽度和频响函数实部相关。其中，较大的磨削力系数和较大的砂轮宽度均会导致磨削稳定性降低。此外，由于磨削力系数和砂轮宽度均为正值，则磨削极限切削深度还与频响函数的负实部相关，负实部越大，磨削稳定性越低。
2.2 针对不同工件位置的外圆磨削稳定性分析
结合仿真得到的工件频响函数以及试验得到的砂轮频响函数，利用式（18）可以得到工件不同位置在CFRP砂轮加工时的磨削稳定性图，如图6所示，其中磨削力系数来自文献[20]中的试验数据，即Kg = 3×1012 N/m3，砂轮宽度和图2中工件的槽宽相等，所考虑的砂轮转速范围包含了高速磨削的50 ～ 400 m/s。从整体来看，靠近尾架顶尖的位置P3处磨削稳定性要明显优于靠近工件中心的位置P1和P2。具体来看，在位置P1处的磨削过程中，计算得到的极限切削深度为3个位置中最低的，为0.121 mm。但是其稳定性曲线也是最光滑的，说明此时的磨削稳定性仅受到工件的第1阶模态的影响。在位置P2处的磨削过程中，所得到的极限切削深度略高于P1位置，为0.229 mm。在较低的50～150 m/s转速范围内，磨削稳定性主要受到工件的第1阶模态影响，仅在126 m/s转速附近受到砂轮模态的影响；在其他转速范围内，磨削稳定性仍然主要受到工件的第1阶模态影响，但在176 m/s、289 m/s和365 m/s等转速附近受到工件第2阶模态的限制。在位置P3处的磨削稳定性非常好，磨削稳定性的极限切削深度远高于P1和P2位置，为1.949 mm。由于工件和砂轮的动力学特性相互接近，因此此处的稳定性曲线受到多重因素影响，其中，砂轮主要影响50 m/s和118 m/s转速附近的磨削稳定性，工件的第1阶模态则影响66 m/s、80 m/s和220 m/s等转速附近的磨削稳定性，此外，90 m/s、288 m/s和364 m/s等较高转速的磨削稳定性还会受到工件第2阶模态的影响。由于同一工件在磨削加工过程中通常采用统一的加工参数，因此该磨削加工过程的稳定性主要受到工件中间位置的弱刚性的影响。
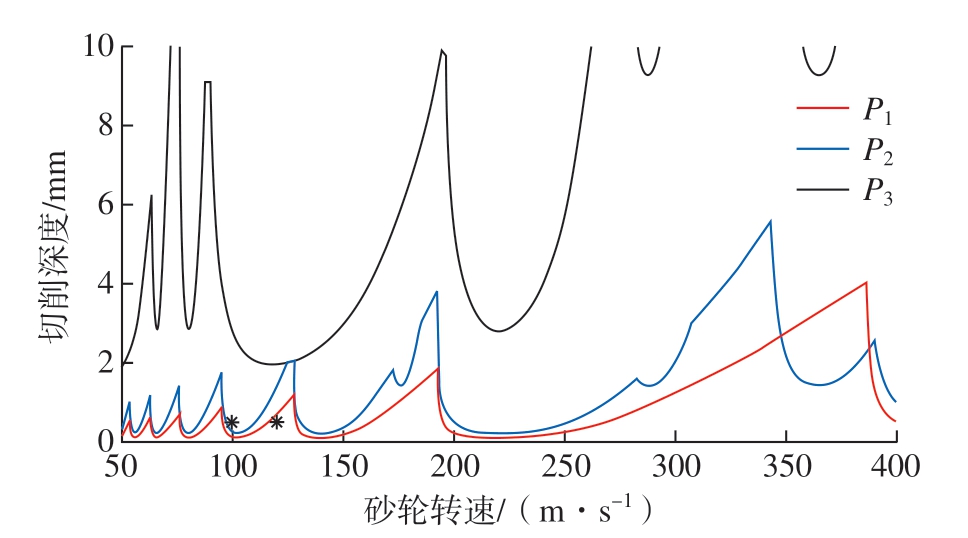
图6 工件不同位置处的磨削稳定性图
Fig.6 Grinding stability diagram with different workpiece positions
3 高速外圆磨削试验
高速磨削试验在CNC8325凸轮轴高速数控复合磨床上进行，采用8 MPa供液压力的水基冷却方式。工件的形状和材料参数如表2所示，所用工件采用同一批次圆柱棒料并在正式磨削试验前采用保守磨削参数进行光磨以保证初始条件的一致性。所用的砂轮以CFRP为基体，工件的全部被磨削位置如图2（b）所示，砂轮参数和磨削加工参数如表5所示，磨削试验的现场布置情况如图7所示。在磨削试验中，主轴和尾架各布置一个三向压电式加速度传感器，主轴处的加速度计用于测量磨削过程中主轴单元的振动信号，位于尾座的加速度计则用于测量工件的振动信号，采样频率均设置为10000 Hz。
表5 砂轮参数和磨削加工参数
Table 5 Parameters of grinding wheel and grinding process
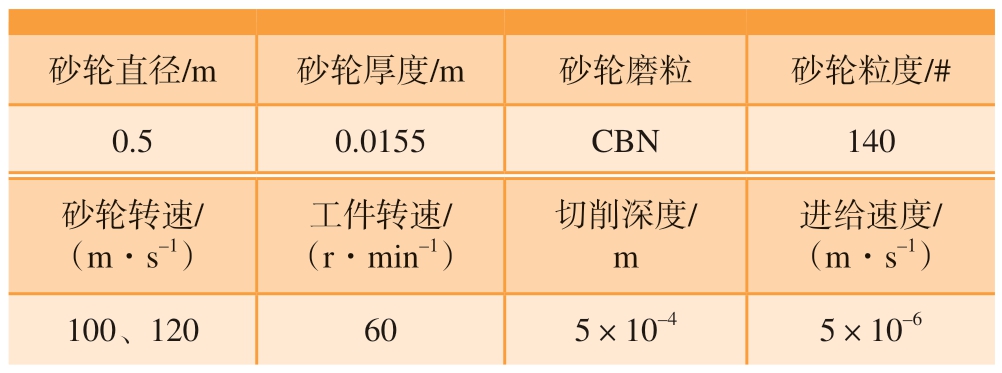
砂轮直径/m砂轮厚度/m砂轮磨粒砂轮粒度/#0.50.0155CBN140砂轮转速/（m·s–1）工件转速/（r·min–1）切削深度/m进给速度/（m·s–1）100、120605×10–45×10–6
图7 磨削试验装置
Fig.7 Grinding experiment setup
在外圆磨削过程中，通常将砂轮转速超过100 m/s的磨削过程认为是高速磨削，同时考虑到试验中较大的砂轮直径对数控磨床主轴功率和刚度的高要求，因此在磨削试验过程中采用了100 m/s和120 m/s两种砂轮转速，其所对应的磨削稳定性情况在图6中用星号进行了标识。需要说明的是，在磨削试验中，每种砂轮转速分别对应一根全新的工件并进行完整的磨削，进一步结合图2（b）所示的磨削位置分布和图6所示的稳定性分析结果，下文选择位置特征和稳定性特征更明显的P1和P3位置的磨削情况进行分析。从图6可以看出，当砂轮转速为100 m/s时，位置P1处的磨削会位于非稳定区域，此时磨削加工过程将极易诱发颤振，而在位置P3处磨削则位于稳定性区域，此时磨削过程稳定进行；当砂轮转速为120 m/s时，磨削位置P1和P3均位于稳定性区域，此时磨削过程稳定进行。
为了展示更详细的频域成分，分别从每一次磨削切入过程中选择长度为1 s的加速度信号，采用快速傅里叶变换算法（Fast Fourier transform，FFT）计算其振动能量在频域内的分布情况，试验结果如图8所示。需要说明的是，实际分析中发现，通过主轴采集的加速度信号在频域中的能量多集中在主轴转速的转频及其倍频上；而通过尾架外壳采集的振动信号则具有更大的时域幅值且更能够反映工件的振动情况，因此所展示的振动频域图均来源于尾架加速度计的X方向振动信号。由图8（a）和（c）可知，当砂轮转速为100 m/s时，此时转频的基频为63.7 Hz，在磨削位置P3时，此位置靠近支撑工件的顶尖，工件刚度良好，振动信号的频域成分大多集中在转频及其倍频，在实际磨削过程中表现为以磨削力为外力的强迫振动；在磨削位置P1时出现颤振现象，具体表现为整个频带内的能量均有所增加，并且在1539 Hz处出现一个能量集中且非常高的频域峰值，该峰值处的能量是P3位置中最大峰值的5倍，并且该峰值频率非常接近工件的一阶固有频率，可判断此时由于工件的弱刚性导致磨削过程出现颤振现象。进一步结合图8（b）和（d）可知，当砂轮转速为120 m/s时，转频的基频为76.4 Hz，此时在位置P1和P3进行磨削时均表现为稳定磨削过程，振动幅度很小，从频谱中可以看到，振动能量多集中在以299 Hz和745 Hz为代表的转频的倍频中。需要注意的是，在砂轮转速为100 m/s和120 m/s时，在825 Hz处振动频域信号均存在一个较大的能量峰值，该频率既是100 m/s转速的13倍频，也接近于120 m/s转速的11倍频，考虑到该频率所在峰值在主轴振动信号的频域中并未出现，因此认为其是尾架中某结构件的固有频率所引入的干扰。
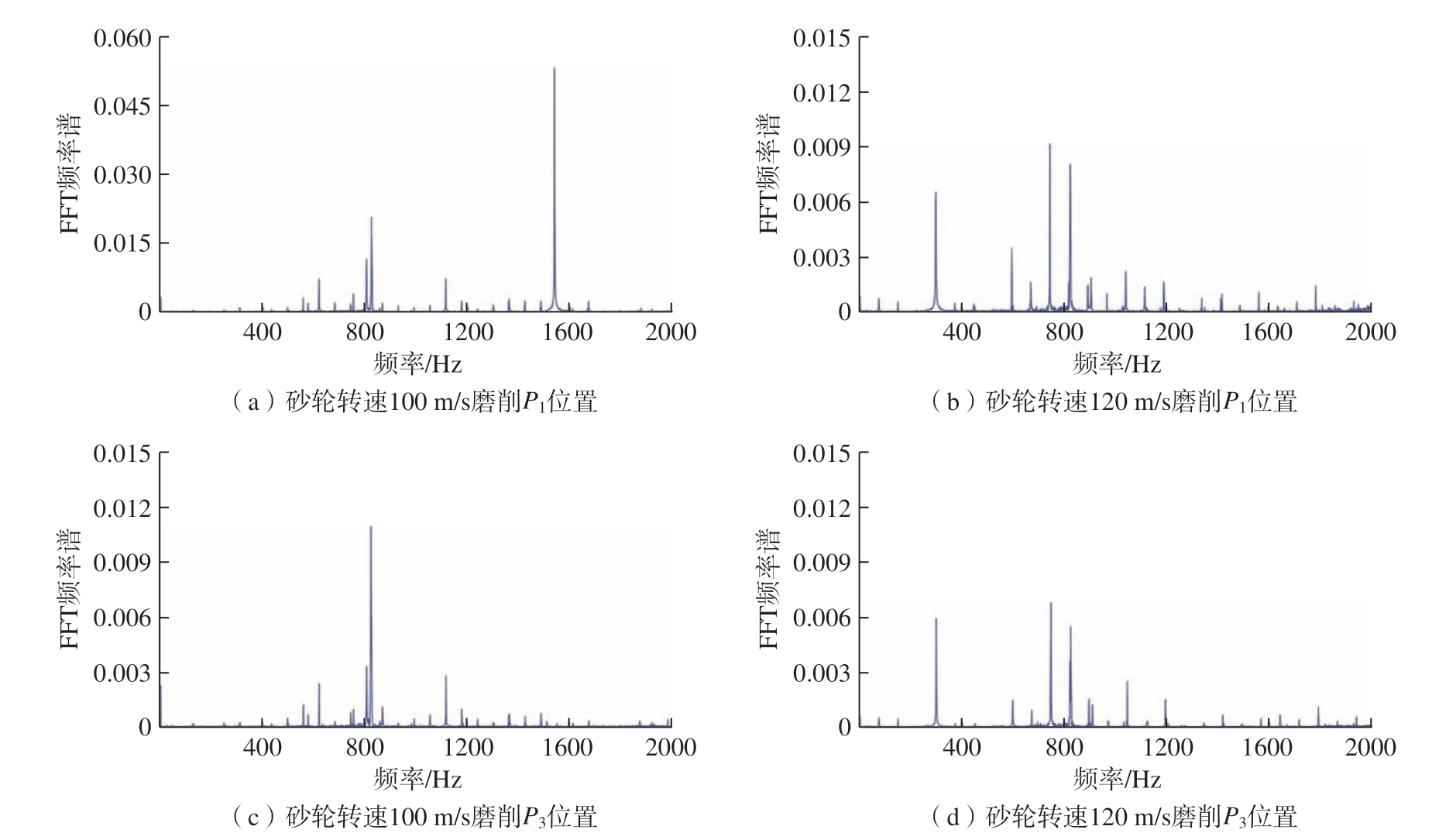
图8 不同砂轮转速在不同磨削位置时的磨削振动频域图
Fig.8 Frequency domain of grinding vibration under different grinding wheel speeds and different workpiece positions
为了进一步分析磨削颤振的影响，利用时代Time 3231粗糙度仪对CFRP砂轮磨削后的工件表面粗糙度进行评定，重点针对高度特征参数中使用最普遍的轮廓算术平均偏差Ra进行测量，每个磨削位置均测量3次后取平均值，测量过程如图9（a）所示，由于粗糙度仪的触针长度有限，对磨削后的工件进行了切割分段。磨削后工件的表面粗糙度结果如图9（b）所示，由于砂轮转速100 m/s时在位置P1处出现磨削颤振现象，该位置磨削后的工件表面粗糙度较大，达到0.138 μm；而在位置P3处稳定磨削时，其表面粗糙度为0.089 μm。此外，当砂轮转速为120 m/s时在位置P1和P3处进行稳定磨削，磨削后的工件表面粗糙度分别为0.091 μm和0.085 μm，可以看出，由于P3位置工件刚度良好，此处的表面粗糙度比P1磨削位置要低6.6%。综上，在磨削位置P1，由于砂轮转速不合理所诱发的磨削颤振，导致工件表面粗糙度增加51.6%，这将严重破坏磨削加工质量和精度，降低加工效率，因此在磨削前对加工过程进行稳定性分析以验证加工参数合理性是非常必要的。
图9 不同砂轮转速在不同磨削位置磨削后的工件表面粗糙度
Fig.9 Surface roughness of workpiece under different grinding wheel speeds and different workpiece positions
4 结论
本文利用铁木辛柯梁理论对高速磨削中的阶梯工件进行动力学分析，并结合CFRP砂轮的动力学特性，分析了不同工件位置对磨削稳定性的影响，并进行了高速磨削试验，得到的主要结论如下。
（1）利用铁木辛柯梁理论对具有阶梯特征的工件进行动力学分析，得到该工件的固有频率和模态振型。通过对比考虑和不考虑阶梯特征的铁木辛柯梁模型计算结果，发现由于工件的槽深较浅，其阶梯特征并不明显。进一步对比铁木辛柯梁模型和欧拉梁模型的计算结果，发现铁木辛柯梁理论的计算结果更为准确。
（2）结合仿真得到的工件动力学特性和试验得到的砂轮动力学特性，对高速磨削过程中的砂轮–工件两自由度系统进行磨削稳定性分析，结果表明，工件和砂轮均会对磨削稳定性产生影响。通过绘制稳定性图发现，当磨削位置靠近工件的中间位置时，工件刚度较差易诱发颤振；当磨削位置接近工件两端的顶尖支撑位置时，工件刚度增加并接近砂轮刚度，两者一起影响不同转速区域的磨削稳定性，并且磨削稳定性随着工件位置的变化并不是线性的。通过采用不同砂轮转速进行磨削试验，验证了磨削稳定性分析所得的稳定性图的准确性。磨削试验还体现了不同工件磨削位置对工件表面质量的影响，由磨削失稳导致的表面粗糙度增幅可达51.6%。
[1] 袁巨龙, 邓朝晖, 熊万里, 等. 高效磨削技术与装备进展及展望[J]. 航空制造技术, 2010, 53(5): 66–70.
YUAN Julong, DENG Zhaohui, XIONG Wanli, et al. Development and prospect of high-efficiency grinding technology and equipment[J].Aeronautical Manufacturing Technology, 2010, 53(5): 66–70.
[2] 丁文锋, 徐九华, 杨长勇, 等. 航空发动机零件高效精密磨削技术的发展与应用[J]. 航空制造技术, 2014, 57(12): 26–29.
DING Wenfeng, XU Jiuhua, YANG Changyong, et al. Development and application of high efficiency and precision grinding technology for aeroengine components[J]. Aeronautical Manufacturing Technology,2014, 57(12): 26–29.
[3] INASAKI I, KARPUSCHEWSKI B, LEE H S. Grinding chatter-origin and suppression[J]. CIRP Annals, 2001, 50(2): 515–534.
[4] 江卓达, 何永义. 磨削颤振特性研究进展[J]. 制造技术与机床, 2012(9): 35–42.
JIANG Zhuoda, HE Yongyi. Advances of research on the character of grinding chatter[J]. Manufacturing Technology & Machine Tool,2012(9): 35–42.
[5] LI H Q, SHIN Y C. A study on chatter boundaries of cylindrical plunge grinding with process condition-dependent dynamics[J]. International Journal of Machine Tools and Manufacture, 2007, 47(10): 1563–1572.
[6] 蒋永翔, 王太勇, 张莹, 等. 外圆切入磨再生颤振稳定性理论及评价方法[J]. 天津大学学报, 2009, 42(4): 283–286.
JIANG Yongxiang, WANG Taiyong, ZHANG Ying, et al. Analysis of regenerative chatter stability theory and evaluation method on cylindrical plunging grinding[J]. Journal of Tianjin University, 2009,42(4): 283–286.
[7] YAN Y, XU J, WIERCIGROCH M. Regenerative and frictional chatter in plunge grinding[J]. Nonlinear Dynamics, 2016, 86(1):283–307.
[8] CHEN Y, CHEN X, XU X P, et al. Quantitative impacts of regenerative vibration and abrasive wheel eccentricity on surface grinding dynamic performance[J]. The International Journal of Advanced Manufacturing Technology, 2018, 96(5–8): 2271–2283.
[9] 张氢, 陈文韬, 陈淼, 等. 数控凸轮轴磨床颤振稳定性研究[J]. 湖南大学学报(自然科学版), 2020, 47(2): 45–52.
ZHANG Qing, CHEN Wentao, CHEN Miao, et al. Study on cutting chatter stability of a computerized numerical control camshaft grinder[J].Journal of Hunan University (Natural Sciences), 2020, 47(2): 45–52.
[10] 刘涛, 邓朝晖, 罗程耀, 等. 基于动态磨削深度的非圆轮廓高速磨削稳定性建模与分析[J]. 机械工程学报, 2021, 57(15):264–274.
LIU Tao, DENG Zhaohui, LUO Chengyao, et al. Stability modeling and analysis of non-circular high-speed grinding with consideration of dynamic grinding depth[J]. Journal of Mechanical Engineering, 2021,57(15): 264–274.
[11] 杨淮文, 冯伟, 朱建辉, 等. CFRP砂轮与钢基体砂轮高速磨削过程中的动力学特性[J]. 金刚石与磨料磨具工程, 2021, 41(5):52–58.
YANG Huaiwen, FENG Wei, ZHU Jianhui, et al. Dynamic characteristics of high speed grinding process of CFRP wheel and steel based wheel[J]. Diamond & Abrasives Engineering, 2021, 41(5): 52–58.
[12] 王民, 秦鹏, 张彦琳, 等. 组合阶梯梁振动特性计算方法及应用[J]. 北京工业大学学报, 2019, 45(1): 1–7.
WANG Min, QIN Peng, ZHANG Yanlin, et al. Solution and application for vibration characteristics of combined stepped beam[J].Journal of Beijing University of Technology, 2019, 45(1): 1–7.
[13] LIN C W, LIN Y K, CHU C H. Dynamic models and design of spindle-bearing systems of machine tools: A review[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(3): 513–521.
[14] 崔灿. 变截面梁振动特性快速算法及其应用[D]. 成都: 西南交通大学, 2012.
CUI Can. A fast calculation methods and application for vibration characteristic of beam with variable cross-section[D]. Chengdu:Southwest Jiaotong University, 2012.
[15] TIMOSHENKO S, YOUNG D H, WEAVER W. Vibration problems in engineering[M]. 4th ed. New York: Wiley, 1974.
[16] HUANG T. The effect of rotatory inertia and of shear deformation on the frequency and normal mode equations of uniform beams with simple end conditions[J]. Journal of Applied Mechanics.1961, 53: 579–584.
[17] WANG M, ZAN T, GAO X S, et al. Suppression of the timevarying vibration of ball screws induced from the continuous movement of the nut using multiple tuned mass dampers[J]. International Journal of Machine Tools and Manufacture, 2016, 107: 41–49.
[18] FENG W, LIU B G, YAO B, et al. An integrated prediction model for the dynamics of machine tool spindles[J]. Machining Science and Technology, 2018, 22(6): 968–988.
[19] MUNOA J, BEUDAERT X, DOMBOVARI Z, et al. Chatter suppression techniques in metal cutting[J]. CIRP Annals, 2016, 65(2):785–808.
[20] QUINTANA G, CIURANA J. Chatter in machining processes:A review[J]. International Journal of Machine Tools and Manufacture, 2011,51(5): 363–376.
[21] ALTINTAS Y. Manufacturing automation: Metal cutting mechanics, machine tool vibrations, and CNC design[M]. New York:Cambridge University Press, 2000.
[22] 钟建琳, 沈山山, 米洁. 外圆磨削过程稳定性预测研究[J].制造业自动化, 2014, 36(13): 48–50.
ZHONG Jianlin, SHEN Shanshan, MI Jie. Research on stability prediction of plung grinding process[J]. Manufacturing Automation,2014, 36(13): 48–50.