镍基合金属于一种典型的高温合金材料，常用于喷气发动机、燃气轮机以及核反应堆等[1–3]。Inconel 718是镍基合金中用量最大的一种，具有高温稳定性，是高温装备领域核心部件的首选材料[4]。Inconel 718具有优异的疲劳耐久性，可以在较宽的温度范围内保持机械性能[5]，但自身高硬度使得其在加工过程中切削力较大，加工硬化明显。此外，在切削加工过程中，产生的大部分热量都是通过切屑传递的[6]，由于Inconel 718的低导热性，热量很难快速传递到切屑中，切削区域温度迅速升高，刀具易发生磨损。因此，研究高温合金切削过程的应力和温度对于切削参数优化和刀具磨损控制具有重要意义。
高温合金切削过程的应力和温度与其自身的力学响应特性有直接关系。材料的力学响应是建立材料微观力学、热力学行为（如变形、应力、绝热温升等）和宏观力学、热力学表现（如切削力、切削温度等）之间内在联系的关键所在[7–8]。对于材料力学响应的研究，一般采用试验法和有限元仿真法，其中试验法是通过测力仪和红外测温仪获取切削过程中的切削力和切削温度的方法，是对宏观力学、热力学表现的重要研究方法。但试验法具有局限性，只能测量切削力和切削温度，应力和切削热无法直接测得。有限元仿真法则可以探究切削过程中热量流动和应力的变化情况，有限元仿真过程是通过材料本构模型[9]、热物理属性模型[10]、摩擦模型[11]以及失效模型[12]等多模型耦合机制完成的，其中，材料本构模型是保证有限元仿真精度的最重要的模型。材料的本构模型是研究金属材料本构关系的理论基础，是建立在弹性理论基础上的用于研究金属材料在变形过程中应力–应变关系的数学模型[13]。在材料成形过程中，材料的本构模型可以反映出材料的力学性能随温度、应变率等参数的变化规律。通过动态拉伸试验和压缩试验可获取金属材料的应力–应变曲线，再对所获取的试验结果进行分析处理，得到合适的材料本构模型[14]。常见的本构模型可以分为经验模型、半物理模型和物理概念模型等，用于金属切削仿真的本构模型主要是经验型本构模型，包括Power–Law[15]、Johnson–Cook[16]模型，两模型均可建立应力–应变、应变率、温度的内在联系。同时可以驱动应力–温度相耦合的有限元仿真算法[17]，因此得到了最广泛的应用。
针对Inconel 718材料力学行为与应变、应变率、温度的关系，Yuan等[18]通过单轴拉伸试验探究Inconel 718在高应变率和高温下的力学性能，研究发现，当应变率小于103 s–1时，流动应力变化不明显，但是，当应变率大于104 s–1时，流动应力变化较大。Forni等[19]通过霍普金森压杆试验得到了Inconel 718在不同温度下及相应的应力–应变曲线，发现Inconel 718对应变率和温度都较为敏感。Xie等[20]研究发现，应变率在5000 s–1、300 ℃以内，材料流动应力变化很小；温度在300～500 ℃时，材料的硬化作用加重；当温度在700℃以上时，材料发生软化，流动应力变化明显。郭必成等[17]研究发现，相同变形时间条件下，应变与应变率成正比变化；不同应变下的应力不同，应力做功产生热量形成温度场，因此应变会间接影响温度场；温度使得材料软化，反过来又影响了不同应变下的应力。由于材料变形过程力学行为与应变、应变率、温度关系的复杂性，已有的研究难以将应变、应变率和温度对材料变形过程力学行为的影响明确。
本文通过霍普金森压杆试验得到了常温下Inconel 718在不同应变率下的真实应力–应变曲线；通过高温硬度试验得到了材料在不同温度下的硬度值以反映材料的热软化行为；通过激光热导试验获得材料在不同温度下的比热容和热导率，用以计算Inconel 718变形过程中的绝热温升。利用上述试验结果，建立Inconel 718的Power – Law（P – L）和 Johnson – Cook（J – C）本构模型表达式。对比两种模型的精度，选择精度较高的P – L本构模型作为有限元仿真中的本构模型，并进行Inconel 718切削仿真。通过试验设计，控制每组仿真中的应变、应变率、温度单因素变化，探讨上述3个因素分别对切削力和应力的影响，建立了材料微观力学、热力学行为与宏观力学、热力学表现之间的映射关系，为高温合金的材料设计、切削工艺参数优化和刀具磨损控制建立理论基础。
1 试验
1.1 霍普金森压杆试验
采用分离式霍普金森压杆（Split Hopkinson pressure bar，SHPB）平台研究Inconel 718在高应变速率（102～104 s–1）下的力学性能。如图1所示，SHPB 试验装置主要由入射杆、透射杆、冲击杆、气缸和数据处理系统组成。首先将试样放置在入射杆与透射杆之间，然后调节气缸上的气压，在气压的作用下，冲击杆撞击入射杆的末端，并产生应力波。该波通过入射杆传播，在到达入射杆的另一端时，入射波部分透射到试样中，部分反射回来，同时试样发生塑性变形，应力波在试样中传播，而后应力波被传递到透射杆中。应力波通过粘在入射杆与透射杆上的应变片传递到数字示波器上，最后被数据处理系统采集。
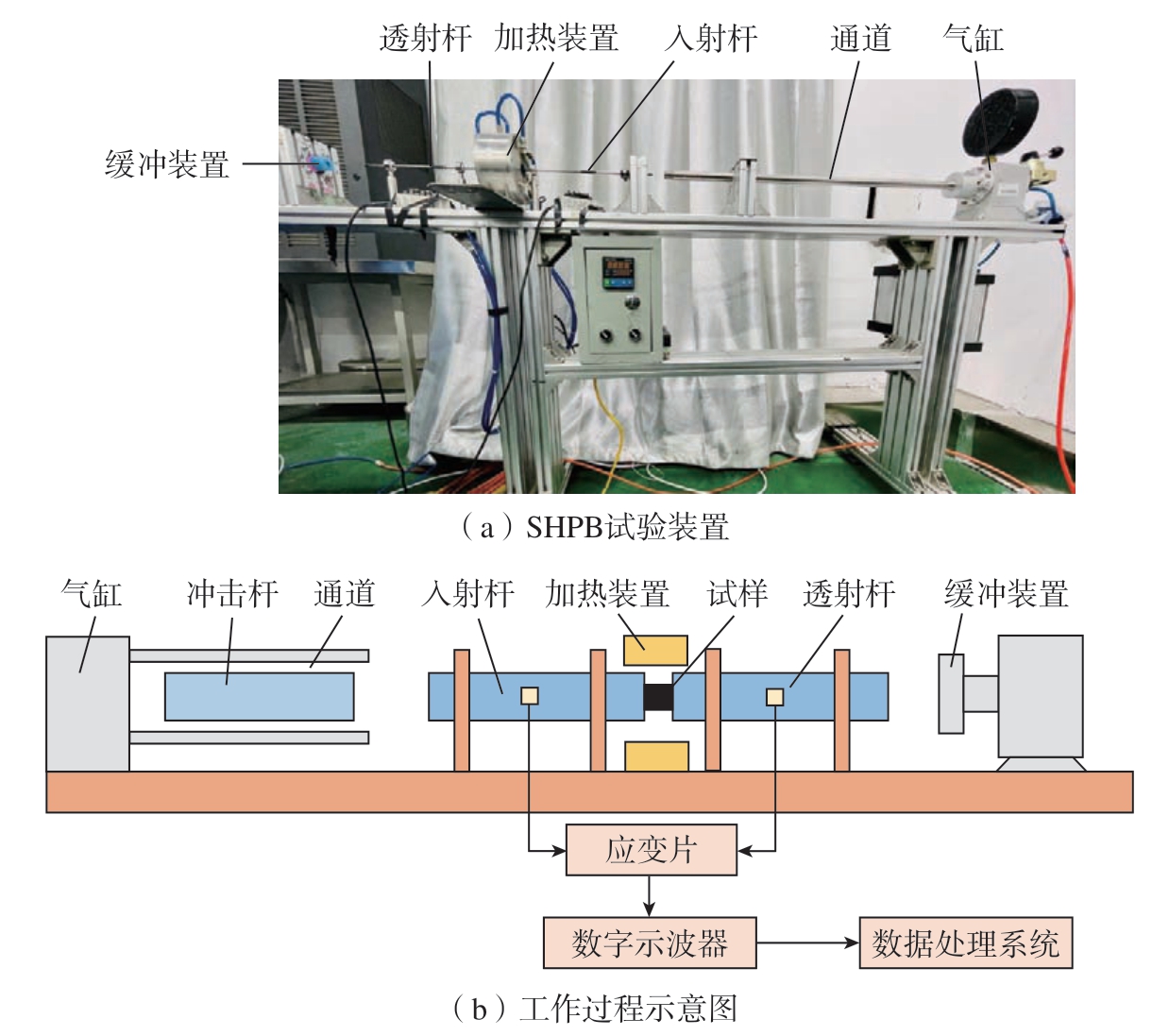
图1 分离式霍普金森压杆设备示意图
Fig.1 Schematic diagram of the SHPB
图2是应力在试样、入射杆及透射杆之间的传递示意图。所有波形，包括入射波、反射波和透射波，均由粘贴在入射杆和透射杆上的应变片获取。
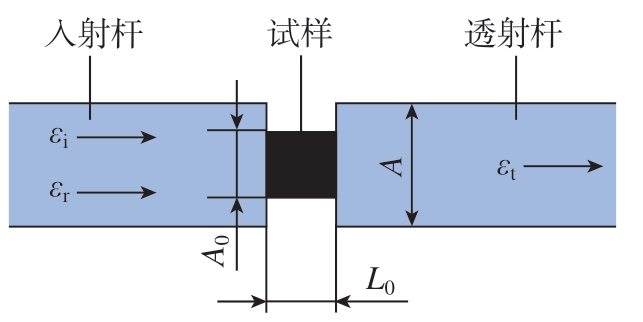
图2 SHPB系统的应力传播示意图
Fig.2 Schematic representation of stress propagation in SHPB system
图3显示了在常温和冲击气压为0.2 MPa时，对Inconel 718材料试样进行SHPB测试后，采集到的入射杆和透射杆的原始波形曲线。
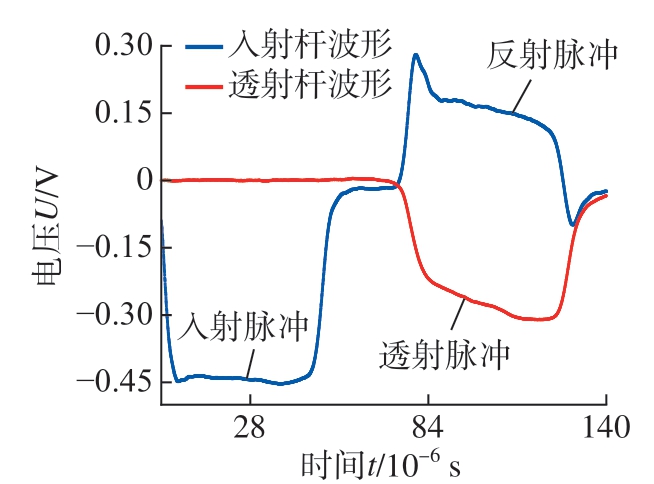
图3 入射杆与透射杆采集原始波形
Fig.3 Raw waveforms acquired by incident and transmission bars
通过得到的波形曲线再结合一维应力波理论计算得到材料的应力–应变曲线。其中应变ε、工程应力σe、工程应变εe、应变率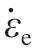
分别与时间t的关系如下[21]。
式中，V（t）是电压随时间的变化表达式；k是应变仪的灵敏度系数；I是应变仪的工作电流；E是杆的弹性模量；A是杆的横截面积；L0是试样的长度；A0是试样的横截面积；εt是透射脉冲的幅值；εi是入射脉冲的幅值；εr是反射脉冲的幅值；C是杆的一维弹性波速度；ρ是杆的密度。各物理参数值如表1所示。真实应力σT和真实应变εT的计算公式为
表1 SHPB试验各物理量参数值
Table 1 Parameter values of various physical quantities in SHPB experiment
kE/GPaA/mm2L0/mmA0/mm2C/（m/s）ρ/（kg/m3）1.9619012.56278.549007.91
试样的尺寸为Φ2 mm×2 mm。为减少试验过程中杆表面与试样之间的摩擦，试样的平均表面粗糙度Ra≤0.8 μm。同时，必须确保入射杆、透射杆和试样的轴线符合轴向要求。因此，试样轴线与两个端面的垂直度以及两个端面的平行度应小于 0.1 mm。该试验在常温下进行，冲击气压分别设定为 0.05 MPa、0.10 MPa、0.15 MPa、0.20 MPa和0.25 MPa，且每个气压下重复测试3次。
1.2 高温硬度试验
本研究采用高温硬度试验获取Inconel 718的热软化系数。试验采用ZD – HVZHT–10高温维氏硬度计（山东宗德机电设备有限公司），图4为高温硬度试验示意图[22]。该高温硬度计的测试温度最高可达1000℃，升温速率高达50 ℃/min。工作过程为首先对试样进行加热处理，为了确保工件在设定温度下完全加热，先对试样进行10 min的温度保持时间。在负载的作用下，压头压入试样表面，试样表面形成压痕，再通过CCD图像采集系统测量压痕对角线长度，载荷设置为30 kgf，加载保持时间为30 s，计算可得到在此设定温度下的维氏硬度值。高温硬度试验设计如表2所示。
表2 高温硬度试验设计
Table 2 High-temperature hardness experiment design
温度/℃ 温度保持时间/min载荷/kgf载荷保持时间/s 25，200，400，600，800，1000103030
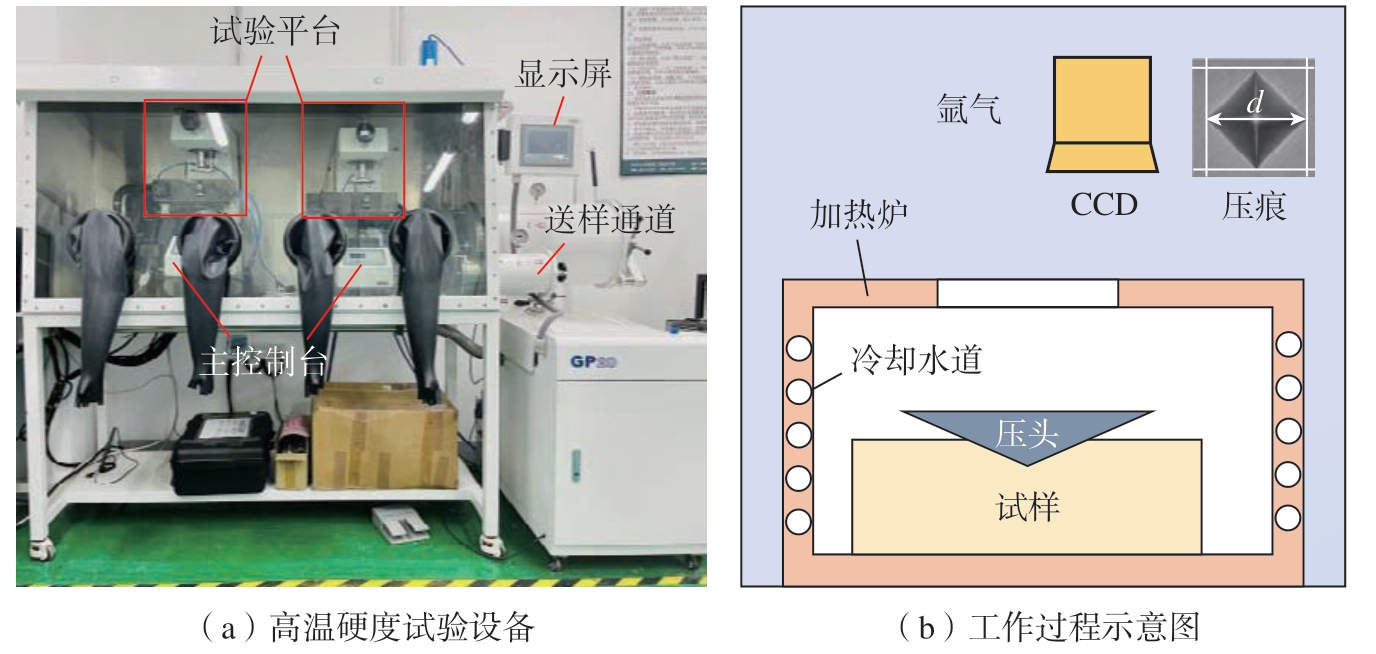
图4 高温硬度试验设备和工作过程示意图[22]
Fig.4 High-temperature hardness experiment equipment and working process diagram[22]
试样尺寸为8 mm×8 mm×8 mm，考虑到试样表面精度对测试结果的影响，应对试样表面进行抛光处理，以保证试样的平均表面粗糙度Ra≤0.05 μm。
1.3 激光热导试验
本研究采用激光热导试验获取材料在不同温度下的比热容和热导率。测试采用LFA457激光热导仪（德国耐驰仪器制造有限公司），图5为激光热导试验设备及工作过程示意图。测试原理为首先激光源发出激光脉冲，然后均匀照射在试样的下表面，使其表层吸收光能，温度瞬间升高，下表面作为热端，再通过一维热传导将能量传播到上表面，并使用红外检测器连续测量上表面中心部位的相应温升。
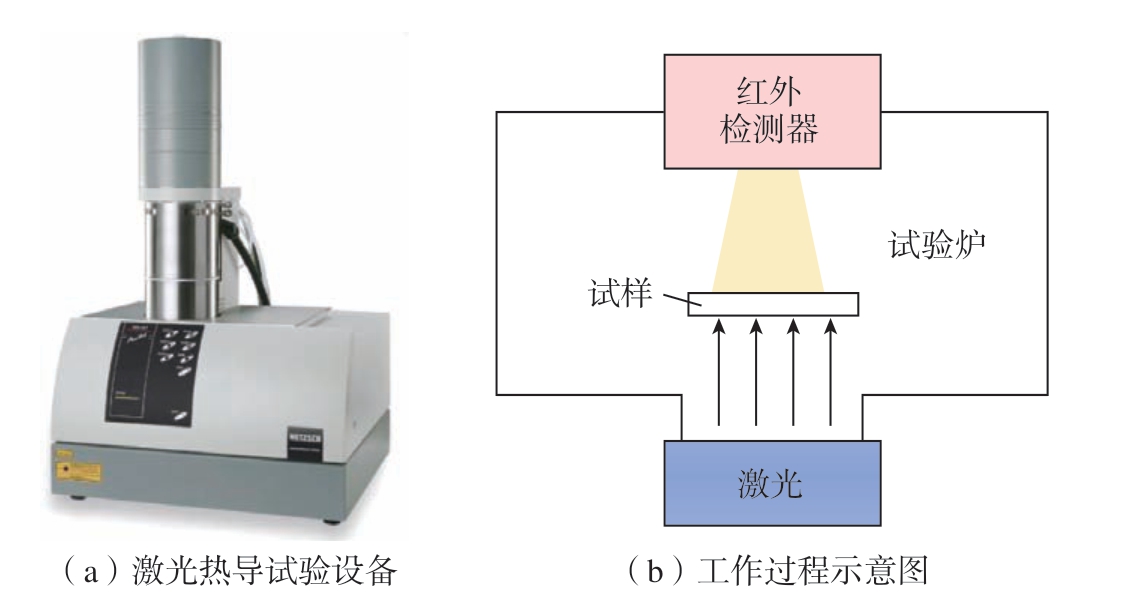
图5 激光热导试验设备及工作过程示意图
Fig.5 Laser thermal conductivity experiment equipment and working process diagram
这款激光热导仪采用模块化设计，可以测量材料在不同温度下的热膨胀系数、热导率和比热容。此试验的试样尺寸为Φ10 mm×4 mm，试验温度分别设定为25 ℃、100 ℃、200℃、400 ℃、600 ℃、800 ℃和1000 ℃，并对每个测试温度进行3次重复测试，平均3次的测试结果作为最后的测试结果。
2 试验结果及分析
对 SHPB 试验获得的波形数据进行数据处理，得到 Inconel 718在不同应变率下的真实应力–应变曲线，如图6所示。可以看出，对于Inconel 718，由于其硬度较大，随着应变率的增大，真实应力变化不明显，应变率敏感性不强。由于SHPB试验是一个绝热过程，因此试验过程中的绝热温升不容忽视，绝热温升计算公式为[23]
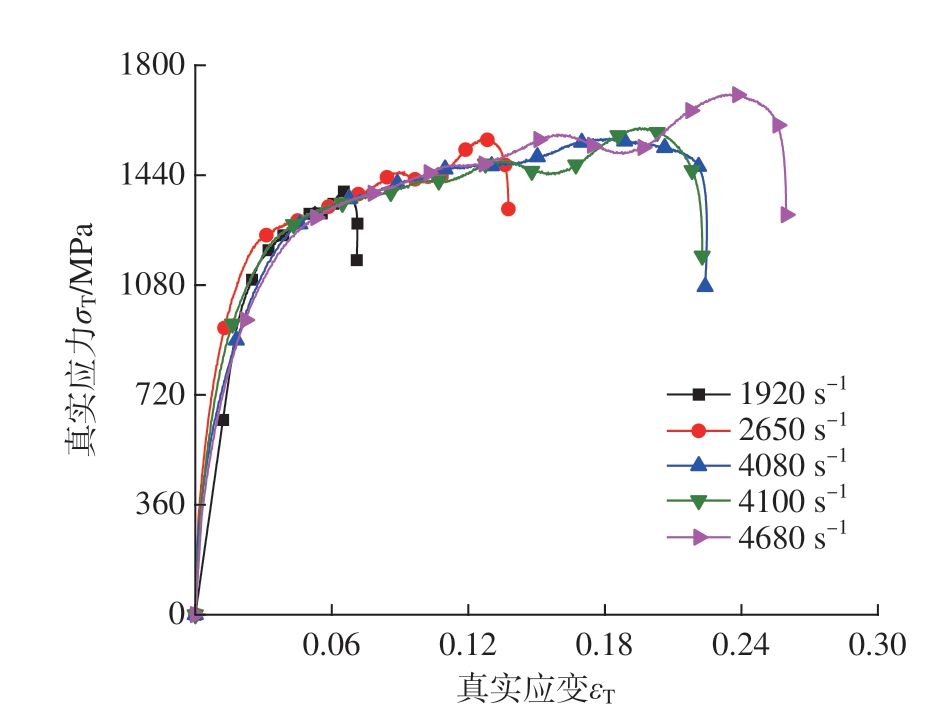
图6 不同应变率下的真实应力–应变曲线
Fig.6 True stress-strain curves at different strain rates
式中，β为塑性功的热转换系数，一般为0.9[24]；ρ0为Inconel 718的密度，为8.2 g/cm3；Cp为材料的比热容，通过上述激光热导试验获取。图7为Inconel 718在不同温度下的比热容和热导率。
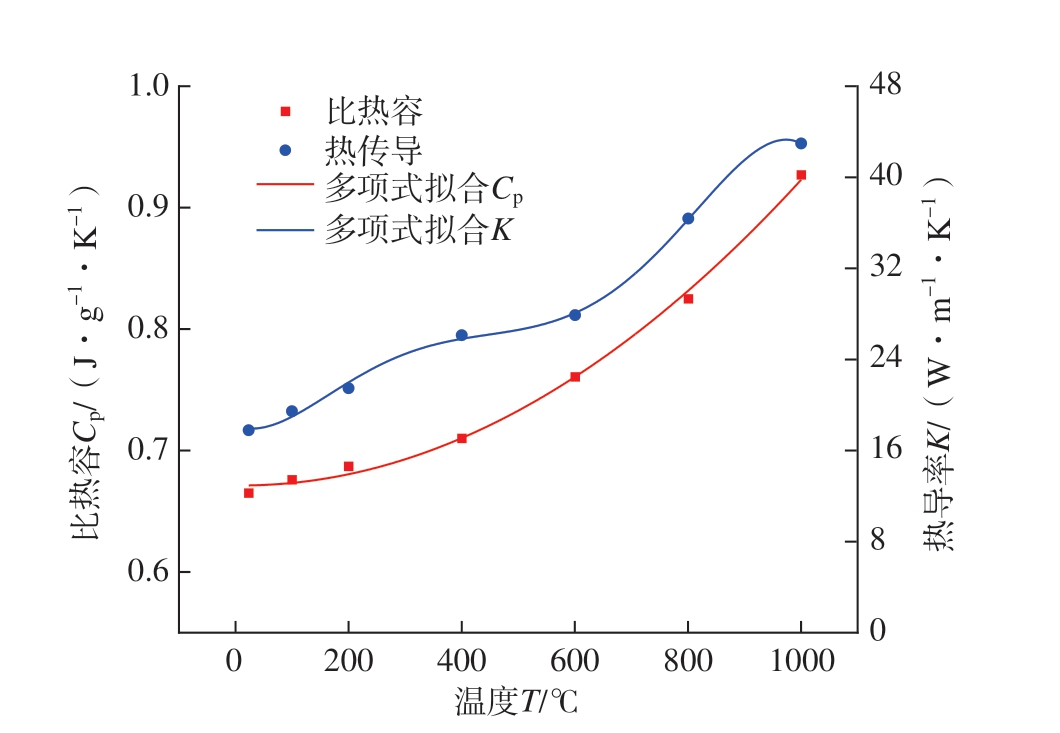
图7 不同温度下的比热容和热导率
Fig.7 Specific heat capacity and thermal conductivity at different temperatures
通过拟合可以得到Inconel 718的比热容和热导率随温度变化的表达式
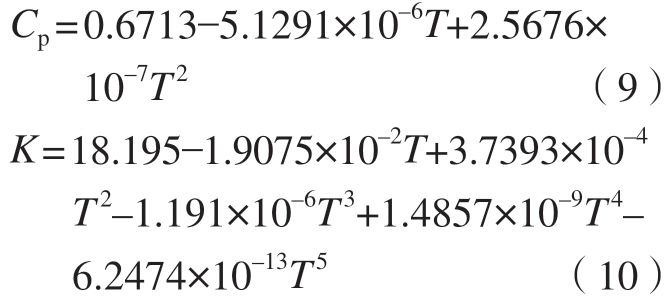
把比热容等相关数值代入式（8），并通过MATLAB软件计算可得到该材料在不同应变率下的绝热温升，结果如图8所示。可以看出，绝热温升随着应变的增大而增大，但在相同应变下，随着应变率的增大，其绝热温升没有明显的上升，进一步说明了该材料的应变率敏感性不强。图6所示的真实应力–应变曲线处于非等温状态，由于绝热温升的存在，所以在拟合本构模型之前，有必要将非等温应力转化为等温应力，变形温度通过公式（11）计算。
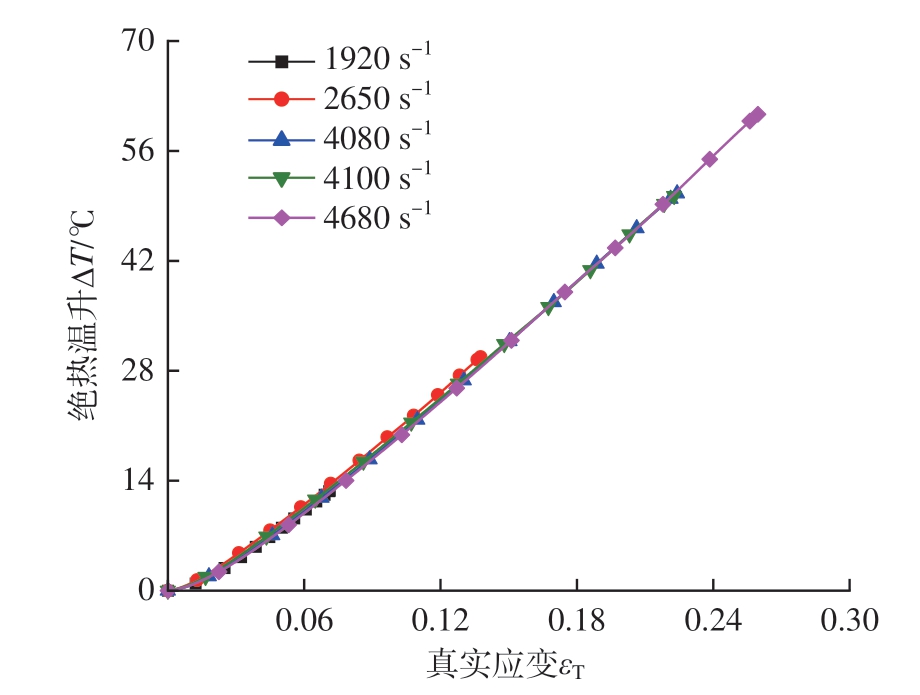
图8 不同应变率下的绝热温升
Fig.8 Adiabatic temperature rise at different strain rates
式中，Tdef为变形温度；Troom为室温；ΔT为绝热温升。
等温应力可由式（12）计算。
式中，σi是等温应力；σT是真实应力；θ（Tdef）是材料的软化系数。
图9显示了材料在不同应变率下的等温应力–应变曲线。
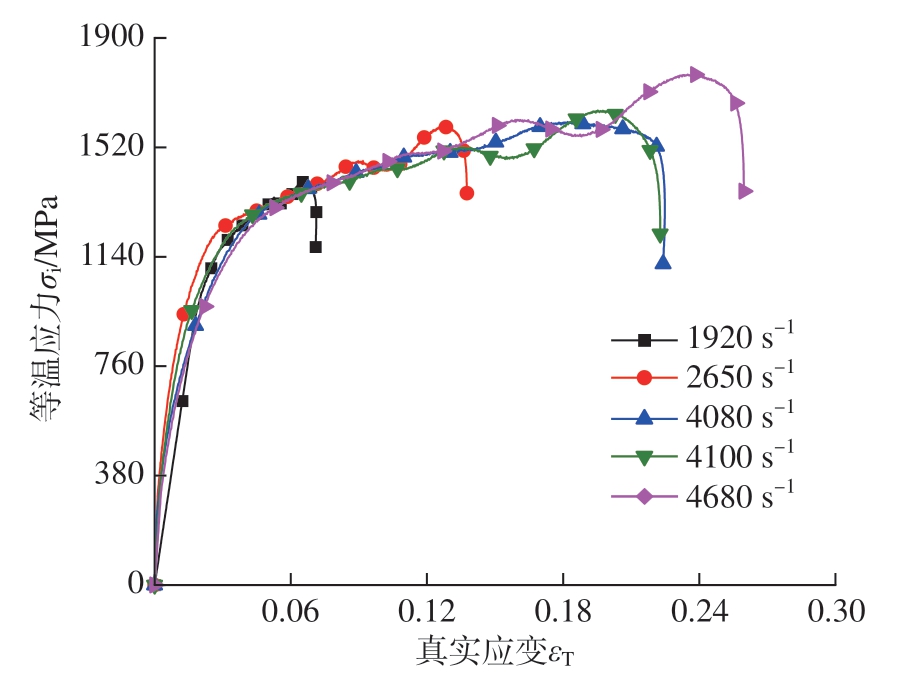
图9 不同应变速率下的等温应力–应变曲线
Fig.9 Isothermal stress-strain curves at different strain rates
3 Inconel 718本构模型拟合
3.1 基于P–L关系的Inconel 718本构方程拟合
P–L本构模型表达式为[25]
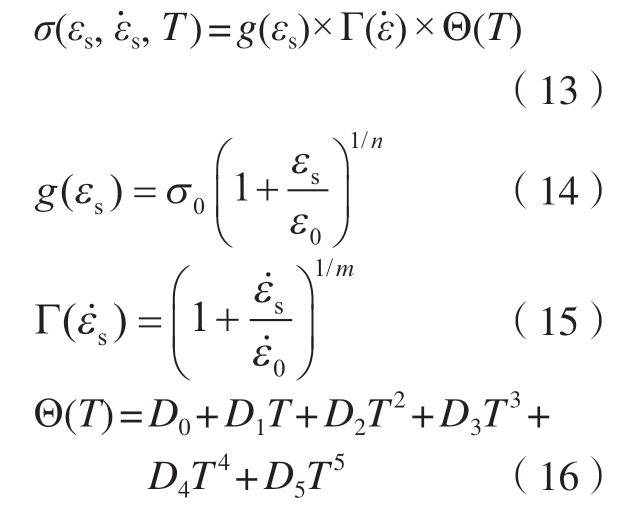
式中，n为材料的应变硬化指数；m为应变率强化指数；σ0是屈服应力；εs是塑性应变；ε0是参考应变；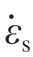
是塑性应变率；
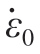是参考应变率；T为材料瞬时温度；D0，D1，…，D5为材料软化参数。
由式（13）可知，该本构模型由g（εs）、Γ（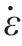
）、Θ（T） 3部分相乘所组成，这3部分分别体现了材料的应变硬化、应变率强化以及材料的温度软化特性，本构模型的拟合前提是假定材料的3个属性彼此独立。
具体拟合过程见附录，最后整合三项拟合可得到基于P–L关系的本构模型表达式为
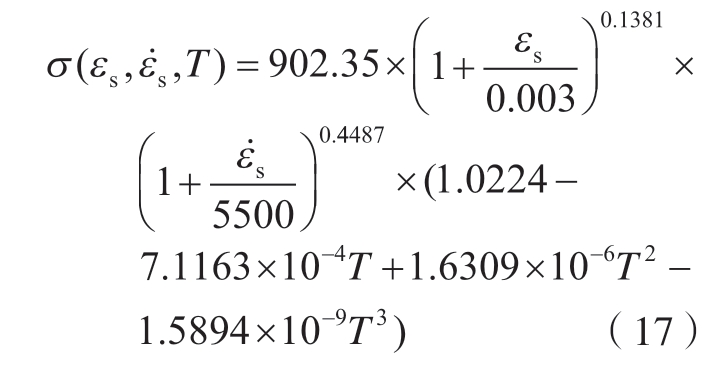
3.2 基于J–C关系的Inconel 718本构模型拟合
J – C本构模型表达式为[26]
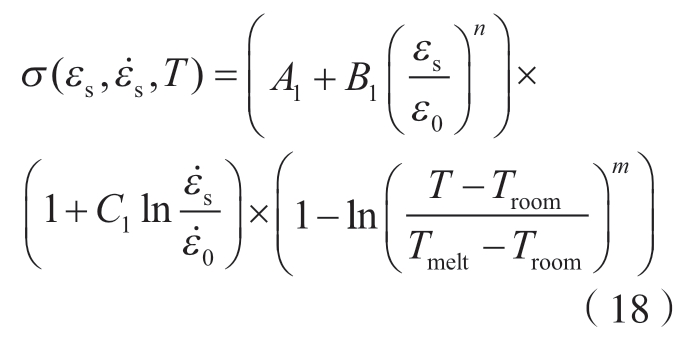
式中，A1是屈服应力；B1是应变硬化系数；C1是应变速率硬化系数；n是应变硬化指数；m是热软化指数；Troom是室温；Tmelt是材料的熔点。
具体拟合过程见附录，最后整合三项拟合可得到基于J – C关系的本构模型表达式为
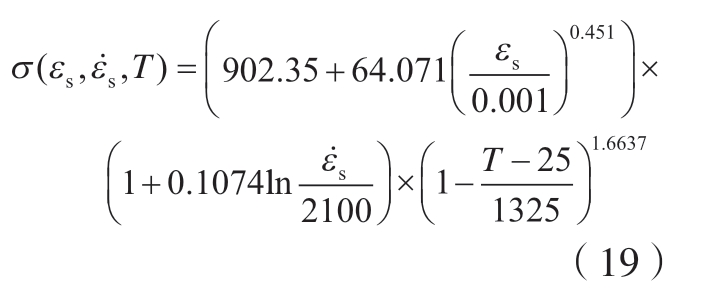
3.3 Inconel 718本构模型的拟合结果与试验结果的比较
为了验证拟合结果的可靠性，将获得的基于J – C和P – L本构模型的Inconel 718本构方程拟合结果与试验结果进行比较，图10为常温下不同应变率的拟合结果和试验结果对比图。
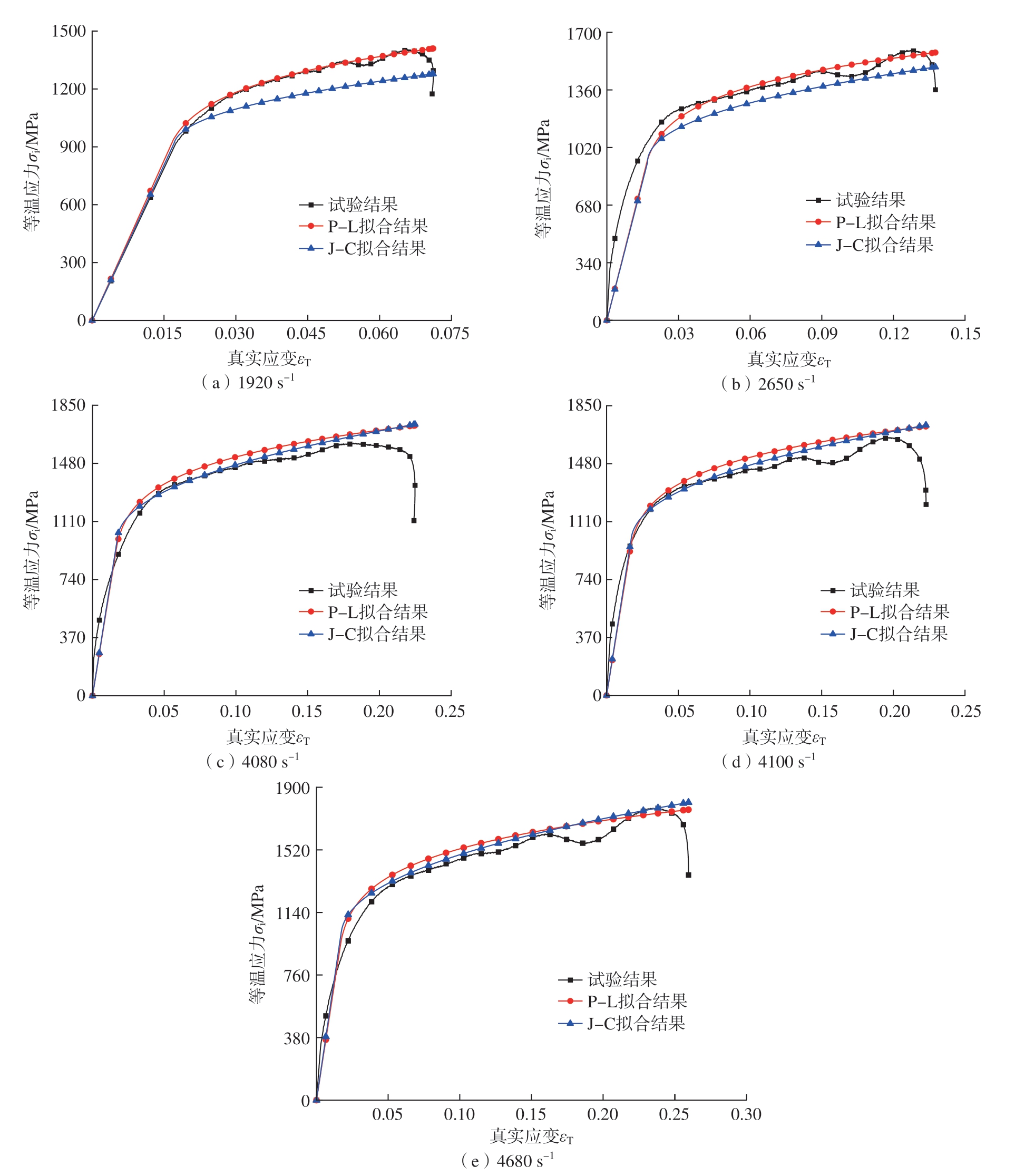
图10 室温下不同应变率的拟合结果和试验结果对比
Fig.10 Comparison of fitting results and experimental results for different strain rates at room temperature
3.4 P–L与J–C本构模型拟合精度对比
通过式（20）可对比分析不同应变率下试验数据和两种本构模型拟合数据的误差，结果如表3所示。
表3 室温下不同应变率下的Inconel 718本构模型的拟合精度误差
Table 3 Errors in fitting accuracy of the Inconel 718 intrinsic model at different strain rates at room temperature
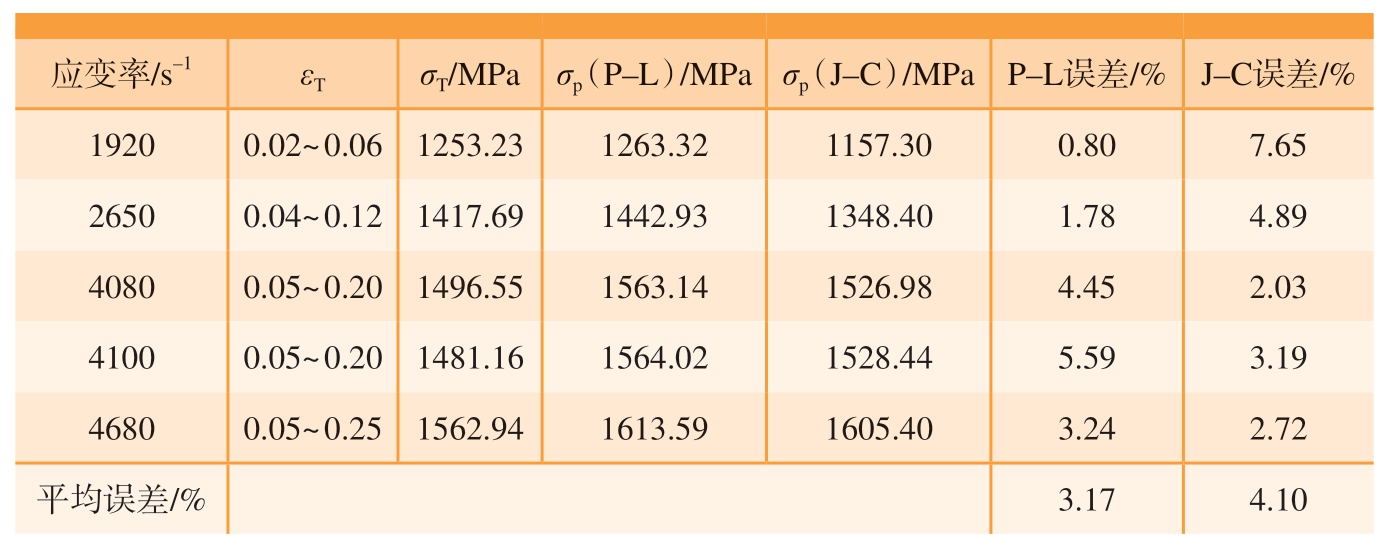
应变率/s–1εTσT/MPaσp（P–L）/MPaσp（J–C）/MPaP–L误差/%J–C误差/%19200.02～ 0.061253.231263.321157.300.807.65 26500.04～ 0.121417.691442.931348.401.784.89 40800.05～ 0.201496.551563.141526.984.452.03 41000.05～ 0.201481.161564.021528.445.593.19 46800.05～ 0.251562.941613.591605.403.242.72平均误差/%3.174.10
式中，σT是通过SHPB试验获得的真实应力；σp是本构模型预测的应力值。
从表3中可以看出，P – L和J – C本构模型的拟合精度都比较高，J – C本构模型最大误差为7.65%，平均误差为4.10%；而P – L本构模型的最大误差为5.59%，平均误差为3.17%。后面的分析选用平均误差较小的P – L模型作为数值仿真中输入的本构模型。
4 Inconel 718力学响应分析
4.1 切削仿真模型的建立
本研究针对直角切削进行有限元仿真，并利用简化模型进行二维车削建模，简化过程如图11所示。首先将切屑沿端面方向展开，得到图示的直角切削示意图，再简化即可得到二维直角切削模型。其中工件尺寸为5 mm×2 mm，刀具后角为10°，刃口钝圆半径为0.02 mm。
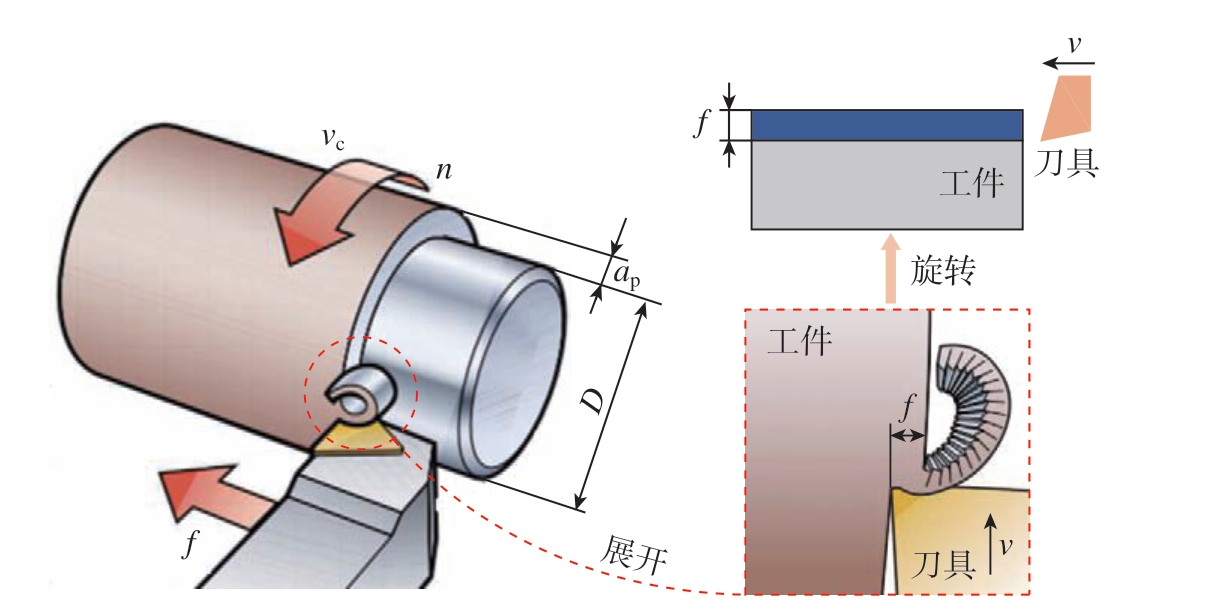
图11 刀具–工件模型示意图
Fig.11 Schematic diagram of tool – workpiece model
将上述试验获得的相关数据输入AdvantEdge切削仿真专用软件，对Inconel 718进行切削分析，探究切削速度、刀具前角以及初始温度对切削力和Mises应力等的影响。对于建模过程中的网格细化设置，在工件网格细化单元中，建议最大网格尺寸为0.025 mm，建议最小网格尺寸为0.005 mm，切削刃细化半径参数为0.1。
4.2 材料的力学响应分析
从式（13）中可以看出，影响应力的因素有应变、应变率和温度，针对这3个影响因素建立了3组不同的仿真参数，并通过单因素分析法对切削力及应力进行分析。首先是应变，在进给量一定的前提下，材料的应变主要受刀具结构的影响，其中影响最大的是刀具前角。因此通过改变前角的方式来探究应变对切削力和应力的影响，但改变前角，切削剪切区的平均温度也会改变，不能实现单因素研究材料力学响应的方法，所以需要不停调整同组另外两个的初始温度。当调至剪切区平均温度相同时，再进行单因素分析。对于应变率而言，在刀具结构一定的情况下，应变率主要受切削速度的影响，因此通过改变切削速度的方式来探究应变率对切削力和应力的影响，同样的，切削剪切区的平均温度会改变，所以需要调整同组另外两个的初始温度。对温度的探究则只需要改变初始温度即可，所设计的3组工艺参数如表4所示。
表4 不同组别的参数设计
Table 4 Parameter design of different groups
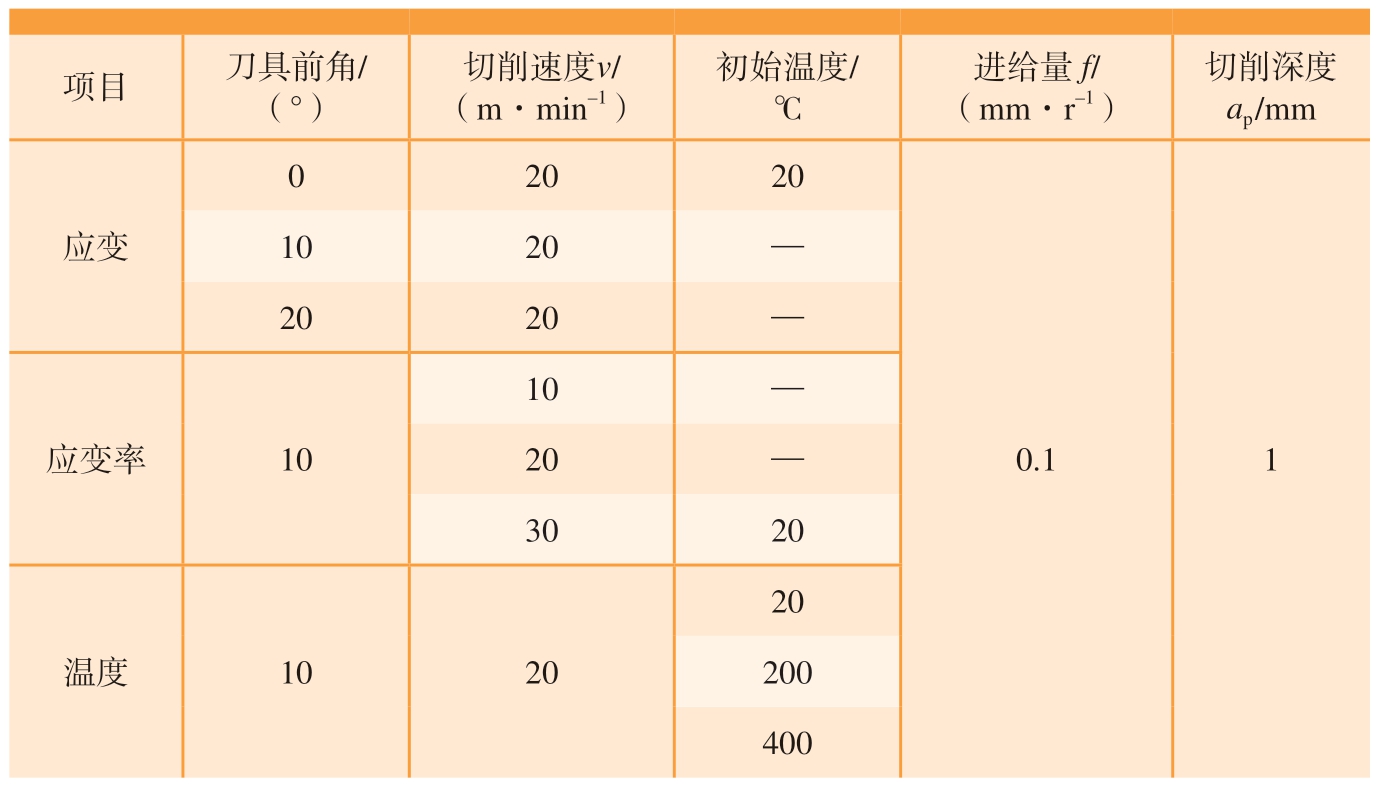
注：“—”指初始温度不确定，需要调整。
项目刀具前角/（°）切削速度v/（m·min–1）初始温度/℃进给量f/（mm·r–1）切削深度ap /mm 0 2020应变1020—2020—应变率10 0.11 10—20—3020温度1020 20 200 400
首先是对应变进行单因素分析，选择的方法是通过改变刀具前角的方式来改变切削过程中的应变。由于前角不一致，必然会导致切削变形区温度不一致，这就会影响单因素分析的准确性。因此，该仿真通过改变初始温度的方式使得在不同前角下的切削变形区温度基本相同，进而达到单因素探究材料的力学响应。由于变形区应变、应变率及温度分布不均匀，所以本研究采用在变形区等距提取应变、应变率及温度的方式获取变形区的平均数值。具体取值方式为：首先在取值线上等距取20个点，然后计算20个点上所得数据的平均值，所得平均值作为该物理量在变形区的平均数值（图12）。
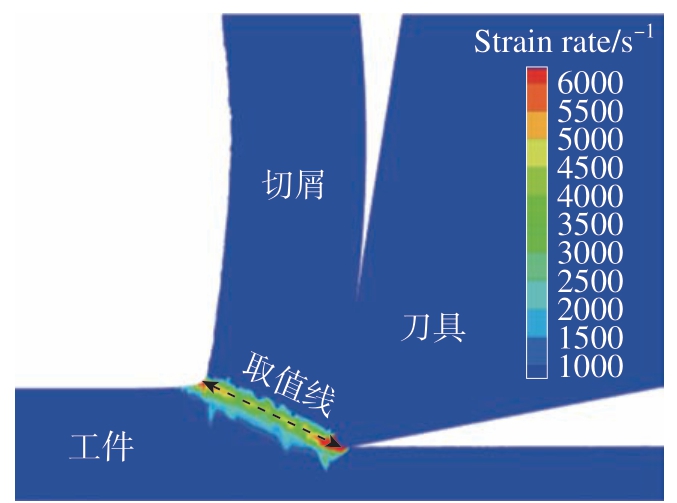
图12 取值示意图
Fig.12 Schematic diagram of value taking
图13显示了不同条件下的各物理量的云图。可以看出，随着前角的增大，剪切区的应变率及温度云图分布基本一致，对剪切区进行取值计算，结果如图14（a）所示，其中剪切区的平均应变率与平均温度变化不大，主要变化的是平均应变，前角越大，应变越小，图14（b）为应变云图。针对应变的变化，对力进行分析，从图14（c）可以看出随着前角的减小，应变增大，切削力与Mises应力也随之增大，图14（d）为Mises应力云图。
图13 不同条件下的各物理量的云图
Fig.13 Cloud of each physical quantity under different conditions
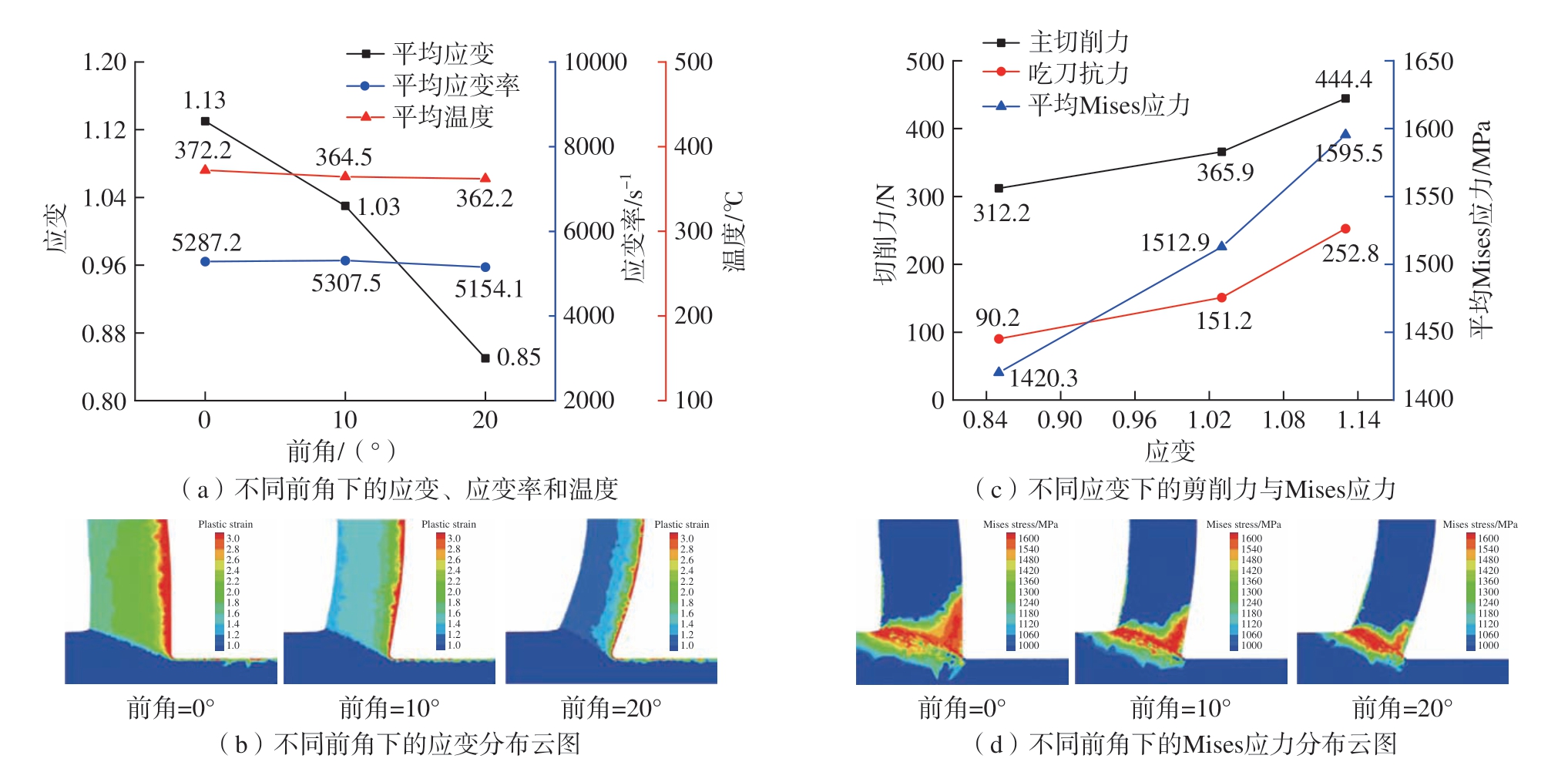
图14 不同前角下的云图及变化图
Fig.14 Cloud diagrams and variation diagrams at different relief angles
结合霍普金森压杆试验得到的真实应力–应变曲线进行分析，可以看出，随着应变的增大，真实应力也增大，与此结果一致。
再对应变率进行单因素分析，选择的方法是通过改变切削速度的方式来改变变形区的应变率。通过调节初始温度的方式，使剪切区平均温度基本相同。图13（b）显示了不同切削速度下的切屑变形区的应变及温度云图，可以看出，在不同切削速度下，剪切区的应变与温度云图分布基本一致。对剪切区平均计算，得到的平均应变、平均应变率和平均温度如图15（a）和（b）所示，其中平均应变与平均温度变化不大，平均应变率变化大，说明随着切削速度的增大，切削变形区的平均应变率逐渐增大。
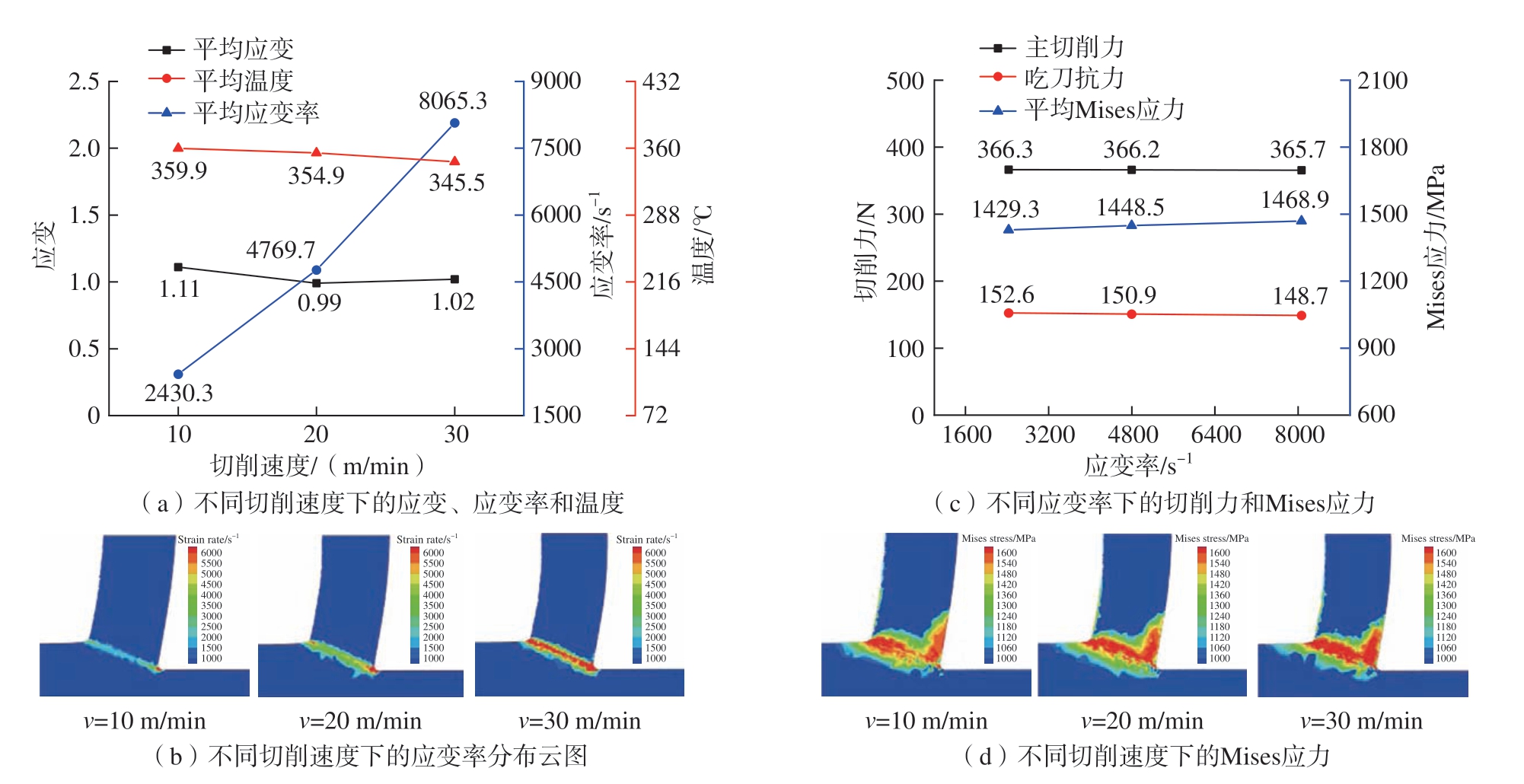
图15 不同切削速度下的云图及变化图
Fig.15 Cloud diagrams and variation diagrams at different cutting speeds
图15（c）显示了切削力和Mises应力的变化，可以看出随着切削速度的增加，Mises应力增大，但增加的不多，Mises应力云图如图15（d）所示。从图9中也可以看出随着应变率的增大，等温应力也增大，但增大的幅度比较小。Mises应力随应变率的变化与霍普金森压杆试验结果保持一致。由于Mises应力变化比较小，不足以使得切削力发生明显的变化，所以切削力基本保持不变。
最后对温度进行单因素分析，通过改变初始温度的形式进行探究，从图13（c）和（d）中可以看出，不同温度下切削变形区的应变及应变率云图分布基本一致。对剪切区进行数据采集，得到平均应变、平均应变率以及平均温度如图16（a）所示，其中应变和应变率变化不大，温度变化较大，温度云图如图16（b）所示。随着初始温度的变化，切削力与Mises应力的变化如图16（c）所示，可以看出随着初始温度的升高，切削力和Mises应力均减小，但随着温度升高幅度的增大，Mises应力减小的幅度也在增大，Mises应力云图如图16（d）所示。回溯到附录在图3高温硬度试验获得的结果，随着温度的上升，材料的热软化系数越小，真实应力减小，与Mises应力下降趋势保持一致。
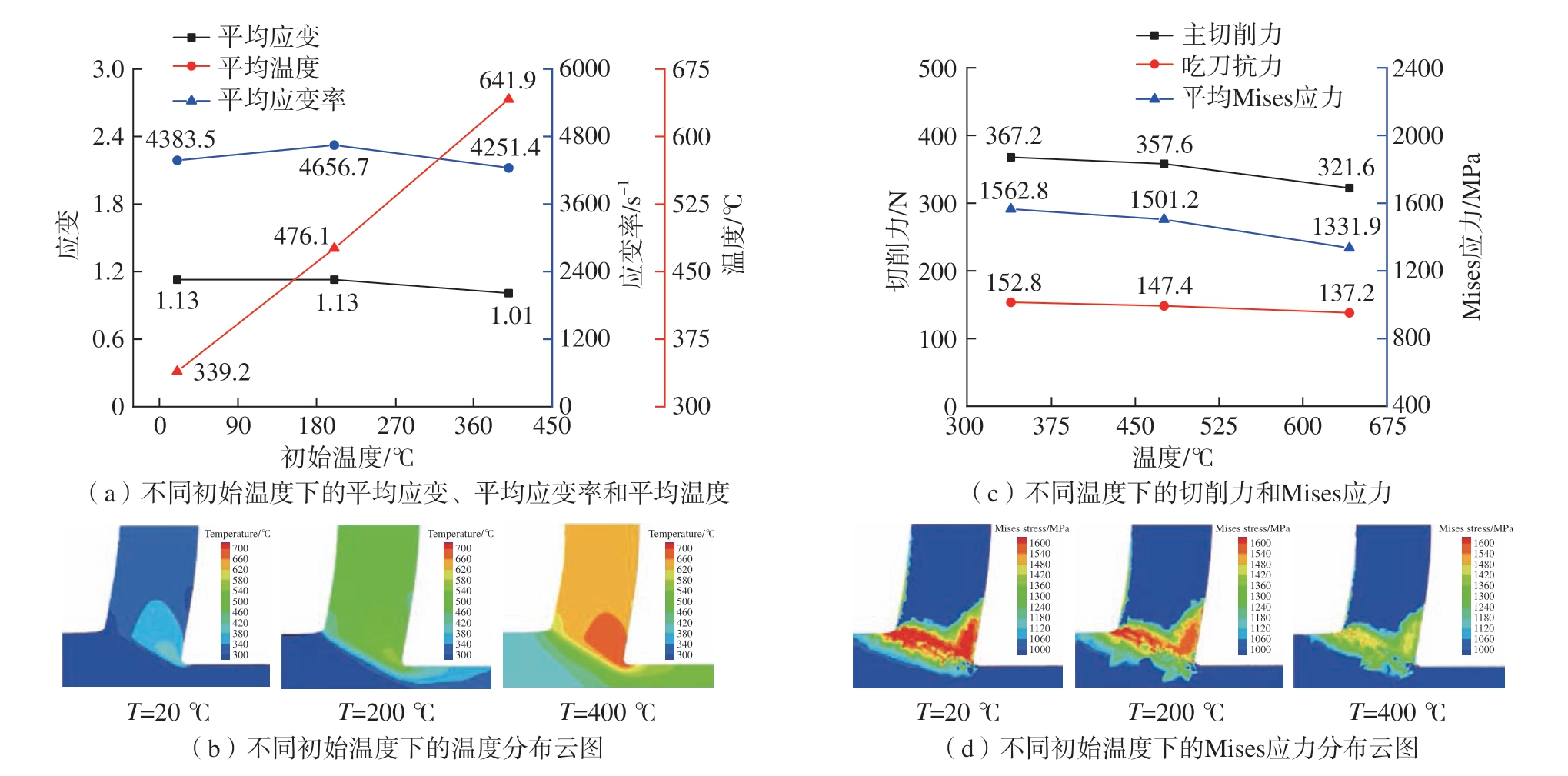
图16 不同温度下的云图与变化图
Fig.16 Cloud diagrams and variation diagrams at different temperatures
5 结论
经过一系列的试验，并对试验结果进行拟合得到Inconel 718的本构模型，再通过单因素分析法分析应变、应变率和温度对Inconel 718力学性能的影响，得到了以下结论。
（1）从真实应力–应变曲线可以看出，随着应变率的增大，流动应力缓慢增加，说明Inconel 718的应变率敏感性不强。
（2）从本构模型的拟合结果中可以发现，J – C和P – L本构模型的拟合效果都比较好。从拟合精度上看，在相对小应变率下P – L本构模型的拟合精度更高；在高应变率下，J – C本构模型拟合精度更高。从总的拟合精度来看，P – L本构模型的拟合精度略高于J – C本构模型。
（3）应变对材料变形应力（Mises应力）的影响最大，温度次之，而应变率对材料变形应力（Mises应力）的影响最小。
（4）从有限元结果分析上看，发现在加工Inconel 718过程中，刀具前角对切削力的影响最大，而切削速度和初始温度对切削力的影响较小。
[1] 屈华鹏, 王留兵, 王东辉, 等. 时效强化高镍合金Inconel-718的高温弹塑性特征及本构模型[J]. 金属热处理, 2021, 46(8): 1–7.
QU Huapeng, WANG Liubing, WANG Donghui, et al. High-temperature elastic-plastic characteristics and constitutive model of aging strengthened high-nickel alloy Inconel-718[J].Heat Treatment of Metals, 2021, 46(8): 1–7.
[2] CHOWDHURY T S, MOHSIN F T,TONNI M M, et al. A critical review on gas turbine cooling performance and failure analysis of turbine blades[J]. International Journal of Thermofluids,2023, 18: 100329.
[3] PATIL N G, ASEM A, PAWADE R S,et al. Comparative study of high speed machining of Inconel 718 in dry condition and by using compressed cold carbon dioxide gas as coolant[J].Procedia CIRP, 2014, 24: 86–91.
[4] ÖZEL T, ULUTAN D. Prediction of machining induced residual stresses in turning of titanium and nickel based alloys with experiments and finite element simulations[J]. CIRP Annals,2012, 61(1): 547–550.
[5] THAKUR A, GANGOPADHYAY S.State-of-the-art in surface integrity in machining of nickel-based super alloys[J]. International Journal of Machine Tools and Manufacture, 2016, 100:25–54.
[6] ASTAKHOV V P. Tribology of cutting tools[M]//DAVIM J. Tribology in manufacturing technology. Berlin: Springer, 2012: 1–66.
[7] 王亮, 梁泽芬, 郭文静. GH4169高温镍基合金微织构刀具切削力优化设计及预测[J]. 机械设计与制造工程, 2023, 52(5): 7–12.
WANG Liang, LIANG Zefen, GUO Wenjing. The cutting force optimization design and prediction for GH4169 nickel-base superalloys micro-texture tool[J]. Machine Design and Manufacturing Engineering, 2023, 52(5): 7–12.
[8] 吴敏, 杨东, 陈建彬, 等. 铝合金直角切削仿真的本构响应行为研究[J]. 制造业自动化, 2022, 44(2): 42–45.
WU Min, YANG Dong, CHEN Jianbin, et al. Study on the constitutive response behavior of aluminum alloy during orthogonal cutting simulation process[J]. Manufacturing Automation,2022, 44(2): 42–45.
[9] SUN Y, LI G H, HE Z, et al. The advance of research on constitutive model used in finite element simulation of metal cutting[J].Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2022, 236(9): 4921–4945.
[10] LAAKSO S V A. Heat matters when matter heats—The effect of temperature-dependent material properties on metal cutting simulations[J].Journal of Manufacturing Processes, 2017, 27:261–275.
[11] MENEZES P L, AVDEEV I V,LOVELL M R, et al. An explicit finite element model to study the influence of rake angle and friction during orthogonal metal cutting[J]. The International Journal of Advanced Manufacturing Technology, 2014, 73(5): 875–885.
[12] ZHANG K, WANG M C, LIU W J, et al. Fracture prediction for an advanced high-strength steel sheet using the fully coupled elastoplastic damage model with stress-state dependence[J]. Acta Mechanica Solida Sinica,2021, 34(2): 263–273.
[13] 彭鸿博, 张宏建. 金属材料本构模型的研究进展[J]. 机械工程材料, 2012, 36(3):5–10, 75.
PENG Hongbo, ZHANG Hongjian. Research development of the constitutive models of metal materials[J]. Materials for Mechanical Engineering, 2012, 36(3): 5–10, 75.
[14] 赵娜, 刘二亮, 张慧萍, 等. 金属切削变形常用本构模型研究进展[J]. 工具技术,2016, 50(1): 3–8.
ZHAO Na, LIU Erliang, ZHANG Huiping,et al. Recent advances of constitutive model used in metal cutting[J]. Tool Engineering, 2016, 50(1):3–8.
[15] YILMAZ O D, NADIMI BAVIL OLIAEI S. Effect of constitutive material model on the finite element simulation of shear localization onset[J]. Simulation Modelling Practice and Theory, 2020, 104: 102105.
[16] GURUSAMY M, SRIRAM S.Investigations on the choice of Johnson–Cook constitutive model parameters for the orthogonal cutting simulation of Inconel 718[J]. Journal of Advanced Manufacturing Systems, 2023, 22(1):1–25.
[17] 郭必成, 王福增, 黄辉, 等. 金属切削仿真的驱动模型及其耦合机制研究[J]. 计算机集成制造系统, 2023(12): 1–18.
GUO Bicheng, WANG Fuzeng, HUANG Hui, et al. Study on driving model and its coupling mechanism for metal cutting simulation[J].Computer Integrated Manufacturing Systems,2023(12): 1–18.
[18] YUAN K B, GUO W G, LI P H, et al. Thermomechanical behavior of laser metal deposited Inconel 718 superalloy over a wide range of temperature and strain rate: Testing and constitutive modeling[J]. Mechanics of Materials,2019, 135: 13–25.
[19] FORNI D, MAZZUCATO F,VALENTE A, et al. High strain-rate behaviour of as-cast and as-build Inconel 718 alloys at elevated temperatures[J]. Mechanics of Materials, 2021,159: 103859.
[20] XIE G L, YU X T, GAO Z F, et al. The modified Johnson-Cook strain-stress constitutive model according to the deformation behaviors of a Ni–W–Co–C alloy[J]. Journal of Materials Research and Technology, 2022, 20: 1020–1027.
[21] WANG X Y, HUANG C Z, ZOU B,et al. Dynamic behavior and a modified Johnson-Cook constitutive model of Inconel 718 at high strain rate and elevated temperature[J]. Materials Science and Engineering: A, 2013, 580: 385–390.
[22] ZHANG T, JIANG F, YAN L, et al.FEM modeling of the relationship between the high-temperature hardness and high-temperature,quasi-static compression experiment[J]. Materials,2017, 11(1): 34.
[23] OSOVSKI S. The dependence of the Taylor-Quinney coefficient on the dynamic loading mode[J]. Journal of the Mechanics and Physics of Solids, 2017, 107: 96–114.
[24] ZHU S S, LIU J, DENG X.Modification of strain rate strengthening coefficient for Johnson-Cook constitutive model of Ti6Al4V alloy[J]. Materials Today Communications, 2021,26: 102016.
[25] 艾建光, 姜峰, 言兰. TC4-DT钛合金材料动态力学性能及其本构模型[J]. 中国机械工程, 2017, 28(5): 607–616.
AI Jianguang, JIANG Feng, YAN Lan.Dynamic mechanics behavior and constitutive model of TC4 DT titanium alloy materials[J].China Mechanical Engineering, 2017, 28(5):607–616.
[26] 张继林, 罗文翠, 贾海深, 等. 高应变率下06Cr19Ni10奥氏体不锈钢Johnson-Cook本构模型研究[J]. 钢铁钒钛, 2022, 43(4):158–166.
ZHANG Jilin, LUO Wencui, JIA Haishen, et al. Research on Johnson-Cook constitutive model of 06Cr19Ni10 austenitic stainless steel at high strain rate[J]. Iron Steel Vanadium Titanium, 2022,43(4): 158–166.
附录
1.基于P–L关系的Inconel 718本构模型的具体拟合过程
P–L本构模型表达式为
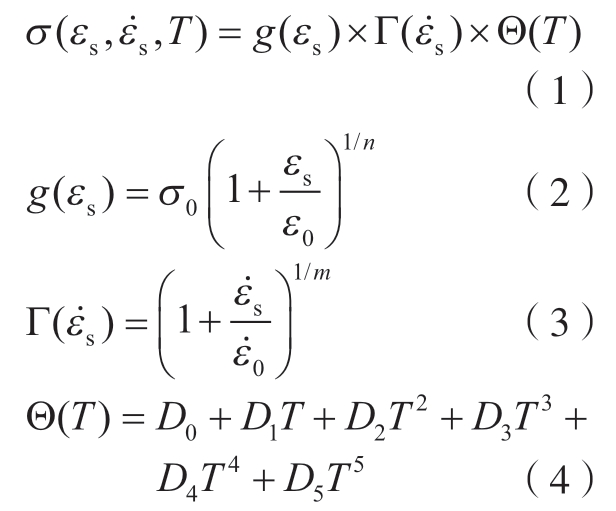
为了拟合应变硬化项g（εs），假设应变率硬化项和温度软化项均为1，可将式（1）简化为式（5）。
如正文图9所示，确定 Inconel 718在最低应变率（1920 s–1）下的屈服应力σ0为902.35 MPa，对应的真实应变为0.0169。εs是材料的真实应变减去屈服点对应的真实应变。对式（5）两边取对数并简化为
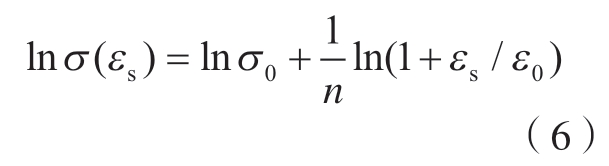
取参考应变ε0为0.003，将常温下1920 s–1的应力–应变曲线上的塑性段区间，即应变为0.018～0.032区间的等温应力–应变值代入式（6）。然后通过最小二乘法线性拟合得到图1所示的拟合曲线，直线斜率（1/n）为0.1381，反求得材料应变硬化指数n为7.24。
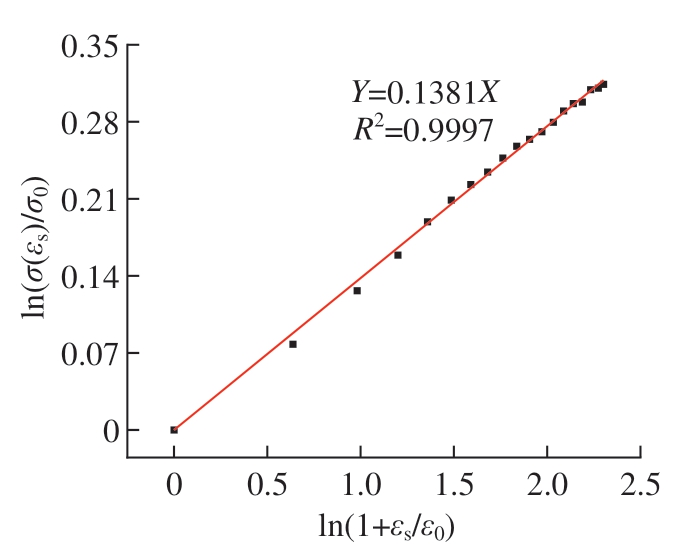
图1 P–L本构模型第一项拟合曲线
Fig.1 First fitting curve of P-L constitutive model
再对应变率强化项进行拟合，假设温度软化项为1，可将式（1）简化为
式中，σ（εs，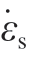
）是真实应变在0.032～0.066时的平均流动应力；g（εs）是应变率为 1920 s–1 时的平均流动应力，经计算g（εs）为 1269.2 MPa。对式（7）两边取对数可简化为
取参考应变率
为5500 s–1，再将图8所示的应变区间为0.032～0.066之间的不同应变率下对应的流动应力的平均值代入式（8）中，然后通过最小二乘法线性拟合得到图2所示拟合曲线，直线斜率（1/m）为0.4487，反求得到应变率强化指数m为2.2286。
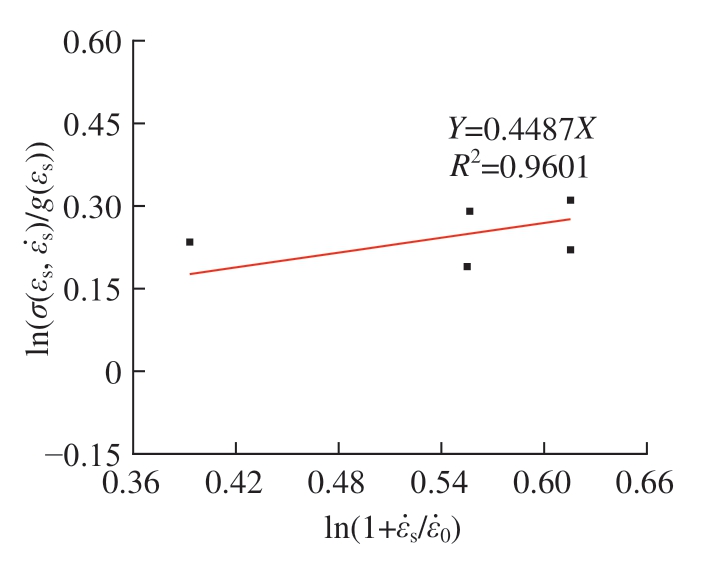
图2 P–L本构模型第二项拟合曲线
Fig.2 Second fitting curve of P-L constitutive model
最后确定材料的温度软化参数D0～D5，利用高温硬度试验可以得到材料在不同温度下的硬度值，再通过式（9）可将硬度转化为软化系数。
式中，α为材料软化系数；HT为测试温度下的硬度值；H20为常温下的硬度值。
图3为材料在不同温度下的热软化系数及拟合曲线图，可以得到Inconel 718在25～1000 ℃温度范围内热软化系数与温度关系的数学表达式
图3 Inconel 718在不同温度下的软化系数
Fig.3 Softening coefficient of Inconel 718 at different temperatures
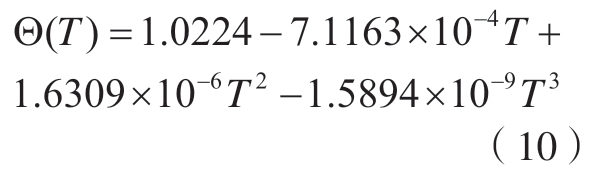
整合三项拟合可得到基于P–L关系的本构模型表达式为
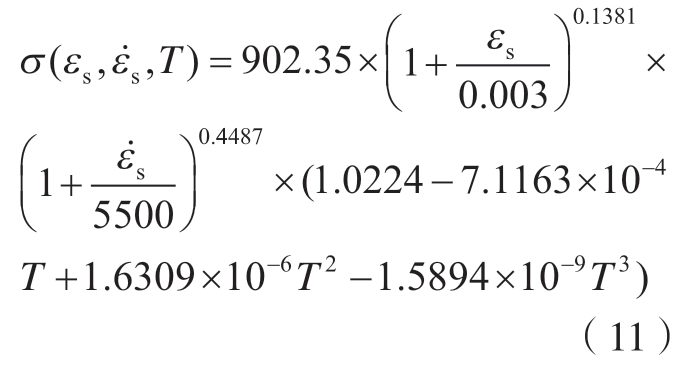
2.基于J–C关系的Inconel 718本构模型的具体拟合过程
J–C本构模型表达式为
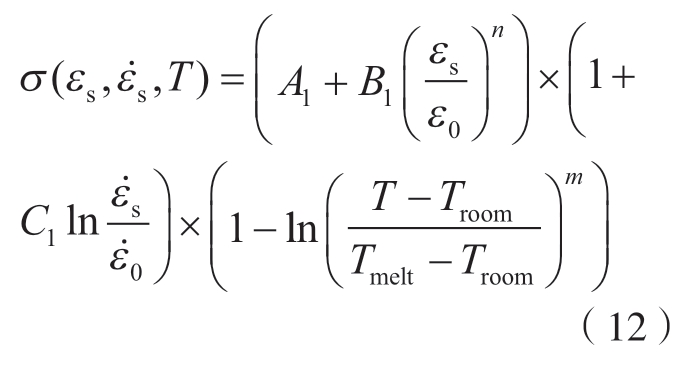
首先拟合应变硬化项，同样假设应变率硬化项和温度软化项均为 1，可将式（12）简化为式（13）。
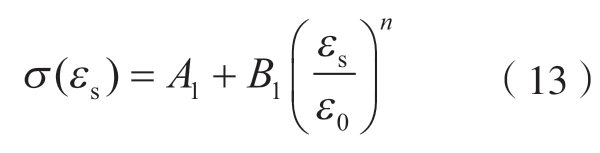
如正文图9所示，确定 Inconel 718在最低应变率（1920 s–1）下的屈服应力A1为902.35 MPa，对应的真实应变为0.0169。εs是材料的真实应变减去屈服点对应的真实应变。对式（13）两边取对数并简化为
取参考应变ε0为0.001，将常温下塑性阶段下的等温应力和真实应变值代入式（14），可拟合得到图4所示的拟合曲线。曲线的斜率n为0.451，截距lnB1为4.16，反求得应变硬化系数B1为64.071。
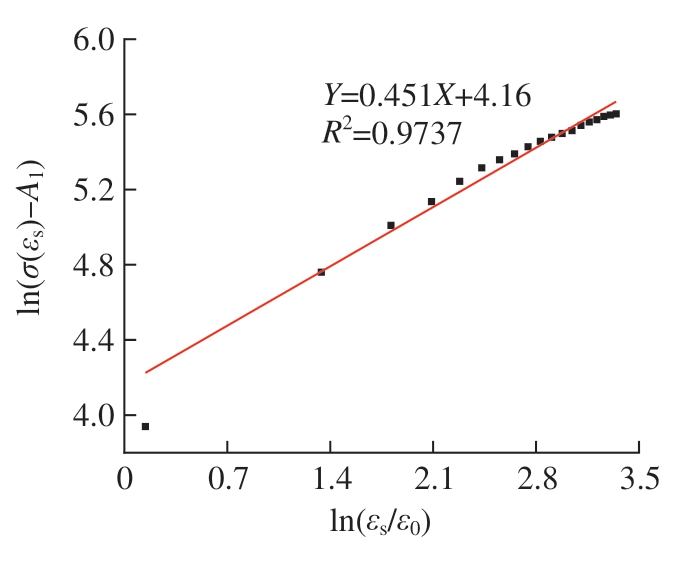
图4 J–C本构模型第一项拟合曲线
Fig.4 First fitting curve of the J-C constitutive model
接着确定J–C本构模型的第二项参数，假设材料的热软化项为1，可将式（12）简化为
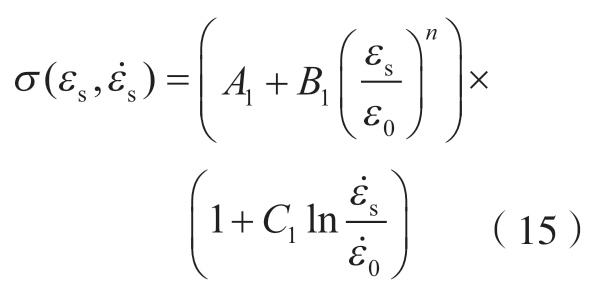
将公式（15）转化为
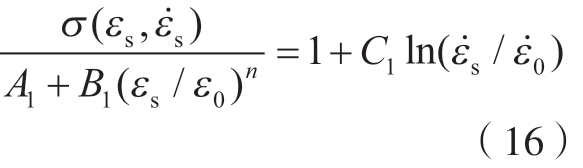
把不同应变率下应变区间在0.032～0.066之间的流动应力平均值代入式（16），设置参考应变率
为2100 s–1，拟合得到图5所示的拟合曲线。可得应变速率硬化系数C1= 0.1074。
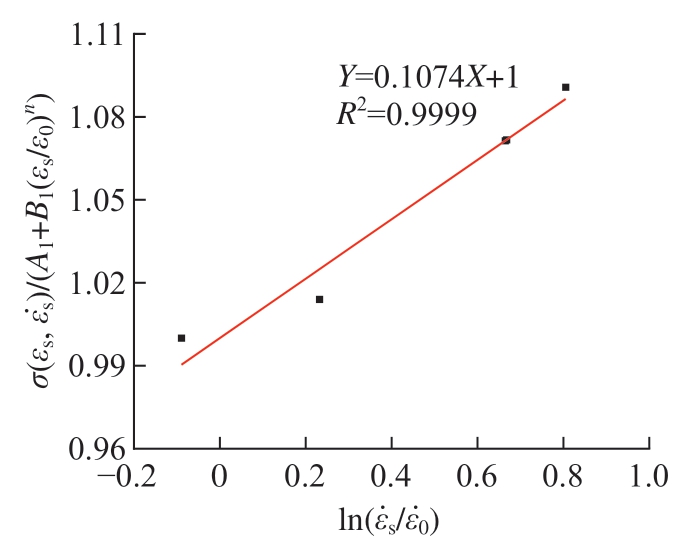
图5 J–C本构模型第二项拟合曲线
Fig.5 Second fitting curve of the J-C constitutive model
最后拟合温度软化项，公式（12）可转化为
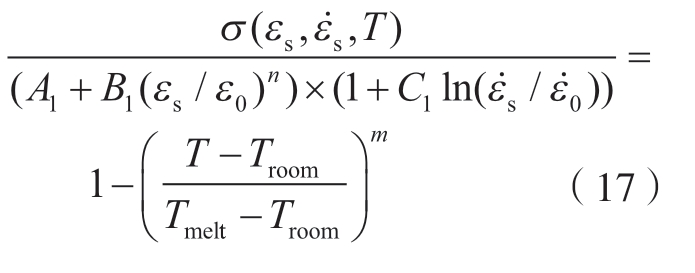
将公式（17）两边取对数得：
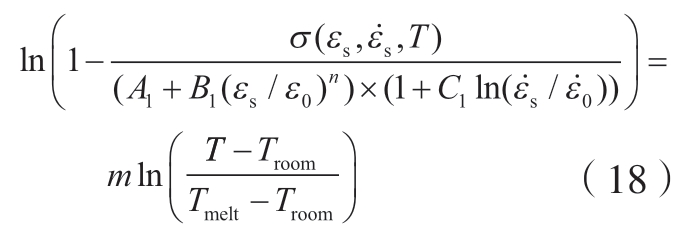
Inconel 718的熔化温度Tmelt为1350 ℃，通过线性拟合可得到图6所示拟合曲线，可得热软化指数m =1.6637。
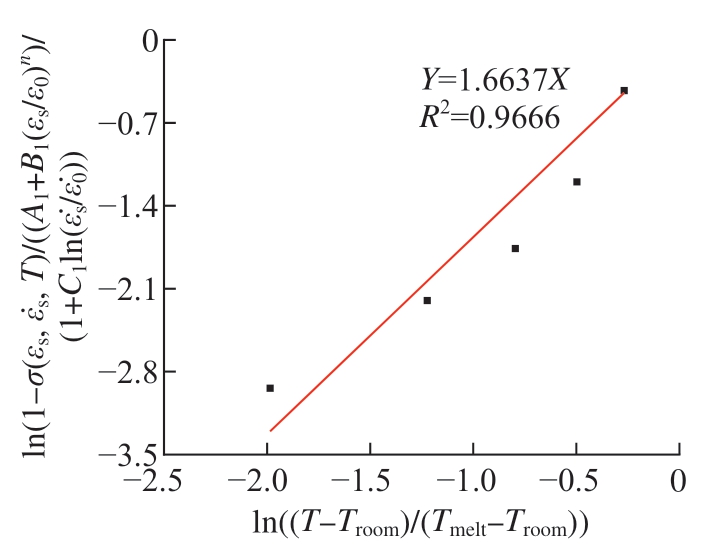
图6 J–C本构模型第三项拟合曲线
Fig.6 Third fitting curve of the J-C constitutive model
根据上述步骤计算出材料各项参数后，得到基于J–C关系的本构模型表达式
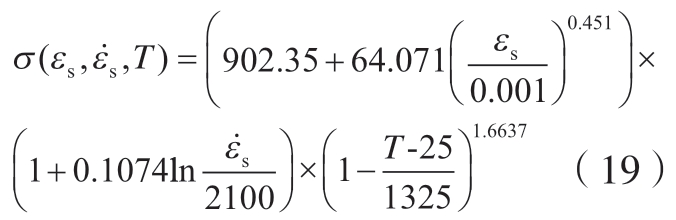
J–C本构模型的拟合过程是对应变硬化项、应变率强化项以及温度软化项三项分别拟合的过程。
首先对材料的等温应力–应变曲线进行拟合，先选择一个最低应变率下的等温应力–应变曲线并对其进行拟合，可得到J–C模型中应变硬化项的各参数。
然后再选取不同应变率下的同一塑性阶段，并求这一阶段的平均流动应力，再进行相应的拟合，即可得到J–C本构模型中应变率强化项的各参数。
最后对高温硬度试验获得的不同温度下的热软化系数进行拟合，得到J–C本构模型中温度软化项的各参数。
