机械系统中较为重要的连接表面大都采用磨削的加工方式进行加工[1]，磨削粗糙表面的摩擦特性直接影响整个系统的稳定性和可靠性，因此研究和预测机械系统的摩擦特性具有重要的意义。
目前粗糙表面静摩擦系数理论建模主要采用统计模型、分形模型和有限元模型。Chang等[2]考虑了表面黏着力的影响，结合Greenwood和Williamson统计学模型[3]（简称GW模型）建立金属粗糙表面间的静摩擦系数模型，研究表明随着法向载荷的增大，静摩擦系数减小。但由于GW模型中统计学参数受限于测量仪器的分辨率和取样长度，对确定粗糙表面的表征和分析不具有唯一性[4]。针对统计学方法的不足，盛选禹等[5]在Majumdar等[6]的分形接触模型（简称MB分形接触模型）的基础上，建立了粗糙表面静摩擦系数的分形模型，研究表明，随着法向载荷的增加，表面静摩擦系数增大，与统计学模型的结论刚好相反。兰国生等[7]根据Yan等[8]三维分形接触模型（简称YK分型接触模型）建立了表面静摩擦系数的改进模型，但该模型未考虑微凸体弹塑性变形的影响。Pan等[9]基于YK分形接触模型[8]和KE弹塑性有限元模型（Kogut和Etsion弹塑性有限元模型）[10]建立了考虑弹塑性变形的粗糙表面静摩擦系数分形模型，但未考虑区域扩展系数的影响。Wu等[11]基于MB分形接触模型[6]和指数弹塑性模型[12]建立了粗糙表面静摩擦系数模型，但该模型中临界接触面积没有考虑动摩擦系数的影响。张学良等[13]基于尺度相关接触模型[14-15]建立了尺度关联的三维静摩擦系数模型。以上静摩擦系数模型研究了分形参数D、G以及材料参数f对静摩擦系数的影响规律，但都没有考虑粗糙表面微凸体之间的相互影响。
基于此，本文综合考虑微凸体间相互作用、微凸体弹性、弹塑性和塑性3种变形机制以及区域扩展系数，建立磨削粗糙表面静摩擦系数的三维分形模型，并通过数值仿真探讨各相关参数对表面静摩擦系数的影响。
1 磨削表面几何模型的建立
1.1 磨削表面几何形貌表征
工件表面质量直接决定了机械系统的性能和使用寿命，对于精密零件，目前大都采用磨削的加工方式进行加工。图1为OLS5000-SAF激光共聚焦显微镜对粗糙度Sa0.046 μm磨削表面的采集结果。采样面积为257 μm×257 μm，采样点数共有1024×1024。
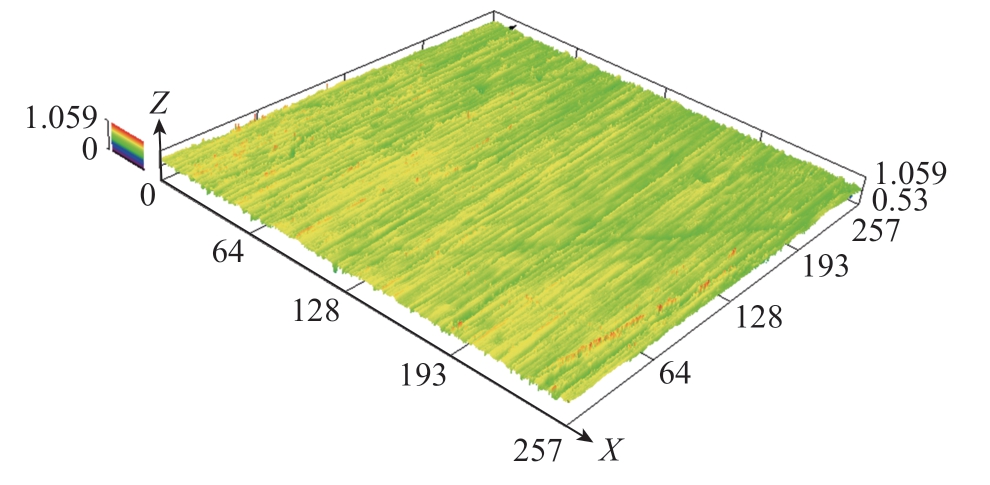
图1 磨削表面形貌（μm）
Fig.1 Grinding surface morphology (μm)
磨削粗糙表面具有自放射和自相似等分形特性[16]，从而可以用分形函数来表征磨削粗糙表面。Yan等[8]用修正后的双变量的Weierstrass-Mandelbrot（W-M）函数来表征磨削表面，表达式为[8]
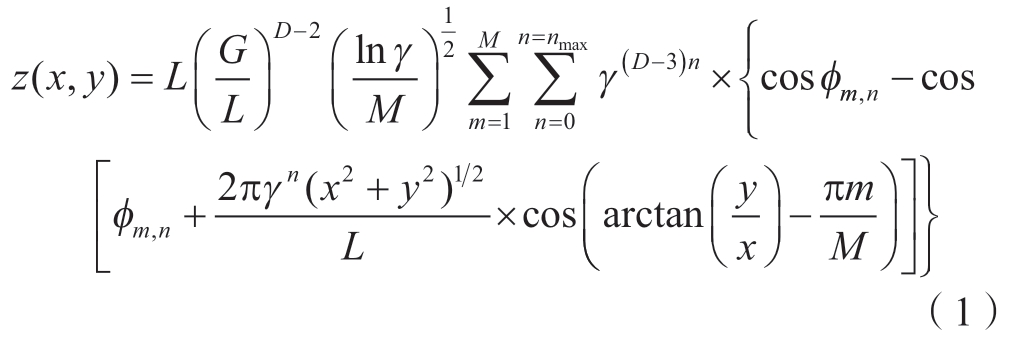
式中，z（x，y）为磨削表面轮廓高度； （x，y）为轮廓高度对应的几何位置；L为表面轮廓的取样长度；D为磨削表面的分形维数（2＜D＜3）；G为高度尺度参数；γ为空间频率的参数，一般取1.5；M为表面隆起的总数；m为表面隆起数；n为频率指数；nmax为最低截止长度Ls对应n的最大值，nmax= int[ln（L/Ls）/lnγ]；fm，n为随机相位，取值为 （0，2π）。
当M=1，则m=1，此时双变量的W-M函数退化成单变量的W-M函数，其表达式为
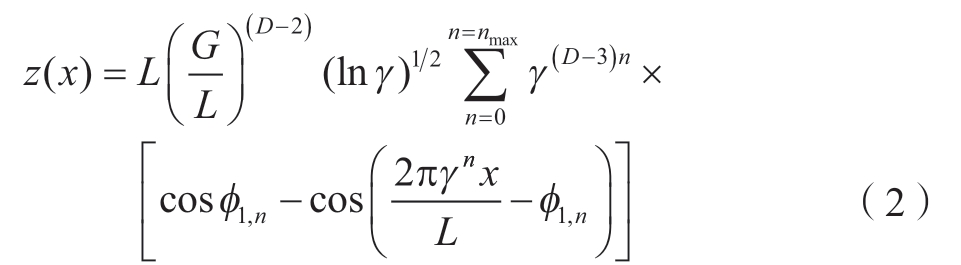
1.2 单个微凸体的几何描述
平面内两微凸体相互接触可以简化为等效的单个微凸体和刚性光滑平面的接触，简化后的接触示意图见图2，其中R为微凸体的峰顶曲率半径；ω为微凸体的变形量；r为微凸体的接触半径，对应面积为接触面积a；r'为微凸体的截断接触半径，对应的面积为截断接触面积a'。
图2 微凸体与刚性平面间的接触示意图
Fig.2 Schematic of microcontact between asperity and rigid flat
由式 （2）可知，对于任意频率指数的微凸体，可得其轮廓表达式为
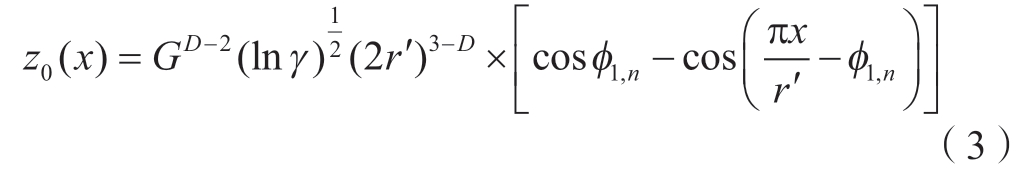
由式 （3）可知，单个微凸体的变形量ω为
式中，a' = πr' 2。
对图2中的直角三角形Δobc利用勾股定理可得
由于R ＞＞ ω，由式 （5）可得微凸体的峰顶曲率半径R近似为
2 单个微凸体的接触特性
2.1 单个微凸体的法向接触载荷
2.1.1 弹性变形阶段
Wang等[17]基于Hertz接触理论和铁木辛柯弹性理论建立了考虑微凸体相互影响的分形接触模型，并推导出单个微凸体的弹性接触载荷Fe为
式中，a为微凸体的接触面积；等效弹性模量E= [（1-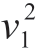
）/E1+（1-
）/E2]-1，其中，E1、E2和v1、v2分别为两相互接触表面的弹性模量和泊松比。
由YK模型可知，微凸体发生弹性变形时，微凸体的截断接触面积a'和接触面积a的关系为
将式 （6）、 （7）和 （8）联立可得，微凸体弹性接触载荷Fe、接触压力Pe与截断接触面积a'的关系为
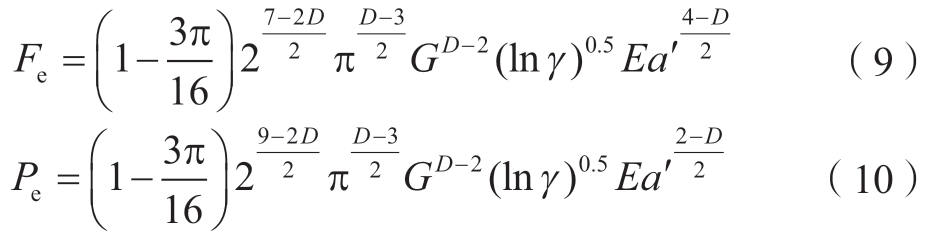
由接触力学可知，考虑摩擦时，微凸体开始发生屈服时的临界平均接触压力Pc为
式中，σy是较软材料的屈服强度；Kf为摩擦力修正因子，与动摩擦系数f有关，其关系式为
联立式 （10）和 （11）可得，临界弹性截断接触面积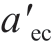
和临界弹性变形量ωec分别为
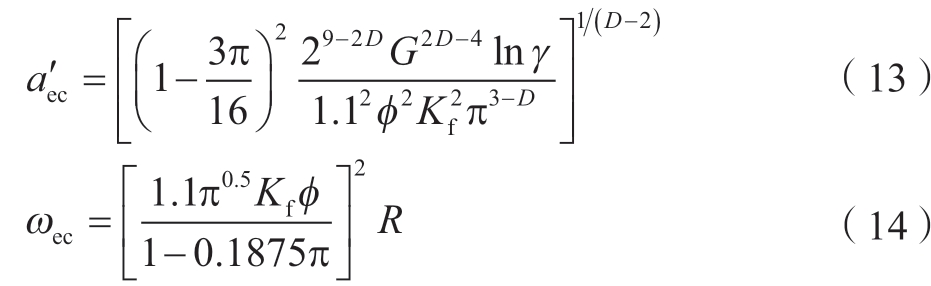
式中，f = σy / E，为材料参数。
联立式 （4）、（13）和 （14）可得，微凸体的变形量与临界弹性变形量的关系为
2.1.2 弹塑性变形阶段
Kogut等[10]利用ANSYS研究了单个球形微凸体的弹塑性接触特性，并将弹塑性分为两个阶段：第一弹塑性变形阶段和第二弹塑性变形阶段，并给出弹性接触面积aep和弹性接触载荷Fep与变形量的关系为
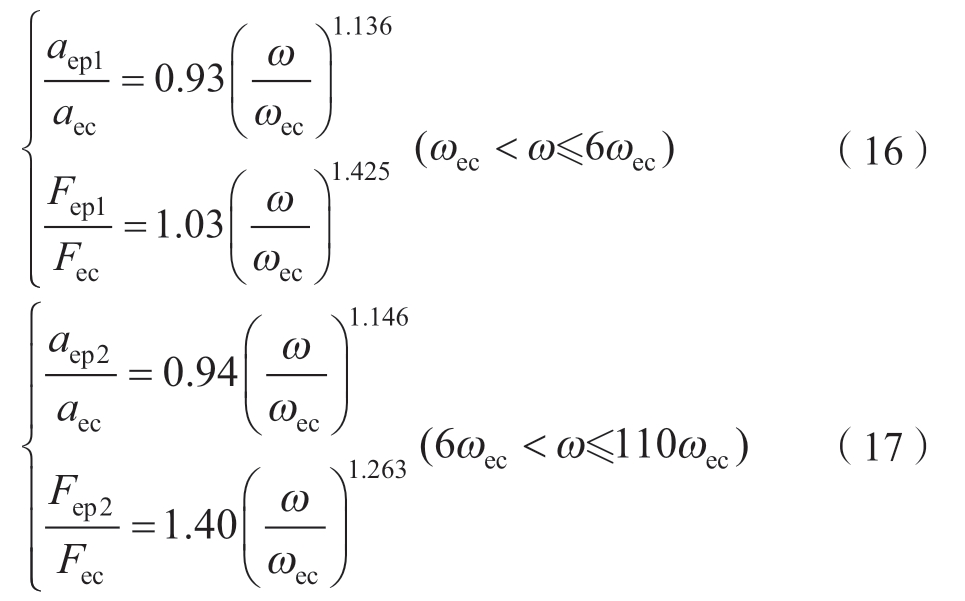
式中，aep1、aep2、Fep1、Fep2分别为第一弹塑性和第二弹塑性的接触面积和接触载荷；aec、Fec分别为临界弹性接触面积和接触载荷。
将式 （4）、（6）、（7）、（8）和 （14）分别代入式 （16）和 （17）中可得弹塑性变形阶段接触面积和接触载荷与截断接触面积的关系为
式中，b = 1.1Kf fE。
由式 （15）可得，临界弹塑性截断接触面积为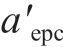
=61/(2-D)
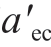和临界塑性截断接触面积为
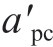=1101/(2-D)
。
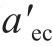2.1.3 完全塑性变形阶段
当a' ＜ a'pc时，微凸体发生完全塑性变形，此时微凸体的塑性接触面积ap、塑性接触载荷Fp与截断面积a'之间的关系为
式中，λ为材料系数，与材料的硬度H和屈服强度σy的关系为λ = H/σy。
2.2 单个微凸体的切向接触载荷
根据哈密顿原理和Tresca屈服条件可知，单个微凸体承受的切向载荷[11]为
式中，F为单个微凸所承受的法向接触载荷。
由式 （8）、（9）、（18）、（19）和（22）可得，单个微凸体发生弹性、弹塑性变形时，所能承受的最大切向接触载荷分别为
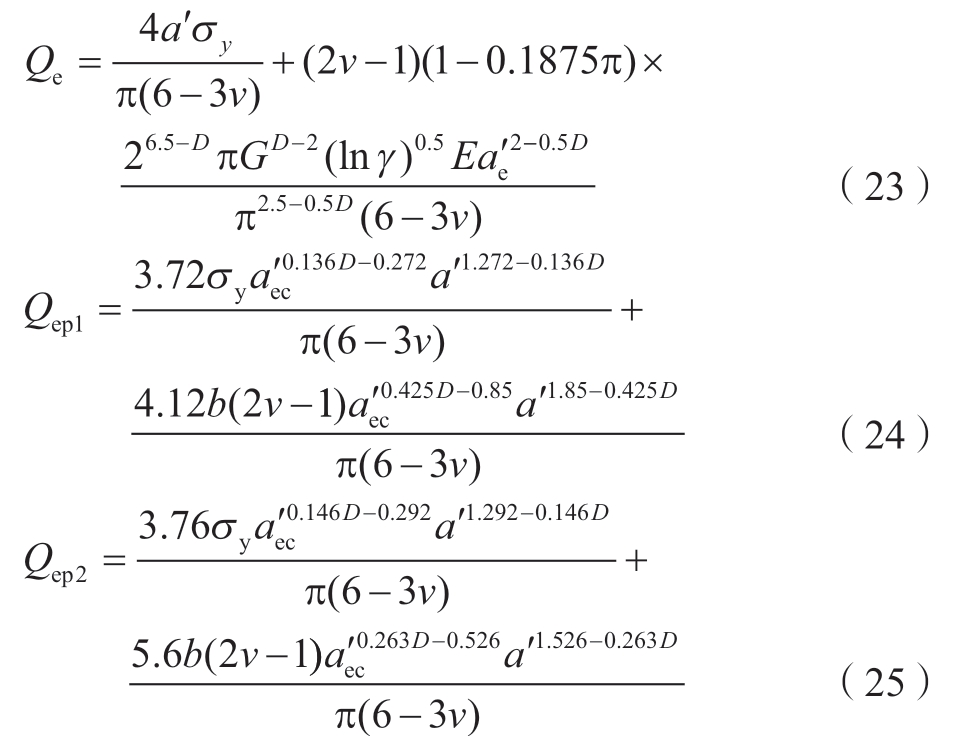
式中，Qe、Qep1、Qep2分别为单个微凸体的弹性切向载荷、第一弹塑性切向载荷和第二弹塑性切向载荷。
3 磨削表面微观接触模型
由第2节可知，根据单个微凸体在不同变形阶段的临界截断接触面积，可将微凸体的变形划分为3个阶段，即弹性变形阶段、弹塑性变形阶段 （第一弹塑性变形阶段和第二弹塑性变形阶段）和完全塑性变形阶段，并且根据单个微凸体的几何参数，得到各变形阶段内微凸体的接触力学表达式。基于分形几何理论，对接触区所有的微凸体进行积分，就可以得到整个磨削粗糙表面的接触特性 （以下都假设接触表面中最大微凸体截断接触面积a'l大于临界弹性截断接触面积a'ec）。
3.1 微凸体的截断接触面积分布密度函数
由YK模型[8]可知，三维分形表面中微凸体的截断接触面积分布函数为
式中，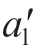
为接触表面中最大微凸体的截断接触面积；φ为分形区域扩展系数，与分形维数之间的关系为φ（3-D）/2-
3.2 真实接触面积
磨削粗糙表面的真实接触面积是所有微凸体在不同变形阶段内的接触面积的总和，其表达式为
式中，Are、Arep1、Arep2、Arp分别表示磨削粗糙表面的弹性接触面积、第一弹塑性接触面积、第二弹塑性接触面积和塑性接触面积，具体表达式如下
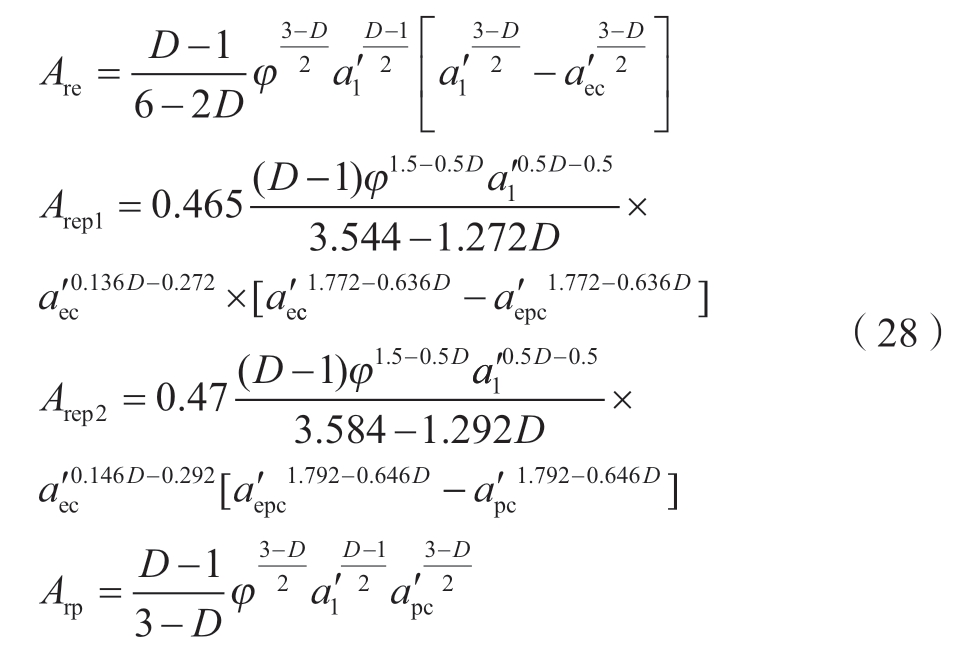
3.3 总法向接触载荷
磨削粗糙表面总的法向接触载荷是所有微凸体在不同变形阶段内的累加和，其表达式为
式中，F1、F2、F3、F3分别表示磨削粗糙表面的弹性接触载荷、第一弹塑性接触载荷、第二弹塑性接触载荷和塑性接触载荷，具体表达式如下
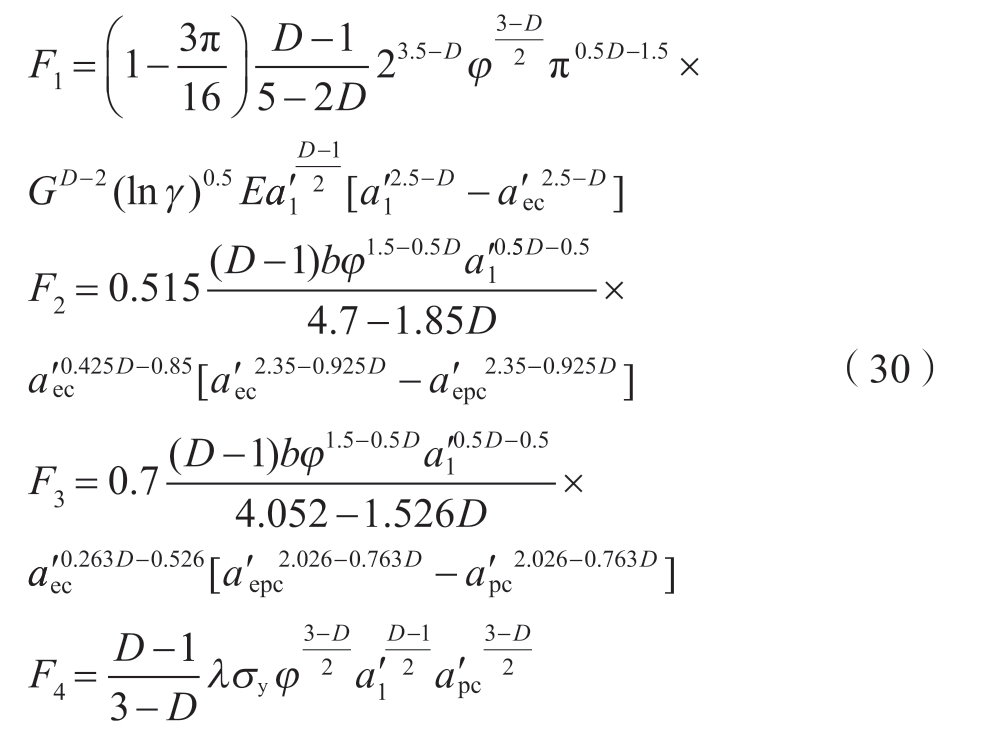
3.4 总切向接触载荷
磨削粗糙表面总的切向接触载荷是所有微凸体在弹性变形和弹塑性变形阶段内切向接触载荷的总和，其表达式为
式中，Q1、Q2、Q3分别为磨削粗糙表面的弹性切向接触载荷、第一弹塑性切向接触载荷及第二弹塑性切向接触载荷，具体表达式如下
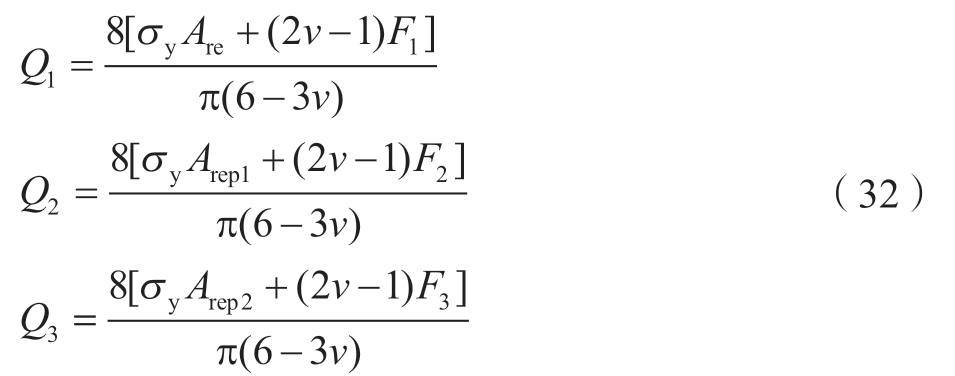
3.5 静摩擦系数
随着切向接触载荷的不断增大，粗糙表面将处于临界滑动状态，此时粗糙表面上微凸体所受的总的切向接触载荷Q就是最大的静摩擦力。
由式 （29）和 （31）可得考虑磨削真实三维形貌的静摩擦系数模型为
4 仿真与结果分析
4.1 模型的验证
为了验证本文模型的有效性，将本文模型与田红亮等[19]的试验结果和Pan等[9]的模型进行对比。上试件的材料为35#钢，其弹性模量和泊松比分别为E1= 197 GPa，ν1= 0.31；下试件的材料为45#钢，其材料参数为：E2 = 205 GPa，ν2 = 0.3。由于35#钢材料较软，所以取35#钢的屈服强度和硬度为等效粗糙表面的屈服强度和硬度，其数值分别为346 MPa和478 MPa。粗糙表面的等效分形参数分别为D = 2.5033，G = 2.0099×10-9 m。对比结果如图3所示。本文模型与Pan模型及试验数据在整体变化规律上是一致的，即粗糙表面的静摩擦系数随着法向总载荷的增加而增大。本文模型的计算值总体上小于试验值，这是由于所建模型中未考虑粗糙表面的基底变形以及材料的强化作用。
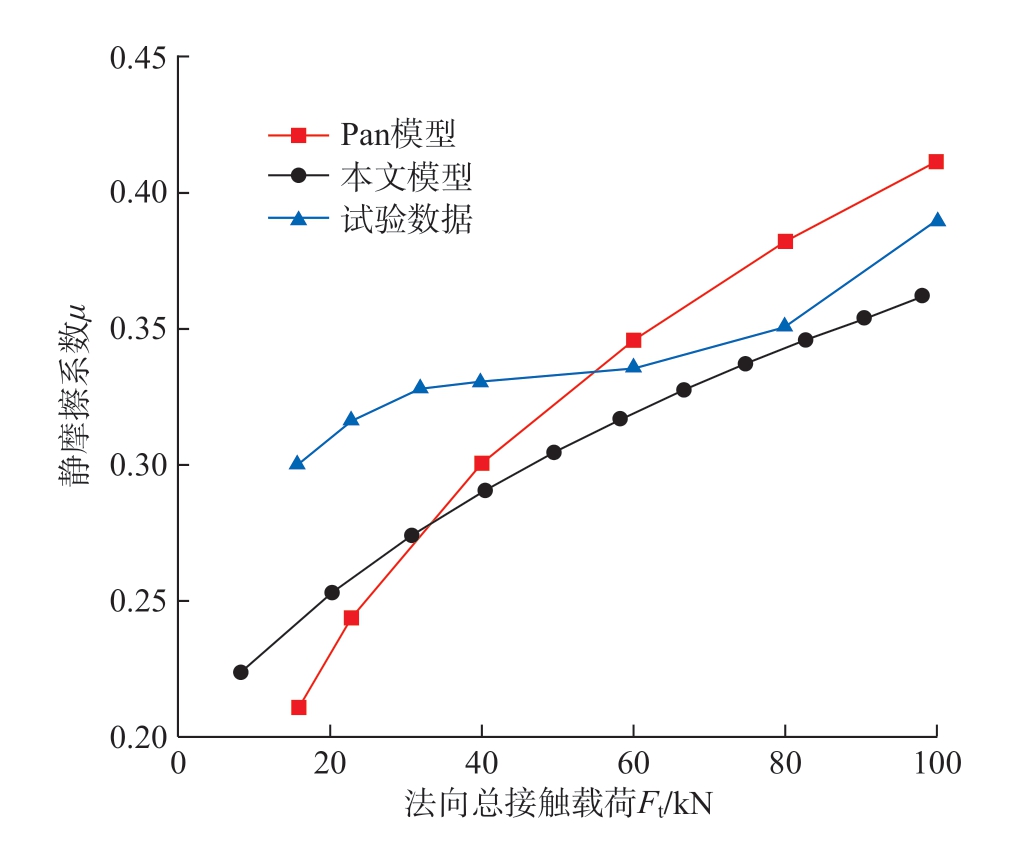
图3 本文模型和Pan模型及试验数据的对比
Fig.3 Comparison of the proposed model, Pan model and experimental data
4.2 分形维数对静摩擦系数的影响
图4中给出了在相同高度尺度参数 （G =10-8 m）条件下磨削粗糙表面静摩擦系数μ随分形维数D和无量纲法向接触载荷Ft*的变化关系。在分形维数2.35≤ D≤2.65范围内，静摩擦系数μ随着分形维数D的增加而增大；在2.65＜ D≤2.95范围内，静摩擦系数随着分形维数的增大而减小，所以分形维数存在一个最佳值，使得该表面的静摩擦系数μ达到最大值。
图4 分形维数与静摩擦系数的关系
Fig.4 Relations of fractal dimensional and static friction factor
4.3 高度尺度参数对摩擦系数的影响
图5中给出了在相同分形维数 （D = 2.45）条件下磨削粗糙表面静摩擦系数μ随高度尺度参数G和无量纲法向接触载荷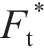
的变化关系。由图5可知，对于确定的高度尺度参数G，磨削粗糙表面的静摩擦系数μ随着无量纲法向接触载荷
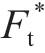的增加而增大；随着高度尺度参数G的增大，静摩擦系数μ减小。
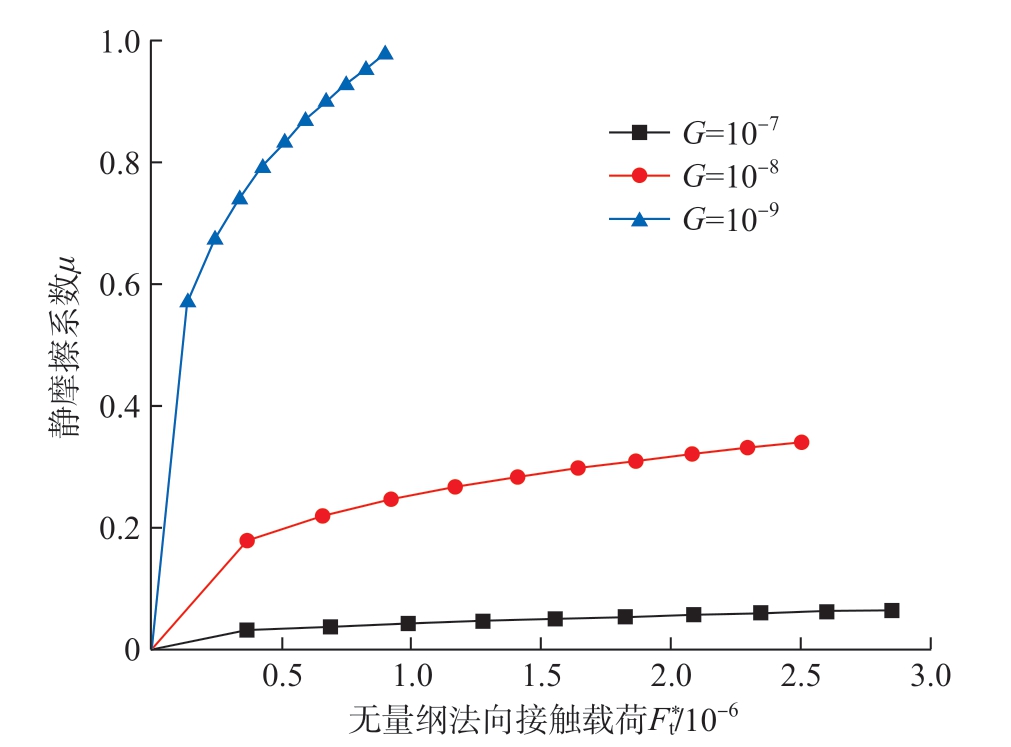
图5 高度尺度参数与静摩擦系数的关系
Fig.5 Relations of height scaling parameter and static friction factor
4.4 材料参数对静摩擦系数的影响
图6中给出了在相同分形参数和高度尺度参数（D = 2.45，G = 10-8 m）条件下磨削粗糙表面静摩擦系数μ随材料参数f和无量纲法向接触载荷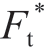
的变化关系。从图6可以看出，静摩擦系数μ随着f的增大而减小。
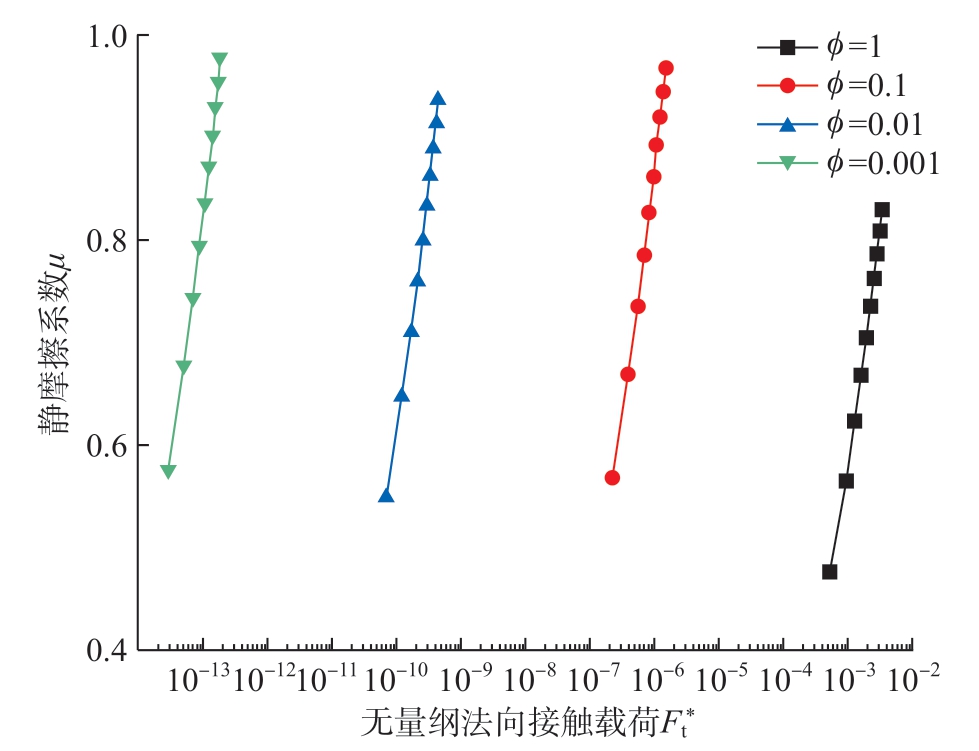
图6 材料参数与静摩擦系数的关系
Fig.6 Relations of material properties and static friction factor
由图4 ～ 6可知，对于确定的分形参数和材料特性，磨削粗糙表面的静摩擦系数μ随着无量纲法向接触载荷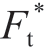
的增加而增大，这和大部分分形接触静摩擦系数模型的变化趋势一致[18]，原因在于随着法向载荷
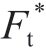的增加，粗糙表面会有更多的微凸体参与接触，从而更多弹性变形和弹塑性变形的微凸体承受切向载荷，进而导致磨削表面的静摩擦系数μ增大。
5 结论
（1）本文提出了一种考虑微凸体相互作用的磨削粗糙表面静摩擦系数分形模型。
（2）在相同的法向接触载荷作用下，粗糙表面静摩擦系数与分形维数存在非线性关系，当分形维数在2.35≤D≤2.65范围内，静摩擦系数随着分形维数的增大而增大；当分形维数在2.65 ＜D≤2.95范围内，静摩擦系数随着分形维数的增大而减小。
（3）静摩擦系数随着高度尺度参数或材料参数的增大均减小。
[1] 安琪, 索双富, 林福严, 等. 平面磨削粗糙表面的微观接触模型[J]. 机械工程学报, 2020, 56(7): 240-248.AN Qi, SUO Shuangfu, LIN Fuyan, et al. A micro-contact model for rough surface of plane grinding[J]. Journal of Mechanical Engineering, 2020,56(7): 240-248.
[2] CHANG W R, ETSION I, BOGY D B. Static friction coefficient model for metallic rough surfaces[J]. Journal of Tribology, 1988, 110(1): 57-63.
[3] GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1966, 295(1442): 300-319.
[4] SAYLES R S, THOMAS T R. Surface topography as a nonstationary random process[J]. Nature, 1978, 271: 431-434.
[5] 盛选禹, 雒建斌, 温诗铸. 基于分形接触的静摩擦系数预测[J]. 中国机械工程, 1998, 9(7): 16-18.SHENG Xuanyu, LUO Jianbin, WEN Shizhu. Static friction coefficient model based on fractal contact[J]. China Mechanical Engineering, 1998, 9(7):16-18.
[6] MAJUMDAR A, BHUSHAN B. Fractal model of elastic-plastic contact between rough surfaces[J]. Journal of Tribology, 1991, 113(1): 1-11.
[7] 兰国生, 张学良, 丁红钦, 等. 基于分形理论的结合面静摩擦因数改进模型[J]. 农业机械学报, 2012, 43(1): 213-218.LAN Guosheng, ZHANG Xueliang, DING Hongqin, et al. Modified model of static friction coefficient of joint interfaces based on fractal theory[J]. Transactions of the Chinese Society for Agricultural Machinery,2012, 43(1): 213-218.
[8] YAN W, KOMVOPOULOS K. Contact analysis of elastic-plastic fractal surfaces[J]. Journal of Applied Physics, 1998, 84(7): 3617-3624.
[9] PAN W J, LI X P, WANG X. Contact mechanics of elasticplastic fractal surfaces and static friction analysis of asperity scale[J].Engineering Computations, 2021, 38(1): 131-150.
[10] KOGUT L, ETSION I. Elastic-plastic contact analysis of a sphere and a rigid flat[J]. Journal of Applied Mechanics, 2002, 69(5): 657-662.
[11] WU J W, WANG H, CHEN T F, et al. Friction mechanism and characteristics of reticle based on contact theory[J]. Journal of Tribology,2022, 144(2): 021501.
[12] LIU W W, YANG J J, XI N, et al. A study of normal dynamic parameter models of joint interfaces based on fractal theory[J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2015, 9(5):JAMDSM0070.
[13] 张学良, 张伟, 温淑花, 等. 结合面静摩擦因数尺度关联三维分形模型[J]. 机械工程学报, 2021, 57(9): 127-138.ZHANG Xueliang, ZHANG Wei, WEN Shuhua, et al. Threedimensional fractal model with scale correlation for static friction factor of joint interfaces[J]. Journal of Mechanical Engineering, 2021, 57(9): 127-138.
[14] YUAN Y, CHENG Y, LIU K, et al. A revised Majumdar and Bushan model of elastoplastic contact between rough surfaces[J]. Applied Surface Science, 2017, 425: 1138-1157.
[15] 陈建江, 原园, 成雨, 等. 尺度相关的分形结合面法向接触刚度模型[J]. 机械工程学报, 2018, 54(21): 127-137.CHEN Jianjiang, YUAN Yuan, CHENG Yu, et al. Scale dependent normal contact stiffness fractal model of joint interfaces[J]. Journal of Mechanical Engineering, 2018, 54(21): 127-137.
[16] 葛世荣, 朱华. 摩擦学的分形[M]. 北京: 机械工业出版社, 2005.GE Shirong, ZHU Hua. Fractal of tribology[M]. Beijing: China Machine Press, 2005.
[17] WANG R Q, ZHU L D, ZHU C X. Research on fractal model of normal contact stiffness for mechanical joint considering asperity interaction[J].International Journal of Mechanical Sciences, 2017, 134: 357-369.
[18] ZHANG C X, LI X, HE J L, et al. Static friction coefficient model of joint surface based on the modified fractal model and experimental investigation[J]. The International Journal of Advanced Manufacturing Technology, 2023, 124(11): 4415-4429.
[19] 田红亮, 刘芙蓉, 赵春华, 等. 金属材料表面静摩擦学特性的预测研究——实验佐证[J]. 振动与冲击, 2014, 33(1): 209-220.TIAN Hongliang, LIU Furong, ZHAO Chunhua, et al. Prediction of static friction performance of metallic material surfaces with experimental proof[J]. Journal of Vibration and Shock, 2014, 33(1): 209-220.