准确的材料力学性能是进行结构安全性、可靠性设计的基础。研究材料或结构冲击载荷作用下的动态力学响应与变形机制,既是一个重大的科学问题,又具有重要的工程实用价值。在现代国防和高端装备制造生产过程中,经常要对产品或结构进行冲击试验。国内外对相关技术的研究已进行了多年,发展了多种冲击测试技术,例如典型的落锤/摆锤试验[1-2]、机载飞行数据记录仪 (俗称“黑匣子”)冲击试验[3-4]、飞机机身结构抗鸟撞试验[5-6]、霍普金森杆试验[7-8]、炮弹穿甲试验[9-10]、航天器遭受太空碎片撞击试验等。此外,像坦克遭受穿甲破坏、军事设施遭受爆炸冲击以及高速动车抗撞击防护设计等都需要进行冲击测试。在这些冲击测试中,如何实现冲击加载是关键,直接决定了装置的冲击测试能力,目前主要采用的冲击加载方法包括重力加载[11]、空气炮加载[12]、液压加载[13]、炸药爆炸加载[14]等。其中,重力加载方法简单可靠,但冲击速度受高度限制,极限冲击速度较低,例如实现20 m/s冲击速度要求冲击高度达20 m,显然无法满足结构强冲击动态力学测试要求;液压加载冲击速度可达20 m/s,但加载重复度低,且设备体积庞大;空气炮加载通过压缩空气的方法可实现高速冲击加载,但是这种装置对气密性要求特别高。现有空气炮发射装置采用电磁阀或活塞气阀,使得装置反应慢、响应时间长、气体释放精度差、耗损大。炸药爆炸加载控制难度大、重复性差,且存在很大的安全隐患。随着现代国防和高端装备技术指标的快速发展,对材料和结构抗冲击性能测试需求日益增加,传统的冲击测试装置的能量不足、模式单一与当下的高标准、多场景的测试要求形成了巨大差异,严重影响了材料、结构及其装备抗冲击防护技术应用的发展,因此研制新的材料/结构动态力学性能测试方法和设备迫在眉睫。
相比传统冲击加载方法,脉冲电磁力加载具有可控性好、稳定性强、安全性高等诸多优势,其相关技术已成熟,并应用于电磁铆接[15-16]、电磁炮[17]、电磁弹射[18]等,创造了明显的技术和军事效益。基于已掌握的电磁加载的核心技术及应用经验,西北工业大学研制了基于电磁加载的霍普金森杆,其成果应用得到国内外高度关注。试验测试结果显示,基于电磁加载的霍普金森杆技术可以实现材料在高应变率(102 s-1~104 s-1)范围内的动态力学性能测试。为实现材料在中应变率(1~102 s-1)范围内的相关动态性能测试,项目组开发了基于电磁加载的中应变率冲击测试系统。初步试验表明,基于电磁加载的冲击测试系统具有控制简单、加载精度高、加载重复性好、试验成本低的优势,为实现传统冲击测试系统的跨越式发展提供了新的途径。本文侧重于电磁加载技术基本原理及已开发的冲击测试试验技术的介绍,并对其可能的应用领域进行展望。
1 电磁加载原理
基于电磁加载的冲击测试平台主要包括电源控制系统、电磁加载结构平台和测试数据采集系统3大部分,如图1所示。试验时,通过电源控制系统调节加载至初级线圈上的电压值,电容放电时使得初级线圈产生第一磁场,次级线圈的一面与初级线圈紧密贴合,当初级线圈产生第一磁场时,次级线圈感应出第二磁场,第一磁场与第二磁场相互排斥,产生冲击测试试验所需要的互斥推力,从而实现对互斥推力的精准调节,提高了试验精度。次级线圈的另一面与应力波放大器贴合,互斥推力中的作用力经放大器放大作用于发射杆,互斥推力中的反作用力作用于缓冲部件,为发射杆提供缓冲,以提高整体装置的稳定性。
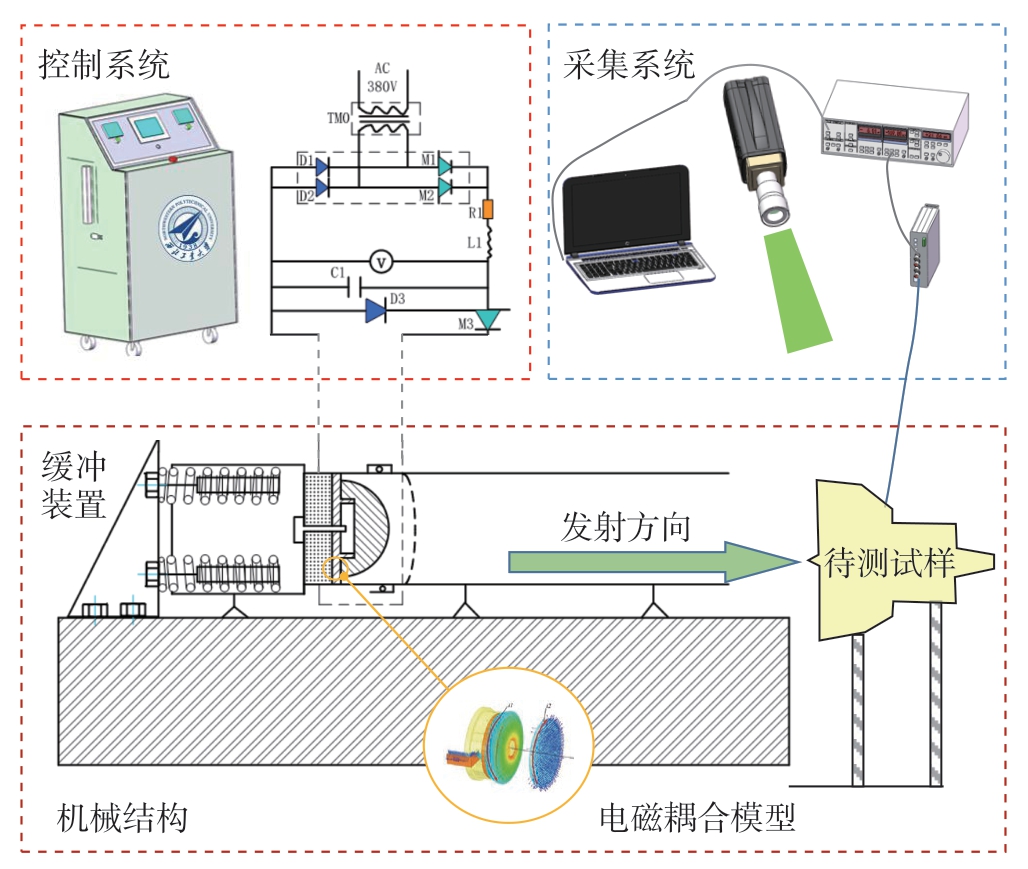
图1 加载平台原理图
Fig.1 Schematic diagram of loading platform
脉冲电磁力加载的动态试验测试方法的加载机理类似于电磁铆接[19]。在这个过程中,380 V的交流电通过变压器升压后经由二极管D1、D2和晶闸管M1、M2组成的双臂整流桥转换成高压直流电,直流电流对电容C充电。当电容进行放电时,放电电流流经初级线圈。在初级线圈周围建立磁场,然后次级线圈产生感应电流,感应电流在次级线圈周围建立1个磁场,该磁场与初级线圈的磁场相互作用产生动态洛伦兹力,动载荷以应力波的形式加载到试件上,完成试件的动态测试。
在电磁加载系统中,存储在系统电容中的放电能量E为
式中,C为系统电容;U为充电电压。
电容放电时,放电线圈中产生的电流为
式中,Im为放电线圈电流幅值;δ = R/2L;ω为放电回路振荡频率;N为放电线圈匝数。
次级线圈经过电磁感应产生涡流
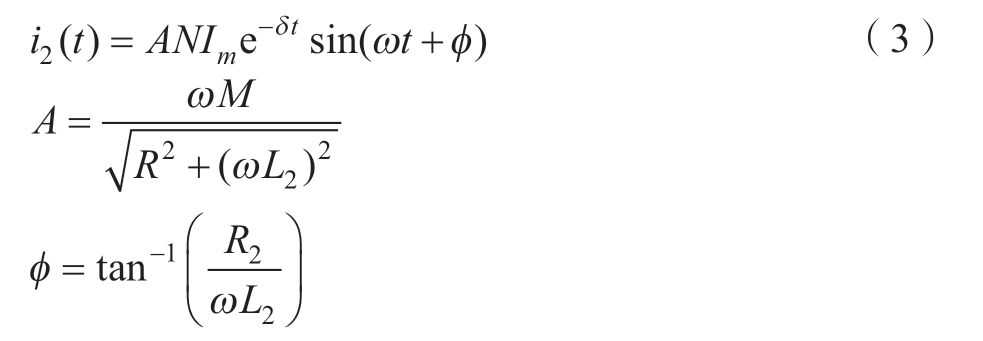
式中,M为放电线圈与次级线圈的互感;R2为次级线圈电阻;R为放电电路电阻;L2为次级线圈电感。动态试验平台的应力波是在控制系统控制的放电电流半波周期内完成的,根据电阻电感电容 (RLC)电路放电周期,应力波脉宽可以通过以下公式计算。
式中,L为系统电感。图2所示[20]为通过对4个2 mF电容器进行不同的并联或串联得到不同电容值所对应的加载脉宽。放电线圈与次级线圈之间的电磁斥力可表示为

图2 不同电容值下的应力波脉宽[20]
Fig.2 Loading period under different capacitance[20]
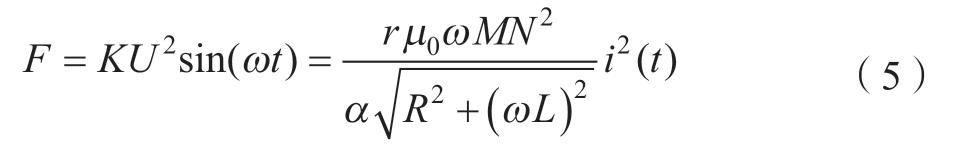
式中,α为放电线圈与次级线圈间距;K为RLC回路系统常数。
图3所示为电容值23.5 mF时,不同充电电压下对应的载荷大小,固定电容下放电脉宽基本相同。发射杆中的应力可表示为
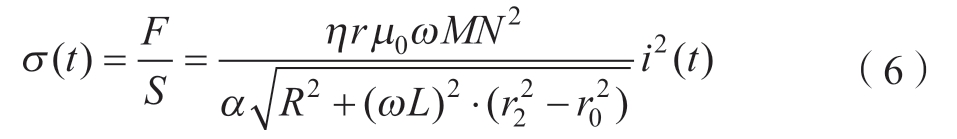
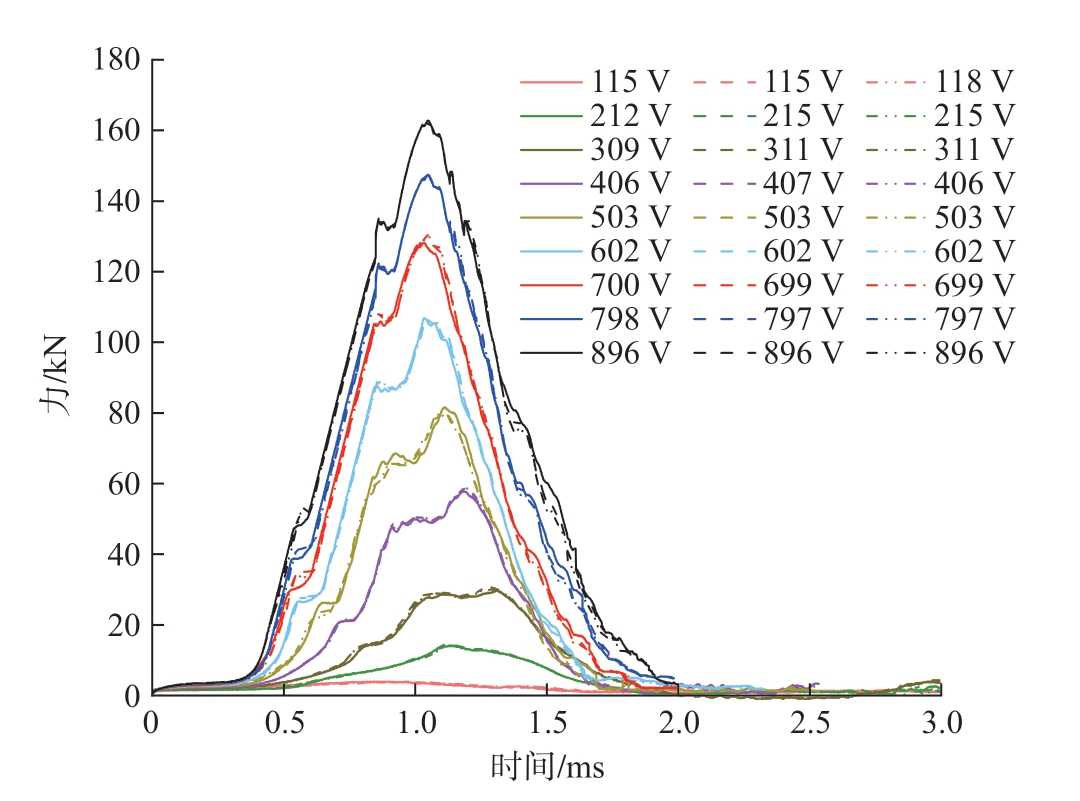
图3 固定电容值(C=23.5 mF)时载荷与电压的关系
Fig.3 Relationship between load and voltage (C=23.5 mF)
式中,η为放大系数;r为放电线圈半径;μ0为真空磁导率;S为入射杆横截面积;r0为线圈导向轴半径;r2为次级线圈半径。应力的幅值主要由匝数N、互感M、间距α、系统电阻R、系统电感L、放电电流幅值决定。然而,对于定型的电磁加载头,其互感、匝数、电阻、电感等固定参数较难调节,因此,应力波幅值可通过调整充电电压实现精确控制。
根据一维杆碰撞方程,结合式 (5)和 (6),最大当量撞击速度Vmax由式 (7)计算得出。
式中,ρ0是加载杆密度;C0是应力波在加载杆中的传播速度。如式 (7)所示,各项设计参数确定的前提下,加载速度可通过改变充电电压U而实现精确控制。理论和试验均表明,基于电磁加载的测试技术具有可靠性高、可控性好和可重复性高的优点。
综上所述,根据RLC电路的基本原理并结合以上公式,电能储能系统存储的能量与电容量成正比,与充电电压平方成正比。理论研究表明,充电电压对脉冲电磁力峰值、波形具有重要影响,而电容量同时影响脉冲电磁力峰值、脉冲宽度以及波形。因此,电磁加载方法可以通过调节充电电压和系统电容精确控制加载持续时间和最大当量冲击速度,为提高加载重复性和降低试验成本提供了可能。且与传统加载方法相比,电磁加载方法的其中一个优点是在测试中不需要子弹或撞击器的加速距离,这将有助于显著减小测试平台的体积。
2 电磁霍普金森杆技术及应用
霍普金森杆试验装置 (SHPB)是研究材料在高应变率下的动态力学行为及材料动态本构关系的主要测试装置。很多学者利用该试验装置开展了大量的材料动态性能研究工作。由于材料与结构的动态变形及破坏过程都是在应力波的作用下发生的,因此应力波的产生方式至关重要。最初的霍普金森杆试验装置冲击脉冲的产生是通过炸药起爆的方式[21],之后经历了炮/枪发射[22]、Hyge速度发生器发射[23]、高压气体驱动的方式,其中通过高压气体驱动子弹撞击入射杆来产生入射波应用最为广泛。其应力波幅值调节方式为调节子弹的加载速度或调节预加载弹性势能大小,脉冲长度则与子弹长度有关。图4为传统分离式霍普金森压杆示意图。然而,正如前文所提到的高压气体加载所存在的气压调节上限低且试验环境危险的局限性,以及加载脉宽受限于加载子弹长度,更换不同长度子弹操作繁琐且有空间限制,很大程度限制了动态加载的试验范围。因此,设想将电磁发射技术应用到霍普金森杆试验技术中。电磁霍普金森杆入射波由应力波加载次级线圈撞击入射杆产生,其驱动原理为电磁发射技术,应力波幅值调节方式为改变脉冲电容器的充电电压,脉冲宽度则与脉冲电容器的电容量有关。
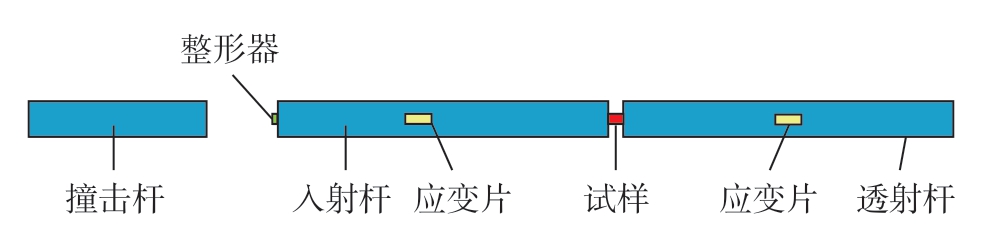
图4 分离式霍普金森压杆示意图
Fig.4 Schematic diagram of separate Hopkinson pressure bar
2.1 电磁霍普金森杆测试原理
基于电磁加载的霍普金森杆试验装置如图5所示,由能量控制系统、机械加载系统、数据采集系统组成。其中控制系统用于提供冲击能量和控制电磁动载荷,主要组成部分包括:电容充电主回路、电容放电主回路、充电触发模块、放电触发模块、HMI人机交互设备。在电容充电主回路中,利用比例积分微分控制 (Proportional integral derivative,PID)回路实现充电电压精确控制,充电误差1 V以内,从而对应力波脉冲幅值的控制更加精确。在电容放电主回路中,使用晶闸管代替开关,可以更加精确地触发放电回路。针对材料受复杂冲击载荷下的动态力学性能测试,在电容放电模块中,引入了数字脉冲延时发生器,实现了放电延时时间误差控制在1 ns以内,保证了材料复杂加载测试过程中加载的同步性。在电容量调节单元中,使用一个开关对应一种电容值的方式,避免了电容间的干扰和一条回路中开关过多带来的影响,降低了电路的复杂程度,增加了电容量调节的精确度和电容的寿命。电容充电主回路和电容泄流主回路中,开关均使用真空接触器,可承受高电压、大电流。机械加载系统主要由应力波加载头、入射杆、透射杆组成。其中应力波加载头代替传统的霍普金森杆中的空气炮和子弹,加载头产生应力波经过入射杆、试样、透射杆完成加载。数据采集系统由应变片、LK2109超动态应变仪、LK2400数据采集器和计算机构成,获得试验样品的应力-应变数据。此外,根据需要,电磁霍普金森杆可改变应力波加载头方向变换拉压模式,增加应力波加载头变为双向加载,通过正交放置装置实现双轴甚至三轴加载。

图5 项目组研发的电磁霍普金森杆试验平台实物图
Fig.5 Physical diagram of the electromagnetic Hopkinson bar developed by the author’s team
以单轴单向压缩试验为例,对电磁霍普金森杆的测试原理与数据处理进行介绍。电磁霍普金森杆测试基于一维弹性应力波和试样应力、应变分布均匀性假定,根据一维波传播理论求解波导杆 (即输入杆和输出杆)与试样断面的应力-位移-时间关系,从而得到试样的应力-应变关系。霍普金森杆单轴单项压缩试验的典型波形图如图6所示,应力波传播至试样处示意图如图7所示。
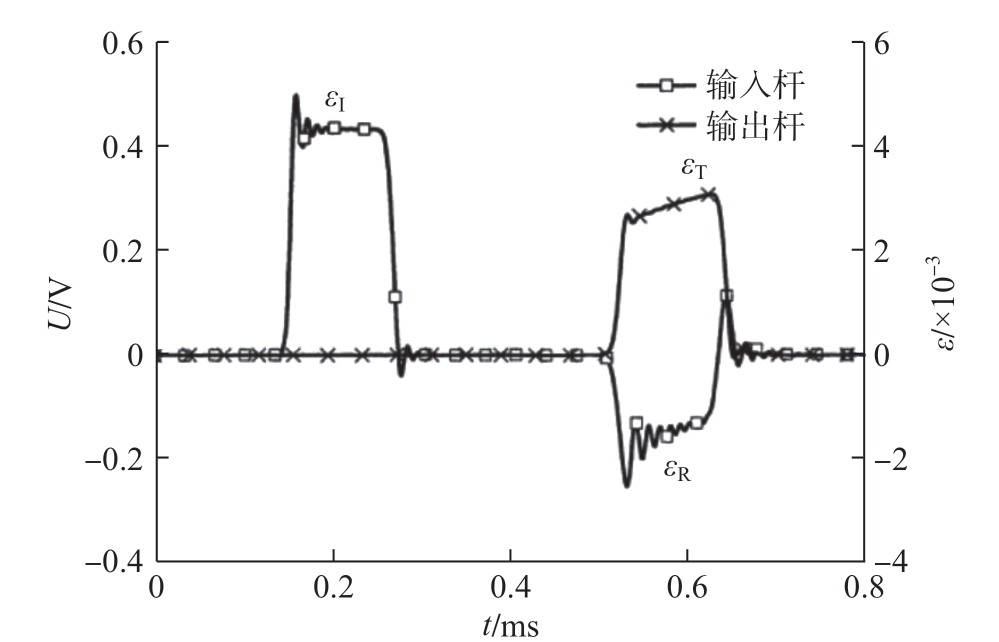
图6 霍普金森杆单轴单向压缩试验的典型波形图
Fig.6 Typical waveform of Hopkinson pressure bar uniaxial test
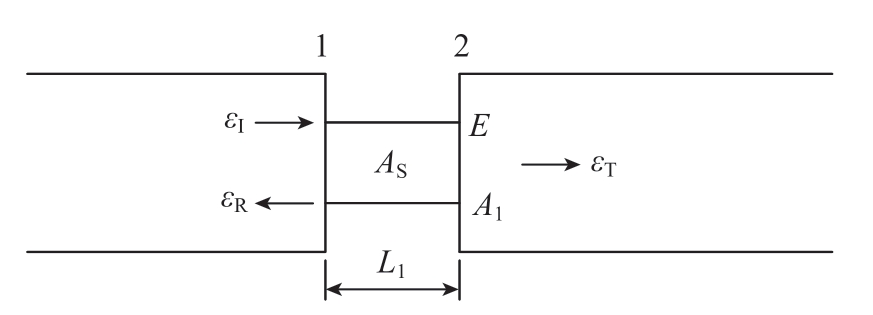
图7 霍普金森杆单向压缩加载示意图
Fig.7 Schematic diagram of unidirectional compression loading of SHPB
图7中,εI、εR、εT分别为入射波、反射波、透射波产生的弹性应变; 1、2分别为试样的前、后端面;AS为试样的截面面积;A1为波导杆的截面面积;L1为试样的标距长度;E为波导杆的弹性模量。移动入射波、反射波和透射波,使其起点位于相同的时刻,以此时刻作为数据处理的起始时刻。起点对齐后的入射波、反射波和透射波应均满足均匀化假设,即满足公式
撞击瞬间,界面1和界面2的应变分别为ε1= εI + εR,ε2= εT;入射杆速度V1与透射杆速度V2分别为
式中,![]() ,为应力波在波导杆中的传播速度,其中ρ为波导杆密度。
,为应力波在波导杆中的传播速度,其中ρ为波导杆密度。
加载应变率为
则作用于试样上的应变率为
根据式 (10),试样的工程应变可表示为
界面1和界面2处的载荷分别为
则平均载荷为
则试样上的工程应力为
根据式 (8)应力-应变均匀性假设,基于电磁霍普金森杆的应力、应变及应变率为
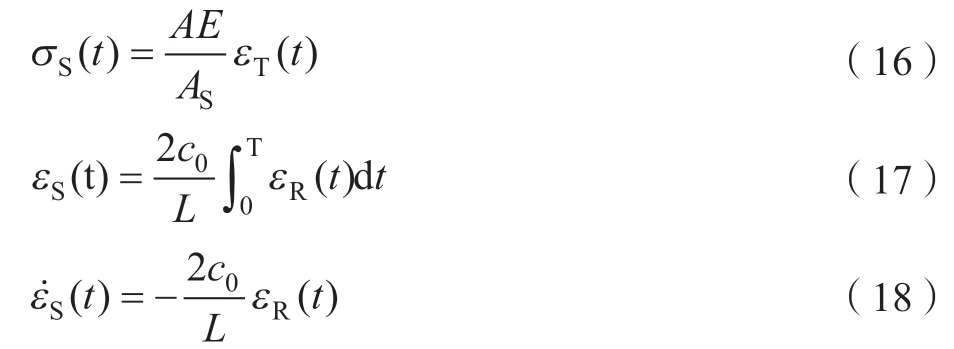
2.2 电磁霍普金森杆的发展与应用
相比于传统高压气体加载的霍普金森杆是通过机械方式产生入射波,电磁霍普金森杆试验加载技术是基于已经成熟的电磁铆接加载技术[16],利用电磁感应原理直接或间接驱动子弹撞击入射杆,从而产生应力波,具有可控性好、加载范围大及试验效率高等优势,对于完善与拓展材料动态力学行为的研究具有重要意义。国内第一套单轴双向和双轴四向电磁霍普金森杆是由西北工业大学曹增强团队和李玉龙团队联合研制,其电磁加载系统由曹增强团队在其多年电磁铆接加载系统的基础上[24]经过对控制系统和电磁加载头的创新设计而研发。霍普金森杆试验系统一般用于测试材料在高应变率范围内的动态冲击试验,因而对试验加载速率的要求很高,而电磁铆接为有效防止镦头中的微裂纹,提高铆接质量,铆接时所需的冲击能量、加载速率不宜太大。因此,电磁铆接控制系统还不能直接用于电磁霍普金森杆。曹增强等[25]提出了一种基于电磁加载的霍普金森压杆试验设备控制系统,用来解决现有控制系统用于电磁霍普金森杆时存在的问题。图8[25]为控制系统结构示意图,具体技术方案包括人机交互控制单元、电容量调节控制单元、加载方式控制单元、放电线圈温度控制单元、电容充电控制单元、电容放电控制单元、泄流控制单元、试验数据采集控制单元和安全控制单元。其中,人机交互控制单元用于控制试验过程;电容量调节控制单元和加载方式控制单元分别用于调节电容量和选择不同的加载方式;电容充电控制单元、电容放电控制单元、泄流控制单元分别用于控制应力波脉冲幅值,产生应力波脉冲,电容器组泄流;安全控制单元用于保证试验人员的生命安全。与低压电磁铆接设备的控制系统相比较,基于电磁力加载的霍普金森压杆试验设备控制系统能够实现对基于电磁力加载的霍普金森压杠试验装置的自动化控制,且冲击能量可调范围大、冲击速率大、响应快,显著提高了控制系统的效率及可靠性。
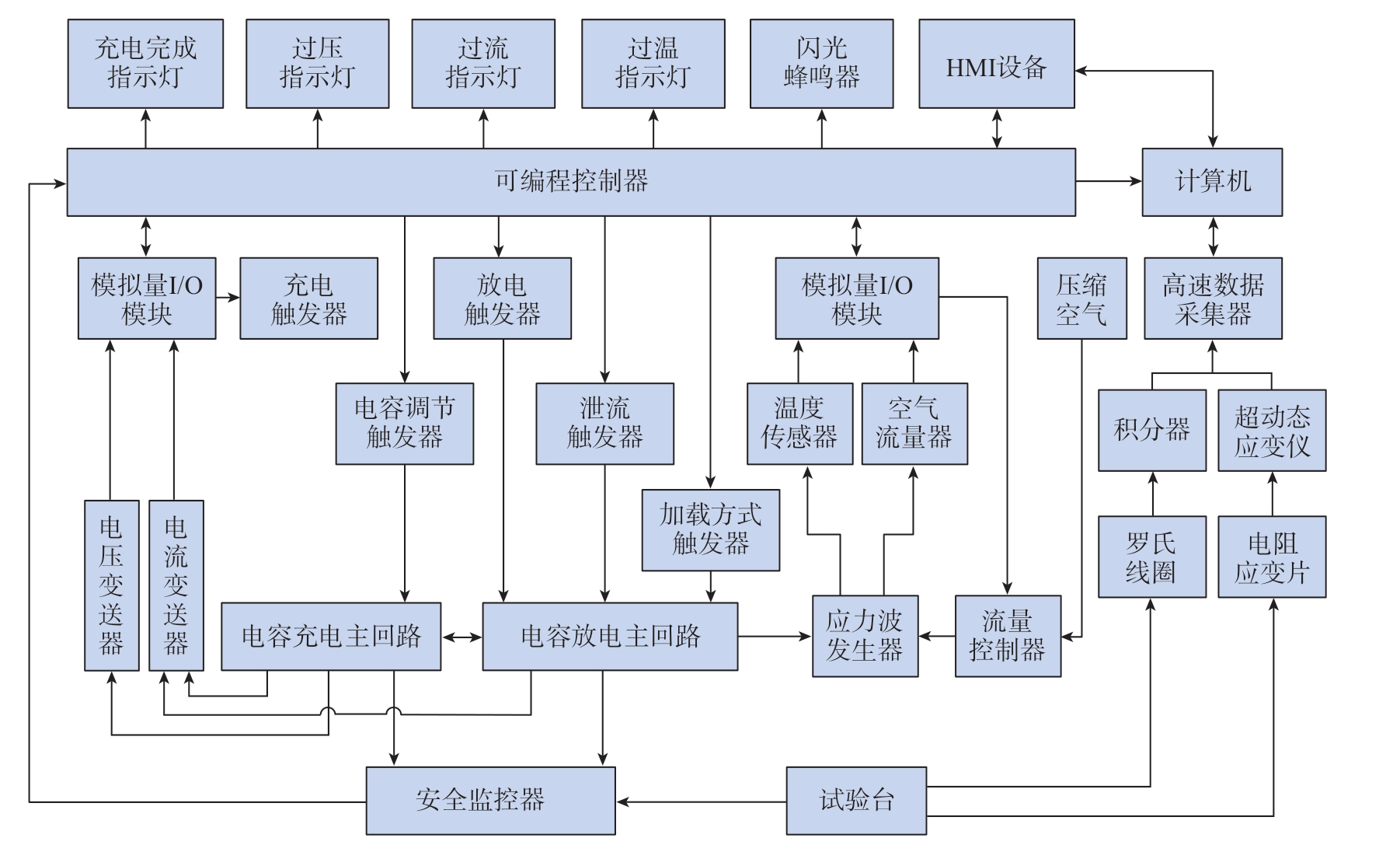
图8 控制系总体结构示意图[25]
Fig.8 Schematic diagram of control system[25]
最初的电磁霍普金森压杆试验装置的加载头是以电磁铆枪作为动力头加载,将电磁铆枪的端面与入射杆的端面紧密接触,使电磁铆接装置产生的应力脉冲输入到入射杆,进而传递到试样,实现试样的冲击压缩试验[26]。随着材料科学领域动态力学性能测试的不断发展,分离式霍普金森压杆由于在加载初期,试样的应力不均匀导致所测材料性能的弹性段不准确,一般用来测量在高应变率下材料的塑性流动行为。因此,在霍普金森压杆的基础上提出了分离式霍普金森拉杆试验技术,用于测量材料在高应变率下的拉伸力学性能。对于传统的霍普金森杆试验技术,由于撞击杆的形状不同、气枪位置的不同导致拉伸杆和压缩杆的应力波驱动系统无法在同一装置上实现。针对这一缺陷,曹增强等[27]以电磁铆接为基础,提出了基于电磁力的霍普金森压杆和拉杆试验方法。就此方法,曹增强等[28]给出了电磁力霍普金森压杆和拉杆试验加载装置的入射波控制方法。具体技术方案:利用电磁力入射波与放电电压、放电电感、放电电容、放电电阻以及次级线圈的厚度的关系,进行加载入射波幅值、脉冲宽度的精确控制,提高了入射波最大脉冲幅值、脉冲宽度和上升沿斜率。Nie等[20]利用基于电磁加载的单向单轴霍普金森(Electromagnetic-Hopkinson)压杆和拉杆试验技术对2024 铝合金和黄铜试样进行了动态压缩/拉伸试验,并将试验结果与对传统霍普金森杆试验装置测试结果进行了对比,如图9和图10所示,可以观察到通过两种不同加载源驱动的霍普金森杆测试技术获得的试验测试结果具有很好的一致性。
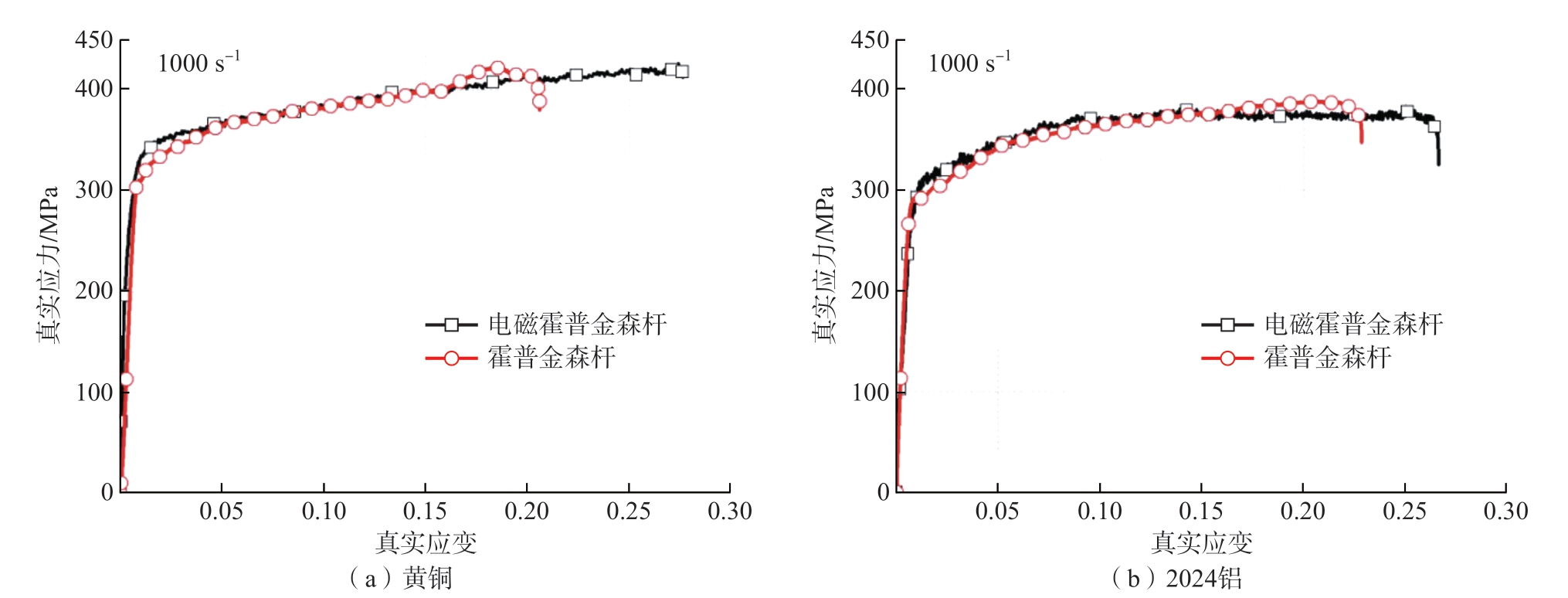
图9 压缩试验结果[20]
Fig.9 Compression test results[20]
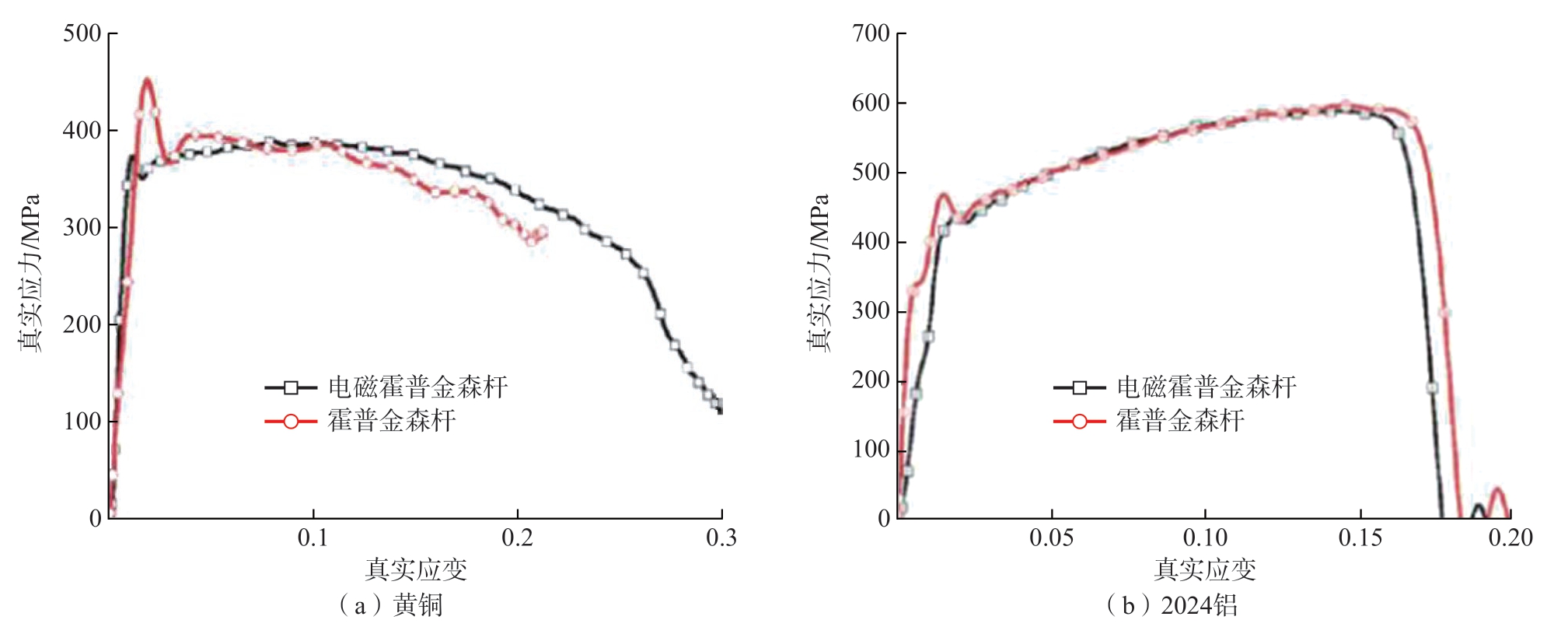
图10 拉伸试验结果[20]
Fig.10 Tension test results[20]
单轴单向的电磁霍普金森拉压杆虽可用于测量材料的高应变率动态力学特性,但由于杆自身属性的限制,其所能达到的最大应变率是有限的。理论上,通过提高撞击杆速度或采用微型试样可以提高应变率,然而,杆的强度限制了冲击速度的极值,且对于很多材料来说,微小试样很难加工。基于电磁加载的霍普金森杆脉冲力是通过触发开关瞬间产生的,在开关触发和应力脉冲的产生之间没有时间延迟,因此脉冲宽度很容易通过电路控制。基于这一优点,聂海亮等[29]通过有限元软件对基于单轴双向加载分离式霍普金森压杆的2024铝合金动态试验进行数值模拟,同样的入射波被用于相同条件下的SHPB模拟,图11(a)为单向加载和双向加载的对比结果。显然,双向加载的应变率比单向加载高了一倍左右;图11(b)所示为基于双向加载在实际试验中测到的两个入射杆中的应力波形,从试验结果可以看出两个入射波幅值和时间误差很小。
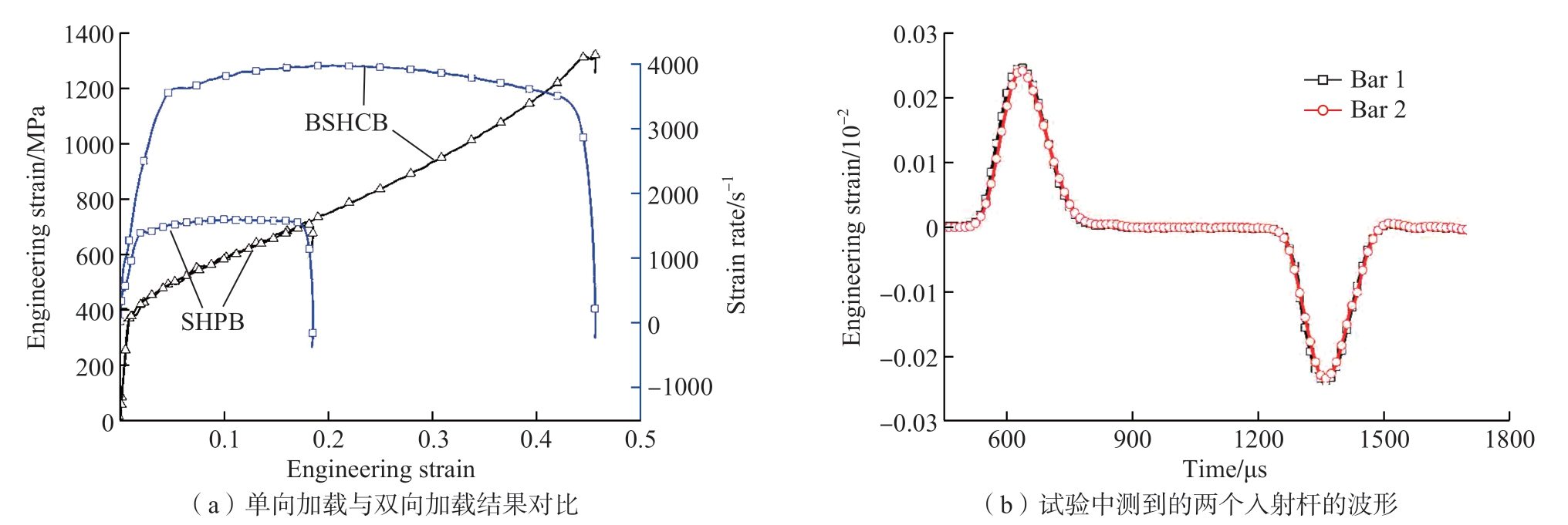
图11 单轴双向分离式霍普金森压杆装置测试结果[29]
Fig.11 Test results of loading sparate Hopkinson pressure bar[29]
考虑到大部分结构实际中所受的载荷通常为复杂应力,因此研究材料在多轴应力状态下的力学性能对于实际工程应用更具有指导意义。采用传统霍普金森杆试验技术很难实现多轴复合加载,而基于电磁加载的双轴霍普金森杆,理论上只需要将两套或三套相同的应力波发生器垂直布置,分别由试样的纵向、横向、竖向垂直加载入射波,即可实现双向霍普金森拉压杆试验加载设备统一,当两套装置的充电电压相同时,纵向、横向入射波等效加载。基于此,曹增强等[30]提出了一种基于双轴分离式霍普金森拉压杆多脉宽加载设备控制系统,在电容充电主回路中,利用PID回路实现充电电压精确控制,充电误差1 V以内,从而对应力波脉冲幅值的控制更加精确。在电容放电主回路中,使用晶闸管代替开关,可以更加精确地触发放电回路;在电容放电模块中,引入了数字脉冲延时发生器,实现了放电延时时间误差控制在1 ns以内,保证了材料测试过程中加载的同步性。在电容量调节单元中,使用1个开关对应一种电容值的方式,避免了电容间的干扰和1条回路中开关过多带来的影响,降低了电路的复杂程度,增加了电容量调节的精确度和电容的寿命。电容充电主回路和电容泄流主回路中,开关均使用真空接触器,可承受高电压,大电流,图12所示为控制系统结构总示意图。

图12 双轴霍普金森杆控制系统结构示意图[30]
Fig.12 Schematic diagram of biaxial Hopkinson bar control system[30]
2.3 小结
相比于传统霍普金森杆通过机械方式产生入射波,电磁霍普金森杆采用电磁驱动技术有以下显著优势。
(1)应力波脉宽与幅值调节范围大。同传统霍普金森杆相比,电磁霍普金森杆试验平台中,改变电容值相当于改变子弹长度,调节充电电压相当于改变空气炮气压。
(2)可实现对称同步加载。电磁霍普金森杆由电子开关控制电路中RLC电路放电,因为脉冲电流在电路中传播速度远大于固体应力波在试验杆中的传播速度,故双向加载时应力波加载头产生的应力可等效为无时差地施加在试件上。
(3)易进行应力波整形。目前的电磁霍普金森杆试验平台应力波由电磁驱动技术产生,波形为与电磁脉冲相近的半正弦波形。对于脆性材料和软性材料来讲可以实现近似的恒应变率变形。但对于金属材料来说,需要梯形应力波来实现恒应变率加载,可利用电磁驱动技术的优势进行应力波整形。根据傅里叶变换,任意形状的波形都可以分解为若干个正弦波时序叠加。将目前控制系统中RLC电路进行改进,通过高频电子开关控制各电容时序放电,所产生的应力波相叠加后可调节为所需要的任意波形梯形波[31]。
3 低速冲击测试技术及应用
在材料科学领域中,材料准静态力学性能的测量有成熟的液压万能测试试验机,而分离式霍普金森杆技术是测量材料在高应变率下力学性能使用最广泛的试验技术。对于材料受中/低速冲击载荷力学性能的研究,已有的少数试验研究是通过伺服液压高速拉伸试验机(HSTM)进行的,HSTM可用于在10-1~103 s-1内的恒定应变率测试[32],但受液压驱动的限制,HSTM无法实现中应变率的冲击载荷测试。然而,在实际应用中材料/构件经常承受中/低速冲击载荷作用,如空中飞鸟与飞行器的撞击、冰雹撞击飞机、应力波干涉铆/螺接及金属零件的高速切削加工等。从应变率的角度来说,中/低速冲击载荷可以等效为中应变速率 (1~500 s-1) 的冲击加载。从热力学的角度来说,中应变率冲击加载既不完全是等温过程,也不完全是绝热过程。因此,中应变速率试验作为材料由应变速率不敏感向应变速率敏感的过渡区,理解材料在该载荷范围内准确的力学特性及失效机理,对保障材料/结构的设计可靠性具有重要意义。当下,对材料/构件中/低速冲击试验使用最多的是落锤试验机,然而落锤试验技术设备庞大的缺点是明显的。为了能够有效地预测材料或结构受中应变率冲击载荷后的力学响应来提高设计效率和结构可靠性,很多学者通过对准静态测试和高应变率测试结果的插值获得材料在中应变率 (1~100 s-1)冲击载荷下的模型参数,显然这是不严谨的。准确的材料动态力学性能是保证数值模拟结果可靠的前提。因此,迫切需要一种新型的中应变率冲击试验测试方法。与传统的冲击加载方法相比,电磁加载的冲击能量由系统电容器中存储的放电能量控制,冲击速度由设定的充电电压自由控制。因此,具有测试精度高、可靠性高、可控性好、重复性好和试验成本低等优点,能大大提升冲击试验测试效率。因此,基于电磁加载的冲击测试方法为更准确地了解材料中应变率 (10-1~102 s-1)的动态特性提供了可能。
电磁力加载的中应变率冲击加载测试平台的核心加载原理与电磁霍普金森杆是基本一致的,即利用脉冲电容器储能并对放电线圈释放脉冲强电流,将放电线圈与次级线圈产生的电磁涡流所激发的电磁场之间的耦合脉冲斥力作为加速力,加速次级线圈和驱动头,再通过驱动头撞击拉伸杆作用于结构试样,实现结构强冲击加载。脉冲电磁力激发原理如图13所示。依据式(9),基于该测试平台的中应变率试验可通过调整充电电压U和初始平行标尺长度L0来实现材料应变率的精确控制,具有控制简单、加载速度快、重复性好等优点。
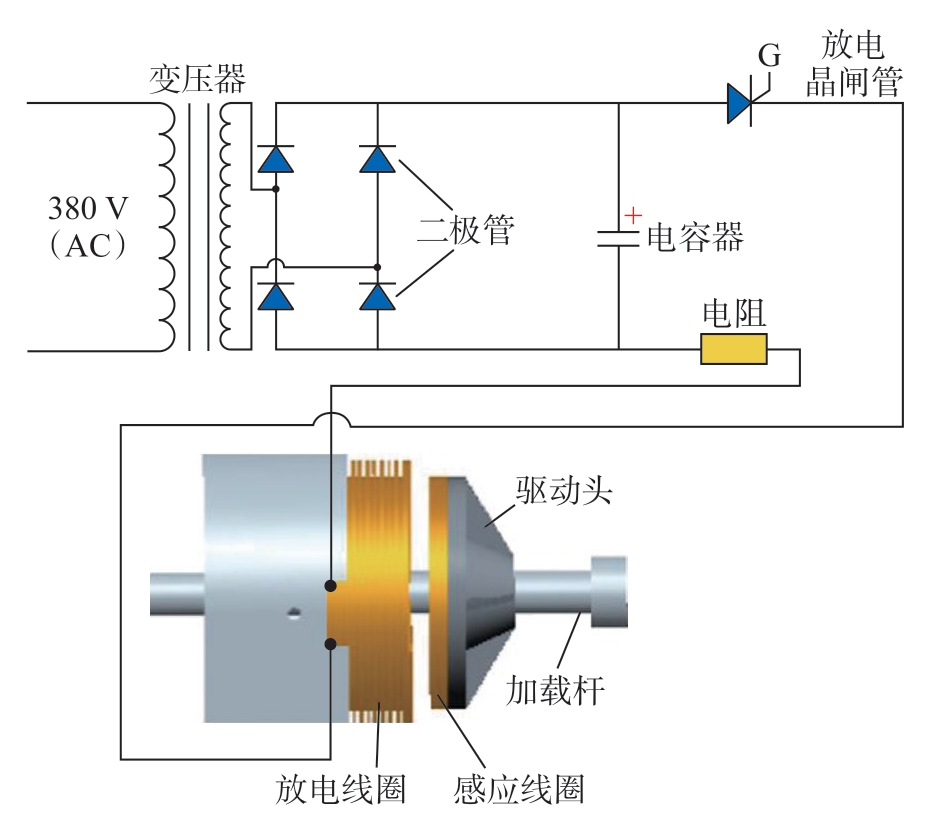
图13 加载原理图
Fig.13 Loading schematic
3.1 加载过程
中应变率冲击测试平台示意图如图14所示,由控制系统、机械结构和数据采集系统组成。控制系统在试验中用于提供冲击能量和控制电磁动载荷。在机械结构中,初级线圈由铜带缠绕而成,初级线圈、次级线圈和应力放大器紧密贴合,依次排列,并由加载杆同轴连接。加载杆和固定杆通过直线轴承限位,保证加载的稳定性。压电力传感器至于固定杆末端。试件用一种特殊的夹具夹紧,以减少负载振铃现象并提高获取应力的准确性,夹持面进行45°滚花处理,以增加摩擦力。通过更换夹具中的楔形块,可实现对不同尺寸和形状试件的夹持。动态加载时,应力放大器、次级线圈、初级线圈、直线轴承、加载杆、固定装置、夹具Ⅰ和Ⅱ与压电力传感器严格同心,以确保测试区处于单向应力状态。当瞬时电流通过初级线圈时,在初级线圈和次级线圈之间产生冲击力,由应力放大器放大,作用于加载杆的端面,完成对试件的加载,试件发生断裂时,真空阻尼器可以缓冲驱动头的冲击。
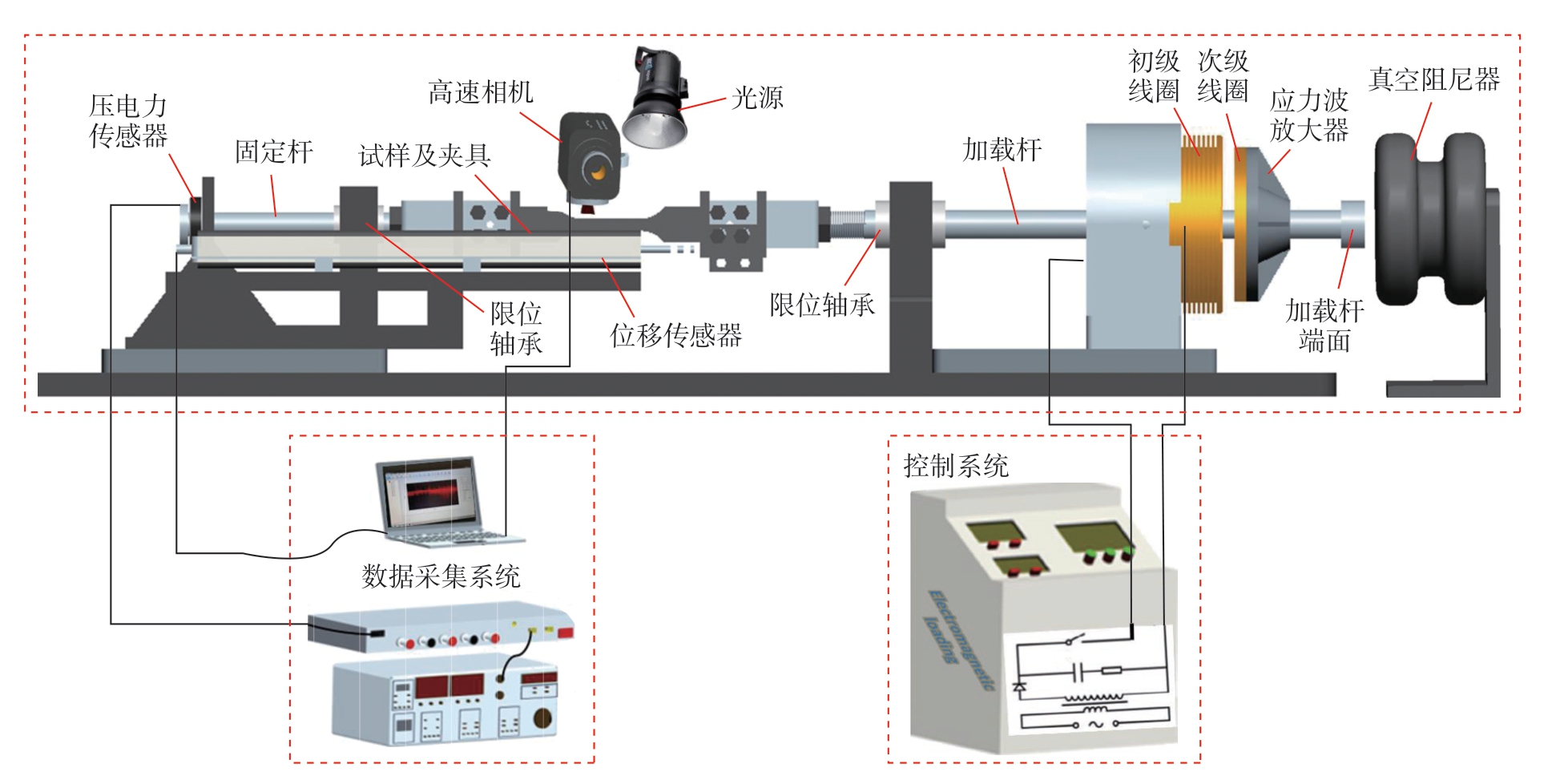
图14 中应变率冲击测试平台示意图
Fig.14 Schematic diagram of intermediate strain rate impact testing platform
3.2 数据采集
试验时,采用Reveler5F01高速摄像系统对试件在试验过程中的变形过程及冲击速度进行监控,光源采用EFⅢ-200LED高效影视灯,显色指数TLCI>98,色温 (5500±200) K。通过位移传感器KTC1(测量精度为±0.01 mm)和高频响应式压电力传感器LC2304(量程300 kN、测量精度40 kHz)测量试验时试件的位移变化和载荷大小,并通过数据采集器采集到电脑端,通过Datalab软件进行试验结果的显示及分析。试验中,通过全局快门同步触发高速摄像机、位移传感器和压电力传感器,实现数据的同步记录,便于数据分析。
3.3 低速冲击测试技术的应用
随着航空领域竞争的加剧,新一代飞机的设计对减轻结构重量、降低生产成本、提高使用效率和寿命提出了广泛的要求。为了应对这些挑战,高性能碳纤维增强复合材料 (CFRP)正越来越多地应用于飞机结构件,发挥其高比刚度、高强度和高抗疲劳的潜在优势。尽管复合材料与传统金属相比具有潜在的优势,但由于复合材料结构的几何复杂性和荷载传递要求,结构连接仍然是复合材料结构设计中不可避免的问题。机械连接技术是目前复合材料结构,特别是承重结构中使用的主要连接方式。为了解CFRP/Ti单搭接节点的动态力学性能,Zuo等[33]基于如图15所示的冲击测试平台,开展了冲击载荷下干涉CFRP/Ti螺栓单搭接构件节点的动态拉剪试验,以了解CFRP/Ti单搭接节点的动态力学性能。图16所示为冲击测试系统[33]在设定电压为400 V、500 V和600 V空载条件下对应的电磁动态载荷的载荷-时间曲线,试验结果显示,400 V、500 V和600 V 3次重复测试的结果一致性很好,这说明基于电磁加载的冲击测试设备具有良好的重复性。Zuo等[33]基于电磁加载方法的冲击测试系统测试得到的CFRP/Ti单搭接接头的动态力学性能曲线显示,在每个冲击速度下,接头的载荷-位移响应重复性与预期的一样。此外,研究发现CFRP/Ti单搭接接头的载荷-位移响应经历了显著的载荷速率依赖性,随着冲击速度的增加,螺接构件的破坏载荷减小,且在低应变率动态加载过程中接头表现出多种失效模式。因此,所开发的基于电磁加载方法的冲击测试系统能够测试CFRP/Ti单搭接接头的动态性能,且为提高加载重复性和降低测试成本提供了可能。

图15 应变率冲击测试平台实物图[33]
Fig.15 Intermediate strain rate impact testing platform based on electromagnetic loading[33]
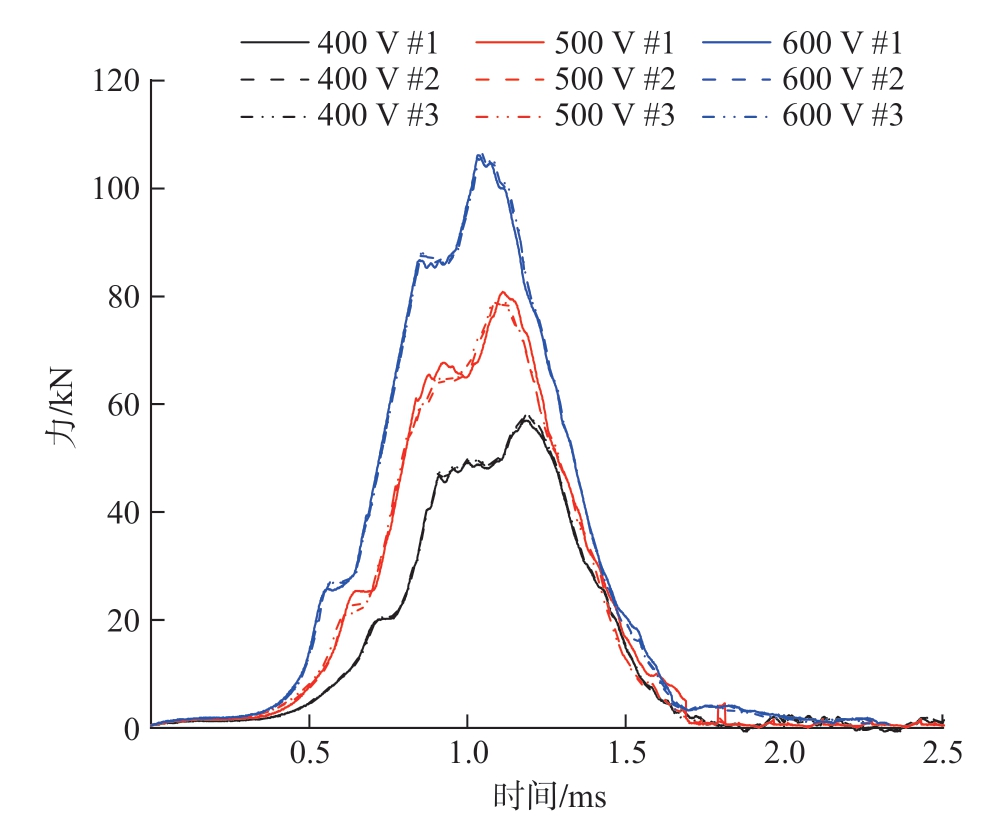
图16 对应于400 V、500 V和600 V的电磁动态负载[33]
Fig.16 Dynamic loads corresponding to the 400 V, 500 V and 600 V[33]
此外,本文作者基于该测试方法,考虑加载应变速率的作用,对TC4-M合金受中应变率冲击拉伸的材料动态性能进行了研究。为了更好地了解TC4-M合金板材在不同中应变率冲击载荷条件下的动态行为,进行了4种不同应变率60/s、70/s、85/s和100/s下的试验。图17所示为对应于4种加载应变率的载荷-位移曲线。可以发现,这些曲线都是同类型的,且每组试验参数得到的两组试验数据误差较小,这表明基于电磁加载的中应变率冲击测试试验具有高的一致性,验证了设备的稳定性。图18显示了通过高速摄像机 (帧速率为2000 fps)获得的TC4-M合金在最大当量应变率值为60/s的单轴冲击拉伸下 (其他应变率下的拉伸过程类似)的试件变形图,可以看出在基于电磁冲击测试平台的TC4-M合金冲击试验中,试样从变形到断裂的加载时间在2 ms以内。
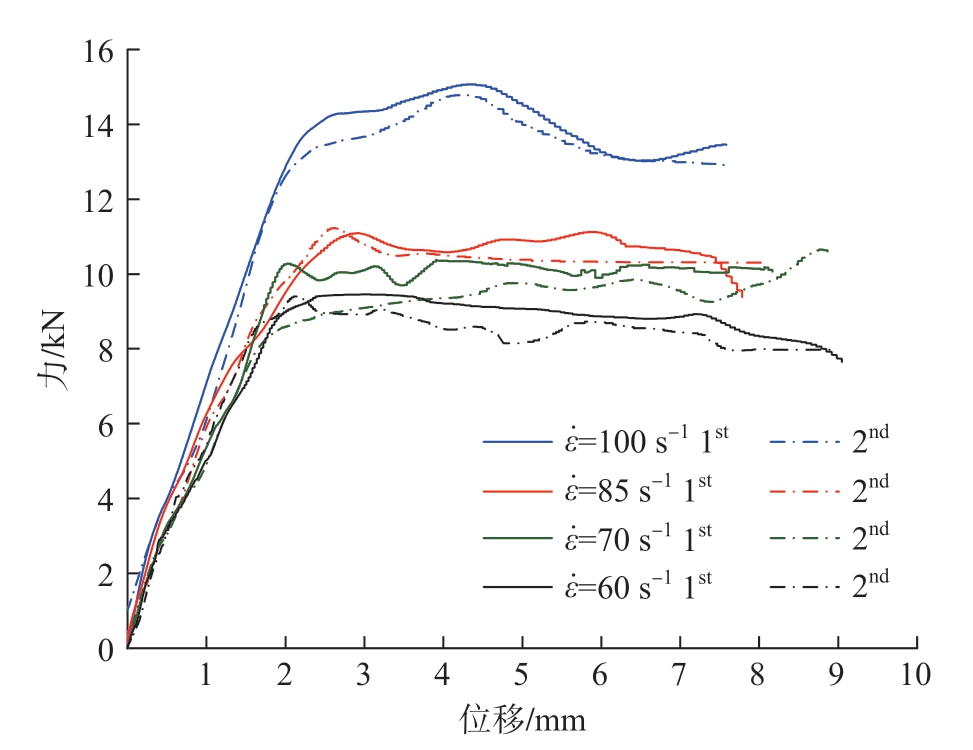
图17 4种应变速率的载荷-位移曲线
Fig.17 Load-displacement curves at four strain rates

图18 应变速率为60/s时的单轴冲击拉伸过程图
Fig.18 Diagram of uniaxial impact tensile process at strain rate of 60/s
3.4 小结
基于电磁加载的动态测试平台可通过调整冲击加载速度V和试件的初始平行标距长度L1来实现材料/构件中应变率动态性能的测试,不同冲击速度的精确控制可通过调整控制系统的充电电压U来实现。从试验测试结果可以得出,该测试技术具有可控性好、加载重复性高、试验成本低的优点,有望填补中应变率下冲击测试技术的空白,为传统冲击试验测试的跨越式发展提供了一种新的途径。
4 结论
电磁加载技术利用电能转化磁能来产生冲击和应力波,是对传统的霍普金森杆和高速拉伸试验机技术的进一步拓展和创新。本文综述了电磁加载技术的理论分析、试验研究、试验结构及在冲击测试领域取得的广泛应用。相比于传统技术,电磁加载具有以下优点。
(1)可控性好。针对不同的试验对象及不同试验要求可以通过调整电源控制参数 (主要是电容值和充电电压值)实现脉冲电磁力脉宽、幅值以及加载速度的精确控制。也正因为如此,电磁加载的测试试验具有高重复性及试验效率高的优势。此外,整个测试过程中可实现“三无”(无尘、无烟、无光)发射,操作简便,操控稳定。
(2)发射速度高。电磁加载原理上是将电能转化为电磁能再转化为发射弹撞击的动能,相比当前采用压缩空气、火药爆炸提供冲击动力的加载方式,从理论上讲,电磁加载技术只要系统的电容量满足条件,就可以提供足够的能量将发射弹加速至音速,甚至高达1000 m/s,从而可以显著提高发射弹的发射速度,以更加接近实际的方式测试试件在极端复杂环境下的力学行为特征,为结构安全设计提供有效的参考依据和技术支持。
(3)试验测试精确高。可依据控制程序计算出加载时的电磁力,较为准确地分析整个试验测试过程中能量的转化和损耗。同时无需考虑传统空气炮发射时发射弹所受气流不均对试验结果造成的不利影响。试验系统重复性好,进而有效保证了试验结果的准确度。
(4)结构简单。电磁加载试验平台在能够满足较大的发射速度同时,可以在几百μs到几ms的时间顺利完成加载,其加载能量来源于电容器储能对初级线圈放电形成的高脉冲电磁力。 因此,相比传统大型空气炮冲击测试装置需建立高压气体站,且发射炮筒很长、占地面积大,电磁加载试验平台具有结构简单、成本低及占地面积小的优点。
(5)安全性高。高压气体站爆炸的报道屡见不鲜,电磁加载技术不需配备高压气体站,安全系数更高。电磁加载极大地提高了材料动态性能测试的试验效率和试验准确性,因此,电磁技术已成为冲击测试领域重要的试验设备。此外,电磁加载技术在冲击领域有非常大的潜力,除了一维霍普金森杆、中应变率冲击测试平台,已研制成功的还有双轴霍普金森杆、立式拉压一体冲击测试平台,正在研制的还有动态三轴霍普金森杆、鸟撞试验测试平台等。
[1] ALI M B, ABDULLAH S, NUAWI M Z, et al. Evaluating instrumented Charpy impact strain signals using curve fitting equations[J].Journal of Central South University, 2014, 21(2): 600-609.
[2] 胡庆贤, 吕子剑. 落锤撞击加速度的测试及讨论[J]. 含能材料, 1999, 7(4): 176-179.HU Qingxian, LÜ Zijian. Determination of impact acceleration in drop weight test[J]. Energetic Materials, 1999, 7(4): 176-179.
[3] 冯九胜, 王小虎. 飞行数据记录器防护壳体强冲击试验数值仿真[C]//中国航空学会国内飞参系统使用状况及发展趋势研讨会. 北京: 中国航空学会, 2001.FENG Jiusheng, WANG Xiaohu. Numerical simulation of strong impact test of flight data recorder protective shell[C]//Symposium on the use and development trend of domestic flight parameter system. Beijing: Chinese Society of Aeronautics and Astronautics, 2001.
[4] 吴显吉, 李寿安, 李曙林, 等. 某型飞行数据记录器防护壳体强度性能分析[J]. 沈阳航空工业学院学报, 2003, 20(1): 12-13, 8.WU Xianji, LI Shouan, LI Shulin, et al. Strength capability analysis of a flight data recorder protecting housing[J]. Journal of Shenyang Institute of Aeronautcal Engineering, 2003, 20(1): 12-13, 8.
[5] 谢灿军, 童明波, 刘富, 等. 民用飞机平尾前缘鸟撞数值分析及试验验证[J]. 振动与冲击, 2015, 34(14): 172-178.XIE Canjun, TONG Mingbo, LIU Fu, et al. Numerical analysis and experimental verification of bird impact on civil aircraft’s horizontal tail wing leading edge[J]. Journal of Vibration and Shock, 2015, 34(14):172-178.
[6] GUAN Y P, ZHAO Z H, CHEN W, et al. Foreign object damage to fan rotor blades of aeroengine part I: Experimental study of bird impact[J]. Chinese Journal of Aeronautics, 2007, 20(5): 408-414.
[7] 胡时胜. 霍普金森压杆技术[J]. 兵器材料科学与工程, 1991,14(11): 40-47.HU Shisheng. Hopkinson pressure bar technique[J]. Ordnance Material Science and Engineering, 1991, 14(11): 40-47.
[8] 李为民, 许金余. 大直径分离式霍普金森压杆试验中的波形整形技术研究[J]. 兵工学报, 2009, 30(3): 350-355.LI Weimin, XU Jinyu. Pulse shaping techniques for large-diameter split Hopkinson pressure bar test[J]. Acta Armamentarii, 2009, 30(3): 350-355.
[9] 王志军, 尹建平. 弹药学[M]. 北京: 北京理工大学出版社, 2005.WANG Zhijun, YIN Jianping. Ammunition science[M]. Beijing:Beijing Insititute of Technology Press, 2005.
[10] 董瀚, 李桂芬, 王步震, 等. 高强度钢在高速冲击载荷下的动态响应[J]. 兵器材料科学与工程, 1995, 18(3): 10-16, 28.DONG Han, LI Guifen, WANG Buzhen, et al. Dynamic response of high strength steel under high speed impact load[J]. Ordnance Material Science and Engineering, 1995, 18(3): 10-16, 28.
[11] 雷建平, 张善元. 落锤冲击加载实验装置及结构耐撞性实验研究[J]. 力学与实践, 1996, 18(5): 51-53.LEI Jianping, ZHANG Shanyuan. Experimental study on impact loading device of falling hammer and structural crashworthiness[J].Mechanics in Engineering, 1996, 18(5): 51-53.
[12] 姚小虎. 鸟撞飞机圆弧风挡的实验研究及数值模拟[D]. 太原: 太原理工大学, 2001.YAO Xiaohu. Experimental investigation and numerical simulation on arc windshields of aircrafts subjected to bird impact[D]. Taiyuan: Taiyuan University of Technology, 2001.
[13] GER G S, KAWATA K, ITABASHI M. Dynamic tensile strength of composite laminate joints fastened mechanically[J].Theoretical and Applied Fracture Mechanics, 1996, 24(2): 147-155.
[14] 李金泉, 彭守凡, 黄德武, 等. 穿甲试验靶板中绝热剪切带特征及与裂纹的关系[J]. 兵器材料科学与工程, 2007, 30(6): 29-32.LI Jinquan, PENG Shoufan, HUANG Dewu, et al. Characteristics of adiabatic shear bands and the relations with cracks in penetration target[J]. Ordnance Material Science and Engineering, 2007, 30(6):29-32.
[15] 曹增强, 刘洪. 电磁铆接技术[J]. 塑性工程学报, 2007, 14(1):120-123.CAO Zengqiang, LIU Hong. Electromagnetic riveting technology[J].Journal of Plasticity Engineering, 2007, 14(1): 120-123.
[16] 邓将华, 李春峰, 于海平, 等. 电磁铆接技术[J]. 锻压技术,2010, 35(3): 1-6.DENG Jianghua, LI Chunfeng, YU Haiping, et al. Electromagnetic riveting technology[J]. Forging & Stamping Technology, 2010, 35(3):1-6.
[17] 王静端. 电磁发射技术的发展及其军事应用[J]. 火力与指挥控制, 2001, 26(1): 5-7.WANG Jingduan. The development and application of military electromagnetic emission technology[J]. Fire Control & Command Control, 2001, 26(1): 5-7.
[18] 张明元, 马伟明, 汪光森, 等. 飞机电磁弹射系统发展综述[J]. 舰船科学技术, 2013, 35(10): 1-5.ZHANG Mingyuan, MA Weiming, WANG Guangsen, et al.Overview on a significant technology of modern aircraft carrierelectromagnetic aircraft launch system[J]. Ship Science and Technology,2013, 35(10): 1-5.
[19] 曹增强. 电磁铆接理论及应用研究[D]. 西安: 西北工业大学,1999.CAO Zengqiang. Study on the theory and application of electromagnetic riveting[D]. Xi’an: Northwestern Polytechnical University, 1999.
[20] NIE H L, SUO T, WU B B, et al. A versatile split Hopkinson pressure bar using electromagnetic loading[J]. International Journal of Impact Engineering, 2018, 116: 94-104.
[21] KOLSKY H. An investigation of the mechanical properties of materials at very high rates of loading[J]. Proceedings of the Physical Society B, 1949, 62(11): 676-700.
[22] KRAFH J M, SULIIVAN A M, TIPPER C F. The effect of static and dynamic loading and temperature on the yield stress of iron and mild steel in compression[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1954, 221(1144): 114-127.
[23] HAUSER F E, SIMMONS J A, DORN J E. Strain rate effects in plastic wave propagation[M]//SHEWMON P G, ZACKAY V F. Response of Metals to High Velocity Deformation, Interscience, New York, 1961: 93-114.
[24] 曹增强, 盛熙.一种低压电磁铆接设备: CN200520079179.0[P]. 2007-02-07.CAO Zengqiang, SHENG Xi. A low voltage electromagnetic riveting equipment: CN200520079179.0[P]. 2007-02-07.
[25] 曹增强,韩超众,杨柳, 等. 基于电磁力加载的霍普金森压杆实验设备控制系统: CN201510050378.7[P]. 2015-06-03.CAO Zengqiang, HAN Chaozhong, YANG Liu, et al. Control system of Hopkinson pressure bar experimental equipment based on electromagnetic force loading: CN201510050378.7[P]. 2015-06-03.
[26] 曹增强. 一种基于电磁力的霍普金森拉压杆应力波加载平台: CN201610012240.2[P]. 2016-04-27.CAO Zengqiang. A stress wave loading platform of Hopkinson tension bar based on electromagnetic force: CN201610012240.2[P].2016-04-27.
[27] 曹增强, 左杨杰, 杨柳. 双轴霍普金森压杆和拉杆实验入射波等效加载的实现方法: CN201510047455[P]. 2017-02-22.CAO Zengqiang, ZUO YangJie, YANG Liu. Realization method of equivalent loading of experimental incident waves for biaxial-Hopkinson compression and tension rods: CN201510047455[P]. 2017-02-22.
[28] 曹增强, 左杨杰, 杨柳, 等. 电磁力霍普金森压杆和拉杆实验加载装置的入射波控制方法: CN201510049642.5[P]. 2015-06-03.CAO Zengqiang, ZUO Yangjie, YANG Liu, et al. The incident wave control method of electromagnetic force Hopkinson compression bar and tension rod experimental loading device: CN201510049642.5[P]. 2015-06-03.
[29] 聂海亮, 石霄鹏, 陈春杨, 等. 单轴双向加载分离式霍普金森压杆的数据处理方法[J]. 爆炸与冲击, 2018, 38(3): 517-524.NIE Hailiang, SHI Xiaopeng, CHEN Chunyang, et al. Data processing method for bidirectional-load split Hopkinson compression bar[J]. Explosion and Shock Waves, 2018, 38(3): 517-524.
[30] 曹增强,郑国. 基于双轴分离式霍普金森拉压杆多脉宽加载设备控制系统: CN201910169952.9[P]. 2019-06-11.CAO Zengqiang, ZHENG Guo. Based on biaxial split Hopkinson tension bar multipulse width loading equipment control system:CN201910169952.9[P]. 2019-06-11.
[31] LINDHOLM U S. Some experiments with the split Hopkinson pressure bar[J]. Journal of the Mechanics and Physics of Solids, 1964, 12(5):317-335.
[32] 惠旭龙, 刘小川, 白春玉, 等. 碳纤维增强复合材料的中低应变率力学性能试验研究[J]. 装备环境工程, 2018, 15(9): 81-84.HUI Xulong, LIU Xiaochuan, BAI Chunyu, et al. Mechanical properties of carbon fiber reinforced composite materials under intermediate strain rate[J]. Equipment Environmental Engineering, 2018,15(9): 81-84.
[33] ZUO Y J, CAO Z Q, CAO Y J, et al. Dynamic behavior of CFRP/Ti single-lap pinned joints under longitudinal electromagnetic dynamic loading[J]. Composite Structures, 2018, 184: 362-371.