薄壁结构具有重量轻、比强度高等优良的特性,被广泛应用于航空航天、汽车制造、电子通信以及船舶工程等领域,如航空发动机以及燃气轮机的高压压气机叶片、复材风扇叶片前缘金属加强边、整体隔框和平板天线等薄壁结构大多数采用铣削加工的方式进行零件成形[1]。然而,薄壁结构大多数具有体积大、结构复杂、壁厚不均匀、材料去除率高、刚性较弱等特点,此外,航空发动机薄壁结构材料多为钛合金或高温合金等难切削材料,在进行铣削加工时受到铣削力和铣削热等作用,极易产生较大的加工误差,影响薄壁结构的使用性能[2]。因此,对薄壁结构的加工误差进行预测和控制具有重要的意义。
随着有限元软件和智能算法的发展,大多数学者通过数值计算、有限元仿真及数据驱动的方式定量分析了薄壁结构的加工误差,提出了众多薄壁结构加工误差的控制方法,主要包括走刀路径优化、工艺参数优化、装夹布局优化及误差补偿技术等,解决了一些薄壁结构加工精度低的问题,但是对于诸如航空发动机整体叶盘叶片、复材风扇叶片前缘金属加强边等强非对称性薄壁结构,由于其型面弯扭程度大、无干涉刀轴空间小,导致其工艺参数优化窗口小,且加工工序复杂,单一的误差控制方法难以满足加工精度要求,因此,需要对薄壁结构加工误差的控制方法进行归纳,旨在为复杂曲面类薄壁结构的加工精度提升提供指导[3]。
本文首先对薄壁结构进行分类并且分析其加工特点,根据薄壁结构的加工特点分析了薄壁结构加工误差来源;然后根据误差来源不同对薄壁结构的加工误差进行了分类,面向不同类型的加工误差简述了现有的误差预测和控制方法;最后阐述了薄壁结构铣削加工误差控制方法的当前挑战和未来发展趋势。
1 薄壁结构的分类及加工特点
薄壁结构通常指轴向或者径向尺寸与其厚度之比大于10的结构。由于使用性能的不同,薄壁结构的种类较多,轴向或者径向尺寸与其厚度之比存在差异,但薄壁结构都具有相对质量低、刚性弱及受力易变形等特点[4]。通常情况下,薄壁结构往往以较轻的质量或较少的材料承受较大的载荷[5]。
1.1 薄壁结构的分类
薄壁结构可以按形状或材料进行划分。按形状可分为平板类、框架类、圆环类和复杂曲面类;按材料可分为铝合金、钛合金、高温合金及复合材料等。如图1所示,电子通信领域的平板天线等为平板类薄壁结构,飞机机身承重部件如整体隔框等为框架类薄壁结构,航空发动机机匣等为圆环形薄壁结构,压气机整体叶盘叶片、复材风扇叶片以及前缘金属加强边等都属于复杂曲面类薄壁结构;在材料方面,为了减轻飞机整体重量,机身承重薄壁结构多为铝合金材料,而航空发动机由于工作时温度较高,薄壁结构多采用钛合金和高温合金等耐高温材料。

图1 薄壁结构的分类
Fig.1 Classification of thin-walled structures
1.2 薄壁结构的加工特点
(1)材料方面。航空发动机上的薄壁结构多为钛合金或者高温合金材料,而这些材料硬度大,属于难切削材料,铣削加工过程中会产生较大的切削力和切削热,极易使刀具-工件系统产生弹塑性变形,最终使薄壁结构产生加工误差。
(2)结构方面。薄壁结构通常具有质量轻、体积大、刚度较弱的特点,对于复杂曲面类零件,刀轴无干涉空间小,会导致加工过程极易出现切削振动和变形,无法保证加工稳定性和加工精度,造成加工误差。
(3)精度方面。薄壁结构的设计尺寸要求较高,如航空发动机叶片要满足一定的气动性能要求,整体隔框要满足一定的装配精度要求,因此较高的铣削加工精度是薄壁结构满足设计要求的前提。
(4)刀具方面。由于复杂曲面类结构曲面曲率大,进行多轴铣削时具有狭窄的刀具无干涉空间,无法用直径较大的刀具进行加工,如前缘金属加强边内腔精铣时采用直径为2.5~6 mm的锥度刀,而小刀具-工件工艺系统刚性较弱,薄壁结构易产生加工误差。
2 薄壁结构加工误差来源及控制
薄壁结构具有结构复杂、刚性较弱、材料去除率大等特点,同时薄壁结构的铣削加工过程往往涉及多道复杂工序(原始毛坯到最终成形),涉及粗加工-半精加工-精加工过程,加工过程中影响加工精度的因素很多,因此,需要对薄壁结构的加工误差来源进行归纳总结,如图2所示,主要包括切削刀具、工件特性、切削参数、装夹系统、机床系统以及其他因素等。
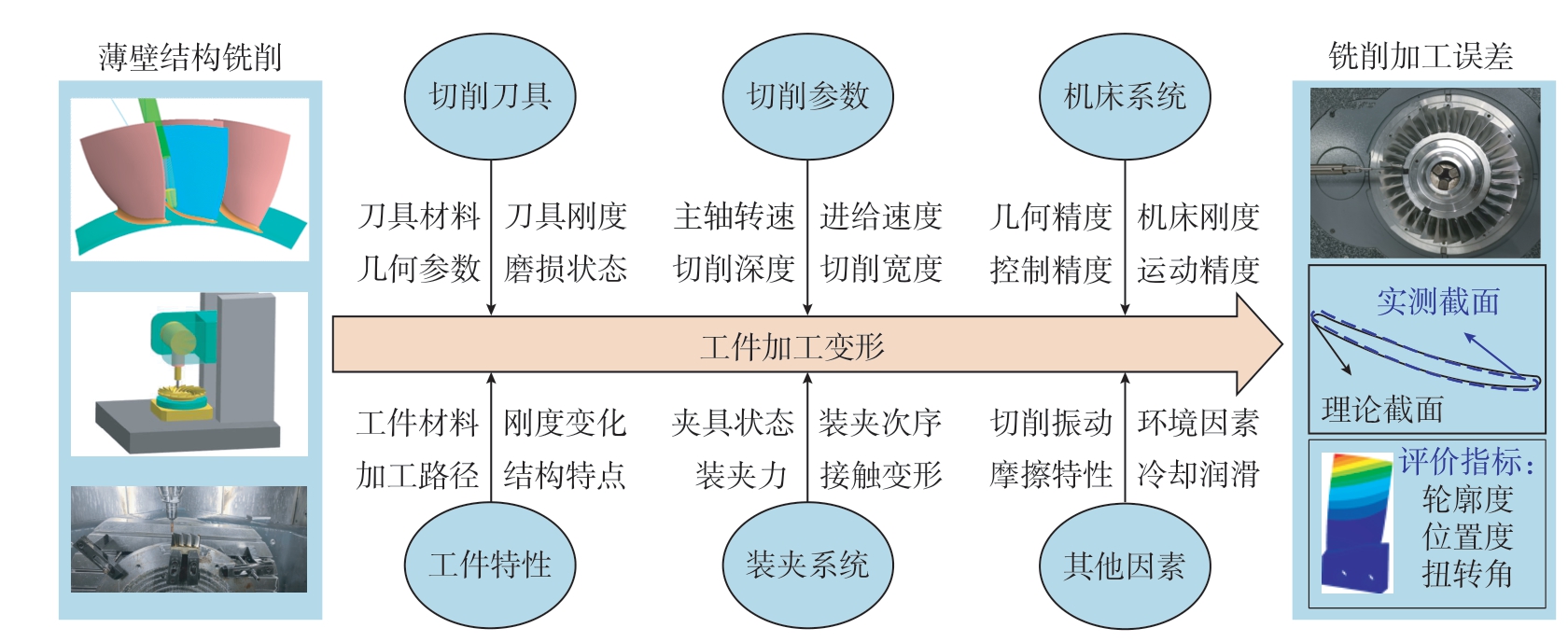
图2 薄壁结构铣削加工误差源
Fig.2 Sources of errors in milling of thin-walled structures
(1)切削刀具。一方面刀具直径的大小会直接影响刀具的弹性让刀变形;另一方面刀具材料的不同以及有/无涂层等都会使得刀具的磨损状态不同,这两者都会使得薄壁结构产生加工误差。 (2)工件特性。薄壁结构的材料包含复合材料、铝合金、钛合金和高温合金等,材料本身的物性参数(如材料的热膨胀系数、弹性模量、硬度等)及工件的结构特性都会造成不同的加工误差。(3)切削参数。切削参数的差异使得切削过程中切削力和切削热不同,从而影响薄壁结构弹性变形及切削残余应力诱导变形,使得薄壁结构产生加工误差。(4)装夹系统。装夹系统的作用是将工件固定到机床上,由于薄壁结构的壁厚较薄,一方面,夹紧力会使得薄壁结构产生弹塑性变形;另一方面,薄壁结构的装夹方式和装夹部位不同也会影响其弹性变形和残余应力释放,影响薄壁结构的加工精度。(5)机床系统。机床的几何误差和跟踪误差使得机床的实际运动轨迹与理想运动轨迹存在偏差,导致薄壁结构产生加工误差。(6)其他因素。切削过程中发生切削振动,造成工件产生较大的表面位置误差;不同的润滑方式对铣削力和铣削热的降低效果不同,产生不同的弹性变形和切削残余应力诱导变形,影响薄壁结构加工精度。
复杂薄壁结构的加工误差可以分为以下以下4类。 (1)系统误差。在加工前加工系统已存在的固有误差,包括毛坯的成形误差、装夹变形、刀具测量误差、机床误差等。(2)累积误差。加工误差在工序间传递而累积的误差,每道工序除了本工序带来的误差外,还要考虑关联工序的累积误差。(3)动态误差。加工过程中切削工艺引入的误差,随加工系统的变化而具有时变特征,包括加工振动、刀具磨损和让刀变形等。(4)时滞误差。薄壁结构加工完成并且卸载夹具后,由毛坯初始残余应力及切削诱导残余应力引起工件产生的滞后误差。如图3所示,毛坯经过铣削加工至最终成品,按照所经历的各个状态分析其加工误差。首先,毛坯在装夹定位时,由于毛坯成形的不确定性,导致出现加工余量包容性问题,使得薄壁结构产生系统误差;然后,在单点静态切削时,一方面,由于刀具磨损,容易使得薄壁结构加工不到位,另一方面,薄壁结构和刀具受到铣削力的作用,使得薄壁结构产生弹性让刀误差;接下来,对于动态切削过程,薄壁结构由于其弱刚性在动态铣削力的作用下会产生加工振动,使其产生表面位置误差,造成其加工表面粗糙度过大;此外,薄壁结构在机床夹持刀具的作用下完成切削过程,机床的静态/动态误差都会造成薄壁结构的轮廓误差;另外,薄壁结构加工完成后,由于其初始残余应力平衡被打破和切削残余应力的形成,薄壁结构需要通过变形使其内部应力重新达到平衡状态(产生的变形属于塑性变形);最后,薄壁结构的加工往往涉及多个工序,工序间存在误差的传递和累积作用。因此,本节将从6个方面对薄壁结构加工误差的预测和控制方法进行归纳总结,进而为其加工工艺优化提供指导。
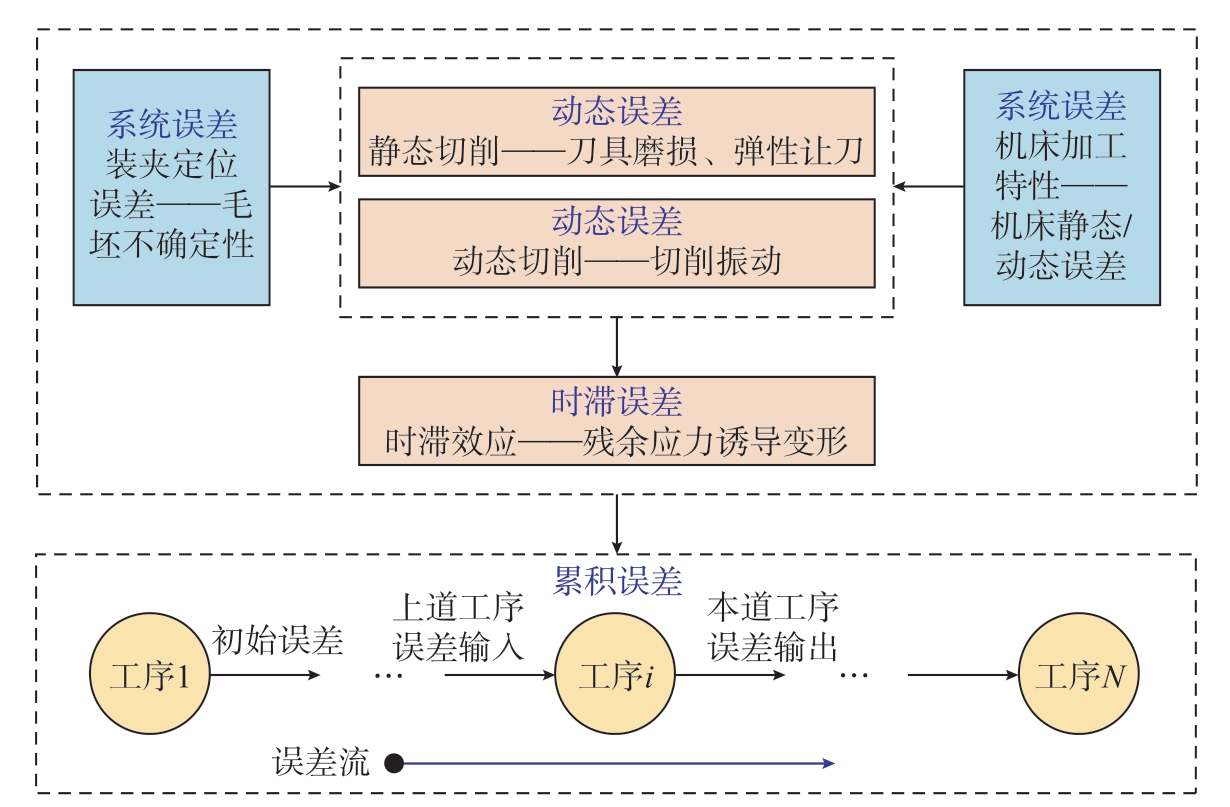
图3 薄壁结构铣削加工误差分类
Fig.3 Classification of milling machining errors of thin-walled structures
2.1 毛坯不确定性等几何问题引起的加工误差——系统误差
薄壁结构的毛坯往往是材料经过轧制、锻造、铸造等工艺制成的,为了提高材料的利用率,有些薄壁结构毛坯成形余量小,由于其壁厚较薄,变形程度大,导致毛坯实际尺寸和理论尺寸存在偏差,余量包容性差。若按照设计基准进行定位,会产生两种情况: (1)毛坯能够“包容”零件,则直接按照理论模型的数控程序进行加工; (2)毛坯不能够“包容”零件或者无精确定位基准,按照理论模型数控程序直接加工会产生超差报废、台阶缺陷等。对于第2类情况,下文以精锻叶片为例对毛坯不确定性等几何问题引起的加工误差控制所涉及的技术进行综述。
精密锻造叶片毛坯如图4所示,主要部位叶盆/叶背的锻造精度满足叶片的设计要求,然而,由于小半径和几何复杂的零件精密锻造成形精度差,精密锻造叶片的前缘和后缘的轮廓精度较低,不能直接用于航空发动机的使用,必须利用数控机床进行精加工,以确保最终精度满足设计要求[6]。由于精锻工艺过程复杂,往往会造成叶片型面不同程度的变形,导致余量包容性差,如图5所示,若以锻造基准直接按叶片名义模型对叶片前/后缘进行数控加工,零件毛坯的几何形状和空间位置的不确定性就会引起拼接处出现台阶、叶片型面位置度和轮廓度易超差,导致叶片前/后缘的形状难以满足设计要求。
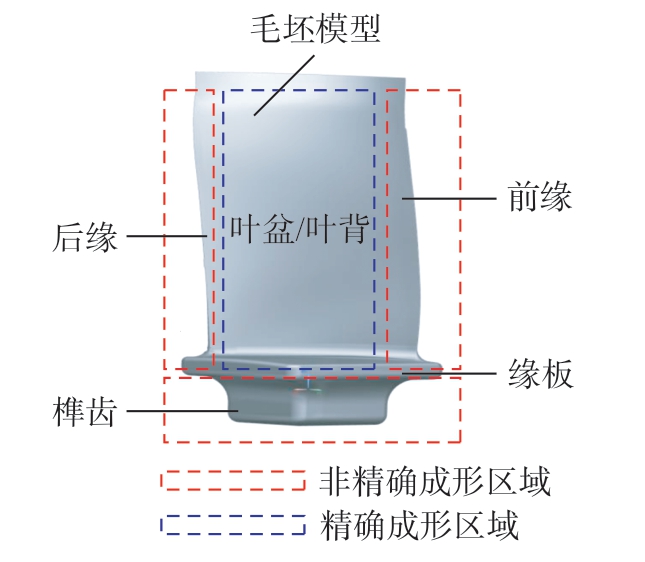
图4 精锻叶片示意图
Fig.4 Schematic diagram of precision forged blades

图5 精锻叶片加工误差示意图
Fig.5 Schematic diagram of machining error of precision forged blades
自适应加工方案可以有效解决由于毛坯不确定性等几何问题引起的加工误差。自适应加工工艺流程如图6所示,首先采用数控铣削的方式加工一个与叶片固连的中介基准,并以该基准建立叶片的测量坐标系,规划测量路径并进行测量和处理数据;然后运用多公差约束配准算法将实际测量数据和理论模型进行配准,获取理论模型在实际毛坯中的位置;最后采用在机测量方式测量装夹状态下的精锻叶片,构建装夹状态下叶片的工艺几何模型,根据工艺几何模型生成数控加工程序进行铣削加工。大量学者对自适应加工中涉及的数字化测量、配准定位、模型构建技术三大技术进行了探索。
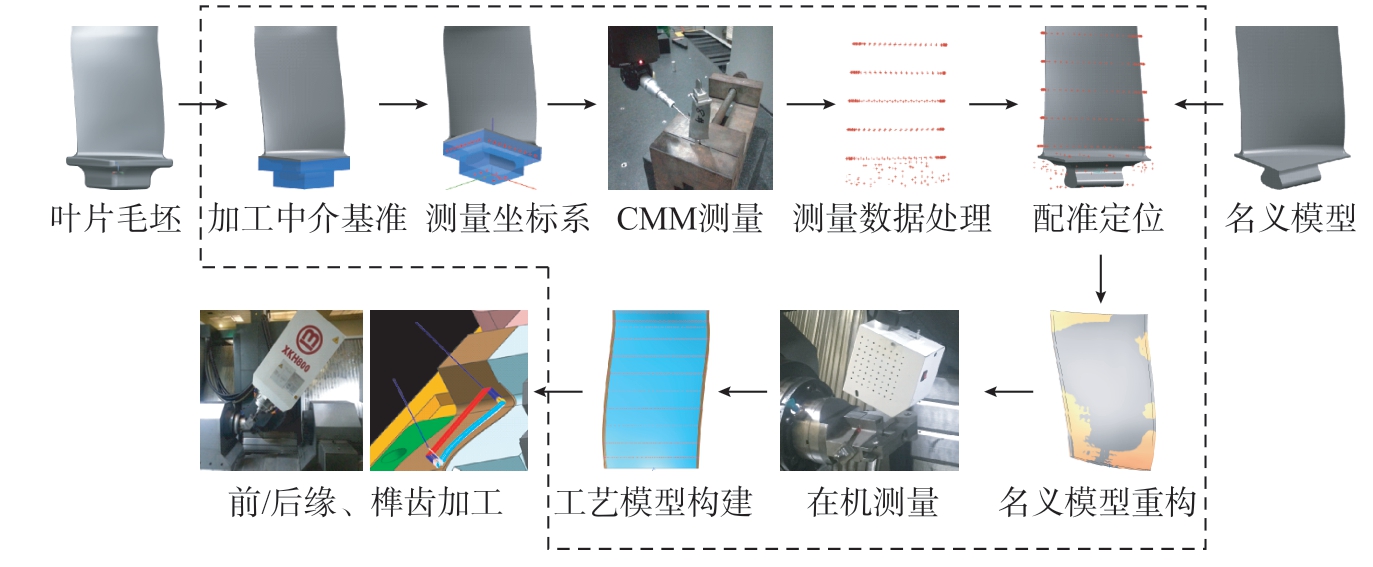
图6 精锻叶片自适应加工工艺方案
Fig.6 Adaptive machining process plan for precision forged blades
在测量路径规划方面,对于自由曲面检测,最常见的方法是使用坐标测量机(CMM)进行检测,首先对设计表面进行离散,获得一系列离散化点,然后以逐点方式进行检测,这种不连续和手动的检测方式造成检测效率极低,一些学者为提高其检测效率,对CMM扫描路径进行优化,Han等[7]建立了测量空间的三维蚁群图,提出一种改进的蚁群算法,该算法比标准蚁群算法更快地收敛到最优路径,提高了CMM的检测效率。Cheng等[8]提出了一种基于深度学习的智能测量方法和系统,用于高效测量常见部件的典型特征。虽然采用智能算法可以实现扫描路径的优化,在一定程度上提高了检测效率,但是对于涡轮叶片等大型复杂薄壁结构,通常也需要数小时甚至数天才能完成测量。为了解决这个问题,一种五轴测量机检测技术于近期被开发[9],五轴检测机的探头不是以逐点方式工作,而是在检测过程中不断接触零件表面并扫描,从而大大减少了测量时间;五轴检测机可以利用两个附加旋转轴提供的灵活性,进一步提高扫描效率。Zhou等[9]介绍了一种自动扫描路径规划系统,该系统使用具有3个平移轴和1个带有两个旋转轴的旋转头组成的五轴测量机生成连续扫描路径,用于检测任意自由曲面,该系统的两个旋转轴具有非常低的转动惯量,因此,具有较好的运动学优势,可以快速覆盖更大的扫描区域,显著提高扫描效率。Liu等[10]提出一种通过结合探头旋转和有效干涉检测来自动编程测量点检测的最优路径规划系统,可以显著缩短检测时间。Chen等[11]将表面扫描率引入五轴检测作为检测效率指标,将表面划分为单个螺旋条,建立了基于螺旋的检测路径生成算法。Shen等[12]提出一种基于图像的算法,用于生成平滑、无干涉的五轴扫描路径,极大地减少了测量机的运动载荷和动态误差。
在模型配准方面,刚性曲面的匹配方法一直受到学术界的密切关注。迭代最近点(ICP)算法假设两个三维曲面在刚性变换下相互关联,是实现刚性曲面配准非常实用且有效的方法。ICP通过搜索两个点集之间的对应关系来计算变换矩阵,但算法需要良好的初始值来保证收敛性,否则可能不收敛。Ji等[13]提出了一种集成遗传算法(GA)和ICP的混合算法,给定的测量点云和理论模型不需要任何初始参数估计,就可以实现点云和CAD模型的自动配准。He等[14]提出了一种从粗到细的配准方法,该方法使用主成分分析实现粗对准,并作为ICP精细配准的输入,所提出的配准方法具有较高的准确性。可见当前探索大多集中在算法加速和准确度等方面,一般为无公差约束情况下的配准。然而,在近净成形叶片的配准过程中,必须考虑叶片的形位公差约束,Feng等[15]提出了一种基于多公差约束的近净成形叶片配准算法,在多公差约束下,建立了基于轮廓度公差约束的全局配准模型和基于位置度和扭转度约束的局部配准模型,该配准方法能够提高近净成形叶片的铣削加工精度。陆正新等[16]在近净成形类零件自适应加工的过程中,针对传统配准算法无法有效约束零件形位公差的问题,提出一种基于满意度函数和灰关联度的多公差约束配准算法,将公差间平衡关系转化为多目标协同优化问题进行求解。对于非刚性大型薄壁零件,如在蒙皮的成型和装夹过程中,变形主要沿法向方向产生,非刚性蒙皮的变形可以被视为等距变形,轮廓特征的加工精度将由等距变形过程中不变的特征如测地线距离或弧长决定。因此,在配准过程中,保留弧长可以保证特征轮廓的相对关系,从而提高加工精度。而ICP算法不能保留弧长等特征,不能应用于蒙皮加工方面的曲面配准。对于等距变形,标称曲面中任意两点的测地线距离应等于实测曲面中两个映射点的测地线距离,通过使用等距不变曲面匹配,可以将标称曲面直接嵌入变形曲面中,该方法侧重于标称表面与实测表面之间的映射,并利用测地线距离偏差之和来估计映射误差。Bi等[17]根据等距曲面映射结果自适应调整刀具路径以补偿变形误差,加工后的变形蒙皮在曲面轮廓精度上得到了显著提高。
在模型重构方面,大多是根据测量数据采用样条曲线重构叶片曲面的截面线,然后经过放样得到薄壁叶片工艺模型,Zhao等[18]运用自由曲面变形技术(FFD)对涡轮叶片铣削工艺模型进行几何模型重构,将叶片原始形状按照其设计方式切成几个截面线,通过FFD技术,根据测量点对每个截面线进行修改,最后通过放样这些修改后的截面线来重建叶片。Yu等[19]基于叶片表面的特点,研究了叶片流道面的重建方法,根据实测点和四元数球面插值方法,提出了速度场的细分方法和积分算法,以提高重建精度。Zhao等[20]开发了一种构造曲面薄壁零件工艺形状的新方法,考虑轮廓约束、厚度约束和加工余量不均匀性,建立非线性约束优化模型,在公差范围内寻找可行点,基于这些可行点构建了新的工艺形状,可用于弯曲薄壁零件的自适应加工。Yan等[21]将叶片模型由一系列平面分割生成截面曲线(CSC),将理论模型和被测模型CSC之间进行配准,使用插值或外推法重建测量的CSC损坏或缺失部分,通过这些测量的CSC重建完整的模型。只根据测量数据重构的叶片模型前后缘不能够满足叶片的气动要求,Hou等[22]提出基于设计意图的补偿叶片几何建模方法,融合设计理念和测量数据,建立了考虑叶片气动性能的工艺模型。冯亚洲等[23]提出基于特征曲线相似变形的模型重构算法,精确重构精锻叶片前/后缘非精确成形区域的工艺几何模型,该方法可有效满足以精锻叶片为代表的复杂薄壁构件自适应加工要求。
综上所述,在测量方面,近几年对于路径规划不仅仅限于三轴测量机,五轴测量机在大型复杂曲面测量方面更有优势,但是现在的测量方式大多是采用的离线测量,对于五轴在机测量的报道较少;在配准方面,使用多个模型评价项组合的评价标准时,各项的权重往往以经验确定为主,未研究评价项之间的相互作用机制;在模型重构方面,主要以贝齐尔等曲线光滑拼接曲率较大的曲面缺失区域,构建的模型与理论叶片形状不相似,尤其是前/后缘区域难以满足设计部门对叶片气动性能的要求。
2.2 切削负载引起的加工误差——动态误差
薄壁结构件在铣削过程中会由于切削负载的作用产生切削力和切削热,一方面,切削力和切削热会使得刀具产生较大的磨损,导致刀具尺寸发生变化,出现加工不到位的情况;另一方面,由于薄壁结构自身的弱刚性,在铣削力的作用下不可避免发生弹性让刀变形,导致实际的切削深度小于理论设置的切削深度,致使部分材料未被切除,在走刀过后会发生回弹,从而造成弹性让刀误差,如图7所示。
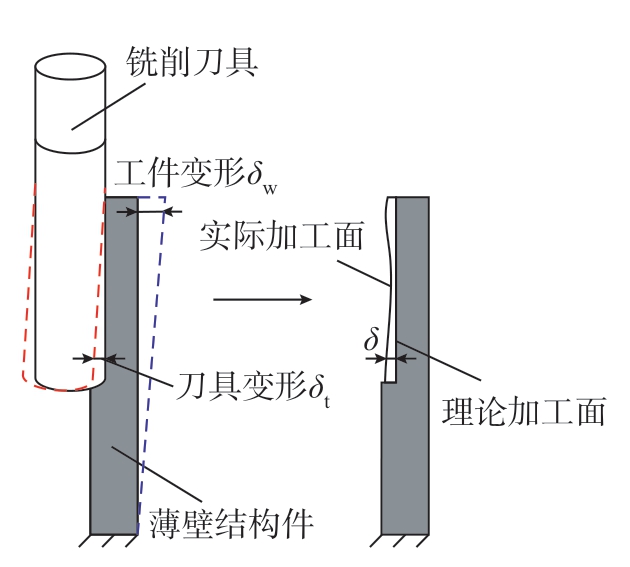
图7 铣削弹性变形示意图
Fig.7 Schematic diagram of elastic deformation in milling
2.2.1 切削负载引起的加工误差预测
一般来说,刀具磨损预测主要可分为直接和间接两种方式。直接预测方法是通过图像视觉和红外测量来量化不同加工时间下刀具的磨损状态,然后利用数据通过曲线拟合建立预测模型。间接预测方法是通过收集特定的传感器信号(如切削力、振动、声音和主轴电机电流等),然后选择适当的方法对信号进行处理,提取对刀具磨损敏感的特征参数,最后建立预测模型。直接预测方法需要中断加工过程,从而影响加工效率,而且,由于刀具与工件的接触,以及恶劣的加工环境(切削液和切屑),直接预测方法的应用在实际加工过程中受到了极大限制。近年来,间接方法因具有易于实施且不会干扰操作过程的突出优势而受到越来越多的关注。Corne等[24]通过主轴功率数据,使用神经网络建立了镍基高温合金Inconel 625钻孔过程中的刀具磨损预测。Zhou等[25]采用声音信号来监测铣削过程中的刀具磨损。随着传感器和信号融合技术的发展,监测的信号不仅限于某一种,出现了多信息融合的混合机器学习模型,解决了单一信号偶然性强、模型精度低等缺点。Cai等[26]提出一种基于长短期记忆网络(LSTM)的混合信息模型,用于刀具磨损预测,将LSTM模型与支持向量回归(SVR)、多层感知机(MLP)、卷积神经网络(CNN)进行了比较,发现混合信息模型在刀具磨损预测中表现出优异的性能。Cheng等[27]通过时域、频域和时频域提取切削力和振动信号的多域特征,提出一种基于鲸鱼优化算法优化支持向量机的刀具磨损预测方法。Huang等[28]通过收集三轴切削力和振动信号,提出一种基于多信息融合的混合机器学习技术的间接刀具磨损测量方法。Cheng等[29]提出了一种基于特征归一化、注意力机制和深度学习算法的刀具磨损监测和预测框架,所提模型在效率和鲁棒性方面具有较大优势。
关于切削力引起刀具和工件弹性变形的研究一直是学者们关注的焦点。对于弹性让刀的计算,大约经历了理论计算、有限元仿真、数据驱动3个过程。Liu等[30]将零件侧壁简化为悬臂梁、简单支承梁等,实现了不同切削力下的加工变形预测。Wu等[31]将有限差分法整合到薄壁板理论的计算过程中,建立了适用于不同加工参数的加工变形预测模型。党建卫等[32]将铣削力和刀具变形作为已知量,并将铣削中铣刀刀齿的运动近似为圆弧轨迹,通过数学模型搭建了铣削加工中铣刀刀齿运动轨迹的离散模型,据此可计算得到刀齿轨迹的位置,进而实现对加工误差的预测。Wan等[33]通过分析加工瞬时切削力系数,得到切削力求解模型,然后建立薄壁零件的有限元模型用于计算工件的加工误差。Habibi等[34]基于悬臂梁模型和有限元法提出了一种虚拟加工系统,通过在虚拟环境中模拟加工过程实现对加工误差的预测。基于加工理论并考虑铣刀跳动,Chen等[35]提出了一种可变螺旋立铣刀的统一解析切削力模型,进一步提高了有限元分析薄壁件变形的精度。Ge等[36]提出了一种考虑材料去除效应的高效变形预测方法,即工件刚度矩阵减小后进行动态修正,避免重新网格划分,减小求解变形的计算复杂度。Li等[37]提出了一种基于几何形状和切削载荷时空相关学习的加工变形预测方法,将理论几何变化和实际切削载荷变化在时间和空间上融合,提出一种深度时空学习网络,对复杂的几何-载荷-变形关系进行预测。
2.2.2 切削负载引起的加工误差控制方法
对于刀具磨损的加工误差控制方法主要是通过改变润滑方式和优化切削参数实现的,Yildirim等[38]考察了冷却方法和铣削参数对镍基高温合金铣削刀具寿命和表面粗糙度的影响,通过使用不同的冷却方法进行试验,发现干式加工产生的磨损值最高,而湿式加工的磨损值最低,虽然湿式加工实现了最佳的冷却/润滑结果,但使用微量润滑(MQL)进行加工的结果与湿式加工的结果非常接近,因此,考虑到生产成本和环境,建议在铣削中使用MQL系统。Wang等[39]通过试验研究了钛合金TC21在不同冷却条件下铣削的刀具磨损机理,在干铣和高速铣削加工过程(HPAC)中发现刀具磨损剧烈,会严重影响加工精度,降低刀具寿命,使用相同的铣削参数加工,MQL润滑条件下,没有观察到剧烈的磨损阶段,并且刀具边缘和刀尖的形态保持完整性。Pei等[40]使用低温气体喷射冷却进行铣削试验,研究了各种低温气体射流参数对刀具磨损的影响,通过优化射流冷却参数控制刀具磨损。Sundaramoorthy等[41]应用田口技术找出硅化镁合金与铝的数控铣削加工中最小刀具磨损的工艺参数,根据优化结果进行试验,刀具磨损减少了20.26%。Vavruska等[42]提出了一种用于复杂形状表面点铣的主轴速度和进给速度控制新方法,刀具寿命延长了28%。Li等[43]提出了一种基于强化学习的刀具磨损预测和切削参数优化集成方法。
对于由于切削力引起的弹性变形误差控制主要是通过工艺优化和误差补偿来实现的,如图8所示,工艺优化主要包括工艺参数优化、走刀路径优化和夹具优化,误差补偿技术主要是通过反变形原理建立工艺模型。
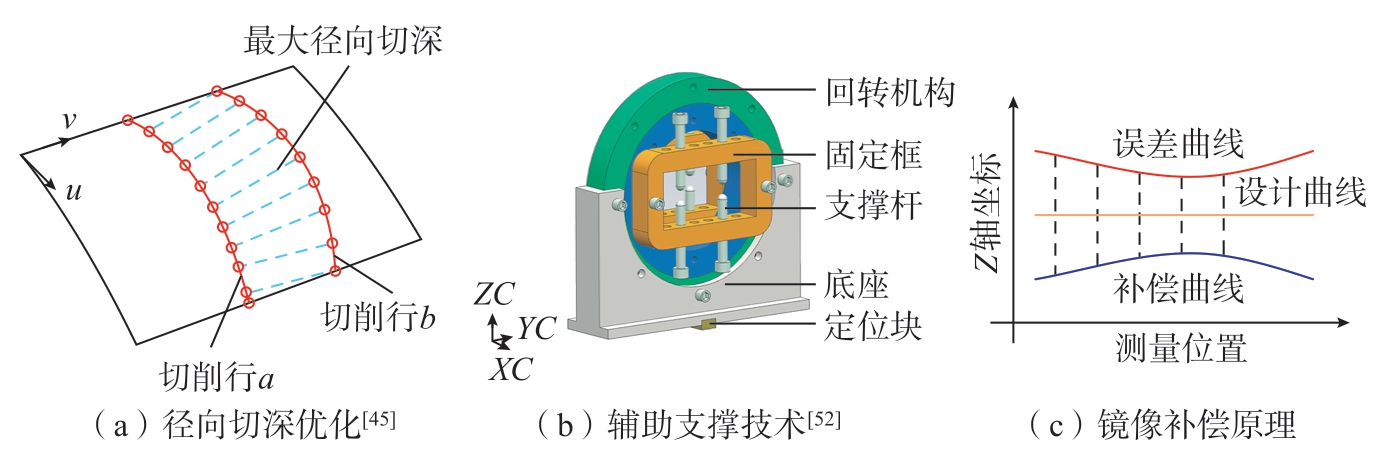
图8 弹性变形主要控制方法
Fig.8 Main control methods of elastic deformation
基于加工误差预测模型,采用智能优化算法,建立包含加工误差最小为目标的优化模型,是目前加工参数优化的主流趋势,Wang等[44]结合田口法、主成分分析法和非支配排序遗传算法II(NSGA-II),提出了一种以尺寸精度为目标的加工参数优化方法。Hou等[45]开发了基于稳态变形场的薄壁叶片可变径向切削深度优化算法,如图8(a)所示,该方法兼顾薄壁叶片的加工精度和效率。Lei等[46]开发了基于线性规划的进给率优化算法,优化后的进给率在切削加工时显著提高加工精度和效率。谢义[47]以材料去除率和最大加工变形量作为优化目标,对铝合金薄壁零件加工参数进行了优化。赵刘生[48]以切削宽度、切削速度、进给量和切削深度为设计变量,建立汽轮机叶片加工误差的响应面模型,将变形量和加工时间作为参数优化的目标,采用自适应变异遗传算法对4个切削参数进行多目标优化设计,优化后的切削参数使变形量减小。在走刀路径优化方面,不同的刀具轨迹会对薄壁结构的刚度产生不同影响,造成不同的弹性让刀误差,田荣鑫等[49]采用同步半精铣-精铣加工方法对线性摩擦焊后的风扇叶片进行加工,从叶尖开始,先以半精铣参数加工叶片上某一区域,再以精铣参数完成这部分区域的加工,如此循环直至完成整个叶片的加工,该方法可以保证叶片精铣时刚度好,减小了弹性让刀误差。Hou等[45]发现对于薄壁叶片铣削工艺,优先铣削叶片低刚度区域的切削路径可以达到较低的弹性让刀误差。在夹具优化方面,主要是通过优化夹具结构使得薄壁结构的刚度得到提升,从而减小弹性让刀变形。Lan等[50]为减小大型薄板工件立铣过程中的挠度误差,建立了智能镜像铣削加工系统,该系统包括两个可移动的支撑头,将其通过真空吸附的方式固定在工件上,从而提高工件在加工过程中的刚度,减小弹性变形误差。Wu等[51]提出一种新型多点辅助支撑技术来抑制叶片挠度误差。郑志阳等[52]设计了四自由度回转辅助支撑机构增加叶片的加工刚度,如图8(b)所示,叶身型面通过上下成对的球头螺杆进行支撑,该回转机构可以绕X轴进行旋转,可以适应不同弯扭程度的叶片,并提出了一种基于遗传算法优化支持向量机回归(GASVR)的薄壁叶片辅助支撑布局优化方法,优化后的辅助支撑布局方案对叶片加工弹性变形的抑制程度可达57.6%。在误差补偿方面,基于弹性变形预测的迭代补偿方法可以减小试验,降低成本,Huang等[53]为了减小切削力引起的静态挠度,通过迭代算法求解轴向切削深度(ACD)与力引起的误差之间的耦合模型,确定了用于补偿静态壁厚误差的改进ACD。Ge等[54]建立了考虑刀具-工件动态相互作用的迭代切削力诱导误差预测模型,基于误差预测模型,利用数控系统的EMZPS函数开发了实时误差补偿系统。然而,由于弹性变形量的计算过程中采用了大量近似计算,导致补偿效果一般,随着在机测量技术的发展,基于测量结果实时修改刀位点的方案可以提高补偿效果。Gao等[55]为减小钛合金等难加工材料制成的薄壁曲面零件的加工变形,提出了一种基于修改刀具定位点的高效补偿方法,以钛合金TC4薄壁弧形件为例进行铣削试验,补偿后最大变形值从104 μm减小到49 μm。Wang等[56]提出了一种在线测量和余量补偿方法,可以应用于薄壁零件加工以提高加工精度。Zhang等[57]提出一种同时考虑轮廓约束和厚度约束的曲面件综合补偿方法,通过使用权重法定义综合约束,将具有轮廓和厚度约束的多目标优化问题转换为单目标优化,从而构建新的模型外表面,然后通过镜像补偿原理计算刀具路径。
综上所述,对于切削负载引起的复杂曲面变形的控制方法较多,但是仍未形成面向变形控制的自适应加工系统,利用多类型传感器实时监控加工过程中切削负载引起的变形,实现薄壁结构加工变形的自适应控制是未来探索的重点。
2.3 切削振动引起的加工误差——动态误差
切削过程中有3种机械振动:自由振动、强制振动和自激振动。自由振动是由撞击引起的;强制振动是由齿轮、轴承、主轴和其他机床部件之间的不平衡引起的;自激振动是由刀具与工件相互作用产生的交变力引起的未衰减振动,这种类型的振动增加了系统的不稳定性和不可控性。根据振动中存在的特定自激机制,颤振可分为3种类型:摩擦颤振、模式耦合颤振和再生颤振。摩擦颤振是由刀具与工件在与切削速度相同的方向上相互摩擦引起的;模式耦合颤振是由两种自然振动模式的耦合引起的,因为振动元件在两个不同方向上的刚度略有不同,可以通过试验建模和分析获得系统的稳定条件;再生颤振是由先前切削过程中形成的振动位移与后续切削过程中的振动位移之间的相位差引起的切屑厚度差异引起的,如图9所示。限制铣削加工生产精度和效率的主要因素是自激颤振,尤其是再生型颤振,会造成薄壁结构产生较大的表面位置误差,影响其表面粗糙度。
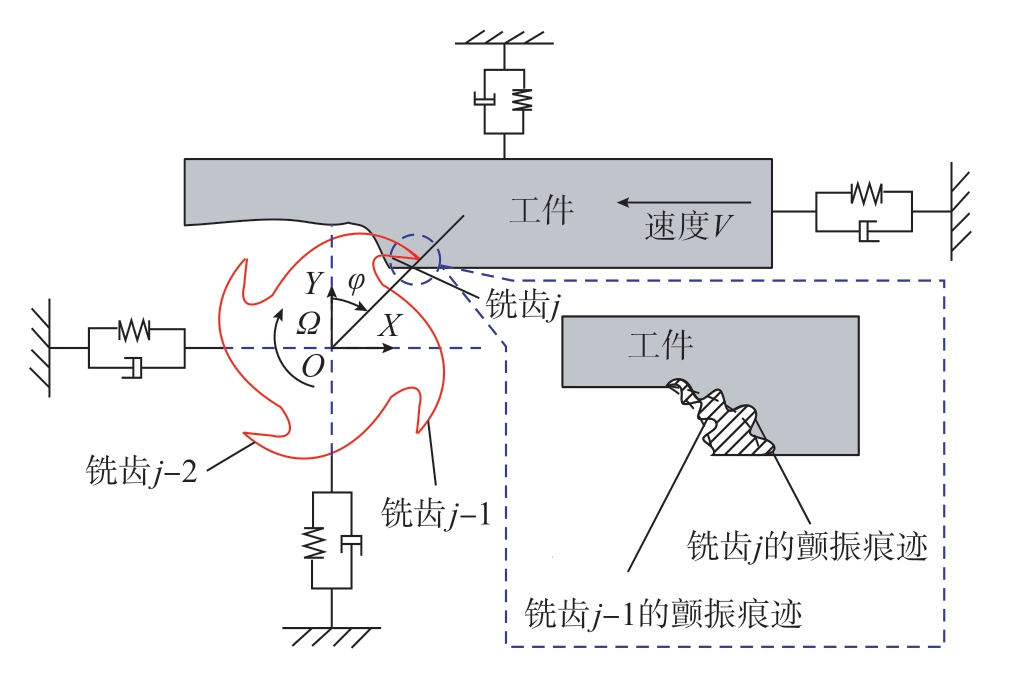
图9 铣削再生型颤振示意图
Fig.9 Schematic diagram of regenerative chatter in milling
2.3.1 切削振动引起的加工误差预测
在数学上,再生效应的切削动力学模型由时间周期参数的延迟微分方程(DDE)构成。因此,求解DDE可以获得铣削过程的稳定性边界,将切削区域划分为稳定和不稳定切削区域,可以从稳定性叶瓣图中选择适当的切削参数,避免颤振,提高加工效率和加工质量。动态响应模型的求解方法一般有3种:频域法、时域法以及试验法,如图10所示。
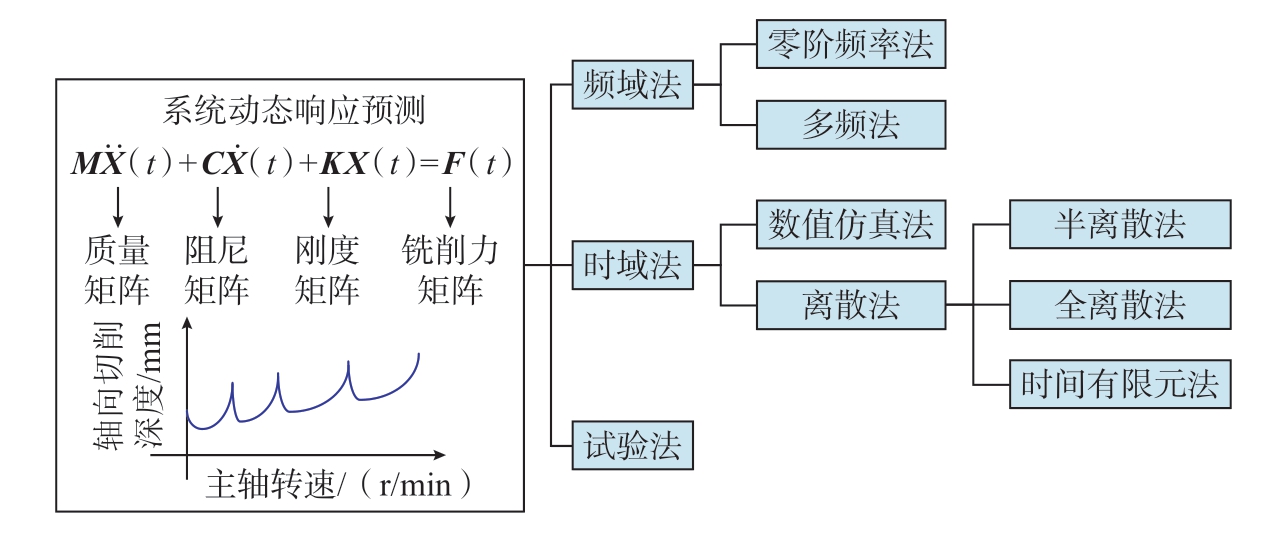
图10 薄壁结构铣削动态响应模型的求解方法
Fig.10 Solution method of dynamic response model of thin-walled structure milling
频域法是在傅里叶变换和控制理论的基础上,将模型的延迟微分方程用频域表示,最终通过计算得到稳定域,可以分为零阶频域法和多阶频域法。时域法是将系统动力学微分方程在时间周期内进行离散,设定初始条件进行迭代求解,通过结果确定颤振稳定域,直接求解了动力学方程,可以引入刀具偏心和刀具跳动等因素,预测精度可以达到更高要求。试验法是通过试验来确定颤振稳定域,选取不同的切削深度进行加工,得到多组振动信号,以此来确定加工状态。3种方法的优缺点对比如表1所示[58-63]。
表1 铣削动态响应模型的求解方法对比
Table 1 Comparative analysis of solving methods for milling dynamic response models
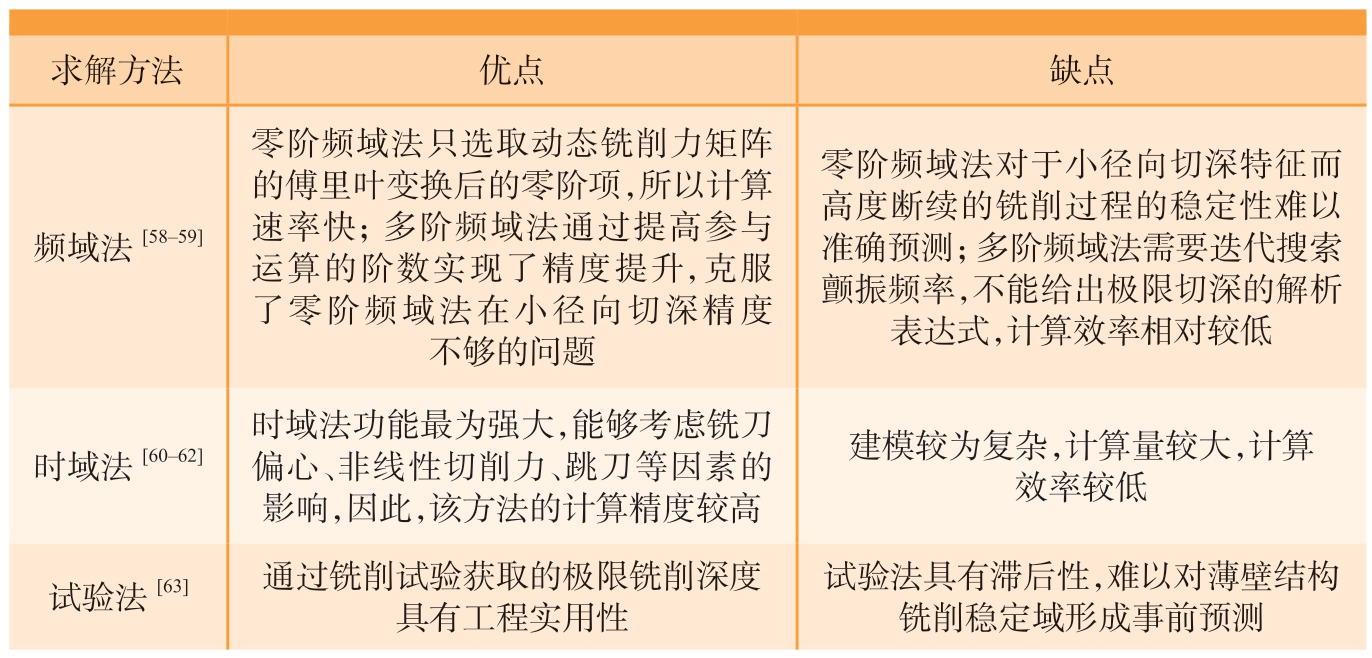
求解方法 优点 缺点频域法[58-59]零阶频域法只选取动态铣削力矩阵的傅里叶变换后的零阶项,所以计算速率快;多阶频域法通过提高参与运算的阶数实现了精度提升,克服了零阶频域法在小径向切深精度不够的问题零阶频域法对于小径向切深特征而高度断续的铣削过程的稳定性难以准确预测;多阶频域法需要迭代搜索颤振频率,不能给出极限切深的解析表达式,计算效率相对较低时域法[60-62]时域法功能最为强大,能够考虑铣刀偏心、非线性切削力、跳刀等因素的影响,因此,该方法的计算精度较高建模较为复杂,计算量较大,计算效率较低试验法[63] 通过铣削试验获取的极限铣削深度具有工程实用性试验法具有滞后性,难以对薄壁结构铣削稳定域形成事前预测
2.3.2 切削振动引起的加工误差控制方法
从广义上讲,颤振抑制技术可分为被动控制和主动控制。被动控制技术通过改进机床设计/使用可以吸收额外能量/消除再生效应的设备来提高加工过程的稳定性,通常使用阻尼器或特殊工具来抑制颤振。Moradi等[64]设计了一种可调谐减振器来抑制悬臂板铣削中的再生颤振,找到吸收器位置及其弹簧刚度的最佳值,从而使板振动最小化,使用可调谐减振器可以极大地改善铣削工艺的稳定性极限,可以获得更大的稳定切削深度,提高铣削加工效率。Butt等[65]设计了非接触式涡流阻尼装置来抑制颤振,该设备的优点是适用于不同尺寸的工件。Zhang等[66]表明在黏性流体条件下,铣削系统的阻尼显著增加,工件的刚性保持不变,而铣削系统的频率由于黏性流体质量的增加而降低,此外,还降低了切削力系数,与干式铣削相比,在黏性流体条件下切削力系数显著降低。Ma等[67]利用磁流变液作为相变材料,构建了面向磁流变可控阻尼支撑夹具-工件系统试验验证平台,试验结果表明,磁流变可控阻尼支撑夹具能够提高叶片铣削稳定性,减小加工误差。张鸿泽[68]提出了一种通过在薄壁零件上使用附加质量和电涡流阻尼来提高铣削过程稳定性的方法。对于飞机常见的大型承重部件(如整体壁板和整体隔框)而言,由于其尺寸较大,无法采用附加质量或者磁流变夹具来抑制颤振,因此,一些学者开发出了可移动支撑夹具来提高薄壁结构加工精度和效率。Wan等[69]设计一个移动夹具,该夹具以相同的速度随铣刀移动,为瞬时加工位置提供额外的刚度和阻尼,以抑制大型薄壁结构铣削过程中发生的颤振。Fu等[70]首次引入了具有双并联运动机床(PKM)配置的同步双面铣削的概念,即双PKM以原位和实时地在薄壁工件的两侧进行同步铣削和支撑,在双PKM协同操作下,工件的刚度得到显著提升,提高了加工表面质量和精度。除了增加工件的质量、刚度和阻尼等方法来抑制颤振外,还有一些学者通过改变铣刀的内部结构和参数来抑制颤振,如Galarza等[71]在长径比为7的球头铣刀中加入冲击阻尼器钢球来减少铣削时的振动。刘建永等[72]采用变螺旋角、变齿距和标准铣刀切削钛合金TB6,发现改变螺旋角和齿距可以有效减小铣削颤振。司博文[73]不仅分析了不等齿距立铣刀的减振机理,还在兼顾效率和精度下对其相匹配的工艺参数进行优化。
主动控制技术通过检测机床的状态来确定铣削的动态行为,然后通过主动执行决策来调整加工状态。主动减振系统通常由监测、诊断和执行元件组成。由于计算机、传感器和驱动器领域技术的不断进步,主动控制技术变得越来越重要,可以显著提高铣削过程的稳定性。Munoa等[74]使用外部加速度传感器获取加工实时状态,控制器根据传感器信号控制驱动器产生驱动力来抑制颤振的发生。Wan等[75]提出了使用滑模控制和电磁致动器的主动铣削颤振抑制。Li等[76]通过将压电致动器和位移传感器集成到主轴-刀具-工件系统中,设计了一种主动颤振控制结构。高顺[77]利用激光位移传感器实时测量刀具的振动状态,基于主动控制律计算控制电压并输出给压电作动器,可实现实时控制,提高了加工准确性。王俊鹏[78]使用磁流变阻尼抑振设备同时作为工件装夹装置和驱动器,对薄壁件的铣削振动进行有效的主动控制。
综上所述,对于铣削振动的预测主要是通过求解动力学方程获取铣削的稳定性叶瓣图,从而得到铣削稳定域,但是复杂薄壁结构铣削系统响应预测方面的模型准确度和算法精度需要进一步探索;对于铣削振动的控制以被动控制研究和应用较多,对于主动控制方面缺少相关理论探索,导致其在复杂薄壁结构方面的应用较少。
2.4 机床误差引起薄壁结构加工误差——系统误差
机床误差包括静态误差和动态误差,如图11所示。静态误差是指机床不移动(主轴不旋转或工作台不移动)或运动速度低时的误差,包括几何误差和热误差。几何误差是机床部件在制造和装配过程中产生的误差,与负载无关;热误差是机床零部件由于环境温度的变化而产生的热膨胀和变形。动态误差是指加工过程中仅在机床运动状态下出现的误差,包括切削力载荷误差和控制系统误差。切削力载荷误差指的是在加工过程中由切削力载荷造成的机床部件应变或振动,从而导致的加工误差。控制系统误差通常定义为在复杂联动加工过程中,由于机床的伺服参数不匹配、进给速度过快引起机床运动不同步产生的跟踪延时,进而通过机床运动传递表现为实际运动轨迹与设置运动轨迹之间的偏差。所有提到的来自机床的误差都会使薄壁结构在加工时产生形状尺寸误差。
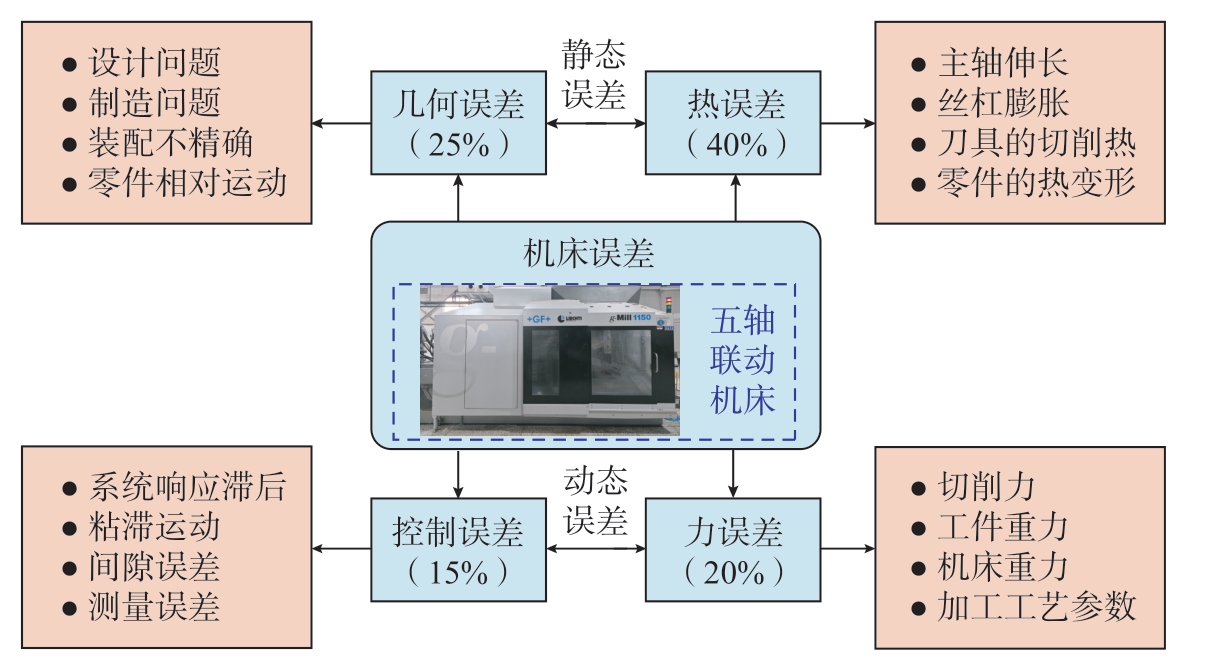
图11 机床的主要误差源
Fig.11 Main sources of error in machine tools
2.4.1 机床误差引起薄壁结构加工误差预测
机床几何误差的模型主要是基于多体系统(MBS)理论建立的,Li等[79]采用一种基于多体系统理论的误差建模方法,构建了某五轴机床误差源与切削刀具位姿误差的映射模型。Niu等[80]提出一种全局敏感性分析方法,基于多体系统理论,建立空间误差模型,分析几何误差与加工精度之间的非线性映射关系。Tao等[81]基于多体系统理论和铣削理论,建立了考虑37个几何误差的加工误差模型,引入一种新的灵敏度分析(SA)方法,以加工误差模型为敏感性分析模型,提出了一种具有表达简单的灵敏度指标,即各几何误差引起的加工误差峰值,该方法可以扩展到多轴机床。对于机床热误差的建模方法主要为有限元法和数据驱动的方法。有限元法首先计算热源的功率得到机床的多维温度分布,然后通过有限元软件在机床主轴模型上施加热载荷和边界条件,最后通过有限元软件计算机床的热致变形,有限元建模的挑战来自机床的复杂性和各种机床结构之间的热相互作用,热边界条件难以准确确定;数据驱动法首先进行主轴温度和热变形测量,然后采用最小二乘法、回归分析、神经网络、灰色系统法等建立热误差模型。Zhang等[82]基于装配尺寸链原理,机床上所有受热误差影响的对象都被选为构成回路,在此基础上建立了热误差传递函数,利用机床热误差传递函数建立了机床热误差模型。Fu等[83]将基于鸡群优化算法的径向基本函数神经网络应用于集成热误差建模。Wei等[84]提出一种基于高斯过程回归(GPR)的热误差建模方法,提供热误差的区间预测,将GPR模型的预测结果与岭回归、主成分回归和长短期记忆网络模型的预测结果进行了比较,所提出的机床主轴热误差建模方法,可以在不同工况下实现较高的预测精度。对于动态加工误差,Li等[85]对XY工作台的动态特性进行了深入分析,建立了XY工作台运动部件的动态定位误差模型,推导了XY工作台动态定位误差的理论模型,将数控机床相关误差试验平台的实际参数代入模型进行理论计算和分析;结果表明,工作台的运动速度、工件的重量、工件的安装位置和摩擦力是造成动态定位误差的主要因素。Yang等[86]提出基于螺杆理论的多轴数控机床运动学建模,基于元作用层分析机床的运动过程,根据运动轴的结构和运动学关系,可以得到机床的运动学和运动学误差模型,从而可以预测多轴机床的加工精度。
2.4.2 机床误差引起薄壁结构加工误差的控制方法
对于机床误差引起薄壁结构的加工误差,如果从提高机床硬件方面来控制机床引起的加工误差会产生较高的成本,同时还要涉及机床的设计原理和硬件改造,难度较大;从加工工艺角度来降低机床误差对薄壁结构加工误差的影响,可以高效地实现薄壁结构加工误差的控制以降低加工成本。目前工艺控制方法主要有优化工件位置、控制机床运动参数及优化刀轴矢量等。Liu等[87]通过有限元仿真,将支撑底座在多种工况下的实时变形转化为运动系统的节点面变形,建立系统的动态误差模型,实现机床复杂误差源的模型解耦,可以根据机床的动态特性有效地识别机床的最佳加工空间,提高机床的加工精度,图12显示了机床加工空间布局的优化,将可加工空间划分为多个加工单元,根据所需的相邻加工单元,遍历加工空间中所有可能的相邻加工单元,通过比较智能找到误差最小的区域。韩江等[88]根据机床的运动学关系建立非线性误差模型,为了限制非线性误差的大小,采用粒子群算法优化五轴机床工件的最佳安装位置。Liu等[89]提出一种考虑机床几何和运动学约束的数控加工自适应进给率规划方法,此种进给率规划方法使机床能够平稳快速的运动,提高了加工质量和加工效率。Lu等[90]提出一种基于新型参数化方法并结合共形变换理论的等参数路径规划策略,该方法适应叶片表面的曲率,提高了机床的运动学性能,降低了多轴协调运动控制的复杂性,提高了加工精度。Ma等[91]提出一种基于曲面加工旋转进给轴运动特性的刀轴矢量优化方法,根据旋转进给轴的运动学特性优化刀轴矢量,提高了复杂曲面件的加工精度。Qian等[92]根据机床的旋转轴需要满足最大角速度、最大角加速度和最大角加加速度的要求,提出基于机床运动学约束优化刀轴矢量。Wu等[93]提出了一种最小加速度局部修正方法来规划五轴球头铣刀加工的刀轴方向,该方法避免了刀轴矢量的剧烈变化,提高五轴机床的两个旋转轴的运动学性能并实现良好的加工精度。

图12 加工空间布局的优化[87]
Fig.12 Optimization of machining spatial layout[87]
综上所述,对于复杂薄壁结构的加工精度提升,同时考虑机床动态特性和机床联动误差的报道较少,探索机床动态特性与动态误差的关系,以机床动态性能为约束,通过优化机床运动参数和刀轴矢量实现复杂薄壁结构加工精度的提升是未来的发展趋势。
2.5 薄壁结构残余应力变形——时滞误差
薄壁结构在铣削时随着材料的去除以及受到铣削力、铣削热的作用,原有的残余应力和加工过后新产生的切削残余应力为达到平衡状态将重新分布,从而导致薄壁结构产生塑性变形。初始残余应力,是由于轧制、锻造、淬火、铸造和挤压等加工工艺中施加在材料上的热载荷和机械载荷而导致毛坯产生的固有应力。在切削加工中材料去除会打破残余应力的初始平衡,导致成品零件卸载夹具后发生变形。图13(a)显示了铝坯料内部由于其先前的制造过程而产生的典型初始应力分布,毛坯内部存在应力平衡系统。当材料的某个部分从原始毛坯上进行加工移除时,切削部分内的应力(虚线轮廓)被移除,如图13(b)所示,剩余材料内部的应力平衡受到干扰,零件需要通过变形使其内部应力重新分布建立新的平衡状态。切削引起的表面残余应力是由于切削过程中的高温、高压、高应变率和相变引起的严重非弹性变形而发生的。应力层的深度很浅,通常不超过0.2 mm,如图13(c)所示。薄壁结构铣削过程是工件在刀具的作用下以非常高的速率完成材料的剪切。这是一种涉及高切削力和温度的热机械现象。目前,一般认为加工残余应力来源于以下3个方面。(1)机械载荷造成的残余应力。切削加工引起工件产生不均匀的塑性变形,从而影响材料的弹性恢复,在材料内部产生应力。 (2)热应力引起的残余应力。切削产生的切削热形成不均匀的温度场,使得材料冷却后内部产生应力。 (3)相变而产生残余应力。切削产生的切削热使得局部温度超过材料的相变温度,组织发生相变,不同相的晶体体积不同,从而诱导材料内部产生残余应力,薄壁结构加工后产生的最终残余应力是这些现象之间平衡的结果。对于不同的结构,初始残余应力与切削残余应力对变形的贡献率有所不同[94]。国内外学者对于切削残余应力引起的变形预测与控制进行了大量的研究。
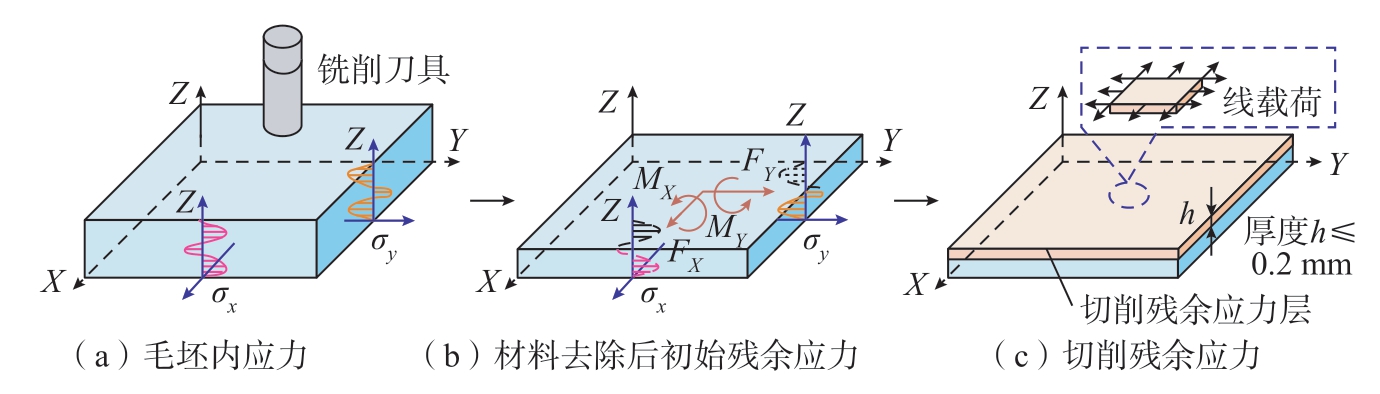
图13 铝坯料典型初始应力和切削残余应力分布
Fig.13 Typical initial stress and cutting residual stress distribution of aluminum billet
2.5.1 薄壁结构残余应力变形预测
在薄壁结构切削残余应力变形预测方面,对于简单的薄板件,可通过切削残余应力建模结合板壳理论计算翘曲变形量;对于框类、曲面类等复杂薄壁结构,主流手段仍然是使用有限元仿真,如图14所示,通过经验模型、有限元模型或者解析模型获取残余应力梯度分布,然后在节点处施加等效应力大小和方向,利用有限元软件计算工件的残余应力变形。Wan等[95]将基本铣削原理与典型接触力学相结合,考虑切削刃的热弹塑性载荷和松弛效应,详细推导出了由机械载荷和热载荷引起的切削残余应力的表达式,从而实现铣削残余应力的预测,进而为残余应力变形预测提供基础。Gao等[96]将薄壁框类零件等效为悬臂梁,并基于弹性理论与有限元仿真计算等效刚度,进而建立起残余应力变形的半解析预测模型。Ma等[97]基于有限元分析研究了铝合金框类零件铣削过程中内应力的演化规律,发现初始残余应力在工件扭曲变形中起主要作用,但加工残余应力同样不可忽略。Chen等[98]将灰色关联分析和反向传播神经网络进行结合,实现镁锂合金铣削过程中残余应力变形机理分析,发现切削速度提高而导致的切削温度升高是引起残余应力变形的首要因素。孔文滕[99]分析了热致残余应力受温度梯度和层深影响的规律,通过有限元软件利用等效弯矩法对薄壁零件的热致残余应力变形进行建模。王骏腾[100]提出了一种基于工况映射和薄壳应力绑定贴合的薄壁件残余应力变形的预测方法,通过试验测量或者模型预测各工况下的零件加工残余应力分布,然后利用有限元软件进行应力再平衡计算,得到零件的残余应力变形状态。对于叶片等复杂曲面类零件,周金华[101]采用了壳-实体界面绑定约束的建模方式来仿真叶片残余应力变形,图15展示了单独加工叶盆/叶背面残余应力引起的变形云图,加工叶盆面时最大变形量为0.527 mm,而加工叶背面时最大变形量为0.493 mm,可以看出,叶盆面对残余应力更加敏感,即相同的切削残余应力在叶盆面比在叶背面上引起更大的翘曲变形。

图14 切削残余应力变形仿真流程
Fig.14 Simulation process of cutting residual stress-induced deformation
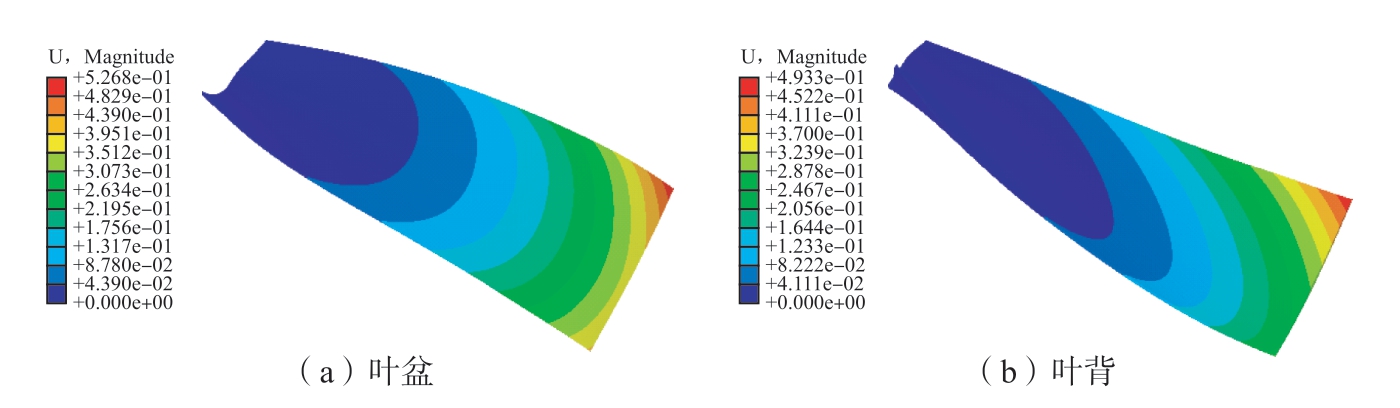
图15 叶盆/叶背切削残余应力变形云图[101]
Fig.15 Cloud diagram of cutting residual stress-induced deformation of blade basin/ blade back [101]
2.5.2 薄壁结构残余应力变形控制方法
在薄壁结构切削残余应力变形控制方面,研究方法包括毛坯初始内应力控制、切削参数优化、余量优化设计、刀轴控制、走刀路径规划、装夹优化等。毛坯初始残余应力对加工变形有着重要的影响[102],材料去除引起的毛坯内应力演化及结构刚性弱化是初始残余应力导致工件变形的主要原因。秦国华等[103]针对飞机结构件,提出以加工变形为约束,反求毛坯初始残余应力的应力规范模型,给出了引起零件加工变形超差的毛坯初始残余应力边界的求解算法。Li等[104]提出了通过优化铣削工艺参数来实现残余应力绝对值的最小化,进而实现薄壁结构切削残余应力变形的控制。Zhang等[105]提出一种通过优化精加工工艺参数的不对称薄壁构件误差控制方法,通过调节加工残余应力的分布,使切削残余应力趋于自平衡,减小残余应力变形,试验结果如图16所示(虚线代表叶片的测量横截面),与叶片1(图16(a))相比,叶片2(图16(b))的误差明显减小。Wang等[106]针对框类零件,提出通过优化零件在毛坯中的位置并在精加工前修正基准,可有效降低框类零件的残余应力变形。张峥[107]采用轮廓法重构残余应力场,结合有限元仿真方法,建立薄壁结构残余应力变形的预测模型,并通过优化余量分配来控制变形。Hao等[108]通过优化框类零件精加工余量,使得由初始残余应力与切削残余应力引起的变形减小了39%~56%。黄涛等[109]推荐采用15°~20°的刀轴倾角加工薄壁叶片,可有效减小叶片的切削残余应力引起的弯曲与扭转变形。Zheng等[110]为了控制因材料初始残余应力和切削残余应力引起的变形,采用元素去除方法进行数值研究,模拟不同的材料去除顺序,获得不同走刀路径下工件的变形量,通过优化走刀路径控制变形。Casuso等[111]采用有限元建模和仿真计算的方法,对航空铝合金零件在不同走刀路径下残余应力引起的变形进行研究,并通过优化走刀路径来控制零件的加工变形。Zhang等[112]提出一种通过精确调整加工过程中的夹具状态改变零件内应力的分布来减小薄壁零件残余应力引起的变形。于建华等[113]则通过设计一种具备6个自由度的自适应夹具,来逐层抵消加工中新产生的变形,实现对叶片加工变形的控制。同时,一些研究者提出,加工时添加加强筋和增加工件等效弯曲刚度可以减少残余应力引起的加工变形。如Li等[114]在工件低刚度方向增加一些加强肋,提高其弯曲刚度,然后对工件进行应力消除后进行二次加工去除加强肋。Gao等[115]探究等效弯曲刚度和残余应力对薄壁零件加工变形的影响,提出了一种同时增加弯曲刚度和降低残余应力来控制加工变形的工艺流程。此外,Pervaiz等[116]指出微量冷却润滑(MQCL)可以有效降低切削区域的温度,减小材料的热膨胀和残余应力的累积,控制加工变形。
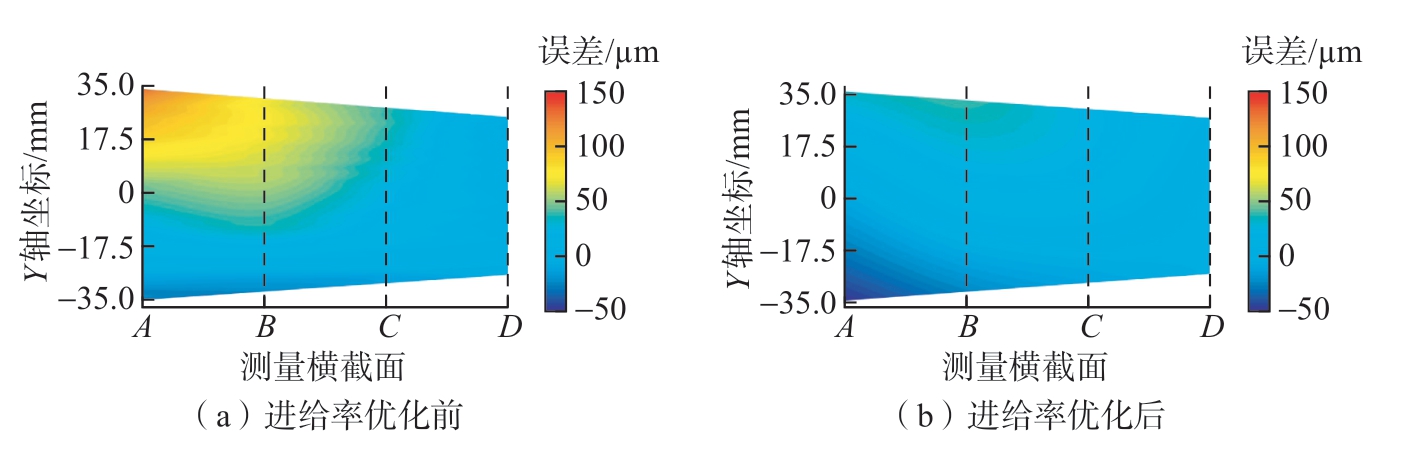
图16 工艺优化前后叶片误差对比[105]
Fig.16 Comparison of blade errors before and after process optimization[105]
综上所述,切削残余应力变形预测与控制主要以薄板与框类零件等简单结构为对象,较少涉及包含复杂曲面特征的薄壁结构。研究手段主要以试验测试与仿真分析为主,控制残余应力变形的思路以正向工艺调控为主。而新型整体叶盘叶片为复杂自由曲面薄壁结构,型面弯扭程度高,属于强非对称性结构,即使叶盆与叶背面残余应力完全对称分布,仍然会发生弯扭变形,使得现有铣削工艺参数控制窗口较小,变形控制难度较大。
2.6 多工序集成综合误差
多源多工序制造过程是指采用多个工序生产产品,最终质量受到刀具、夹具、机床等多个误差源影响的一个制造过程,相应的制造系统为多源多工序制造系统。综合误差指的是零件最终的实际尺寸和理论模型尺寸之间的偏差,是多源误差之和,一般利用测量机或者蓝光等测量设备对零件尺寸进行测量。薄壁结构的弱刚性特点使得其加工过程的误差形式和误差源种类复杂多样,各误差源耦合效应强且难控制加工工艺系统,如图17所示,零件的加工经过多个工序,多个工序之间存在加工误差的传递与累积,多源误差造成的薄壁结构单工序加工误差经过工序传递和累积形成薄壁结构的多工序综合误差。
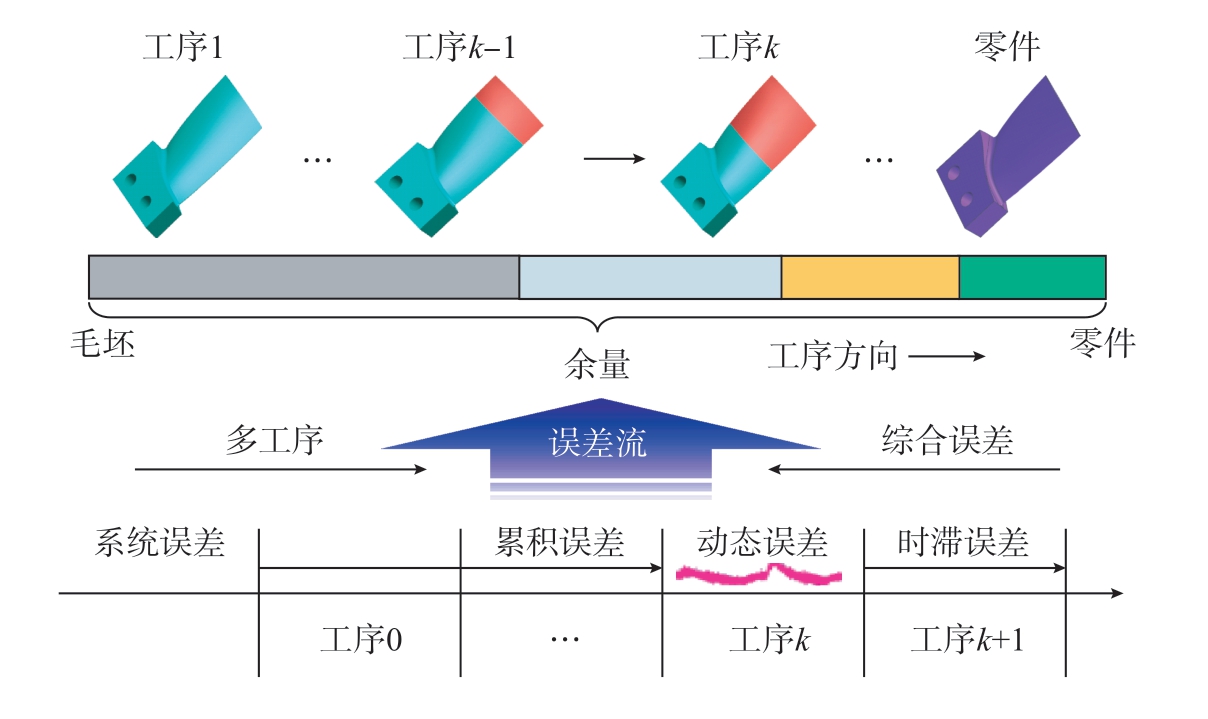
图17 多工序集成综合误差
Fig.17 Comprehensive error of multi-process integration
2.6.1 多工序集成综合误差预测
基于误差流理论的机理模型可以实现多工序加工误差流的建模。美国密西根大学的Hunter教授[117]提出了一种基于多个零件的误差传递特性的机械产品装配误差流理论方法,用以解决车身装配质量控制问题。关于状态空间模型有很多扩展的研究,都是在状态方程上进行了改善[118-119]。虽然上述研究方法和思路以多产品装配过程为导向,但所提出的空间域误差累积效应和时域传递效应是多源多工序误差传递的本质,即应考虑误差在时域的传递特性,在研究多源、多工序加工误差时,也应考虑误差在空间域的累积效应。李贵龙等[120]分析了基准误差、夹具误差和刀具误差等误差源在多工序之间的传递、耦合关系,提出基于有限元仿真和点集微分运动矢量(DMV)描述的方法,建立了考虑切削力所致变形的误差流模型,并对发动机缸体的特征尺寸误差进行了预测。Yang等[121]通过定位基准面引起的误差变化及其相应的夹具误差变化来扩展当前误差流模型,修改了基于微分运动向量的误差传递模型,可以扩展到一些复杂工件的误差预测。随着智能算法和数字化测量设备的发展,从机械加工过程可以获得海量测量数据,一些学者将数据驱动方法运用到多工序加工误差预测中,Jiang等[122]建立了基于人工神经网络的加工误差网络传播模型,用于多级加工过程中的误差分析。Wang等[123]改进了小样本条件下误差流分析的网络架构,提出了一种扩展的误差传播网络模型。江平宇等[124]提出了一种误差传递网络,基于支持向量机对单工序质量进行预测,通过合并多个单工序构建了多工序质量预测模型,此外,基于上述算法研发了质量预测软件,并在相关的质量预测试验中证明了有效性。王亚军[125]提出了基于长短期记忆网络时序预测模型对工件质量监控的方法,收集精密数控机床加工过程中工件的历史和实时数据,基于收集到的数据对模型进行训练,学习数据之中的内在规律,通过训练好的模型对实际生产过程中的工件质量情况进行分析预测。
2.6.2 多工序集成综合误差控制方法
在多工序加工误差控制方面,王佩等[126]以航空发动机复杂薄壁零件为对象,基于扩展误差流,建立了薄壁零件多工序加工过程误差耦合模型和监控方法,进而提出了几何定位误差与受力变形误差的溯源方法及相应的误差调控方法,但是该种方法是从质量管理与统计的角度来进行误差溯源与控制的,对误差的控制存在滞后性。李菲[127]面向工作台交换的柔性生产线制造过程,引入在机检测夹具的方式,补偿工件与夹具装配体偏离机床加工刀具的误差,间接改变制造过程变量误差,实现零件加工精度的提高。Guo等[128]分析了多工序铣削过程中残余应力的分布机理,根据薄壁零件的多工序铣削过程,建立有限元仿真模型,计算了不同加工参数下粗加工、半精加工、精加工过程中残余应力的分布,试验结果表明,从半精加工到精加工,随着切削深度的减小,加工表面的残余应力和变形减小,通过热处理工艺消除残余应力提高了薄壁零件的加工精度,但是仅仅考虑了残余应力引起的变形。Wu等[129]建立了近净成形叶片多源多工序加工误差传递模型,通过自适应数控加工工艺试验,发现自适应数控加工工艺可以合理减少定位基准引起的加工误差,在叶片夹具系统刚度足够的前提下,减小叶片的轮廓误差和位置误差。由于闭式整体叶盘加工时需要分别从正反两面进刀来完成加工,二次装夹引入了新的误差因素,导致叶型型面上不可避免地存在一条接刀痕迹,邱文旺等[130]提出通过增加前置的磨削工序提高上下两端面的平面度及平行度,控制多工序误差耦合因素带来的影响。
综上所述,对于多源多工序加工误差预测与控制方面,大多数预测模型是刚体方面的误差传递模型,由于薄壁结构误差源种类多且耦合效应强,误差流模型适用于刚体,但不适用于薄壁结构的误差传递。现有的多工序综合误差控制方法无法对整体叶盘叶片等复杂曲面类薄壁结构产生有效的事前(加工前)控制,因此,需要进一步探索薄壁结构的误差传递模型与控制方法。
3 未来发展方向
(1)机理模型和试验数据混合驱动的加工误差预测。
随着人工智能的不断发展,数据驱动的模式被引入到传统制造领域。数据驱动的方法为解决预测问题开辟了新天地,但是,航空领域的薄壁结构往往具有多品种、小批量的特点,从试验中获取试验数据的成本很高,模型的训练需要大量的数据作为基础,这限制了数据驱动在制造领域的应用。为了解决上述问题,近期提出了一种混合驱动方法,将机理模型与试验数据相结合,一方面,该方法利用机理分析模型提供的先验知识来建立输入和输出之间的关系;另一方面,利用有限的试验数据对模型进行校准或校正,从而提高预测精度,降低训练成本。目前,机理和实验数据混合驱动模型已被应用到切削力预测、简单薄壁结构弹性让刀变形预测、切削残余应力预测等方面,如何面向复杂薄壁结构建立机理和数据混合驱动的加工误差预测模型是未来发展方向之一。
(2)复杂薄壁结构自适应精密加工技术。
复杂薄壁结构加工过程时变性强、动态响应复杂,难以事先精确建模预测具体的加工工况,导致加工工艺与实际复杂加工状态和时变工况不匹配,难以对加工过程进行精确的控制和调节,造成薄壁结构加工精度和表面质量极难保障。复杂薄壁结构自适应精密加工技术通过在薄壁结构加工过程中依据当前工件的工艺几何、切削负载、动态响应、机床特性等多源信息及时做出装夹位姿、刀具-工件接触状态、加工工艺参数、刀轴控制方向、刀位轨迹等的优化调整,以适应当前工件的加工状态和时变工况,从而实现复杂薄壁结构多轴数控加工的高效和高精度控制。复杂薄壁结构自适应精密加工技术是未来的又一大发展方向。
(3)基于数字孪生技术的薄壁结构加工误差控制平台。
随着新一代信息技术和传感器技术的发展,数字孪生技术应运而生。数字孪生技术为复杂薄壁结构加工误差的预测和控制提供了新的解决思路,通过使用传感器和其他数据收集工具来收集有关加工过程的实时数据,例如机床状态、温度、铣削力和其他参数等,然后将这些数据输入到数字模型中模拟加工系统的行为,以实现实时可视化的监控机器状态和加工过程,可以及时发现加工误差并进行调控,保证加工过程的稳定性和可靠性。然而,目前对于数字孪生技术大多是概念探索,尚未形成基于数字孪生技术的薄壁结构加工误差控制平台,因此,如何实现数字孪生技术在加工领域的落地应用是另一个重要的发展方向。
4 结论
本文从装夹定位、切削负载、切削振动、机床误差、残余应力和多工序加工6个方面对薄壁结构加工误差预测和控制方法进行了综述,尽管薄壁结构的加工误差预测和控制取得了长足的进步,但是仍存在巨大挑战。
(1)对于薄壁结构加工误差预测方面,大多数是采用仿真模拟的方式展开的,但是有限元仿真难以模拟有些实际加工情况,造成仿真结果不准确。建立有限元仿真和试验数据相结合的混合驱动模型可以有效解决有限元仿真模型不准确的问题。
(2)对于薄壁结构加工误差控制方面,大多数控制方法仅控制薄壁结构的精加工过程和某单一类型的加工误差,后续工作应以薄壁结构设计公差为约束进行各工序公差设计,整合多种变形控制方法实现薄壁结构各工序加工误差控制,降低误差传递与累积效应,从而减小薄壁结构的综合误差。
(3)发展数字孪生和智能加工技术。利用传感器技术对薄壁件铣削加工过程中的海量数据进行采集,构建基于数字孪生技术的加工过程诊断和控制系统,即“人-信息-物理”系统,实现薄壁结构加工误差的实时监测和控制。
[1] WANG X, ZHAO B, DING W F, et al. A short review on machining deformation control of aero-engine thin-walled casings[J].The International Journal of Advanced Manufacturing Technology, 2022, 121(5): 2971-2985.
[2] YAN B, HAO Y, ZHU L, et al.Towards high milling accuracy of turbine blades: A review[J]. Mechanical Systems and Signal Processing, 2022, 170: 108727.
[3] ZHAO B, DING W F, SHAN Z D, et al. Collaborative manufacturing technologies of structure shape and surface integrity for complex thin-walled components of aero-engine: Status,challenge and tendency[J]. Chinese Journal of Aeronautics, 2023, 36(7): 1-24.
[4] JIANG X H, WEI Y X, ZHOU J H, et al. Residual stress generation and evaluation in milling: A review[J]. The International Journal of Advanced Manufacturing Technology, 2023,126(9): 3783-3812.
[5] WANG F B, WANG Y Q. Milling performance of cryogenic cooled titanium alloy thin-walled parts based on cantilever sheet[J]. The International Journal of Advanced Manufacturing Technology, 2023, 128(5): 2261-2270.
[6] WAN N, SHI S, ZHAO H, et al.Localization method for precision forged blade edge considering multiple constraints[J].The International Journal of Advanced Manufacturing Technology, 2019, 104(9): 4641-4653.
[7] HAN Z H, LIU S G, YU F, et al.A 3D measuring path planning strategy for intelligent CMMs based on an improved ant colony algorithm[J]. The International Journal of Advanced Manufacturing Technology, 2017,93(1): 1487-1497.
[8] CHENG Z Y, SUN Y, HU K, et al.Deep learning-based intelligent measurement methods and system for CMM[J]. Measurement,2023, 221: 113474.
[9] ZHOU Z, ZHANG Y, TANG K.Sweep scan path planning for efficient freeform surface inspection on five-axis CMM[J].Computer-Aided Design, 2016, 77: 1-17.
[10] LIU Y H, ZHAO W Z, SUN R,et al. Optimal path planning for automated dimensional inspection of free-form surfaces[J].Journal of Manufacturing Systems, 2020, 56:84-92.
[11] CHEN L F, ZHANG R, TANG K,et al. A spiral-based inspection path generation algorithm for efficient five-axis sweep scanning of freeform surfaces[J]. Computer-Aided Design, 2020, 124: 102838.
[12] SHEN Y J, ZHANG W Z, ZHU L M,et al. An image-based algorithm for generating smooth and interference-free five-axis sweep scanning path[J]. Robotics and Computer-Integrated Manufacturing, 2021, 71: 102159.
[13] JI S J, REN Y C, JI Z, et al. An improved method for registration of point cloud[J]. Optik, 2017, 140: 451-458.
[14] HE W T, LI Z W, GUO Y Y, et al.A robust and accurate automated registration method for turbine blade precision metrology[J].The International Journal of Advanced Manufacturing Technology, 2018, 97(9): 3711-3721.
[15] FENG Y Z, ZHENG H, REN J X. Registration algorithm for near-net-shape blade based on multi-tolerance constraints[J].The International Journal of Advanced Manufacturing Technology, 2023, 127(9): 4959-4969.
[16] 陆正新, 梁永收, 楚亚松, 等. 基于满意度函数和灰关联度的多公差约束配准算法[J]. 航空制造技术, 2022, 65(6): 90-98.LU Zhengxin, LIANG Yongshou,CHU Yasong, et al. A registration algorithm with multiple tolerance constraints based on satisfaction function and gray correlation[J].Aeronautical Manufacturing Technology, 2022,65(6): 90-98.
[17] BI Q Z, HUANG N D, ZHANG S K, et al. Adaptive machining for curved contour on deformed large skin based on on-machine measurement and isometric mapping[J].International Journal of Machine Tools and Manufacture, 2019, 136: 34-44.
[18] ZHAO Z C, FU Y C, LIU X, et al.Measurement-based geometric reconstruction for milling turbine blade using free-form deformation[J]. Measurement, 2017, 101: 19-27.
[19] YU H Y, LYU X G, LIU P. Stream surface reconstruction of aero engine blade based on limited measured points[J]. Advances in Engineering Software, 2019, 131: 90-101.
[20] ZHAO Z C, XU T R. A novel approach for process shape construction in adaptive machining of curved thin-walled part[J]. Precision Engineering, 2021, 67: 282-292.
[21] YAN C Y, WAN W Q, HUANG K T, et al. A reconstruction strategy based on CSC registration for turbine blades repairing[J]. Robotics and Computer-Integrated Manufacturing, 2020, 61: 101835.
[22] HOU Y H, ZHANG D H, MEI J W, et al. Geometric modelling of thin-walled blade based on compensation method of machining error and design intent[J]. Journal of Manufacturing Processes, 2019, 44: 327-336.
[23] 冯亚洲, 任军学, 刘战锋, 等. 复杂薄壁构件自适应加工工艺几何模型重构[J].航空学报, 2021, 42(10): 524820.FENG Yazhou, REN Junxue, LIU Zhanfeng, et al. Model construction of complex thin-wall structure parts for adaptive machining[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(10): 524820.
[24] CORNE R, NATH C, EL MANSORI M, et al. Study of spindle power data with neural network for predicting real-time tool wear/breakage during inconel drilling[J].Journal of Manufacturing Systems, 2017, 43:287-295.
[25] ZHOU C A, GUO K, SUN J.Sound singularity analysis for milling tool condition monitoring towards sustainable manufacturing[J]. Mechanical Systems and Signal Processing, 2021, 157: 107738.
[26] CAI W L, ZHANG W J, HU X F, et al. A hybrid information model based on long short-term memory network for tool condition monitoring[J]. Journal of Intelligent Manufacturing, 2020, 31(6): 1497-1510.
[27] CHENG Y N, GAI X Y, JIN Y B, et al. A new method based on a WOA-optimized support vector machine to predict the tool wear[J]. The International Journal of Advanced Manufacturing Technology, 2022, 121(9): 6439-6452.
[28] HUANG Z W, SHAO J J, GUO W C, et al. Hybrid machine learning-enabled multiinformation fusion for indirect measurement of tool flank wear in milling[J]. Measurement,2023, 206: 112255.
[29] CHENG M H, JIAO L, YAN P, et al. Intelligent tool wear monitoring and multistep prediction based on deep learning model[J].Journal of Manufacturing Systems, 2022, 62:286-300.
[30] LIU C Q, LI Y G, ZHOU X, et al. Interim feature-based cutting parameter optimization for aircraft structural parts[J].The International Journal of Advanced Manufacturing Technology, 2015, 77(1): 663-676.
[31] WU Q, LI D P, REN L, et al.Detecting milling deformation in 7075 aluminum alloy thin-walled plates using finite difference method[J]. The International Journal of Advanced Manufacturing Technology, 2016,85(5): 1291-1302.
[32] 党建卫, 张卫红, 万敏, 等. 周铣过程中加工误差预测新模型[J]. 机械工程学报, 2011, 47(17): 150-155.DANG Jianwei, ZHANG Weihong,WAN Min, et al. A novel model for predicting machining error in peripheral milling process[J].Journal of Mechanical Engineering, 2011,47(17): 150-155.
[33] WAN M, ZHANG W H, QIN G H, et al. Efficient calibration of instantaneous cutting force coefficients and runout parameters for general end mills[J]. International Journal of Machine Tools and Manufacture, 2007, 47(11):1767-1776.
[34] HABIBI M, SOORI M, AREZOO B. Accuracy analysis of tool deflection error modelling in prediction of milled surfaces by a virtual machining system[J]. International Journal of Computer Applications in Technology, 2017, 55(4): 308.
[35] CHEN D, ZHANG X J, XIE Y K,et al. A unified analytical cutting force model for variable helix end mills[J]. The International Journal of Advanced Manufacturing Technology,2017, 92(9): 3167-3185.
[36] GE G Y, XIAO Y K, FENG X B,et al. An efficient prediction method for the dynamic deformation of thin-walled parts in flank milling[J]. Computer-Aided Design, 2022,152: 103401.
[37] LI E M, ZHOU J T, YANG C S,et al. Part machining deformation prediction based on spatial-temporal correlation learning of geometry and cutting loads[J]. Journal of Manufacturing Processes, 2023, 92: 397-411.
[38] YILDIRIM Ç V, KiVAK T,ERZINCANLI F. Influence of different cooling methods on tool life, wear mechanisms and surface roughness in the milling of nickel-based waspaloy with WC tools[J]. Arabian Journal for Science and Engineering, 2019, 44(9): 7979-7995.
[39] WANG Z Y, LIANG Y D, LI H Y,et al. Milling force and tool wear mechanisms on milling TC21 titanium alloy under different lubrication conditions[J]. The International Journal of Advanced Manufacturing Technology,2022, 123(1): 169-185.
[40] PEI S H, XUE F, ZHOU Y F, et al.Effects of cryogenic gas jet cooling on milling surface roughness and tool life for GH4169 alloy additive manufacturing parts[J]. Journal of Manufacturing Processes, 2023, 86: 266-281.
[41] SUNDARAMOORTHY R,RAVINDRAN R. Tool wear optimization in CNC milling operation of Al-Mg2Si alloys by Taguchi method[J]. SN Applied Sciences, 2019,1(9): 1093.
[42] VAVRUSKA P, BARTOS F,STEJSKAL M, et al. Increasing tool life and machining performance by dynamic spindle speed control along toolpaths for milling complex shape parts[J]. Journal of Manufacturing Processes, 2023, 99: 283-297.
[43] LI C B, ZHAO X K, CAO H J, et al.A data and knowledge-driven cutting parameter adaptive optimization method considering dynamic tool wear[J]. Robotics and Computer-Integrated Manufacturing, 2023, 81: 102491.
[44] WANG P, BAI Q S, CHENG K, et al. Optimization of the process parameters for micro-milling thin-walled micro-parts using advanced algorithms[J]. The International Journal of Advanced Manufacturing Technology,2022, 121(9): 6255-6269.
[45] HOU Y H, ZHANG D H, ZHANG Y, et al. The variable radial depth of cut in finishing machining of thin-walled blade based on the stable-state deformation field[J].The International Journal of Advanced Manufacturing Technology, 2021, 113(1): 141-158.
[46] LEI Y, PENG J F, DING Y. Feedrate optimization for pocket machining considering cutting force constraints[C]//International Conference on Intelligent Robotics and Applications. Cham: Springer, 2021: 732-742.
[47] 谢义. 铝合金薄壁零件铣削工艺参数优化及仿真研究[D]. 广州: 广东工业大学, 2020.XIE Yi. Optimization and simulation of milling process parameters for aluminum alloy thin-walled parts[D]. Guangzhou: Guangdong University of Technology, 2020.
[48] 赵刘生. 汽轮机叶片的切削加工分析与切削参数优化[D]. 镇江: 江苏大学,2019.ZHAO Liusheng. Machining analysis and cutting parameter optimization of steam turbine blades[D]. Zhenjiang: Jiangsu University, 2019.
[49] 田荣鑫, 皮雨欣, 文学谦, 等. 线性摩擦焊后叶片数控加工技术研究[J]. 航空精密制造技术, 2023, 59(5): 1-4.TIAN Rongxin, PI Yuxin, WEN Xueqian,et al. Research on NC machining technology of linear friction welded blade[J]. Aviation Precision Manufacturing Technology, 2023,59(5): 1-4.
[50] LAN J, LIN B, HUANG T, et al.Path planning for support heads in mirrormilling machining system[J]. The International Journal of Advanced Manufacturing Technology,2017, 91(1): 617-628.
[51] WU B H, ZHENG Z Y, WANG J,et al. Layout optimization of auxiliary support for deflection errors suppression in end milling of flexible blade[J]. The International Journal of Advanced Manufacturing Technology, 2021,115(5): 1889-1905.
[52] 郑志阳, 张阳, 张钊, 等. 基于GA-SVR的薄壁叶片辅助支撑布局优化方法[J]. 航空学报, 2023, 44(4): 426805.ZHENG Zhiyang, ZHANG Yang, ZHANG Zhao, et al. Layout optimization of auxiliary support for thin-walled blade based on GASVR[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(4): 426805.
[53] HUANG W W, ZHANG Y, ZHANG X Q, et al. Wall thickness error prediction and compensation in end milling of thin-plate parts[J]. Precision Engineering, 2020, 66: 550-563.
[54] GE G Y, DU Z C, YANG J G.Rapid prediction and compensation method of cutting force-induced error for thin-walled workpiece[J]. The International Journal of Advanced Manufacturing Technology, 2020,106(11): 5453-5462.
[55] GAO Y Y, MA J W, JIA Z Y, et al.Tool path planning and machining deformation compensation in high-speed milling for difficultto-machine material thin-walled parts with curved surface[J]. The International Journal of Advanced Manufacturing Technology, 2016,84(9): 1757-1767.
[56] WANG G, LI W L, TONG G, et al. Improving the machining accuracy of thinwalled parts by online measuring and allowance compensation[J]. The International Journal of Advanced Manufacturing Technology, 2017,92(5): 2755-2763.
[57] ZHANG S K, JI Y L, HUANG N D, et al. Integrated profile and thickness error compensation for curved part based on on-machine measurement[J]. Robotics and Computer-Integrated Manufacturing, 2023, 79:102398.
[58] ZHOU X, ZHANG D H, LUO M,et al. Chatter stability prediction in four-axis milling of aero-engine casings with bull-nose end mill[J]. Chinese Journal of Aeronautics,2015, 28(6): 1766-1773.
[59] OTTO A, RAUH S, IHLENFELDT S, et al. Stability of milling with nonuniform pitch and variable helix tools[J].The International Journal of Advanced Manufacturing Technology, 2017, 89(9): 2613-2625.
[60] GUO M X, ZHU L D, YAN B L,et al. Research on the milling stability of thinwalled parts based on the semi-discretization method of improved Runge-Kutta method[J].The International Journal of Advanced Manufacturing Technology, 2021, 115(7): 2325-2342.
[61] LI Z Q, YANG Z K, PENG Y R,et al. Prediction of chatter stability for milling process using Runge-Kutta-based complete discretization method[J]. The International Journal of Advanced Manufacturing Technology,2016, 86(1): 943-952.
[62] 张钊. 薄壁结构铣削过程颤振分析及抑制研究[D]. 上海: 上海交通大学, 2018.ZHANG Zhao. Chatter analysis and mitigation for the milling of thin-walled structure[D]. Shanghai: Shanghai Jiao Tong University, 2018.
[63] 田卫军. 薄壁叶片多轴加工颤振抑制方法研究[D]. 西安: 西北工业大学, 2018.TIAN Weijun. Study on flutter suppression method of thin-walled blade in multi-axis machining[D]. Xi’an: Northwestern Polytechnical University, 2018.
[64] MORADI H, VOSSOUGHI G,BEHZAD M, et al. Vibration absorber design to suppress regenerative chatter in nonlinear milling process: Application for machining of cantilever plates[J]. Applied Mathematical Modelling, 2015, 39(2): 600-620.
[65] BUTT M A, YANG Y Q, PEI X Z,et al. Five-axis milling vibration attenuation of freeform thin-walled part by eddy current damping[J]. Precision Engineering, 2018, 51:682-690.
[66] ZHANG Z, LI H G, MENG G, et al. Milling chatter suppression in viscous fluid:A feasibility study[J]. International Journal of Machine Tools and Manufacture, 2017, 120:20-26.
[67] MA J J, LI Y F, ZHANG D H,et al. Dynamic response prediction model of thin-wall workpiece-fixture system with magnetorheological damping in milling[J].Journal of Manufacturing Processes, 2022, 74:500-510.
[68] 张鸿泽. 附加质量和电涡流阻尼对薄壁件加工振动状态的影响分析[D]. 大连:大连理工大学, 2022.ZHANG Hongze. Influence of added mass and eddy current damping on machining vibration state of thin-walled parts[D]. Dalian:Dalian University of Technology, 2022.
[69] WAN M, DANG X B, ZHANG W H,et al. Chatter suppression in the milling process of the weakly-rigid workpiece through a moving fixture[J]. Journal of Materials Processing Technology, 2022, 299: 117293.
[70] FU R, CURLEY P, HIGGINS C,et al. Double-sided milling of thin-walled parts by dual collaborative parallel kinematic machines[J]. Journal of Materials Processing Technology, 2022, 299: 117395.
[71] GALARZA F A M, DE ALBUQUERQUE M V, ANTONIALLI A Í S,et al. Design and experimental evaluation of an impact damper to be used in a slender end mill tool in the machining of hardened steel[J]. The International Journal of Advanced Manufacturing Technology, 2020, 106(5): 2553-2567.
[72] 刘建永, 乔立红, 陈五一. 减振铣刀切削钛合金TB6颤振和切削力分析[J]. 中南大学学报(自然科学版), 2020, 51(2): 349-358.LIU Jianyong, QIAO Lihong, CHEN Wuyi. Chatter and cutting forces analysis in machining of titanium alloy TB6 with vibrationfree milling cutters[J]. Journal of Central South University (Science and Technology), 2020,51(2): 349-358.
[73] 司博文. 不等齿距立铣刀铣削力建模与关键结构参数及工艺优化[D]. 哈尔滨:哈尔滨理工大学, 2023.SI Bowen. Modeling of milling force, key structural parameters and process optimization of end mill with unequal pitch[D]. Harbin: Harbin University of Science and Technology, 2023.
[74] MUNOA J, BEUDAERT X,ERKORKMAZ K, et al. Active suppression of structural chatter vibrations using machine drives and accelerometers[J]. CIRP Annals,2015, 64(1): 385-388.
[75] WAN S K, LI X H, SU W J, et al.Active chatter suppression for milling process with sliding mode control and electromagnetic actuator[J]. Mechanical Systems and Signal Processing, 2020, 136: 106528.
[76] LI D H, CAO H R, CHEN X F.Active control of milling chatter considering the coupling effect of spindle-tool and workpiece systems[J]. Mechanical Systems and Signal Processing, 2022, 169: 108769.
[77] 高顺. 基于压电作动器的多轴铣削加工颤振主动控制[D]. 武汉: 华中科技大学,2022.GAO Shun. Active control of chatter in multi-axis milling based on piezoelectric actuator[D]. Wuhan: Huazhong University of Science and Technology, 2022.
[78] 王俊鹏. 基于磁流变阻尼调控的薄壁件加工抑振研究[D]. 大连: 大连理工大学,2022.WANG Junpeng. Research on vibration suppression of thin-walled parts based on magnetorheological damping control[D]. Dalian:Dalian University of Technology, 2022.
[79] LI J, XIE F G, LIU X J. Geometric error modeling and sensitivity analysis of a fiveaxis machine tool[J]. The International Journal of Advanced Manufacturing Technology, 2016,82(9): 2037-2051.
[80] NIU P, CHENG Q, LIU Z F, et al. A machining accuracy improvement approach for a horizontal machining center based on analysis of geometric error characteristics[J]. The International Journal of Advanced Manufacturing Technology, 2021, 112(9): 2873-2887.
[81] TAO H H, FAN J W, LI T J, et al.An approach to enhancing machining accuracy of five-axis machine tools based on a new sensitivity analysis method[J]. The International Journal of Advanced Manufacturing Technology,2023, 124(7): 2383-2400.
[82] ZHANG C X, GAO F, YAN L.Thermal error characteristic analysis and modeling for machine tools due to timevarying environmental temperature[J]. Precision Engineering, 2017, 47: 231-238.
[83] FU G Q, GONG H W, GAO H L, et al. Integrated thermal error modeling of machine tool spindle using a chicken swarm optimization algorithm-based radial basic function neural network[J]. The International Journal of Advanced Manufacturing Technology, 2019,105(5): 2039-2055.
[84] WEI X Y, YE H H, MIAO E M, et al. Thermal error modeling and compensation based on gaussian process regression for CNC machine tools[J]. Precision Engineering, 2022,77: 65-76.
[85] LI L, YANG H T, ZHANG Y, et al. Dynamic positioning error analysis and modeling of CNC machine tool guideway system[J]. Journal of Mechanical Science and Technology, 2021, 35(5): 1955-1967.
[86] YANG B, ZHANG G B, RAN Y, et al. Kinematic modeling and machining precision analysis of multi-axis CNC machine tools based on screw theory[J]. Mechanism and Machine Theory, 2019, 140: 538-552.
[87] LIU X J, XU J R, WANG Y, et al.A systematic spatial-variably volumetric error model and machining optimization method based on continuous moving support variation of machine tool[J]. The International Journal of Advanced Manufacturing Technology, 2023,129(3): 1189-1211.
[88] 韩江, 刘秀钰, 姜阳, 等. 考虑非线性误差的五轴工件安装位置优化[J]. 制造技术与机床, 2019(7): 28-32.HAN Jiang, LIU Xiuyu, JIANG Yang, et al. On the workpiece setup optimization for fiveaxis machining considering nonlinear errors[J].Manufacturing Technology & Machine Tool,2019(7): 28-32.
[89] LIU H, LIU Q, YUAN S M.Adaptive feedrate planning on parametric tool path with geometric and kinematic constraints for CNC machining[J]. The International Journal of Advanced Manufacturing Technology, 2017,90(5): 1889-1896.
[90] LU Z Y, YANG X, ZHAO J.Tool-path planning method for kinematics optimization of blade machining on five-axis machine tool[J]. The International Journal of Advanced Manufacturing Technology, 2022,121(1): 1253-1267.
[91] MA J W, HU G Q, QIN F Z, et al. Optimization method of tool axis vector based on kinematical characteristics of rotary feed axis for curved surface machining[J].The International Journal of Advanced Manufacturing Technology, 2019, 100(5): 2007-2020.
[92] QIAN L, ZHANG L Q, GAO Q G,et al. Optimization of tool axis vector for mirror milling of thin-walled parts based on kinematic constraints[J]. The International Journal of Advanced Manufacturing Technology, 2023,124(3): 847-861.
[93] WU L, CHEN M S, XU J T, et al. Minimum-acceleration local modification method for planning tool orientations in 5-axis ball-end machining[J]. The International Journal of Advanced Manufacturing Technology, 2021,114(7): 2271-2287.
[94] LI J G, WANG S Q. Distortion caused by residual stresses in machining aeronautical aluminum alloy parts: Recent advances[J]. The International Journal of Advanced Manufacturing Technology, 2017,89(1): 997-1012.
[95] WAN M, YE X Y, YANG Y, et al.Theoretical prediction of machining-induced residual stresses in three-dimensional oblique milling processes[J]. International Journal of Mechanical Sciences, 2017, 133: 426-437.
[96] GAO H J, ZHANG Y D, WU Q, et al. Investigation on influences of initial residual stress on thin-walled part machining deformation based on a semi-analytical model[J]. Journal of Materials Processing Technology, 2018, 262:437-448.
[97] MA Y, ZHANG J F, YU D W, et al. Modeling of machining distortion for thinwalled components based on the internal stress field evolution[J]. The International Journal of Advanced Manufacturing Technology, 2019,103(9): 3597-3612.
[98] CHEN Z J, QIAN L Y, CUI R K, et al. Machining-induced residual stress analysis and multi-objective optimization for milling process of Mg-Li alloy[J]. Measurement, 2022,204: 112127.
[99] 孔文滕. 薄壁铣削工件热变形建模方法研究[D]. 武汉: 华中科技大学, 2021.KONG Wenteng. Research on modeling method of thermal deformation of thin-walled milling workpiece[D]. Wuhan: Huazhong University of Science and Technology, 2021.
[100] 王骏腾. 薄壁件铣削残余应力变形的感知预测与工艺优化方法[D]. 西安: 西北工业大学, 2018.WANG Junteng. Perceptual prediction and process optimization method of milling residual stress and deformation of thin-walled parts[D].Xi’an: Northwestern Polytechnical University,2018.
[101] 周金华. 薄壁结构切削残余应力建模及变形预测[D]. 西安: 西北工业大学, 2018.ZHOU Jinhua. Modeling and deformation prediction of cutting residual stress of thinwalled structure[D]. Xi’an: Northwestern Polytechnical University, 2018.
[102] 王民, 刘宇男, 孙国智, 等. 初始残余应力和切削残余应力对薄壁件加工变形的影响[J]. 北京工业大学学报, 2017, 43(8):1141-1147.WANG Min, LIU Yunan, SUN Guozhi,et al. Influence of initial residual stress and cutting stress on machining deformation of thinwalled parts[J]. Journal of Beijing University of Technology, 2017, 43(8): 1141-1147.
[103] 秦国华, 王华敏, 林锋, 等. 基于铝合金板材应力反求与应力评测的飞机结构件加工变形控制新方法[J]. 中国科学: 技术科学, 2020, 50(1): 85-102.QIN Guohua, WANG Huamin, LIN Feng,et al. A new approach to deformation control of aeronautical monolithic components of aluminum alloy plates based on stress inverse and stress evaluation[J]. Scientia Sinica(Technologica), 2020, 50(1): 85-102.
[104] LI J, YANG X Y, REN C Z, et al. Multiobjective optimization of cutting parameters in Ti-6Al-4V milling process using nondominated sorting genetic algorithm-II[J]. The International Journal of Advanced Manufacturing Technology, 2015, 76(5): 941-953.
[105] ZHANG Z X, WANG L H, WANG S Q, et al. A novel deflection control method for the asymmetric thin-walled component by optimizing the feed rate of the finishing process[J]. The International Journal of Advanced Manufacturing Technology, 2023,127(7): 3385-3395.
[106] WANG Z B, SUN J F, LIU L B, et al. An analytical model to predict the machining deformation of frame parts caused by residual stress[J]. Journal of Materials Processing Technology, 2019, 274: 116282.
[107] 张峥. 飞机弱刚性铝合金结构件的残余应力和加工变形控制技术研究[D]. 南京: 南京航空航天大学, 2015.ZHANG Zheng. Research on residual stress and machining distortion of aeronautic weak rigidity in aluminum structure[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2015.
[108] HAO X Z, LI Y G, CHENG Y H,et al. A time-varying geometry modeling method for parts with deformation during machining process[J]. Journal of Manufacturing Systems,2020, 55: 15-29.
[109] 黄涛, 刘志兵, 王西彬, 等. 刀轴侧倾角对薄壁叶片加工变形的影响[J]. 兵工学报, 2018, 39(3): 577-583.HUANG Tao, LIU Zhibing, WANG Xibin, et al. Effect of inclination angle of cutter shaft on machining deformation of thin-walled blade[J]. Acta Armamentarii, 2018, 39(3): 577-583.
[110] ZHENG J Y, VOYLE R, TANG H P, et al. Study of distortion on milled thin-wall aluminum parts influenced by initial residual stress and toolpath strategy[J]. The International Journal of Advanced Manufacturing Technology,2023, 127(1): 237-251.
[111] CASUSO M, POLVOROSA R,VEIGA F, et al. Residual stress and distortion modeling on aeronautical aluminum alloy parts for machining sequence optimization[J]. The International Journal of Advanced Manufacturing Technology, 2020, 110(5): 1219-1232.
[112] ZHANG Z X, LUO M, TANG K,et al. A new in-processes active control method for reducing the residual stresses induced deformation of thin-walled parts[J]. Journal of Manufacturing Processes, 2020, 59: 316-325.
[113] 于建华, 陈志同. 双臂自适应夹具加工变形控制方法[J]. 航空学报, 2016,37(5): 1657-1665.YU Jianhua, CHEN Zhitong. A control method of machining distortion using adaptive fixture with dual-arm[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(5): 1657-1665.
[114] LI B H, GAO H J, DENG H B,et al. A machining deformation control method of thin-walled part based on enhancing the equivalent bending stiffness[J]. The International Journal of Advanced Manufacturing Technology,2020, 108(9): 2775-2790.
[115] GAO H J, LI X, WU Q, et al.Effects of residual stress and equivalent bending stiffness on the dimensional stability of the thinwalled parts[J]. The International Journal of Advanced Manufacturing Technology, 2022,119(7): 4907-4924.
[116] PERVAIZ S, ANWAR S,QURESHI I, et al. Recent advances in the machining of titanium alloys using minimum quantity lubrication (MQL) based techniques[J].International Journal of Precision Engineering and Manufacturing-Green Technology, 2019,6(1): 133-145.
[117] HUNTER J S. Statistical design applied to product design[J]. Journal of Quality Technology, 1985, 17(4): 210-221.
[118] ZHU M R, GE G Y, FENG X B, et al. A novel error compensation method for multistage machining processes based on differential motion vector sets of multiple contour points[J]. Journal of Manufacturing Science and Engineering, 2021, 143(6): 061010.
[119] YACOB F, SEMERE D, ANWER N. Variation propagation modeling in multistage machining processes considering form errors and N-2-1 fixture layouts[J]. The International Journal of Advanced Manufacturing Technology,2021, 116(1): 507-522.
[120] 李贵龙, 杜世昌. 发动机缸体多工序加工变形误差传递的建模与分析[J]. 上海交通大学学报, 2017, 51(4): 385-392.LI Guilong, DU Shichang. Modeling and analyzing for stream of variations in multistage manufacturing processes of cylinder block[J].Journal of Shanghai Jiao Tong University, 2017,51(4): 385-392.
[121] YANG F Y, JIN S, LI Z M. A modification of DMVs based state space model of variation propagation for multistage machining processes[J]. Assembly Automation,2017, 37(4): 381-390.
[122] JIANG P Y, JIA F, WANG Y, et al. Real-time quality monitoring and predicting model based on error propagation networks for multistage machining processes[J]. Journal of Intelligent Manufacturing, 2014, 25(3): 521-538.
[123] WANG Y, JIANG P Y, LENG J W. An extended machining error propagation network model for small-batch machining process control of aircraft landing gear parts[J].Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2017, 231(7): 1347-1365.
[124] 江平宇, 王岩, 王焕发, 等. 基于赋值型误差传递网络的多工序加工质量预测[J]. 机械工程学报, 2013, 49(6): 160-170.JIANG Pingyu, WANG Yan, WANG Huanfa, et al. Quality prediction of multistage machining processes based on assigned error propagation network[J]. Journal of Mechanical Engineering, 2013, 49(6): 160-170.
[125] 王亚军. 面向航天复杂结构件的数控加工过程质量波动预测与监控方法研究[D]. 西安: 西安电子科技大学, 2021.WANG Yajun. Research on quality fluctuation prediction and monitoring method of NC machining process for aerospace complex structural parts[D]. Xi’an: Xidian University,2021.
[126] 王佩, 李翌辉, 吴毅, 等. 复杂零件加工过程质量控制与改进方法研究[J]. 航空精密制造技术, 2014, 50(6): 36-40, 45.WANG Pei, LI Yihui, WU Yi, et al.Research on complex part machining process quality control and improvement method[J].Aviation Precision Manufacturing Technology,2014, 50(6): 36-40, 45.
[127] 李菲. 采用在机检测的五轴多工序加工误差控制及成本优化研究[D]. 成都:电子科技大学, 2018.LI Fei. Research on cost analysis and optimization relate to error transmission for multistage manufacturing process with onmachine detecting fixture on five-axis machine tool[D]. Chengdu: University of Electronic Science and Technology of China, 2018.
[128] GUO M X, JIANG X H, YE Y, et al. Investigation of redistribution mechanism of residual stress during multi-process milling of thin-walled parts[J]. The International Journal of Advanced Manufacturing Technology, 2019,103(1): 1459-1466.
[129] WU D B, WANG H, YU J.Research on machining error transmission mechanism and compensation method for nearnet-shaped jet engine blades CNC machining process[J]. The International Journal of Advanced Manufacturing Technology, 2021,117(9): 2755-2773.
[130] 邱文旺, 杨继平, 王永飞, 等. 闭式叶盘加工过程接刀误差控制方法研究[J].航空制造技术, 2021, 64(7): 95-102.QIU Wenwang, YANG Jiping, WANG Yongfei, et al. Research on control method of blade adjoining error in machining operation of closed blisk[J]. Aeronautical Manufacturing Technology, 2021, 64(7): 95-102.
