开式整体叶盘具有结构紧凑和超高强度重量比等优良特性,因而在航空航天领域获得了广泛应用[1]。然而,如图1所示的航空发动机开式叶盘结构复杂,开式悬伸叶片的刚度差、厚度薄且普遍采用钛合金等难加工材料,在切削力作用下极易产生弹性变形,造成其加工误差大、加工周期长[2]。因此,薄壁叶片的加工精度和效率的提升一直以来都是学术界和工业界的难点问题。

图1 开式整体叶盘叶片
Fig.1 Open blisk blades
薄壁叶片在铣削过程中除了受到切削力所致误差外,还会受到刀具磨损、机床几何误差以及热误差的综合影响[3],且在不同的加工工况下各个误差源对叶片最终加工误差贡献的比例不同。通常来说,由于薄壁叶片的弱刚性结构特点,切削力所致变形在其加工误差的占比最大,可达60%以上。因此,当前的大部分研究围绕切削力作用下薄壁件所产生弹性变形的预测和抑制开展,并发展出了加工工艺调整法和有限元预测补偿法。其中,加工工艺调整法的典型代表包括修改加工参数以减小切削力[4]、采用柔性夹具[5-6]或镜像铣削[7]等方式增强工件支撑刚度;有限元预测补偿法则采用有限元法将切削力作用于工件各刀位点[8],提前预测出变形值并通过修改数控加工代码等方式进行补偿[9-10]。上述研究对薄壁件的切削力所导致的弹性变形有较好的抑制效果,然而难以考虑到刀具磨损、热误差等多源误差的影响。
近年来,在机测量由于具备高精度、高可靠性、无需复杂的机理建模以及可方便集成到数控机床等优良特性,被广泛应用到薄壁件的精度提升过程[11],形成测量-加工一体化的趋势。黄诺帝等[12-13]将在机测量应用于叶轮及火箭箱体加工误差的控制中,并在测点规划和型面重建领域开展了工作[14];东北大学朱立达等[15]针对航空叶片的在机检测提出了测点优化规划方法和基于3次样条节点的轮廓重建方法;毕庆贞等[16]开发了基于在机测量的大型蒙皮件的自适应铣削加工,进而开发了一种非接触式超声波在机测厚系统,并应用于航空发动机外壳的车削厚度控制[17]。上述基于在机测量的研究在薄壁件加工精度提升方面均取得了一定的效果。然而,目前大部分研究中的补偿方式为修改数控加工代码,存在集成化程度低、灵活性不足、补偿精度差等缺陷,难以形成薄壁件测量-加工一体化。针对上述问题,本文提出一种基于在机测量的薄壁叶片加工误差建模与补偿方法,用于实现薄壁叶片加工精度的提升。
1 薄壁叶片加工误差建模与补偿方法
1.1 薄壁叶片加工误差分析
薄壁叶片加工过程中,对加工精度影响最大的因素通常为受力变形导致的加工误差,如图2所示,其中的黑色虚线表示薄壁叶片的理想型线,而在加工过程中薄壁叶片在铣削力的作用下可能会形成蓝色虚线所示的受力变形,在加工完成后形成红色实线所示的铣削力所致加工误差。
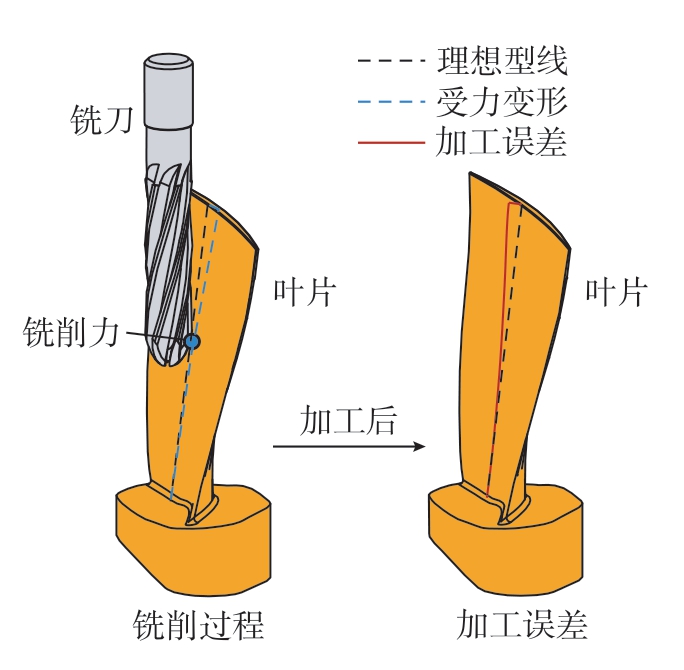
图2 薄壁叶片铣削加工误差
Fig.2 Milling error of the thin-walled blade
薄壁叶片在实际加工过程中受力复杂多变,可能同时存在弹性变形和塑性变形,导致采用基于弹性变形的模型预测(图2)的加工误差存在精度差,甚至预测值与实际误差值方向相反的情况。此外,薄壁叶片加工误差还受到刀具磨损、机床热误差以及机床精度衰退等误差源的综合影响,长期下来,这些误差源对加工精度的影响也难以忽略,但由于机理复杂,使其存在建模成本高的问题。针对上述问题,提出基于在机测量的薄壁叶片加工误差建模与补偿方法,可采用在机测量的方式直接测量获取包含弹性变形、塑性变形、刀具磨损以及机床精度演变等多源因素影响下的综合误差值,进而建立对应的加工误差模型并实施补偿加工,从而提高薄壁叶片的加工精度和效率。
1.2 薄壁叶片加工误差建模与补偿方法流程
基于在机测量的薄壁叶片加工误差建模与补偿方法的流程如图3所示。除了测头标定、数控系统通信测试等前期准备工作外,主要包括以下步骤。
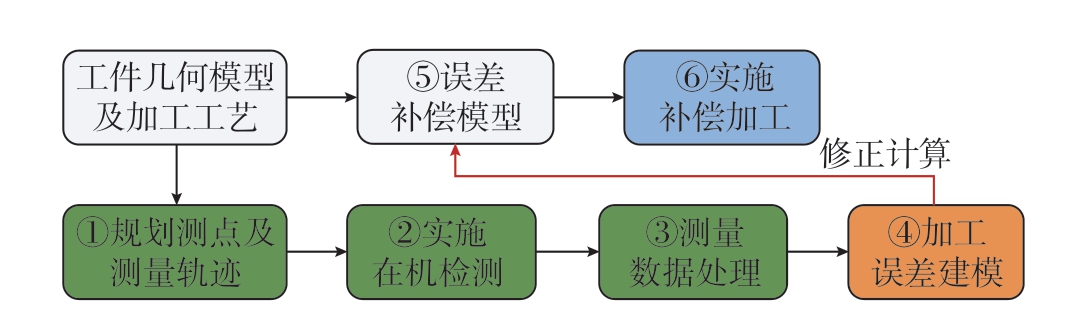
图3 薄壁叶片加工误差建模与补偿流程
Fig.3 Modeling and compensation procedure for thin-walled blades machining
(1)规划在机测点及测量轨迹。在机测点及测量轨迹直接决定最终检测精度和可靠性,因此需根据工件几何模型以及加工工艺规划测点和测量轨迹。在机测点的分布一般采用等参数法、等间距法、形状采样法或基于智能算法的采样法来确定。而在测点确定以后,在机测量轨迹即可根据最小路径法或最优测角法确定。
(2)实施在机检测。根据建立的在机测点及测量轨迹,生成在机测量数控代码,开展加工工件的在机测量,并将各测量点信息传输到数控系统指定数据区。
(3)测量数据处理。将各测点测得的坐标信息全部导出,计算各个测量的误差信息。在此基础上,对上述误差数据中的异常值进行剔除处理。
(4)建立加工误差模型。基于处理后的误差数据对工件误差曲面进行重建,以获取各个刀位点的误差值。工件的加工误差曲面通常较为复杂,多项式拟合等常规拟合方法难以精确表示,因此通常采用非均匀有理B样条曲面或机器学习等拟合能力较强的方法进行建模。
(5)修正计算误差补偿模型。基于加工误差模型,考虑由于弹性回弹等造成的实际和理想补偿值之间的耦合关系,建立误差补偿计算模型。进而,利用建立的工件误差补偿模型修正原有的模型,实现薄壁叶片批量加工过程中误差补偿模型的动态修正,保持薄壁叶片批量加工精度的稳定。
(6)实施补偿加工。开发薄壁叶片加工误差实时补偿系统,导入误差补偿模型,实施补偿加工。
上述方法可根据薄壁叶片的几何特征自动规划测点、实施在机检测、建立误差模型、计算补偿值并实施补偿加工,从而避免了工业界常用的“三坐标测量-调整加工程序”这种反复离线测量和修改G代码的过程。此外,经过5次以内在机测量和修正后的误差模型可达到较高的精度,后续可通过间隔抽样式在机测量保持模型精度,从而进一步缩短加工周期。
在上述方法中,测点规划的采样点越多、分布越密,所能达到的测量精度越高。但更多的测量意味着耗费更多的测量时间,这将会对生产效率造成影响。因此,测点规划的目的在于在测点数量有限的情况下采用最优采样策略对待测工件表面进行精确反映,或在测量精度一定的情况下选用最少的测点达到要求的精度。而在机测点的采样研究在国内外均相对成熟,常用的测点采样法包括均布和等参数等传统采样法,等弧长、等弦高等基于间距的采样法以及基于曲率和曲面片的形状采样法等。根据上述方法进行测点采样后,需判断所采样的测点是否能满足精度要求。首先,利用采样点处的三维坐标及测得的数据,对待测工件表面进行NURBS曲面重建。进而将重建的三维表面与待测工件的理想三维表面进行对比,当采样点满足式(1)的判定准则时,即可认为所采样的测点可达到精度要求。

式中,xr、yr和zr分别为重建工件表面的测点所在位置的坐标;xnorm、ynorm和znorm分别为理想工件表面对应点所在位置的坐标;Δ为允许的最大测量误差值。
2 基于在机测量数据的误差建模与补偿值计算
在图3所示的基于在机测量的薄壁叶片加工误差建模与补偿方法流程中,高效获取在机测量数据、根据测量数据计算加工误差以及根据加工误差建立误差模型是关键的3个步骤,因此本节内容重点围绕这3个步骤开展。
2.1 在机测量数据获取
接触式触发测头由于其高精度和高可靠性,在在机测量系统中使用最为广泛。经过多年的发展,接触式触发测头的技术已经较为成熟,可以非常方便地集成到机床主轴上,无需复杂设置即可快速实施在机测量,其基本测量原理如图4所示。假设在测量工件的过程中,测头触发时测球球心为点Op=(xp,yp,zp),测球与被测工件接触点Oc的坐标为
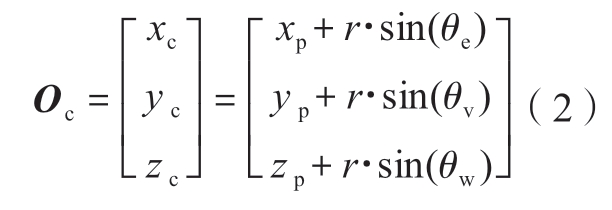
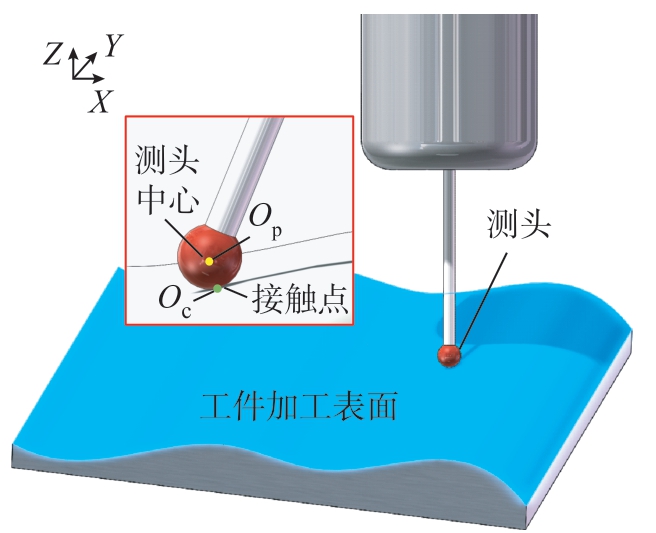
图4 在机测量设置
Fig.4 Setup of the on-machine measurement
式中,r为测球半径;θe、θv和θw分别为测球球心与接触点的连线在YZ平面、XZ平面及XY平面的夹角。那么,当前被测点的综合加工误差值u即为点Oc与理想坐标点Onorm之差。
需要说明的是,在机测量过程中测球应以法向方向靠近待测表面,以保证接触点的准确性,且在机测头在使用前应使用环规或标准球进行标定以尽可能减小测头的方向偏差。
2.2 在机测量数据处理
基于在机测量数据计算加工误差的过程中主要涉及测量数据的分析、处理、计算。虽然常用的接触式触发测头的精度和可靠性均很高,但是由于铣削过程的复杂性,最终测得的加工误差数据可能存在一些异常值。因此,首先采用Hampel滤波法[18]对所测得的加工误差数据进行处理,以检测数据集中的异常值,并将其替换为合理值。Hampel滤波法首先根据窗函数构建数据值序列,基于数值序列服从指定概率分布模型的假设,即可根据指定的概率分布模型对数值序列进行检测和处理。假设数据值序列的窗函数中包含的数据个数为m,那么此数值序列中所有数据的中位数可表示为
式中,meadian(u)为数值序列中的中位数;ui为原始数据集中的第i个数据值。接下来,定义上述数值序列的绝对偏差中值(Median of absolute deviation,MAD)为
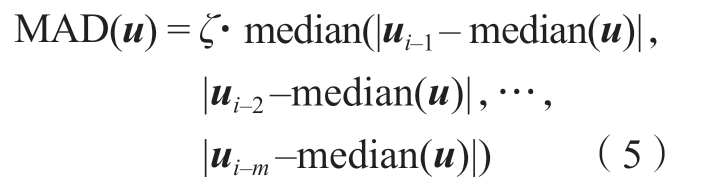
式中,ζ为选用概率分布模型的偏差估计值,例如,正态分布时,ζ= 1.4826。最后,对于每个窗口内的数值序列,其中的数值是否被判断为异常值并进行替换应遵循以下规则。
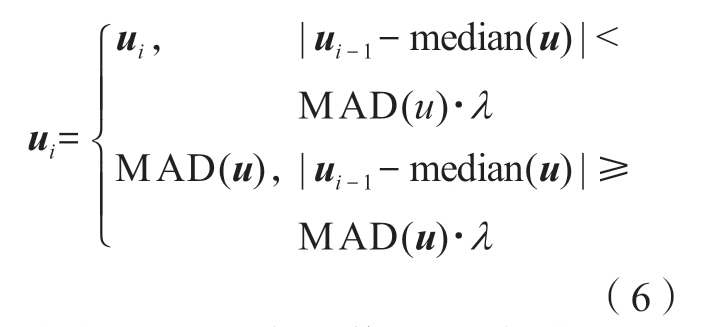
式中,λ为判定阈值,可根据实际工况动态调整。
2.3 基于在机测量数据的加工误差建模
在采用Hampel滤波法对原始数据进行处理后,接下来重要的一步是铣削加工误差的建模,主要涉及误差曲面的精确拟合。工件的加工型面通常是规律的平面或者曲面,但其加工误差通常较为复杂,难以采用多项式拟合等常规方法精确表示。大多数情况下,即使采用5次以上的多项式对整个误差曲面进行拟合,最终的拟合误差可能仍然大到无法接受。因此,此处采用一种泛化能力强且计算性能高的机器学习算法——梯度提升决策树(Gradient boosting decision tree,GBDT)[19]来对误差曲面进行拟合。
薄壁叶片铣削加工误差的建模可以描述为一个回归任务,其目标在于根据当前坐标值预测对应的误差值。在机测量数据可总结为一个具有以下形式的数据集。
式中,ci =(xi,yi,zi,ai,bi)为五轴坐标值向量;ui=(ux,i,ub,i,uz,i,ua,i,ub,i)为综合误差值向量;i为第i个测量数据;n为数据集点数;ci为输入数据;梯度提升决策树的任务就是构建一个可以根据五轴坐标值ci预测综合误差值ui的模型。
梯度提升决策树是由多个分类与回归树构成的,其最终预测值为所有分类与回归树预测值的累加。假设其中第k个分类与回归树的函数为Tk(ci),则前k个分类与回归树的预测值为
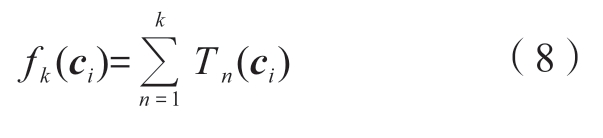
在训练第k个分类与回归树时,构建一个最小化目标函数。
式中,L为损失函数。加工误差的建模属于典型的回归任务,因此此处采用回归任务最常用的残差平方和损失函数,则目标函数变为
接下来采用梯度下降法,使目标函数的值尽快降低以满足最终训练阈值要求。目标函数对于前k-1个分类与回归树的预测值fk-1的梯度为![]() ,则可得fk为
,则可得fk为
式中,η为学习率,是模型中较为重要的一个超参数。此时,模型中第k个分类与回归树Tk(ci)可表示为
将上式中fk(ci)的k改为实际采用的分类与回归树的数量,即可根据在机测量数据训练获得薄壁叶片铣削加工误差模型。进而,根据建立的误差模型可进行后续的补偿加工,提高薄壁叶片铣削加工精度。
2.4 薄壁叶片加工误差补偿值准确计算
在建立加工误差模型后,可根据误差模型实施补偿加工。目前,大多数薄壁件加工误差补偿过程中,采用“与误差值大小相等且方向相反”的镜像补偿法。该方法简单直观、易于操作,但由于刀具和工件的弹性变形等因素的影响,补偿过程中实际与理想补偿位置之间会产生较大偏差,从而导致实际补偿量无法达到预期值。如图5所示,假设无补偿工况下的初始加工误差为u0,按照与初始加工误差大小相等方向相反的规则,令初始补偿量cp0=-u0实施初始误差补偿,则补偿后误差并不能被完全消除而是剩余了u1。在此基础上,第1次迭代后的补偿量为cp1= cp0-u1,补偿后仍剩余误差值u2。如此反复,直至第i次迭代结束后实际补偿位置与设计的补偿位置之间的差值小于给定阈值,此时最终误差补偿量cpi= cpi-1-ui。
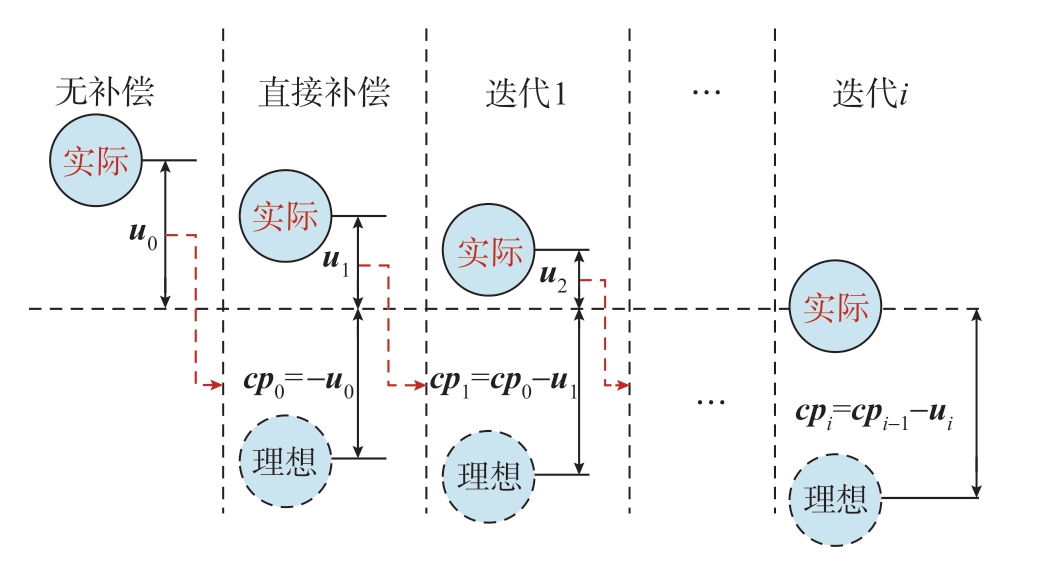
图5 误差补偿值的迭代计算
Fig.5 Iterative process of error compensation values
通过上述迭代过程计算补偿值的效率较低,为了满足实时补偿的要求,应考虑减少补偿值迭代计算消耗的时间。本文提出一种能避免迭代的计算过程,基于初始误差值直接计算出满足阈值要求的误差补偿值的计算方法,可大幅提高补偿值计算效率。首先,假设在刀具和工件的弹性变形等因素影响下的补偿值偏差比例为ρ,则初始补偿量可表示为
式中,ae为切削宽度。根据图5所示的迭代流程,将初始补偿量叠加到切削宽度上,可得初始补偿后再次形成的u1为
将再次形成的误差量u1代入,可得第1次迭代的补偿量cp1为
同理可得第i次迭代的补偿量cpi,并根据次方求和公式简化为
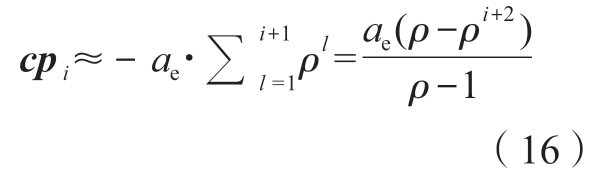
通过上述推导建立了基于迭代系数的误差补偿量修正计算方法,可实现无需迭代的情况下直接计算出与迭代计算流程一致的补偿值,兼顾了计算效率和补偿精度。
3 薄壁叶片加工误差补偿
薄壁件铣削加工误差的补偿方法通常分为修改数控程序法、内置功能补偿法及实时补偿法3类。其中,实时补偿法基于数控系统的原点偏移功能,以较高的频率不断地与数控系统通信并修正加工误差以实现各刀位点的误差修正,对加工程序以及加工参数均无任何影响,可取得较好的精度提升效果。
误差实时补偿的流程如图6所示。首先向误差实时补偿系统输入建立好的误差模型,进而通过误差模型计算误差值、综合补偿值及各轴解耦补偿值,最后基于通信协议实现与数控系统的双向实时数据交互并实现实时补偿。在每个补偿周期内误差实时补偿系统需要完成以下主要步骤。
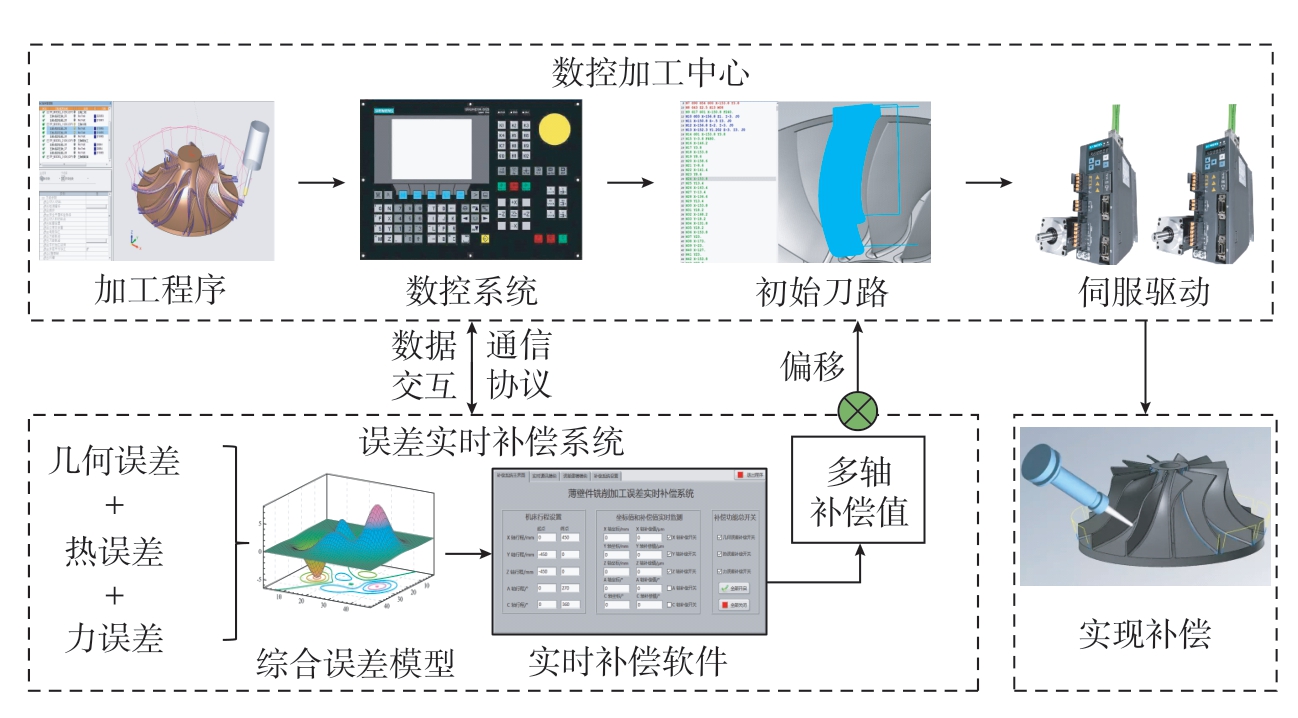
图6 薄壁件加工误差补偿系统
Fig.6 Error compensation system for the thin-walled parts
(1)从数控系统读取当前刀位点的各轴坐标、进给速度和主轴转速等加工信息。
(2)将读取的当前刀位点加工信息作为参数输入综合误差预测模型,用于计算加工误差以及补偿量。
(3)将计算的补偿量通过逆运动学解耦为各个轴的偏移量。
(4)将解耦出的各轴偏移量写入数控系统内部原点偏移变量区。
(5)数控系统控制伺服驱动,在初始刀路基础上叠加偏移量,实现实时补偿。
除了能实现上述补偿流程外,为了能够稳定可靠地应用于环境复杂的工业现场,误差实时补偿系统还需要同时满足补偿实时性、补偿安全性、数据交互可靠性和数据交换规范性等要求。开发的误差实时补偿系统分为补偿信息展示模块、数控系统实时通信模块、误差建模模块和系统设置模块,可便捷地实现机床信息的监测、连接各类数控系统、建立加工误差模型以及修改补偿系统设置。其兼容试验中采用的FANUC数控系统,补偿分辨率为0.1 μm,支持以太网连接和高速光纤总线连接两种方式,分别可达到40 ms和10 ms的补偿周期。试验中采用高速光纤总线通信,经测试补偿周期在10 ms以内,满足本试验中的补偿实施要求。需要说明的是,补偿分辨率为0.1 μm的实现依赖于两个方面:首先是开发的误差补偿系统可计算并输出0.1 μm或更高分辨率的补偿值;其次是数控系统自身支持接收并执行0.1 μm或更高分辨率的补偿值。
4 试验验证
4.1 试验设置
试验以航空发动机压气机开式整体叶盘叶片为对象,面向其关键的精铣加工工艺步骤开展铣削加工-在机测量-实时补偿一体化闭环加工对比验证试验。在实际铣削过程中,对叶片三维模型的叶型轮廓进行完整保留的同时,对叶片的扭度进行了简化,形成了图7所示的直纹薄壁叶片工件,以实现其三轴铣削加工。工件的3个叶片固定在同一个底座上,均为6061铝合金材料,每个叶片的高度和宽度分别为35 mm和32 mm。叶片最厚的地方为中间区域,厚度约为1.72 mm,厚度最薄处为叶缘区域,厚度约为0.35 mm。此外,工件底座上还设计了3个基准面,用于后续三坐标检测的定位基准。刀具采用1把6 mm直径的2刃钨钢球头铣刀,其螺旋角为30°。
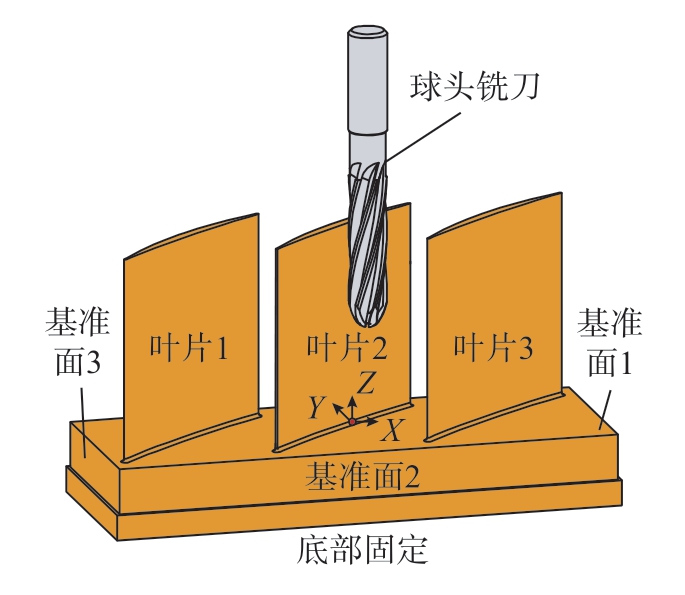
图7 试验加工的薄壁叶片工件
Fig.7 Thin-walled blade workpiece machined in the experiment
试验整体的流程主要分为薄壁叶片工件铣削加工-实施在机测量-加工误差建模-误差补偿对比铣削加工4个步骤,其中用于在机测量和误差建模的为叶片1,基于在机测量数据补偿前后的分别为叶片2和叶片3。试验中叶片的铣削轨迹均为围绕叶片轮廓的侧铣闭环,工件坐标系的原点为叶片2的底部中心位置。侧铣过程中,切削深度为0.3 mm,切削厚度方向的精加工余量为0.2 mm,进给速度为300 mm/min,主轴转速为2000 r/min。
经过几何-热复合误差补偿后,其直线轴运动精度稳定保持在3.0 μm以内,满足试验的精度要求。试验中叶片的铣削过程如图8所示,采用的机床为1台配备FANUC 0i-MF数控系统的沈阳机床VMC 850E三轴立式加工中心,支持发那科的FOCAS外部通信协议。加工过程中的补偿基于FANUC数控系统的外部机械原点偏移功能实施,所开发误差实时补偿系统的补偿分辨率为0.1 μm,补偿周期为10 ms,支持加工结束后自动在机测量、从数控系统中读取测量数据、自动建立加工误差模型等流程的自动化控制。

图8 整体叶盘叶片加工过程
Fig.8 Manufacturing process of blisk blades
叶片的在机测量过程如图9所示,测头采用英国雷尼绍RMP-60型号的无线电测头,配备一颗1 mm直径的红宝石测球,测头系统测量重复精度为1.0 μm。在机测点按照均布采样法获得,在最大测量误差值设为2 μm后,获得的测点分布如图10所示,分别在高度为Z=34.5 mm、Z=31.5 mm、Z=28.5 mm、Z=25.5 mm及Z=22.5 mm处的5条轮廓线处各选取了40个采样点。需要说明的是,在试验开始之前,机床的几何误差和热误差已被预先建模和补偿抑制,为铣削加工-在机测量-实时补偿提供良好的精度基础。经过几何-热复合误差补偿后,机床3个直线轴加工区域的定位精度稳定保持在3.0 μm以内。在测量过程中,在机测头的测球均以法向方向靠近待测表面,以保证接触点的准确性。并且,在机测头在测量前使用环规进行了标定以尽可能减小测头的方向偏差。

图9 整体叶盘叶片在机测量过程
Fig.9 On-machine measurement process of blades
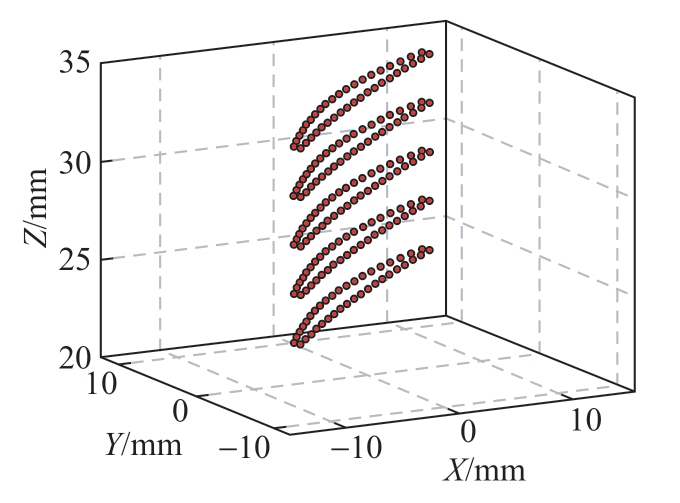
图10 整体叶盘叶片在机测量点
Fig.10 On-machine measurement points of blades
最后,补偿加工前后的薄壁叶片表面采用蔡司V3696型三坐标机进行检测(图11),对比补偿前后叶片轮廓的精度情况。该三坐标机的测量精度为(2.5+L/300) μm,测点与图10所示的在机测量测点保持一致。

图11 叶片的测量过程
Fig.11 Measurement process of the blades
4.2 试验结果及讨论
上述加工过程中,每件薄壁叶片精铣步骤耗时约15 min,接着在10 min内可完成全部200个点的在机测量,因此每件叶片加工周期约为25 min。目前,业界主流的薄壁叶片在精铣工序时采用反复“三坐标测量-调整加工程序”的方式来保证加工精度,每次三坐标测量和调整加工程序需要约32 min,按照一次测量和调整来计算每件叶片加工周期约为62 min。因此,相比于主流的“三坐标测量-调整加工程序”法,本文所提方法在满足加工精度的同时加工周期缩短了59.7%。在机测量完成后,测量数据自动导入误差建模软件,通过GBDT算法建立补偿模型并用于下一件叶片的实时补偿。在计算精度方面,GBDT算法所拟合模型的均方差以及根均方差分别为1.203和1.082,满足试验的精度要求;在计算效率方面,该模型每次预测耗时不足1 ms,完全可在一个补偿通信周期(10 ms)内完成计算,因此满足试验的效率要求。
在补偿前薄壁叶片(叶片2)的加工误差曲面如图12所示。可以看出,叶片2背部误差曲面的范围为[-2.6412 μm,43.3676 μm],而 前部误差曲面的范围为[-0.7182 μm,21.2135 μm]。背部误差曲面的趋势为两边大、中间小、顶部大、底部小,较为符合叶片刚度分布结果。但是,前部误差曲面的整体范围仅为背部误差曲面整体范围的一半左右,且整体趋势性也不如背部明显。图13所示的轮廓误差曲线也印证了这种差别,Z=34.5 mm处叶片背部的轮廓误差范围为[13.8438 μm,43.3675 μm],前部轮廓误差范围为[8.56 μm,21.0456 μm];Z=28.5 mm处叶片背部的轮廓误差范围为[5.8022 μm,19.3518 μm],前部轮廓误差范围为[5.0612 μm,16.0143 μm]。误差可能是由于叶片的厚度太薄,侧铣过程中发生了部分塑性变形所导致的。这种塑性变形导致的加工误差是传统的基于切削力所致弹性变形的模型难以准确判断和预测的。
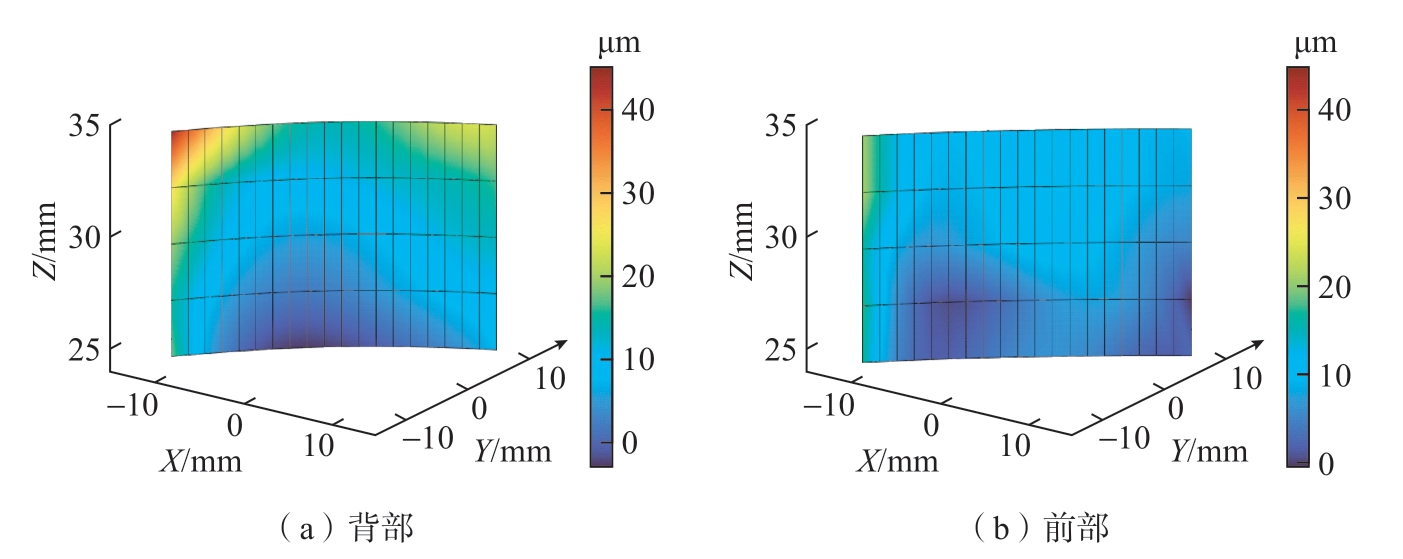
图12 补偿前的叶片加工误差曲面(叶片2)
Fig.12 Error surfaces of the blisk blades before compensation (blade 2)
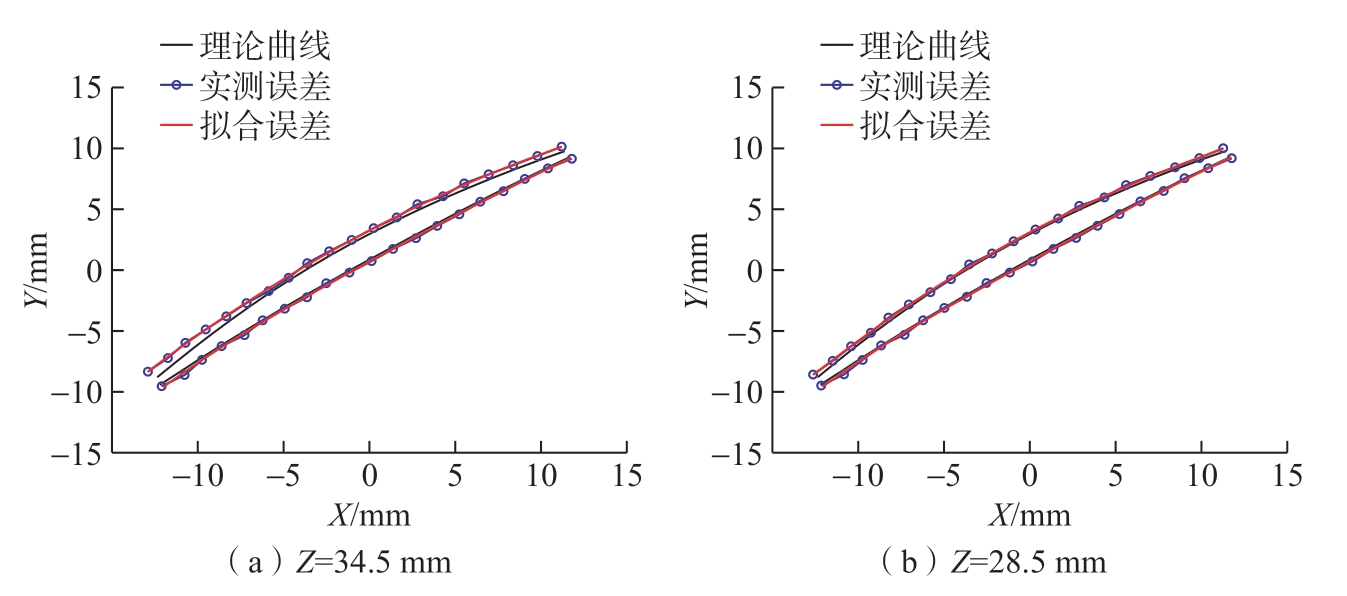
图13 补偿前的叶片加工误差曲线(叶片2)
Fig.13 Error lines of the blisk blades before compensation (blade 2)
在机测量-补偿加工工况下,叶片3的加工误差曲面和对应的两条轮廓误差线如图14和15所示。可以看出,在机测量-补偿加工后,无论是弹性变形为主的背部还是塑性变形为主的前部误差均得到较好的消除,误差范围分别降低到[-3.1084 μm,7.0060 μm]和[-7.8703 μm,6.2440 μm]。综合考虑背部和前部的总误差范围降低至[-7.8703 μm,7.0060 μm],相比于无补偿工况降低了67.7%。
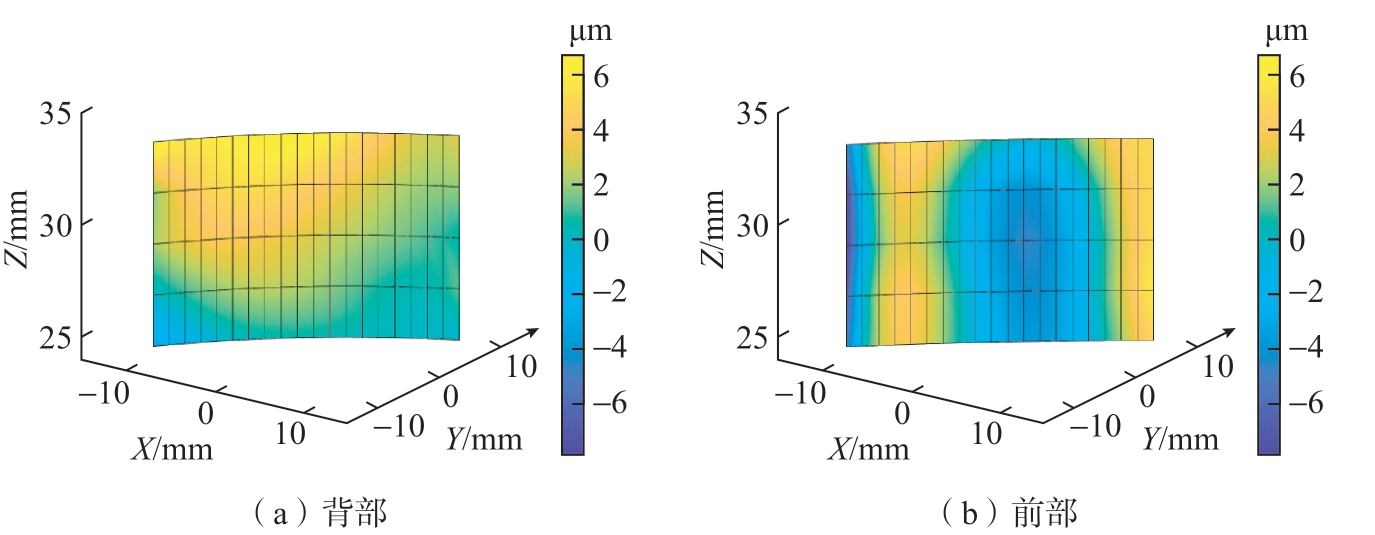
图14 补偿后的叶片加工误差曲面(叶片3)
Fig.14 Error surfaces of the blisk blades after compensation (blade 3)
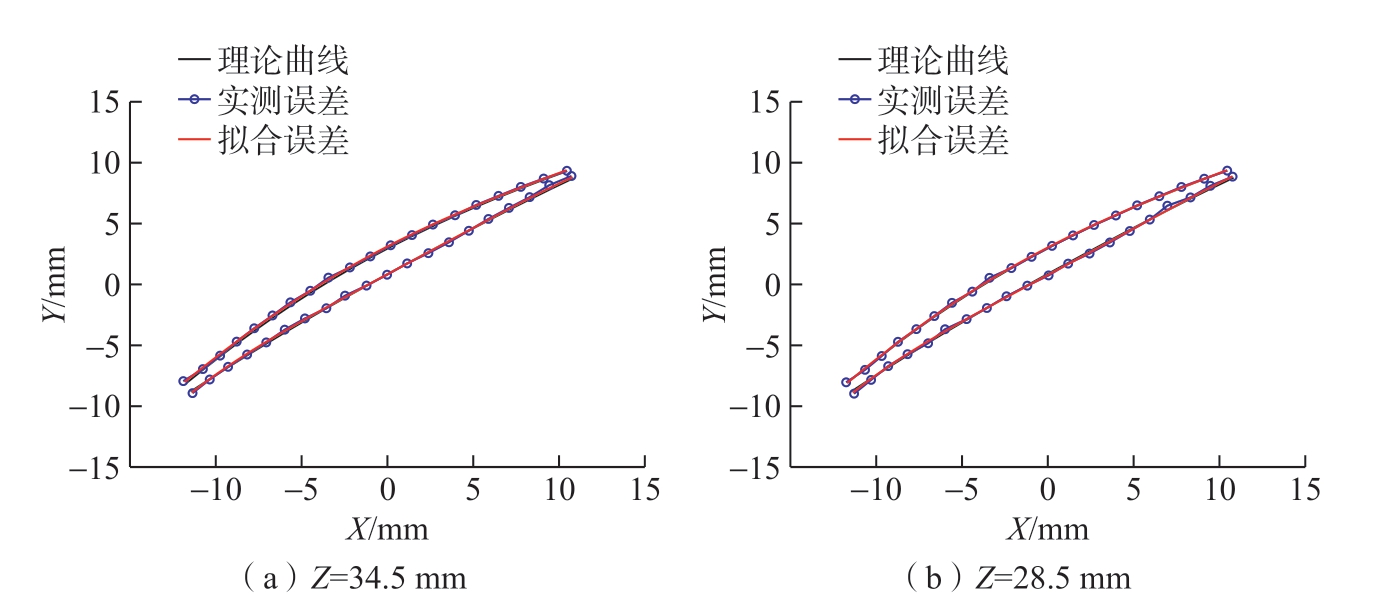
图15 补偿后的叶片加工误差曲线(叶片3)
Fig.15 Error lines of the blisk blades after compensation (blade 3)
综上所述,所提的在机测量-补偿加工一体化制造方法可有效适用于机理复杂、难以建模的薄壁叶片铣削加工误差建模与补偿,并且适用于薄壁叶片批量加工过程。由于同一批次薄壁叶片的结构相同、加工工艺相同且工况类似,因而通常可在前5件的在机测量和模型修正过程中逐渐将模型的精度迭代至较高水平。后续加工时无需每件都进行在机测量,仅需进行抽样式的在机检测和模型修正,实现加工效率和精度的兼顾。
5 结论
本文针对薄壁叶片加工误差的检测、建模与实时补偿,所开展的主要工作总结如下。
(1)提出了基于在机测量的薄壁叶片加工误差建模与补偿方法,主要包括规划在机测点以及测量轨迹、实施在机检测、测量数据处理、建立加工误差模型、修正计算误差补偿模型及实施补偿加工6个步骤。
(2)提出了基于Hampel滤波的在机测量数据处理方法、基于机器学习算法的加工误差建模以及补偿值计算方法,实现了复杂工况下薄壁叶片加工误差在机检测、自动建模与实时补偿。
(3)开发了基于数控系统原点偏移功能的薄壁叶片加工误差实时补偿系统,开展了薄壁叶片铣削加工验证试验。试验结果表明,在机测量-补偿加工后的薄壁叶片无论是弹性变形为主的背部还是塑性变形为主的前部,其误差均得到较好的消除,整体加工误差范围降低了67.7%,有效提高了其加工精度。
[1] YAN B, HAO Y, ZHU L, et al.Towards high milling accuracy of turbine blades: A review[J]. Mechanical Systems and Signal Processing, 2022, 170: 108727.
[2] CHEN W F, XUE J B, TANG D B, et al. Deformation prediction and error compensation in multilayer milling processes for thin-walled parts[J]. International Journal of Machine Tools and Manufacture, 2009, 49(11):859-864.
[3] DU Z C, GE G Y, XIAO Y K, et al.Modeling and compensation of comprehensive errors for thin-walled parts machining based on on-machine measurement[J]. The International Journal of Advanced Manufacturing Technology,2021, 115(11): 3645-3656.
[4] KOIKE Y, MATSUBARA A,YAMAJI I. Optimization of cutting path for minimizing workpiece displacement at the cutting point: Changing the material removal process, feed direction, and tool orientation[J].Procedia CIRP, 2013, 5: 31-36.
[5] 刘述明, 扈博琴, 张春龙, 等. 基于浮动装夹自适应加工工艺的薄壁件加工变形控制技术研究[J]. 航空制造技术, 2023, 66(3):70-77.LIU Shuming, HU Boqin, ZHANG Chunlong, et al. Research on deformation control technology for thin-walled parts based on responsive fixture adaptive machining process[J]. Aeronautical Manufacturing Technology, 2023, 66(3): 70-77.
[6] 王张浩, 李东升, 翟雨农. 弱刚性薄壁件夹具布局优化方法研究概述[J]. 航空制造技术, 2023, 66(14): 118-135.WANG Zhanghao, LI Dongsheng, ZHAI Yunong. A review of fixture layout optimization method for weakly-rigid thin-walled workpieces[J]. Aeronautical Manufacturing Technology, 2023, 66(14): 118-135.
[7] ZHANG S K, BI Q Z, JI Y L, et al.Real-time thickness compensation in mirror milling based on modified Smith predictor and disturbance observer[J]. International Journal of Machine Tools and Manufacture, 2019, 144:103427.
[8] GE G Y, XIAO Y K, FENG X B,et al. An efficient prediction method for the dynamic deformation of thin-walled parts in flank milling[J]. Computer-Aided Design, 2022,152: 103401.
[9] WU Q, LI D P, REN L, et al.Detecting milling deformation in 7075 aluminum alloy thin-walled plates using finite difference method[J]. The International Journal of Advanced Manufacturing Technology, 2016,85(5): 1291-1302.
[10] LI Z L, TUYSUZ O, ZHU L M,et al. Surface form error prediction in fiveaxis flank milling of thin-walled parts[J].International Journal of Machine Tools and Manufacture, 2018, 128: 21-32.
[11] GAO W, HAITJEMA H, FANG F Z, et al. On-machine and in-process surface metrology for precision manufacturing[J]. CIRP Annals, 2019, 68(2): 843-866.
[12] HUANG N D, BI Q Z, WANG Y H, et al. 5-Axis adaptive flank milling of flexible thin-walled parts based on the onmachine measurement[J]. International Journal of Machine Tools and Manufacture, 2014, 84:1-8.
[13] HUANG N D, YIN C H, LIANG L,et al. Error compensation for machining of large thin-walled part with sculptured surface based on on-machine measurement[J]. The International Journal of Advanced Manufacturing Technology,2018, 96(9): 4345-4352.
[14] YI B W, LIANG R B, WANG X S,et al. Free-form surface form error evaluation based on smaller-scale sampling points in touchtrigger probing[J]. Precision Engineering, 2022,76: 255-260.
[15] ZHU L D, YAN B L, WANG Y L,et al. Inspection of blade profile and machining deviation analysis based on sample points optimization and NURBS knot insertion[J].Thin-Walled Structures, 2021, 162: 107540.
[16] BI Q Z, HUANG N D, ZHANG S K, et al. Adaptive machining for curved contour on deformed large skin based on on-machine measurement and isometric mapping[J].International Journal of Machine Tools and Manufacture, 2019, 136: 34-44.
[17] WANG J H, BI Q Z, YU J H, et al.On-machine ultrasonic thickness measurement and compensation of thin-walled parts machining on a CNC lathe[J]. Procedia CIRP,2021, 101: 246-249.
[18] DAVIES L, GATHER U. The identification of multiple outliers[J]. Journal of the American Statistical Association, 1993,88(423): 782-792.
[19] FRIEDMAN J H. Greedy function approximation: A gradient boosting machine[J].The Annals of Statistics, 2001, 29(5): 1189-1232.
