镜像加工技术是实现大型复杂曲面薄壁件（以飞机蒙皮、火箭燃料贮箱为代表）高效稳定加工的有效手段之一[1-3]。毛坯成形误差、装夹变形等常导致工件装夹后实际面型与设计模型存在偏差[4-5]。现有的加工轨迹规划方法广泛采用测量-加工一体化方案，即在加工前在机获取装夹后工件实际状态，根据测量结果和加工要求重建加工基准，确定镜像加工轨迹。然而，在加工过程中工件刚度敏感方向局部受力变形，使得构件关联基准浮动，会导致壁厚精度失控、定位基准失效。
康晓军等[6]利用在机线激光扫描获得蒙皮实际面型，并基于特征映射移植加工程序，生成适用于实际面型的加工程序。Hao等[7]根据大尺寸薄壁自由曲面零件的在线检测结果，得到零件毛坯表面的误差分布情况，在理想模型刀具轨迹的基础上进行刀具轨迹移植，得到适应工件实际形状的新刀具轨迹。Xiao等[8-9]通过集成在混联双机器人镜像加工系统支撑侧的蓝光三维扫描系统，获取装夹后工件支撑表面的形位信息，重构得到工件支撑表面数学模型，对支撑端位姿进行规划。Bi等[10]利用线激光扫描仪在机测量获得工件变形表面的真实几何形状，采用曲面匹配算法构建实际曲面与理想曲面之间的映射关系，根据等距曲面映射结果自适应调整刀具轨迹，补偿变形误差。上述基于在机测量的镜像加工轨迹规划研究均提高了薄壁件加工精度，但普遍采用离线加工轨迹规划方法，未考虑加工过程中工件受力变形。Zhang等[11]建立了在线测量系统获取工件的厚度和局部变形，通过测量变形数据和机床的几何姿态估算壁厚，通过加工侧刀具轴向进给轴实现壁厚补偿。Bi等[12]提出了一种基于Fv-SVM的壁厚误差分解方法，将镜像加工壁厚误差分解为空间相关误差和时间相关误差，对空间相关误差进行离线补偿，对时间相关误差利用间接测量壁厚通过调整刀具轨迹实现壁厚在线补偿。然而，当前研究仅考虑了对装夹后工件变形进行轨迹规划，加工轨迹在线调整只调整刀具轨迹以保证壁厚精度，尚未建立完整的镜像“加工-支撑”运动学模型。
针对上述问题，本文研究了基于旋量理论的镜像加工运动学建模及轨迹自动修调方法。首先，基于旋量理论建立了镜像加工运动学模型；其次，建立了镜像加工轨迹生成模型和轨迹修调模型；最后，开展了薄壁件栅格镜像加工试验，验证了本文方法可以满足薄壁件镜像加工剩余壁厚要求。
1 基于旋量理论的镜像加工运动学建模
在连续等壁厚镜像加工过程中，加工侧和支撑侧位姿随工件曲面形状各自按照加工轨迹和支撑轨迹进行运动，但两者相对位姿关系保持不变，进而推导出镜像加工剩余壁厚运动学表达。
目前机床运动学建模方法主要基于齐次坐标变换理论和旋量理论，齐次坐标变化理论必须合理建立多个局部坐标系，在建模和运算上有一定的难度和复杂性，且基于雅克比矩阵的逆运动学求解法仅能得到5个轴运动量的数值近似解，不能得到解析解。而基于旋量理论的建模方法所有点和坐标均表示在机床坐标下，具有简化模型计算的优点，同时基于旋量理论可得到逆运动学的解析解，能够提高支撑轨迹生成和修调的计算精度。因此，本文采用旋量理论建立镜像加工运动学模型。
基于旋量理论的运动学建模基本单位是螺旋运动 eξθ。一个刚体从一个位置到另一个位置的运动分解为绕某直线的转动和沿这条直线的平动，所以螺旋运动 eξθ 由一个旋量ξ和一个运动量θ组成。旋量ξ的表达式为
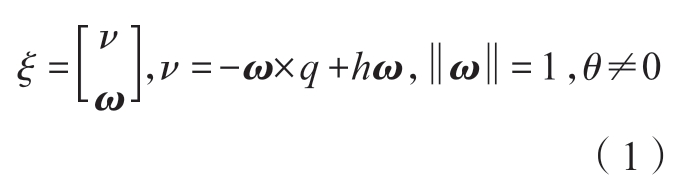
式中，ω是该转轴的单位向量；q为轴线上任意一点；h为旋量运动的节距。
旋量运动对应的齐次变换矩阵为
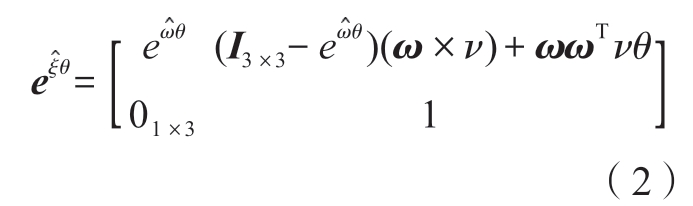
机床整机运动链可以分为工件运动链和刀具运动链。其中，工件运动链从机床坐标系开始到达工件坐标系，刀具运动链从机床坐标系开始到达刀具坐标系。而整机运动链则是从工件坐标系开始，经过机床坐标系最终到达刀具坐标系。沿着工件运动链和刀具运动链分别建立正向运动学模型，描述从机床坐标系到工件坐标系和刀具坐标系的运动学关系。将二者做差，得到在工件坐标系下刀具切削运动位姿向量R（t） =（P（t），O（t））T=（Px（t），Py（t），Pz（t），Oi（t），Oj（t），Ok（t））T，是机床5个运动轴的实时位置M（t） =（x（t），y（t），z（t），θp（t），θs（t））T的函数，如图1所示。
图1 正向运动学示意图
Fig.1 Schematic diagram of forward kinematics
根据旋量理论，运动链的各轴经过一定位移后，第n个轴相对于机床坐标系的齐次变换矩阵为
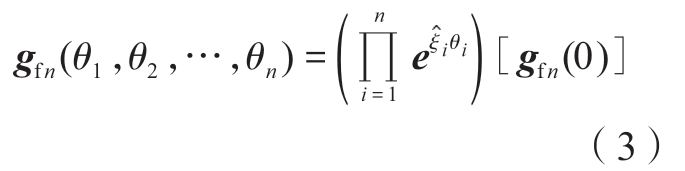
式中，ξi和θi（i=1，2，…，n）表示运动轴n在全局坐标系下的旋量和运动量；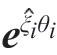
（i=1，2，…，n）表示对应旋量运动的齐次变换矩阵，可根据式（1）和（2）计算得到；gfn（0）为初始状态第n个轴相对于全局坐标系的齐次变换矩阵。定义gft（0）和gfw（0）为初始状态下刀具坐标系和工件坐标系相对于全局坐标系的齐次变换矩阵
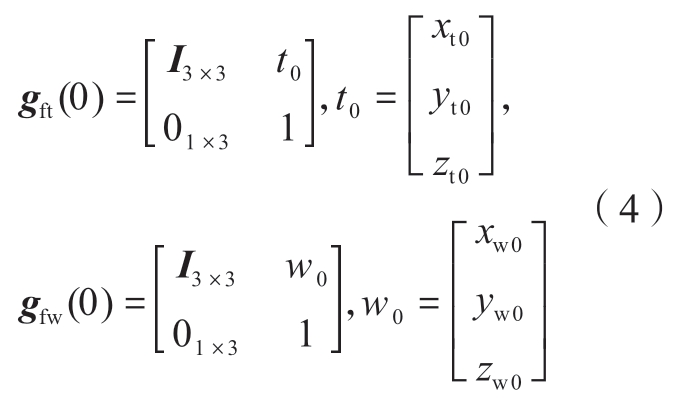
镜像加工系统整机运动链由加工侧运动链和支撑侧运动链组成，单侧运动链即机床运动链。镜像加工系统运动学建模即分别建立加工侧和支撑侧运动链，在工件坐标系下将两侧运动链做差得到镜像加工剩余壁厚运动学模型。
对于加工侧，设在刀具运动链和加工工件运动链中分别有m和n个运动轴，则刀具坐标系相对于机床坐标系的齐次变换矩阵为
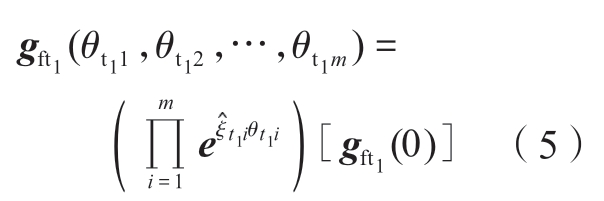
式中
和θt1i（i=1，2，…，m）是机床坐标系下刀具运动链中第i个运动轴的运动旋量和运动距离（或角度）。
工件坐标系相对于机床坐标系的齐次变换矩阵为
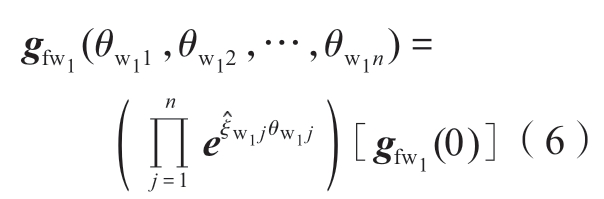
式中，ξwj和θwj（j=1，2，…，n）是机床坐标系下工件运动链中第j个运动轴的运动旋量和运动距离（或角度）。因此，刀具坐标系相对于工件坐标系的齐次变换为
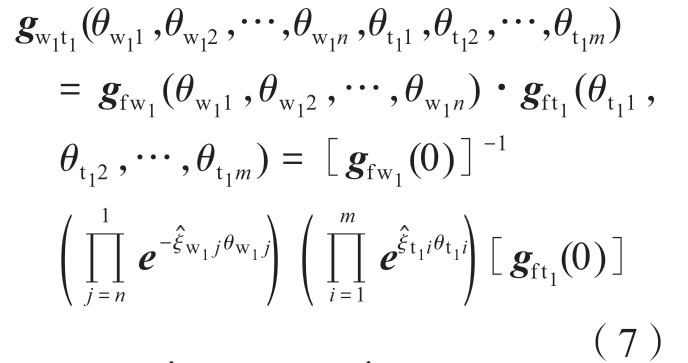
式中，
是变换矩阵的逆，其值与反向变换矩阵
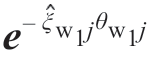相等。
在刀具坐标系中的位置向量rp1t1和姿态向量ro1t1基础上，通过式（7）计算加工工件坐标系下的刀具位姿向量rp1w1和ro1w1。
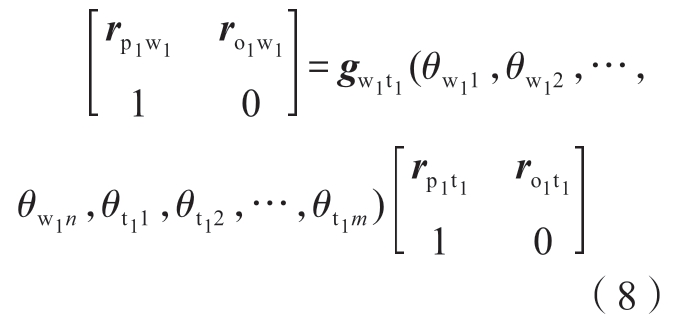
同理，可得到支撑坐标系相对于支撑工件坐标系的齐次变换为
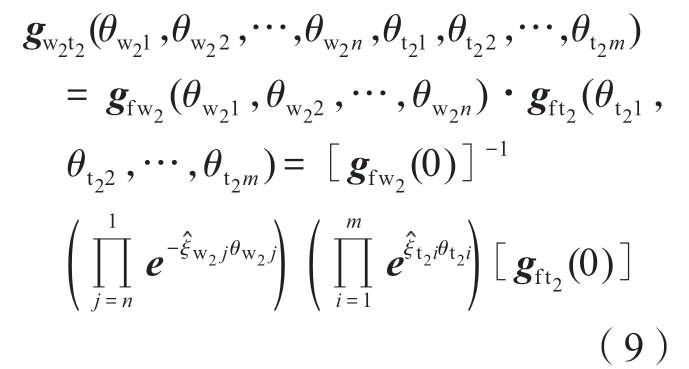
为建立镜像加工壁厚运动学表达模型，需将支撑坐标系相对于支撑工件坐标系的齐次变换转换为支撑坐标系相对于加工工件坐标系的齐次变换关系
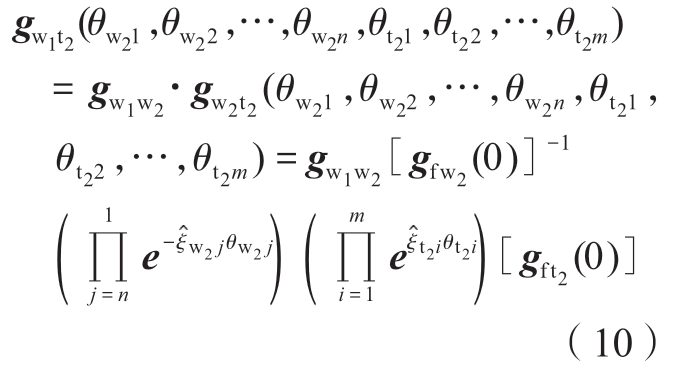
式中，gw1t2为支撑侧刀具坐标系相对于加工侧工件坐标系的变换矩阵。
基于支撑坐标系中位置向量rp2t2和姿态向量ro2t2，通过式（10）计算加工工件坐标系下支撑位姿向量rp2w1和ro2w1。
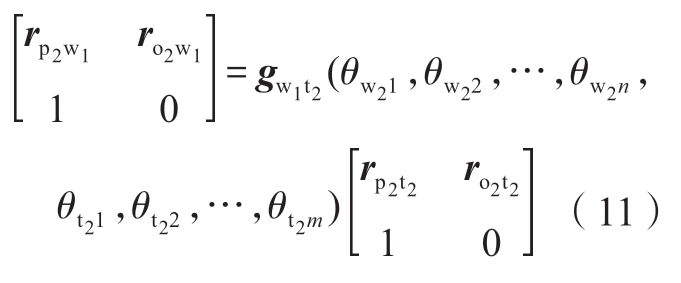
将加工工件坐标系下的刀具与支撑位置向量做差，得到镜像加工剩余壁厚运动学表达为
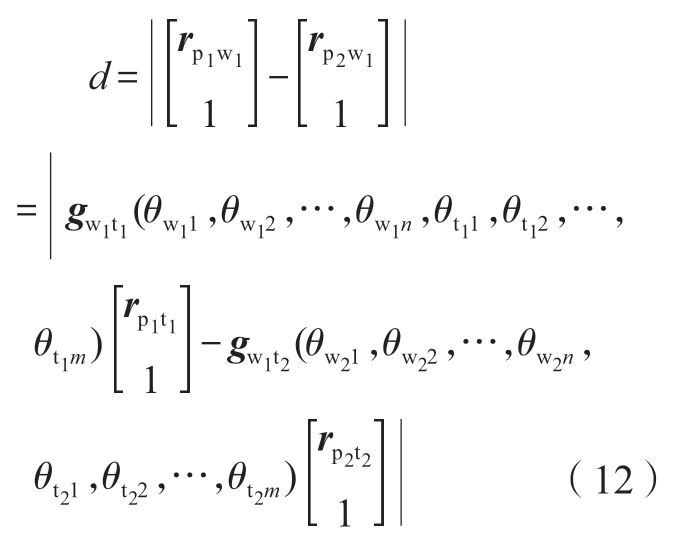
2 面向工件变形补偿的轨迹修调建模
2.1 镜像加工“支撑-铣削”轨迹关联模型
在镜像加工过程中，刀具和支撑头分别位于工件两侧，支撑头方向矢量位于支撑表面法向，刀具矢量和支撑头矢量始终保持反向共线。当前层完成加工后刀具向下一层进刀时，支撑头位姿保持不变，刀具沿轴线方向进行切深进给，加工过程中通过控制刀具与支撑头之间的相对距离保证工件剩余壁厚，如图2所示。镜像加工约束关系总结为：刀具矢量和支撑头矢量始终沿着工件表面的法向矢量，且两者保持反向共线；刀具中心点和支撑中心点在工件表面的公法线，且距离等于壁厚，得出
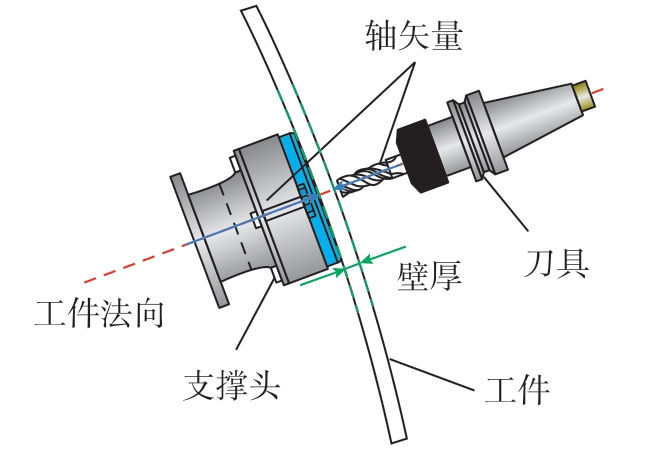
图2 镜像加工约束关系
Fig.2 Mirror milling constraints
式中，VT和VH分别为刀具和支撑头的矢量，nw为工件法向矢量，PT和PH分别为刀具中心点和支撑头中心点，d为工件壁厚。
生成加工侧轨迹后得到加工侧运动轴位置M1（t） =（x1（t），y1（t），z1（t），θp1（t），θs1（t））T，基于运动学模型（式（8））可得到在加工工件坐标系下的刀具切削运动位姿向量R1（t）=（P1（t），O1（t））T=（Px1（t），Py1（t），Pz1（t），Oi1（t），Oj1（t），Ok1（t））T。根据式（13）得到支撑头在加工工件坐标系下的位姿态向量R2（t）=（P2（t），O2（t））T=（Px2（t），Py2（t），Pz2（t），Oi2（t），Oj2（t），Ok2（t））T为
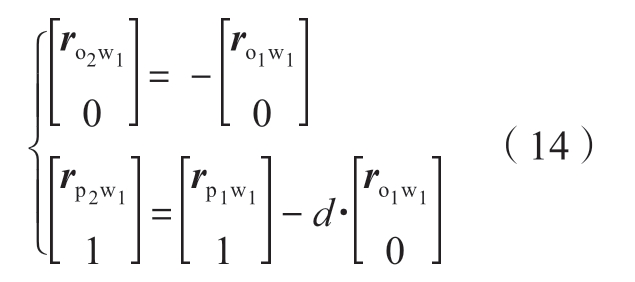
通过逆向运动学求解式（14）得到支撑侧运动轴位置M2（t） =（x2（t），y2（t），z2（t），θp2（t），θs2（t））T。首先，直线轴运动对姿态向量没有影响，设直线轴运动变换矩阵和旋转轴运动变换矩阵分别为
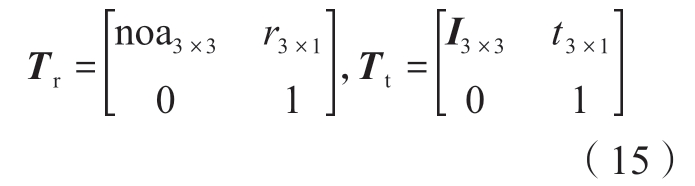
不论是将直线轴变换矩阵左乘还是右乘，都不会影响旋转向量部分。
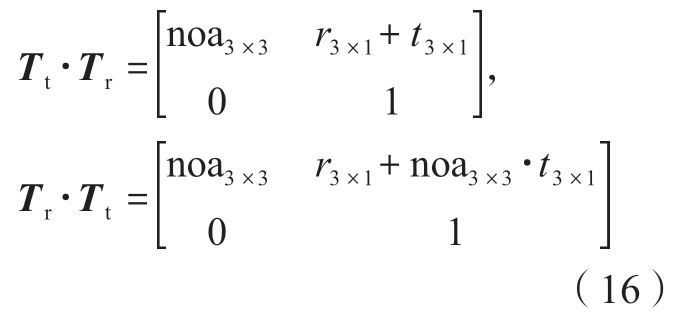
因此，可以将式（14）姿态向量部分简化为
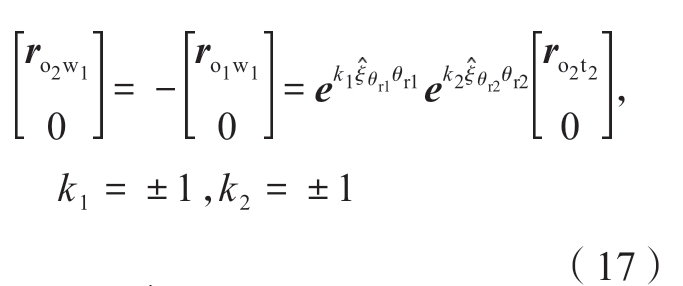
式中，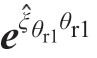
代表更靠近工作台的旋转轴齐次变换矩阵，而
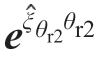代表更靠近刀具的旋转轴齐次变换矩阵。k1和k2取值为+1或者-1，这取决于旋转轴1和旋转轴2在刀具运动链上还是在工件运动链上。
通过Paden-Kahan子问题1和2求解式（17）得到θr1和θr2的解析解[13]，通过引入中间变量c，式（17）可转变为
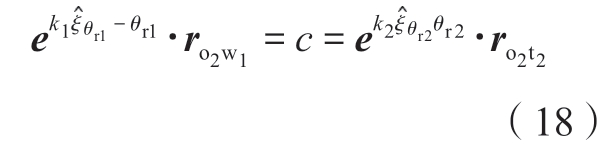
中间变量c存在如下关系
式中，
，γ取值带有正负号是由于方程可能存在2个解、1个解或者无解的情况，u=ro2t2，v =ro2w1=-ro1w1。
计算得到中间变量c后，式（18）将分解为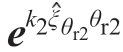
·u=c和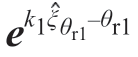
· v=c，应用Paden-Kahan子问题1求解θr1和θr2为
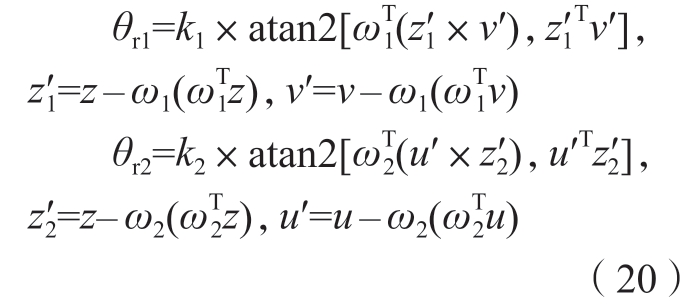
在完成旋转轴求解后，进一步计算直线轴X2、Y2、Z2的运动量。根据运动学模型可将式（14）位置向量部分改写成
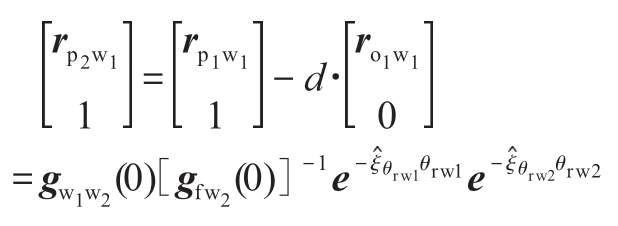
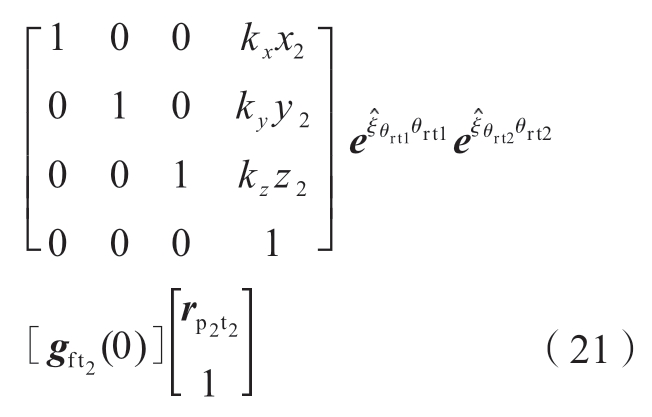
式中，θrw1和θrw2是工件运动链上转轴的运动量，θrt1和θrt2是刀具运动链上转轴的运动量。kx、ky和kz可以取±1，这取决于直线轴在运动链中的位置。若直线轴在床身F之前，k值取-1；若直线轴在床身F之后，k值取+1。
对式（21）直接求解可以得到直线轴的逆运动学解[x2，y2，z2，0]T，为
2.2 镜像加工轨迹自动修调模型
在镜像加工过程中，支撑装置的引入能够为加工提供稳定定位基准，以确保镜像加工的准确性和精度，然而在加工过程中由于支撑力作用，工件不可避免地产生一定程度变形，使得镜像加工初始基准失效，影响工件轮廓和厚度精度。因此，需要对定位基准进行修调，确定新的定位基准，保证刀具-工件-支撑始终满足镜像加工约束，如图3所示。
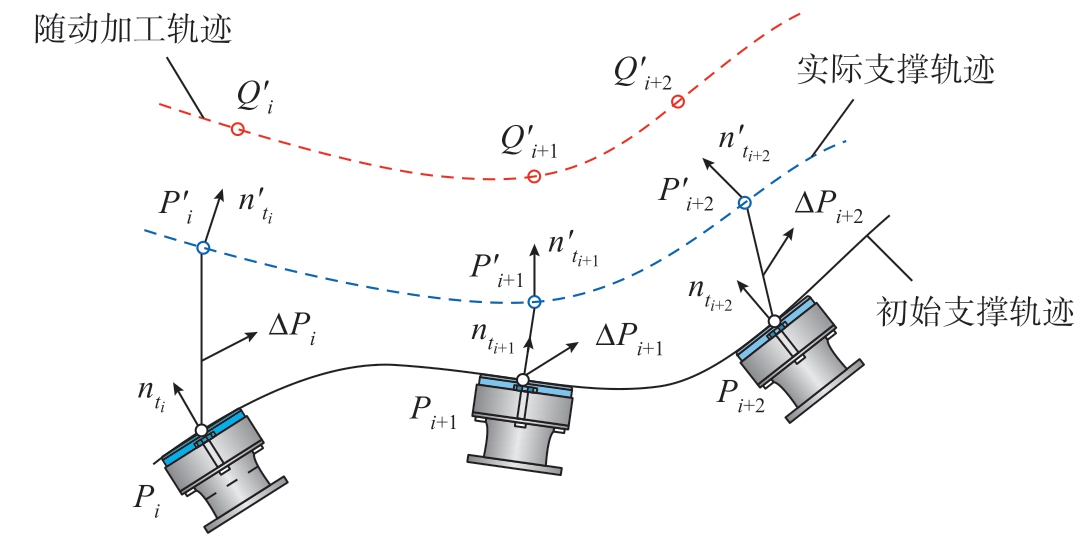
图3 镜像加工轨迹自动修调
Fig.3 Automatic adjustment of mirror milling trajectory
当支撑端依据初始轨迹运动到Pi点R2（ti） = （Px2（ti），Py2（ti），Pz2（ti），Oi2（ti），Oj2（ti），Ok2（ti））T时，由于工件变形，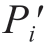
′点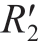
（ti）=（
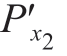（ti），
（ti），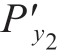
（ti），
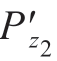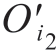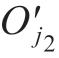（ti），
（ti），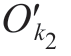
（ti））T为实际支撑位置，因此需要将支撑位置修调至Pi′点以保证镜像稳定支撑。
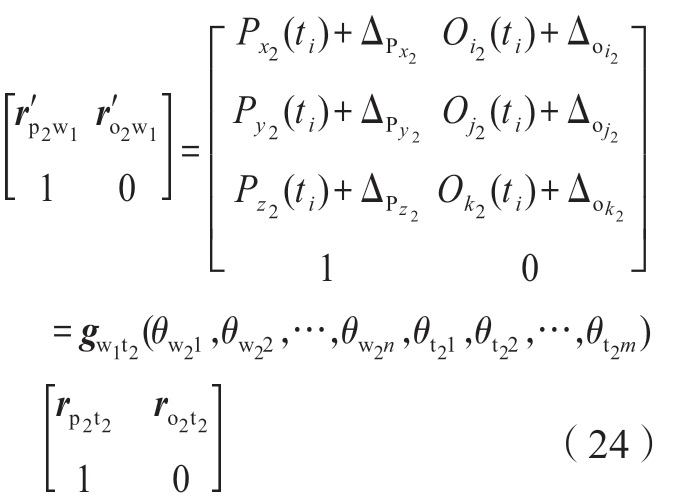
利用式（15）～（22）逆向求解式（24）得到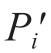
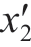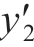′点空间位姿对应的支撑侧运动轴坐标M′2（ti） =[
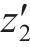（ti），
′（ti），
（ti），
（ti），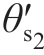
（ti）]T，
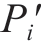点对应运动轴坐标为
支撑侧运动轴修调量为
计算得到Pi′点支撑端刀位点后，基于“支撑—铣削”轨迹关联模型得到加工侧修调后刀位点Qi′点，对应加工侧运动轴坐标为M′1（ti）=
3 栅格壁板镜像加工试验验证
为验证镜像加工“支撑-铣削”轨迹关联模型和修调模型的有效性，利用本课题组自行研制的双四轴镜像加工设备进行加工试验验证。镜像加工装备如图4所示，其主体采用双立柱两侧对称布置结构，单侧四联动，8个伺服轴分别为X1、Y1、Z1、B1和X2、Y2、Z2、B2，其中X1、Y1、Z1、B1轴为加工侧直线轴和旋转轴，X2、Y2、Z2、B2轴为支撑侧直线轴和旋转轴。
图4 镜像加工设备
Fig.4 Mirror milling system
以栅格壁板作为试件，分别在使用轨迹修调模型（2.2节）进行变形补偿和未进行变形补偿情况进行试验，栅格壁板尺寸为1000 mm×750 mm×5 mm，曲率半径为4000 mm，材料为7075铝合金，加工剩余壁厚要求（1.5±0.1） mm。利用海克斯康RigelScan Pro手持式三维扫描仪（精度为0.03 mm）测量工件面型，获得支撑侧实际面型点云数据，将测量点云数据导入Design X软件逆向建模，利用UG建立工件实际模型并生成加工侧轨迹，通过建立的镜像“支撑-铣削”轨迹关联模型生成支撑侧轨迹，将加工侧轨迹与侧支撑轨迹关联得到“支撑-铣削”轨迹，基于镜像加工设备支撑头传感器测量数据修调镜像加工轨迹，如图5所示。依据加工轨迹开展镜像加工验证试验，采用表1中的加工参数进行加工，刀具为不等齿距变螺旋角整体硬质合金立铣刀，刀具直径10 mm，螺旋角30°～45°，支撑端采用3层支撑环结构支撑，支撑环末端为圆弧支撑，刚性环中径为30 mm，柔性外环中径分别为104 mm和126 mm。加工后的工件表面如图6所示。
表1 镜像加工参数
Table 1 Machining parameters for mirror milling
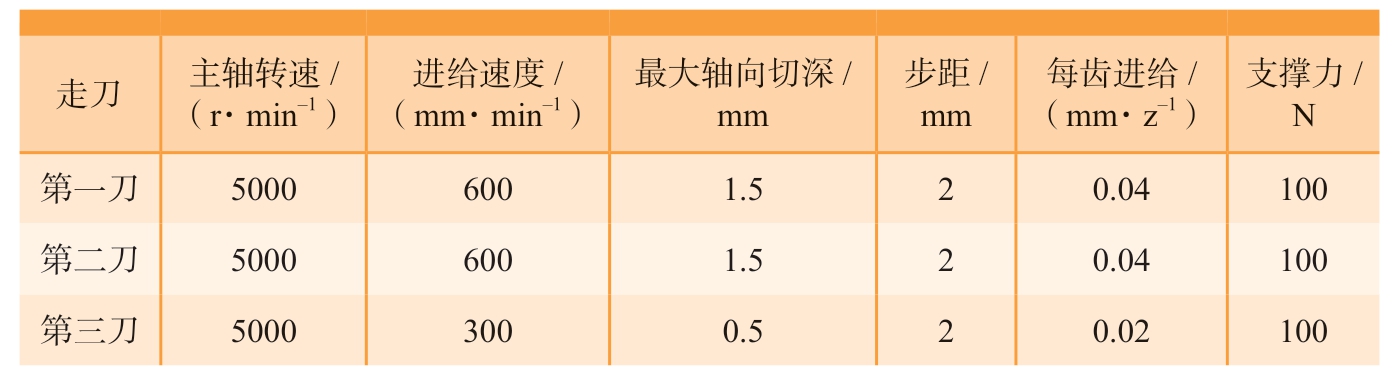
走刀 主轴转速/（r·min-1）进给速度/（mm·min-1）最大轴向切深/mm步距/mm每齿进给/（mm·z-1）支撑力/N第一刀 5000 600 1.5 2 0.04 100第二刀 5000 600 1.5 2 0.04 100第三刀 5000 300 0.5 2 0.02 100
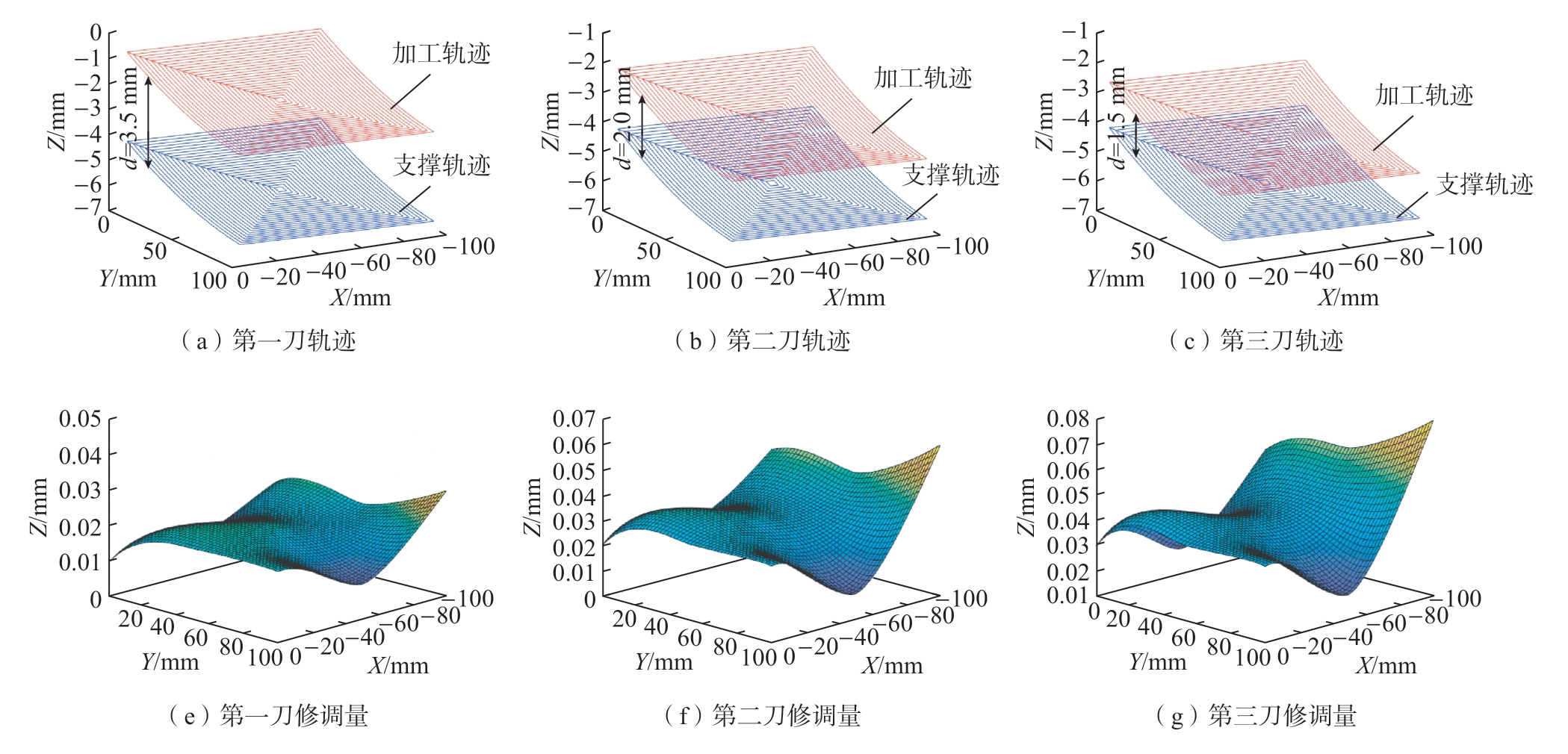
图5 栅格“支撑-铣削”轨迹及修调量
Fig.5 Support-milling path and trimming volume of grid
图6 加工后栅格表面
Fig.6 Machined surface of grid
采用Innerspec超声测厚仪（精度为0.02 mm）测量加工后栅格剩余壁厚。栅格测量9个点，每个测点测量3次，取平均值作为剩余壁厚，使用变形修调和未使用变形修调的测量结果如表2和3所示。工件剩余壁厚加工要求为（1.5±0.1）mm，使用变形修调壁厚测量结果为（1.5±0.07） mm，标准差为0.012 mm；未使用变形修调测量结果为（1.5±0.11） mm，标准差为0.026 mm。结果表明，本文提出的镜像加工“支撑—铣削”关联轨迹生成和修调方法可以满足剩余壁厚加工要求，且壁厚分布较均匀。
表2 使用变形修调的工件剩余壁厚测量结果
Table 2 Measuring results of thickness with trajectory adjustment mm
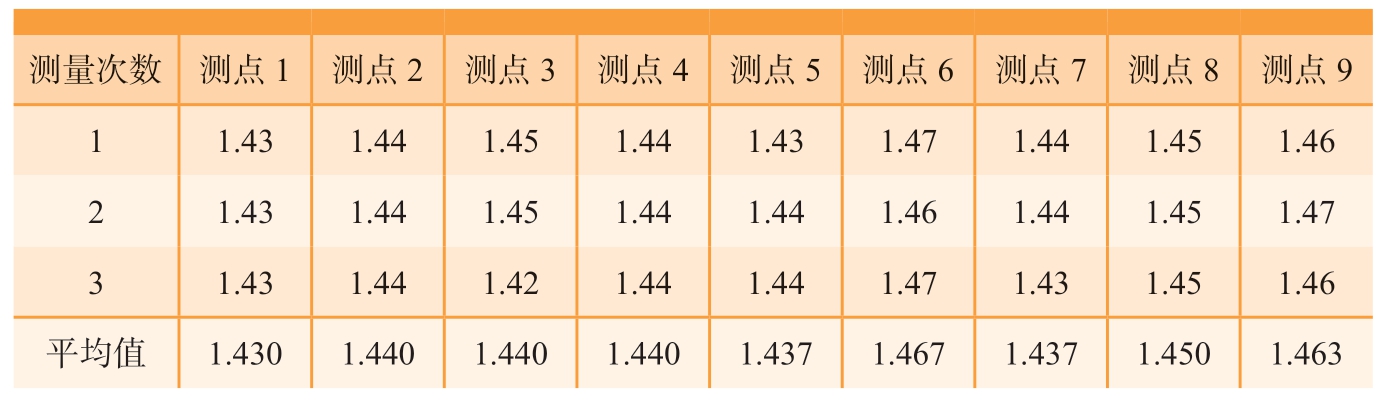
测量次数 测点1 测点2 测点3 测点4 测点5 测点6 测点7 测点8 测点9 1 1.43 1.44 1.45 1.44 1.43 1.47 1.44 1.45 1.46 2 1.43 1.44 1.45 1.44 1.44 1.46 1.44 1.45 1.47 3 1.43 1.44 1.42 1.44 1.44 1.47 1.43 1.45 1.46平均值 1.430 1.440 1.440 1.440 1.437 1.467 1.437 1.450 1.463
表3 未使用变形修调工件剩余壁厚测量结果
Table 3 Measuring results of thickness without trajectory adjustment mm
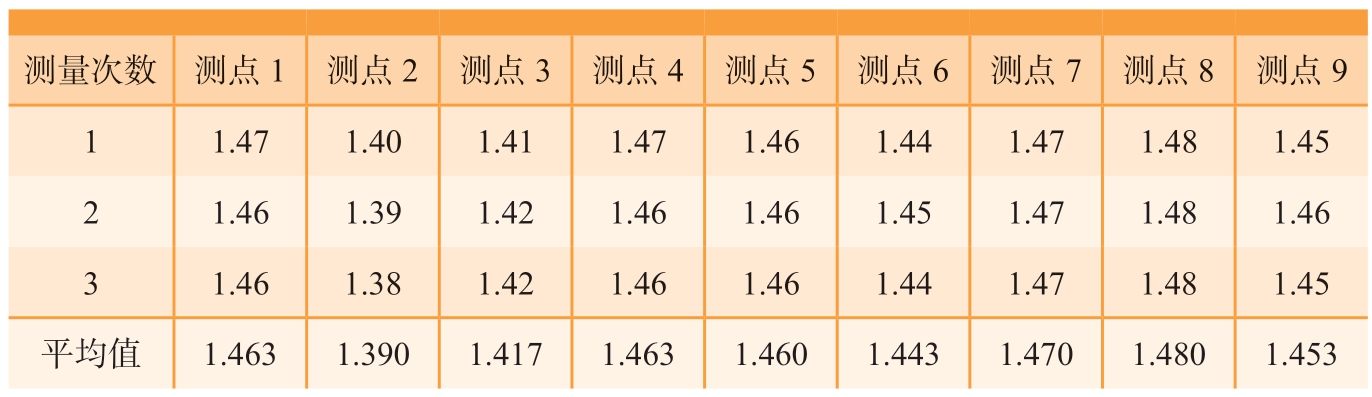
测量次数 测点1 测点2 测点3 测点4 测点5 测点6 测点7 测点8 测点9 1 1.47 1.40 1.41 1.47 1.46 1.44 1.47 1.48 1.45 2 1.46 1.39 1.42 1.46 1.46 1.45 1.47 1.48 1.46 3 1.46 1.38 1.42 1.46 1.46 1.44 1.47 1.48 1.45平均值 1.463 1.390 1.417 1.463 1.460 1.443 1.470 1.480 1.453
4 结论
本文基于旋量理论建立了镜像加工剩余壁厚运动学模型，提出了“支撑—铣削”轨迹生成和自动修调方法，基于在机测量数据生成镜像加工双侧轨迹，开展了栅格壁板镜像加工试验，所提出的方法可满足薄壁件镜像加工剩余壁厚要求，得到以下主要结论。
（1）分析镜像加工“支撑—铣削”运动学闭链，基于旋量理论建立了镜像加工壁厚运动学模型。
（2）综合考虑零件加工要求及其镜像约束关系，建立了镜像加工“支撑—铣削”生成模型，为补偿加工过程中工件变形，建立了镜像加工轨迹自动修调模型。
（3）开展了栅格壁板镜像加工验证试验，加工工件剩余厚度（1.5±0.07） mm，试验结果表明，镜像加工“支撑—铣削”轨迹生成和自动修调方法可以满足剩余壁厚加工要求。
[1] 毕庆贞, 丁汉, 王宇晗. 复杂曲面零件五轴数控加工理论与技术[M]. 武汉: 武汉理工大学出版社, 2016.BI Qingzhen, DING Han, WANG Yuhan. Theory and technique for five-axis NC machining of complex surface part[M]. Wuhan:Wuhan University of Technology Press, 2016.
[2] 鲍岩, 董志刚, 朱祥龙, 等. 蒙皮镜像铣削支撑技术的研究现状和发展趋势[J].航空学报, 2018, 39(4): 021817.BAO Yan, DONG Zhigang, ZHU Xianglong, et al. Review on support technology for mirror milling of aircraft skin[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(4):021817.
[3] BO Q L, WANG P F, CHAI X L,et al. Mirror milling trajectory planning for large thin-walled parts based on Fuzzy-ADRC controlled force pre-supporting[J]. Journal of Manufacturing Processes, 2023, 85: 192-204.
[4] BAO Y, KANG R K, DONG Z G,et al. Model for surface topography prediction in mirror-milling of aircraft skin parts[J].The International Journal of Advanced Manufacturing Technology, 2018, 95(5): 2259-2268.
[5] WASEEM A, ISMAIL L, LIANG STEVEN Y. Prediction and control of residual stress-based distortions in the machining of aerospace parts: A review[J]. Journal of Manufacturing Processes, 2022, 76: 106-122.
[6] 康晓军, 向兵飞, 李迎光, 等. 基于快速扫描的飞机大型蒙皮自适应加工技术[J].航空制造技术, 2019, 62(6): 85-90, 94.KANG Xiaojun, XIANG Bingfei,LI Yingguang, et al. Adaptive machining technology of large aircraft skin based on rapid scanning[J]. Aeronautical Manufacturing Technology, 2019, 62(6): 85-90, 94.
[7] HAO X Z, LI Y G, DENG T C,et al. Tool path transplantation method for adaptive machining of large-sized and thinwalled free form surface parts based on error distribution[J]. Robotics and Computer-Integrated Manufacturing, 2019, 56: 222-232.
[8] LIU Q, LIU H T, XIAO J L, et al. Open-architecture of CNC system and mirror milling technology for a 5-axis hybrid robot[J]. Robotics and Computer-Integrated Manufacturing, 2023, 81: 102504.
[9] XIAO J L, ZHAO S L, GUO H, et al. Research on the collaborative machining method for dual-robot mirror milling[J].The International Journal of Advanced Manufacturing Technology, 2019, 105(10):4071-4084.
[10] BI Q Z, HUANG N D, ZHANG S K, et al. Adaptive machining for curved contour on deformed large skin based on on-machine measurement and isometric mapping[J].International Journal of Machine Tools and Manufacture, 2019, 136: 34-44.
[11] ZHANG S K, BI Q Z, JI Y L, et al. Real-time thickness compensation in mirror milling based on modified Smith predictor and disturbance observer[J]. International Journal of Machine Tools and Manufacture, 2019, 144:103427.
[12] BI Q Z, WANG X Z, WU Q, et al. Fv-SVM-based wall-thickness error decomposition for adaptive machining of large skin parts[J].IEEE Transactions on Industrial Informatics,2019, 15(4): 2426-2434.
[13] MURRAY R M, LI Z, SASTRY S. A Mathematical Introduction to Robotic Manipulation[M]. Boca Raton: CRC Press,1994.
