大型薄壁件结构（如飞机蒙皮和火箭贮箱壁）由于具有强度高与重量轻的优势，在航空航天、汽车、船舶等工业领域得到广泛应用[1-2]。相比于化学加工，铣削方式不但能满足绿色和环保的要求，而且可以实现薄壁件高精度和高效率的减薄加工[3-4]。然而，薄壁件由于尺寸大、材料去除量高，在铣削过程中容易发生严重的再生颤振[5]、受迫振动[6]和静态变形[7]，导致加工误差，甚至损坏刀具。为改善薄壁件的加工质量，一些学者把焦点放在研发新型支撑装置与设备上[8-10]。
从支撑角度来看，大型薄壁件加工方案有3种，分别为固定支撑[11-12]、随动支撑[13-14]和镜像支撑[15-17]。为克服固定位置支撑不能保证铣削表面质量一致性的问题[11-12]，Wan等[13]开发了一种安装在主轴外壳上并在刀具铣削区域对侧同步施加支撑的随动装置，成功抑制了薄壁件颤振。Liu等[14]设计一款可安装在机器人末端的磁吸随动支撑夹具，通过试验验证了该装置对改善加工质量的有效性。上述随动支撑装置需根据工件类型和适用场合进行特定的设计和安装。
为了能够灵活地用于大型复杂薄壁件的加工，支撑头与铣刀主动同步运动并镜像支撑是改善薄壁件任意铣削位置刚度和阻尼的有效方法[15-16]。结合混联机器人刚度和工作空间大的优势，Xiao等[17]设计了一种气动多点柔性支撑头，将其安装在混联机器人末端与加工机器人一起工作可实现镜像协同运动[18]，试验证明其可有效减小工件的变形与振动。值得注意的是，制约机器人镜像协同运动精度的因素主要体现在两方面：商用数控系统限制二次开发与功能定制；双机器人的同步运动轨迹规划不合理且存在镜像同步误差。
在数控系统方面，作为混合机器人的典型代表，Tricept和Exechon均采用西门子专门定制的840D数控系统。该系统可将运动学程序写入程序缓冲区，并按照五轴数控机床标准开发用户操作界面[19]。虽然西门子和ABB公司的机器人控制器具有标准化、可靠性和稳定性等优势，但由于软硬件访问权限和改造的限制，商用数控系统阻碍了双混联机器人运动学和控制算法的开发和应用[20]，已不能满足双机器人镜像协同加工的要求，需要搭建开放式架构的数控系统并对功能进行特殊定制。
在机器人轨迹规划方面，Xiao等[21]考虑单个混联机器人加工路径和关节约束并以加工时间最小为目标，提出一种基于粒子群算法优化的启发式进给速度规划方法，该方法在保证加工质量的同时，可提高加工效率。由于薄壁件内外廓形面几何路径不同，镜像铣削过程中双机器人的进给速度是相互制约的，不能直接采用单机器人的速度规划算法[22]。此外，准确补偿双机镜像同步运动误差仍是一个具有挑战性的问题。离线修正NC代码耗时长且精度低[23]，而在线补偿方法则要通过传感器实时测量机器人当前位置并反馈来实现误差补偿[24]。
为减小大型薄壁件镜像铣削中的变形与颤振，结合混联机器人刚度高与工作空间大的优点，本文提出了基于TriMule-600机器人的镜像铣削协同运动控制策略。首先研发了双CPU开放式架构的数控系统，实现了人机交互和运动控制。然后，为提高双机器人协同运动精度，在数控系统中开发并集成了双机镜像路径生成、双机同步速度规划、双机协同运动学和采用光栅编码器的实时误差补偿4项关键技术。最后，通过一系列薄壁件镜像铣削试验验证了所提出关键技术对改善工件加工质量的有效性。
1 双机器人镜像铣削系统
1.1 混联机器人镜像铣削设备
图1展示了双混联机器人镜像铣削加工系统。该系统由1台带有电主轴的加工机器人、1台装有多点柔性支撑头的支撑机器人和夹持工装等组成。两台混联机器人本体为天津大学自主研发的TriMule-600，该机器人主要由用于定位的1T2R（T平移，R旋转）空间并联机构和连接在动平台上的A/C摆头构成。为更好地模拟大型薄壁件的加工工况，工件采用一端悬臂夹紧的方式（图1中O-XYZ为工件坐标系）。与此同时，优化薄壁件与工装的摆放位置，防止双机器人发生碰撞和超出工作空间。
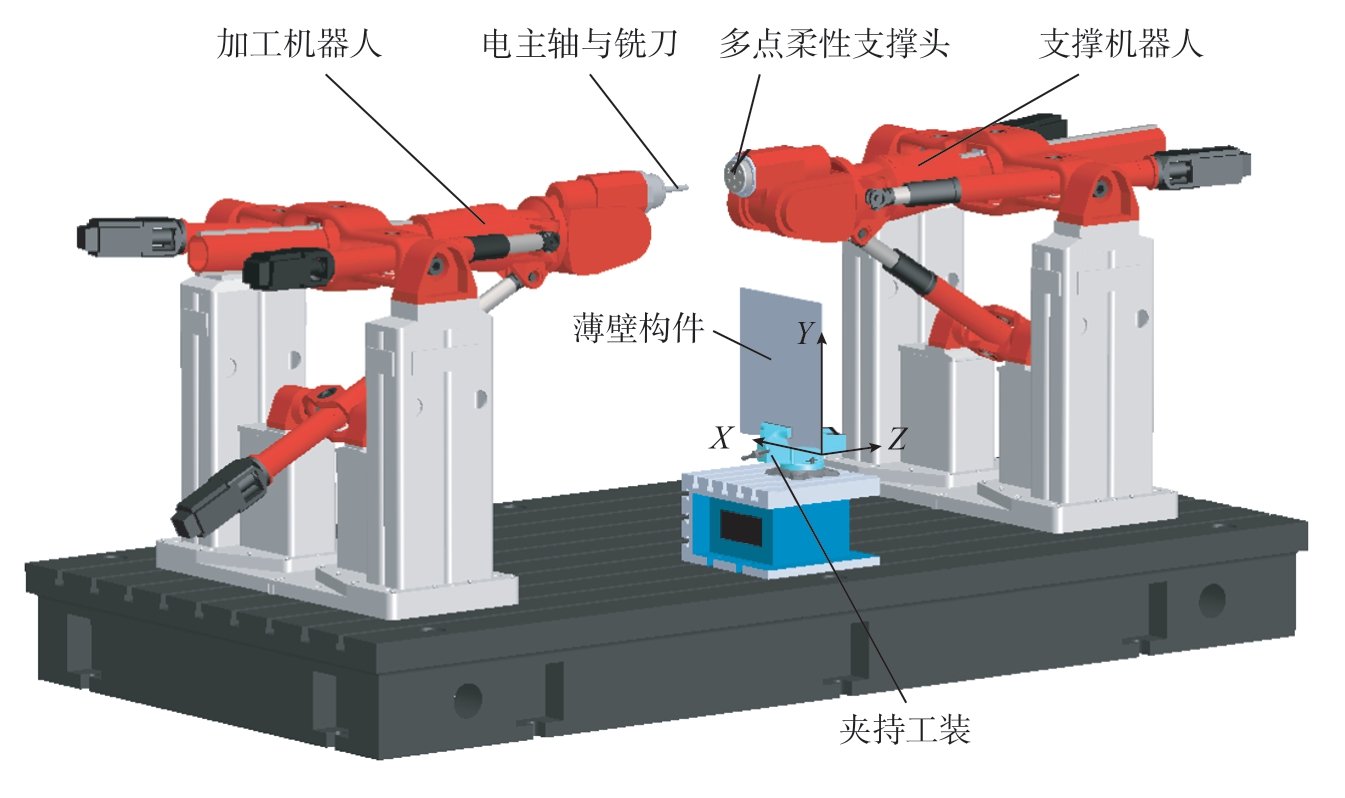
图1 双混联机器人镜像铣削加工设备
Fig.1 Dual hybrid robots mirror milling equipment
多点柔性支撑头由7个支撑杆、SMC-CJPB10-15B微型单动针形气缸、直径15 mm的球形支撑滚珠和端盖组成。7个支撑杆为“中心+外围多点阵列”的位置分布，中间支撑杆为刚性支撑，均布在半径为35 mm圆周上的6个支撑杆尾部连接气缸可形成外围柔性支撑，如图2（a）所示。此外，气缸气压采用SMCITV3030-312CS电气比例阀控制。图2（b）展示了气缸和支撑滚珠的具体结构，相关参数如表1所示。无论是加工平面或曲面薄壁件，刀轴和支撑头方向应沿工件表面法线方向。为避免支撑头与工件发生干涉并结合支撑头的尺寸，可选择曲率半径大于52.2 mm的薄壁件。多点支撑头能够提高薄壁件在加工区域的局部刚度，并有效减小工件在铣削区域的变形与振动。此外，气缸的可伸缩性可以提高支撑头与工件表面的贴合效果。每个支撑杆的末端都装有一个球形滚珠，可减小支撑头随铣刀移动时在工件表面的摩擦和划伤，且在加工曲率较大的薄壁件时也有较好的适应性与贴合性。
表1 针形气缸和支撑滚珠参数
Table 1 Needle shaped cylinder and supporting ball parameters
气缸内径dc/mm 活塞杆直径dr/mm 气缸行程L/mm 气缸气压/MPa 滚珠直径D/mm 滚珠套高度h1/mm 滚珠套直径d1/mm 10 5 15 0.1～0.5 15 16 24
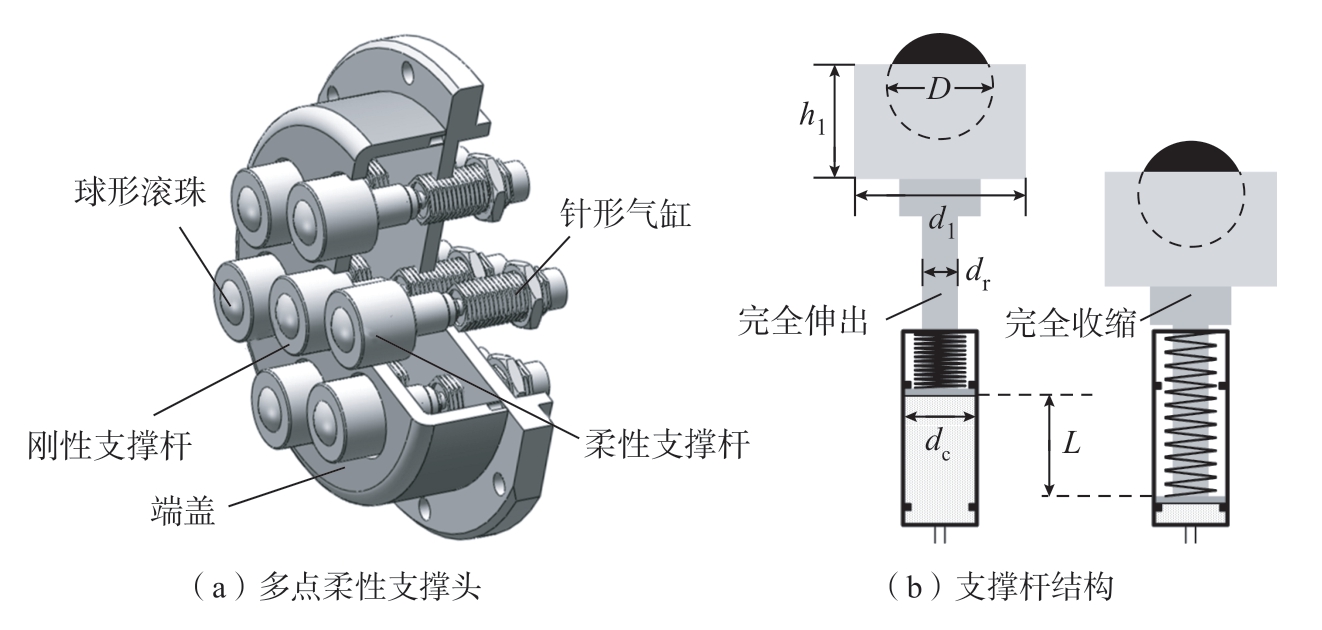
图2 多点柔性支撑头与支撑杆结构
Fig.2 Multi-point flexible support head and support rod structure
考虑到混联机器人关节具有非线性耦合特性，同时为保证镜像铣削系统中两台机器人的运动同步，本研究重点考察和利用开放式数控系统在二次开发、定制特殊功能和提高运动精度方面所具备的优势。
1.2 数控系统的开放式架构与关键功能
图3为双混联机器人镜像铣削数控系统的开放式架构与功能，该系统的硬件主体是由1台工控机IPC（上位机）和1台运动控制器PMAC（下位机）组成的双CPU主从控制结构。用户操作上位机的人机交互界面，通过TCP/IP总线实现与下位机之间的数据传递。PMAC由EtherCAT通信协定与I/O设备、两台机器人的驱动器、电主轴系统等硬件传输控制信号与交换数据。伺服驱动器的PID反馈和速度/加速度前馈算法控制电机实现运动。作为关键环节，软件设计包括人机交互界面设计和PMAC程序开发两部分。
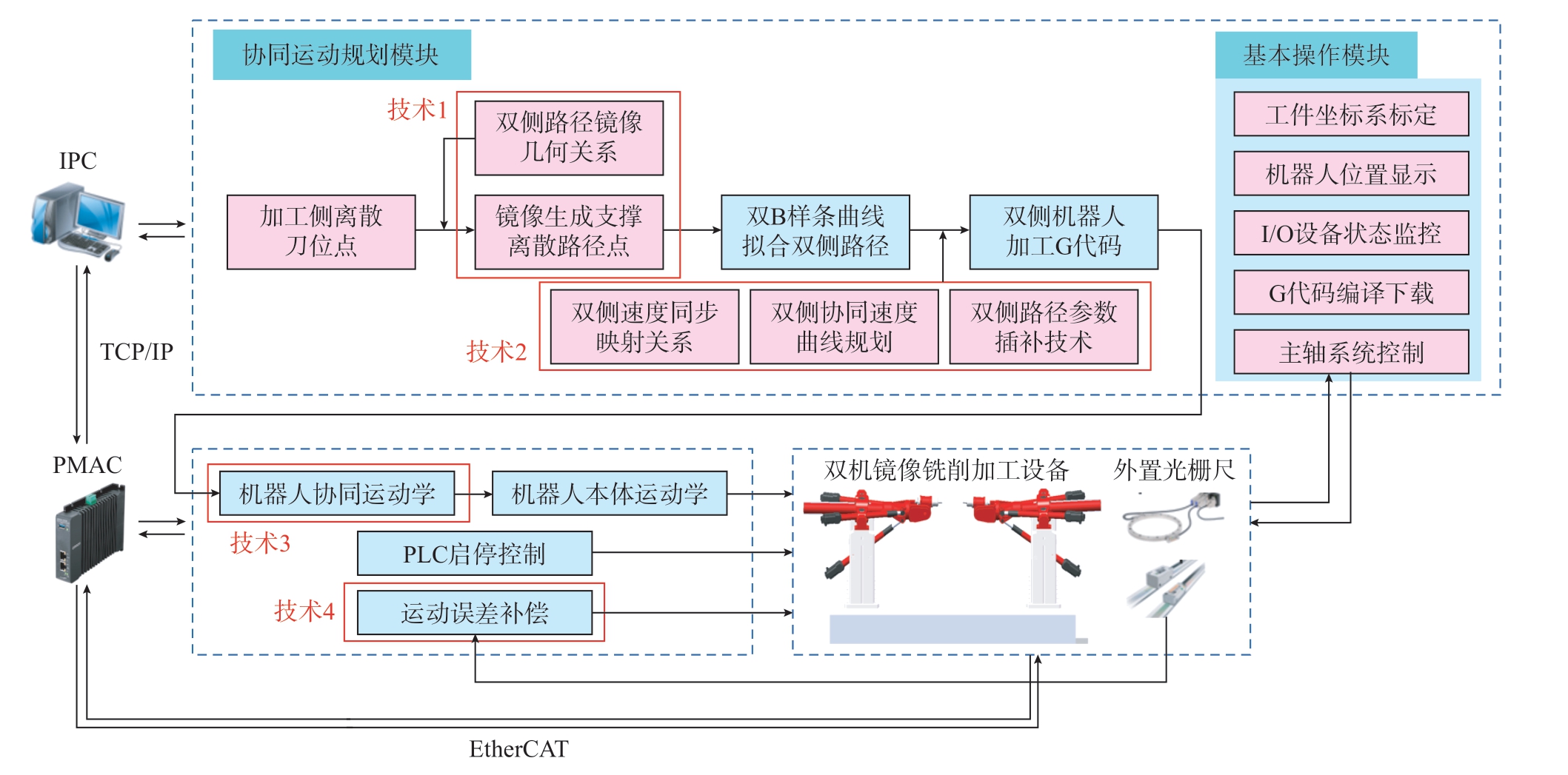
图3 数控系统开放式架构与功能
Fig.3 Open architecture and functions of CNC system
人机交互界面设计主要有协同运动规划模块和机器人基本操作模块。协同运动规划模块包括镜像路径生成和速度规划功能。在交互界面输入加工机器人在工件坐标系下的离散刀位点，结合薄壁件的厚度和铣削深度等信息，可生成满足镜像几何约束的双侧机器人高阶光顺路径（具体见2.1节）。在保证机器人路径的空间镜像外，实现时间维度的运动协同显得更加重要。首先，规划加工机器人的速度曲线，然后通过双机器人的镜像速度映射关系，生成支撑机器人的速度曲线。结合双侧路径，由参数插补技术生成双机器人的加工G代码（具体见2.2节）。机器人基本操作模块的功能包括工件坐标系标定、机器人运动位置显示、I/O设备状态监控、G代码编译下载和主轴系统控制等。
PMAC程序开发主要包括双机器人协同运动学、运动误差补偿和PLC启停控制等。双机器人协同运动学主要是把在工件坐标系下生成的双机运动指令变换到机器人各自的基坐标系下，再通过逆运动学计算得到关节运动指令，从而实现机器人运动（具体见2.3节）。机器人因自身重力、装配误差及关节跟随误差等，使刀尖和刀轴的运动精度下降。引入外置角度/直线光栅传感器测量刀尖位置和刀具方向，然后将修正量分配到各驱动关节的所需指令来补偿刀具运动的动态误差（具体见2.4节）。此外，PLC程序通过判断上位机指令信号，将高低电平信号发送给I/O模块，实现接触器和电磁阀的通断，进而控制伺服系统和主轴系统。
2 镜像铣削协同运动控制策略
2.1 镜像路径生成
针对等壁厚薄壁件的镜像铣削加工，为保证铣刀与支撑头路径之间相对位姿关系，提出一种生成满足镜像几何约束的双侧机器人光顺加工路径方法。
第一步，由镜像几何约束生成支撑机器人离散刀位点。首先，根据加工路径信息和弦高误差，由UG软件给出加工机器人在工件坐标系下的离散刀位路径点Ωi=[xi，yi，zi，Ai，Bi]T，i=0，1，…，m（m为路径点的个数），则第i个离散刀尖点位置为Pi=[xi，yi，zi]T，对应的刀轴单位向量为
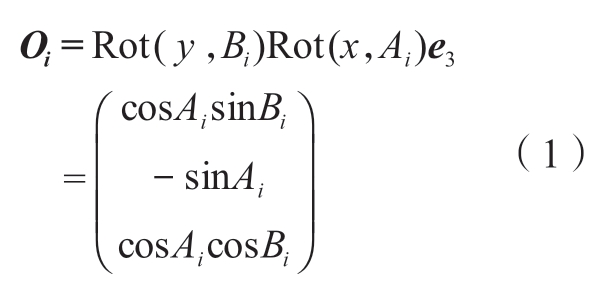
式中，Ai为绕工件坐标系x轴的旋转角度；Bi为绕工件坐标系y轴的旋转角度；单位方向e3=[0，0，1]T，则刀轴上除刀尖点外一点的位置Qi可表示为
式中，L为不为0的任意长度。然后，结合薄壁件的几何特征，铣刀与支撑头路径的镜像位置关系可定义为
式中，
为支撑机器人支撑头中心滚珠位置坐标；H为工件厚度；d为铣削深度；
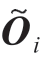为支撑机器人支撑头轴线方向单位向量，式（3）表示的镜像几何关系如图4所示。由此可生成双机器人镜像的离散刀位点对
图4 铣刀与支撑头镜像位置几何关系
Fig.4 Mirror position relationship between milling cutter and support head
第二步，拟合生成加工机器人和支撑机器人的五轴双B样条路径。为避免离散小直线段路径在转接点处高阶导数不连续的问题，同时保证机器人运动的平稳性，借助B样条曲线拟合生成刀尖点和刀轴矢量光顺连续的五轴路径。此外，由全局光顺方法得到统一参数的路径，可便于机器人进给速度的规划。以加工机器人为例，双B样条参数化路径定义为
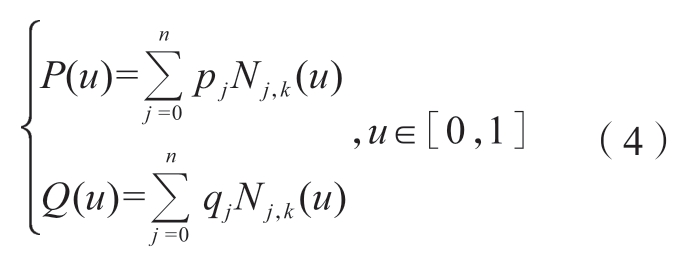
式中，P（u）为刀尖点路径曲线；Q（u）为刀轴上除刀尖点外一点的路径曲线；pj和qj为B样条曲线的控制顶点；n+1为控制顶点的数目；k为曲线的阶数；Nj，k（u）为B样条基函数。需要指出的是，样条曲线P（u）与Q（u）具有相同的路径参数u，即刀轴矢量是跟随刀尖点运动的，这样可保证刀尖点位置和刀轴矢量是一一对应的。
在拟合误差约束下，利用平均节点矢量法得到节点矢量，可由最小二乘法方法[25]拟合得到k=3阶双B样条曲线P（u）和Q（u）。然后，刀轴单位向量O（u）=[ox（u），oy（u），oz（u）]T可通过参数u表示。
最后，可得到机器人光顺的加工参数路径Ω（u） =[x（u），y（u），z（u），A（u），B（u）]T，其中，P（u）=[x（u），y（u），z（u）]T为刀尖点位置，A（u）=-arcsin[oy（u）]为绕工件坐标系x轴旋转的角度，B（u）=atan2[ox（u）/cosA（u），oz（u）/cosA（u）]为绕工件坐标系y轴旋转的角度。
同样的，采用双B样条曲线拟合支撑机器人的支撑头离散路径点
可得到支撑机器人支撑头的光顺路径
，其中w为支撑头双B样条路径参数，w∈[0，1]。需要指出的是，满足镜像几何约束关系的双机器人连续路径是保证镜像协同运动的前提条件。
2.2 双机器人同步速度规划
在生成双机器人光顺路径后，双机器人需要在全路径的每一个时刻保证同步镜像运动。因此，提出一种双机器人速度协同规划方法，具体流程如图5所示。
图5 双机器人速度协同规划流程
Fig.5 Collaborative planning process of dual robots velocity
第一步，规划加工机器人的刀具速度并插补离散路径点。为避免机器人不连续的运动和产生不必要的振动，引入S形加减速曲线[26]作为加工机器人进给速度曲线f1（t）。在弓高误差限制δlim、最大工艺速度fmax、最大刀轴角速度ωlim、最大法向加速度An，lim、最大法向加加速度Jn，lim约束下，路径参数u处的速度应满足
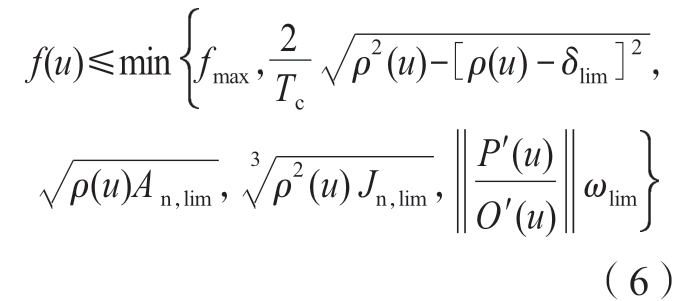
式中，ρ（u）为刀尖点路径P（u）处的曲率半径；Tc=2 ms是机器人控制系统插补周期；P′（u）和O′（u）分别是曲线P（u）和O（u）对参数u的一阶导数。此外，切向加速度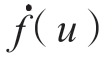
和切向加加速度
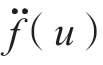需满足以下约束
式中，At，lim是最大切向加速度；Jt，lim是最大切向加加速度。在满足加工工艺约束的前提下，规划时间最优的速度曲线对于提高加工效率很有意义，具体方法见文献[27]。为减少低阶插补算法的截断误差引起机器人的速度波动，结合路径和速度信息，对参数uj=u（tj）在第j个插补点处进行二阶泰勒展开，得到
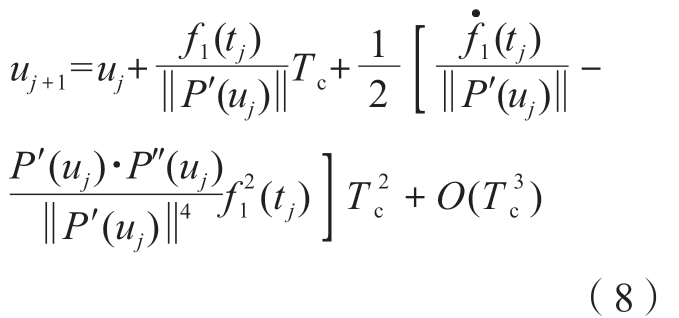
式中，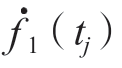
为f1（t）对时间t的一阶导数在tj时刻的值；P′（uj）和P″（uj）分别表示刀尖点样条曲线P（u）对参数u的一阶和二阶导数在uj处的值，O（
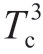）是三阶截断误差。
第二步，建立双机器人进给速度同步映射关系。将插补参数uj和uj+1代入加工机器人路径方程，可得到刀尖位置点Pj和Pj+1。同时，利用式（3）可得到支撑机器人支撑头镜像位置点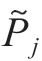
和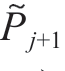
。然后，考虑到Pj和Pj+1、
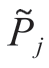和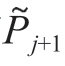
之间运动时间均为插补周期Tc，可认为在很短的时间内Pj和Pj+1、
和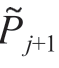
之间为匀速运动。因此，利用弦长‖Pj-Pj+1‖与
可计算出在tj时刻加工机器人进给速度f1（tj）与支撑机器人进给速度f2（tj）的比值λ（tj），得出
重复式（8）所示的插补过程，并结合式（9）可计算出整条路径上支撑机器人的进给速度曲线f2（t）。若支撑机器人进给速度不满足工艺约束，则以较小的步长降低加工机器人的最大速度，重复步骤1和2，直到支撑机器人进给速度满足工艺约束为止。最后，结合双机器人的光顺路径和规划的速度曲线，以Tc=2 ms周期进行参数插补（式（8））可生成双机器人的NC程序，并通过TCP协议离线下载到PMAC控制器中。
2.3 双机器人协同运动学
为将工件坐标系下的双机NC程序转换成电机的驱动指令，需要在PMAC程序中建立双机器人的协同运动学，如图6所示。
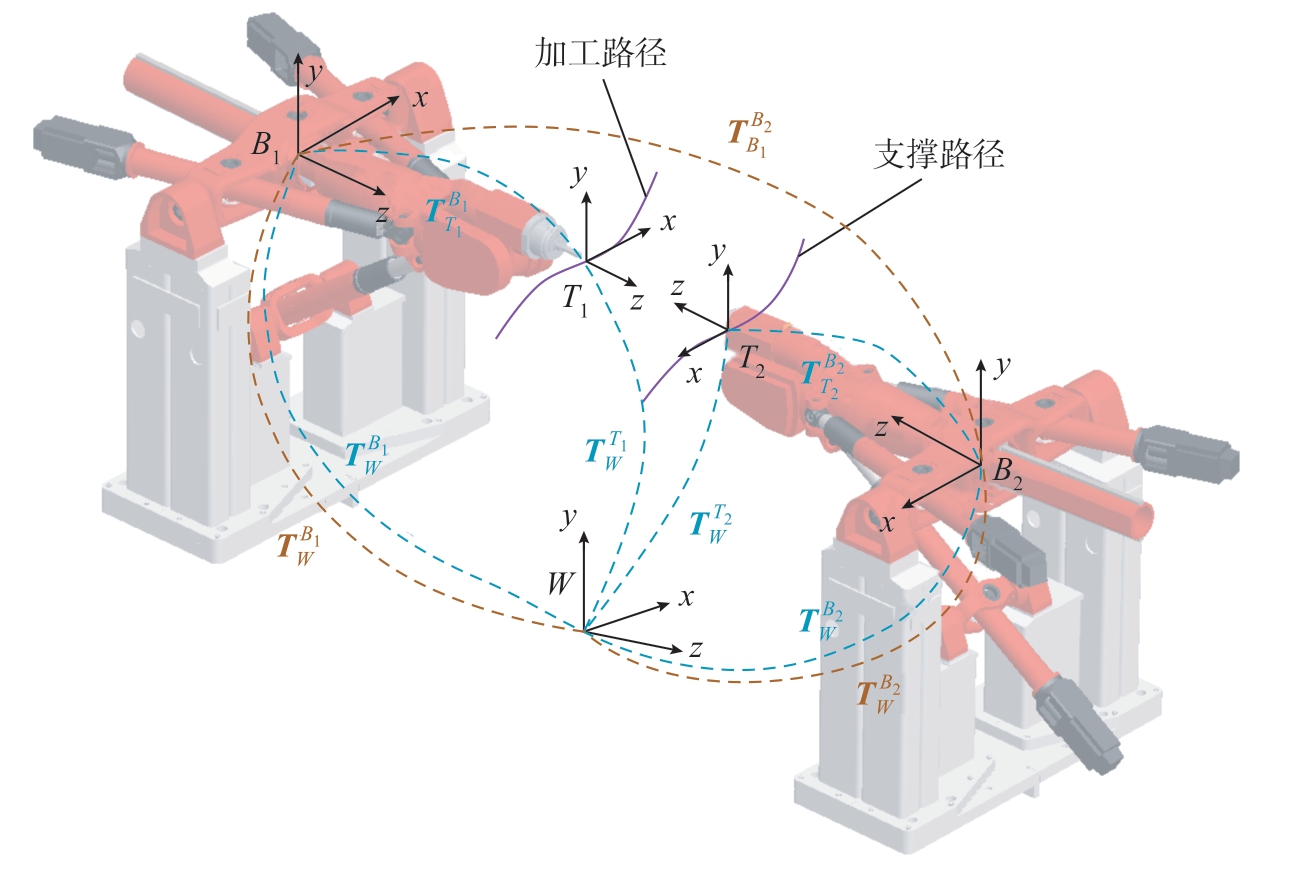
图6 双机器人协同运动学
Fig.6 Collaborative kinematics of dual robots
首先，定义加工机器人刀具坐标系T1和支撑机器人支撑头坐标系T2分别固连在刀尖点和支撑头中心滚珠处，由双机NC程序可分别得到相对于工件坐标系W的变换矩阵为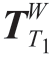
和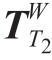
。借助激光跟踪仪可标定出加工机器人基坐标系B1相对于支撑机器人基坐标系B2的齐次变换矩阵
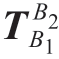。同样可获得工件坐标系W相对于加工机器人基座标系的变换矩阵
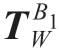。然后，通过式（10）所示的坐标变换可得到工件坐标系W相对于支撑机器人基座标系B2的变换矩阵。
在此基础上，可得到双机器人刀具坐标系T1和支撑坐标系T2分别相对于各自基坐标系的齐次变换矩阵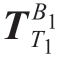
和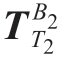
。
最后，通过双机器人各自的逆运动学可获得各关节角度值，然后驱动电机运动，实现双机协同运动。
2.4 机器人运动误差实时补偿
采用双机器人的镜像路径生成、同步速度规划、协同运动学3项关键技术，并借助PMAC运动控制器实时性强和运动控制精度高的优势，理论上能够完全实现且保证双机器人镜像协同运动。但由于机器人自身重力、装配误差、关节跟随误差和其他因素导致机器人末端实际位姿与指令位姿存在误差，使双机器人间的协同运动位置精度降低。为解决这个问题，提出了一种基于外置光栅传感器的实时测量与补偿算法。
圆光栅和直线光栅的安装位置如图7（a）所示，圆光栅1、圆光栅2和直线光栅3分别安装在由转动支架和RP支链组成的RRP被动支链的3个关节上，所测量的实际角位移和线位移分别为θ1，θ2和q3。此外，圆光栅4和圆光栅5分别安装在C轴和A轴的减速器输出端，可测量实际关节角度θ4和θ5，如图7（b）所示。
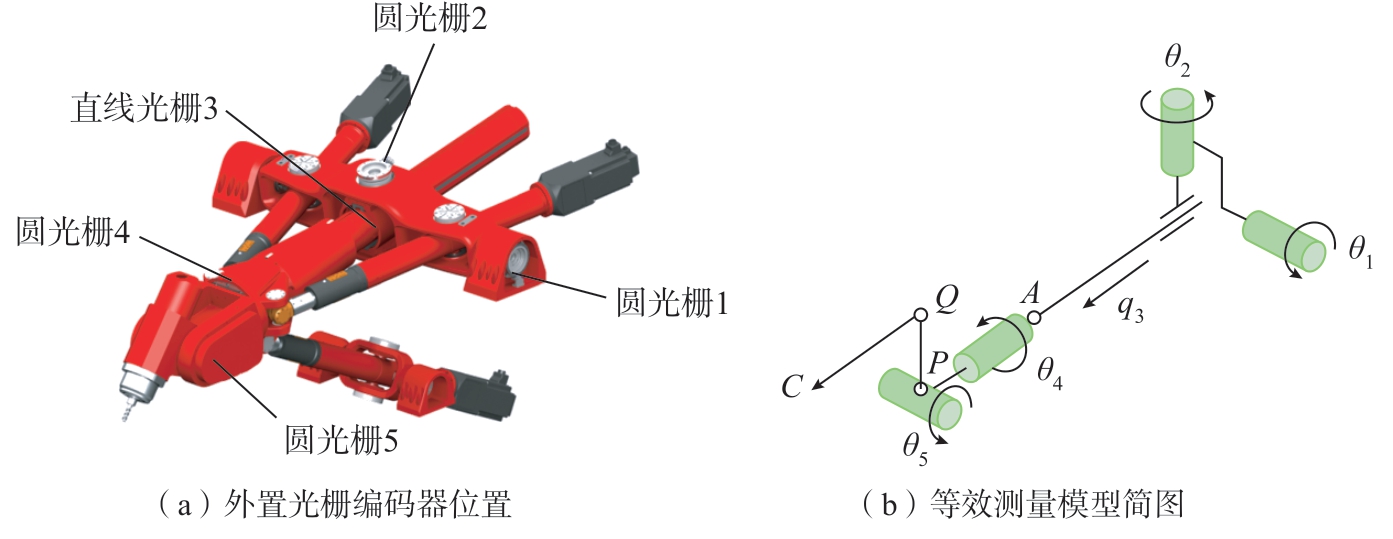
图7 外置光栅编码器测量装置
Fig.7 External grating encoder measurement device
以加工机器人为例，结合混联机器人的运动学和光栅的实际测量值，可计算出加工机器人在第j个插补周期Tc实际的刀尖位置Pm（jTc）和刀轴矢量Om（jTc）为
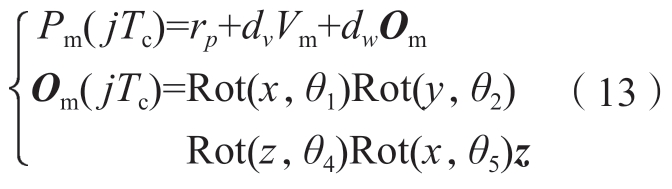
式中，rp=（q3+e）Rot（x，θ1）Rot（y，θ2）z，Vm=Rot（x，θ1）Rot（y，θ2）Rot（z，θ4）Rot（x，θ5）y，z =[0，0，1]T，y =[0，1，0]T，
根据在第j个插补周期Tc处的理论刀尖位置P（jTc）和刀轴矢量O（jTc），可得到刀尖位置偏差ΔP（jTc）和刀轴矢量偏差ΔO（jTc）为
然后，通过机器人逆运动学可计算出第i个关节值Δθi（jTc），i=1，2，…，5。最后，在下一个插补周期（j+1）Tc内，将各关节的补偿量Δθi（jTc）累加到相应的理论值θi[（j+1）Tc]上。因此，双机器人能够实时补偿位姿误差，实现高精度的协同运动。
3 薄壁件镜像铣削试验
3.1 铣削试验设置
为进一步验证双机器人镜像铣削的协同运动效果，基于天津大学自主研发的TriMule-600混联机器人加工平台开展一系列镜像铣削试验，如图8所示。试验采用6061铝合金薄壁件，试件一端悬臂夹紧，尺寸为400 mm×450 mm×4 mm。选用的钨钢平底立铣刀几何参数：直径12 mm、齿数3、螺旋角45°、悬伸长度60 mm。试验的铣削工艺参数：轴向铣削深度1 mm、径向切深12 mm、加工路径长度300 mm、主轴转速3400 r/min、主轴旋转频率56.67 Hz、每齿进给量0.01 mm/z。
图8 双混联机器人镜像铣削加工试验平台
Fig.8 Experimental platform of dual hybrid robots mirror milling
在图8中，为准确测量工件沿法向方向振动信号，并避免与铣刀和支撑头发生干涉，两个单向加速度传感器（RPN 8701-1W两线制加速度传感器，灵敏度为100 mV/g，湖北开航智能装备有限公司）分别固定在工件最上方的左右两角。此外，采用DH5902N坚固型数据采集分析系统（江苏东华测试技术股份有限公司）对工件振动数据进行采集与分析，采样频率设定为2560 Hz。
3.2 平面薄壁件镜像协同铣削试验
针对单点支撑、多点支撑，以及每种支撑方式下铣刀与支撑头协同运动与非协同运动4种方式，开展镜像协同槽铣削加工试验，其中每种铣削方式的工艺参数见3.1节。为保证试验结果的严谨性，每一条加工槽的位置都在工件的同一高度处，距薄板上沿的高度为80 mm。在单点非协同支撑方式中，铣刀与支撑滚珠之间横向偏移为6 mm，而在多点非协同支撑方式下铣刀与支撑头中心滚珠之间的横向偏移为17 mm。为更直观地展示薄壁件的铣削效果，截取加工区域的典型部分，如图9所示。
图9 协同镜像槽铣削加工试验及加工形貌
Fig.9 Collaborative mirror milling experiment and morphologies
图10为单点支撑方式下的加速度信号和快速傅里叶变换（FFT）频谱。由图10（a）和（b）可以看到，在单点支撑条件下非协同加工时工件的加速度幅值整体都超过15g。当双机器人实现单点协同加工后，加速度幅值明显低于15g。为更好地分析工件振动情况，对加速度信号进行快速傅里叶变换，得到图10（c）和（d），其中受迫振动频率是主轴转速频率及其倍频（图中虚线），其他不同于受迫振动的频率是工件铣削时的颤振频率。虽然单点支撑的协同和非协同都发生了颤振，但是单点协同支撑的颤振幅值和数目明显低于非协同支撑方式。这是由于铣刀与滚珠完全镜像时，铣削点处的工件局部刚度得到较大提高。
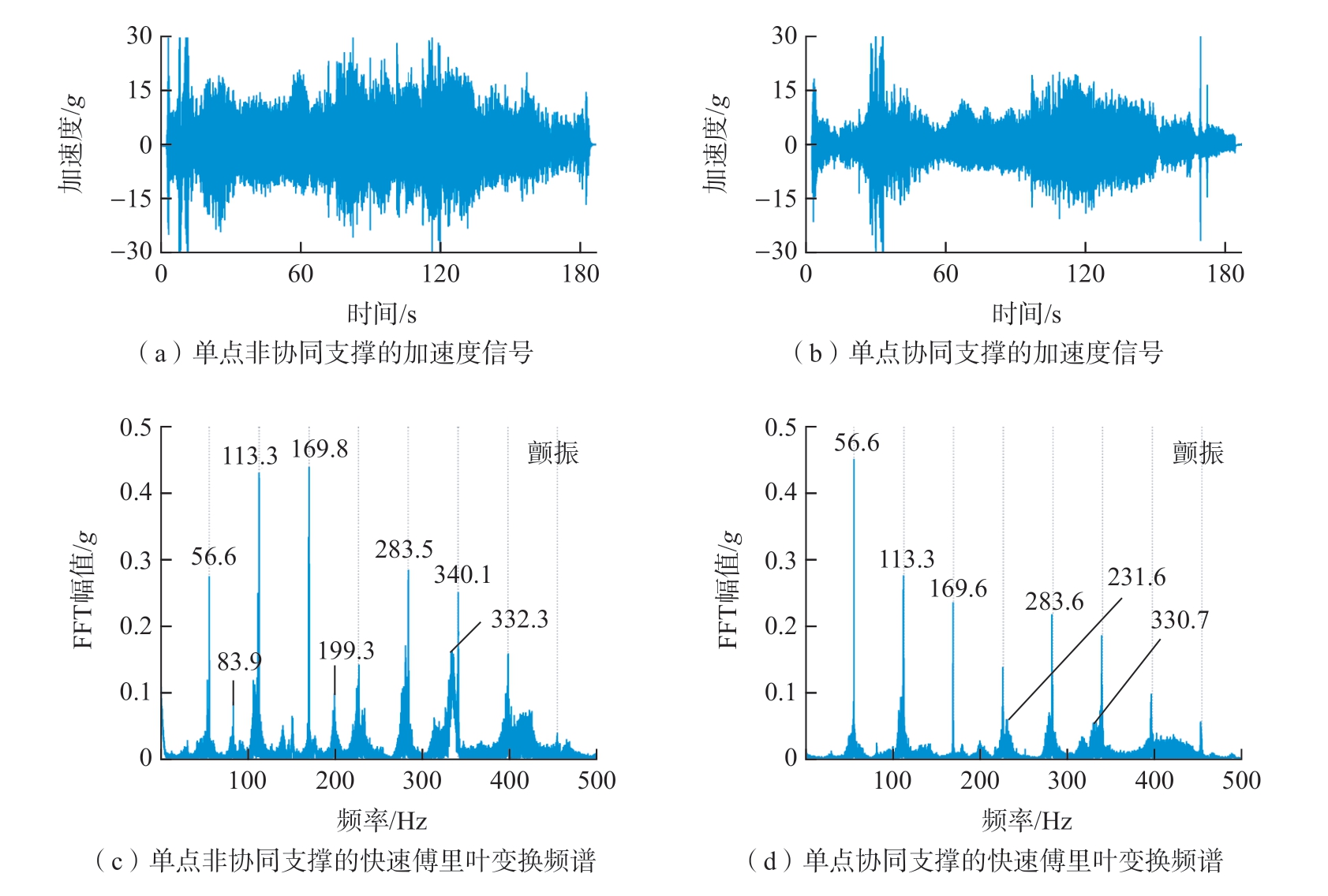
图10 单点支撑方式下的加速度信号和快速傅里叶变换频谱
Fig.10 Acceleration signal and fast Fourier transform (FFT) under single point support mode
图11为多点支撑方式下的加速度信号和快速傅里叶变换频谱。由图11（a）和（b）可见，由于多点支撑方式提高了整个支撑区域的工件刚度，不管支撑方式是否协同，加速度幅值都小于15g。由图11（c）和（d）可知，即使在多点非协同支撑时仍存在少量颤振，但远少于单点支撑方式。而多点协同支撑时，工件是处于稳定铣削状态。这表明单点支撑提供的支撑效果有限，不一定能在铣削区域周围提供足够稳定的刚度和阻尼。在多点支撑时，双机器人即使存在少量的协同误差，也不会对工件加工效果产生较大影响。此外，图9中槽铣的表面粗糙度值分别是2.1 μm（单点不协同支撑）、1.8 μm（单点协同支撑）、1.3 μm（多点非协同支撑）、1.1 μm（多点协同支撑），可见当多点协同支撑时工件表面粗糙度最低，比单点非协同时的表面粗糙度减少45%以上。综上所述，双机器人多点协同支撑加工策略对于抑制薄壁件铣削颤振和减少受迫振动有效。
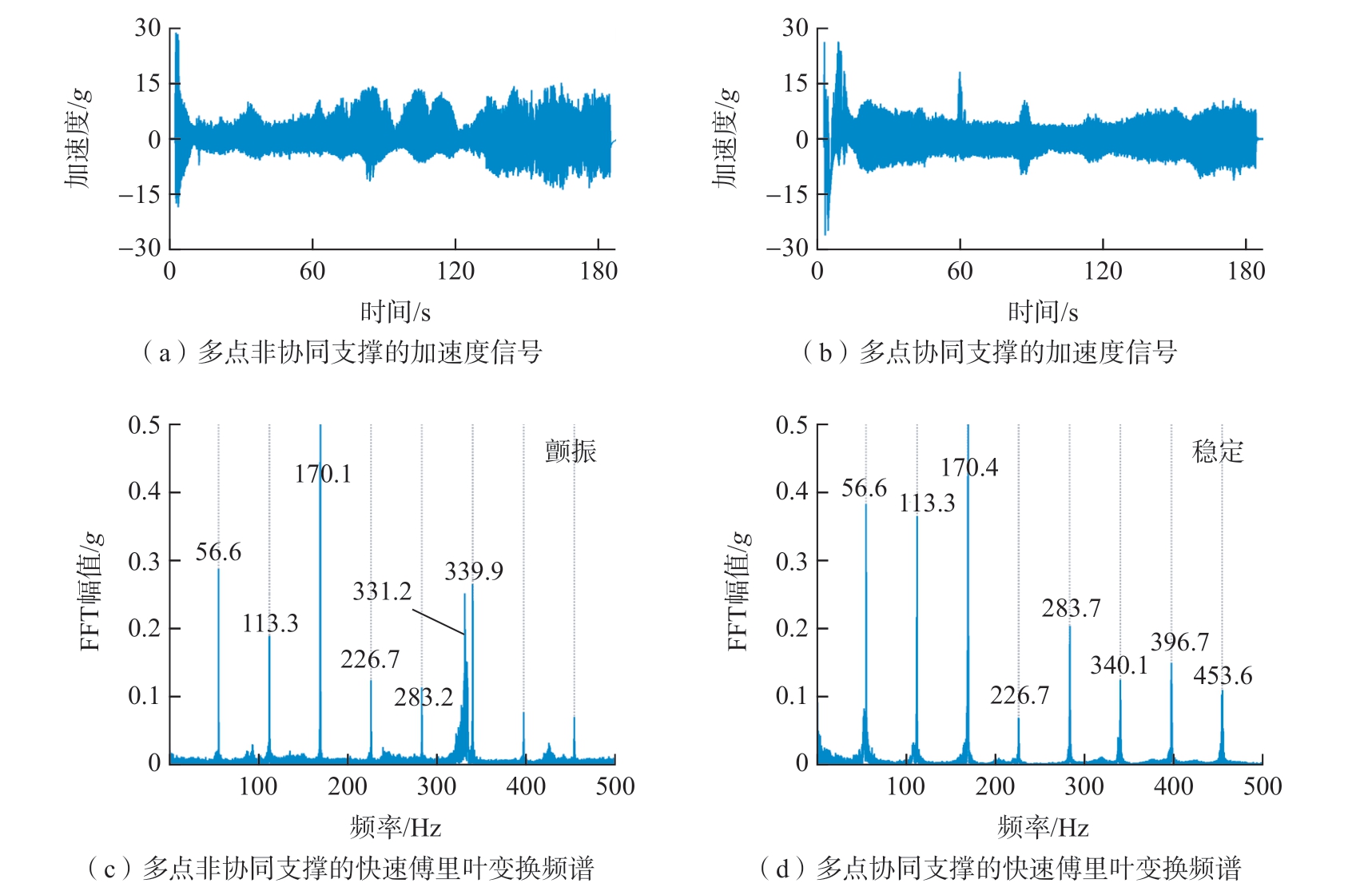
图11 多点支撑方式下的加速度信号和快速傅里叶变换频谱
Fig.11 Acceleration signal and FFT under multi-point support mode
为验证双机器人镜像协同策略对保证工件加工壁厚的能力，在薄壁件上铣削160 mm×300 mm的矩形面，铣削深度为1 mm（理论剩余壁厚为3 mm），面铣削位置如图12（a）所示。图12（b）展示了平面铣削过程。然后，使用超声测厚仪对加工表面进行厚度测量（图12（c）），取20个点位，每行5个点位，每列4个点位，每列间隔80 mm，外侧两列与槽边缘间隔30 mm，每行间隔40 mm，外侧两行与槽边缘之间的距离为20 mm，测量点位置如图12（d）所示。由表2可见，工件的壁厚误差（实际壁厚-理论壁厚）在0.02～0.10 mm，即使在机器人绝对定位误差和工件坐标系标定误差等综合影响下，这也足够证明本文所提出的双机器人镜像协同加工策略对保证工件的壁厚具有很好的能力与效果。需要指出的是，材料去除对镜像铣削中薄壁件的动刚度和振动会产生影响，之后会对此开展重点研究。
表2 工件壁厚误差
Table 2 Wall thickness error of workpieces at different positions
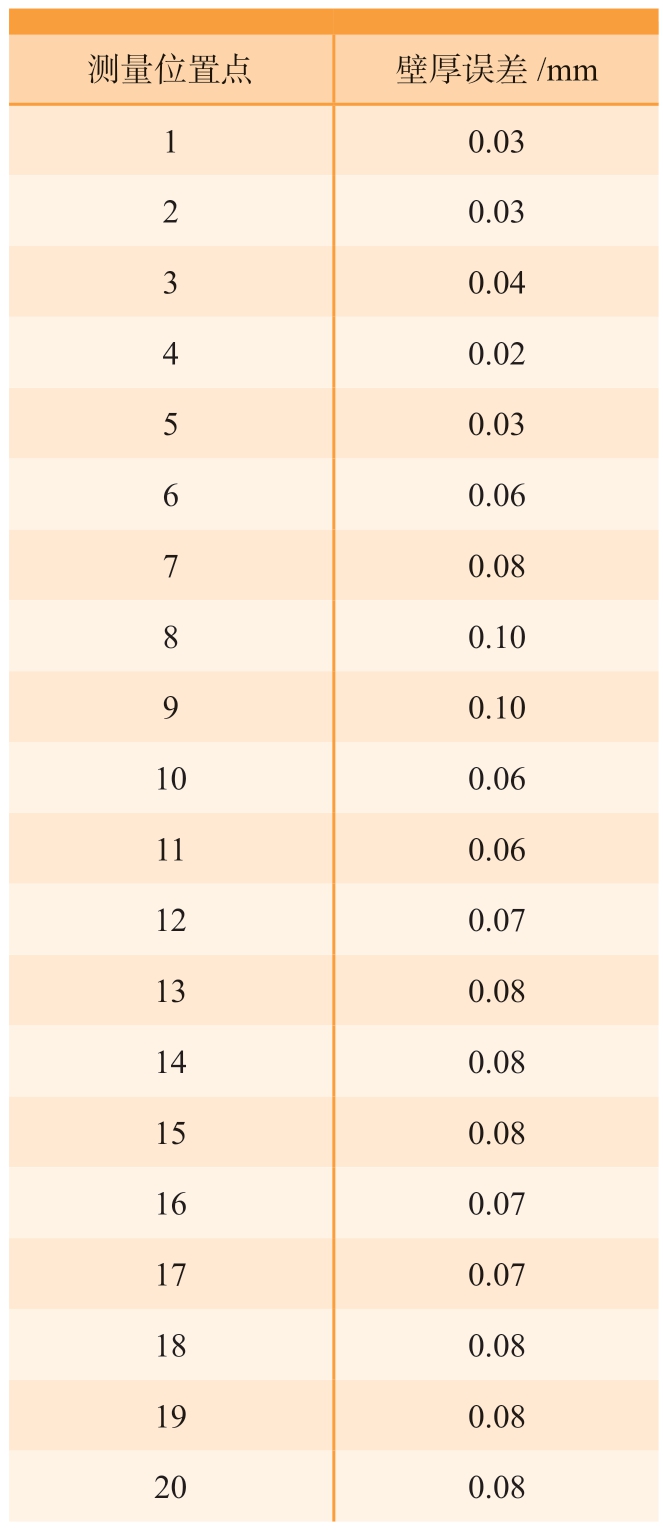
测量位置点 壁厚误差/mm 1 0.03 2 0.03 3 0.04 4 0.02 5 0.03 6 0.06 7 0.08 8 0.10 9 0.10 10 0.06 11 0.06 12 0.07 13 0.08 14 0.08 15 0.08 16 0.07 17 0.07 18 0.08 19 0.08 20 0.08
图12 平面铣削加工试验与面铣壁厚测量
Fig.12 Plane milling machining experiment and surface milling wall thickness measurement
3.3 曲面薄壁件镜像协同铣削试验
3.3.1 高速大曲率协同运动试验
为进一步验证本文提出的镜像协同控制策略对保证双机器人同步运动精度的有效性，开展了高速大曲率协同运动试验。试验路径信息如图13所示，加工侧路径半径为400 mm，支撑侧路径半径为500 mm，双侧路径对应圆心角为30°。首先给定加工机器人刀具运动的S形曲线最大进给速度为20 mm/s，然后利用在2.1和2.2节提出的方法离线生成双机器人末端NC代码。图14展示了在运动误差补偿下加工机器人和支撑机器人末端进给速度和角速度，加工侧进给速度最大值保持在20 mm/s，支撑侧进给速度最大值保持在25 mm/s，双机器人角速度是相同的。试验发现，双机器人不仅运动时间一致而且满足内外协同运动关系，证明了本文提出的双机器人进给速度规划方法的正确性。
图13 高速大曲率双机器人协同运动路径
Fig.13 Dual robots collaborative motion path with high speed and large curvature
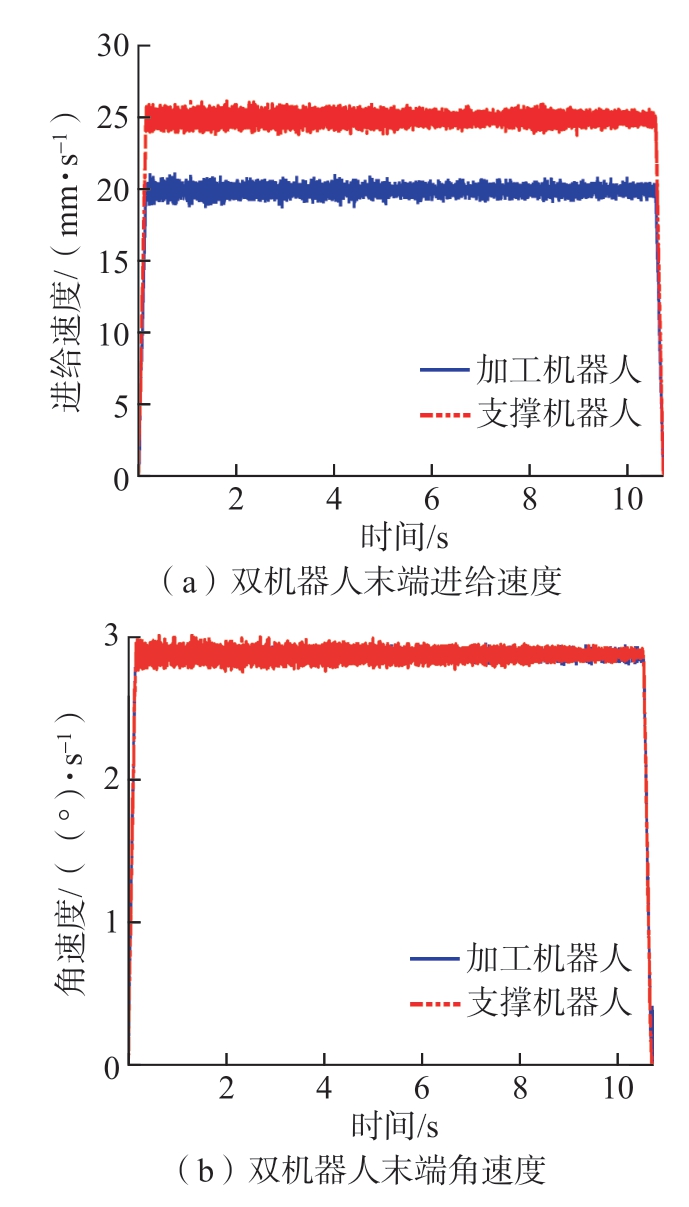
图14 双机器人高速协同运动中的末端速度
Fig.14 End velocity in high-speed collaborative motion of dual robots
为验证2.4节提出的双机器人运动误差实时补偿策略的效果，分别在关闭和开启误差补偿算法情况下利用外置光栅传感器测量并计算出双机器人末端实际运动位移和协同误差，如图15和16所示。利用式（3）计算出加工机器人当前实际位置对应的支撑机器人期望位置，并与支撑机器人的实际位置作差，得到每一个时刻双机器人的协同运动误差。对比图14与15可以看出，在开启补偿算法后，双机器人协同运动误差相较于关闭补偿算法时显著降低。即便在大曲率路径高速协同运动下，双机器人末端协同位置误差仍可控制在30 μm以下，刀轴矢量方向误差可控制在0.004°以下，这证明了双机器人镜像协同控制策略能够实现高精度同步运动。
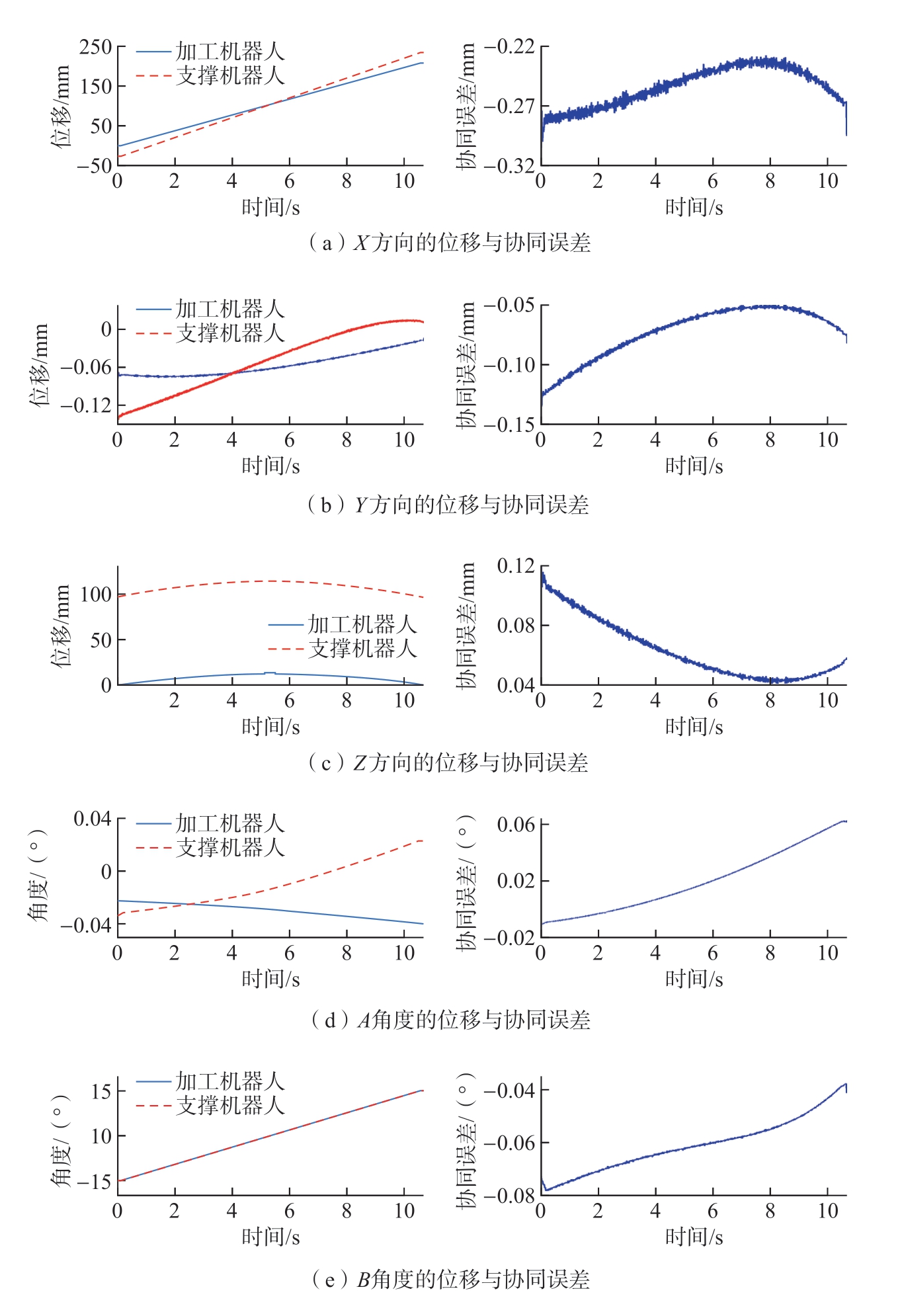
图15 关闭补偿策略下的双机器人末端位移与协同误差
Fig.15 Displacement and collaborative error at the end of dual robots with compensation strategy turned off
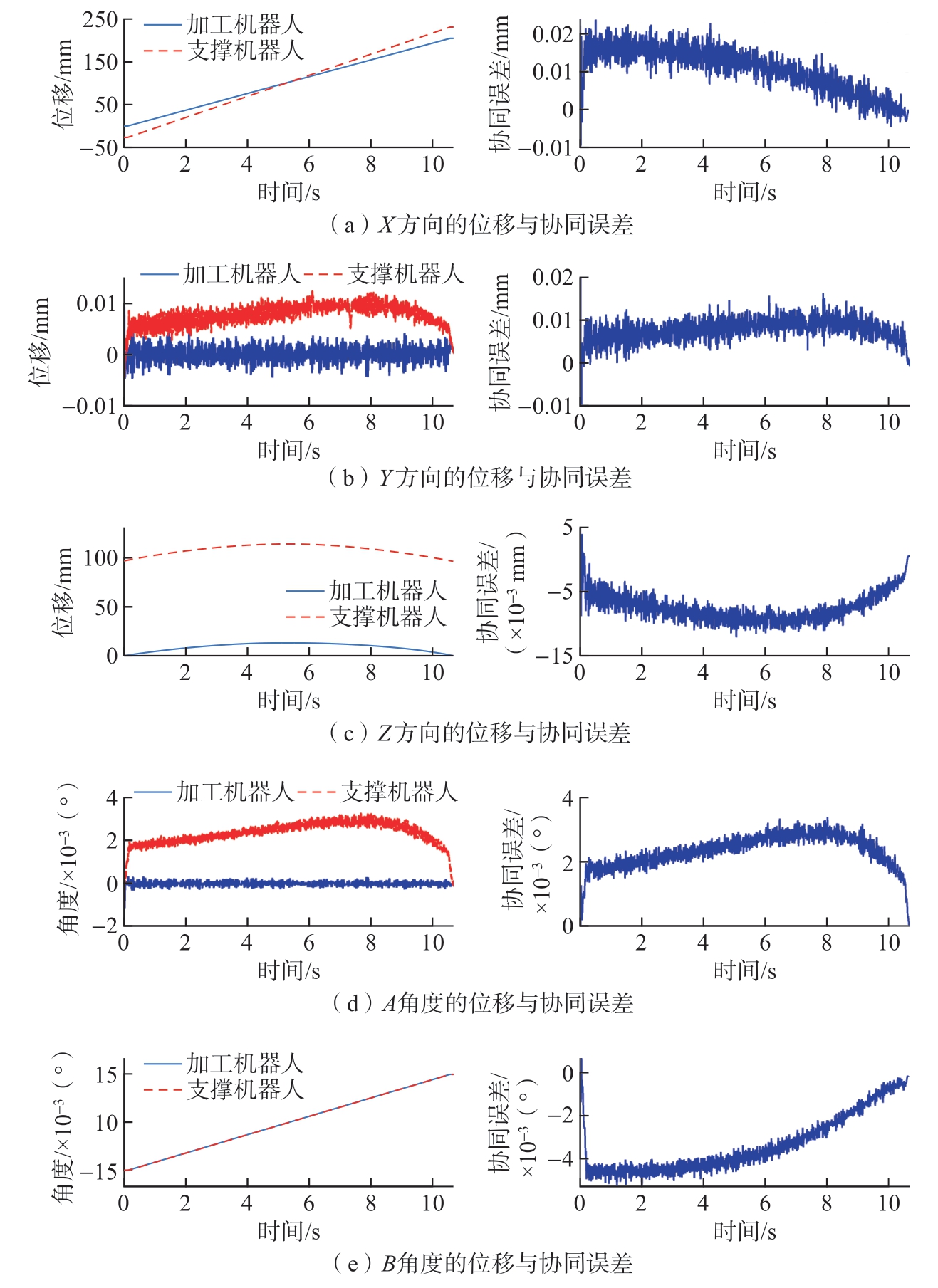
图16 开启补偿策略下的双机器人末端位移与协同误差
Fig.16 Displacement and collaborative error at the end of dual robots under the compensation strategy
3.3.2 曲面薄壁件槽铣试验
为验证双机器人镜像铣削系统加工曲面薄壁件的能力，在开启运动误差补偿策略的情况下进行槽铣削试验。工件特征如图17所示。加工参数为轴向铣削深度1 mm、径向切深12 mm、加工路径长度260.9 mm、主轴转速3400 r/min、主轴旋转频率56.67 Hz、每齿进给量0.05 mm/z。铣削采用多点支撑方式，气缸提供的气压为0.15 MPa。槽铣过程如图18（a）所示，为更清楚地展示铣削表面，截取铣削表面的典型部分（图18（b）），可以看到槽铣表面没有明显的颤振纹。同时，在加工过程中加速度信号小于10g，平均值为6g（图18（c））。由快速傅里叶变换后的频谱图（18（d））可知在铣削加工过程中只有受迫振动，没有颤振的出现。这证明了多点柔性支撑对于抑制薄壁件颤振和改善表面质量有效。
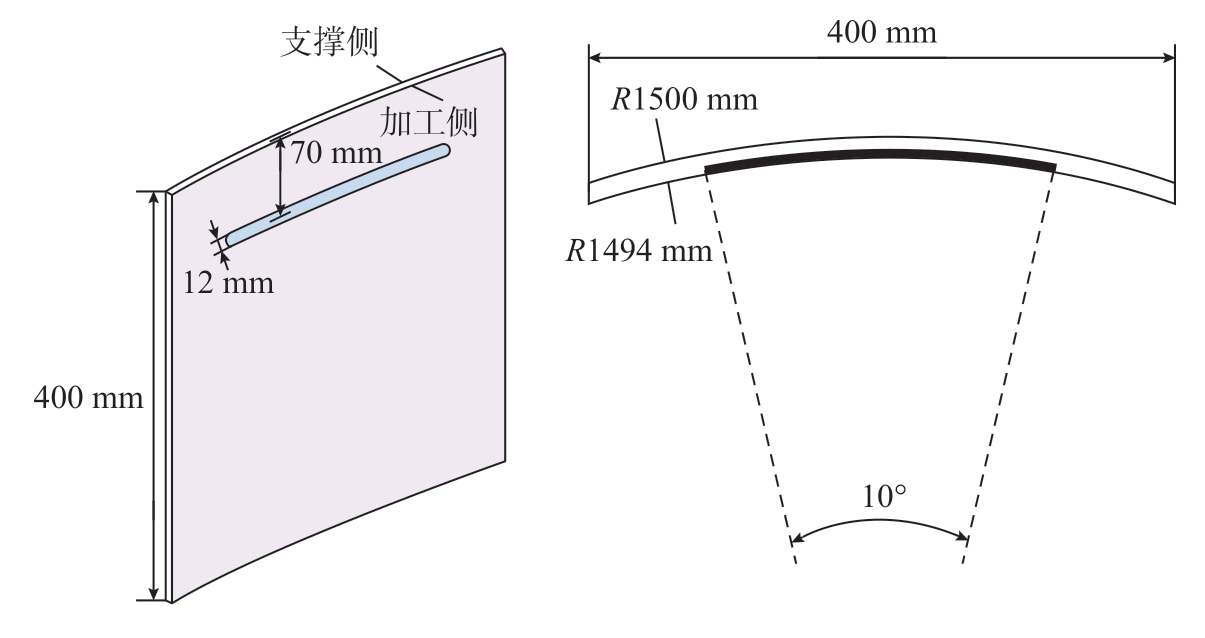
图17 工件与槽铣特征参数
Fig.17 Characteristic parameters of workpiece and slot milling
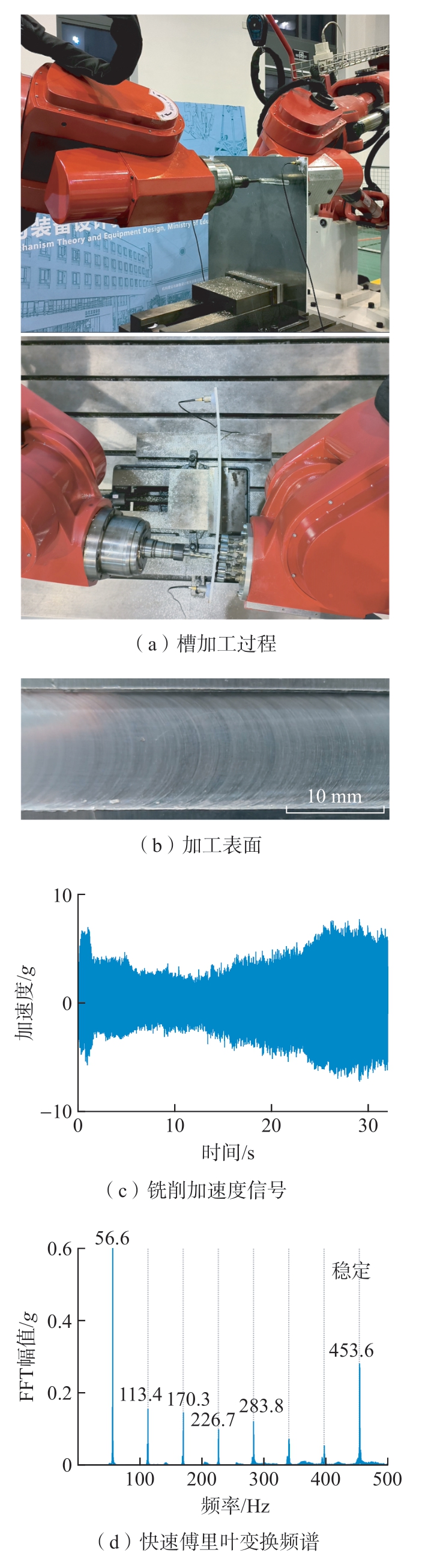
图18 曲面槽加工试验与结果
Fig.18 Curved surface slot machining experiment and results
在铣削过程中，铣刀与支撑头进给速度和角速度能够保证同步运动关系，如图19所示。由图20可以看到，在速度较低的情况下协同位置误差与图16所示的高速误差基本一致，各个方向的末端位置协同误差均小于30 μm，刀轴矢量方向误差均小于0.004°。这表明在曲面薄壁件铣削过程中双机器人镜像协同策略能够实现较高精度的同步运动。
图19 槽铣削加工双机器人末端速度曲线
Fig.19 Dual robots end speed curve for slot milling machining
图20 在槽铣加工且开启补偿策略下双机器人末端位移与协同误差
Fig.20 Displacement and collaborative error of dual robots end effectors during slot milling with compensation strategy enabled
4 结论
（1）为实现双机器人镜像铣削协同运动，研发了一种双CPU主从式开放式架构的数控系统，上位机IPC工控机集成协同运动规划模块与机器人基本操作模块，下位机PMAC控制器支持运动学、PLC、插补及闭环控制等功能。该控制系统可编译底层代码并实现二次开发，也可自主定制其他数控功能。
（2）为保证铣刀与支撑头间位置与运动的镜像协同关系，提出了一种适用于双混联机器人镜像铣削加工的协同控制策略。在上位机通过镜像路径生成和同步速度规划两个功能，离线生成双机器人加工代码；再由下位机的协同运动学和实时误差补偿功能，实现并保证双机器人镜像铣削协同运动。
（3）基于双TriMule机器人镜像铣削加工设备，在4 mm厚度的铝板上开展平面薄壁件槽铣试验。试验结果表明，基于协同加工策略的多点支撑方式能够抑制铣削颤振并减少受迫振动幅值。在4 mm厚度的平面铝板上开展平面铣削试验，结果表明双机器人镜像铣削策略可保证薄壁件的铣削壁厚，误差控制在0.02～0.10 mm，满足加工要求。
（4）开展大曲率路径双机器人高速协同运动试验与曲面薄壁件槽铣削加工试验。试验发现铣刀与支撑头的进给速度和角速度能够保持同步运动，同时双机器人末端各方向的位置协同误差小于30 μm，刀轴矢量方向误差小于0.004°。试验表明提出的双机器人运动误差补偿策略可实现较高精度的同步运动。
[1] TIAN Y, XIAO J L, LIU S J, et al.Vibration and deformation suppression in mirror milling of thin-walled workpiece through a magnetic follow-up support fixture[J]. Journal of Manufacturing Processes, 2023, 99: 168-183.
[2] LI W T, WANG L P, YU G. Forceinduced deformation prediction and flexible error compensation strategy in flank milling of thin-walled parts[J]. Journal of Materials Processing Technology, 2021, 297: 117258.
[3] WANG X Z, BI Q Z, ZHU L M, et al. Improved forecasting compensatory control to guarantee the remaining wall thickness for pocket milling of a large thin-walled part[J]. The International Journal of Advanced Manufacturing Technology, 2018, 94(5): 1677-1688.
[4] BI Q Z, WANG X Z, WU Q, et al. Fv-SVM-based wall-thickness error decomposition for adaptive machining of large skin parts[J].IEEE Transactions on Industrial Informatics,2019, 15(4): 2426-2434.
[5] 杨昀, 张卫红, 党建卫, 等. 航空薄壁件铣削加工动力学仿真技术[J]. 航空制造技术, 2018, 61(7): 42-47, 69.YANG Yun, ZHANG Weihong, DANG Jianwei, et al. Dynamic modelling technology on milling process of aerospace thin-walled workpiece[J]. Aeronautical Manufacturing Technology, 2018, 61(7): 42-47, 69.
[6] YUAN X, WANG S T, MAO X Y, et al. Forced vibration mechanism and suppression method for thin-walled workpiece milling[J].International Journal of Mechanical Sciences,2022, 230: 107553.
[7] SUN Y W, JIANG S L. Predictive modeling of chatter stability considering forceinduced deformation effect in milling thinwalled parts[J]. International Journal of Machine Tools and Manufacture, 2018, 135: 38-52.
[8] BAO Y, WANG B, HE Z X, et al. Recent progress in flexible supporting technology for aerospace thin-walled parts: A review[J]. Chinese Journal of Aeronautics, 2022,35(3): 10-26.
[9] LIU H B, WANG C X, LI T, et al.Fixturing technology and system for thin-walled parts machining: A review[J]. Frontiers of Mechanical Engineering, 2023, 17(4): 55.
[10] LI Z M, SONG Q H, JIN P J, et al. Chatter suppression techniques in milling processes: A state of the art review[J/OL].Chinese Journal of Aeronautics, 2023. https://doi.org/10.1016/j.cja.2023.10.001.
[11] 刘海波, 张鸿泽, 王诚鑫, 等. 基于附加质量和电涡流阻尼的薄壁件铣削振动抑制[J]. 航空制造技术, 2023, 66(3): 53-60.LIU Haibo, ZHANG Hongze, WANG Chengxin, et al. Vibration suppression of thinwalled parts based on additional mass and eddy current damping[J]. Aeronautical Manufacturing Technology, 2023, 66(3): 53-60.
[12] JIA J J, NIU J B, SUN Y W.Dynamics modeling and stability improvement in the machining of thin-walled workpiece with force-tunable pneumatic fixture[J].The International Journal of Advanced Manufacturing Technology, 2021, 117(3): 1029-1043.
[13] WAN M, DANG X B, ZHANG W H,et al. Chatter suppression in the milling process of the weakly-rigid workpiece through a moving fixture[J]. Journal of Materials Processing Technology, 2022, 299: 117293.
[14] LIU S J, XIAO J L, TIAN Y, et al. Chatter-free and high-quality end milling for thin-walled workpieces through a followup support technology[J]. Journal of Materials Processing Technology, 2023, 312: 117857.
[15] BO Q L, LIU H B, LIAN M, et al.The influence of supporting force on machining stability during mirror milling of thin-walled parts[J]. The International Journal of Advanced Manufacturing Technology, 2019, 101(9): 2341-2353.
[16] OZTURK E, BARRIOS A, SUN C, et al. Robotic assisted milling for increased productivity[J]. CIRP Annals, 2018, 67(1):427-430.
[17] XIAO J L, ZHANG Q Y, LIU H T, et al. Research on vibration suppression by a multipoint flexible following support head in thinwalled parts mirror milling[J]. The International Journal of Advanced Manufacturing Technology,2020, 106(7): 3335-3344.
[18] XIAO J L, ZHAO S L, GUO H,et al. Research on the collaborative machining method for dual-robot mirror milling[J].The International Journal of Advanced Manufacturing Technology, 2019, 105(10):4071-4084.
[19] NEUMANN K E. The key to aerospace automation[C]//SAE Technical Paper Series of Aerospace Manufacturing and Automated Fastening Conference and Exhibition. Warrendale: SAE International,2006.
[20] LIU Q, LIU H T, XIAO J L, et al. Open-architecture of CNC system and mirror milling technology for a 5-axis hybrid robot[J]. Robotics and Computer-Integrated Manufacturing, 2023, 81: 102504.
[21] XIAO J L, LIU S J, LIU H T, et al. A jerk-limited heuristic feedrate scheduling method based on particle swarm optimization for a 5-DOF hybrid robot[J]. Robotics and Computer-Integrated Manufacturing, 2022, 78:102396.
[22] SUN Y W, SHI Z F, XU J T.Synchronous feedrate scheduling for the dualrobot machining of complex surface parts with varying wall thickness[J]. The International Journal of Advanced Manufacturing Technology,2022, 119(3): 2653-2667.
[23] MEKID S, OGEDENGBE T. A review of machine tool accuracy enhancement through error compensation in serial and parallel kinematic machines[J]. International Journal of Precision Technology, 2010, 1(3/4): 251-286.
[24] TIAN W J, YANG G, WANG L N,et al. The application of a regularization method to the estimation of geometric errors of a threeaxis machine tool using a double ball bar[J].Journal of Mechanical Science and Technology,2018, 32(10): 4871-4881.
[25] 孙玉文, 徐金亭, 任斐, 等. 复杂曲面高性能多轴精密加工技术与方法[M]. 北京: 科学出版社, 2014.SUN Yuwen, XU Jinting, REN Fei, et al. High-performance multi-axis precision machining technology and method for complex surfaces[M]. Beijing: Science Press, 2014.
[26] WANG M L, XIAO J L, ZENG F,et al. Research on optimized time-synchronous online trajectory generation method for a robot arm[J]. Robotics and Autonomous Systems,2020, 126: 103453.
[27] 王铭礼. 协作机器人在线轨迹规划仿真与实验研究[D]. 天津: 天津大学, 2019.WANG Mingli. Simulation and experimental study on online trajectory planning of cooperative robot[D]. Tianjin: Tianjin University, 2019.
