在航空领域中,工业零件往往具有高度精密和复杂的机械构造,常年工作在高温、高压等恶劣环境中。因此保证零件良好的表面质量和工作状态对整个飞行器的正常运行至关重要。这对航空工业零件的表面精密测量技术提出了迫切的需求。
非接触式光学三维测量方法具有精度高、不会造成表面划痕等优点,成为目前针对零件表面形貌测量的主流方法。该类方法主要包括激光三角法[1]、立体视觉法[2]、主动结构光法[3]、散斑干涉法[4]、光纤传感法[5]等。其中,基于主动结构光的光栅投影法是向被测物表面投射光栅相移条纹图案,然后工业相机对经过被测物表面调制的条纹图案进行采集,识别图像中的对应匹配点,重建零件表面三维形貌[6],具有测量效率高、重建精度高、获取数据稠密等优势,在工业三维形貌测量中广泛应用。
然而,使用光栅投影法对高光零件表面进行三维形貌测量时却存在测量失效问题。高光零件包括铝材合金结构件、金属结构件和碳纤维结构件等,曲面形状复杂,加工后其表面较为光亮平滑。投影仪向测量目标表面投射相移光栅条纹后,零件表面容易出现强反光和多次反光这两种复杂光照特性。强反光导致部分像素灰度值超出相机感光元件动态范围,引起相位解算失败、点云缺失等问题。多次反光出现在凹陷或突出的局部表面,是由入射光线在目标表面经过多次反射而形成的,这会导致测量误差增大、精度严重下降,进而使得传统结构光三维测量方法失效。
针对光学三维测量中的强反光问题,一些研究学者提出多次曝光法[7]、条纹亮度调节法[8]、颜色不变量法[9]、偏振片法[10–11]、条纹反射法[12]、视角选择法[13]等,但是这些方法都具有一定的局限性。多次曝光法、条纹亮度调节法和视角选择法增加了测量的复杂性,颜色不变量法容易受到被测物自身颜色的干扰,偏振片法对于偏振性质不明显的强反光表面测量可能失效,条纹反射法难以测量表面加工痕迹较多的结构件。为了解决高光零件三维测量中的强反光问题,亟须一种高动态范围下的高精度三维测量方法。
为解决多次反光问题,国内外学者提出了高频图案法[14]、微相移[15]、高频格雷码结构光法[16]等,但这些方法都适用于特定的应用场景,不具有一般性。在该问题中,探测器像素接收到的光强是直接反射光和多次反射光的混合光。直接反射光只在目标表面反射一次,就直接被探测器捕获;多次反射光在目标表面经过多次反射后才进入探测器,会对计算过程造成干扰。为了提高高光零件三维测量精度,需要一种方法将直接反射光和多次反射光分离,从而去除多次反射光干扰。
综上,针对航空工业高光零件表面强反光和多次反光现象导致测量失效的问题,本文提出基于高动态多步相移和单像素成像相结合的三维测量技术,有效地实现了高光零件表面的精密三维测量,为航空工业零件表面质量检测、余量加工等后续工作提供了必要的先验数据,具有重要的工程意义。
1 测量原理
1.1 光栅投影法原理分析
光栅投影法的基本原理如图1所示。使用一个投影仪向被测目标表面投射光栅相移条纹图案,同步触发两个工业相机拍摄目标表面调制后的条纹图像。空间点P是两个工业相机公共视场内一点,其在两个相机图像平面内分别成像。通过外差多频相移原理[17],能够得到点P在两个相机图像平面内的全场连续相位值。根据极线约束和提前标定好的系统内外参数,能够重建空间点P,得到P点在测量坐标系下的三维点坐标。
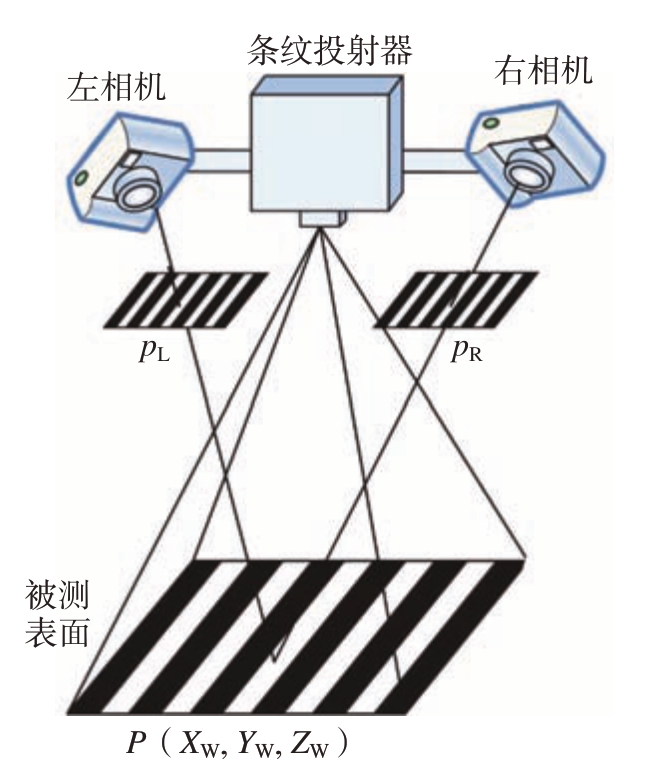
图1 光栅投影法原理示意图
Fig.1 Schematic diagram of fringe projection profilometry
投影仪发出的光线经过测量目标表面反射进入相机,以相机像素点(x0,y0)为例,考虑多次反光的影响,相机采集的条纹图像强度为

式中,Ω为对相机像素点 (x0,y0)的亮度有影响的投影仪像素范围;β(xj,yj;x0,y0)为扩散系数,与相机镜头的点扩散函数有关;α为相机的响应系数;r(xj,yj)为物体表面反射率;a为条纹图像的平均亮度,也称直流分量;b为条纹图案的调制度;φ(xj,yj)为初相位;O为进入到相机的环境光强。
根据相机像素 (x0,y0)接收光的来源,像素接收到的光为对应物点直接反射光和周围多次反射光的混叠光,如图2所示。
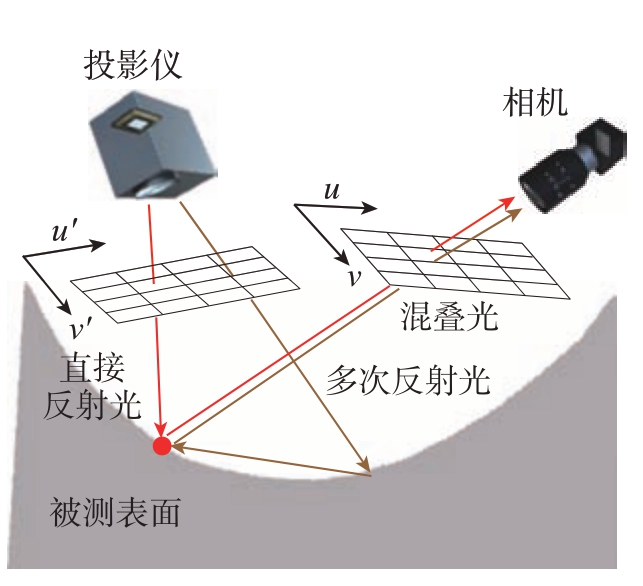
图2 复杂零件表面成像过程示意图
Fig.2 Schematic diagram of surface imaging process for complex parts
因此式 (1)可以分解成
式中,I d(x0,y0)为直接反射光的亮度分量;ΔI(x0,y0)为多次反射光的亮度分量。分别可以表示为
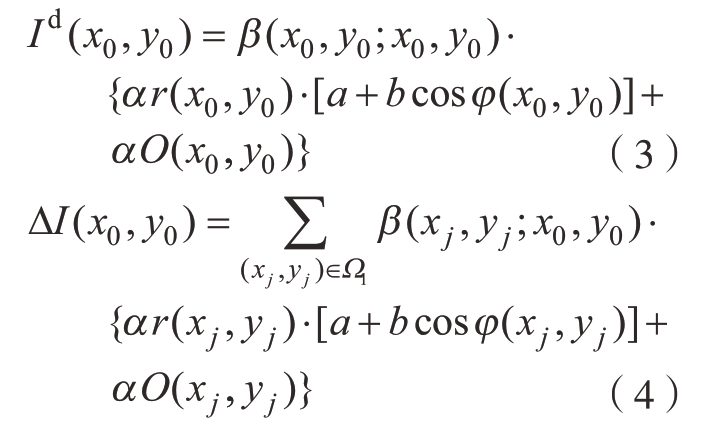
式中,Ω1={(x,y) |(x,y)∈Ω,(x,y)≠(x0,y0)}。直接反射光包含该点的相位信息,且β(xj,yj;x0,y0)系数在相移算法中会被抵消,不会影响相位解算结果。而多次反射光会干扰直接反射光,从而引入相位解算误差,多次反射光分量越大,对像素中直接反射光的亮度干扰也就越大。而由式(4)可知,多次反射光分量与表面反射率相关,表面反射率越大,多次反射光亮度也就越大。高光零件表面较为平滑,粗糙度低,表面反射率较高,因此多次反射光对高光零件表面三维测量的干扰较为严重,其影响不可忽视。
1.2 基于高动态多步相移的强反光表面三维测量方法
投影仪向高光零件投射相移条纹后,大部分区域能够正确解算相位,但是局部区域的反射光亮度超出了相机传感器的动态范围,导致精度下降或点云缺失。若降低投射条纹亮度,保证强反光区域处于相机动态范围之内,那么其余测量区域则会过暗,同样会降低测量精度和准确性。使用基于高动态多步相移的三维测量方法,克服高光零件表面因强反光导致的三维重构精度下降问题。
基于高动态多步相移的三维测量方法包含两部分,一是多步相移技术,二是多亮度投射技术。多步相移技术是指向测量目标投射N步相移条纹图案,通过对调制条纹图像进行相位解算和相位展开,得到绝对相位图,从而进行立体匹配的三维测量技术。强反光表面测量时,图像饱和会导致相位解算出现偏差,相位偏差与相移步数有关,因此考虑通过优化相移步数使相位偏差最小,从而达到抑制强反光的效果。
当投射条纹周期λ是奇数时,相移步数选择N=λ·k,其中k=1,2,…;或者当投射条纹周期λ是偶数时,相移步数选择N=λ/2·k,其中k=1,2,…,此时相位偏差Δφ(x,y)=0。同一像素点即使在部分相移条纹图上饱和,该像素点的包裹相位仍可以通过传统多步相移算法准确解算出,消除图像饱和引入的相位偏差,对局部强反光干扰具有较好的抑制作用,提高了高光零件三维测量精度。
然而在某些情况下,零件强反光区域的所有相移条纹图可能全部饱和,即使采用多步相移算法也无法正确解算出相位。因此引入多亮度投射技术。多亮度投射技术是指在相位解算过程中,投射一系列亮度不同的条纹图案,对于反射率不同的区域,通过掩膜选择合适亮度等级下的相移条纹图。掩膜图像与条纹图像大小相同,数量与投射亮度等级数相同,即每一张掩膜都对应一个亮度等级。每个像素的掩膜值与调制度有关,第m个亮度的正弦条纹调制度为
为每一个像素的掩膜赋值,将条纹调制度最大的亮度等级所对应的掩膜值设置为1,其余亮度等级所对应的掩膜值设置为0,这样就能够通过掩膜筛选出当前像素调制度最大的亮度,即
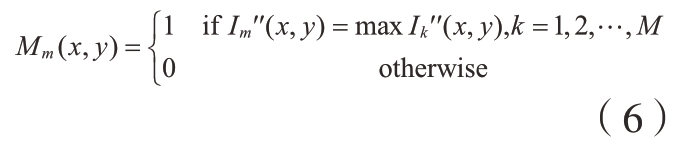
由于各个像素之间相互独立,最终可以逐像素合成一组完整高动态相移条纹图,用于相位解算[18]。多亮度投射技术示意图如图3所示,以两个亮度等级为例,分别生成掩膜,并最终合成一幅高动态图像。
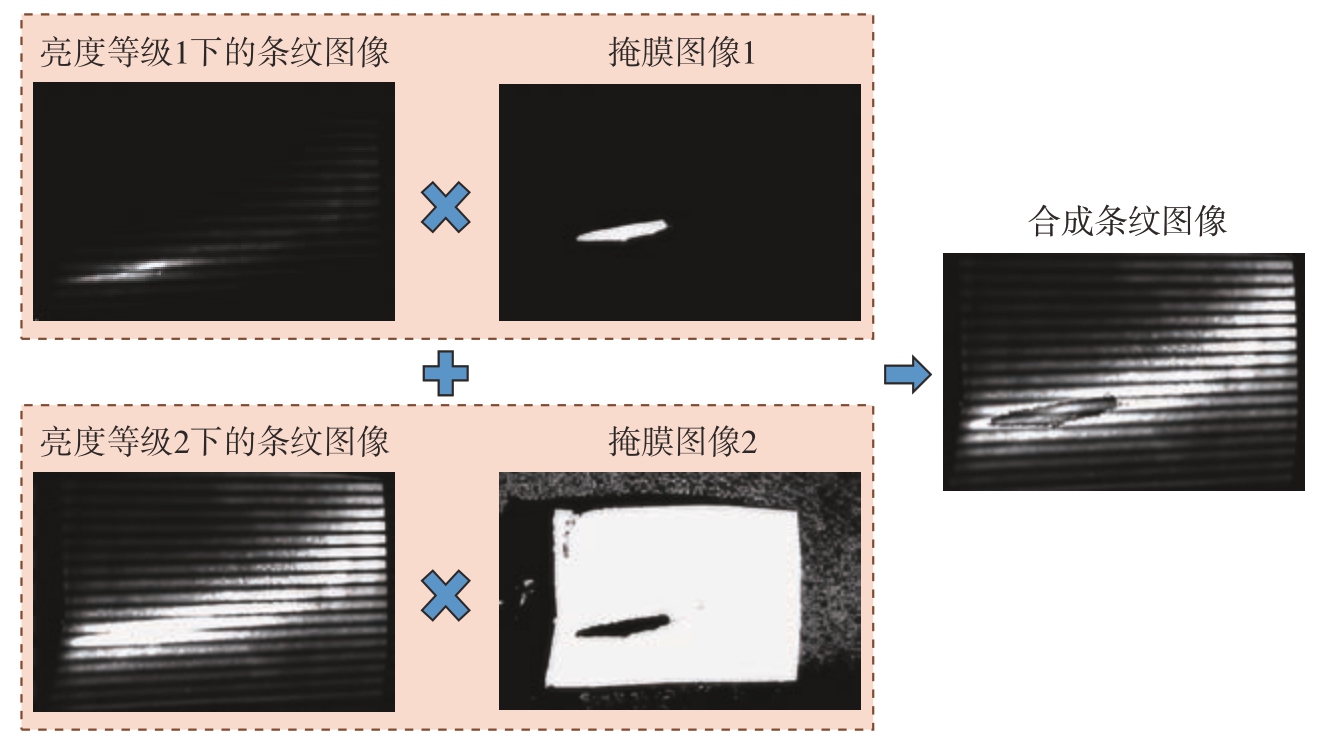
图3 多亮度投射技术示意图
Fig.3 Schematic diagram of multi-brightness projection technology
在合成的高动态相移条纹图中,每个像素的亮度为
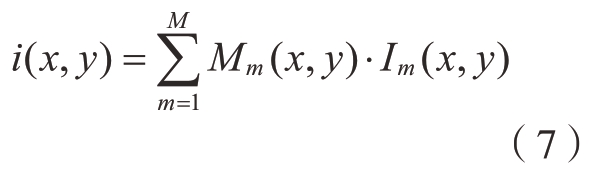
经过上述掩膜操作,合成图中每一个像素的亮度值都源自相机采集的原始条纹图,且没有改变原始亮度值,因此不影响对应点的相位解算结果。所有像素亮度均处于相机的动态范围内,不会出现过亮或过暗的情况,避免了强反光区域由于图像饱和而造成点云缺失问题。
将多步相移技术和多亮度投射技术结合在一起,所采取的测量策略是逐亮度依次投射并采集多步相移条纹。使用原始条纹图生成相对应的掩膜,按照上述原理合成一系列高动态多步相移条纹图。根据每个独立像素的亮度解算其相位,并进行相位展开、立体匹配、三维重建等后续计算工作。
1.3 基于单像素成像的多次反光表面三维测量方法
投影仪发出的光线入射到待测零件表面,由于待测零件复杂的几何形貌而进行多次反射,最终直接反射光和多次反射光同时被相机捕获,其中的多次反射光分量会对相位解算造成干扰。为了分离直接反射光和多次反射光,采用基于单像素成像的三维测量方法。
假设投影仪向平面某点Q'=(x',y')T发出的光能量为P(x',y'),Q'点到相机探测器的光传输系数为h(x',y'),则相机接收到的光能量为
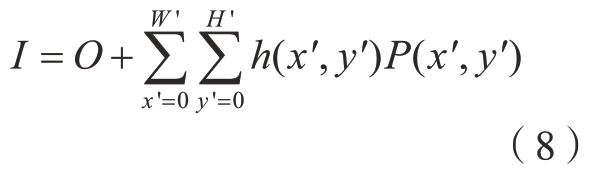
式中,I表示单像素探测器的亮度响应;O表示环境光亮度;W'和H'分别代表投影仪横、纵方向的分辨率。
向测量目标投射的相移正弦条纹为
式中,(fxj,fyj)为条纹图案的空间频率;ϕ为条纹图案的初始相位。探测器响应为
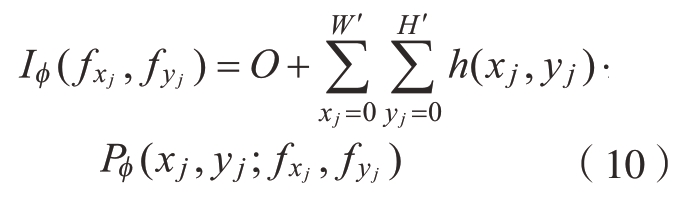
对于每一个空间频率,都可通过投射相移图像计算得到其对应的傅里叶系数。以四步相移为例,某一空间频率的傅里叶系数为
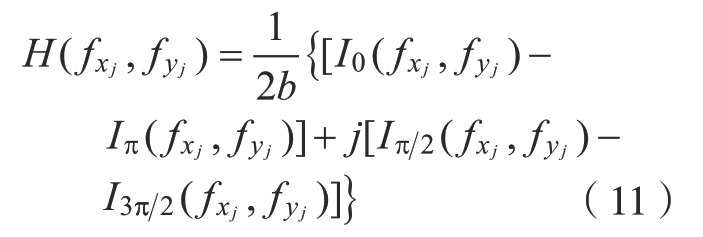
通过投射相移条纹可以消除环境光亮度O和直流分量a的影响。对所有空间频率都投射相移条纹并按照式 (11)计算,可以获得图像的傅里叶频谱,再对其进行傅里叶反变换,可以解算得到光传输系数为
式中,IFT{*}表示傅里叶反变换。
在多次反光的条件下,相机像素对应的光传输系数图像存在多个光斑,如图4所示,两个光斑代表直接反射光和多次反射光。
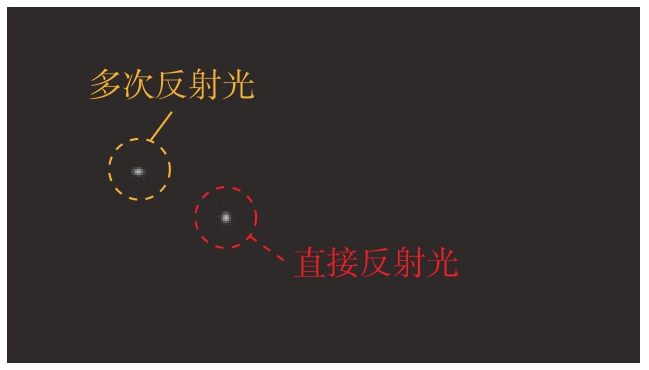
图4 相机像素对应的光传输系数图像
Fig.4 Image of the light transport coefficients corresponding to the camera pixel
因此,通过单像素成像的方法获得投影仪–相机像素对之间的光传输系数后,相机接收到的混合光可以分解为直接反射光和多次反射光,即可利用极线约束[19]等方法去除多次反射光的干扰,进行高光零件表面的高精度三维重构[20]。
2 试验结果
搭建一套用于验证本文提出方法可行性的三维测量系统,如图5所示。试验中使用的相机分辨率为2048 pixel×1080 pixel,投影仪分辨率为1920 pixel×1080 pixel。拍摄的帧频为60 fps。

图5 试验所用三维测量系统
Fig.5 3D measurement system used in the experiment
首先进行强反光表面三维测量试验。使用基于高动态多步相移的三维测量方法,对典型航空工业零件进行三维重构,验证本文所提出方法的效果及测量精度。测量目标为航空发动机涡轮叶片的叶边局部,如图6(a)所示。向测量目标投射5个亮度等级的条纹图案,保证最低的亮度等级能够使得强反光区域处于相机动态范围内,最高的亮度等级能够照亮暗处区域。其中两个亮度等级的调制条纹图如图6(b)和(c)所示,这两个亮度等级对应的掩膜图像如图6(d)和(e)所示。根据合成的相移条纹图进行包裹相位解算,并通过相位展开得到绝对相位进行立体匹配,最后根据匹配点计算出测量目标的三维点云数据。测量结果如图6(f)所示,可以看到发动机叶片的叶边局部得到了完整重构,精细结构处没有点云缺失,重建效果好。

图6 基于高动态多步相移的三维测量方法过程及结果
Fig.6 Process and results of 3D measurement method based on high-dynamic range N-step fringe projection profilometry
为了验证基于高动态多步相移的三维测量方法的测量精度,使用该方法对具有强反光特征的标准量块进行三维测量,标准量块如图7(a)所示。对测量结果进行平面拟合,使用拟合均方根误差来评价测量精度。平面拟合的结果如图7(b)所示,得到平面拟合均方根误差为0.0066 mm。试验结果证明,使用高动态多步相移方法对高光物体表面进行三维测量能够实现较高的测量精度。

图7 基于高动态多步相移的三维测量方法精度评价
Fig.7 Accuracy evaluation of 3D measurement method based on high-dynamic range N-step fringe projection profilometry
接下来进行多次反光表面三维测量试验。使用基于单像素成像的三维测量方法,对由两个垂直的不锈钢标准量块组成的具有多次反光现象的表面进行三维重构,验证单像素成像方法的效果及测量精度。不锈钢标准量块如图8(a)所示,将生成的相移条纹图案投射至测量目标,通过工业相机拍摄图像,如图8(b)所示。根据前文所述原理获得单个像素的光传输系数,对全部相机像素的光传输系数进行叠加,得到全局光传输系数。根据计算结果分离多次反射光和直接反射光,去除多次反射光对测量目标三维重构的干扰。测量结果如图8(c)所示,可以看到测量的数据结果非常完整,没有点云缺失。为了验证该方法的精度,对标准量块的测量结果进行平面拟合,使用拟合均方根误差来评价测量精度。标准量块平面拟合的结果如图8(d)所示,得到平面拟合均方根误差为0.0046 mm。试验结果证明,单像素成像方法能够有效地去除多次反射光的干扰,提高高光表面的测量精度,实现多次反光情况下高光表面精密三维测量。

图8 基于单像素成像的三维测量方法效果及精度评价
Fig.8 Accuracy evaluation of 3D measurement method based on single pixel imaging
在实际生产测量中,使用本方法重建出的航空零件三维点云模型通常用于后续的尺寸比对、余量分析等。为了评估本方法对于绝对尺寸测量的精度,进一步开展了精度验证试验。使用具有强反光和多次反光特征的台阶标准器作为测量目标,每一级台阶的高度为10.000 mm,台阶标准器如图9(a)所示。使用本文所述高动态多步相移和单像素成像相结合的方法对台阶标准器进行三维重建,重建结果如图9(b)所示,然后对台阶标准器的1~5号工作面分别进行平面拟合,并计算相邻两个工作面的拟合平面距离。以2号工作面平面拟合为例,拟合结果如图9(c)所示。所有相邻工作面之间的平面距离和标准偏差如表1所示。试验结果表明,测量得到的平面距离与真值的绝对偏差不大于0.007 mm,具有很高的尺寸测量精度,验证了本方法在反光零件绝对尺寸测量中的精度优势。
表1 平面距离计算结果
Table 1 Plane distance calculation results mm
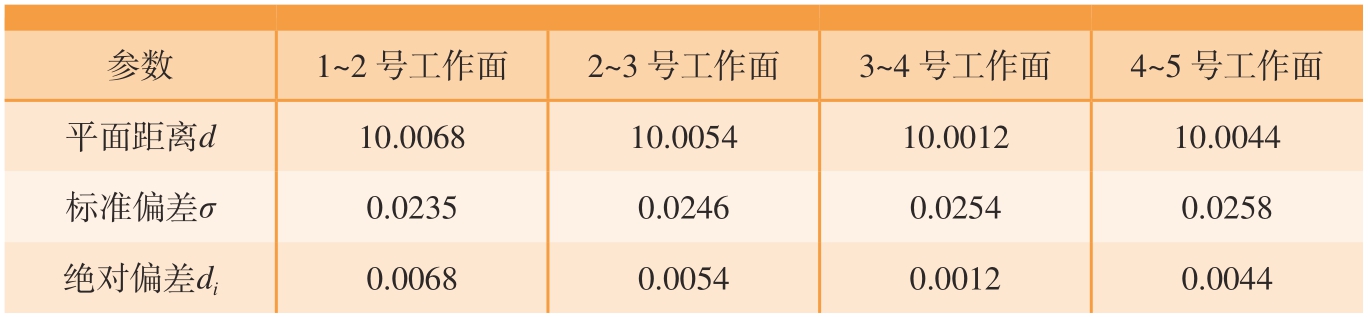
参数1~2号工作面2~3号工作面3~4号工作面4~5号工作面平面距离d 10.006810.005410.001210.0044标准偏差σ 0.02350.02460.02540.0258绝对偏差di0.00680.00540.00120.0044
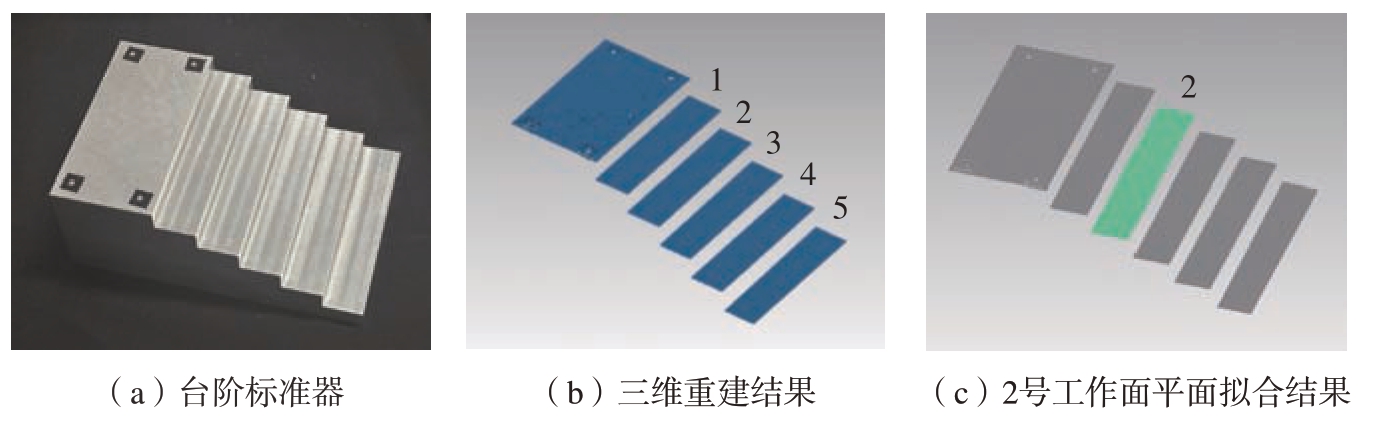
图9 绝对尺寸测量精度验证试验过程及重建结果
Fig.9 Experimental process and reconstruction results of absolute dimension accuracy measurement verification
最后,使用测量系统对航空工业高光零件表面进行三维重建,验证本文所述方法在实际工业测量中的可行性。对多个航空工业零件 (例如航空发动机叶轮、涡轮叶片和碳纤维结构件)分别使用传统三频四步光栅投影法、高动态多步相移法及本文所述高动态多步相移和单像素成像相结合的方法开展三维测量对比试验。试验结果如图10所示。

图10 航空工业高光零件三维测量方法结果对比
Fig.10 Comparison of results of 3D measurement methods for industrial shiny parts
由图10试验结果可以看出,传统三频四步光栅投影法点云缺失严重,三维测量失效。高动态多步相移法能够补全部分强反光区域的点云数据,但仍然存在一定程度的多次反射光干扰,导致点云部分缺失,测量精度较低。使用本文所述高动态多步相移和单像素成像相结合的方法,能够避免强反光影响,同时去除多次反射光的干扰。最终重建的点云结果完整,三维重构精度高,解决了传统测量方法对航空工业高光零件三维测量时产生的点云缺失和精度下降问题。
3 结论
(1)针对航空工业制造领域中高光零件表面三维测量时所产生的强反光和多次反光问题,提出了基于高动态多步相移和单像素成像相结合的三维测量方法,并搭建了三维测量系统。
(2)基于高动态多步相移的三维测量方法向测量目标投射多个亮度的多步相移条纹图案,消除了强反光条件下的相位偏差。试验表明,拟合均方根误差为0.0066 mm,有效地抑制了强反光干扰。基于单像素成像的三维测量方法,根据探测器响应计算得到光传输系数,分离直接反射光和多次反射光,降低了多次反射光的影响。试验表明,拟合均方根误差为0.0046 mm,解决了高光零件多次反光区域三维测量失效的问题。
(3)为了评估本方法对于绝对尺寸测量的精度,以具有强反光和多次反光特征的台阶标准器作为测量目标,开展了精度验证试验。试验结果表明,测量值与真值的绝对偏差不大于0.007 mm,具有很高的尺寸测量精度。
(4)对航空发动机叶轮、涡轮叶片和碳纤维结构件进行三维测量试验。与传统测量方法相比,本文所述方法无点云缺失,能够三维重建出完整的零件表面模型,解决了零件表面强反光区域测量失效问题,去除了由多次反光现象引起的多次反射光干扰,实现了航空工业高光零件复杂表面的高精度三维测量。测量得到的完整点云数据可以作为零件表面质量检测、精密尺寸测量、余量加工等后续工作的重要依据,具有较高的应用价值。
[1] HUA L X, LU Y, DENG J H, et al.3D reconstruction of concrete defects using optical laser triangulation and modified spacetime analysis[J].Automation in Construction, 2022,142: 104469.
[2] ZHANG J J, DU R X, GAO R Z.Passive 3D reconstruction based on binocular vision[C]//Tenth International Conference on Graphics and Image Processing (ICGIP 2018).Chengdu, 2019.
[3] CHEN H, CUI W.A comparative analysis between active structured light and multiview stereo vision technique for 3D reconstruction of face model surface[J].Optik, 2020, 206:164190.
[4] YU Z J, MA K, WANG Z J, et al.Surface modeling method for aircraft engine blades by using speckle patterns based on the virtual stereo vision system[J].Optics Communications,2018, 411: 33–39.
[5] JIANG Y, YAN J, ZHANG L, et al.Array FBG sensing and 3D reconstruction of spacecraft configuration[J].Optoelectronics Letters, 2022, 18(4): 193–199.
[6] HARDING K.3D profilometry:Next requests from the industrial viewpoint[C]//Photonics Asia 2010.Beijing, 2010.
[7] ZHOU P, WANG H Y, WANG Y, et al.A 3D shape measurement method for highreflective surface based on dual-view multiintensity projection[J].Measurement Science and Technology, 2023, 34(7): 075021.
[8] LIN H, GAO J, MEI Q, et al.Adaptive digital fringe projection technique for high dynamic range three-dimensional shape measurement[J].Optics Express, 2016, 24(7):7703–7718.
[9] BENVENISTE R, ÜNSALAN C.Nary coded structured light-based range scanners using color invariants[J].Journal of Real-Time Image Processing, 2014, 9(2): 359–377.
[10] ZHU Z M, XIE Y L, CEN Y G.Polarized-state-based coding strategy and phase image estimation method for robust 3D measurement[J].Optics Express, 2020, 28(3):4307–4319.
[11] ZHU Z M, DONG Y W, YOU D D,et al.Accurate three-dimensional measurement based on polarization-defocused encoded structured light[J].Measurement, 2022, 205:112128.
[12] XIAO Y L, LI S K, ZHANG Q C,et al.Optical fringe-reflection deflectometry with bundle adjustment[J].Optics and Lasers in Engineering, 2018, 105: 132–140.
[13] LI Z C, KANG Y C, MOON J H,et al.The optimum projection angle of fringe projection for ball grid array inspection based on reflectance analysis[J].The International Journal of Advanced Manufacturing Technology, 2013,67(5): 1597–1607.
[14] CHEN Y C, YAO P C, GAI S Y, et al.A self-alignment XOR coding strategy resistant to global illumination[J].Measurement, 2022, 193:110767.
[15] NAYAR S K.Micro phase shifting[C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition(CVPR).New York: ACM, 2012: 813–820.
[16] 王晋疆, 张烜瑜.反射光干扰下的格雷码结构光三维测量方法[J].光学技术,2018, 44(1): 69–74.
WANG Jinjiang, ZHANG Xuanyu.3D Measurement method of Gray code structured light under interference of reflected light[J].Optical Technique, 2018, 44(1): 69–74.
[17] REICH C, RITTER R, THESING J.White light heterodyne principle for 3D-measurement[C]//Sensors, Sensor Systems,and Sensor Data Processing.Munich, 1997.
[18] JIANG H Z, ZHAO H J, LI X D.High dynamic range fringe acquisition: A novel 3-D scanning technique for high-reflective surfaces[J].Optics and Lasers in Engineering, 2012, 50(10):1484–1493.
[19] JIANG H Z, YANG Q Y, LI X D, et al.3D shape measurement in the presence of strong interreflections by using single-pixel imaging in a camera-projector system[J].Optics Express, 2021,29(3): 3609–3620.
[20] JIANG H Z, LI Y X, ZHAO H J,et al.Parallel single-pixel imaging: A general method for direct–global separation and 3D shape reconstruction under strong global illumination[J].International Journal of Computer Vision, 2021,129(4): 1060–1086.
