光面塞规是用于孔径检验的光滑极限量规[1],具有使用简单、测量精度和效率高等优点,在飞机的大批量孔类零件快速检验中应用极为广泛。但光面塞规本身的制造误差及在使用过程中产生的工作面磨损等,会导致在检测零件孔时产生误判[2]。因此,计量部门在光面塞规使用前和使用过程中均需对其做定期检定[3]。
传统的光学计[4]和测长机[5]等测量设备虽然检定精度高,但需要通过相对测量和人工找拐点,操作过程烦琐,检定效率低。天津大学的程大林[6]研制了一种透射式激光扫描直径测量装置,对汽车发动机曲轴外径进行测量,测量结果的标准差小于0.01 mm。吉林大学的高飞[7]研究了基于机器视觉的轴类零件外径测量方法,利用超分辨率重构及亚像素边缘提取技术来提高测量精度,测量误差不超过0.02 mm。这些新方法尽管能提高测量效率,但测量精度普遍无法达到塞规检定的要求[8]。
为此,本文将误差修正技术应用于塞规检定,即通过机器视觉[9–10]测量塞规的姿态,进而对激光测径仪的测量结果进行修正。同时采用气浮运动机构和自动控制系统提高测量运动精度和自动化程度,实现了光面塞规直径的快速高精度检定。
1 系统总体结构
光面塞规自动检定系统的总体结构如图1所示。激光测径仪立式安装在大理石工作台上,用于测量塞规直径尺寸。在激光测径仪下方安装了对射式光电开关和机器视觉模块,当光电开关感知到被检塞规上升至指定位置时,机器视觉模块采集塞规端部图像并检测塞规姿态,作为修正激光测径仪测量结果的依据。
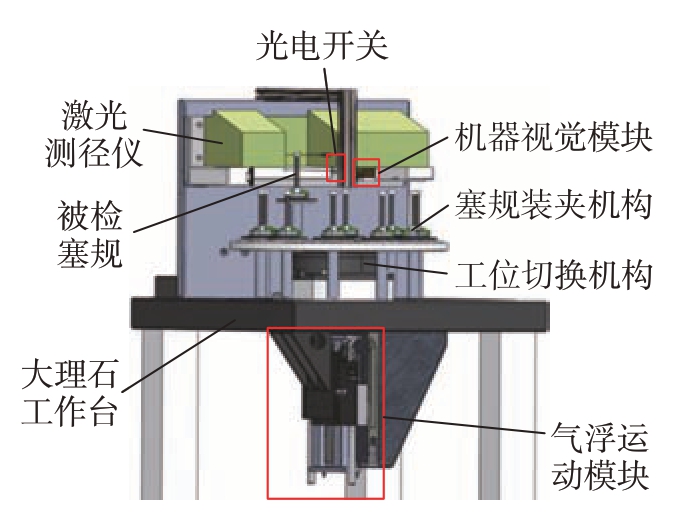
图1 光面塞规自动检定系统总体组成
Fig.1 Overall composition of the automatic verification system for plug gauge
工位切换机构由直驱电机和安装在电机上的转台组成。转台的一周均匀分布有10个安装孔,被检塞规通过专用夹具装夹于各个孔内,并可随转台一起在直驱电机驱动下旋转,从而实现多个塞规的批量化检定。
如图2所示,大理石工作台下方安装有气浮升降台和气浮转台。塞规检定时,气浮转台上的气动夹爪夹住专用夹具下端的轴,在气浮升降台的带动下将被检塞规升至激光测径仪光幕中央,气浮转台则带动塞规旋转,实现塞规多截面多角度的直径测量。
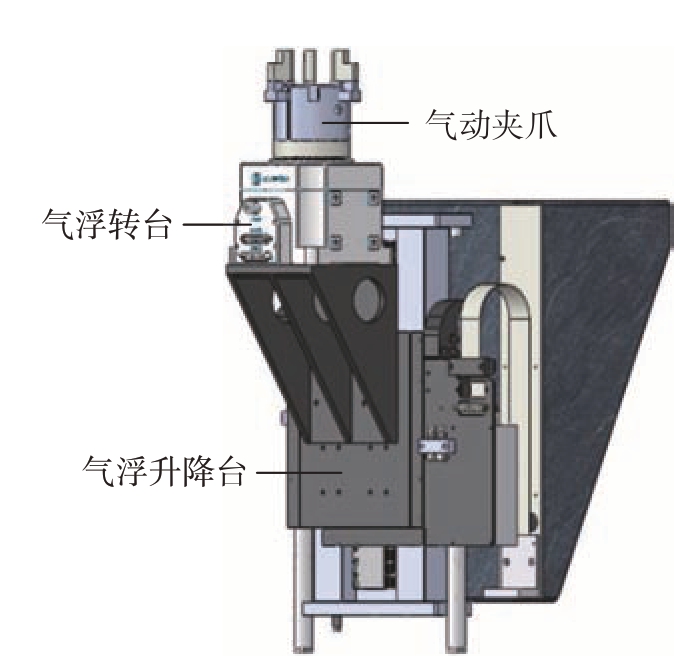
图2 检定系统气浮运动模块
Fig.2 Air flotation module of the verification system
2 测量模型
激光测径仪是一种基于激光扫描的非接触式测量仪器,其发射端发出的平行光幕被塞规遮挡后在接收端形成阴影,阴影宽度即为塞规的直径L[11]。如图3所示,当塞规轴线与光幕平面不垂直时,激光测径仪测得的塞规直径存在系统误差,该误差需要根据塞规相对于光幕的倾斜角度来进行修正。

图3 激光测径仪测量塞规直径
Fig.3 Measuring the diameter of the plug gauge with a laser caliper
如图4所示,以塞规轴线与激光测径仪光幕平面的交点O为坐标原点,光幕平面为XOY坐标平面,并以光幕投射方向作为OY轴正方向建立系统坐标系OXYZ。令塞规轴线与OZ轴之间的夹角为θ,同时令塞规轴线在XOY平面上的投影与OX轴之间的夹角为β,在XOZ平面上的投影与OZ轴之间的夹角为γ。
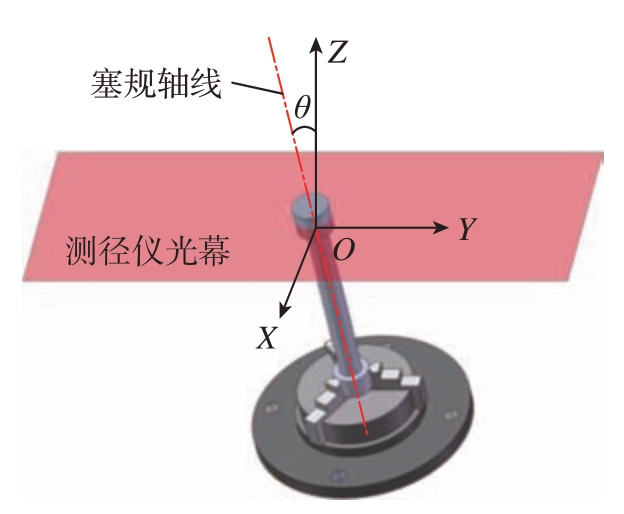
图4 塞规直径测量坐标系
Fig.4 Coordinate system in measurement of plug gauge diameter
假设塞规轴线的方向向量为→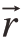 ,则
,则
夹角γ满足
如图5所示,直径为D的光面塞规被激光测径仪测量光幕所截的轮廓为椭圆。不难看出该椭圆的短半轴长度b = D/2,长半轴长度a = D/2cosθ,椭圆长轴与OX轴正方向的夹角为β。因此,椭圆方程为
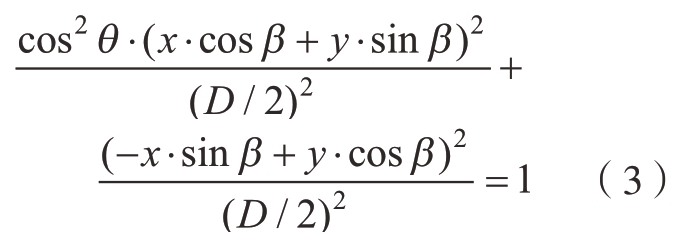
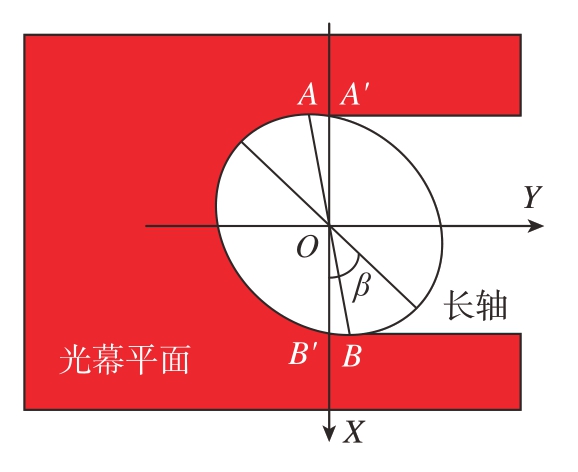
图5 测径仪光幕平面上的塞规截面轮廓
Fig.5 Cross-sectional profile of the plug gauge on the light curtain plane of the caliper
假设图5中塞规截面与光幕相切于A、B两点,其在OX轴上的投影分别为点A'(m,0) 和点B'(–m,0),m>0。代入椭圆方程可计算出m为
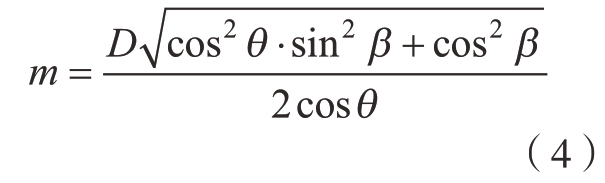
所以,激光测径仪的测得值L可由式 (5)计算得到。
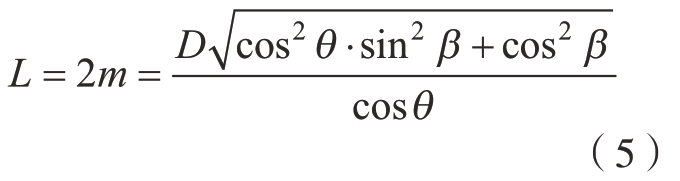
由式 (2)等号两边同时平方得
通过简单的三角函数变换可得
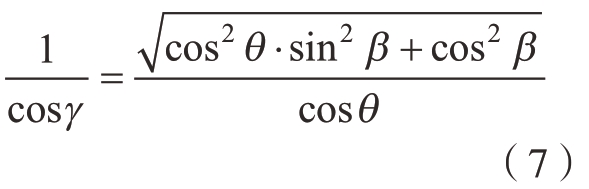
由式 (5)和 (7)可得
式 (8)给出了塞规直径的测量模型。可以直观看出,塞规直径只与在XOZ平面上的投影和OZ轴之间的夹角γ相关,夹角是表示塞规沿X方向上的倾斜,由沿Y方向上部署的相机拍摄得到。
测量系统总误差可以由测量模型函数的全微分表示,结合式 (8)推导其算术合成误差传递公式,即

式中,Δd表示直径测量误差;ΔL和Δγ分别表示激光测径仪与视觉测量系统测量直径与角度的测量误差。
根据国标GB/T 10920—2008,本测量系统对光面塞规直径测量精度要求Δd范围在± 1 μm,ΔL由激光测径仪精度决定为± 0.25 μm,本系统量程L小于50 mm,根据实际情况塞规倾斜角度γ不超过1°,则Δγ需不超过0.064°。故视觉测量系统角度测量精度为± 0.064°。
3 塞规直径测量
3.1 基于激光测径仪的直径测量
Z–mike激光测径仪是检定系统的关键设备,它通过标准RS232接口与工控机之间进行串口通信,实现工控机对激光测径仪的数据采集和测量控制。Z–mike测径仪的采集速率为0.02 s/点,在测量塞规直径时,每个测量位置上采集100个测量数据。为了消除激光异常波动等对测量结果带来的影响,首先采用3σ准则从测量数据中剔除粗大误差[12],然后将余下的数据求平均值作为最终的测量结果。
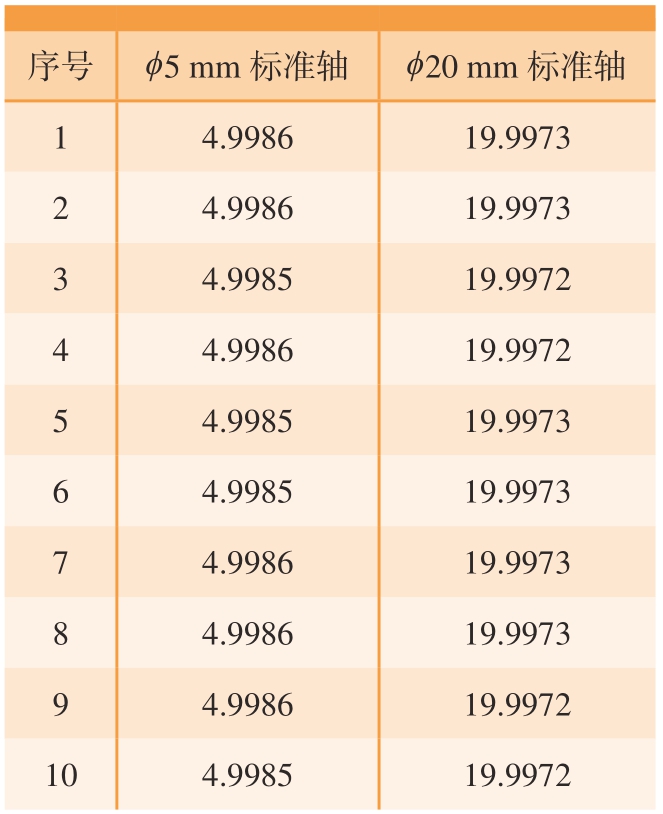
在 (20±1)℃的实验室环境下,使用Z–mike测径仪分别对公称直径ϕ5 mm和ϕ20 mm的两根标准轴进行重复测量试验,测量结果如表1所示。根据表1中数据可计算出两根标准轴10次重复测量的极差为0.1 μm,表明该激光测径仪具有很高的重复测量精度。
表1 Z–mike激光测径仪重复测量结果
Table 1 Repeated measurement results of Z–mike laser caliper mm
序号ϕ5 mm标准轴ϕ20 mm标准轴14.998619.9973 24.998619.9973 34.998519.9972 44.998619.9972 54.998519.9973 64.998519.9973 74.998619.9973 84.998619.9973 94.998619.9972 104.998519.9972
但由于测径仪内部光学元件的制造与装配误差及电机转速等因素的影响,测量光幕表现出非线性[13],即同一尺寸在光幕中的不同位置会被测成不同的测量值。因此在塞规直径这样的高精度测量应用中,应将被测件在测径仪光幕中的位置限定在一个较小的区域内,以减小非线性误差。
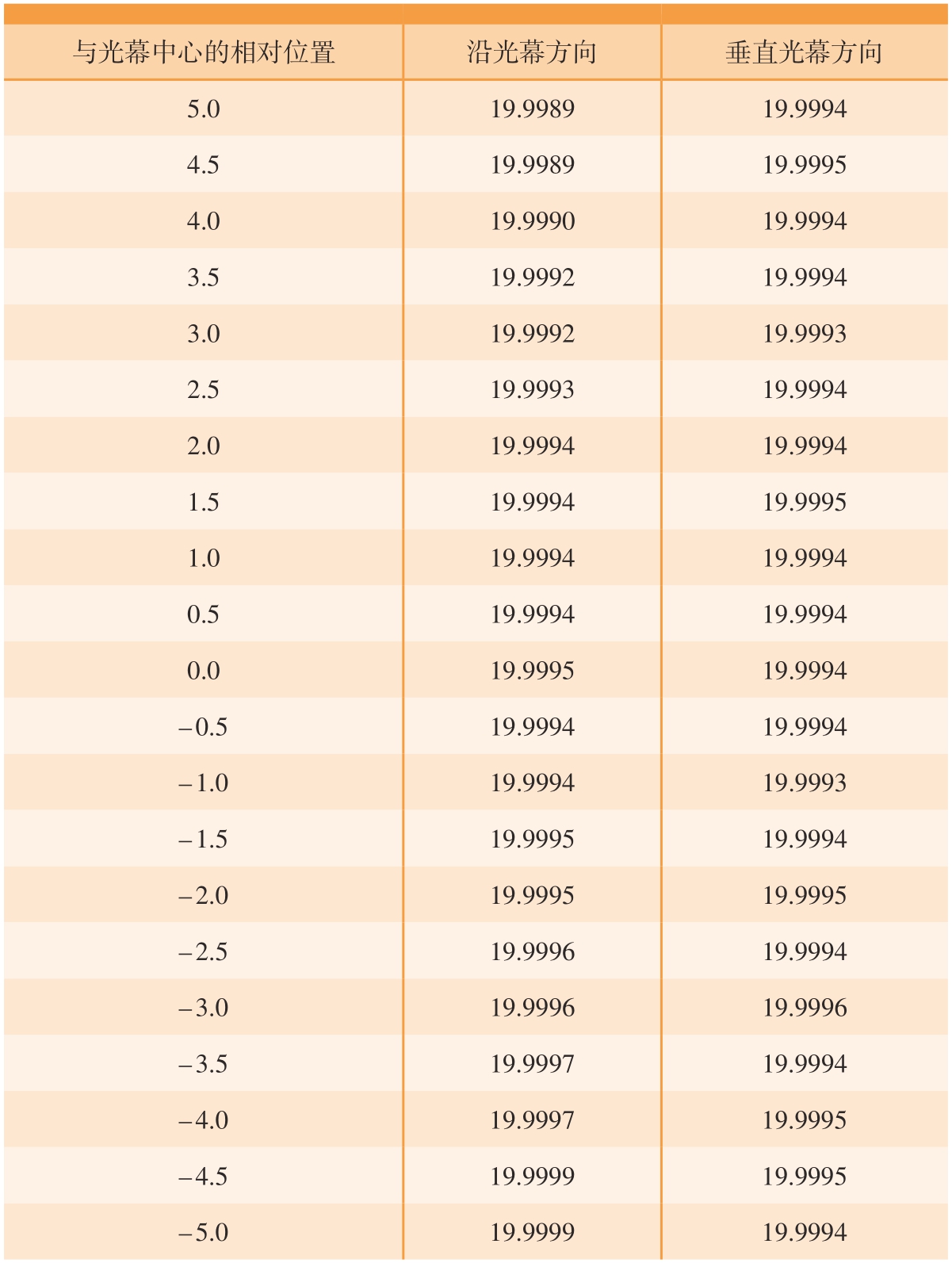
为了确定测径仪光幕中的这一最佳测量区域,本文通过直线位移台带动ϕ20 mm直径的标准轴在光幕中心附近± 5 mm范围内分别沿着光幕方向及垂直于光幕方向做平移,移动间隔为0.5 mm。标准轴直径的测量数据如表2所示,图6为两个方向上的测量点分布图。
表2 标准轴在光幕不同位置处直径测量结果
Table 2 Measurement results of the diameter of the standard shaft at different positions in the light curtain mm
与光幕中心的相对位置沿光幕方向垂直光幕方向5.019.998919.9994 4.519.998919.9995 4.019.999019.9994 3.519.999219.9994 3.019.999219.9993 2.519.999319.9994 2.019.999419.9994 1.519.999419.9995 1.019.999419.9994 0.519.999419.9994 0.019.999519.9994–0.519.999419.9994–1.019.999419.9993–1.519.999519.9994–2.019.999519.9995–2.519.999619.9994–3.019.999619.9996–3.519.999719.9994–4.019.999719.9995–4.519.999919.9995–5.019.999919.9994
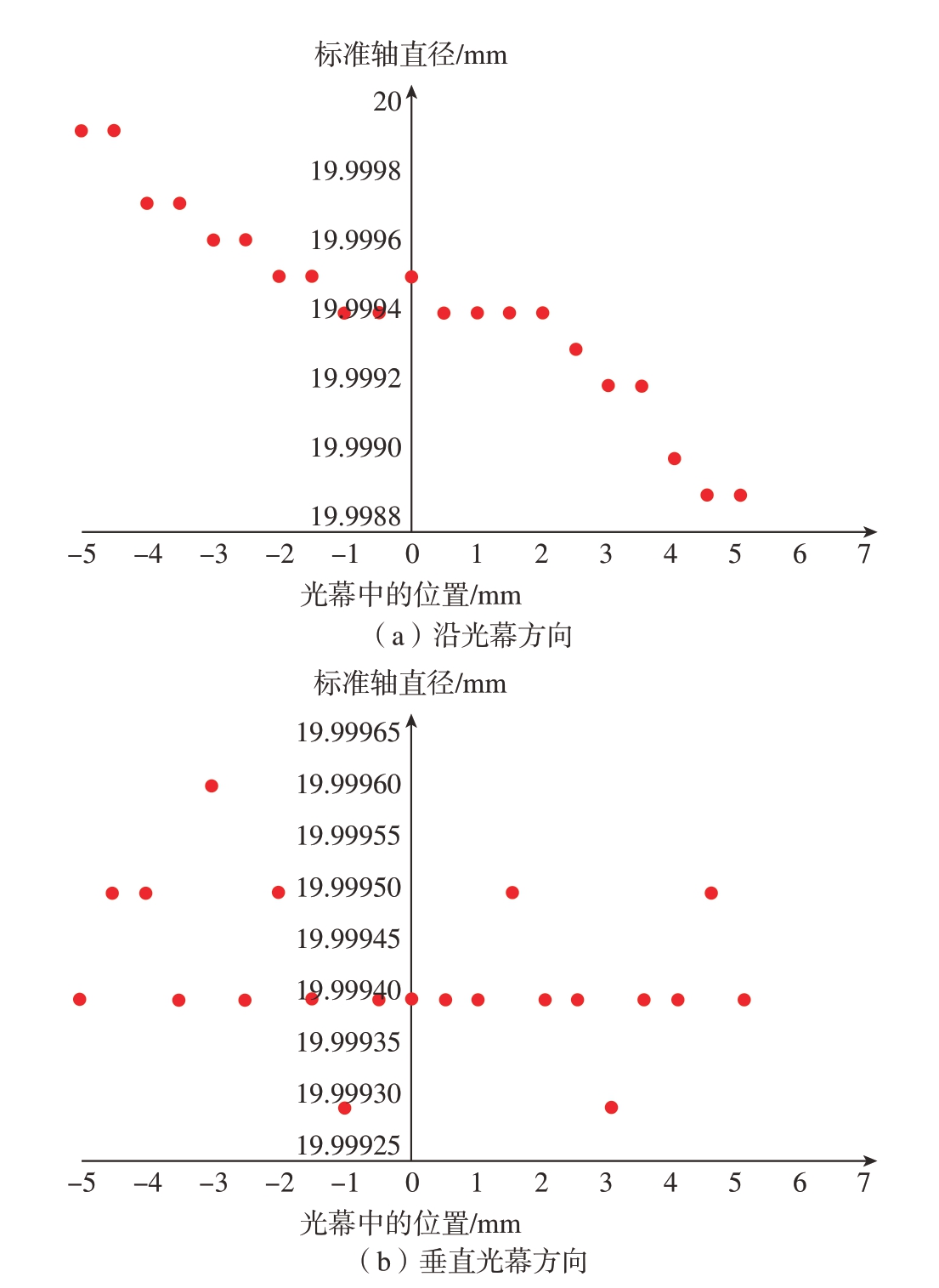
图6 标准轴移动时直径测量结果
Fig.6 Diameter measurement results during standard shaft movement
测量结果表明,垂直于光幕方向的位置变化对标准轴的直径测量影响很小,而沿着光幕方向的标准轴直径测量值近似呈线性变化。当标准轴的轴线处于光幕中心附近± 2 mm的正方形区域内时,其直径的测量值几乎不变,因此本系统控制该区域为激光测径仪检定塞规时的测量区域。
3.2 基于机器视觉的塞规位姿修正
根据式 (8)给出的塞规直径测量模型,塞规装夹误差以及激光测径仪与气浮升降台之间的安装位置误差等都会造成被检塞规处于测径仪光幕当中时存在倾斜角度γ。必须实时测出该角度值,然后代入式 (8)才能计算出塞规的直径。为此,本系统在测径仪下方安装了机器视觉模块,通过背光打光方式清晰呈现塞规轮廓,相机采集塞规图像并由计算机对图像进行处理,最终测得塞规的倾斜角γ。
图7(a)为相机采集的塞规原始图像。首先通过OpenCV库[14–15]中的threshold函数对原始图像做二值分割,得到图7(b)所示的二值化图像。接下来,利用findContours函数在二值图像中寻找轮廓点,并通过drawContours函数将这些轮廓点连接成图7(c)所示的闭合轮廓。闭合轮廓中包含了塞规端部和背光源边缘的轮廓信息,根据两者的位置分布特点,利用Rect函数对轮廓进行裁剪,即可得到只包含塞规端部轮廓的图像,结果如图7(d)所示。最后,提取塞规轮廓的两侧边缘,通过最小二乘法对边缘进行直线拟合,从而得到塞规的倾斜角γ,即
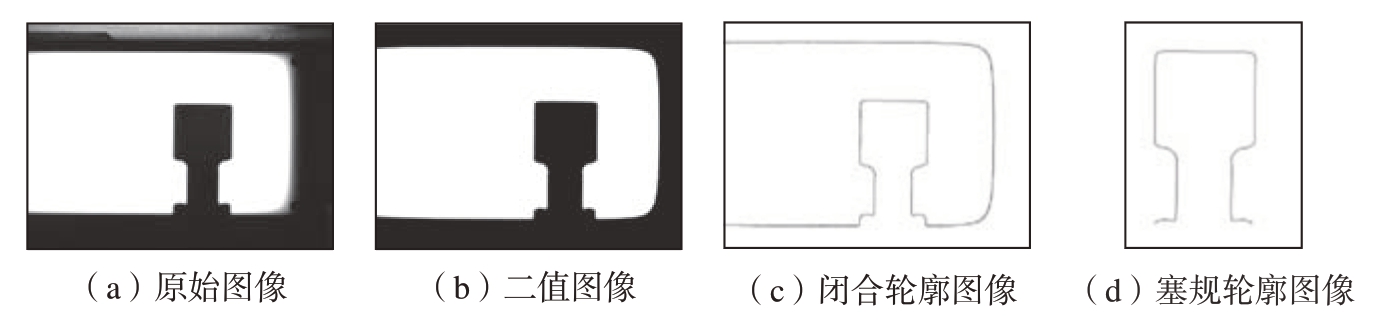
图7 塞规轮廓图像处理
Fig.7 Image processing of plug gauge contour
式中,k1、k2分别为塞规左右两侧边缘最小二乘法直线的斜率。
如图8所示,为了验证检定系统对不同姿态塞规直径的测量精度,将直径为ϕ25 mm的标准轴装夹在精密角位移台上,手动调整角位移台旋钮使标准轴倾斜不同角度。机器视觉模块和激光测径仪同步测量标准轴的倾斜角度γ(沿X方向倾斜角度)和直径L,测量结果如表3所示。
表3 不同姿态的标准轴直径测量结果
Table 3 Measurement results of the diameter of standard shaft in different postures
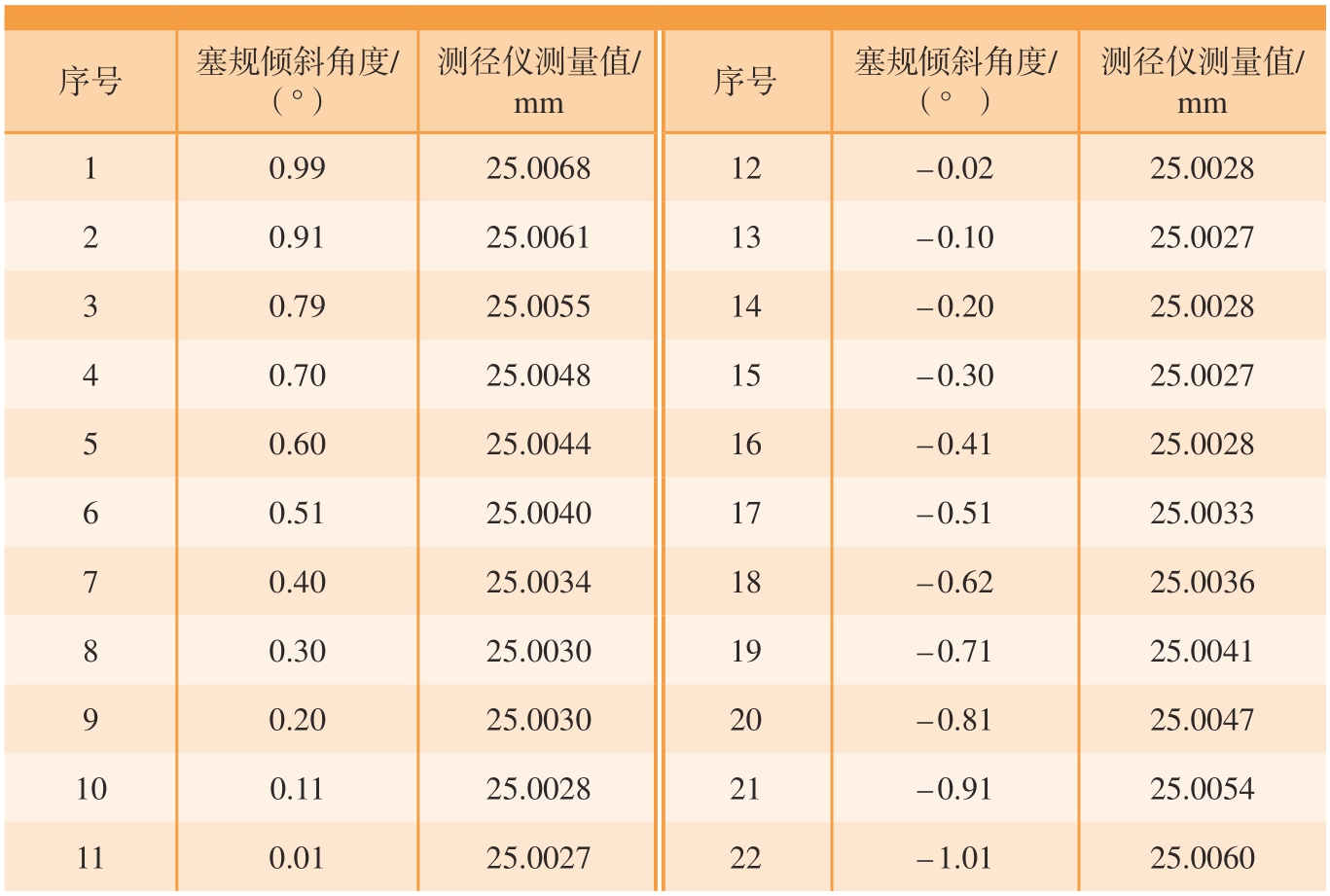
序号塞规倾斜角度/(°)测径仪测量值/mm 1 0.9925.006812–0.0225.0028 2 0.9125.006113–0.1025.0027 3 0.7925.005514–0.2025.0028 4 0.7025.004815–0.3025.0027 5 0.6025.004416–0.4125.0028 6 0.5125.004017–0.5125.0033 7 0.4025.003418–0.6225.0036 8 0.3025.003019–0.7125.0041 9 0.2025.003020–0.8125.0047 100.1125.002821–0.9125.0054 110.0125.002722–1.0125.0060测径仪测量值/mm序号塞规倾斜角度/(°)

图8 不同姿态的标准轴直径测量试验
Fig.8 Measuring experiment for the diameter of standard shaft in different postures
以标准轴倾斜角度为横坐标,激光测径仪测量值为纵坐标,将测量结果绘制成图9所示的散点图。可以看出,当标准轴相对于垂直光幕方向倾斜1°时,激光测径仪的测量值偏离4.5 μm左右。也就意味着,直接以测径仪测量值作为标准轴直径的测量结果是无法达到测量精度要求的。

图9 测径仪直接测得的不同姿态标准轴直径
Fig.9 Diameters of standard shaft in different postures measured by the laser caliper
将表3中测得的标准轴倾斜角度γ和直径L代入式 (8)计算得到姿态修正后的标准轴直径,然后绘制成图10所示的散点图,结果表明修正后的标准轴直径测量值的极差小于0.5 μm,取得了很好的修正效果。
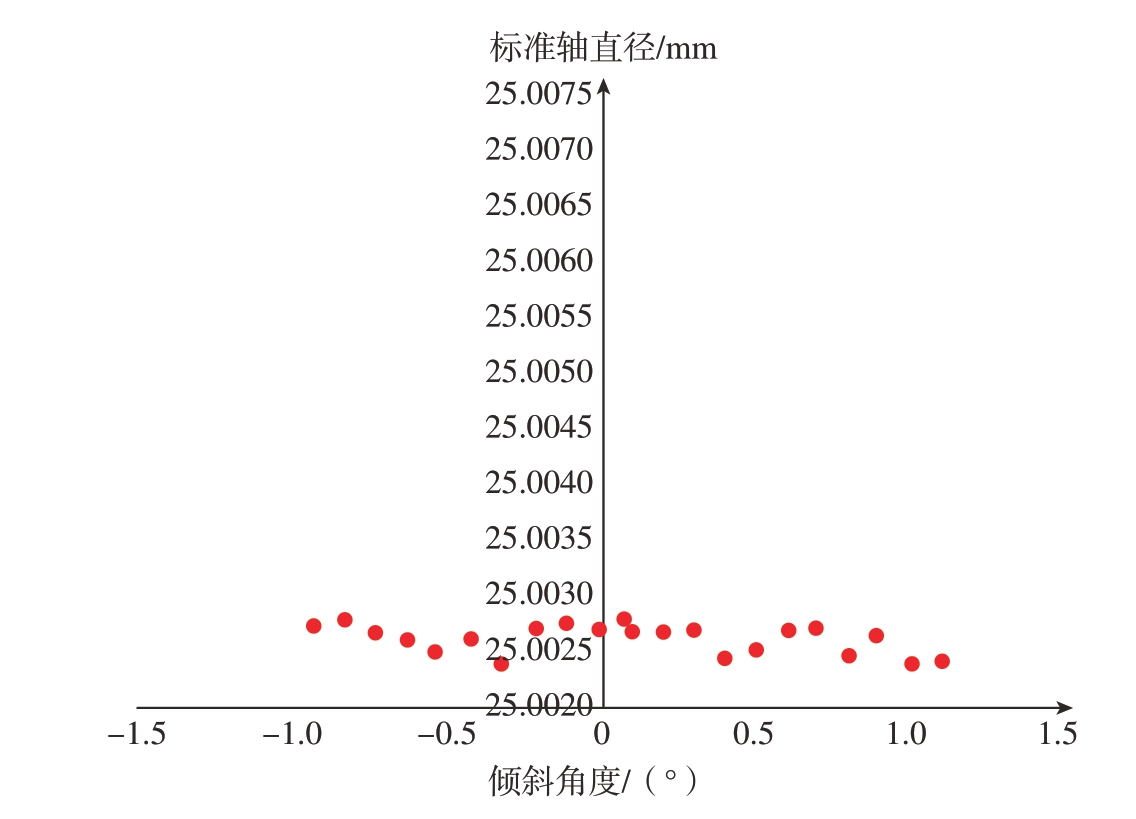
图10 修正后的不同姿态标准轴直径
Fig.10 Corrected diameters of standard shaft in different postures
4 试验结果
测量精度是光面塞规检定系统最重要的技术指标,接下来主要从测量重复性和测量结果的绝对误差两个方面进行测试。
将表面擦拭干净的Φ7H6标准塞规在 (20±1)℃的温度环境下静置30 min以上,然后将标准塞规装夹到检定系统上开始测量。表4给出了10次重复测量的数据,测量值的极差为0.5 μm,标准差为0.16 μm,达到了很高的重复测量精度。
表4 Φ7H6标准塞规直径的重复测量结果
Table 4 Repeated measurement results of diameter of Φ7H6 standard plug gauge
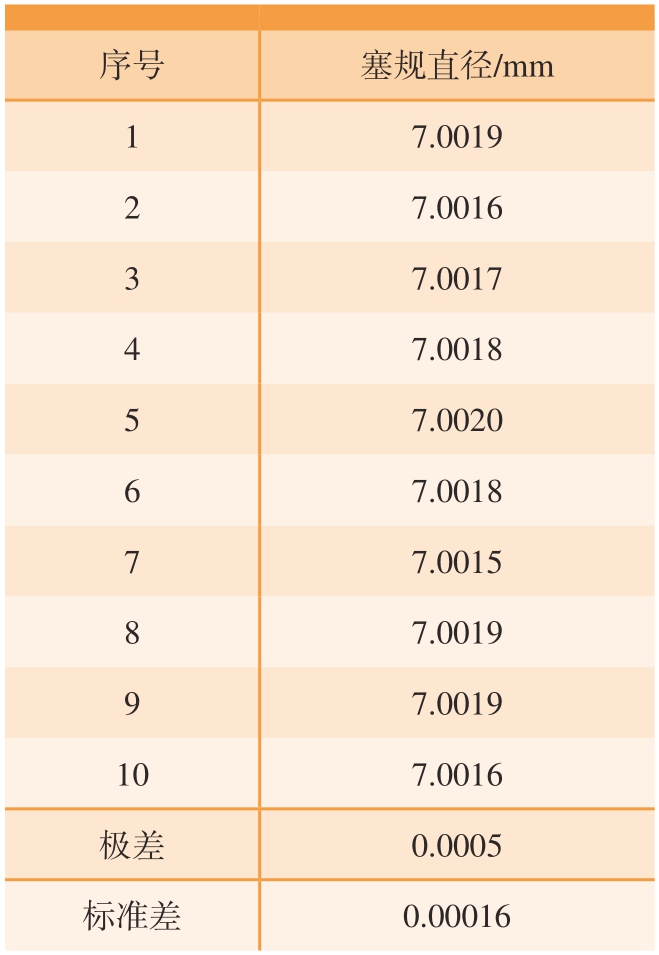
序号塞规直径/mm 1 7.0019 2 7.0016 3 7.0017 4 7.0018 5 7.0020 6 7.0018 7 7.0015 8 7.0019 9 7.0019 107.0016极差0.0005标准差0.00016
对于Φ7H6标准塞规,其标准公差为0.009 mm,根据MSA分析原理中对测量系统重复性、再现性的评定准则计算其Gage R&R%数值。
式中,T表示Φ7H6标准塞规的标准公差;σ表示测量结果标准差。
计算的Gage R&R% = 10.3%,结果约为10%,故此判断,本测量系统重复性佳、再现性好,满足测量需求。
为了进一步验证系统测量结果的正确性,还将本系统与立光计进行了对比测量试验,测量数据如表5所示。对比结果可以看出,本检定系统对4种不同规格标准塞规直径的测量结果与立光计的绝对误差在0.5 μm以内,能够满足生产中常用塞规的检定精度要求。
表5 本系统与立光计的塞规直径测量结果对比
Table 5 Comparison of the plug gauge diameter measurement results between this system and the standing light meter mm

序号立光计本系统绝对误差1 7.00227.00240.0002 2 10.001810.00190.0001 3 12.000412.00090.0005 4 19.999519.99980.0003
5 结论
(1)研究了基于机器视觉的误差修正技术,通过机器视觉模块测量塞规相对于激光测径仪光幕的姿态角,然后根据塞规直径测量模型对激光测径仪的测量值进行修正,使系统的重复测量标准差达到0.16 μm,与立光计测量值相比的绝对测量误差≤0.5 μm,实现了光面塞规直径的高精度测量。
(2)通过专用装夹机构、旋转工作台和高精度气浮运动台,实现了塞规的批量化自动检定,并对检定流程进行优化,使塞规单端测量时间≤45 s,实现了光面塞规的快速自动检定。
[1] 国家质量监督检验检疫总局, 中国国家标准化管理委员会.螺纹量规和光滑极限量规 型式与尺寸: GB/T 10920—2008[S].北京: 中国标准出版社, 2009.
General Administration of Quality Supervision, Inspection and Quarantine of China,National Standardization Administration of China.Types and dimensions of thread gauges and smooth limit gauges: GB/T 10920—2008[S].Beijing: Standards Press of China, 2009.
[2] 孔晓玲.几何量精度设计与测量技术[M].北京: 电子工业出版社, 2013.
KONG Xiaoling.Precision design and measurement technology of geometric quantities[M].Beijing: Publishing House of Electronics Industry, 2013.
[3] 国家技术监督局.光滑极限量规检定规程: JJG 343—1996[S].北京: 中国计量出版社, 2004.
The State Administration of Technical Supervision.Verification regulation for smooth limit gauges: JJG 343—1996[S].Beijing: China Metrology Publishing House, 2004.
[4] 吴呼玲, 窦益华.立式光学计测量塞规分析其测量不确定度[J].机械研究与应用,2016, 29(5): 84–85, 89.
WU Huling, DOU Yihua.Analysis on the measurement uncertainty of plug gauge measured by vertical optical meter[J].Mechanical Research & Application, 2016,29(5): 84–85, 89.
[5] 吕军.测长机直接比较测量误差和测量不确定度分析[J].计量技术, 2020(4):52–56, 72.
LÜ Jun.The measurement error of direct comparison and measurement uncertainty of length measurement machine[J].Measurement Technique, 2020(4): 52–56, 72.
[6] 程大林.透射式激光扫描轴径测量系统的设计[D].天津: 天津大学, 2012.
CHENG Dalin.Design of transmission laser scanning diameter measurement system for shafts[D].Tianjin: Tianjin University, 2012.
[7] 高飞.基于机器视觉技术测量轴类零件尺寸的研究[D].长春: 吉林大学, 2007.
GAO Fei.The study of measuring the dimension of shaft-type elements by the machine vision[D].Changchun: Jilin University,2007.
[8] 黄开元.光滑极限量规快速综合检定系统的研发[D].南京: 南京航空航天大学,2018.
HUANG Kaiyuan.Research and development of the rapid and comprehensive verification system for the plain limit gauge[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2018.
[9] 赵庆斌.机器视觉技术在轴零件检测中的应用研究[J].科学技术创新, 2018(22):171–172.
ZHAO Qingbin.Research on the application of machine vision technology in shaft parts inspection[J].Scientific and Technological Innovation, 2018(22): 171–172.
[10] WANG L H.Key technology and application of computer artificial intelligence recognition based on machine vision[J].Journal of Physics: Conference Series, 2021, 1982(1):012112.
[11] CHURSIN Y A, FEDOROV E M.Methods of resolution enhancement of laser diameter measuring instruments[J].Optics &Laser Technology, 2015, 67: 86–92.
[12] 叶川, 伍川辉, 张嘉怡.计量测试中异常数据剔除方法比较[J].计量与测试技术,2007, 34(7): 26–27.
YE Chuan, WU Chuanhui, ZHANG Jiayi.Comparision about how to get rid of abnormal data in metrology & measurement[J].Metrology& Measurement Technique, 2007, 34(7): 26–27.
[13] 段长超, 彭松, 谭骏, 等.扫描式激光测径仪中电机转速波动对精度的影响及误差修正研究[J].现代电子技术, 2020, 43(4):112–116.
DUAN Changchao, PENG Song, TAN Jun, et al.Influence of motor speed fluctuation in laser scanning diameter measuring gauge on accuracy and its error correction[J].Modern Electronics Technique, 2020, 43(4): 112–116.
[14] GONZALEZ R C, WOODS R E.数字图像处理[M].阮秋琦, 阮宇智, 译.北京:电子工业出版社, 2003.
GONZALEZ R C, WOODS R E.Digital image processing[M].RUAN Qiuqi, RUAN Yuzhi, Trans.Beijing: Publishing House of Electronics Industry, 2003.
[15] 黄佳.基于OPENCV的计算机视觉技术研究[D].上海: 华东理工大学, 2013.
HUANG Jia.Computer vision technology based on OPENCV[D].Shanghai: East China University of Science and Technology, 2013.
