铆钉作为飞机装配中使用最广泛的紧固件,在强度、尺寸、耐腐蚀性、寿命、变形量等方面都必须达到很高的要求。根据行业标准,飞机蒙皮表面的航空沉头铆钉不允许凹进蒙皮,凸出量应符合各机型的设计技术条件,安装在非气动外缘处的铆钉相对于安装面的凹凸量应在±0.1 mm以内[1]。
目前,国内大多数飞机制造企业主要依靠有经验的工人通过目视、借助塞尺或是使用带辅助支架的千分表等方法来检查飞机铆钉的凹凸量是否合格。不仅容易损伤飞机表面,而且无法准确得到铆钉的凹凸量值,检测精度及效率低,难以对铆接工艺提供有效反馈。因此,航空制造现场迫切需要一种量化的铆钉凹凸量测量方法。
蒋滔等[2]构建了一套铆接质量视觉检测系统,采用改进遗传算法结合OSTU方法对铆钉图像进行阈值分割,在此基础上实现了铆钉亚像素边缘提取;该系统主要用于铆钉识别,并未对凹凸量进行测量。王红涛等[3]研发出飞机蒙皮铆钉阶差检测装置,该装置由支架、深度尺、转轴等组成,但由于采用的是接触式测量,操作烦琐,不适合铆钉数量较多的情况。李红卫[4]提出了一种局部自适应密度算法提取三维点云,根据获得的铆钉头点云和局部非铆钉点云数据计算铆钉凹凸量,但该方法需要处理的点云数据量庞大,测量效率不高。王德重等[5]提出了一种基于双目多线激光的铆钉凹凸量测量方法,对双目视觉系统采集的被测表面多线激光图像进行匹配与重建,计算分布于激光线上的铆钉头部及蒙皮表面点的坐标,进而计算出铆钉凹凸量;该测量方法灵活、效率较高,但只采集了线激光上的点云数据,以此来计算铆钉的凹凸量容易产生较大误差。
近年来,基于结构光的三维重建技术[6]取得了很大进展,通过被测对象表面三维重建可实现对物体特征尺寸的测量。与二维图像相比,重建的三维形貌能够提供更加丰富的细节信息。本文利用工业投影仪的投影条纹对比度高、亮度非线性误差小等优点,将结构光编码后投射到铆钉区域,然后由双目相机采集图像,再经过相位解算、形貌重建和型面拟合等一系列处理后计算出铆钉的凹凸量。该方法在满足现场测量效率要求的前提下,提高了铆钉凹凸量的测量精度。
1 双目视觉检测系统
1.1 系统组成
如图1所示,检测装置主要由结构光源和双目视觉模块组成。其中,结构光源采用S52型投影仪 (腾聚科技),其结构紧凑、帧率高,且投影条纹可编程。视觉模块选用VEN–134–90U3M/C–D型CMOS相机和HN–P–1628–6M–C2/3镜头 (大恒图像)。整个检测装置体积小巧、质量轻,可以手持或机械臂夹持,移动便捷,适合用于航空制造现场的检测。

图1 基于结构光的双目视觉检测装置
Fig.1 Binocular vision inspection device based on structured light
检测系统的视场范围约50 mm×70 mm,通过工业投影仪对铆接表面连续投射多帧结构光条纹,利用双目相机同步采集条纹图像,经图像处理和计算后得到铆钉凹凸量。
1.2 相机标定
系统构建完成后,首先采用张正友方法[7]对双目相机进行标定,定制的棋盘格标定板的角点位置精度为1 μm。双目相机在不同角度和位置上采集10幅以上的标定板图像,提取图像中角点的亚像素坐标。以其中一个角点作为原点Ow,以标定板平面作为XwOwYw平面,建立世界坐标系Ow XwYwZw。则二维图像中的角点像素坐标 (u,v)与其对应的空间点的世界坐标 (Xw,Yw,Zw)之间的转换关系可用式 (1)表示。
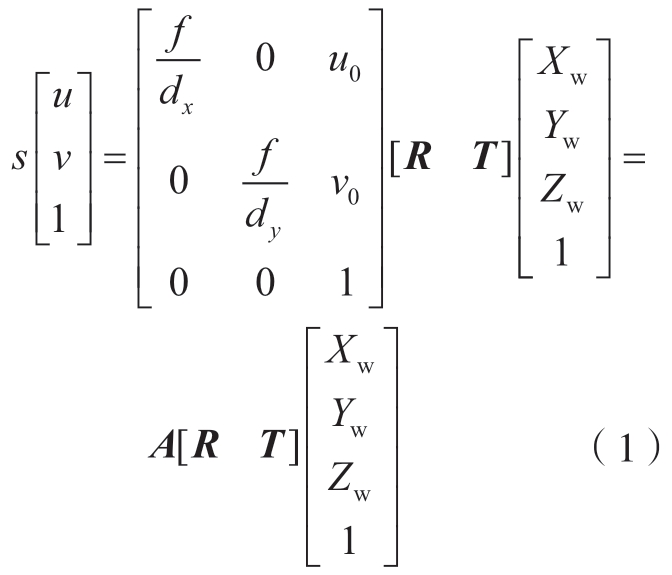
式中,s为空间点到镜头光心的距离沿相机光轴方向上的投影长度;dx、dy分别为图像在水平方向和竖直方向的像素尺寸; (u0,v0)为相机光心图像映射点的像素坐标;f为镜头的焦距;A为相机内部参数矩阵;R和T分别为世界坐标系相对相机坐标系的旋转矩阵和平移矩阵。
以镜头光心在相机成像平面上的投影点为原点,水平方向为x轴,竖直方向为y轴建立图像坐标系。考虑到相机本身存在径向畸变和切向畸变,经校正后的像点坐标 (xp,yp)与原坐标 (xd,yd)的关系为
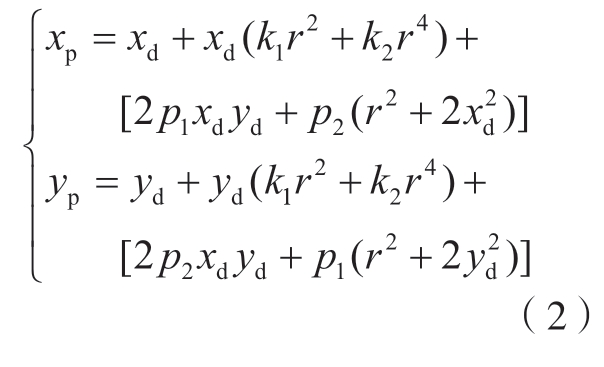
式中,r为校正前的像点到图像坐标系原点的距离,r=![]() ;k1、k2分别为径向畸变系数;p1、p2分别为切向畸变系数。
;k1、k2分别为径向畸变系数;p1、p2分别为切向畸变系数。
利用Levenberg-Marquard算法[8]对式 (1)和 (2)联立的包含多个角点的方程组进行迭代优化,可获得相机的内部参数A和外参数[R T]的最优解。然后根据两个相机的外部参数计算得到右相机坐标系相对于左相机坐标系的旋转矩阵R1和平移矩阵T1。
1.3 系统校正
双目视觉系统采用的是类似人眼的平行光轴模型[9],但在实际应用时由于视场范围的要求及相机安装误差的原因,左右相机的光轴往往并不平行,这时就需要对双目相机采集的图像进行立体校正。参照Bouguet算法[10],首先将左右相机之间的旋转矩阵R1拆分成左、右相机的合成矩阵,即rl和rr。

然后将平移矩阵T1归一化,得到单位平移矩阵e1。定义与e1正交的单位矩阵e2,将e1与e2叉积得到e3,从而得到行对齐矩阵为
联立式 (3)和 (4),得到左右相机的立体校正矩阵为
如图2所示,利用上述矩阵可将左右图像中的对应点转换到同一水平线上,从而实现左右相机的立体校正。这样,后续图像匹配时的特征点搜索范围就从二维平面缩小至一维水平线,大幅降低了计算量,提高了算法效率。
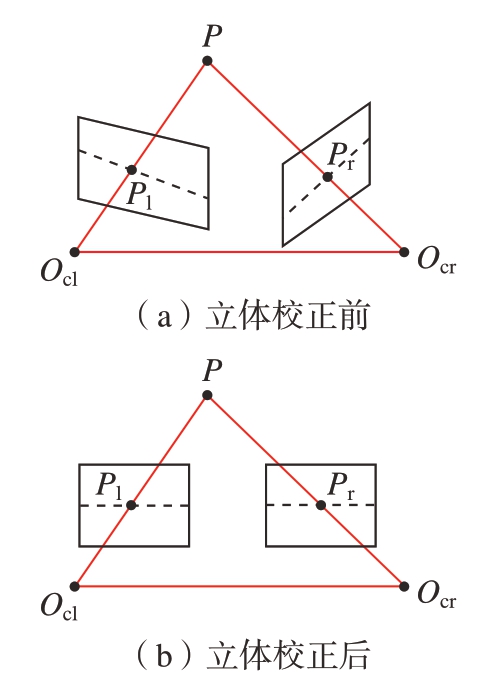
图2 立体校正前后的双目视觉成像对比
Fig.2 Comparison of visual imaging before and after binocular stereo correction
2 凹凸量测量原理
2.1 改进的格雷码解相位方法
如图3所示,工业投影仪向铆钉周围表面投射正弦相移条纹[11]与格雷码条纹[12],给铆钉区域表面赋予独特的相位信息。其中,正弦相移条纹用于计算包裹相位,格雷码用于将包裹相位展开成绝对相位。根据相位信息匹配铆钉区域表面任意一点在双目视觉图像中的同名特征点,从而克服了因蒙皮表面缺乏纹理特征带来的特征点匹配难题。

图3 结构光投影图像
Fig.3 Image of structured light projection
包裹相位由式 (6)计算得到。

式中,φw(x,y)为像素点(x,y)的包裹相位;Ii(x,y)为像素点(x,y)在第i步正弦条纹投影图像中的灰度;N为正弦相移条纹的步数,本文这里采用的是4步相移,即N=4。
计算出包裹相位后,再对格雷码图像解码,计算出相位阶数G1(x,y)。然后根据G1(x,y)对包裹相位进行展开,获得连续的绝对相位φ(x,y)。
解码时格雷码条纹的边缘容易发生跳变,将导致最终生成的点云存在条带状突变。为此,本文提出了一种改进的格雷码解相位方法,即对相位阶数图进行分区,在可能发生跳变的分区内根据邻域像素的相位阶数推测当前像素的相位阶数并进行修正。该方法的具体步骤如下。
(1)制作模板。
首先根据包裹相位图中的相位信息制作3个模板Mask1、Mask2和Mask3,这3个模板的灰度信息与包裹相位φw(x,y)之间的关系满足式(8)。
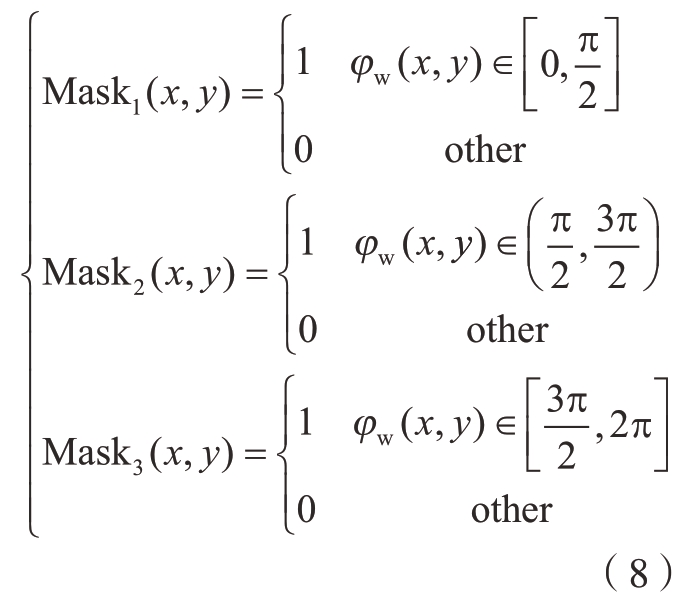
(2)掩模、修正。
利用上面的模板按式 (9)对相位阶数图进行掩模,将相位阶数图按照包裹相位的区间分为Ka、Kb、Kc 3个区域。
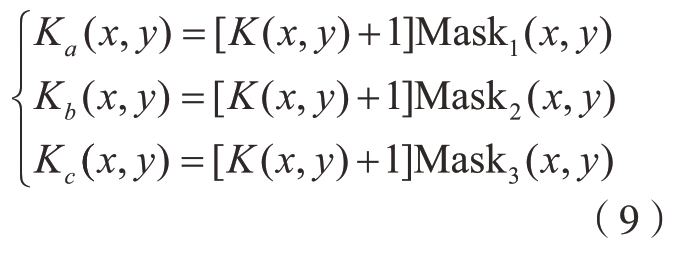
式中,将阶数K(x,y)加1是因为第1级相位台阶的阶数为0,加1后可与图像中灰度值为0的无条纹区域区分。
根据邻域相位阶数的分布特征对跳变区域 (Ka中的截断相位0右侧附近及Kc中的截断相位2π左侧附近)进行修正。根据其右侧邻域的相位阶数对Ka(x,y)进行修正 (式(10)),对Kc(x,y)则根据其左侧邻域的相位阶数进行修正 (式(11))。
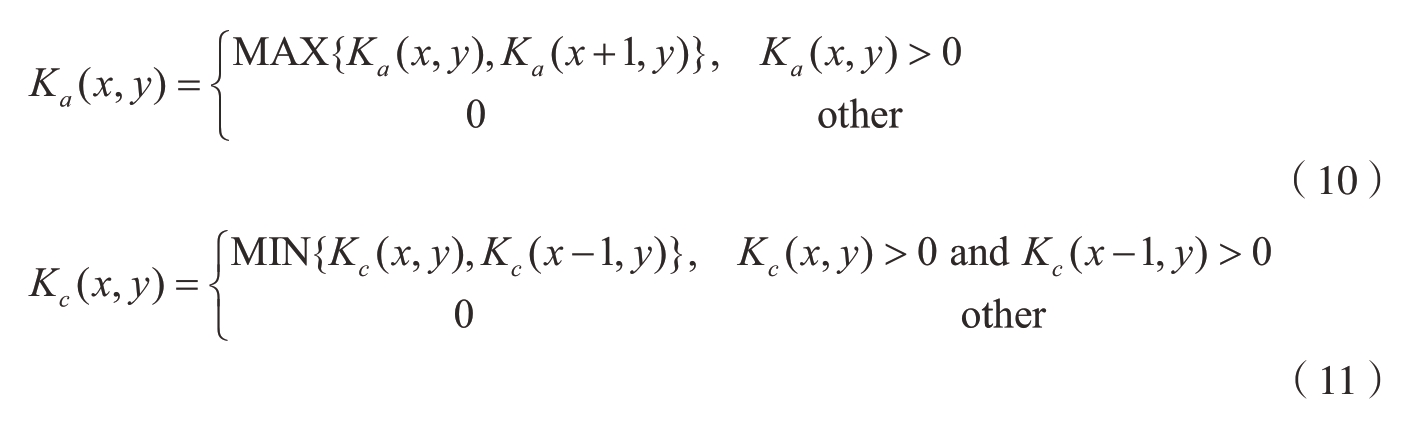
式中,Ka中的像素沿着同一图像高度从右往左修正;Kc中的像素沿着同一图像高度从左往右修正。
根据修正的阶数和包裹相位合成绝对相位图,绝对相位的表达式为
本方法的图像处理过程如图4所示。
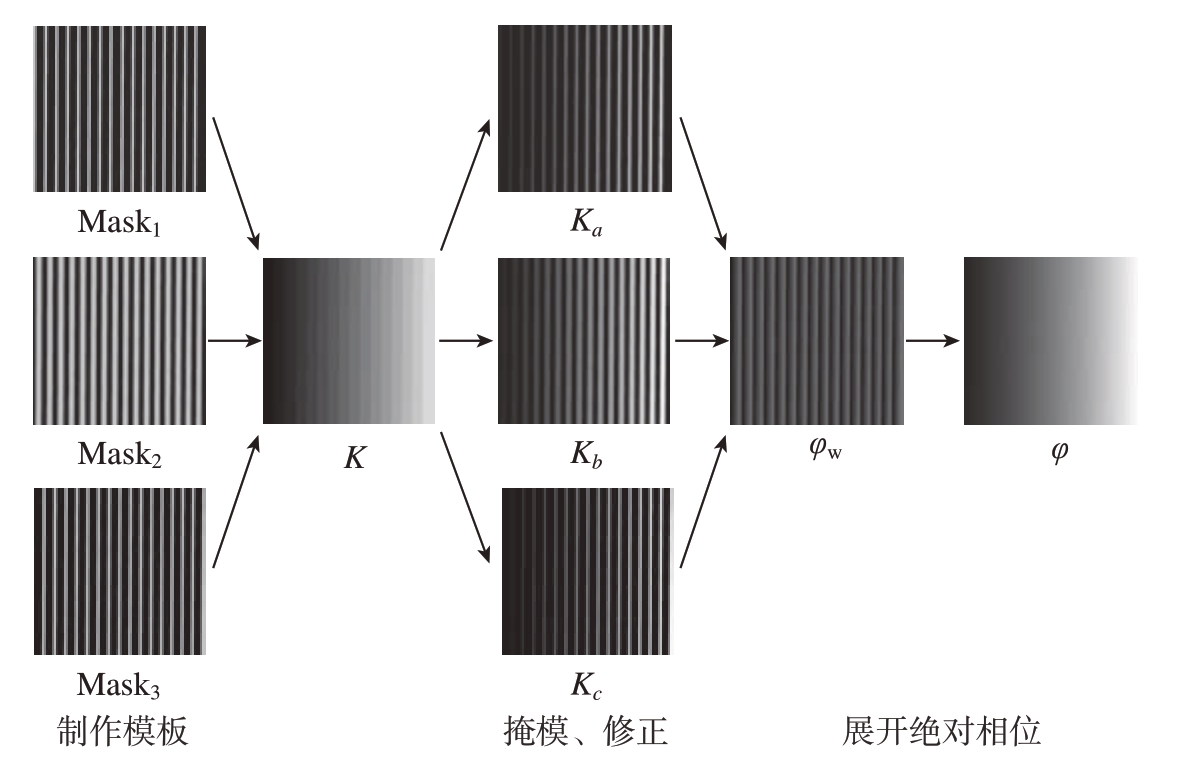
图4 基于邻域阶数推测的跳变相位修正示意图
Fig.4 Schematic diagram of hop phase correction based on neighborhood order estimation
图4给出了改进的格雷码解相位方法的图像处理过程,对同一铆接表面,将本文方法与常用的互补格雷码法[13]进行对比,在各自生成的绝对相位图中任取相同一行,其相位值如图5所示。
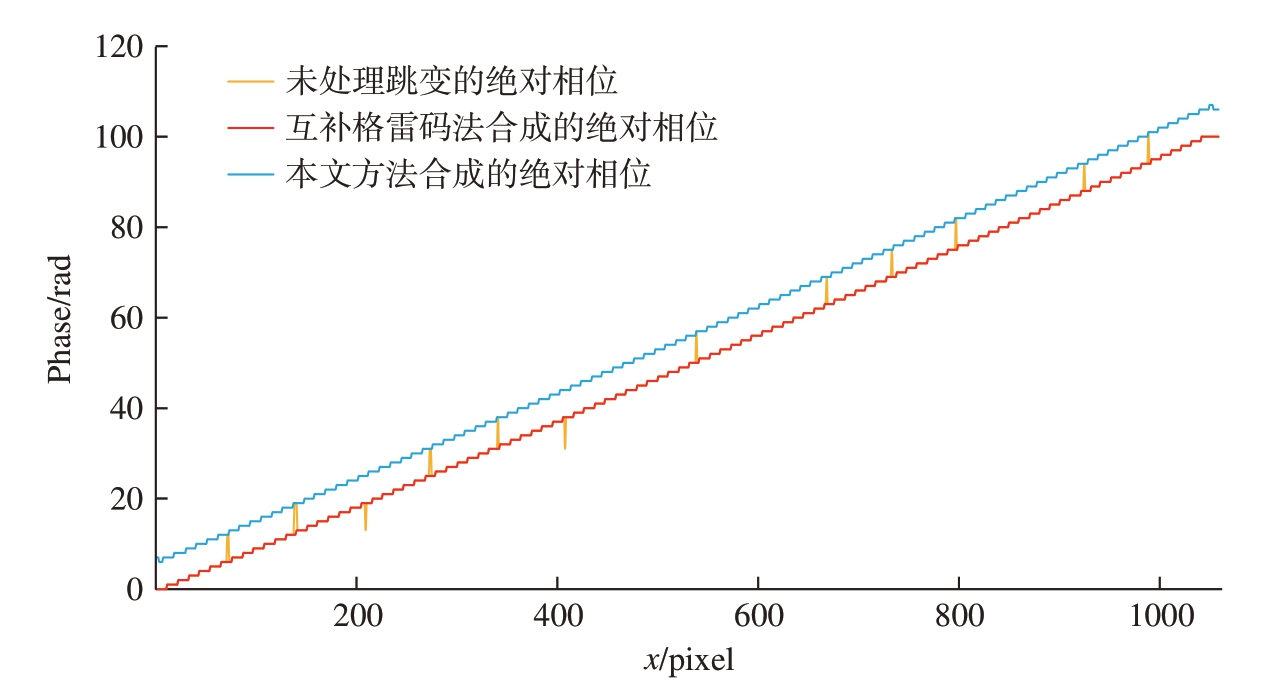
图5 本文方法与互补格雷码法生成的绝对相位对比
Fig.5 Comparison of absolute phase by this method and complementary Gray code method
由图5可以看出,本文方法可以准确修正跳变相位,获得较为理想的绝对相位拓展结果。本文方法合成的绝对相位比互补格雷码法合成的绝对相位整体增大了2π,这是第1级相位阶数加1造成的。由于左右相位图的相位值同时增加了2π,因此并不会影响双目匹配的结果。此外,对比试验还表明,在相同硬件条件下互补格雷码法解算相位用时5.2 s,而本文方法仅3.5 s,节省了约30%。
2.2 基于边缘特征的铆钉区域表面重建
根据解算的相位信息即可匹配双目图像中的特征点对,生成三维点云。由于相位解算是一个非常耗时的过程,为了提高效率,本文首先提取铆钉所在的感兴趣区域,后续只匹配感兴趣区域内的特征点对。
首先采用基于霍夫变换的圆检测算法[14]从图像中检测出铆钉,拟合出铆钉边缘轮廓并计算轮廓圆的圆心和半径;然后以轮廓圆为边界分割出铆钉钉头区域和邻近蒙皮区域,如图6所示。
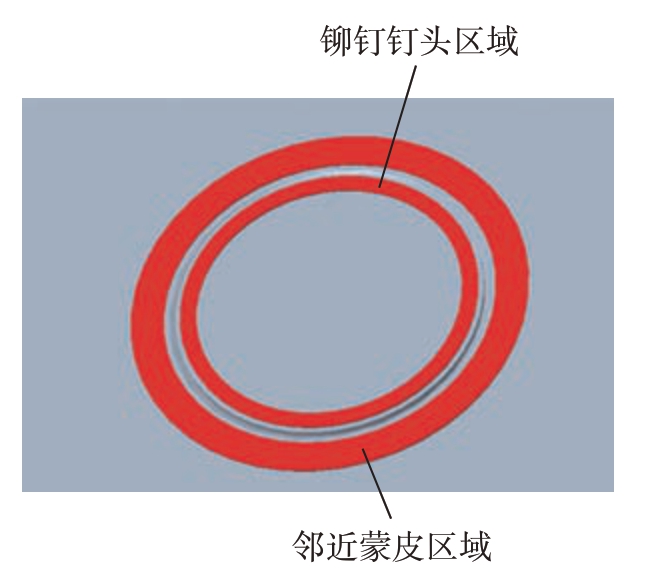
图6 铆钉感兴趣区域分割结果示意图
Fig.6 Schematic diagram of feature region segmentation
由于飞机体型非常庞大,例如波音787客机的机身宽度为5.75 m,因而表面蒙皮的曲率很小。而常用的航空沉头铆钉头部直径范围为ϕ5~16 mm,铆接区域的面积也很小,因此可将感兴趣区域内的蒙皮表面近似当作平面来处理。这样,铆钉凹凸量的最大值发生在铆钉钉头的边缘区域。
对于空间中的一点,其在双目视觉图像中的映射点的相位值理论上是相同的,并且图像校正后受到极线约束,因此可在同一图像高度上搜索相位值接近的点作为特征点对。图7给出了特征点匹配过程示意图,以左图中的待匹配像素及其8邻域像素设置左匹配框,以右图中的待匹配像素及其8邻域像素设置右匹配框,通过匹配框计算左右像素的相似代价,即
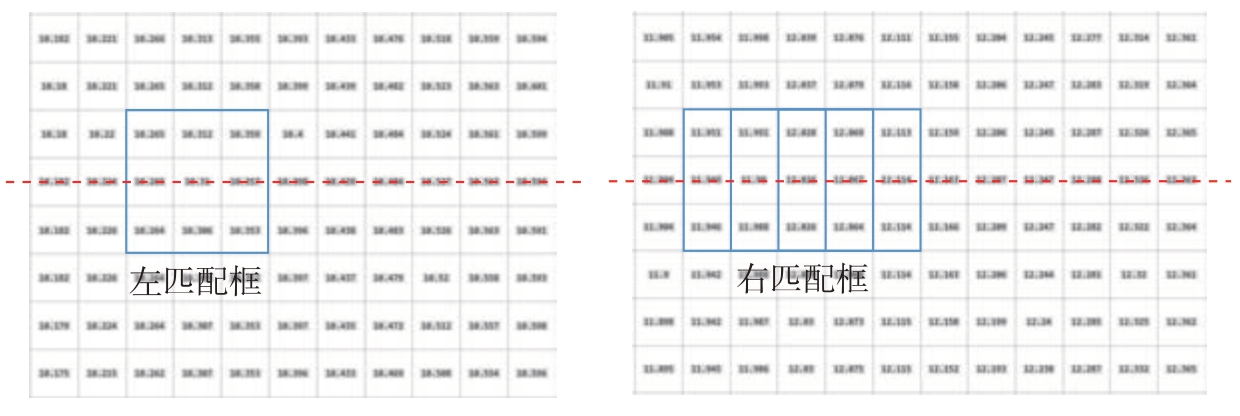
图7 特征点匹配过程示意图
Fig.7 Schematic diagram of corresponding points matching

式中,(xl,yl)、(xr,yr)分别为图7左、右两图中待匹配像素的坐标;R为相似代价;I为相位值。相似代价值越小说明相似程度越高。
图8是特征点匹配流程图,详细匹配步骤如下:
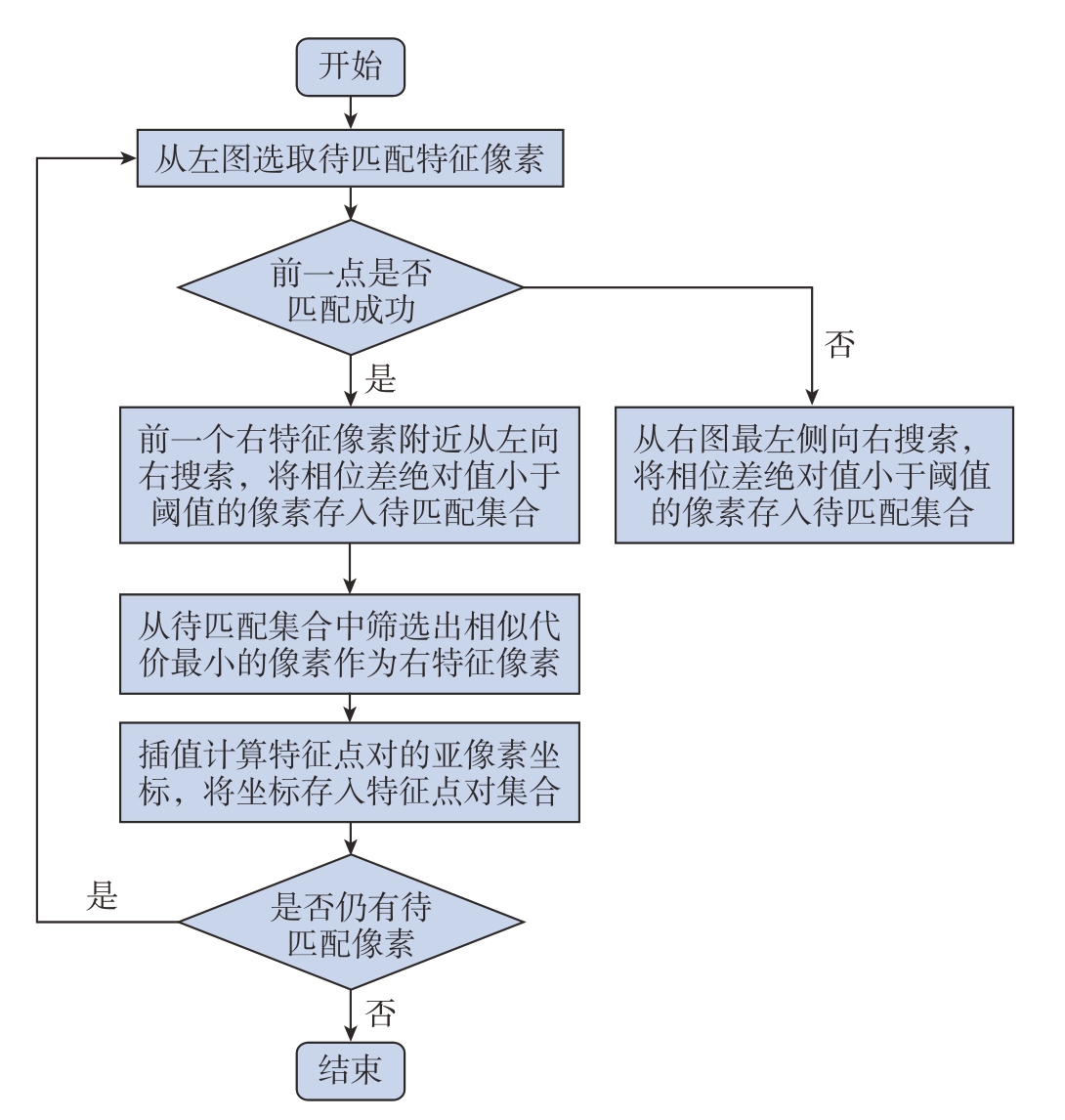
图8 特征点匹配流程图
Fig.8 Flow chart of corresponding points matching
(1)在右相位图中与左相位图特征像素纵坐标相同的一行,从左往右依次遍历每个像素,计算每个像素与左特征像素的相位值差的绝对值ΔI,并设置阈值I0,将 ΔI≤I0的像素点放入待匹配集合;
(2)将待匹配集合中的像素依次取出,通过式 (13)计算该像素与左特征像素的相似代价,筛选出相似代价最小的像素作为右特征像素;
(3)以右特征像素为中心,选取左右两边各两个像素进行3次样条曲线插值,计算出右特征点的亚像素坐标,将坐标存入特征点对集合;
(4)继续匹配下一个特征点,若上一个点匹配成功,从上一个点的横坐标附近开始匹配,若上一个点匹配失败,则仍然从同一行最左端开始向右搜索。
获得左右相机图像中匹配特征点对的集合后,结合相机标定得到的重投影矩阵Q,由式(14)计算特征点对空间点云的三维坐标。
式中,(x,y)为左相机图像中的特征点像素坐标;dis(x,y)为特征点对的视差,即左特征点与右特征点的横坐标之差; (Xw,Yw,Zw)为特征点对应的空间点的三维坐标。
重建后的铆钉区域表面点云如图9所示,本文提出的重建算法只对铆钉区域表面进行重建,与对整个表面进行无差别重建的常规方法相比,本算法大幅减少了无关区域的数据计算量,使检测效率得到了显著提高。

图9 铆钉区域表面点云
Fig.9 Surface point cloud of rivet area
2.3 基于RANSAC的铆钉凹凸量计算
实际测量获得的点云数据中总会存在一定数量的噪声点,这些噪声点的坐标误差大,对测量结果产生较大影响。因此,如图10所示,这里提出了一种基于RANSAC的平面拟合算法来剔除噪声点,具体步骤如下:
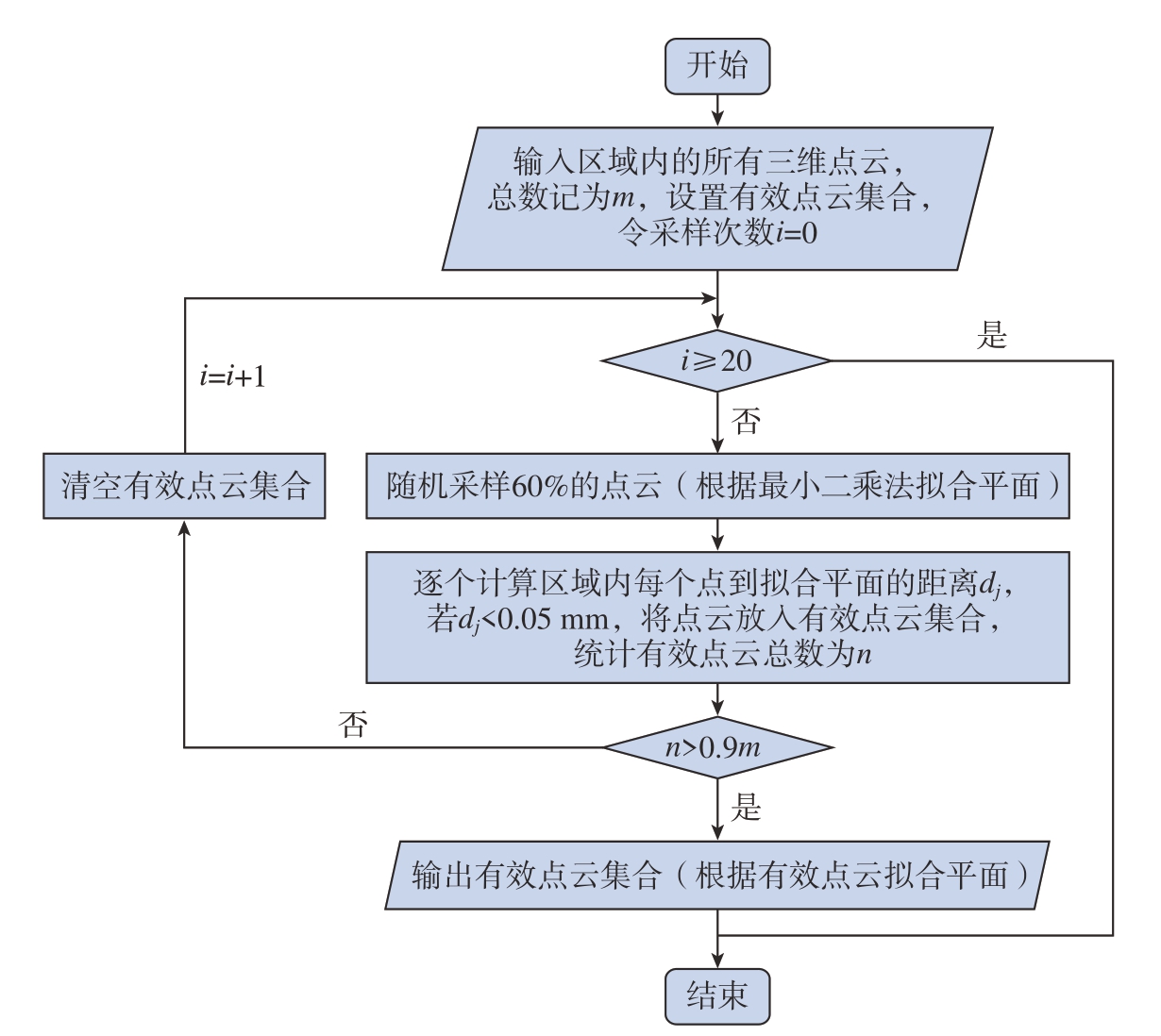
图10 基于RANSAC的噪声点剔除算法流程图
Fig.10 Flow chart of noise point removal based on RANSAC
(1)在点云数据中随机抽取占样本总量60%的点,利用这些点拟合最小二乘平面;
(2)计算点云中每个点到拟合平面的距离,将距离小于设定阈值的点放入有效点云集合;
(3)若有效点云集合的规模达到样本总量的90%,则输出有效点云集合,转入下一步;否则重复步骤(1)~(3),直到满足条件或者迭代达到20次;
(4)利用有效点云集合中的点云数据重新拟合最小二乘平面。
剔除噪声点后的点云如图11所示,通过上述算法分别剔除铆钉头平面点云和附近蒙皮表面点云中的噪点后,即可根据保留的有效点云计算铆钉的凹凸量。
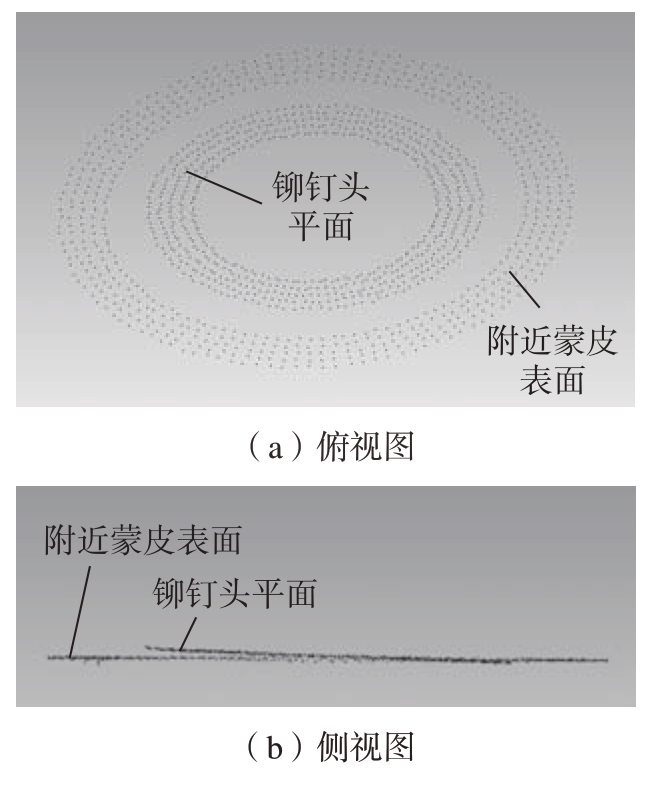
图11 剔除噪声点后的点云数据
Fig.11 Point cloud data after removing noise points
由图11(b)可以看出,铆钉铆接时钉头平面与蒙皮表面不一定平行,可能存在较大倾斜。因此,铆钉钉头平面上的点到蒙皮表面的距离是变化的,基于这一特征,本文在钉头平面区域内设置了一个滑动窗口。如图12所示,通过滑动窗口遍历整个钉头平面,每次只计算滑动窗口内的点云到蒙皮表面拟合平面的距离均值,从而获得钉头平面到蒙皮表面距离的变化范围。最后将距离的极限值与设定的允许值进行比较,即可判断铆钉凹凸量是否合格。
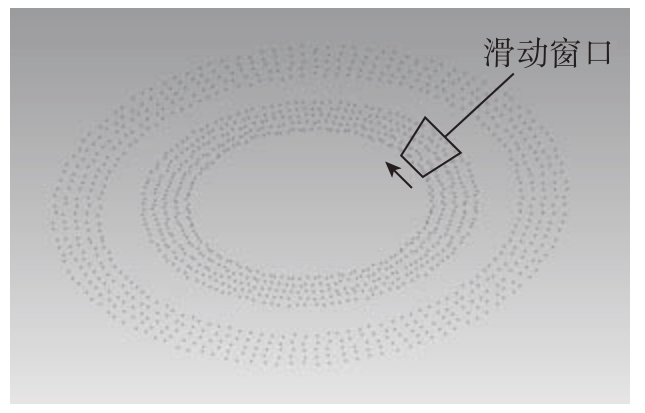
图12 滑动窗口示意图
Fig.12 Schematic diagram of sliding window
3 试验与分析
3.1 表面重建精度试验
为了测试重建的三维点云精度,对厚度分别为1.010 mm、1.020 mm、1.030 mm和1.500 mm的精密量块(尺寸偏差±0.12 μm)进行测量试验。首先将待测量块按照图13所示方式叠置,然后采集量块上表面的结构光投影图像,并根据图像重建出量块上表面的三维形貌。

图13 叠放在一起的量块
Fig.13 Gauge blocks stacked together
通过点云处理软件提取出图13所示的A、B、C 3个区域的点云数据,结果如图14所示。
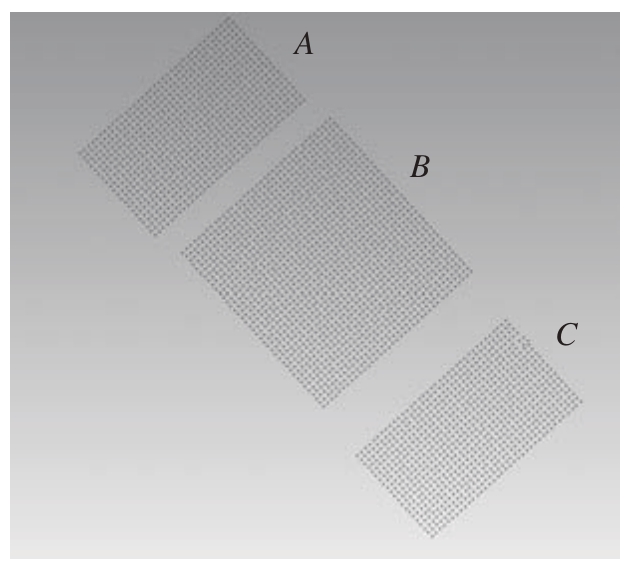
图14 量块点云
Fig.14 Point cloud of gauge blocks
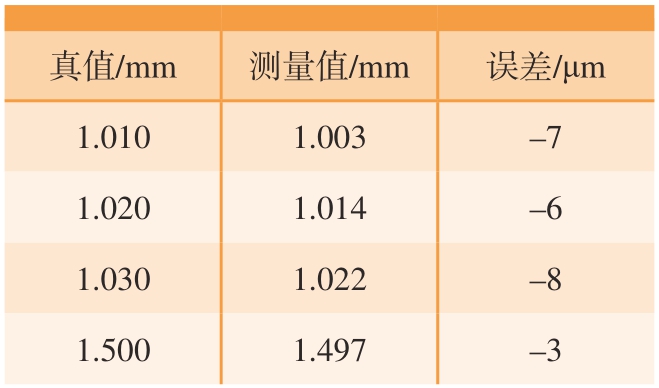
通过RANSAC拟合算法对A区与C区的点云进行拟合,得到下方量块表面的平面方程。然后再通过RANSAC方法剔除B区点云中的粗大误差点,并计算出B区中保留下来的有效点到下方量块表面的距离均值,即为量块的厚度值。如表1所示,对4种不同厚度的量块分别进行测量,测量误差均在10 μm以内,说明上述表面重建算法达到了较高的精度。
表1 量块厚度测量结果
Table 1 Measurement results of gauge block thickness
真值/mm测量值/mm误差/μm 1.0101.003–7 1.0201.014–6 1.0301.022–8 1.5001.497–3
3.2 铆钉凹凸量测量试验
如图15所示,为了进一步验证测量装置对铆钉凹凸量的测量精度和稳定性,本文设计定制了与飞机蒙皮铆接表面特征相似的凹凸量标准件,标准件上有10个高度各不相同的圆柱形凹/凸台。

图15 凹凸量标准件
Fig.15 Standard part of flatness
考虑到实际加工的标准件尺寸存在误差,本文使用图16所示测量精度±5 μm的3D轮廓扫描仪测出凸/凹台的实际高度值作为相对真值,然后使用本测量系统对标准件进行测量,每个凸/凹台重复测量10次,测量结果如表2所示。
表2 标准件凹凸量测量结果
Table 2 Measurement results of flatness of the standard parts
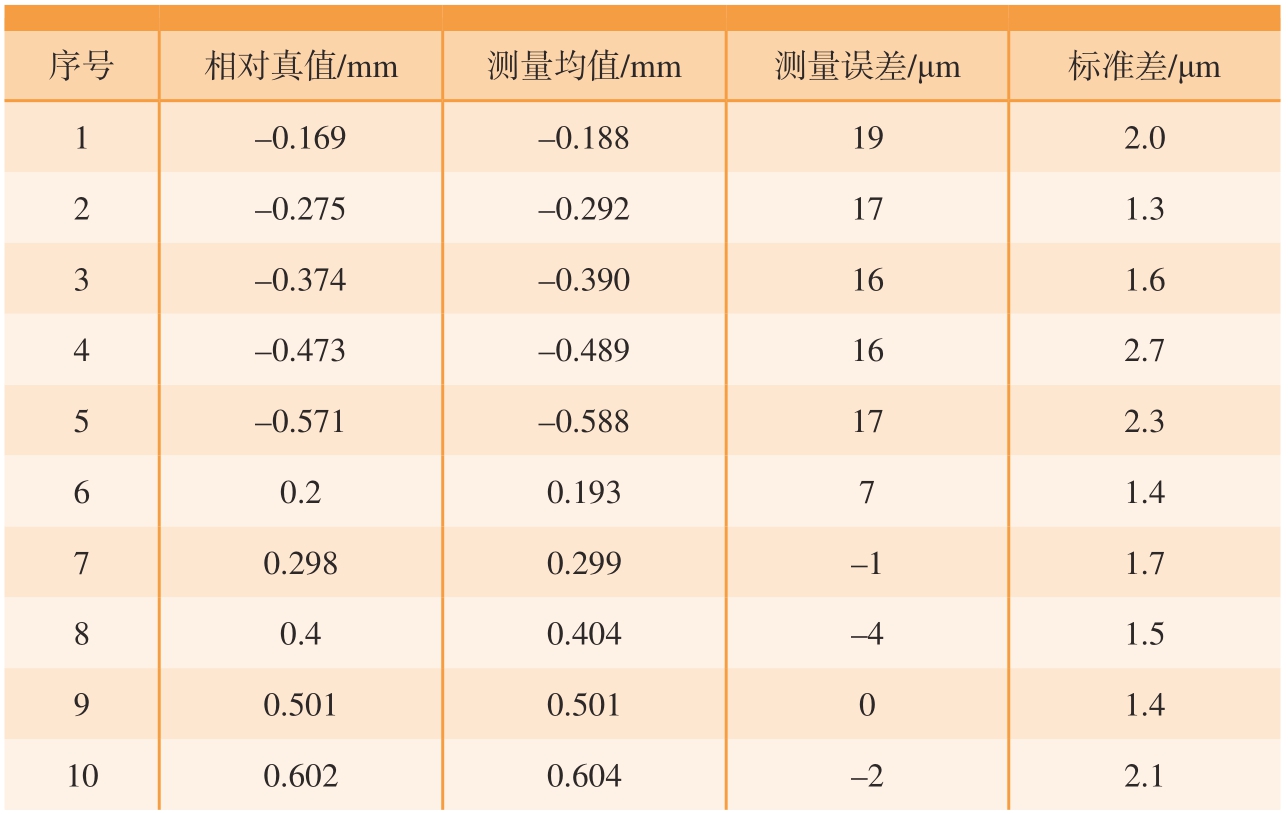
序号相对真值/mm测量均值/mm测量误差/μm标准差/μm 1–0.169–0.188192.0 2–0.275–0.292171.3 3–0.374–0.390161.6 4–0.473–0.489162.7 5–0.571–0.588172.3 6 0.20.19371.4 7 0.2980.299–11.7 8 0.40.404–41.5 9 0.5010.50101.4 100.6020.604–22.1

图16 3D轮廓扫描仪
Fig.16 3D profile scanner
由表2中的测量结果可知,本系统的测量误差在±20 μm以内,重复测量的标准差在3 μm以内。并且单个凸/凹台的平均测量时长约2.2 s。本系统的测量精度和测量效率均可满足航空制造现场的应用要求。
4 结论
(1)提出了一种基于结构光的铆钉凹凸量双目视觉检测方法。对常规格雷码解相位方法进行改进,解决了条纹边缘存在跳变误差的问题,相比传统互补格雷码法效率更高。通过基于铆钉边缘的特征区域提取方法,缩小了型面重建的范围,提高了测量算法的效率。研究了一种基于RANSAC的铆钉凹凸量计算方法,提高了测量结果的稳定性。
(2)构建了基于结构光的飞机铆钉凹凸量双目视觉检测系统,并完成了测量试验。试验结果表明,本系统测量误差小于±20 μm,重复测量标准差小于3 μm,单个铆钉测量时间约2.2 s,达到了较高的测量精度和检测效率。
[1] 国防科学技术工业委员会.飞机装配工艺 实心铆钉铆接后的检查及验收: HB/Z 223.15—2002[S].北京: 中国标准出版社,2002.
National Defense Science, Technology and Industry Committee.Aircraft assembling technology check and acceptance inspection for solid rivet after riveting: HB/Z 223.15—2002[S].Beijing: Standards Press of China, 2002.
[2] 蒋滔, 方辉, 董秀丽.飞机蒙皮铆接质量视觉检测系统的构建[J].航空制造技术,2017, 60(6): 88–91.
JIANG Tao, FANG Hui, DONG Xiuli.Construction of visual inspection system for riveting quality of aircraft skin[J].Aeronautical Manufacturing Technology, 2017, 60(6): 88–91.
[3] 王红涛, 焦悦, 冯连强, 等.一种飞机蒙皮铆钉阶差检测装置: CN212030420U[P].2020–11–27.
WANG Hongtao, JIAO Yue, FENG Lianqiang,et al.A detection device for the step difference of rivets on aircraft skin: CN212030420U[P].2020–11–27.
[4] 李红卫.基于三维点云的飞机机体结构铆钉轮廓提取算法研究[J].机电工程,2020, 37(6): 719–723.
LI Hongwei.Algorithm of rivet contour extraction for aircraft body structure based on 3D point cloud[J].Journal of Mechanical &Electrical Engineering, 2020, 37(6): 719–723.
[5] 王德重, 黄翔, 李泷杲, 等.基于双目多线结构光的铆钉齐平度测量方法[J].航空制造技术, 2021, 64(23/24): 57–65.
WANG Dezhong, HUANG Xiang, LI Shuanggao, et al.Measurement method of rivet flatness based on binocular multi-line structured light[J].Aeronautical Manufacturing Technology,2021, 64(23/24): 57–65.
[6] WILL P M, PENNINGTON K S.Grid coding: A preprocessing technique for robot and machine vision[J].Artificial Intelligence, 1971,2(3–4): 319–329.
[7] ZHANG Z.Flexible camera calibration by viewing a plane from unknown orientation[C]//Proceedings of the Seventh IEEE International Conference on Computer Vision.New York: IEEE Computer Society, 1999.
[8] 王笛.基于双目立体匹配的三维视觉方法研究[D].西安: 西安理工大学, 2021.
WANG Di.Research on 3D vision method based on binocular stereo matching[D].Xi’an:Xi’an University of Technology, 2021.
[9] 武紫凝.基于结构光的双目视觉三维测量技术研究与应用[D].成都: 电子科技大学, 2021.
WU Zining.Research and application of binocular vision three-dimensional measurement technology based on structured light[D].Chengdu:University of Electronic Science and Technology of China, 2021.
[10] 任继昌, 杨晓东.双目视觉系统的立体标定与校正[J].导航与控制, 2012, 11(4):74–76, 56.
REN Jichang, YANG Xiaodong.Stereo calibration and rectification of binocular vision system[J].Navigation and Control, 2012, 11(4):74–76, 56
[11] CHEN S L, XIA R B, ZHAO J B,et al.Analysis and reduction of phase errors caused by nonuniform surface reflectivity in a phase-shifting measurement system[J].Optical Engineering, 2017, 56(3): 033102.
[12] 侯风芝.格雷码结合相移的编码结构光三维重建技术研究[D].西安: 西安电子科技大学, 2011.
HOU Fengzhi.Research on 3D reconstruction technology of coded structured light based on Gray code and phase shift[D].Xi’an:Xidian University, 2011.
[13] 孙学真, 苏显渝, 邹小平.基于互补型光栅编码的相位展开[J].光学学报, 2008,28(10): 1947–1951.
SUN Xuezhen, SU Xianyu, ZOU Xiaoping.Phase-unwrapping based on complementary structured light binary code[J].Acta Optica Sinica,2008, 28(10): 1947–1951.
[14] 肖亮.编码结构光投影双目视觉三维测量技术研究[D].合肥: 合肥工业大学,2019.
XIAO Liang.Research on binocular vision three-dimensional measurement technology of coded structured light projection[D].Hefei:Hefei University of Technology, 2019.
