随着我国工业技术的发展，国防、航空、航天、汽车等诸多领域对机床加工精度的要求日益提高。机床的加工精度会受几何误差、热误差、切削力诱导误差等因素的综合影响。其中，几何误差是由机床零部件制造和装配不精确等因素造成的，在误差源中占有很大比例。由于几何误差项较多，逐项测量并补偿全部误差成本很高，有必要对其进行灵敏度分析[1]。从而降低补偿成本、提高效率，对优化机床加工精度具有重要意义。
近年来，数控机床几何误差灵敏度分析方法发展迅速。Cheng等[2]通过旋量理论对五轴机床空间误差进行了建模，并通过改进的Morris法对37项几何误差进行了全局灵敏度分析。Li等[3]基于多体系统理论构建了五轴机床误差源与刀具位姿误差之间的误差映射，通过定义局部灵敏度指数、全局灵敏度指数和全局灵敏度波动指数对机床误差进行了灵敏度分析。Zou等[4]基于蒙特卡洛法 （Monte Carlo simulation, MCS），求解Sobol灵敏度指数，量化了几何误差对加工精度的影响，并根据分析结果对关键几何误差元素进行调整和分布。Fu等[5]根据坐标系微分运动关系，建立了机床各轴的几何误差灵敏度矩阵，分析得出误差关键轴为A轴和X轴，并验证其正确性。郭世杰等[6]采用拉丁超立方法 （Latin hypercube sampling，LHS）在整个参数空间内抽样，利用Spearman系数进行几何误差相关性分析并辨识出影响机床精度的关键几何误差。王培桐等[7]采用截断傅里叶级数表征与位置有关的几何误差，将求解灵敏度指数转换为求取傅里叶幅值，该方法具有较好的鲁棒性。综上所述，目前机床的灵敏度分析方法主要有偏微分法、Morris法、MCS法、LHS法、傅里叶幅值法等，这些方法普遍样本需求量大且计算效率不高。
针对上述局限性，本文提出一种以多项式混沌展开 （Polynomial chaos expansion，PCE）为理论基础的全局灵敏度分析方法。将双转台五轴数控机床作为研究对象，运用旋量理论建立空间误差模型，构建几何误差的PCE模型，通过Sobol指数表征41项误差的关键程度。最后，与MCS法和LHS法进行对比，验证其正确性与高效性。
1 五轴数控机床空间误差建模
1.1 运动链拓扑描述
本文的研究对象为AC型双转台五轴数控机床，其主要结构及运动链拓扑如图1所示。其中，机床坐标系设于回转工作台的中心，即旋转轴轴线交点处。根据该机床运动链拓扑可知，旋转轴A、C彼此相邻并与床身构成工件运动链，平动轴X、Y、Z与床身构成刀具运动链。
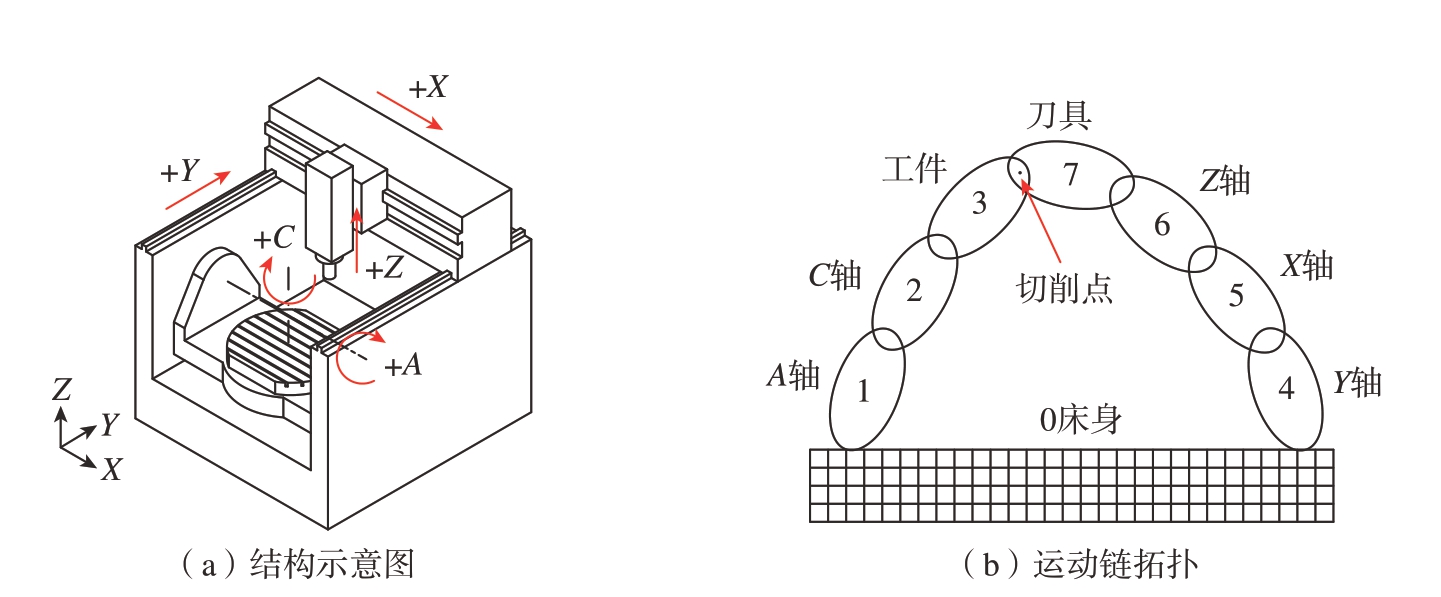
图1 双转台五轴数控机床结构示意图与运动链拓扑
Fig.1 Structure diagram and kinematic chain topology of double turntable five-axis CNC machine tool
1.2 几何误差描述
在几何误差综合作用下，刀具相对于工件的实际位姿与理想位姿间存在偏差。根据各几何误差与机床运动轴位置的相关性，可将其分为位置无关几何误差 （Position independent geometric error，PIGEs）和位置相关几何误差 （Position dependent geometric errors，PDGEs）。目前在国际学术界，针对旋转轴PIGEs有“绝对表示”和“相对表示”两种定义方法。由于“高”旋转轴的PIGEs会受“低”旋转轴运动的影响，绝对表示法对于双转台五轴机床并不适用。因此，本文采用相对表示法[8]，41项几何误差及其编号如表1所示。
表1 五轴数控机床几何误差及其编号
Table 1 Geometric errors and their numbering of five-axis CNC machine tool
运动轴几何误差项编号X轴δxx，δyx，δzx，εxx，εyx，εzx1，2，3，4，5，6 Y轴δxy，δyy，δzy，εxy，εyy，εzy7，8，9，10，11，12 Z轴δxz，δyz，δzz，εxz，εyz，εzz13，14，15，16，17，18 A轴δxa，δya，δza，εxa，εya，εza19，20，21，22，23，24 C轴δxc，δyc，δzc，εxc，εyc，εzc25，26，27，28，29，30 PDGEs PIGEs X/Y/Z轴Sxy，Syz，Sxz31，32，33 A/C轴δxAM，δyAM，δzAM，αAM，βAM，γAM，δyCA，βCA34，35，36，37，38，39，40，41
1.3 基于旋量理论的空间误差模型
根据旋量理论[9]，刚体的位姿变换运动可以由围绕空间某一直线的旋转运动以及沿该直线的平移运动合成。其运动学模型的基本单元是旋量运动eξ·θ，由旋量ξ和运动量θ构成。
对于旋转轴，旋量ξ可以表示为
式中，v为平动轴轴线方向的单位向量；ω为旋转轴轴线方向的单位向量。v =–ω×q，q为轴线上的任意一点。
旋转轴旋量运动的变换矩阵可以表示为
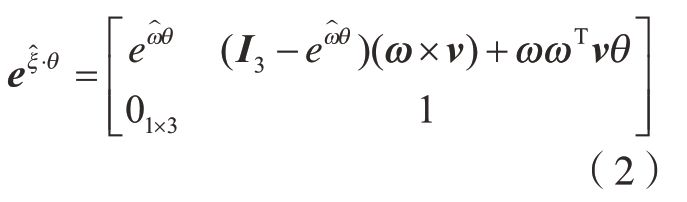
式中，
为3阶单位矩阵；^为叉乘算子；θ为旋转轴转动量。
对于平动轴，旋量ξ可以表示为
平动轴旋量运动的变换矩阵可以表示为
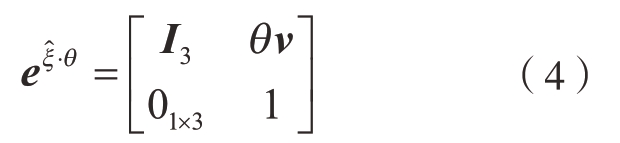
式中，θ为平动轴运动量。
结合图1描述的运动链拓扑，可得到刀具链位姿变换矩阵gbt（θ）和工件链位姿变换矩阵gbw（θ），即
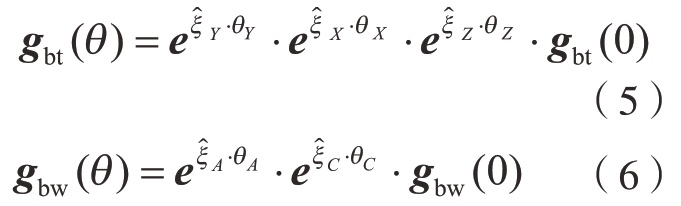
式中，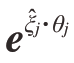
为j轴的变换矩阵；gbt（0）和gbw（0）分别为刀具和工件相对于机床坐标系的4×4初始变换矩阵。
根据式 （5）和 （6），可得到理想状况下刀具相对于工件的位姿变换矩阵
（θ），即
式中，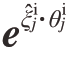
为理想状况下j轴的变换矩阵。
结合表1和式（7），可得到实际状况下刀具相对于工件的位姿变换矩阵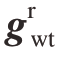
（θ），即
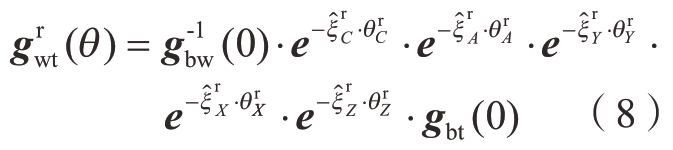
式中，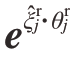
为实际状况下j轴的位姿变换矩阵，以A轴为例
式中，
为A轴PIGEs变换矩阵；
为A轴PDGEs变换矩阵。
由式 （7）和 （8）可得到五轴数控机床的位姿误差矩阵E，即
位姿误差矩阵中包含位置误差和姿态误差，各个方向的位置误差分量PX、PY、PZ为
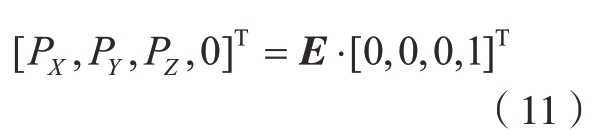
各个方向的姿态误差分量VX、VY、VZ为
2 基于PCE的全局灵敏度分析方法
2.1 多项式混沌展开模型
多项式混沌展开最早由Wiener[10]提出，用于研究Brown运动；Sudret[11]后续将PCE应用到灵敏度分析中。其基本原理是将含有N维随机输入变量的响应函数Y=M（x），用一组关于变量x的多项式混沌展开模型表示
式中，ψb（x）为正交的多项式基底，其最优类型取决于变量的分布函数[12]；yb为多项式基底对应的系数。
系数的求解是PCE方法的关键，一般利用最小二乘回归求解。
式中，A为回归矩阵，包含回归样本所对应的多项式基底；y为多项式系数构成的列向量。
在实际工程应用中，通常会对式（13）进行截断。当最高阶次为p阶时，PCE模型可近似为
式中，P为截断近似保留的多项式总项数，可由式 （16）确定。
不难看出，PCE方法的计算量会随着输入变量维数的增多呈阶乘增长，高维下存在“维数灾难”问题。该问题可通过对PCE模型进行稀疏化来解决，其思想是通过去除模型中对输出响应影响不大的正交多项式项来减少多项式系数的个数，从而降低计算量。根据这一思想，式 （14）可以转换为求解多项式系数向量中非零元素最少的优化问题。
式中，ε为允许容差。
直接求解式 （17）是一个NP–hard难题，为了以可接受的计算成本获得近似的最稀疏解，可采取一系列重构算法。其中，正交匹配追踪（Orthogonal matching pursuit，OMP）具有计算成本低、收敛速度快、适合交叉验证等优势，本文使用该方法实现多项式系数的快速求解。
2.2 基于OMP的多项式系数求解
正交匹配追踪由Pati等[13]提出，其工作原理是在A矩阵中检索与当前残差最相关的多项式基底，并将其添加到已有的索引集中，通过最小二乘法更新相应的多项式系数，不断迭代，直至残差降至指定的容差范围内，算法流程如图2所示。
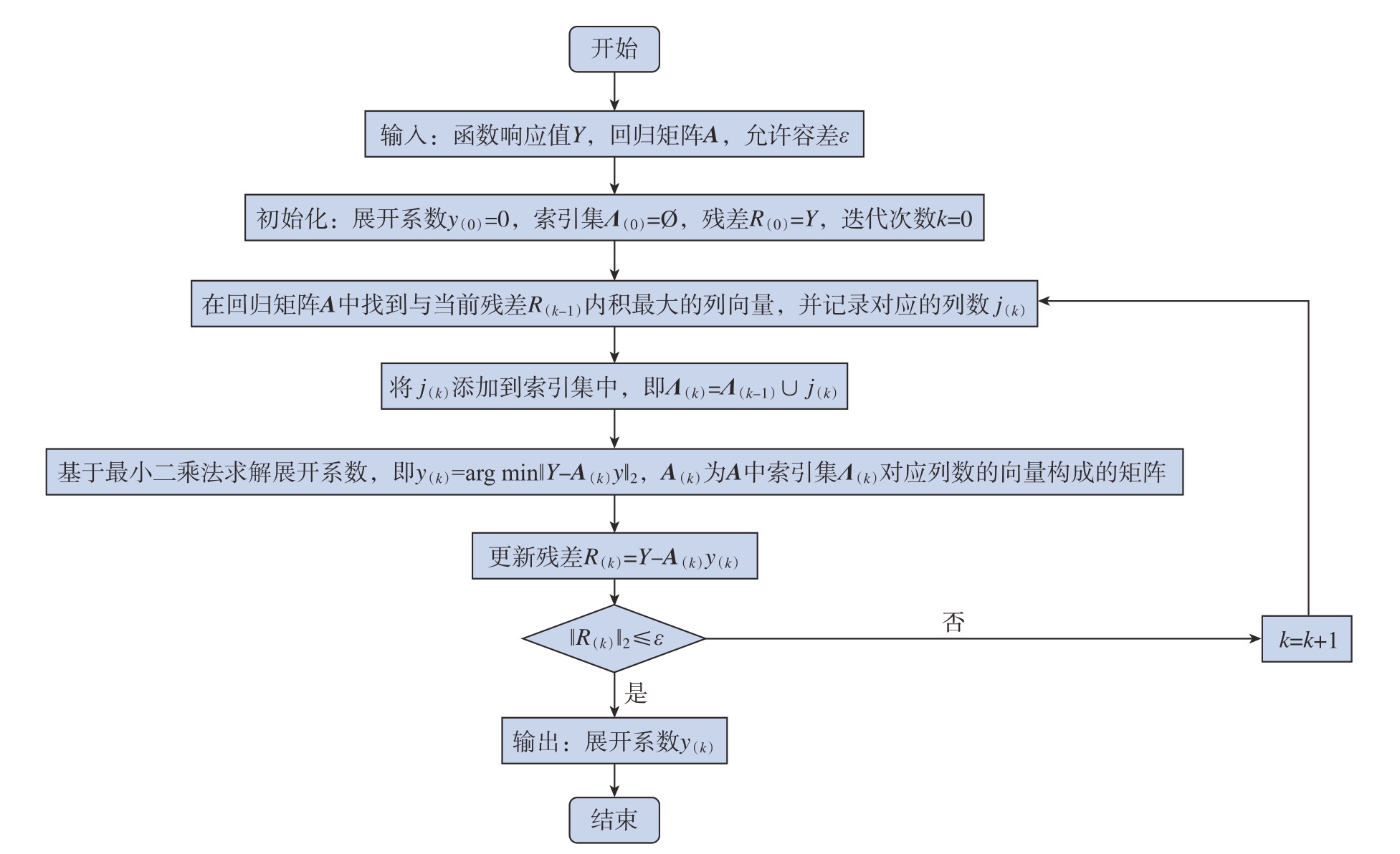
图2 OMP算法流程图
Fig.2 Flowchart of OMP algorithm
由于在每一个迭代步，OMP都寻找能使残差下降最快的多项式基底，因此能够快速求解多项式系数。
2.3 基于PCE的全局灵敏度指数
基于方差分解的Sobol灵敏度指数[14]因简单有效而得到了广泛应用，可通过多项式系数直接得到。根据该方法，可将含有N维随机输入变量的响应函数Y=M（x），唯一地分解成2N个子函数之和，即
式中，s=1，2，…，N；M0为0阶常数项；Mi（xi）为与xi有关的1阶子函数；
为与
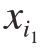和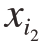
有关的2阶子函数；
为与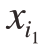
，…，
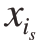有关的s阶子函数；M1，2，…，N（x1，…，xN）为与所有输入变量有关的N阶子函数。
对式 （18）等式两边取方差，可得
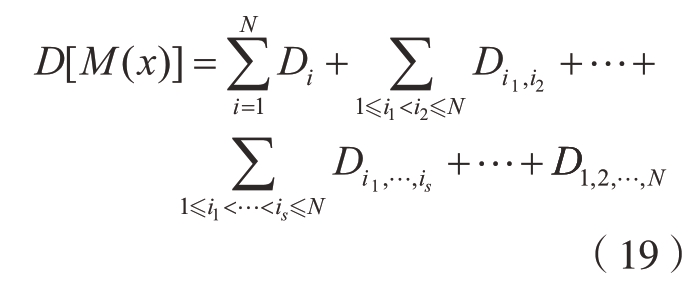
可以看出，子函数的方差表征了不同单个输入及其相互作用对输出响应方差的贡献。因此，变量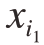
，…，
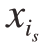的Sobol灵敏度指数被定义为
再对截断后的PCE模型 （式（15））进行改写，可得
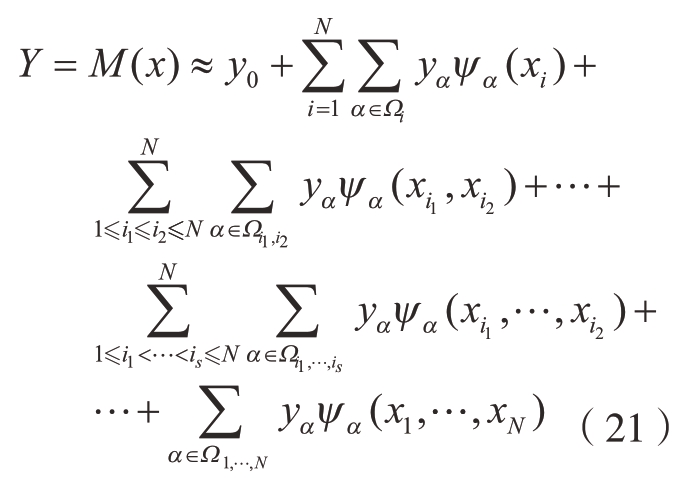
式中，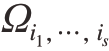
={α∈（α1，α2，…，αN）|αu=0 u （i1，…，is），u=1，…，N}为包含α中所有非0元素的集合。
对比式 （18）和 （21）可知，Sobol分解式中变量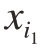
，…，
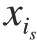的s阶子函数就是PCE模型中含相同变量的s阶正交多项式之和，即
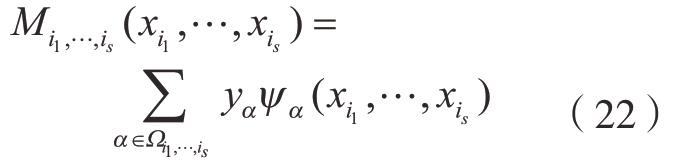
由此，结合式 （20）和 （22）就可得到基于PCE的Sobol灵敏度指数，即
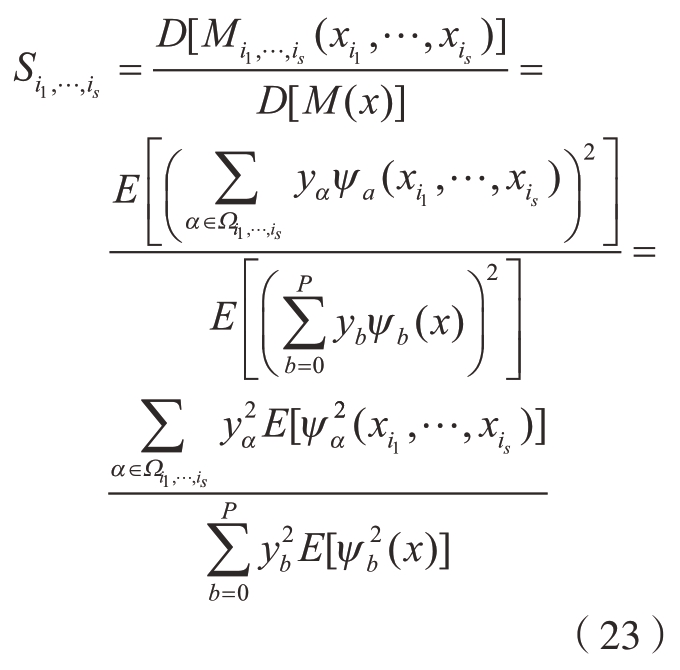
3 五轴数控机床几何误差全局灵敏度分析实例
3.1 几何误差测量试验
为获得几何误差的概率分布，基于四川普什宁江机床有限公司生产的VMC80IV型五轴数控机床搭建试验平台，如图3所示。选择Renishaw XL–80激光干涉仪作为测量仪器，运用“15线法[15]”测量机床平动轴几何误差；再利用Renishaw QC20–W球杆仪，依据Tsutsumi等[16]提出的策略测量机床旋转轴几何误差，重复进行多次试验。期间，测试环境保持 （20±0.5） ℃恒温，以抑制机床热致空间误差对测试结果的影响。辨识并统计测量数据，可以得到各个误差的近似概率分布。结果表明，41项几何误差服从正态分布，对误差范围进行合理缩放后，取位置误差范围为±15 μm，角度误差范围为±10″。
图3 几何误差测量试验平台
Fig.3 Experimental platform of geometric errors measurement
3.2 基于PCE的全局灵敏度分析
在灵敏度分析前，首先要确定几何误差采样测试点。VMC80IV型机床X轴、Y轴和Z轴的行程分别为±400 mm、±425 mm和±275 mm，C轴的回转范围为0～360°，A轴的摆角范围为–130°～+130°。将机床的工作空间沿对角线划分，并在每条对角线上等距取5个点作为测试点，如图4所示。这样选取的测试点适用于全尺寸的被加工件，且接近实际工作空间附近，位于机床常用的坐标范围内。越接近工作空间中心，越为常加工区域，测试点越密集，与实际加工的逻辑相符，在这些点进行灵敏度分析将得到更有意义的结果。
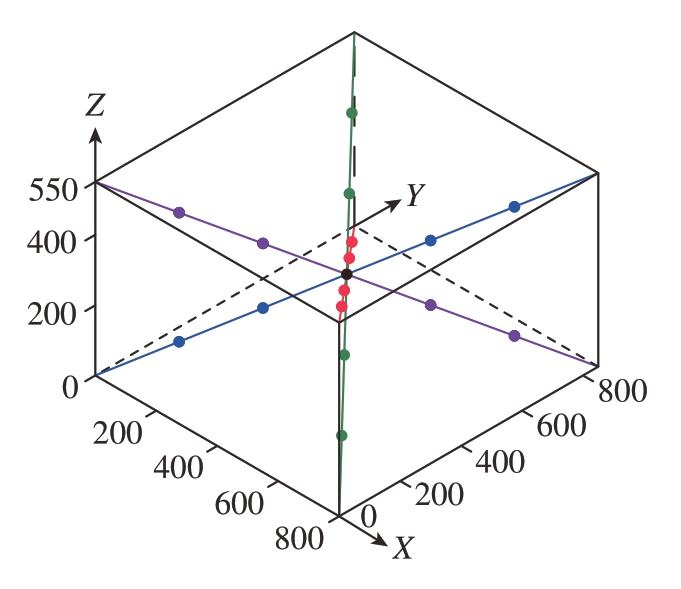
图4 机床空间测试点分布（mm）
Fig.4 Spatial test points distribution of machine tool (mm)
借助UQLab[17]编程构建几何误差的PCE模型。多项式基底选择Hermite正交多项式，根据Cameron-Martin理论[18]，其对服从正态分布的输入变量具有指数收敛速度。模型的最高阶次和样本量可通过收敛性测试确定，经过测试，取阶次p =3，样本量m=1×103。采用OMP求解多项式系数，再通过Sobol指数表征几何误差对各方向位姿误差分量的影响程度。由于几何误差相对较小，且误差项之间具有低耦合性，一阶灵敏度与总灵敏度结果相差不大。因此，本文仅讨论总灵敏度指数，归一化结果如图5和6所示。
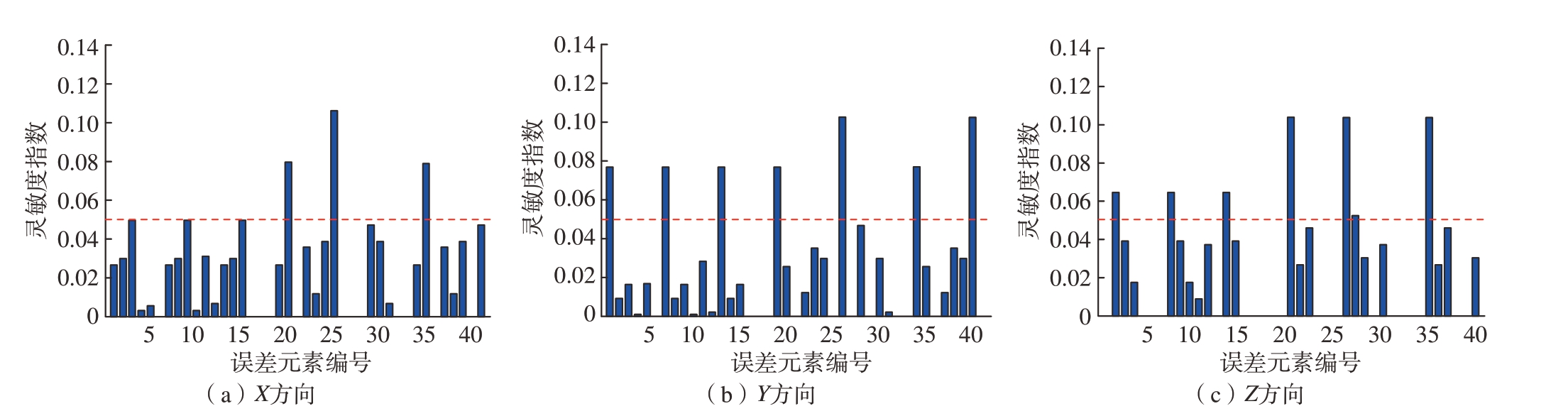
图5 位置误差全局灵敏度分析结果
Fig.5 Global sensitivity analysis results of position error
将灵敏度指数大于0.05（大约是平均灵敏度指数的两倍）的误差项作为关键几何误差。根据图5可知，影响X方向位置误差的关键几何误差为δxc、δya、δyAM；对Y方向位置误差影响最大的为δyc和δyCA，此外，δxx、δxy、δxz、δxa、δxAM也有较大影响；Z方向上影响最大的为δza、δzc、δzAM，此外，δyx、δyy、δyz、εxc的影响也不容忽视。从分析结果中不难发现，位置误差的影响要明显超过角度误差，而旋转轴的影响要超过平动轴，PIGEs和PDGEs的影响差别不大。
根据图6可知，影响X方向姿态误差最关键的几何误差为εyx、εyy、εyz、Sxz，此外，εza、εzc、γAM、εyc、βCA也有较大影响；Y方向上的关键几何误差除εyc和βCA外，与X方向完全相同，且影响权重更高；对Z方向影响最大的几何误差为εxx、εxy、εxz、εxa、Syz、αAM，同时εyc和βCA也不容忽视。可以看出，对姿态误差影响较大的全部都是角度误差，旋转轴和平动轴的影响差别不大。
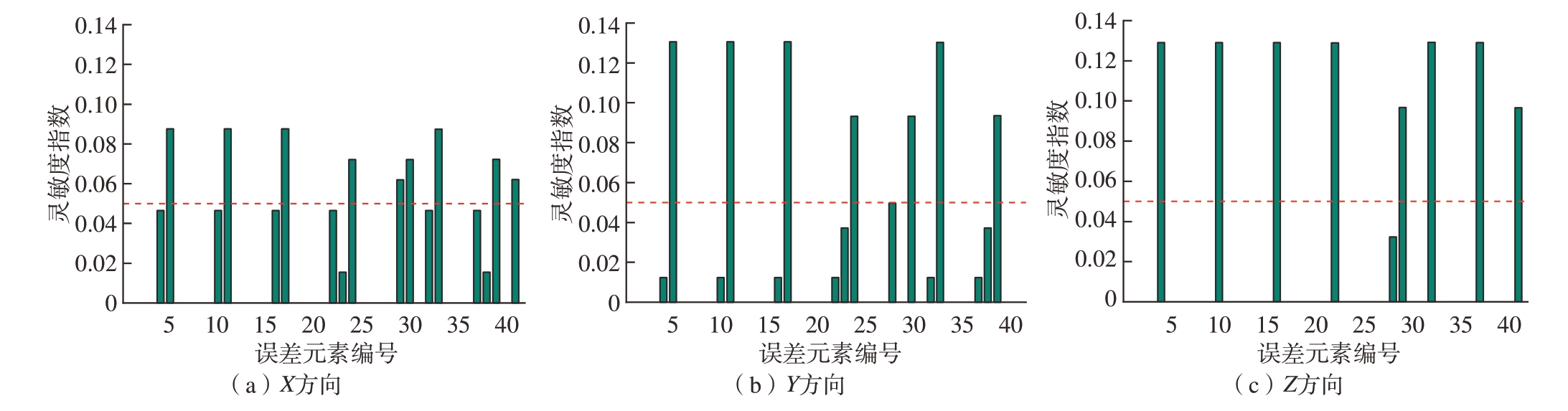
图6 姿态误差全局灵敏度分析结果
Fig.6 Global sensitivity analysis results of attitude error
3.3 灵敏度分析方法对比与验证
为验证本文方法的正确性与高效性，与MCS法和LHS法进行对比。这两种方法是目前灵敏度分析的常用方法，且都需要大规模采样，以样本量为1×105的结果作为验证标准。3种方法所得的关键几何误差及其灵敏度指数如表2所示。不难看出，3种方法得到的关键误差完全相同，且灵敏度指数接近，最大相对误差不超过5%。因此，本文方法的正确性得到验证。
表2 关键几何误差灵敏度指数对比
Table 2 Comparison of sensitivity index for key geometric errors
误差方向位置误差姿态误差关键几何误差PCE法灵敏度指数MCS法灵敏度指数LHS法灵敏度指数关键几何误差PCE法灵敏度指数MCS法灵敏度指数LHS法灵敏度指数εyx0.08760.08610.0889——εyy0.08760.08760.0882————εyz0.08760.09090.0903 δya0.07970.08020.0771εza0.07210.0720.0701 δxc0.10620.10590.1060εyc0.06190.06040.0618 δyAM0.07890.07950.0805εzc0.07210.07330.0716——Sxz0.08740.08560.0856——γAM0.07230.07320.0734————X方向————βCA0.06200.06360.0612 δxx0.07690.07930.0758εyx0.13050.12880.1299 δxy0.07690.08000.0757εyy0.13050.13080.1300 δxz0.07690.07660.0761εyz0.13050.13500.1292 δxa0.07680.07790.0755εza0.09330.09310.0934 δyc0.10260.10410.1046εzc0.09330.09470.0930 δxAM0.07700.07430.0782Sxz0.13020.12750.1285 δyCA0.10250.10110.1031γAM0.09350.09460.0929 Y方向δyx0.06460.06510.0633εxx0.12900.12840.1280 δyy0.06460.06570.0629εxy0.12900.12790.1278 δyz0.06460.06570.0631εxz0.12900.13120.1285 δza0.10390.10320.1025εxa0.12890.12490.1266 δzc0.10380.10480.1034Syz0.09680.09490.0972 εxc0.05240.04960.0547εyc0.12920.12700.1280 δzAM0.10370.10380.1031αAM0.12910.13620.1354——βCA0.09660.09860.0971 Z方向
此外，对3种方法分别进行收敛性能测试。以X、Y、Z方向上的最关键的几何误差δxc、δyc、δza为例，测试在不同采样规模下的收敛过程，并用波动率R来量化灵敏度指数的波动状况，即
式中，l为测试样本量。
以R≤3%作为收敛标准。根据图7所示结果，误差δxc在PCE法采样规模为1×103时达到收敛标准；而MCS法和LHS法在采样规模为1×103时波动率仍在10%以上，在1×105时才达到收敛标准。误差δyc和δza测试结果也相同，这意味着本文方法具有更高的收敛性能，且在样本量减小两个数量级的情况下达到相同的计算精度。
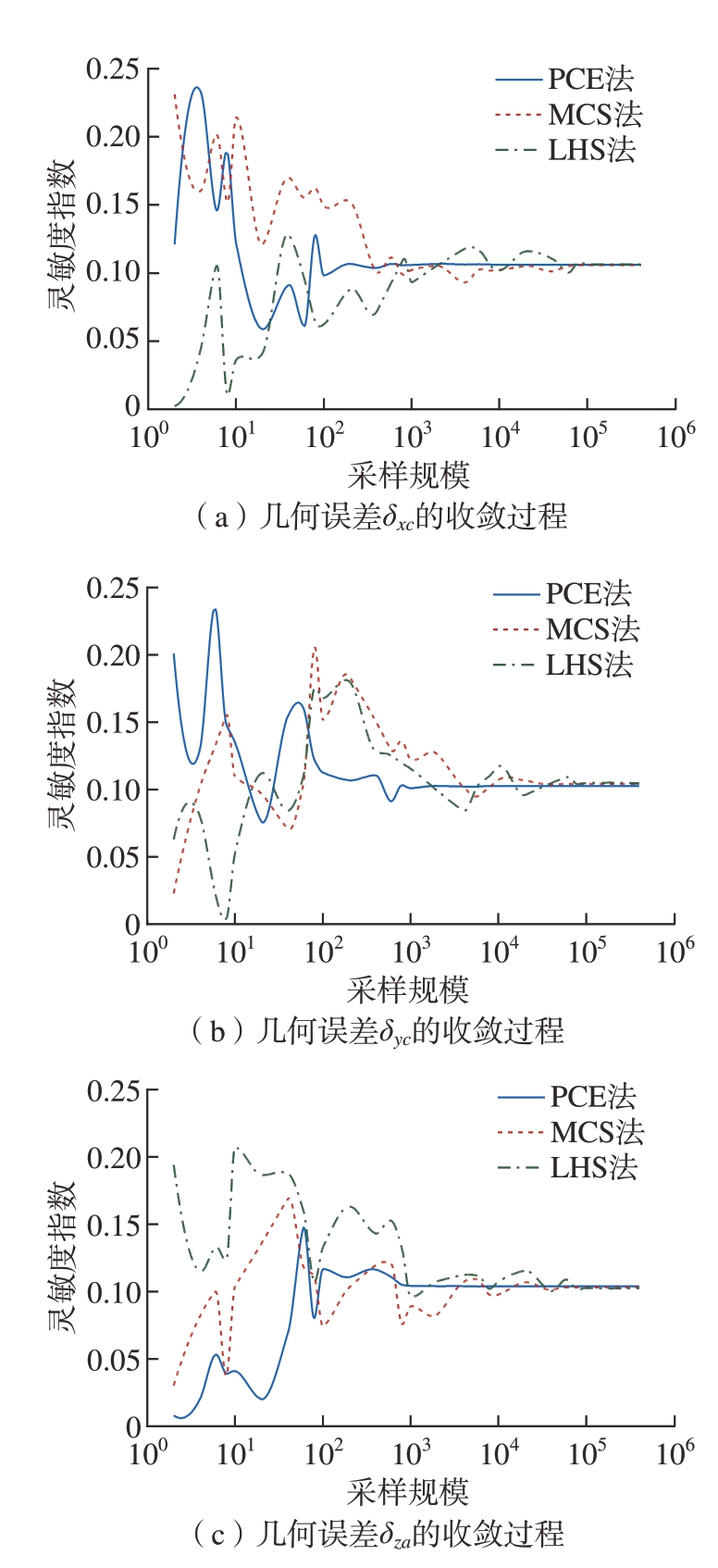
图7 收敛性能测试结果对比
Fig.7 Comparison of convergence performance test results
表3还对比了3种方法的计算时间。结果显示，本文方法在不降低计算精度的前提下，计算时间相对MCS法减少了96.8%，相对LHS法减少了98.1%。此外，本文方法中大部分时间用于PCE建模，只要模型构建完成，便可快速求解灵敏度指数。随着机床日益复杂，面对更多轴类型的机床和更多的几何误差，本文方法的优势将更加显著。
表3 计算时间对比
Table 3 Comparison of calculation time
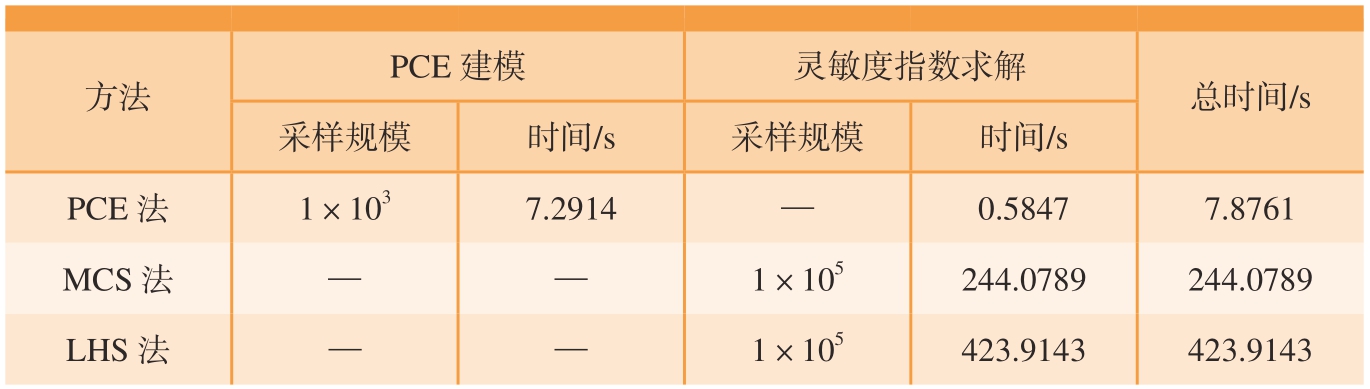
方法PCE建模灵敏度指数求解总时间/s采样规模时间/s采样规模时间/s PCE法1×103 7.2914—0.58477.8761 MCS法——1×105 244.0789244.0789 LHS法——1×105 423.9143423.9143
4 结论
（1）本文提出了基于多项式混沌展开的全局灵敏度分析方法，运用正交匹配追踪算法实现多项式系数的快速求解，并给出了基于该方法的Sobol灵敏度指数。
（2）测量得到机床41项几何误差的近似概率分布，在确定采样测试点后，使用PCE法对几何误差进行全局灵敏度分析，得到了影响各方向位姿误差分量的关键几何误差。
（3）与MCS法和LHS法进行对比，本文方法的正确性得到验证，且在保证计算精度的前提下，具有更高的收敛性能，样本量从1×105降低到1×103，计算时间分别减少了96.8%和98.1%。
[1] 项四通, 吴铖洋.灵敏度分析在数控机床精度优化中的应用研究现状[J].航空制造技术, 2021, 64(22): 40–47, 55.
XIANG Sitong, WU Chengyang.Application of sensitivity analysis in precision optimization of CNC machine tools: A state-of-the-art review[J].Aeronautical Manufacturing Technology, 2021,64(22): 40–47, 55.
[2] CHENG Q, FENG Q N, LIU Z F, et al.Sensitivity analysis of machining accuracy of multi-axis machine tool based on POE screw theory and Morris method[J].The International Journal of Advanced Manufacturing Technology,2016, 84(9): 2301–2318.
[3] LI J, XIE F G, LIU X J.Geometric error modeling and sensitivity analysis of a fiveaxis machine tool[J].The International Journal of Advanced Manufacturing Technology, 2016,82(9): 2037–2051.
[4] ZOU X C, ZHAO X S, WANG Z W,et al.Error distribution of a 5–axis measuring machine based on sensitivity analysis of geometric errors[J].Mathematical Problems in Engineering, 2020, 2020: 8146975.
[5] FU G Q, GONG H W, FU J Z, et al.Geometric error contribution modeling and sensitivity evaluating for each axis of fiveaxis machine tools based on POE theory and transforming differential changes between coordinate frames[J].International Journal of Machine Tools and Manufacture, 2019, 147:103455.
[6] 郭世杰, 梅雪松, 姜歌东, 等.数控机床几何误差相关性分析方法研究[J].农业机械学报, 2016, 47(10): 383–389.
GUO Shijie, MEI Xuesong, JIANG Gedong,et al.Correlation analysis of geometric error for CNC machine tool[J].Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(10):383–389.
[7] 王培桐, 范晋伟, 任行飞, 等.一种新的机床位置误差灵敏度分析方法[J].仪器仪表学报, 2022, 43(12): 129–138.
WANG Peitong, FAN Jinwei, REN Xingfei,et al.A novel sensitivity analysis method for machine tool position error[J].Chinese Journal of Scientific Instrument, 2022, 43(12): 129-138.
[8] SAKAMOTO S, INASAKI I.Influenceof structure errors in five-axis machining centers on the machining accuracy[J].Transactions of the Japan Society of Mechanical Engineers Series C,1996, 62(594): 748–753.
[9] MURRAY R M, LI Z X, SASTRY S S.A mathematical introduction to robotic manipulation[M].Boca Raton: CRC Press, 1994.
[10] WIENER N.The homogeneous chaos[J].American Journal of Mathematics, 1938,60(4): 897.
[11] SUDRET B.Global sensitivity analysis using polynomial chaos expansions[J].Reliability Engineering & System Safety, 2008,93(7): 964–979.
[12] XIU D B, KARNIADAKIS G E.Modeling uncertainty in flow simulations via generalized polynomial chaos[J].Journal of Computational Physics, 2003, 187(1): 137–167.
[13] PATI Y C, REZAIIFAR R,KRISHNAPRASAD P S.Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition[C]//Proceedings of 27th Asilomar Conference on Signals, Systems and Computers.Pacific Grove:IEEE Comput.Soc.Press, 1993.
[14] SOBOL′ I M.Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J].Mathematics and Computers in Simulation, 2001, 55(1–3):271–280.
[15] CHEN G Q, YUAN J X, NI J.A displacement measurement approach for machine geometric error assessment[J].International Journal of Machine Tools and Manufacture, 2001,41(1): 149–161.
[16] TSUTSUMI M, SAITO A.Identification and compensation of systematic deviations particular to 5–axis machining centers[J].International Journal of Machine Tools and Manufacture, 2003, 43(8): 771–780.
[17] MARELLI S, SUDRET B.UQLab:A framework for uncertainty quantification in Matlab[C]//Vulnerability, Uncertainty, and Risk.Liverpool: American Society of Civil Engineers,2014: 2554–2563.
[18] CAMERON R H, MARTIN W T.The orthogonal development of non-linear functionals in series of fourier-Hermite functionals[J].The Annals of Mathematics, 1947, 48(2): 385.
