高速切削加工是集高效、优质、低耗于一体的先进制造技术，在航空航天领域中被广泛应用。但是由于高速机床结构、刀具系统构成、工件材料特性、切削参数选用和加工环境状况等原因，极易在加工过程中引发颤振，影响零件表面加工质量、降低材料去除率、加剧刀具磨损[1]。目前学术界及工业界最广泛使用的颤振抑制方法是基于稳定性叶瓣图选取无颤振加工参数[1–2]。而加工刀具的刀尖点模态参数是构建稳定性叶瓣图的重要输入[3–4]。刀尖点模态参数与机床结构密切相关，在加工过程中随刀具位姿变化而发生改变[5–6]。因此，准确获得随位姿变化的刀尖点模态参数是构建稳定性叶瓣图的重要前提[7]。
目前，获得刀尖点模态参数最为可靠的方法是锤击试验[1]，通过冲击锤敲击刀具尖端，同时用传感器收集响应信号，然后基于冲击力和响应数据，利用模态参数识别方法辨识出刀尖点的模态参数，其准确性高。但是测量刀具全工作空间下的刀尖点模态参数时，锤击试验工作量大且需要停机测量，成本高、效率低。现有的刀尖点模态参数预测方法主要有响应耦合子结构分析法（Receptance coupling substructure analysis，RCSA）和基于数据驱动的方法。
RCSA 方法将机床划分成多个子结构，通过耦合各结构的频率响应函数（Frequency response function，FRF）来计算机床刀尖点的模态参数。Schmitz 等[8]将机床分成刀具伸出部分和机床剩余部分，通过计算和锤击试验分别获取两部分的频响函数，最后通过单点弹簧阻尼模型进行耦合。Movahhedy 等[9]提出一种子结构之间的连接模型，避免了主轴–刀柄系统旋转动态特性的测量难题。为了解决更换刀具导致的重复测量问题，Duncan[10]和Schmitz[11]等又将机床进一步划分为刀具、外露刀柄与刀柄底座、主轴3 个部分。Kivanc 等[12–13]将刀具划分为刀杆和刀刃两个子结构，然后参考刀刃部分的实际几何特性，搭建了较精确的刀具频率响应函数模型。
zsahin 等[14]将非对称刀具划分成许多具有相同惯性矩的小单元，计算了各单元的惯性矩，随后计算每个单元的频响函数，最后耦合得到整个刀具频率响应函数。Ertürk 等[15–16]也进一步研究了主轴、刀柄和刀具的几何参数对整个机床系统频响函数的影响。朱坚民等[17]则将机床分成主轴–刀柄–部分刀杆、其余部分刀杆及刀刃，计算得出刀柄的频响函数，通过锤击试验和逆RCSA 方法得出主轴–刀柄–部分刀杆的频响函数，最后刚性耦合得到刀尖点频响函数。子结构之间的连接处的动力学特性也是影响RCSA 方法精度的一个主要因素，Duncan[10]和Schmitz[11]等使用单点弹簧阻尼模型作为连接状态模型，并使用非线性优化算法对连接处的动力学特性进行求解。王二化[18]和王军[19]等也采用了类似的求解方法。闫蓉等[20]通过在刀柄和刀具结合面上均匀布置多点弹簧阻尼连接来模拟连接处动力学特性，然后通过遗传算法对连接处的连接参数进行了求解。目前大部分的研究致力于提高RCSA 方法的准确性[21]。
近年来，迁移学习在机器学习领域中被广泛关注，可从已有任务的大量训练数据中学习有用的知识来提升只有少量训练数据的相似预测任务的学习性能，以此来避免机械重复且耗时的数据采集[22]。Liu 等[23]通过试验发现，不同刀具随位姿变化的刀尖点模态参数间存在一定的相似性，进而利用迁移学习算法进行刀尖点模态参数预测，避免了RCSA 方法中连接参数不准确带来的影响，但是作者仅考虑迁移一把源刀具模态参数数据，当源刀具和目标刀具的相似性较低时，预测的效果有限。
本文提出一种基于多源迁移学习的刀尖点模态参数预测方法，使得新刀具预测模型可以从多把源刀具数据中获取相似性更强的知识。当更换新刀具后，仅需通过锤击试验获取少量位姿下的刀尖点模态参数，再利用已有多把刀具的刀尖点模态参数数据进行多源迁移，便可得到新刀具的刀尖点模态参数预测模型。
1 基于多源迁移学习的刀尖点模态参数预测
1.1 刀尖点模态参数预测问题建模
本文所用的一些符号和定义如下。
用X 表示输入空间，即机床的整个工作空间。对于xi∈X，xi={x1i，x2i，x3i，x4i，x5i}，表示第i 个输入数据，其中，x1i、x2i、x3i 为五轴机床的3 个平动轴坐标；x4i、x5i 为机床的两个回转轴的坐标；X Sp 和X T 分别表示第p 个源刀具和目标刀具的输入空间。
用Y 表示由刀尖点模态参数组成的标签空间。对于yi∈Y，yi={wi，ξi，Ki}，表示xi 位姿下的刀尖点模态参数，其中，wi 代表固有频率；ξi 代表阻尼比；Ki 代表刚度；Y Sp 和Y T 分别代表X Sp 和X T 对应的标签空间。
f（x）表示xi∈X 和f（xi）∈Y 之间的刀尖点模态参数预测函数。f Sp（X）和f T（X）分别代表第p 个源刀具和目标刀具的预测模型。
多个源域数据集，即多把源刀具的刀尖点模态参数数据，表示为DS={DS1，…，DSp}，其中，p 为源刀具个数。对于每个源域，有DSp={（xiSp，yiSp）}，其中xiSp ∈X Sp，yiSp∈Y Sp，且i =1，2，…，nSp，nSp为第p个源域中的数据个数。
目标域数据集，即少量的目标刀具的刀尖点模态参数数据，表示为DT={（xiT，yiT）}，其中，xiT∈X T，yiT∈Y T，且i=1，2，…，nT，nT 为目标域中的数据个数，其远小于源域的训练数据个数，即nT<<nSp，p=1，2，…，P。
本文所提方法旨在利用可获得的多个源域数据集DS={DS1，…，DSp}来帮助仅有少量数据的目标域数据集DT 建立准确的刀尖点模态参数预测模型f T（X）。
1.2 基于多源迁移学习的刀尖点模态参数预测
由于不同刀具间的刀尖点模态参数相似性不同，为了更好地实现目标刀具模态参数预测，本文引入一种基于高斯过程回归的多源迁移学习方法，可以评估不同源刀具和目标刀具之间的相似性。在具体介绍该方法之前，首先阐述其所用到的迁移核函数。
1.2.1 基于高斯过程回归的迁移核函数
高斯过程回归是一种常见的机器学习算法，可直接学习训练数据和测试数据输出之间的关系，并且可以给出预测值的方差，广泛应用于工程领域。高斯过程回归对一维数据的建模效果如图1 所示。刀尖点模态参数的采集依赖于传感器测量及模态参数识别，数据处理易引起多种不确定度，因此高斯过程回归更加适用于本文的测量方差大而预测精度要求高的刀尖点模态参数预测问题。
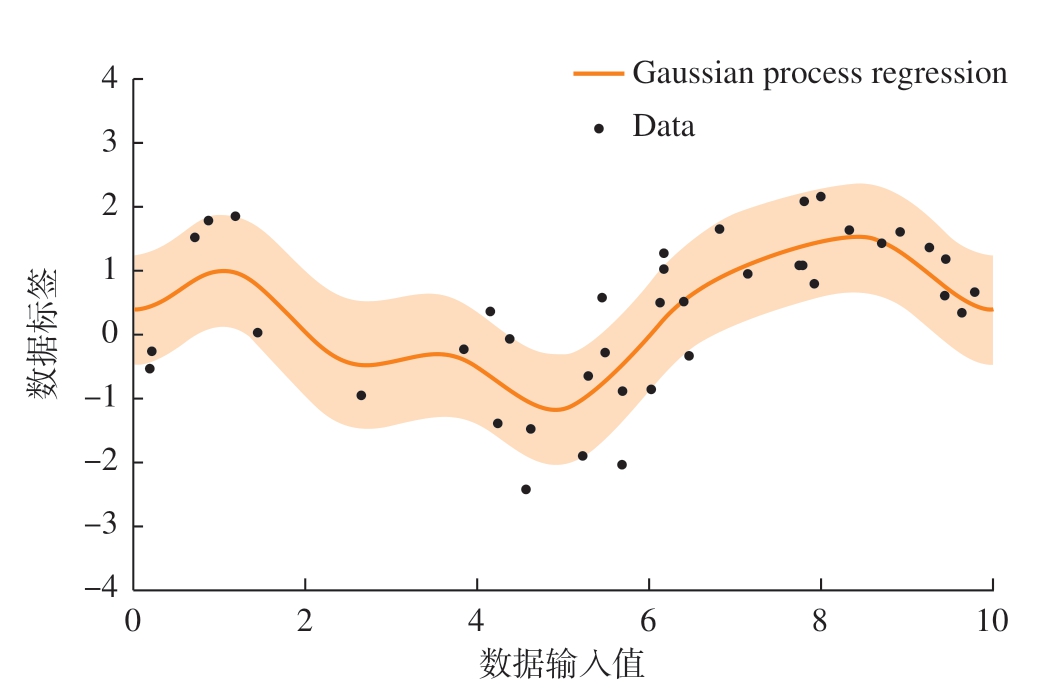
图1 高斯过程回归
Fig.1 Gaussian process regression
给定指定刀具的模态参数训练数据，输入
，输出
，n为训练数据的个数；d为训练数据输入的维度。对于待预测位姿数据
，m为测试数据的个数。高斯过程回归建模得到的预测值为
式中，N 表示高斯分布；I 为单位矩阵；σn 为训练数据噪声的标准差。
可以看出，高斯过程给出了预测的正态分布，在此认为均值便是相应的预测值。其中，K 矩阵中的元素由核函数κ（·，·）确定，即
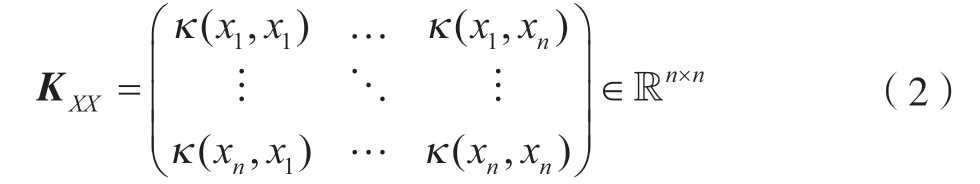
常见的核函数有线性核函数、多项式核函数和高斯核函数等。在迁移学习任务过程中，需要从源域中提取相似的可重用的信息至目标域，因此在目标建模过程中，首先要衡量源域数据对于目标域模型训练的价值。由于核矩阵中的核函数能够描述数据之间的相关关系，因此可通过设计核函数来实现对数据价值的衡量。
Pan 等[24]提出一种迁移核函数，用于衡量源域和目标域之间的相似性，即
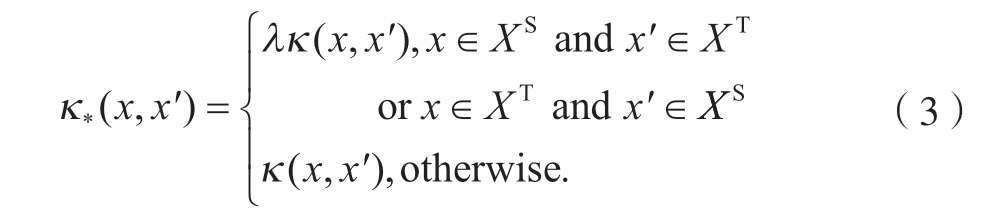
式中，λ 为描述源域与目标域间相似性的衡量指数，可通过构造先验分布求解，也可以通过共轭梯度下降等优化方法求解。
基于迁移核函数，可定义同时包括目标数据和源数据的核矩阵，矩阵的维度为源数据和目标数据的尺寸和，由于核矩阵要保证半正定性质，因此根据目标数据和源数据的数量将矩阵分为分块矩阵，即
式中，K11 为刀尖点模态参数源数据与源数据间的核矩阵；K12 为刀尖点模态参数源数据与目标数据间的核矩阵；K21 为刀尖点模态参数目标数据与源数据间的核矩阵；K22 为刀尖点模态参数目标数据与目标数据间的核矩阵。
为了保证核矩阵的半正定性质，迁移核也应当对称使用。因此考虑核矩阵K12 及其所定义的迁移核函数，此时核矩阵表示为
1.2.2 基于迁移核函数的多源迁移学习方法
为了更好地将多把刀具中的模态参数数据用于目标刀具建模，本文采用Wei 等[25]提出的一种基于高斯过程回归的多源迁移学习算法用于刀尖点模态参数预测。首先在每一组源刀具数据{X Sp，Y Sp}和目标刀具数据{X T，Y T}上利用迁移核函数得到单源迁移模型f（Sp，T）（x，Ωp，λp）；然后通过相似性系数λp 对每个单源迁移模型加权得到目标刀具刀尖点模态参数预测模型，即
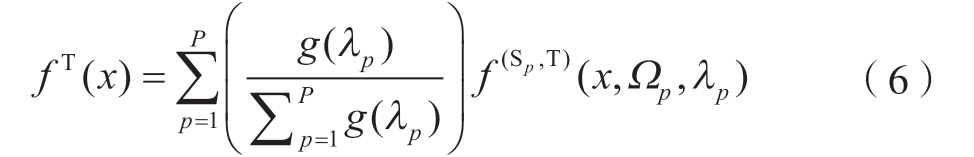
式中，Ωp 和λp 为单源迁移模型中的参数；g（λp）建立相似性系数λp 和模型权重系数之间的关系。考虑到源域之间的依赖性，多个单源迁移模型同时训练。目标函数为
式中，f T(xiT)为目标刀具模态参数预测模型对目标数据xiT 的预测值；yiT 为xiT 相应的测量值。最终通过共轭梯度方法最小化目标函数求解模型中的参数。
因此刀尖点模态参数多源迁移学习过程可分为以下步骤： （1）获取多组源数据以及目标数据； （2）基于上文定义的迁移核函数及高斯过程回归，建立单把源刀具至目标刀具的初始迁移模型； （3）利用多源迁移学习方法集成上述多组初始迁移模型，通过共轭梯度法优化模型相似性系数及模型权重； （4）对于待预测位姿，利用加权多源迁移模型求解刀尖点模态参数预测结果。
刀尖点模态参数包括固有频率、阻尼比及刚度，当刀尖频率响应函数为多自由度时，待预测标签为一组向量，本文所提高斯过程回归对向量中每个维度的元素预测均采用相同处理，因此本文方法适用于多自由度多模态参数同时预测。
2 试验验证
为验证本文所提算法的有效性，选取一台五坐标加工中心开展试验验证。加工中心具有X、Y、Z 3 个平动轴和A、C 两个回转轴，在实际铣削加工中，由于零件复杂的几何变化导致加工过程中各轴位姿发生剧烈变化，因此需要对变位姿情况下的刀尖点模态参数进行建模，通过前期仿真及试验分析发现，X、Y、Z 3 个平动轴对刀尖点模态参数的影响较小，而A/C 摆头的位姿变化会导致固有频率和模态刚度发生剧烈变化，因此本节重点关注A 轴、C 轴摆角变化下的刀尖点模态参数预测问题，对于其他类型的机床，方法通用。对于本文验证，特征变量具体定义为
，其中A轴的旋转范围是x1i ∈[–90°，90°]，C 轴的旋转范围是x2i∈[0°，360°]。
试验用机床常用于加工飞机结构件，所涉及刀具规格、材料、尺寸较广，本文选取精加工中最常用的刀具尺寸，T1、T2、T3、T4 刀具各一把，同时为验证相似规格材料情况下刀具材质对迁移效果的影响，本试验中T1 及T4 为硬质合金刀具，T2 及T3 为高速钢刀具。由于刀具伸出长度影响刀具子结构的动力学性能，从而对模态参数产生影响，因此本文所有试验中保证伸出长度的数值固定，试验所需的刀具具体信息如表1 所示。
表1 试验刀具
Table 1 Test tools
刀具序号刀具材质直径/mm长度/mm T1images/BZ_108_1417_1803_1743_1845.png硬质合金650 T2images/BZ_108_1417_1889_1827_1941.png高速钢865 T3images/BZ_108_1417_1983_1859_2036.png高速钢1085 T4images/BZ_108_1417_2080_1867_2149.png硬质合金1285
2.1 数据集建立
本案例验证选取T2、T3 和T4 3 把刀具的变位姿刀尖点模态参数数据作为3 个源数据集，选取刀具上的少量变位姿作为目标数据，同时在刀具上大量采集模态参数数据作为算法验证所用的测试数据。
为体现不同源域的差异性，多组源域模态参数的采集过程中对机床回转轴的离散方式不同，对于刀具T3与T4，将A 轴从–90° ～10°以10°的步距角离散，将C轴从0° ～30°以30°的步距角离散，因此刀具T3 与T4 分别在247 组位姿下采集了频响函数数据；对于刀具T2，将A 轴从– 90° ～90°以10°的步距角离散，将C 轴从0° ～360°以20°的步距角离散，得到这把刀具的361 组位姿下的频响函数数据。锤击试验具体过程如图2 所示，激振力的方向应始终垂直于A 轴和刀具方向，同时在相对侧用加速度传感器收集响应信号，激励和振动信号由数据采集单元分析，每个位姿的最终模态参数是5次重复锤击试验的平均值。使用有理分数多项式的方法[26]，可以根据试验测得的频率响应函数识别得到刀架组件的固有频率、模态刚度以及阻尼比。
图2 五轴试验平台
Fig.2 Five-axis test platform
本文所提方法在源刀具训练数据足够的情况下，只要获取小部分的目标刀具数据就能够训练得到目标刀具预测模型。然而，多源迁移学习的预测效果依赖于目标数据的数量及具体分布，当目标数据数量不足以描述各域之间的领域偏差时，仅能实现试验目标数据局部位置的分布适配，从而引起负迁移，而目标数据的数量过多时，迁移学习本身便失去了意义。其次目标数据的分布也对迁移学习效果有很大影响，应尽可能表示目标域的数据分布，因此本试验首先考虑目标数据与源数据的实例空间边界重合，同时目标数据应在工作空间内分布均匀。根据以上准则共确定了10 个位姿，如表2 所示。根据这10 个位姿来进行锤击试验，获取目标数据。
表2 构建目标数据的关键位姿
Table 2 Construct the key poses of target data
回转轴P1P2P3P4P5P6P7P8P9P10 A 轴 /（°）–90–909090004040–40–40 C 轴 /（°）036003601202409027090270
2.2 试验验证结果
在获得DS 和DT 后，根据上文介绍的方法训练目标刀具的刀尖模态预测模型。最终得到刀具T1 的固有频率、模态刚度和阻尼比的预测模型，如图3 所示。
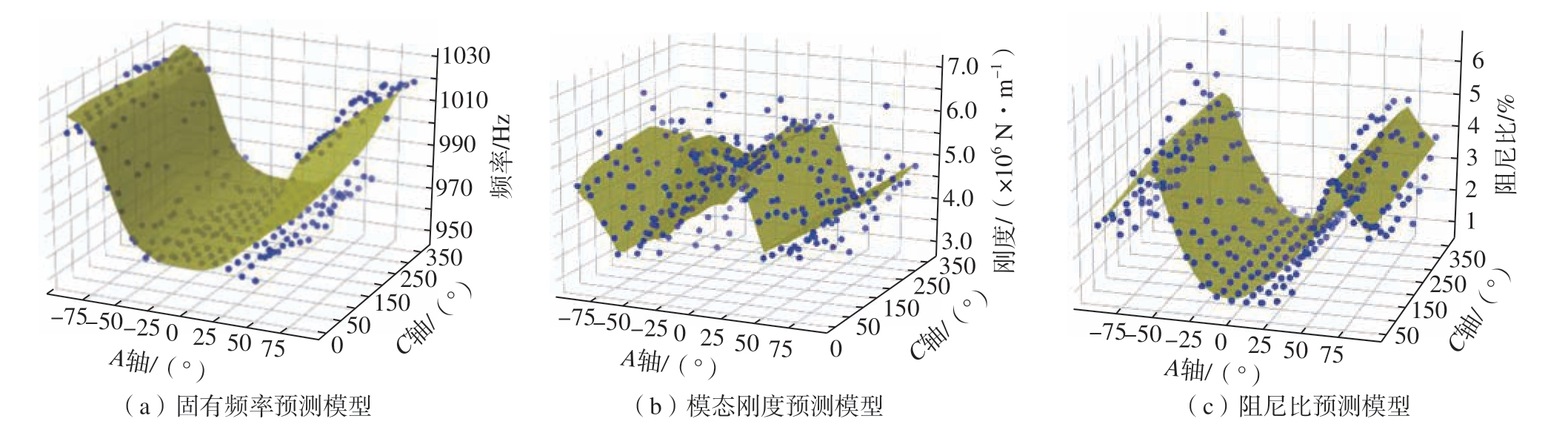
图3 目标刀具刀尖点模态参数预测模型
Fig.3 Prediction model of tool point modal parameters of target tool
用均方根误差（Root mean square error，RMSE）和平均相对误差（Mean relative error，MAE）来衡量所提方法得到的模态参数预测模型的准确性，RMSE 和MAE 分别被定义为
式中，yipred 和yitest 分别是第i 个位姿下预测和测量的刀尖点模态参数，包括固有频率、刚度和阻尼比；N 是测试数据集的大小，N=247。根据式 （8）和 （9）可计算得到目标刀具模态参数预测模型的预测误差，如表3 所示，预测精度表明本文所提方法是有效的。
表3 目标刀具刀尖点模态参数预测模型精度
Table 3 Prediction model accuracy of tool point modal parameters of target tool
误差固有频率模态刚度阻尼比RMSE5.76 Hz0.33×106 N/m0.59%MAE0.42%6.8%8.72%
2.3 与机理模型进行对比
为进一步分析，将所提方法与Deng 等[27]提出的基于RCSA 的方法进行比较。该方法首先通过测量主轴在少量位姿的频响函数，建立Kriging 预测模型，然后基于RCSA 生成刀尖的频响函数。对于目标刀具，通过在位姿A=0°，C=0°下进行锤击试验，并利用Mehrpouya等[28]提出的逆响应耦合（IRC）方法计算关节频响函数矩阵，然后利用关节频响函数矩阵和该位姿的刀架频响函数计算其刀尖点频响函数。本节分别在A=10° C=0°、A=30° C=0°、A=50° C=0°和A=80° C=0° 4 组刀具位姿下与Deng 等[27]的方法进行比较，模态参数预测精度如表4 所示 （括号中的数值表示预测值与测量值的相对误差）。
表4 4 个刀具位姿下本文方法与RCSA 方法预测精度对比
Table 4 Comparison of the prediction accuracy between the proposed method and RCSA method under four tool poses
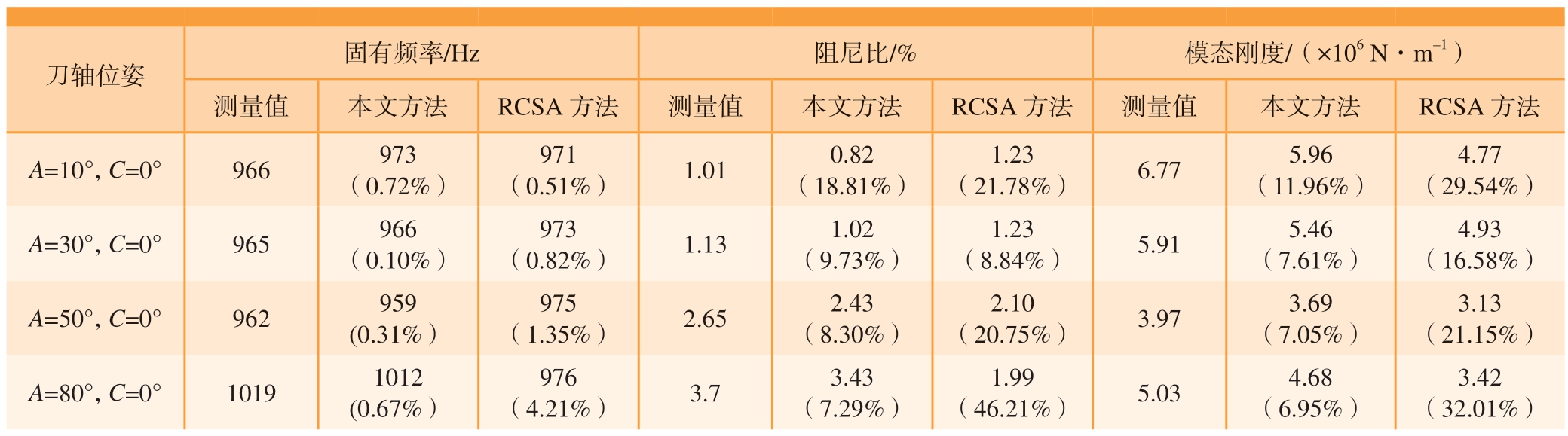
刀轴位姿固有频率/Hz阻尼比/%模态刚度/（×106 N·m–1）测量值本文方法RCSA 方法测量值本文方法RCSA 方法测量值本文方法RCSA 方法A=10°，C=0°966 973（0.72%）971（0.51%）1.01 0.82（18.81%）1.23（21.78%）6.77 5.96（11.96%）4.77（29.54%）A=30°，C=0°965 966（0.10%）973（0.82%）1.13 1.02（9.73%）1.23（8.84%）5.91 5.46（7.61%）4.93（16.58%）A=50°，C=0°962 959(0.31%）975（1.35%）2.65 2.43（8.30%）2.10（20.75%）3.97 3.69（7.05%）3.13（21.15%）A=80°，C=0°1019 1012(0.67%）976（4.21%）3.7 3.43（7.29%）1.99（46.21%）5.03 4.68（6.95%）3.42（32.01%）
将本文方法、RCSA 方法[27]、锤击试验测量法进行对比，如图4 所示。从预测精度及频响函数曲线可以看出，在位姿A=10°、C=0°下，本文方法和对比方法的预测结果均接近于测量值，但在其余3 个位姿下本文方法优于对比方法，尤其是在位姿A=50°、C=0°和A=80°、C=0°下，对比方法所得结果与测量值有明显偏差。这是因为Deng 等[27]的方法中，关节频响函数矩阵在位姿A=0°、C=0°下计算所得，因此当目标刀具的测试位姿接近于A=0°、C=0°时，其结果准确；当位姿差异较大时，该方法的预测效果较差。综上所述，本文方法对于变位姿下的模态参数预测效果更加准确。
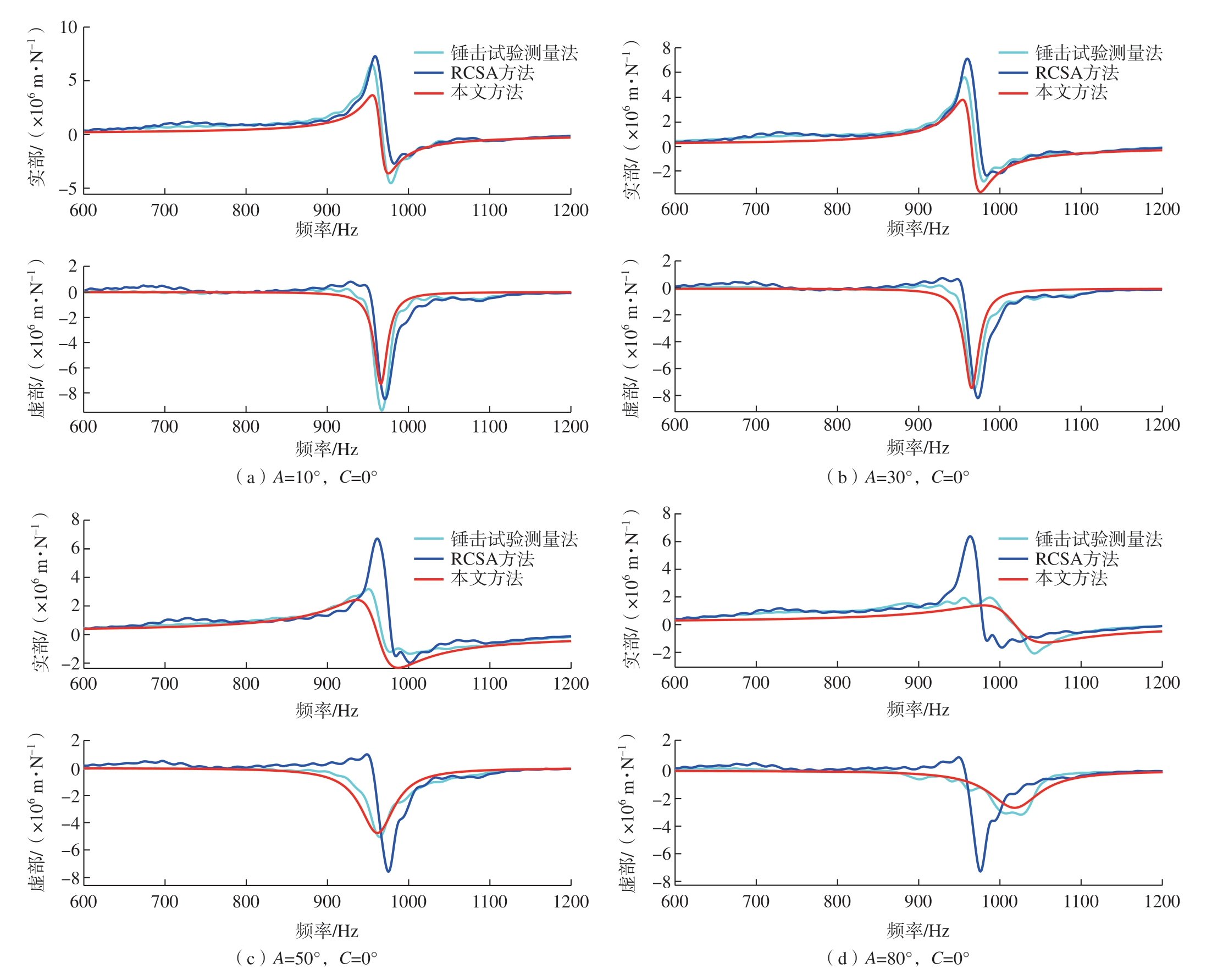
图4 不同刀具位姿下频率响应函数对比
Fig.4 Comparison of frequency response functions under different tool poses
3 结论
本文针对刀尖点模态参数预测问题，提出一种基于多源迁移学习的刀尖点模态参数预测方法。当更换新刀具后，仅需通过锤击试验获取少量位姿下的刀尖点模态参数，再利用已有多把刀具的刀尖点模态参数数据进行多源迁移，便可得到新刀具的刀尖点模态参数预测模型。最后，在五轴铣削机床上进行试验验证，且与现有基于RCSA 方法试验结果进行对比，结果表明，本文提出的方法是有效的。
[1] MUNOA J, BEUDAERT X, DOMBOVARI Z, et al. Chatter suppression techniques in metal cutting[J]. CIRP Annals–Manufacturing Technology, 2016, 65(2): 785–808.
[2] 汤爱君, 马海龙. 机床再生颤振系统研究现状的综述[J]. 机床与液压, 2007, 35(8): 223–225.
TANG Aijun, MA Hailong. Survey on the regenerative chatter of the machine tool[J]. Machine Tool & Hydraulics, 2007, 35(8): 223–225.
[3] YUE C X, GAO H N, LIU X L, et al. A review of chatter vibration research in milling[J]. Chinese Journal of Aeronautics, 2019,32(2): 215–242.
[4] ÖZSAHIN O, ÖZGÜVEN H N, BUDAK E. Analysis and compensation of mass loading effect of accelerometers on tool point FRF measurements for chatter stability predictions[J]. International Journal of Machine Tools and Manufacture, 2010, 50(6): 585–589.
[5] POSTEL M, ÖZSAHIN O, ALTINTAS Y. High speed tooltip FRF predictions of arbitrary tool–holder combinations based on operational spindle identification[J]. International Journal of Machine Tools and Manufacture, 2018, 129: 48–60.
[6] LAW M, ALTINTAS Y, PHANI A S. Rapid evaluation and optimization of machine tools with position–dependent stability[J].International Journal of Machine Tools and Manufacture, 2013, 68: 81–90.
[7] ALTINTAS Y. Modeling the orientation-dependent dynamics of machine tools with gimbal heads[J]. Race Gender & Class, 2006,13(1/2): 7–25.
[8] SCHMITZ T L, DONALSON R R. Predicting high-speed machining dynamics by substructure analysis[J]. CIRP Annals–Manufacturing Technology, 2000, 49(1): 303–308.
[9] MOVAHHEDY M R，GERAMI J M. Prediction of spindle dynamics in milling by sub-structure coupling[J]. International Journal of Machine Tools and Manufacture, 2006, 46(3–4): 243–251.
[10] DUNCAN G S, SCHMITZ T. An improved RCSA model for tool point frequency response prediction[C]//Proceedings of the 23rd International Modal Analysis Conference. New Delhi: Springer, 2005.
[11] SCHMITZ T L，DUNCAN G S. Three-component receptance coupling substructure analysis for tool point dynamics prediction[J].Journal of Manufacturing Science and Engineering, 2005, 127(4): 781–790.
[12] KIVANC E B, BUDAK E. Structural modeling of end mills for form error and stability analysis[J]. International Journal of Machine Tools and Manufacture, 2004, 44(11): 1151–1161.
[13] KIVANC E B, BUDAK E. Development of analytical endmill deflection and dynamics models[C]//ASME 2003 International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers. Washington DC: ASME, 2003: 85–94.
[14] ÖZSAHIN O, ALTINTAS Y. Prediction of frequency response function (FRF) of asymmetric tools from the analytical coupling of spindle and beam models of holder and tool[J]. International Journal of Machine Tools and Manufacture, 2015, 92: 31–40.
[15] ERTÜRK A, ÖZGÜVEN H N, Budak E. Effect analysis of bearing and interface dynamics on tool point FRF for chatter stability in machine tools by using a new analytical model for spindle–tool assemblies[J]. International Journal of Machine Tools and Manufacture,2007, 47(1): 23–32.
[16] ERTÜRK A, BUDAK E, ÖZGÜVEN H N. Selection of design and operational parameters in spindle-holder-tool assemblies for maximum chatter stability by using a new analytical model[J]. International Journal of Machine Tools and Manufacture, 2007, 47(9): 1401–1409.
[17] 朱坚民, 王健, 张统超, 等. 一种改进的基于响应耦合子结构法的刀尖点频响函数预测方法[J]. 中国机械工程, 2015(3): 285–292.
ZHU Jianmin, WANG Jian, ZHANG Tongchao, et al. An improved tool point frequency response function prediction method based on response coupled substructure method[J]. China Mechanical Engineering,2015(3): 285–292.
[18] 王二化, 吴波, 胡友民, 等. 主轴–刀柄与刀柄–刀具结合面参数辨识研究[J]. 振动与冲击, 2014, 33(10): 50–54.
WANG Erhua, WU Bo, HU Youmin, et al. Parametric identification of spindle-holder and holder-tool interfaces[J]. Journal of Vibration and Shock, 2014, 33(10): 50–54.
[19] 王军. 数控铣削加工过程稳定性分析与预测[D]. 武汉: 华中科技大学, 2013.
WANG Jun. Stability analysis and prediction of NC milling process[D].Wuhan: Huazhong University of Science and Technology, 2013.
[20] 闫蓉, 蔡飞飞, 彭芳瑜, 等. 基于响应耦合方法的铣刀刀尖点频响函数预测[J]. 华中科技大学学报(自然科学版), 2013(4): 1–5.
YAN Rong, CAI Feifei, PENG Fangyu, et al. Frequency response function prediction of milling tool point based on response coupling method[J]. Joural of Huazhong University of Science and Technology(Natural Science Edition), 2013(4): 1–5.
[21] JI Y, BI Q, ZHANG S, et al. A new receptance coupling substructure analysis methodology to predict tool tip dynamics[J].International Journal of Machine Tools & Manufacture, 2017, 126: 18–26.
[22] PAN S J, QIANG Y. A Survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345–1359.
[23] LIU X, LI Y, CHEN G . Multimode tool tip dynamics prediction based on transfer learning[J]. Robotics and Computer-Integrated Manufacturing, 2019, 57: 146–154.
[24] PAN W, XIANG E W, LIU N N, et al. Proceedings of the twenty-fourth AAAI conference on artificial intelligence (AAAI-10)transfer learning in collaborative filtering for sparsity reduction[C]//Twenty-Fourth AAAI Conference on Artificial Intelligence. Atlanta,2010: 17–38.
[25] WEI P, RAMÓN S, KE Y, et al. Source-target similarity modelings for multi-source transfer Gaussian process regression[C]//Proceedings of the 34th International Conference on Machine Learning.Caserta: Mondadori Press, 2017.
[26] RICHARDSON M H, FORMENTI D L, Parameter estimation from frequency response measurements using rational fraction polynomials[C]//Proceedings of the 1st International Modal Analysis Conference. New York: ASME, 1982: 167–186.
[27] DENG C, MIAO J, WEI B, et al. Evaluation of machine tools with position-dependent milling stability based on Kriging model[J].International Journal of Machine Tools and Manufacture, 2018, 124: 33–42.
[28] MEHRPOUYA M, GRAHAM E, PARK S S. FRF based joint dynamics modeling and identification[J]. Mechanical Systems & Signal Processing, 2013, 39(1/2): 265–279.