随着“中国制造2025”战略的提出，工业机器人在航空航天制造领域的布置不断增多[1]，不仅可以完成传统的涂胶、喷涂、装配及检测等任务[2–4]，在钻孔、铆接、复合材料铺敷等特种作业上也发挥着优异性能[5–6]。工业机器人在从事复杂加工任务时，通常要在末端执行器上加装钻孔设备、折弯机、超冗余探测机械臂等实施装置进行二次开发[7–9]，持续性的负载对RV 减速器的可靠性及安全性提出了更高要求[10]。RV 减速器作为工业机器人重要的支撑、旋转部件，使用不当会造成整机的颤振、损坏等，并且RV 减速器在过载、周期性疲劳应力等不良工况下，易出现各种强磨损、齿根裂纹、断齿等故障[11]。为确保其定位精度，对RV 减速器运行工况进行监测是必要环节[12]。
近年来，国内外学者从温度、振动、传递特性等领域对减速器进行工况监测分析以评判减速器的综合性能，进而提高智能产线的生产效率。机械部件从正常运行到轻微磨损再到报废无法使用，其各阶段温度状态是不断变化的。通过温度情况判断部件状况相对简单明了，但极易造成耦合现象，往往需要进行其他关键信息的采集[13]。基于振动信号监测的相关研究比较成熟，是现阶段使用最多的一种方法。振动信号多是用加速度传感器采集得到，面对复杂工况时，传动特征就会明显降低，并且传感器的寿命往往低于机械部件，不利于实时在线监测[14–15]。传递特性是衡量减速器性能优劣的标准，监测其传动误差、传递扭矩、回程差等可以精确地反映出减速器的运行状态[16–18]，但此类办法需要进行拆机检查。王庆锋等[19]利用K-means 聚类识别模型计算出实时监测数据的聚类中心，利用直观距离判据实现离心压缩机故障模式自动识别。柴娜[20]利用伺服电机反馈信号监测传动链不对中、齿轮故障的问题，识别效果优异。Hamadache 等[21]采集转子系统的电流、转速信号，实现了恒定负载变转速工况下的轴承故障识别。
综上所述，针对现有的RV 减速器工况监测方法复杂、计算较多，以及需要其他传感器采集数据支撑的问题，本文采用伺服系统反馈的转速、电流等特征信息对RV 减速器运行工况进行识别，该方法可以做到不使用外置传感器，为伺服系统集成机械智能诊断功能提供技术支撑，继而为航空航天制造提供保障。
1 理论分析
RV 减速器是一种具有两级减速的双摆线针轮传动机构，具有传动精度高、传递扭矩大、传动平稳等优点，广泛应用于精密和重载机器人。本文以RV-20E 型减速器为研究对象，外部主要由1 个渐开线中心轮、2 个渐开线行星轮构成一级减速，内部主要由2 个摆线轮、2个曲柄轴、针齿壳、行星架等构成二级减速，两级减速共同组成减速比为121 的新型减速器。因其结构复杂、装配工艺要求高，高质量减速器的生产技术近几年才被国内突破，RV 减速器的结构简图与实物图如图1 所示。
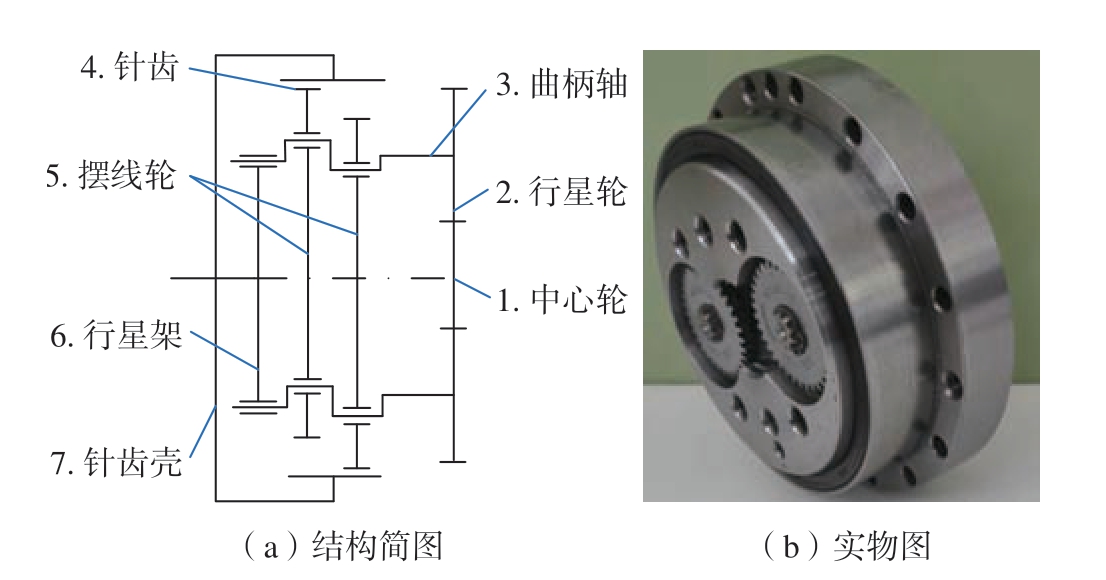
图1 RV-20E 减速器
Fig.1 RV-20E reducer
RV 减速器的动力由伺服电机驱动渐开线中心轮提供，中心轮齿轮与行星轮齿轮啮合将动力通过曲柄轴传输到摆线轮。偏心位置成180°安放的摆线轮与针齿轮相互作用，产生的反作用力通过转臂轴承作用到曲柄轴，形成曲柄轴的公转，最终通过行星架输出 （针齿壳固定行星架输出是现行工业机器人使用最多的一种装配形式），RV-20E 减速器部分结构参数见表1。
表1 RV-20E 减速器部分结构参数
Table 1 Partial structural parameters of RV-20E reducer
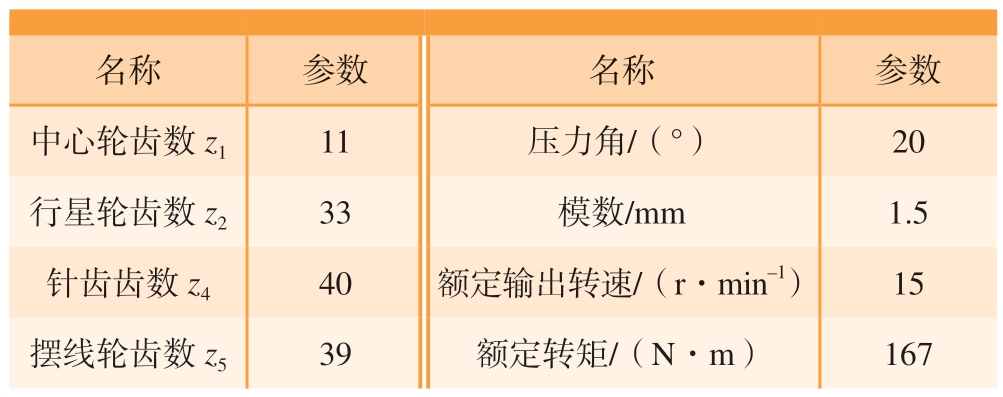
名称参数名称参数中心轮齿数z111压力角/（°）20行星轮齿数z233模数/mm1.5针齿齿数z440额定输出转速/（r·min–1）15摆线轮齿数z539额定转矩/（N·m）167
1.1 输入转速与频率关联分析
RV 减速器作为一种典型的高精密、大速比摆线针轮减速器，其传动比可以通过转化机构法进行求解[22]。对外部一级减速进行求解时，可以假设中心轮与行星轮啮合时行星轮保持架无自转，根据行星传动的原理，可得到
图1（a）中序号1～7 对应下文各变量的下角标，式中，nj（j=1～6）分别表示中心轮、行星轮、曲柄轴、针齿、摆线轮及行星架的转速；i1、i2 分别表示各级减速比。
摆线轮与针轮传动作为二级减速，行星轮自转带动两个摆线轮旋转。假设曲柄轴无公转，根据上述转化机构法进行求解可得到二级减速比 （式 （2）），其中针齿壳固定，n4=0。
行星轮驱动曲柄轴进行旋转运动可知其转速相同，即n2=n3；当针齿壳固定时，摆线轮与行星架保持相同的转速进行运动，它们之间只有平动，无转动，即n5=n6。结合上式可解得RV-20E 减速器的总传动比为
式中，i 为减速器传动比，取121。
利用式 （1）～（3）可求得减速器运动学的齐次表达式 （式 （4））。当输入转速已知时，可以求出任意传动机构的转速。
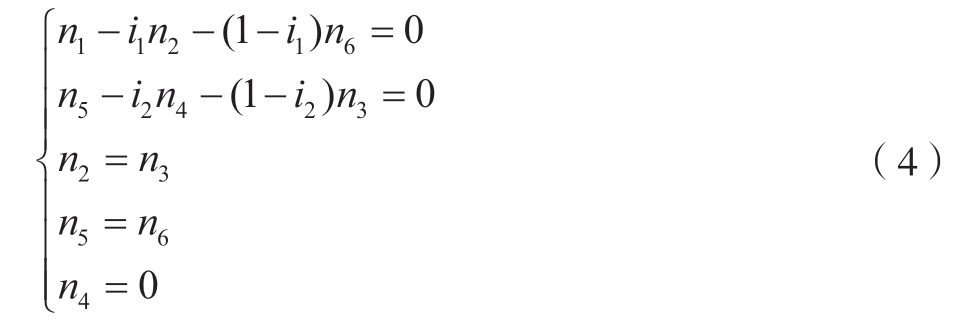
结合伺服电机与RV 减速器的工作原理可得到电机驱动减速器工作时的理论转速计算公式，即
式中，f 为变频器输出频率；P 为伺服电机极对数，取5。
根据式 （4）和 （5），可知针齿壳固定时RV 减速器的工作转频和两级传动的啮合频率[23]。结合文中研究需要，列举RV 减速器主要部件的转动频率及啮合频率（Hz），具体计算公式如下。
伺服电机转频fe= （n1·P）/60；
中心轮转频f1= n1/60；
行星轮 （曲轴）转频f2=（f1·z5）/i；
行星架转频f3= f1/i；
一级传动啮合频率fsp=（f1·z2·z4）/i；
二级传动啮合频率fcs=（f1·z4·z5）/i
1.2 伺服特征信息与负载关联分析
工业机器人在智能制造产线中，沿着预先设置好的路径进行循环往复运动，在一个运动周期内负载变化是相对平稳的。RV 减速器通常安放在工业机器人关节处，运行到不同姿态时承受着不同形式的作用力，大部分用来承载径向的负载转矩Tl，少部分用来承受轴向作用力Fa。Fx、Fy 分别表示在x 轴和y 轴上的径向力分量；G 为机械臂的重力，减速器输出盘上的负载形式如图2所示。减速器传递转矩的理论公式为T l= i × Tm × η（i为减速比；Tm 为电机输出转矩值；η 为减速器的传递效率），试验表明，减速器在相同转速和负载下其传递效率η 稳定于某一值[24]。
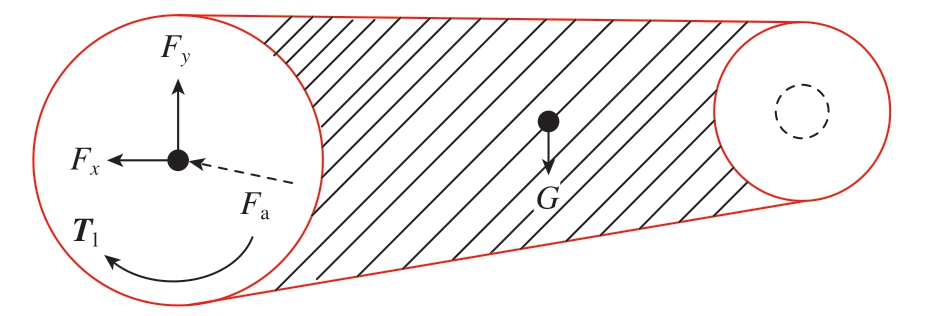
图2 RV 减速器输出盘受力分析
Fig.2 Force analysis of RV reducer output disk
交流伺服电机采用速度控制模式时会根据负载情况调节电流大小控制输出转矩。根据理论分析可知，相同负载下，减速器工作的一个周期内变频器输出的电流信号应是相对稳定的，可以使用电流信号对其传动系统进行状态监测。
对于旋转机械而言，转速同样可以为减速器工况分析和状态监测提供重要的特征信息。本文中采用速度控制模式进行试验，对工业机器人运动轴进行单轴简化处理。分析传动链结构得到理想状态下的机电系统，其机电一体化等效系统原理图如图3 所示。
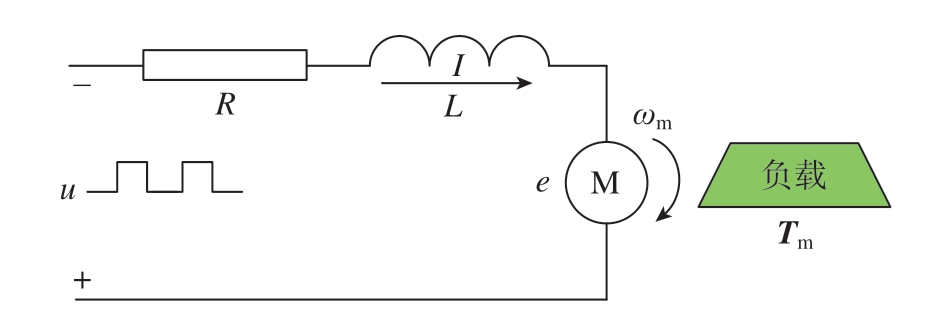
图3 机电一体化等效系统
Fig.3 Equivalent electromechanical system
伺服电机驱动RV 减速器运行时，电枢回路会产生一个与电机转速成正比的反向电动势e，电机的电磁转矩Tem 与电枢回路电流I 成正比[25]。根据图3 并利用相关知识可得到其运动系统方程，即
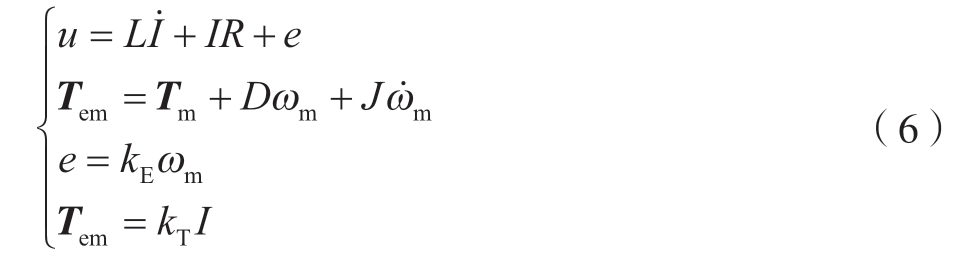
式中，u 为电枢电压；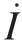
为电流的一阶倒数，表示电流变化率；R、L 分别表示回路等效电阻值、电感值；ωm、
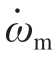分别表示电机角速度、角加速度；D、J 分别表示电机的黏滞阻尼系数、转动惯量；kE、kT 分别表示电机的反电势常数、电机转矩系数。
当负载不随运动过程发生变化时，考虑电机的黏滞阻尼系数，可得到
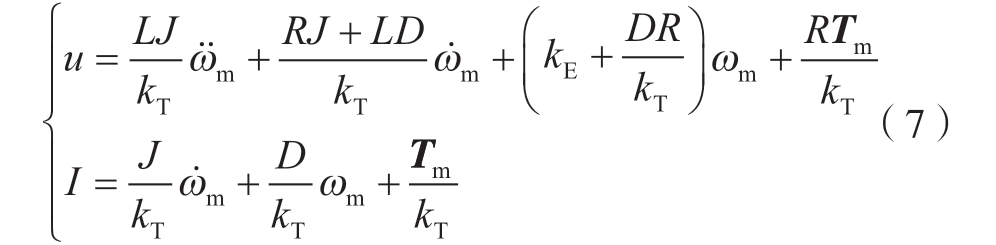
式中，
为角加速度的变化率，是角速度的二阶导数。
由式 （7）可知，伺服运动控制系统是一个二阶系统，在转动过程中系统稳定性受到阻尼比、超调量等因素的影响。电流I 与角加速度、角速度、负载均有一定的关系。因此，仅利用电流信息或转速信息通过相应的理论公式去评估传动链装置运行状态是比较困难的，需借助相应的机器学习算法对采集到的伺服特征信息进行处理，进而对RV 减速器的运行状态进行监测。
2 关联性辨识
2.1 K-means 聚类原理
K-means 是一种经典的聚类识别算法，凭借其原理简单、效率高的优势在数据分类中广泛得到使用[26]。作为一种基于距离度量的简单迭代性“无监督”、自适应聚类方法，K-means 将一个W 维的数据点集A={xw | w=1，…，W}不断重新分配数据点并更新聚类中心，从而得到K 个类簇及其聚类中心，其中每个数据点到其归属类簇的聚类中心距离最小。
K-means 聚类常使用欧式距离 （式8–I）、曼哈顿距离 （式8–Ⅱ）、切比雪夫距离 （式8–Ⅲ）作为其相似性度量计算准则。本文中采用最常用的欧式距离公式进行度量计算[27]，并以数据点与初始聚类中心的误差平方和 （SSE）公式作为度量聚类质量的目标函数。
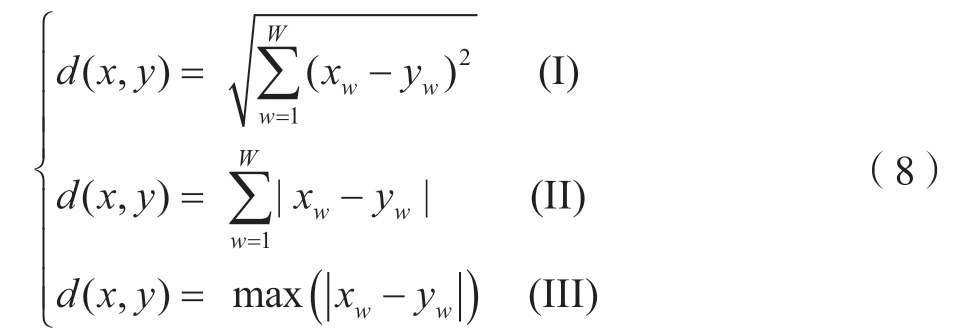
计算数据集A 中的数据点集xw 与第k 个类簇的聚类中心ck 的欧式距离，即
计算出K 个类簇中总的误差平方和SSE，即
上述算法是一种动态聚类算法，首先选择K 个数据点作为初始聚类中心，其中K 值在本文中根据试验要求进行人为设定。通过计算数据点到各个初始聚类中心的距离，不断将数据点以距离最小准则分配到对应的类簇，从而更新聚类中心。经过重复计算与分配，当SSE取最小时算法结束，并获得相应的各类簇聚类中心。
2.2 辨识建模
当减速系统承受负载转矩工作时，仅从简单的某一信息进行状态监测是极其困难的。伴随着伺服系统的发展，其反馈信息在实际应用中变得越发广泛，不仅限于运动精度的控制，在对其传动链的状态监测上也起到了积极作用。基于转速/电流信号的特征分析具有低成本且简单可靠的优点，目前在其他旋转机械的状态监测中起到了一定的应用效果，具体识别原理如图4 所示（其中，数字1～6 表示第1 轴～第6 轴）。
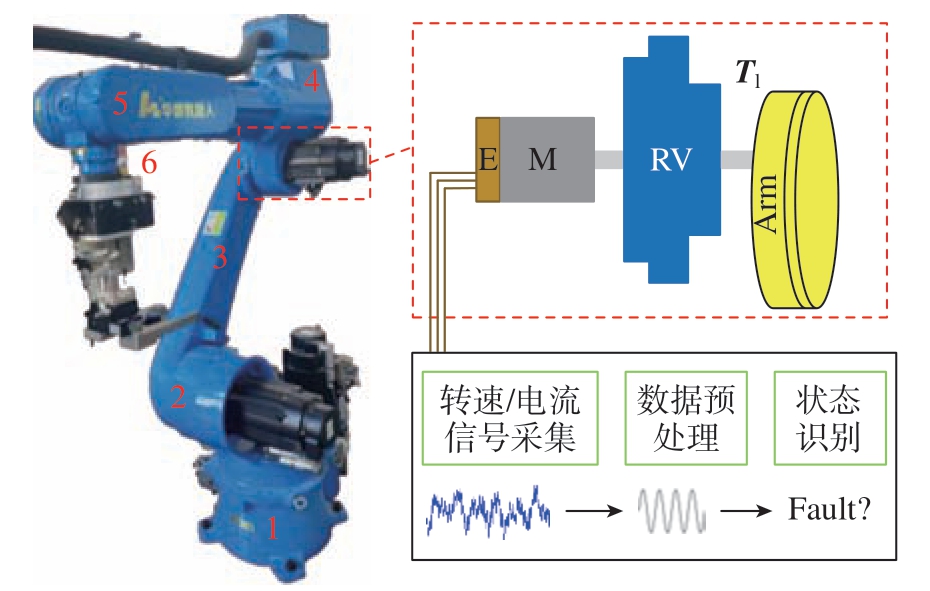
图4 伺服反馈信息状态监测原理图
Fig.4 Principle diagram of servo feedback information status monitoring
对RV 减速器在不同负载工况下采集到的信息使用K-means 聚类识别算法，训练出相应的关键参数，实现多种传动模式识别。伺服特征信息与RV 减速器负载关联性辨识模型由Python 编程实现，具体分类预测流程如图5 所示。
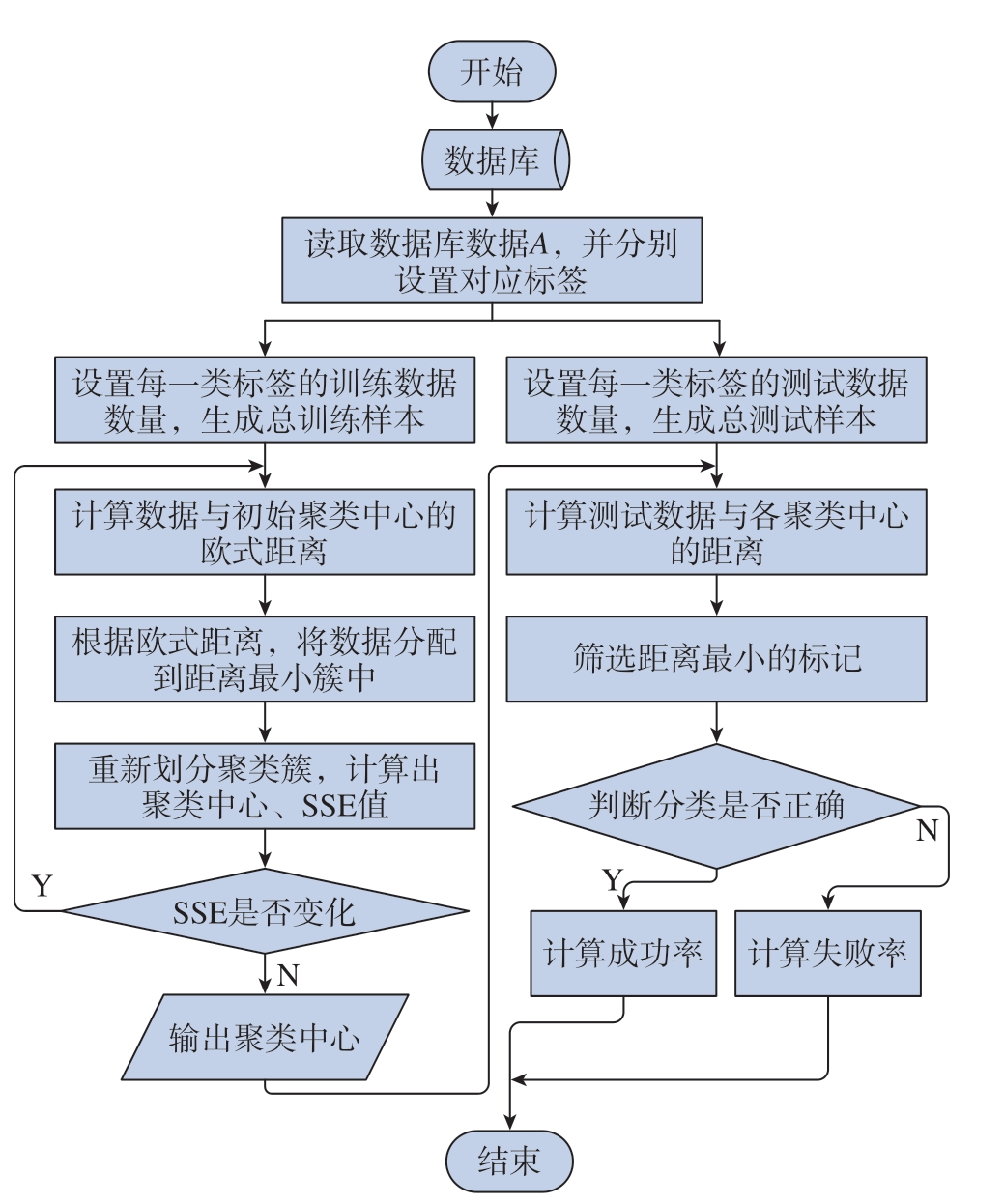
图5 K-means 聚类识别流程图
Fig.5 K-means clustering recognition flowchart
3 试验研究
3.1 测试平台搭建与数据获取
本文采用国产某公司出厂合格的减速器作为研究对象，具体参数见表1。通过RV 减速器试验测试台获取相应的试验数据，验证开发模型的适用性，具体测试平台如图6 所示。
图6 RV 减速器试验测试台
Fig.6 RV reducer test bench
试验平台主要包括数据存储与分析的笔记本电脑、用于驱动RV 减速器运动的伺服系统、对减速器输出量测量的扭矩/转速传感器、模拟负载的磁粉制动器以及联轴器等。驱动装置采用汇川技术生产的0.75 kW 具有23 位绝对值编码器的MS1H4 型交流伺服电机，其运行转速、电流、电压等信息均可由上位机软件进行实时采集。
本次试验设置了不同转矩、转速下的单因素单水平试验。用磁粉制动器模拟负载，分别设置10%、50%、100%、120%的RV 减速器额定负载转矩。使用PLC 控制伺服电机的输出转速，分别为减速器额定输入的10%、50%、80%、100%。遵循上述要求对磁粉制动器、伺服系统设置对应参数并开展试验，共计采集到16 组相应的转速与电流反馈信号，采样频率为1 kHz，每组采集32000个数据点。获得的原始电流数据如图7 所示 （部分）。
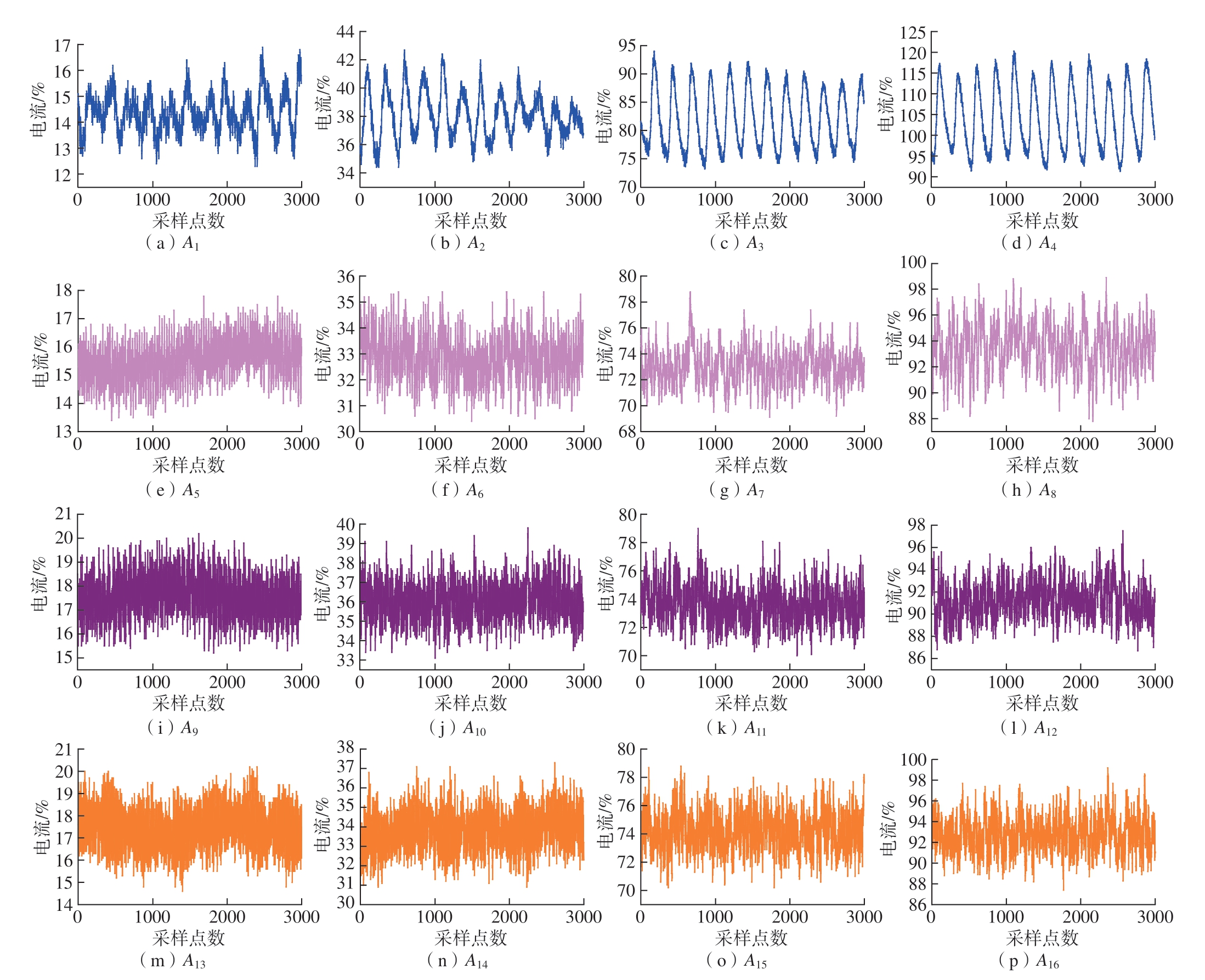
图7 反馈电流信号波形图 （部分）
Fig.7 Waveform of feedback current signal (partial)
图7 中，A1～A4 表示在10%额定转速下不同负载转矩时采集的数据；A5～A8 表示在50%额定转速下不同负载转矩时采集的数据；A9～A12 表示在80%额定转速下不同负载转矩时采集的数据；A13～A16 表示在额定转速下不同负载转矩时采集的数据。
3.2 数据处理与分析
在进行数据分析处理前，首先检查采样数据的完整性，避免在数据采集时遇到因模数转换设备异常、传输线通信错误、数据生成缺陷等问题导致的某段时间内出现空值等异常数据。如果存在缺失的现象，本文将采用均值填补，以确保数据的完整性。
因试验过程中，外界环境的变化容易导致奇异数据点及噪声产生，并且其对正确结果的预测影响比较大。文中利用3σ 准则统计识别方法剔除假数，剔除完数据点后对新数据进行重新验证，直到满足要求为止。
根据前文中的理论分析可知，伺服系统中的相电流与负载状况、转速等密切相关。利用RV 减速器主要部件的转动频率及啮合频率的计算公式计算出RV 减速器在上述4 种转速下的理论特征频率，如表2 所示。
表2 不同转速下RV 减速器重要频率
Table 2 Important frequency of RV reducer at different speeds
转速/（r·min–1） fe/Hzf1/Hzf2/Hzf3/Hzfsp/Hzfcs/Hz 181.515.125 3.0250.9750.0253339 907.575.625 15.125 4.8750.125165195 145212124.27.80.2264312 1815151.25 30.259.750.25330390
为突出核心问题，文中简化分析过程，并考虑实际工作中RV 减速器的传递速度和扭矩均会有所波动，仅使用上文中A1（181.5 r/min）、A6（907.5 r/min）、A11（1452 r/min）、A16（1815 r/min） 4 种时域电流信号对信号进行快速傅里叶变换并提取相应的特征频率，得到图8 所示的频谱图。
图8 不同工况下的频谱图
Fig.8 Spectrograms under different operating conditions
通过上述时频域转换后，对特定频率使用红色星形进行标记。经分析发现，除图8（c）部分频率特征不明显以外，在多数情况下可以很好地提取到RV 减速器的工作频率，与理论值相差较小。上述结果证明伺服系统相电流频谱中包含RV 减速器的固有频率，利用其反馈信息可以进行状态监测。但是也不难发现，利用频谱信息并不能对负载情况进行清晰判断识别，接下来将采用电流、转速信息聚类融合的方法对负载工况进行分类识别。
3.3 关联性验证与对比分析
为进一步验证伺服系统运行特征与负载的关联性，继而基于伺服系统反馈的信息开发出RV 减速器运行状态准确识别模型。本文将采集到的数据分为训练集与测试集，分别输入到K-means 聚类识别模型中进行训练与分类预测，从而对减速器的16 种运行状态进行聚类识别，各状态下的标签从1～16 依次命名，即K 值取16。本次试验在A1～A16 的每组数据中各随机选取30000 个数据点作为训练集，通过K-means 聚类模型获得各簇的聚类中心。经聚类模型识别处理后，各数据点会被划分到16 个类簇，聚类中心位置如图9 中的五角星所示。
图9 聚类中心分布情况
Fig.9 Distribution of clustering centers
可以看出，在10%额定转速下产生了聚类混叠现象，这是因为在低转速、超额负载下，伺服电机接近报警状态，需要短时间内提供超额转矩导致电流波动较大；在低负载状态下聚类中心较重载更明确，可以清楚地划分出其边界；RV 减速器工作在额定转速时，对4 种工况辨识也比较清晰。
在采集的每组数据中各随机选取300 个数据点作为测试集，用于测试上述模型的准确性。结果表明，整体试验预测准确率可以达到97.45%以上，分类结果如图10 所示。
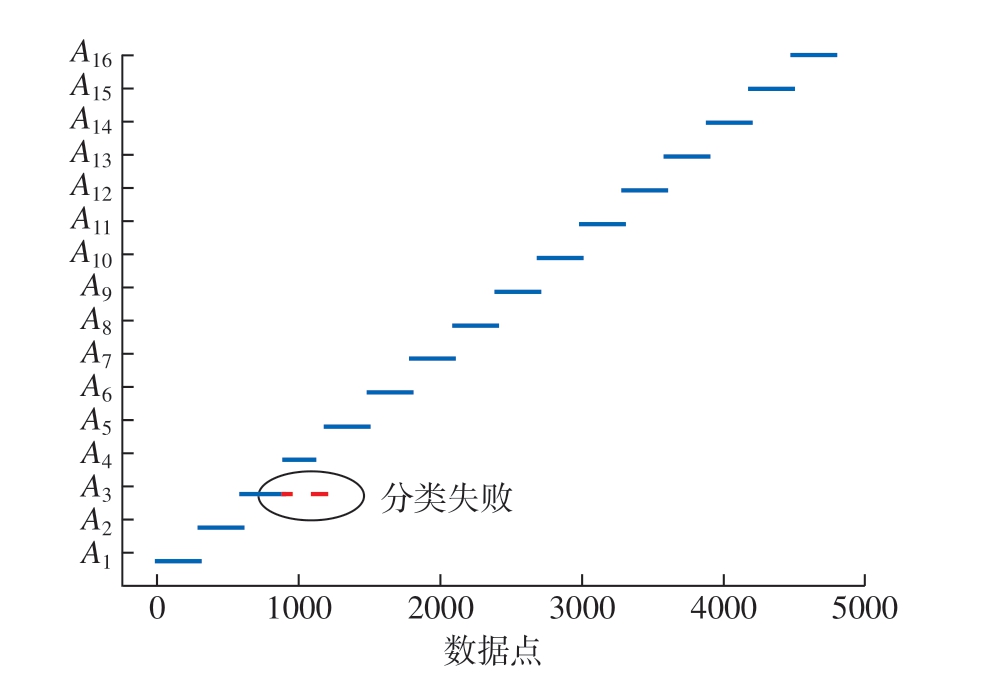
图10 分类预测结果
Fig.10 Classification prediction results
观察图10 中的数据可知，分类失败点主要集中于低转速重负载情况，在其余的试验工况下分类预测准确率均较高。预测结果很好地印证了RV 减速器运行稳定情况下，其负载与伺服系统反馈信号有很好的关联性，也说明了工业机器人在重负载状态下特征信息分布不均，不利于传动精度控制。
4 结论
研究了基于K-means 聚类的伺服系统运行特征信息对RV 减速器传动负载识别方法，分析了输入转速与RV 减速器关键频率、伺服特征信息与负载的关系，搭建对应的试验平台，试验验证了该方法的有效性，得到以下结论。
（1）对伺服传动链系统进行理论分析得到电机运行受负载角速度、角加速度、负载等因素影响，仅采集单一反馈信号，难以实现负载工况的准确识别。
（2）对试验采集的电流信号进行频谱分析发现，频率谱中可以有效提取到RV 减速器的转动频率及啮合频率，伺服特征信息可用于RV 减速器运行工况识别。
（3）使用训练集数据对伺服特征信息与RV 减速器负载关联性模型进行训练，计算出不同工况下的聚类中心点，可用于负载状态的识别监测。测试集的验证表明，通过伺服电机的特征信息可以对减速器的传动负载进行实时的监测，预测精度可以达到97.45%，可为“无”传感故障诊断提供技术支撑。
[1] 王皓, 陈根良. 机器人型装备在航空装配中的应用现状与研究展望[J]. 航空学报, 2022, 43(5): 41–63.
WANG Hao, CHEN Genliang. Research progress and perspective of robotic equipment applied in aviation assembly[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(5): 41–63.
[2] 许斌, 周新房, 王伟华, 等. 面向飞机长桁壁板的柔性化机器人涂胶系统[J]. 航空制造技术, 2022, 65(19): 100–106, 118.
XU Bin, ZHOU Xinfang, WANG Weihua, et al. Flexible robot gluing system for aircraft stringer and skin[J]. Aeronautical Manufacturing Technology, 2022, 65(19): 100–106, 118.
[3] DA SILVA SANTOS K R, VILLANI E, DE OLIVEIRA W R,et al. Comparison of visual servoing technologies for robotized aerospace structural assembly and inspection[J]. Robotics and Computer-Integrated Manufacturing, 2022, 73: 102237.
[4] SÉGUIN-CHARBONNEAU L, WALTER J, THÉROUX L D, et al. Automated defect detection for ultrasonic inspection of CFRP aircraft components[J]. NDT & E International, 2021, 122: 102478.
[5] MEI B, ZHU W D. Accurate positioning of a drilling and riveting cell for aircraft assembly[J]. Robotics and Computer-Integrated Manufacturing, 2021, 69: 102112.
[6] 孙守政, 赵尧旭, 王扬, 等. 热塑性复合材料机器人铺放系统设计及工艺优化研究[J]. 机械工程学报, 2021, 57(23): 209–219.
SUN Shouzheng, ZHAO Yaoxu, WANG Yang, et al. Design of robotic fiber placement machine and process optimization for thermoplastic composites[J]. Journal of Mechanical Engineering, 2021, 57(23): 209–219.
[7] LI B, TIAN W, ZHANG C F, et al. Positioning error compensation of an industrial robot using neural networks and experimental study[J].Chinese Journal of Aeronautics, 2022, 35(2): 346–360.
[8] 刘春梅, 郑硕, 郭文凤, 等. 基于工业机器人的数字化弯管成形技术研究[J]. 航空制造技术, 2022, 65(13): 63–69.
LIU Chunmei, ZHENG Shuo, GUO Wenfeng, et al. Research on digital tube bending technology based on industrial robot[J]. Aeronautical Manufacturing Technology, 2022, 65(13): 63–69.
[9] BUCKINGHAM R O, GRAHAM A C. Dexterous manipulators for nuclear inspection and maintenance—Case study[C]//2010 1st International Conference on Applied Robotics for the Power Industry (CARPI 2010). Montreal, Piscataway, NJ: IEEE, 2010.
[10] 廖文和, 郑侃, 孙连军, 等. 大型复杂构件机器人加工稳定性研究进展[J]. 航空学报, 2022, 43(1): 156–175.
LIAO Wenhe, ZHENG Kan, SUN Lianjun, et al. Review on chatter stability in robotic machining for large complex components[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(1): 156–175.
[11] GONG T, YANG J H, LIU S Y, et al. Non-stationary feature extraction by the stochastic response of coupled oscillators and its application in bearing fault diagnosis under variable speed condition[J]. Nonlinear Dynamics, 2022, 108(4): 3839–3857.
[12] 韩特, 李彦夫, 雷亚国, 等. 融合图标签传播和判别特征增强的工业机器人关键部件半监督故障诊断方法[J]. 机械工程学报, 2022,58(17): 116–124.
HAN Te, LI Yanfu, LEI Yaguo, et al. Semi-supervised fault diagnosis method via graph label propagation and discriminative feature enhancement for critical components of industrial robot[J]. Journal of Mechanical Engineering, 2022, 58(17): 116–124.
[13] WANG X F, GUO Y X, XIONG L. Hybrid fiber Bragg grating sensor for vibration and temperature monitoring of a train bearing[J]. Chinese Optics Letters, 2018, 16(7): 070604.
[14] YU Z, QIU Z R, LI H, et al. Measuring the no-load running torque of RV reducer based on the SVD and MCSA[J]. Measurement, 2022,190: 110697.
[15] FENG K, BORGHESANI P, SMITH W A, et al. Vibrationbased updating of wear prediction for spur gears[J]. Wear, 2019, 426–427:1410–1415.
[16] AMINI F, HEDAYATI Y, ZANDDIZARI H. Exploiting the inter-correlation of structural vibration signals for data loss recovery: A distributed compressive sensing based approach[J]. Mechanical Systems and Signal Processing, 2021, 152: 107473.
[17] ZHANG R H, ZHOU J X, WEI Z. Study on transmission error and torsional stiffness of RV reducer under wear[J]. Journal of Mechanical Science and Technology, 2022, 36(8): 4067–4081.
[18] HE W D, SHAN L J. Research and analysis on transmission error of RV reducer used in robot[M]//Recent Advances in Mechanism Design for Robotics. Cham: Springer International Publishing, 2015: 231–238.
[19] 王庆锋, 刘家赫, 卫炳坤, 等. 数据驱动的聚类分析故障识别方法研究[J]. 机械工程学报, 2020, 56(18): 7–14.
WANG Qingfeng, LIU Jiahe, WEI Bingkun, et al. Research on data-driven clustering analysis fault identification method[J]. Journal of Mechanical Engineering, 2020, 56(18): 7–14.
[20] 柴娜. 伺服电机系统传动链典型故障诊断技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2021.
CHAI Na. Diagnosis technology investigation of typical faults of drive chain in servo motor system[D]. Harbin: Harbin Institute of Technology, 2021.
[21] HAMADACHE M, LEE D, VELUVOLU K C. Rotor speedbased bearing fault diagnosis (RSB-BFD) under variable speed and constant load[J]. IEEE Transactions on Industrial Electronics, 2015,62(10): 6486–6495.
[22] 孙桓, 葛文杰. 机械原理[M]. 9 版. 北京: 高等教育出版社,2021.
SUN Huan, GE Wenjie. Mechanical principle[M]. 9th ed. Beijing:Higher Education Press, 2021.
[23] GU J J, HUANG D S, TAN J, et al. Manufacturing quality assurance for a rotate vector reducer with vibration technology[J]. Journal of Mechanical Science and Technology, 2019, 33(5): 1995–2001.
[24] WANG H, SHI Z Y, YU B, et al. Transmission performance analysis of RV reducers influenced by profile modification and load[J].Applied Sciences, 2019, 9(19): 4099.
[25] XU K, WU X, WANG D X, et al. Electromechanical coupling modeling and motor current signature analysis of bolt loosening of industrial robot joint[J]. Mechanical Systems and Signal Processing,2023, 184: 109681.
[26] 谢刚. 基于数据挖掘的设备状态知识获取方法研究[J]. 航空制造技术, 2014, 54(1/2): 12–15.
XIE Gang. Device status knowledge acquisition method based on data mining[J]. Aeronautical Manufacturing Technology, 2014, 54(1/2): 12–15.
[27] 曲福恒, 潘日涛, 杨勇, 等. 基于加权空间划分的高效全局K-means 聚类算法[J/OL]. 吉林大学学报(工学版): 1–8(2022–12–16)[2023-11-20]. https://doi.org/10.13229/j.cnki.jdxbgxb20221338.
QU Fuheng, PAN Ritao, YANG Yong, et al. An efficient global K-means clustering algorithm based on weighted space partitioning[J/OL]. Journal of Jilin University (Engineering and Technology Edition): 1–8(2022–12–16)[2023-11-20]. https://doi.org/10.13229/j.cnki.jdxbgxb20221338.