商用航空市场需求的快速增长使得大量飞机订单积压,飞机制造商面临着提高产能的巨大挑战。空客公司预测至2036 年全球百座以上客机数量将会增加1 倍[1],中国将需要近6000 架新客机与货机[2]。这种强劲的需求增长导致订单的数量远远超过当前的生产制造能力。传统飞机装配过程中,主要采用刚性工装 (或定制化非标准柔性工装)结合手工作业的装配模式,导致装配周期长、成本高、质量稳定性较差等诸多问题,难以满足新一代飞机高精度、高性能、高效率、低成本批产制造要求。因此,广泛应用模块化、柔性灵活、稳定一致的工业机器人成为商用飞机装配生产线的发展趋势。空客公司在A320 系列新的装配生产线中应用了机器人自动化装配连接单元,可实现钻孔、紧固件的插入与紧固等装配连接工艺的自动化[3]。波音公司使用两台串联机器人协作完成波音777、777X 以及787 客机尾翼壁板中碳纤维长桁与复材蒙皮的装配[4]。针对机身筒段装配,波音公司在波音777 机身装配站位中采用固定式机器人与移载式机器人协同工作的形式完成机身壁板的连接[5],同时在波音787 筒段装配中使用了一种更为先进的机器人装配单元[6],该单元由4 台相同的机器人组成,在装配过程中同步工作,每台机器人都可以完成钻孔、锪窝、检测、密封以及紧固件安装等功能,大幅提高了装配效率与工艺质量。
随着新一代商用飞机服役性能的不断提高,其装配过程中对装配力控制的要求更为严苛[7]。然而,传统工业机器人多采用位移控制,装配过程中无法直接对装配力进行及时调整。因此,国内外学者围绕机器人力控制开展了大量的研究工作。卫月娥等[8]面向航天器装配开展了工业机器人柔性力控研究。Fernandez 等[9]提出了多面导纳控制方法并应用于飞机大型复杂零件装配定位。Lee等[10]基于隐式力位控制改善了碳纤维材料钻孔质量。Wang 等[11]提出了一种新型力控末端执行器,提高了机器人磨削薄壁零件的工艺质量。Wu等[12]采用可变导纳控制实现了飞机大部件柔性辅助装配。在机器人力控制过程中,由于重力场的影响,机器人末端传感器测量值包含了末端负载的重力分量,且其会随着机器人末端位姿的改变而变化,传感器示值无法准确表征真实的外部装配力,因此,需要对末端负载的重力分量进行补偿。Vougioukas[13]通过将机器人运动到特定的姿态以抵消重力分量。缪新[14]、高强[15]、文科[16]等通过不同姿态下机器人控制器中的姿态数据与力传感器数据进行标定。上述研究都在一定程度上实现了对重力分量的补偿,但是受限于机器人末端姿态测量的方法以及机器人的安装误差,其补偿效果仍存在一定的局限性。
为更加精准地补偿机器人末端负载的重力分量,需要精确获取机器人末端负载的位姿。激光跟踪仪作为飞机装配中常用的测量设备,其测量精度可达10 μm + 5 μm/m,结合T-Mac 可实现空间位姿的高精度测量。因此,本文提出一种基于激光跟踪仪的机器人末端负载重力辨识与在线补偿方法,通过建立机器人全局运动学模型获取末端负载的空间位姿,基于卡尔曼滤波方法对力感知信息进行降噪预处理,同时在考虑力传感器的零点偏移与机器人安装偏差的条件下构建末端负载重力分量与位姿的映射关系,最终通过试验验证了本文方法的有效性。
1 机器人系统组成与全局运动学模型建立
该系统主要由机器人、激光跟踪仪、T-Mac、六维力传感器、控制系统组成,如图1 所示。其中,激光跟踪仪与T-Mac 用于测量机器人末端位姿,六维力传感器用于测量外界环境作用于机器人末端的力与力矩,控制系统包含了数据采集处理系统与机器人运动控制器,数据采集处理系统实现位姿与力/力矩测量数据的采集,在处理后得到的机器人运动量通过以太网发送至机器人运动控制器,从而控制机器人运动。
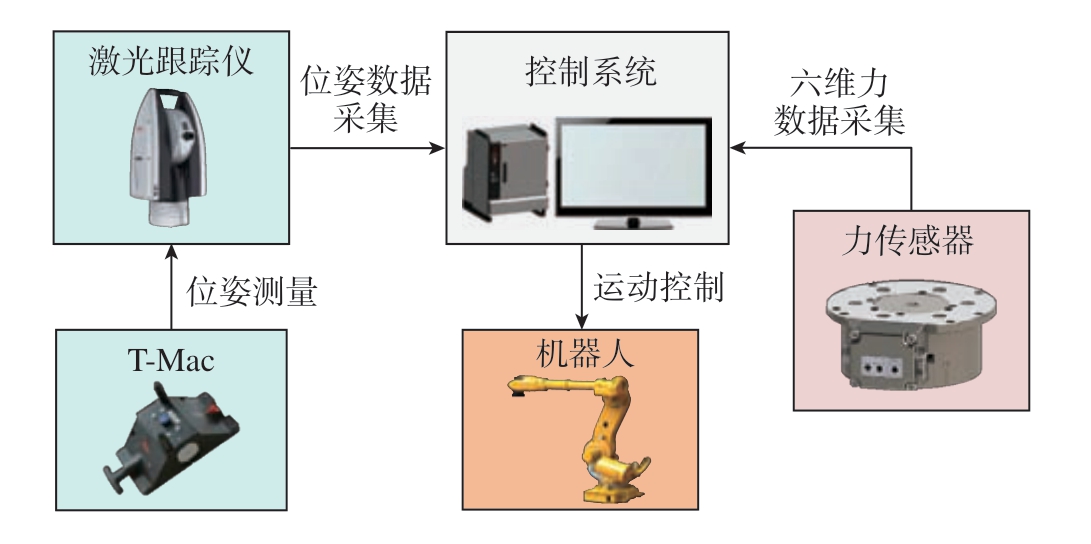
图1 机器人系统结构图
Fig.1 Structure diagram of robot system
机器人末端重力分量的在线计算需要机器人移动六维力传感器等末端工作负载至空间中的特定位置,而机器人控制器中的法兰位姿与激光跟踪仪测量得到的位姿并不一致。因此,需要建立机器人系统的全局运动学模型,获取六维力传感器坐标系与T-Mac、机器人法兰间的相对位姿变换关系,统一运动坐标系。为了建立机器人系统全局运动学关系,采用激光跟踪仪结合T-Mac 作为外部测量设备,如图2 所示,定义各坐标系如下:OLT 为激光跟踪仪坐标系;OB为机器人基座坐标系;OF 为机器人法兰中心坐标系;OT 为T-Mac 坐标系;OS 为六维力传感器坐标系。其中,T-Mac、力传感器均固定于机器人法兰之上,因此坐标系OT、OS 与OF 相互之间的变换关系应保持不变。同理,激光跟踪仪坐标系OLT 与机器人基座坐标系OB 间的变换关系恒定。采用齐次变换矩阵定义坐标系OY 相对于OX 的变换,即
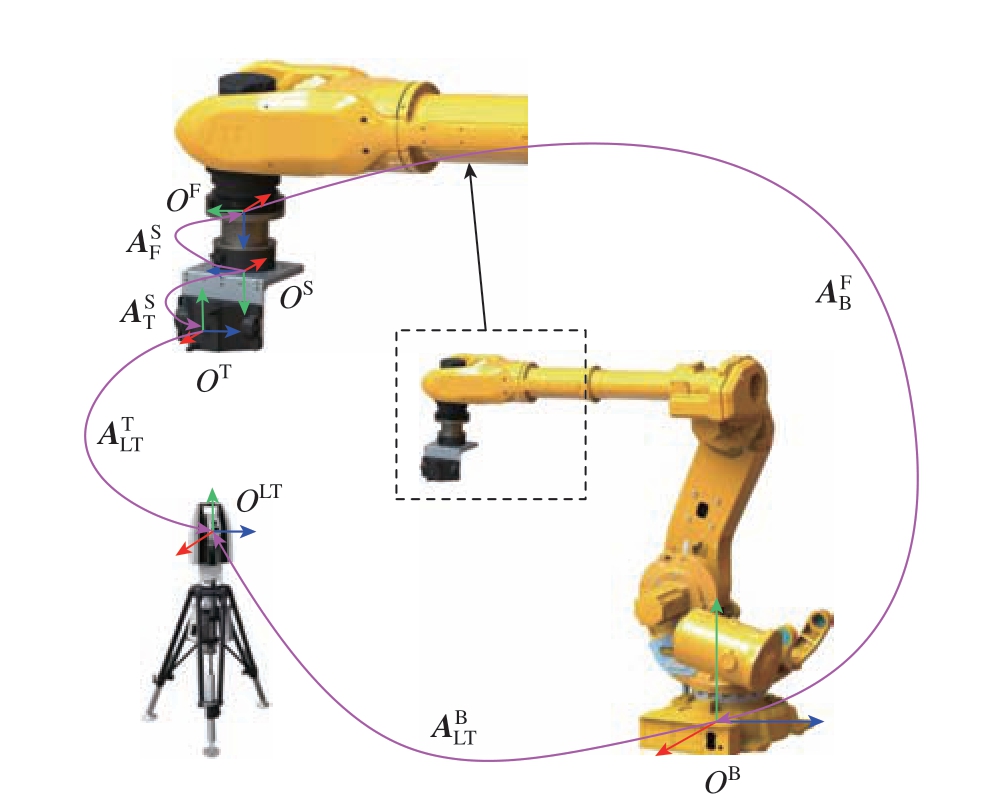
图2 机器人系统全局运动学模型
Fig.2 Global kinematic model of robot system
式中,![]() 表示OY 相对于OX 的旋转矩阵
表示OY 相对于OX 的旋转矩阵![]() 为平移向量。
为平移向量。
机器人系统中各坐标系间的齐次变换矩阵满足式 (2)。
式中,![]() 前期可通过激光跟踪仪与靶球进行标定;
前期可通过激光跟踪仪与靶球进行标定;![]() 在机器人工作过程中由激光跟踪仪实时跟踪T-Mac测量获取;
在机器人工作过程中由激光跟踪仪实时跟踪T-Mac测量获取;![]() 由机器人控制器直接读取。
由机器人控制器直接读取。![]() 与
与![]() 为未知常量,需要通过机器人的多次相对运动进行辨识。
为未知常量,需要通过机器人的多次相对运动进行辨识。
在经过第i 次运动后,六维力传感器坐标系![]() 与机器人法兰坐标系
与机器人法兰坐标系![]() 与运动后的坐标系
与运动后的坐标系![]() 满足:
满足:
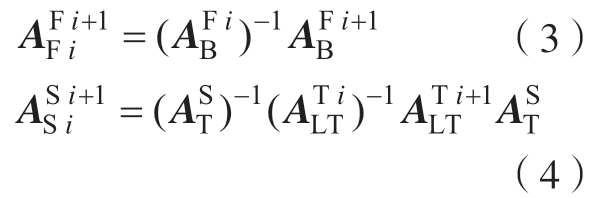
为求解![]() ,构建方程:
,构建方程:
令![]()
![]() X,其中α,β,γ,δ∈R3,将式(5)改写为
X,其中α,β,γ,δ∈R3,将式(5)改写为
对式 (6)的系数进行重新排列,可得
式中,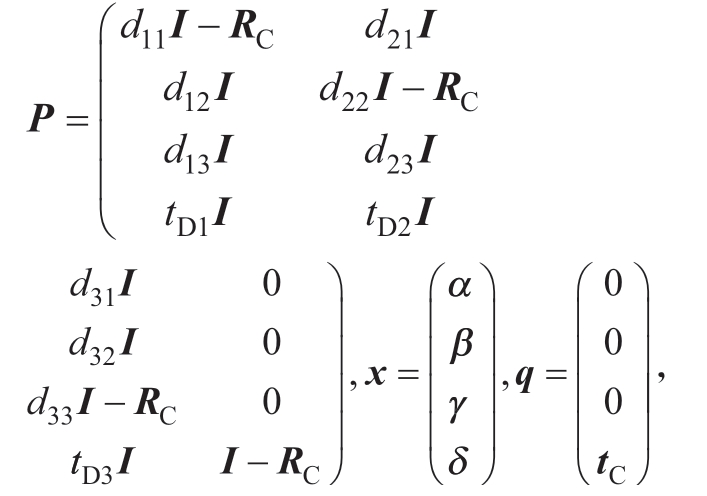 dij 为矩阵RD 第i 行第j 列元素;tDi 为向量tD 的第i 个元素;I 为单位矩阵。
dij 为矩阵RD 第i 行第j 列元素;tDi 为向量tD 的第i 个元素;I 为单位矩阵。
由于RC 为标准旋转矩阵,具有正交性,det(I – RC)=0,矩阵P 不满秩。因此,通过多次非纯平移且旋转线性无关的运动建立多个方程,采用最小二乘的方法求解x,即未知常量![]() ,代回式 (2)即可获取所有未知常量,建立起机器人系统的全局运动学模型。
,代回式 (2)即可获取所有未知常量,建立起机器人系统的全局运动学模型。
2 力感知信息预处理
作用在机器人末端上的外力/力矩通过力传感器测量获取。受电压、温度、振动等外部因素的影响,力传感器实际采集到的六维力信号会在一定范围内波动。因此,为了获得更加准确平稳的外部力信息,需要对采集到的六维力信号进行预处理,减少外部因素产生的噪声。
为满足实时获取力感知信息的要求,采用卡尔曼滤波对六维力信号进行预处理。卡尔曼滤波考虑系统的当前状态以及系统的过程噪声与测量噪声,通过迭代的方式对系统状态进行最优估算,无须系统整体的数据,适用于对力感知信息的实时处理。
六维力传感器数据采集的系统状态变量为力/力矩数值xj 与力/力矩变化率x.j,其中j∈{Fx,Fy,Fz,Mx,My,Mz},代表力/力矩的形式与方向。系统状态空间方程可表示为
式中,![]()
![]() 分别表示tk+1 时刻与tk 时刻的系统状态变量;
分别表示tk+1 时刻与tk 时刻的系统状态变量;![]() 为系统状态转移矩阵;ΔT 表示力传感器的采样周期;
为系统状态转移矩阵;ΔT 表示力传感器的采样周期;![]() 表示系统过程噪声向量,一般认为这些噪声是标准差为σ 的随机白噪声,且变化相互独立,因此,系统过程的噪声的协方差矩阵Qj 可表示为
表示系统过程噪声向量,一般认为这些噪声是标准差为σ 的随机白噪声,且变化相互独立,因此,系统过程的噪声的协方差矩阵Qj 可表示为
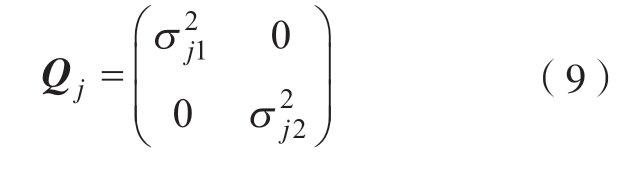
此外,力传感器数据采集的系统观测方程可表示为
式中,![]() 表示tk+1 时刻系统的观测值;H=(1 0)表示系统观测矩阵;
表示tk+1 时刻系统的观测值;H=(1 0)表示系统观测矩阵;![]() 表示力的观测噪声,一般认为各方向的力/力矩的观测噪声为相互独立的标准差为σmj 的随机白噪声。
表示力的观测噪声,一般认为各方向的力/力矩的观测噪声为相互独立的标准差为σmj 的随机白噪声。
由此,该系统的卡尔曼滤波过程可表示为[17]
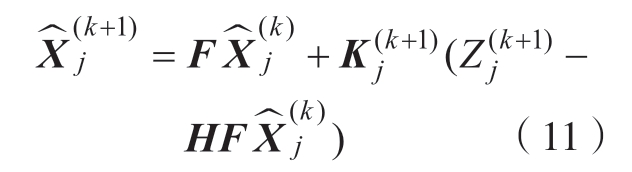
式中,![]() 分别表示tk+1 时刻与tk 时刻的最优估计值。
分别表示tk+1 时刻与tk 时刻的最优估计值。![]() 代表卡尔曼增益,其满足以下方程:
代表卡尔曼增益,其满足以下方程:
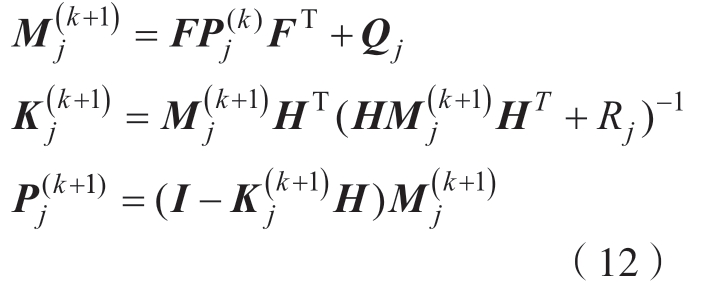
式中,![]() 表示更新前与更新后的误差协方差矩阵,观测噪声
表示更新前与更新后的误差协方差矩阵,观测噪声![]() 。
。
通过式(11)和 (12)的迭代计算,可实现对力传感器信息的预处理,使其更加平稳。
3 末端负载重力分量与位姿的映射关系
在装配过程中,六维力传感器的测量示值主要包含了装配力、机器人末端所有负载的重力分量、惯性力以及在末端负载不受其他外力条件下力传感器的零点偏移 (“零漂”)。惯性力在装配中低速运动的工况下可以忽略不计。因此,为了获得真实的装配力,需要对机器人末端负载进行重力辨识,并考虑力传感器的“零漂”,建立重力分量与位姿的映射关系,将力传感器测量值中的重力分量补偿去除。
构建重力分量与位姿的映射关系需要求解末端负载的重量G 与重心在力传感器坐标系OS 下的位置xcog,如图3 所示。由于“零漂”的存在,在仅有重力作用下六维力传感器的力与力矩测量值Fm、Mm 应为
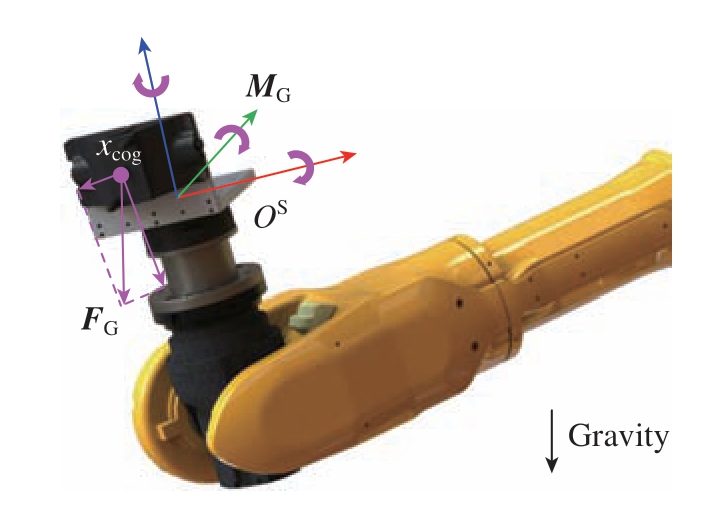
图3 末端负载重力分量示意图
Fig.3 Gravity component of end-effector
式中,FG 为重力分量;F0 与M0 为力传感器的“零漂”,其为随机常量,在每一个上电工作周期中可认为保持不变;S(xcog)为叉乘矩阵,用于计算xcog 与其他向量的叉乘,即
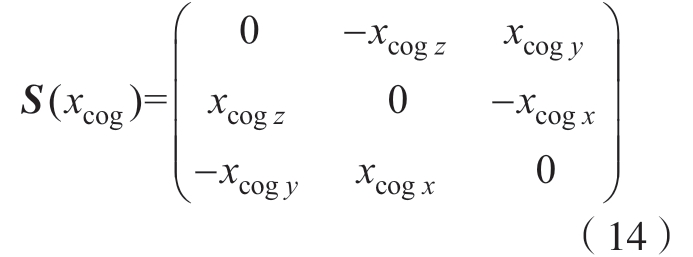
机器人末端负载在任意姿态下,力传感器测量值中的重力分量可表示为
为了消除“零漂”的影响,在每个上电工作周期中设定一个末端负载的初始姿态,即![]() 。在该姿态下末端负载的重力分量为
。在该姿态下末端负载的重力分量为![]() ,力与力矩的测量值
,力与力矩的测量值![]() 设置为“零点”,随后力与力矩的测量值均为相对于该“零点”的变化量,即
设置为“零点”,随后力与力矩的测量值均为相对于该“零点”的变化量,即
可以看出,此时力传感器的测量值不再与“零漂”有关。
为了快速准确地获取末端负载的重量G,在激光跟踪仪测量位姿的修正下,令机器人末端负载初始姿态下传感器坐标系OS 的Z 轴沿重力加速度方向竖直向下,此时记力传感器的力示值![]() 为 “零点”;随后,控制机器人运动使OS 的Z 轴沿重力加速度方向竖直向上,力传感器示值为
为 “零点”;随后,控制机器人运动使OS 的Z 轴沿重力加速度方向竖直向上,力传感器示值为
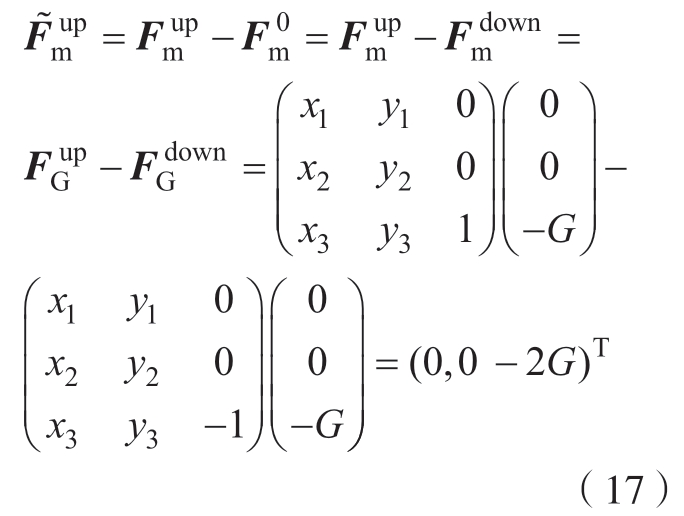
基于前述建立的机器人全局运动学模型,利用激光跟踪仪获取当前力传感器的相对位姿并进行修正,消除了机器人底座安装时的偏差造成的机器人基座坐标系OB 的Z 轴方向与重力加速度方向不平行的影响,确保了末端负载重量测量的准确性。
对于设置“零点”后力传感器的力矩测量值,可表示为
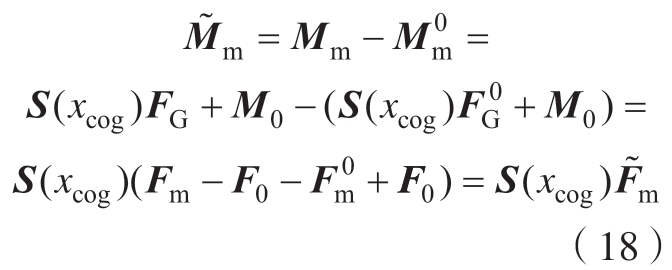
此时,六维力传感器力矩与力的测量值的关系不再与“零漂”有关,且“零点”设置的数值不影响测量外部力与力矩的变化。为求解末端负载重心在力传感器坐标系OS 下的位置xcog,需要测量机器人末端负载在j(j≥4)个不同姿态下力与力矩的测量值,利用最小二乘方法进行求解,即
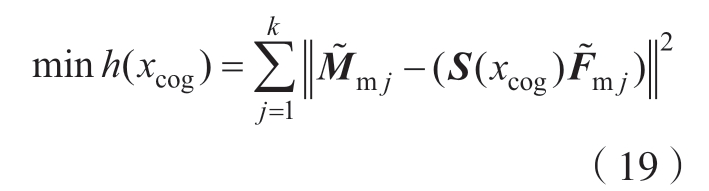
在获得末端负载重量G 与重心位置xcog 后,即可计算出当前姿态下的重力分量。至此,末端负载重力分量与位姿的映射关系建立完成。
4 末端负载重力辨识与在线补偿试验验证
为了验证上述方法的有效性,开展并完成了末端负载重力辨识与在线补偿试验,如图4 所示。试验中使用的机器人为ABB IRB 6640机器人,六维力传感器采用ATI Omega 160 型力传感器,激光跟踪仪型号为Leica AT960 MR,搭配T-Mac TMC30 – B。

图4 末端负载重力辨识与在线补偿试验
Fig.4 Experiment of gravity identification and online compensation
根据力传感器现场采集的数据,基于卡尔曼滤波对六维力感知信息进行预处理,设定系统的过程噪声![]()
![]() ,各通道系统的观测噪声均为
,各通道系统的观测噪声均为![]() ,采样频率为1000 Hz。六维力传感器的原始数据与实时预处理后的数据如图5 所示。可以看出,经过处理后的信号仍然能够跟随原始信号变化,并且信号波动的幅值明显减小,说明力感知信息预处理能够有效抑制原始测量数值中的噪声,使力与力矩的测量值更加平稳准确。
,采样频率为1000 Hz。六维力传感器的原始数据与实时预处理后的数据如图5 所示。可以看出,经过处理后的信号仍然能够跟随原始信号变化,并且信号波动的幅值明显减小,说明力感知信息预处理能够有效抑制原始测量数值中的噪声,使力与力矩的测量值更加平稳准确。
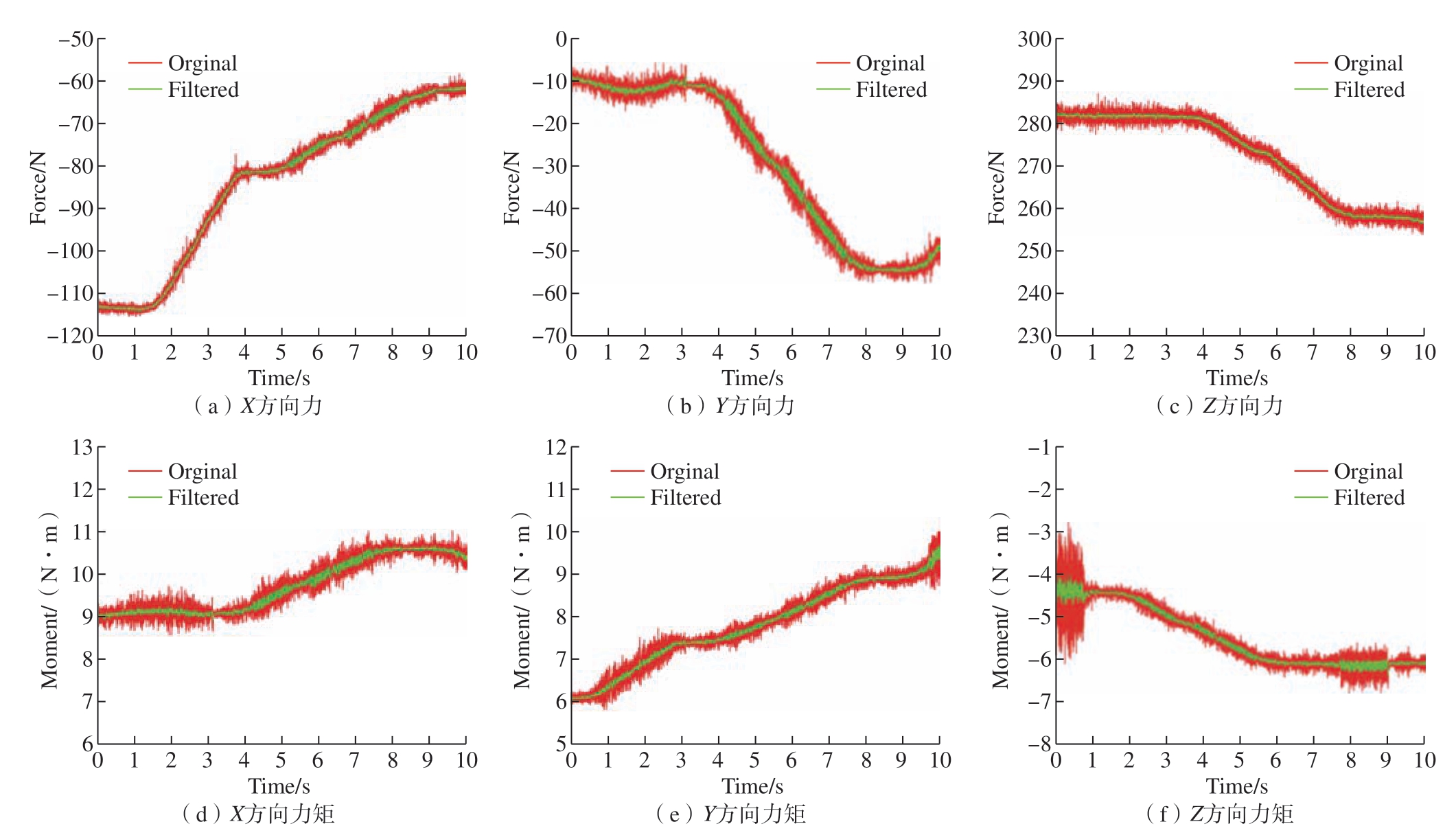
图5 力感知信息预处理结果
Fig.5 Result of pre-process of F/T signals
在重力辨识试验中,机器人末端负载的总重量约为175 N,在经过“零点”设置以及图6 所示的一系列的重力辨识运动后,辨识结果为末端重量G = 176.032 N,重心位置坐标为(0.032 m,0.013 m,0.043 m)。结合激光跟踪仪测量得到的T-Mac 空间位姿与机器人全局运动学模型,获取六维力传感器在空间中的位姿,基于辨识结果建立重力分量测量值与位姿的映射关系。随后,令末端负载在各方向进行任意旋转,并对该过程中六维力传感器测量值进行在线补偿,结果如图7 所示。在仅受重力情况下,未经补偿时,六维力传感器测量值随着机器人末端位姿的改变而变化,通过在线补偿,使得六维力传感器测量值不再受到负载重力分量的影响 (补偿后力测量值在±0.5 N 内波动,力矩测量值在±0.8 N·m 内波动),由此,力传感器测量值可以更加真实地反映机器人末端所受外力。

图6 机器人重力辨识运动
Fig.6 Movement of robot gravity identification
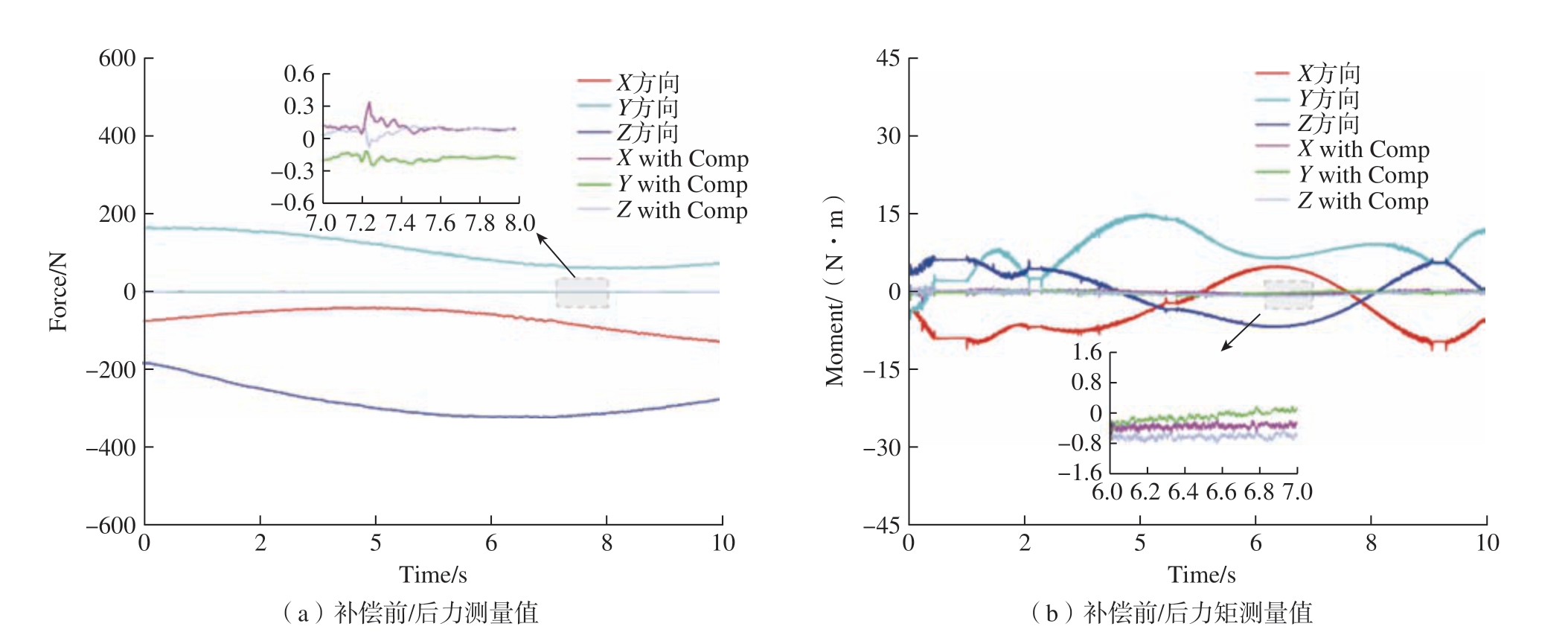
图7 重力在线补偿结果
Fig.7 Result of gravity online compensation
5 结论
本文提出了一种基于激光跟踪仪的机器人末端负载重力辨识与在线补偿方法,利用激光跟踪仪建立机器人的全局运动学模型,将测量得到的T-Mac空间位姿转换为力传感器位姿,在基于全局运动学模型与最小二乘法求解机器人末端负载重力参数的过程中,对力感知信息进行了预处理,同时考虑了传感器“零漂”,并消除了机器人底座安装时的误差带来的影响,最后通过试验验证了该方法的有效性,取得了良好的补偿效果。
[1] AIRBUS. Global services market set to double over the next 20 years[EB/OL].(2017–06–21)[2023–03–04]. https://www.airbus.com/en/newsroom/press-releases/2017-06-global-services-market-set-to-double-overthe-next-20-years.
[2] AIRBUS. China will need almost 6,000 new aircraft in the next 20 years[EB/OL]. (2016–11–02)[2023–03–04]. https://www.airbus.com/en/newsroom/press-releases/2016-11-china-will-need-almost-6000-new-aircraftin-the-next-20-years.
[3] AIRBUS. Airbus inaugurates new A320 structure assembly line in Hamburg[EB/OL]. (2019–10–01)[2023–03–04]. https://www.airbus.com/en/newsroom/press-releases/2019-10-airbus-inaugurates-new-a320-structureassembly-line-in-hamburg.
[4] LANDAU C. High accuracy assembly of large aircraft components using coordinated arm robots[R]//SAE Technical Paper Series. 400 Commonwealth Drive, 2016: 2016–01–2133.
[5] Boeing. Boeing introduces new method for building 777 fuselages[EB/OL]. (2014–07–14)[2022–03–04]. https://boeing.mediaroom.com/2014-07-14-Boeing-Introduces-New-Method-for-Building-777-Fuselages.
[6] EVERHART T. Neighboring mobile robot cell with drilling and fastening[R]//SAE Technical Paper Series. 400 Commonwealth Drive, 2017: 2017–01–2094.
[7] 杨应科, 李东升, 沈立恒, 等. 大型复合材料机身壁板多机器人系统装配调姿控形方法[J]. 航空学报, 2023, 44(14): 428006.
YANG Yingke, LI Dongsheng, SHEN Liheng, et. al. Pose and shape adjustment method for CFRP fuselage panel based on multi-robot collaboration[J]. Acta Aeronautica et Astronautica Sinica, 2023, 44(14): 428006.
[8] 卫月娥, 张成立, 孟伟, 等. 面向航天器装配的机械臂柔性力控研究[J]. 航空制造技术, 2014, 57(21): 147–152.
WEI Yuee, ZHANG Chengli, MENG Wei,et. al. Study on flexible force control on robot arm for spacecraft assembly[J]. Aeronautical Manufacturing Technology, 2014, 57(21): 147–152.
[9] FERNANDEZ S R, OLABI A,GIBARU O. Multi-surface admittance control approach applied on robotic assembly of largescale parts in aerospace manufacturing[C]//International Conference on Advanced Robotics.Belo Horizonte, 2019.
[10] LEE J, HONG T, SEO C, et al.Implicit force and Position control to improve drilling quality in CFRP flexible robotic machining[J]. Journal of Manufacturing Processes.2021, 68: 1123–1133.
[11] WANG Q, WANG W, ZHENG L,et. al. Force control-based vibration suppression in robotic grinding of large thin-wall shells[J].Robotics and Computer Integrated Manufacturing.2021, 67: 102031.
[12] WU C, SHEN Y, LI P, et. al.Compliance auxiliary assembly of large aircraft components based on variable admittance control[C]//Intelligent Robotics and Applications:14th International Conference. Yantai, 2021.
[13] VOUGIOUKAS S. Bias estimation and gravity compensation for force-torque sensors[C]//Proceedings of International Conference on Mathematical Methods and Computational Techniques in Electrical Engineering. Athens, 2001.
[14] 缪新, 田威. 机器人打磨系统控制技术研究[J]. 机电一体化, 2014(11): 8–14.
MIU Xin, TIAN Wei. The control technology on robotic grinding system[J].Mechatronics, 2014(11): 8–14.
[15] 高强, 田凤杰, 杨林, 等. 机器人自动研抛系统平台搭建及重力补偿研究[J]. 工具技术, 2015, 49(8): 47–50.
GAO Qiang, TIAN Fengjie, YANG Lin,et. al. Research on platform of robot automatic polishing system and gravity compensation[J].Tool Engineering, 2015, 49(8): 47–50.
[16] 文科, 杜福洲, 张铁军, 等. 舱段类部件数字化柔性对接系统设计与试验研究[J].航空制造技术, 2017, 60(11): 24–31.
WEN Ke, DU Fuzhou, ZHANG Tiejun, et al. Research on design and experiment for digital flexible aligning system of cabin component[J].Aeronautical Manufacturing Technology, 2017,60(11): 24–31.
[17] ZARCHAN P, MUSOFF H.Fundamentals of kalman filtering: A practical approach[M]. Forth Edition. Reston: American Institute of Aeronautics and Astronautics, Ivnc.,2015.
