高性能齿轮是重要的机械基础件，工况多为高速重载[1]。为提高齿轮疲劳寿命，优化齿轮服役性能，一般在全流程制造末端加入喷丸工序[2–4]。喷丸强化利用高速弹丸冲击零件表面，使工件受喷表面发生不均匀塑性变形，诱导残余压应力产生[5]。较好的残余应力分布可提高齿轮的接触疲劳强度、弯曲疲劳强度、抗胶合能力，从而改善零件服役性能[6–7]。
采用喷丸工艺提高齿轮疲劳强度，需充分发挥喷丸强化因素影响效果，即最大程度提高残余压应力值。因此，了解喷丸后齿面残余应力分布与工艺参数关联规律，优化喷丸工艺参数是提高齿轮服役性能的关键[8]。生产中利用试验摸索进行工艺编制，需耗费大量的时间和精力，开展喷丸工艺仿真研究可以节约资源，为工业制造提供指导。
现有喷丸残余应力预测模型主要基于有限元方法。Miao 等[9]建立了与实际喷丸过程相近的随机多弹丸有限元模型，因此被广泛应用。基于此，李源等[10]利用Python 语言编写了ABAQUS 子程序，模拟多弹丸随机入射Q235 钢板的过程，结果表明多弹丸模型模拟的残余压应力峰值和试验结果很接近。Bagherifard 等[11]利用试验对仿真结果进行了验证，并研究了部分工艺参数（如喷丸速度和弹丸尺寸等）与喷丸后残余应力的关系。目前喷丸工艺仿真模型主要针对平面或圆柱面试样，无需考虑弹丸之间的碰撞。但对于螺旋锥齿轮而言，其复杂曲面使弹丸间碰撞概率大大提高，弹丸碰撞成为仿真模型中必须考虑的因素。基于离散元的方法建立模型，可计算弹丸从喷嘴口到齿面的运动过程。结合离散元和有限元方法计算螺旋锥齿轮喷丸工艺强化效果，提高了仿真结果计算的准确性[12]，受到广泛使用。
本文通过建立螺旋锥齿轮的喷丸工艺仿真模型，计算喷丸后轮齿齿面表层残余应力分布状态。对比喷丸试验结果与仿真结果，以验证仿真计算准确性。基于该仿真模型，研究喷丸时间、弹丸速度、弹丸直径与喷丸后齿面残余压应力场的关联规律。
1 喷丸工艺试验
1.1 试验样件
喷丸样件为某型号螺旋锥齿轮，材料为AISI 9310高强度合金钢，齿部经渗碳淬火处理。齿面为喷丸强化的重要区域，其表面至0.56 mm 深度内，硬度均高于60HRC。
1.2 试验参数
试验采用MP1000Ti 型号数控喷丸机开展。弹丸类型采用ASH110（55～62HRC），喷丸强度为0.178～0.228 mmA，覆盖率200%、喷嘴角度17°、空气压力0.25 MPa、移动速度70 mm/min、喷丸时间144 s。对齿根、凸面、凹面分别进行强化，喷嘴与目标表面垂直，且距离150 mm，齿轮转台转速30 r/min，弹丸流量5 kg/min。
1.3 残余应力测量
对齿面进行残余应力测量，测量点位置如图1所示，a、b、c 均位于齿面节锥线上，依次为齿宽的四分点，a 靠近轮齿大端。为得到齿轮表层残余应力场，沿齿面法向对轮齿进行电解抛光，电解抛光深度由白光干涉仪测量得到。
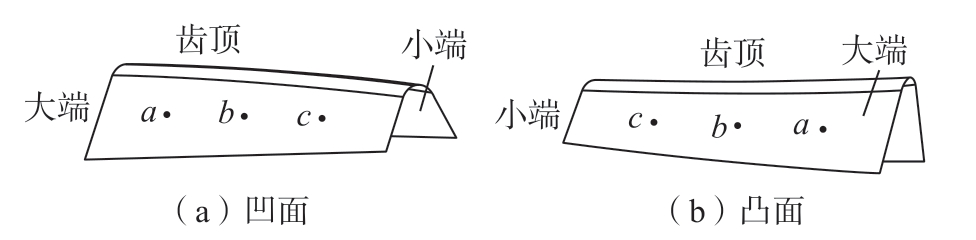
图1 残余应力测量点（a、b、c）位置示意图
Fig.1 Location diagram of residual stress measuring points (a,b and c)
利用加拿大Proto 公司的X 射线衍射仪测量齿面残余应力。管电压25 kV，管电流5 mA，X 射线管Cr_K–Alpha，光圈直径1 mm，波长2.291 A，曝光时间3 s，曝光次数7，最大β 角20°。测试照片如图2所示。电解抛光所用仪器为8818–V3 型号电解抛光仪，设置电压40 V，流量8，抛光时间3 s，抛光电流2.8～3 A。
图2 残余应力测试示意图
Fig.2 Measurement of residual stresses
2 仿真模型建立
由于螺旋锥齿轮曲面复杂，弹丸在齿面附近易发生相互碰撞，从而影响弹丸实际冲击速度及次数。为提高计算准确度，本文基于离散元及有限元耦合的方法建立喷丸工艺仿真模型，计算螺旋锥齿轮喷丸后齿面表层残余应力分布，计算流程如图3所示。建立螺旋锥齿轮喷丸离散元模型，获取齿面弹丸冲击速度矢量、单位面积冲击次数。将离散元计算结果作为输入，结合喷丸前齿面三维粗糙度、残余应力场、齿轮及弹丸材料模型，建立有限元模型，计算喷丸后轮齿表层残余应力场，分析喷丸时间、弹丸速度、弹丸直径等对喷丸后齿面残余应力场的影响。
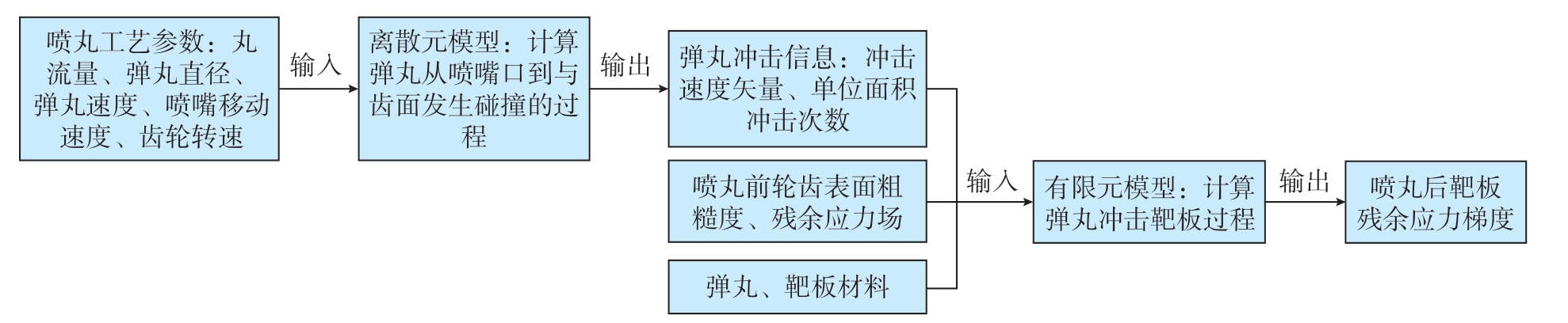
图3 离散元与有限元耦合计算模型流程图
Fig.3 Modeling diagram of coupling of discrete element method and finite element metho
2.1 离散元模型
2.1.1 模型建立
利用EDEM 仿真软件设置离散元模型，模拟弹丸从喷嘴到齿面的过程。
根据1.2 节工艺参数设置模型参数，几何模型如图4所示。为提取轮齿表面目标位置冲击信息，利用Hypermesh 软件对轮齿表面进行网格划分。在模型中，导入齿面单元作为齿轮模型，设置喷嘴分别垂直于齿轮的齿根、凸面、凹面，且距离目标表面 150 mm，并沿齿宽方向进行移动。弹丸初始速度由经验公式（1）确定[13]。
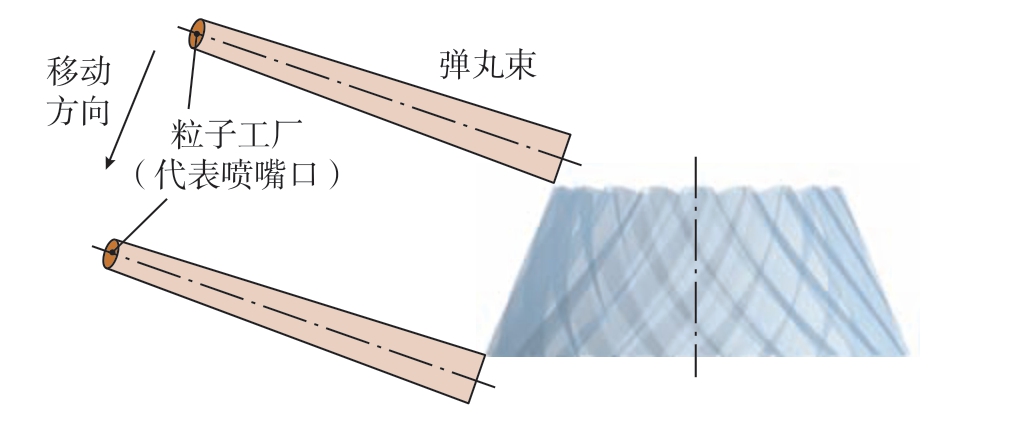
图4 DEM 几何模型示意图
Fig.4 Schematic view of DEM geometry
式中，d 为弹丸直径，mm；qm 为丸流量，kg/min；P 为喷嘴气压，MPa。
2.1.2 数据提取与处理
利用EDEM 软件导出计算结果，并利用单元编号判断冲击点位置，筛选出齿面节锥线上四等分点处的冲击，进行数据处理。
（1）冲击速度矢量。
由于齿轮为曲面，各位置与弹丸束的夹角不同，且有限元模型中靶板为齿面上的局部区域。因此，需将弹丸的绝对速度转换为齿面单元与弹丸的相对速度。
如图5所示，曲面OABC 为齿面上某一区域，划分为网格后简化为四边形OABC。以O 为坐标原点，OA为x′轴，OC 为y′轴，根据空间坐标系右手法则确定z′轴，建立笛卡尔坐标系。其坐标轴的单位向量在大地坐标系中表示为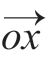
（x1，y1，z1），
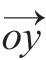（x2，y2，z2），
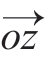（x3，y3，z3）。在大地坐标系中，弹丸i 的速度矢量表示为νi（xi，yi，zi，0），在新坐标系中表示为νi′（x′i，y′i，z′i，0）。根据转轴变换原理得[14]
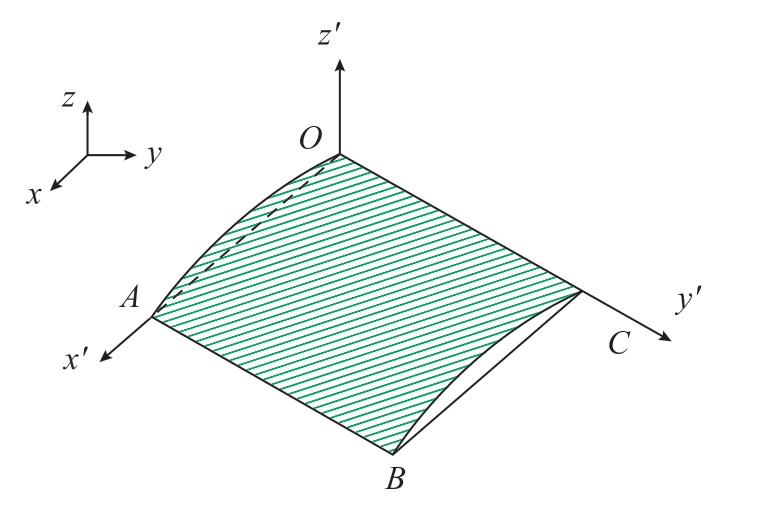
图5 弹丸速度场坐标系变化示意图
Fig.5 Diagram of coordinate system of shot velocity changes
（2）冲击次数。
当实际喷丸时间为t1 时，利用式（3）计算目标位置的单位面积冲击次数n。
式中，n1 为该单元与弹丸发生的冲击次数；S1 为该单元面积；tdem 为EDEM 模型计算时间。
2.2 有限元模型
基于ABAQUS/CAE 商业有限元软件建立有限元模型，计算喷丸后轮齿齿面的残余应力场[15]。
2.2.1 网格划分及边界条件
弹丸直径为0.3 mm，单元类型为C3D8R[16]。靶板尺寸如图6所示，除无限单元体网格外，靶板尺寸为1 mm×1 mm×0.5 mm，单元类型为C3D8R，在该区域内设置预定义场，以喷丸前齿面残余应力实测值作为模型的初始残余应力。其中区域Ⅰ用于限制弹丸冲击中心点位置和提取残余应力计算结果。区域Ⅰ和区域Ⅱ为网格细化部分，单元尺寸均为10 μm×10 μm×10 μm。区域Ⅲ为有限元网格由细到粗的过渡区。区域Ⅳ的网格类型为无限单元体CIN3D8，用于消除应力波在靶板边界的反射[17]。
图6 冲击靶板几何示意图
Fig.6 Schematic view of impact model geometry
模型中对靶板底面进行完全固定。弹丸与靶板之间的接触关系为Surface to Surface，法向行为定义为“硬”接触，切向行为定义为罚摩擦，摩擦系数设置为0.2[18]。
2.2.2 材料模型
弹丸设置为弹塑性体，采用各向同性本构模型，弹丸参数设置为杨氏模量E=210 GPa，泊松比μ=0.3，密度ρ=7800 kg/m3，屈服强度σs=1400 MPa。靶体材料为9310渗碳淬火钢，材料参数设置为杨氏模量E=210 GPa，泊松比μ=0.3，密度ρ=7800 kg/m3，塑性应力应变曲线采用Johnson–Cook 模型，其基本模型如式（4）和 （5）所示，参数由Hopkinson 压杆试验获得，分别为A=1234.38，B=881，C=0.018，n=0.238，m=0.686。为防止应力波振荡[19]，设置靶板材料阻尼α=6×106 s–1。
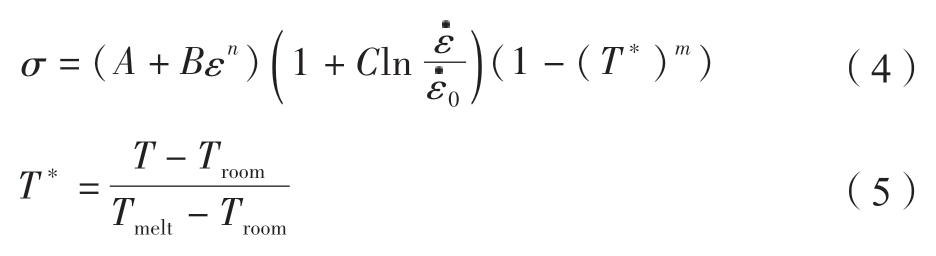
式中，A、B、n、C、m 为材料物理特性参数，由压杆试验结果拟合得到；A 为参考应变率下的屈服强度；B 为应变硬化系数；n 为应变硬化指数；C 为应变率硬化系数；m 为温度软化指数；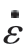
为试验应变率；
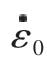为参考应变率；T 为试验温度；Tmelt 为材料的熔点（9310 合金钢的熔点为1510 ℃）；Troom 为参考温度，值为25 ℃。
2.2.3 弹丸冲击信息
弹丸冲击角度、速度、次数由2.1.2 节计算结果确定。根据ASH110 型号弹丸尺寸标准，设置弹丸为球形，直径为0.3 mm。考虑实际情况下弹丸冲击位置随机分布，仿真中利用Python 语言编程，采用Random 函数产生随机位置，弹丸冲击中心点均在图6所示的区域Ⅰ内。
3 结果与讨论
3.1 仿真与试验结果对比
为验证仿真模型准确性，在所建立的喷丸工艺仿真模型中，设置与试验相同的工艺参数。图7为喷丸后凸面b 点实测和仿真三维形貌。根据式（6）计算三维粗糙度Sa 值，实测值为0.35 μm，仿真计算结果0.386 μm，误差10.3%。其中，在x、y 方向，仿真结果分辨率低于实测结果，原因在于实测数据的采样间距为0.5 μm，有限元模型的靶板网格尺寸为10 μm×10 μm。
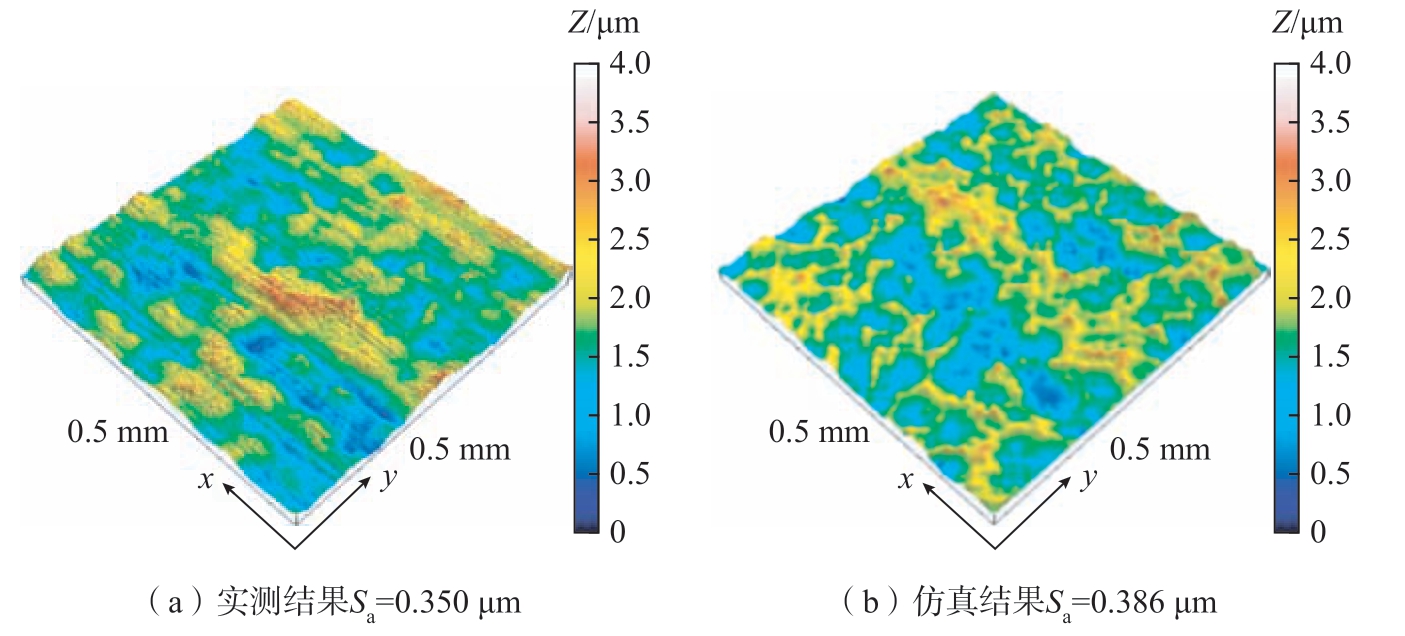
图7 喷丸后齿面三维形貌
Fig.7 Three-dimensional surface topography of tooth flank after shot peening
式中，n 为数据点个数；Zi 为第i 个节点的高度值。
对比喷丸后实测与仿真计算的轮齿表面齿高方向残余应力值，如表1所示。其中，a、b、c 点位置与图1标注一致。结果表明，轮齿各点的表面残余应力均在–800～–880 MPa 之间，计算误差在6%以内。图8展示了凸面、凹面b 点的实测与仿真计算的残余应力沿深度方向的分布，其中σx 为齿宽方向残余应力；σy 为齿高方向残余应力。喷丸处理后，轮齿凸面、凹面残余应力变化趋势一致，凹面残余压应力值略大于凸面。且齿宽方向残余应力和齿高方向分布相近，表面残余应力约为–800～–850 MPa，最大残余压应力值在1200～1300 MPa 之间，深度约为20～30 μm。统计轮齿表面残余压应力和最大残余压应力值，如表2所示，实测值与仿真结果误差均小于10%，证明该仿真模型可准确预测螺旋锥齿轮喷丸后的轮齿表层残余应力场。
图8 凸面、凹面b 点的试验与仿真计算残余应力场对比
Fig.8 Measured and simulated residual stress distribution of point b in convex and concave
表1 试验与仿真计算的轮齿表面齿高方向残余应力对比
Table 1 Measured and simulated surface residual stress along direction of tooth height
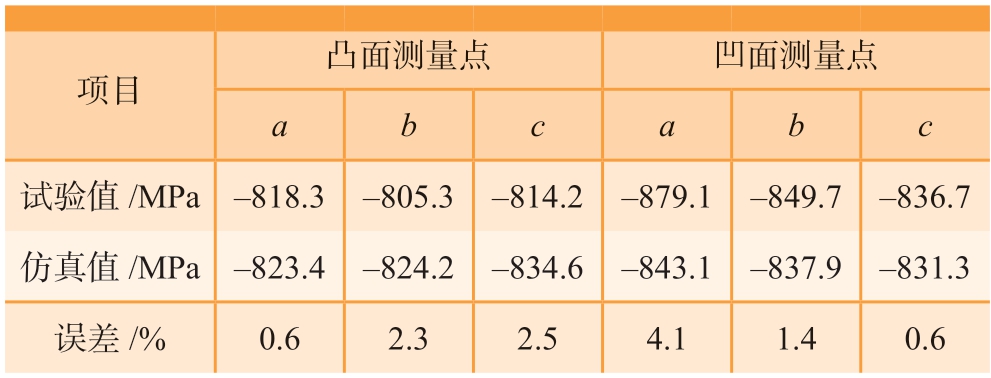
项目凸面测量点凹面测量点abcabc试验值/MPa –818.3 –805.3 –814.2 –879.1 –849.7 –836.7仿真值/MPa –823.4 –824.2 –834.6 –843.1 –837.9 –831.3误差/%0.6 2.3 2.54.1 1.4 0.6
表2 凸面、凹面b 点试验与仿真计算残余应力结果对比
Table 2 Measured and simulated residual stress values of point b in convex and concave
注：σxs、σxm 指齿宽方向的表面残余压应力和最大残余压应力；σys、σym 指齿高方向的表面残余压应力和最大残余压应力。
项目凸面凹面σxs σxm σys σymσxs σxm σys σym试验值/MPa–826.8–1248.5–805.3–1218.2–813.4–1286.6–849.7–1291.2仿真值/MPa–838.7–1145.0–824.2–1148.9–847.1–1161.0–837.9–1169.18误差/%1.4 8.3 2.3 5.74.1 9.8 1.4 9.5
3.2 喷丸时间影响
喷丸覆盖率受丸流量和喷丸时间影响，丸流量和喷丸时间的增加都会提高弹丸冲击次数，增加喷丸覆盖率。本文主要研究喷丸时间对残余应力场的影响，结果如图9所示。基于Miao 等[9]的方法，对喷丸覆盖率进行了计算。
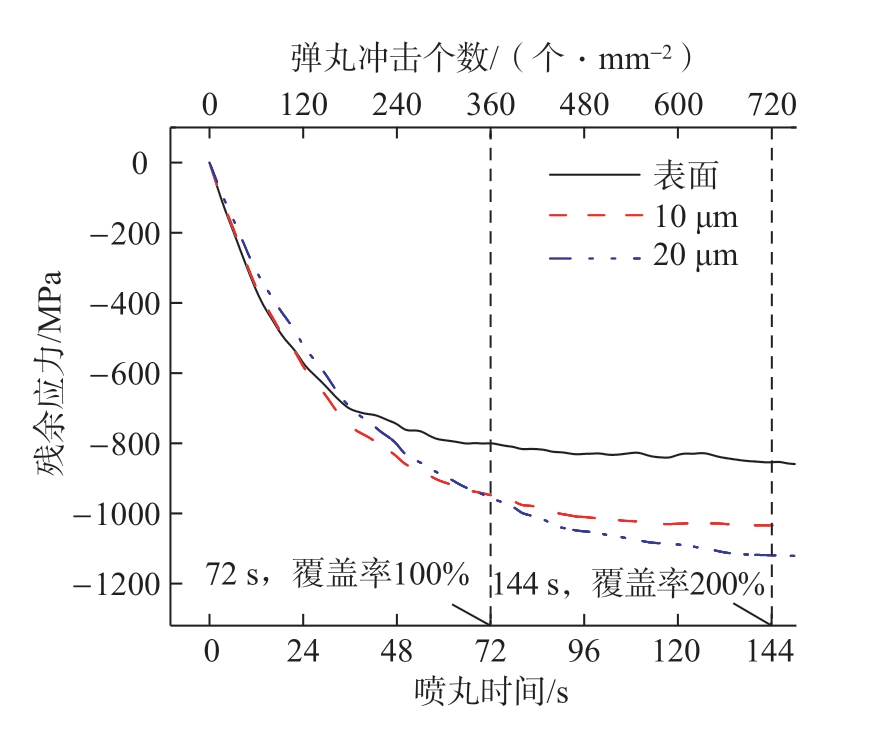
图9 喷丸时间对残余应力结果的影响
Fig.9 Influence of shot peening time on residual stress results
在弹丸初始速度为40 m/s 的条件下，喷丸时间达到72 s 时，弹丸冲击次数为360 个/mm2，喷丸覆盖率达到98%，即满覆盖率[11]。当喷丸时间为144 s 时，覆盖率为200%。随着喷丸时间的增加：（1）靶板表面残余压应力升高，当喷丸时间达到72 s 后，逐渐稳定在800 MPa左右；（2）10 μm 处残余压应力呈现逐渐升高的趋势，并在喷丸时间达到96 s 后稳定，约为1000 MPa；（3）20 μm处残余压应力持续提高，在72 s 后，20 μm 处残余压应力高于10 μm 处，表明最大残余压应力深度由10 μm提高至20 μm。这表明，提高喷丸时间，会有效增加材料次表层残余压应力值，提高最大残余压应力层深。
3.3 弹丸速度影响
由式（3）可知，弹丸初始速度由喷嘴气压、丸流量、弹丸直径确定，其中喷嘴气压为主要因素[20]。喷嘴气压的提升，会使弹丸速度明显增加，提高喷丸强度。
参考Nordin 等[21]的试验弹丸速度范围设置弹丸初始速度，残余应力计算结果如图10所示，云图如图11所示。结果表明，弹丸速度由30 m/s 提高至40 m/s、50 m/s 时，喷丸诱导的残余压应力提高，表面残余压应力值变化较小，最大残余压应力值分别为–1104.7 MPa、–1144.9 MPa、–1167.3 MPa，最大残余压应力深度分别为20 μm、25 μm、30 μm。结果表明，随着弹丸速度的提高，靶板表面残余压应力值变化不大，但最大残余压应力值、最大残余压应力深度会不断提高。
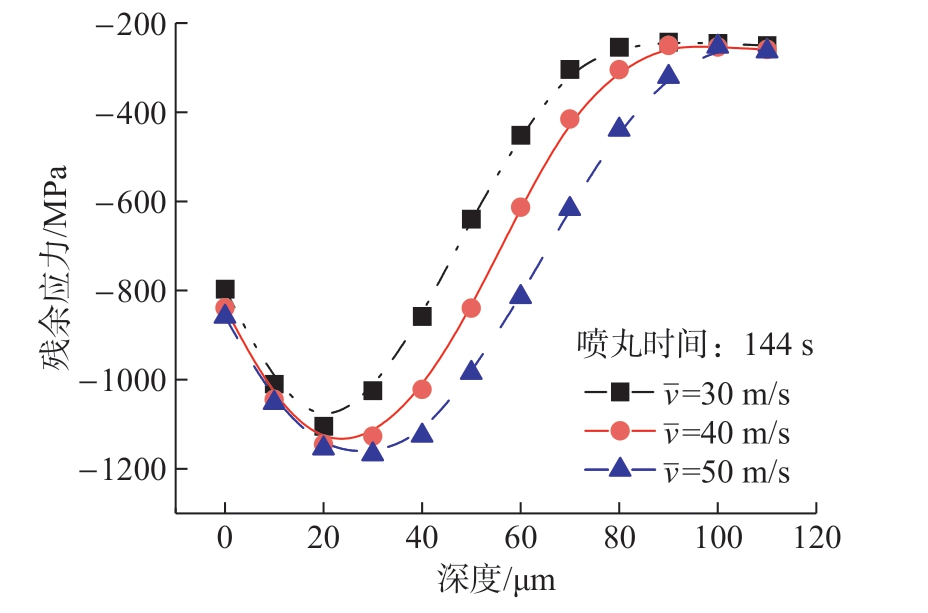
图10 弹丸速度对残余应力结果的影响
Fig.10 Influence of shot velocity on residual stress results
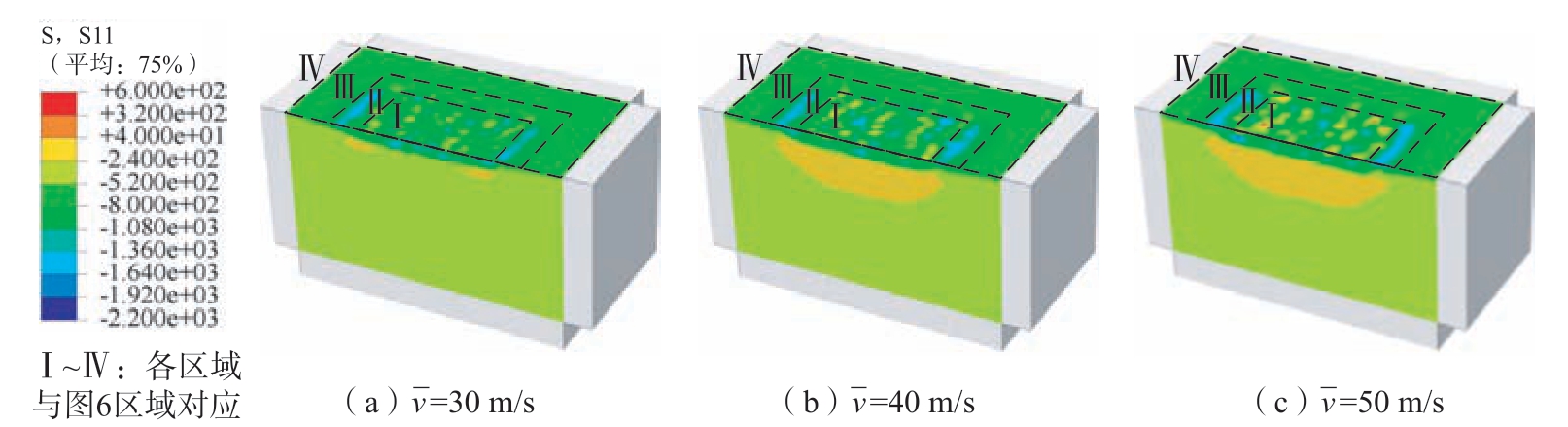
图11 不同弹丸速度冲击结果云图
Fig.11 Simulated residual stress of target impacted by different shot velocities
3.4 弹丸直径影响
计算不同弹丸直径冲击下的残余应力场如图12和13 所示。其中弹丸直径根据SAE 标准设置，采用ASH70、ASH110、ASH170 类型弹丸，表3展示了各类型弹丸与其直径的对应关系。结果表明，弹丸直径提高时，表面残余应力值变化较小，但会明显提高最大残余压应力值和最大残余压应力深度。当弹丸直径由0.18 mm提高至0.30 mm 和0.42 mm 时，表面残余压应力均在–760～–840 MPa 之间，最大残余压应力值由–893.6 MPa提高至–1145.0 MPa 和–1251.5 MPa，最大残余压应力深度由 10 μm 提高至 30 μm 和 40 μm。但弹丸直径提高会增加齿轮表面粗糙度。其原因在于当弹丸直径较高时，弹丸动能增加，与齿面冲击时，材料塑性应变增加，从而增大弹坑半径，会使齿轮表面粗糙度明显提高。
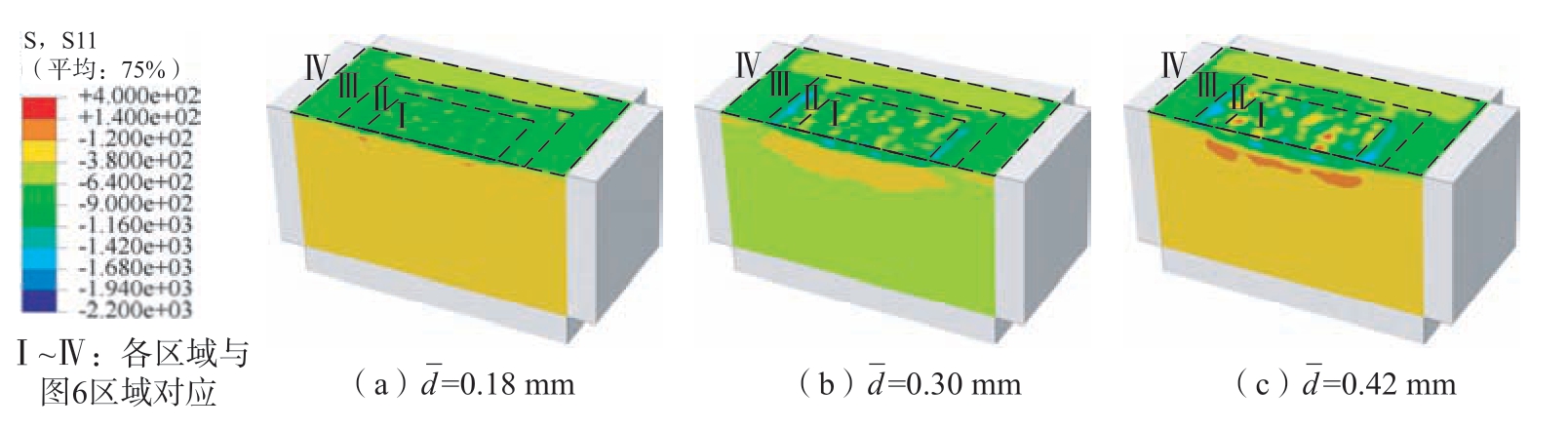
图12 不同弹丸直径冲击结果云图
Fig.12 Simulated residual stress of target impacted by different shot diameters
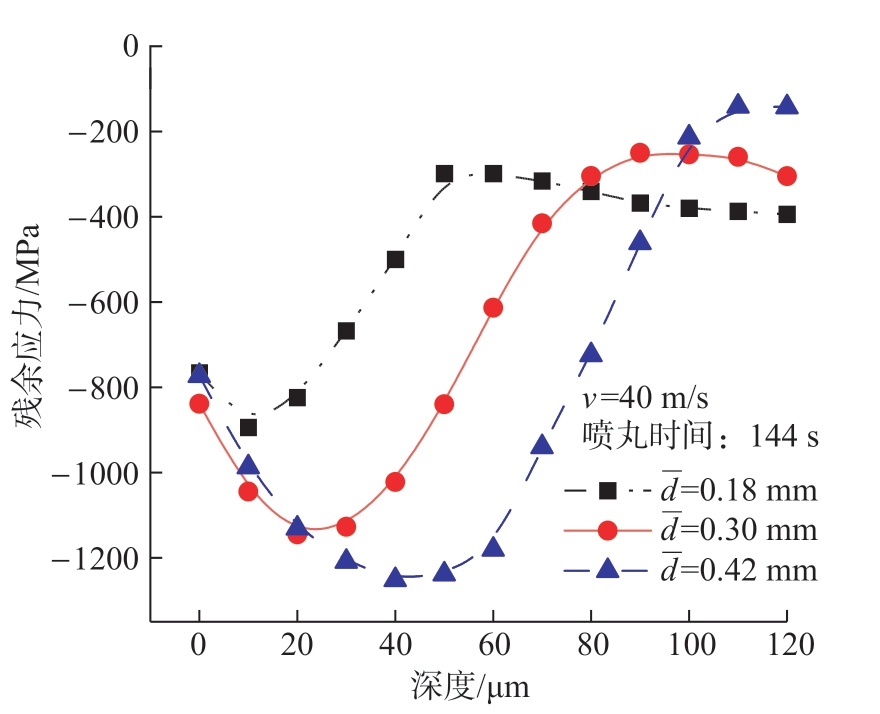
图13 弹丸直径对靶板表层残余应力的影响
Fig.13 Influence of shot diameter on residual stress results
表3 不同类型弹丸对应直径及残余应力计算结果
Table 3 Diameter of different types of shots and residual stress calculation results
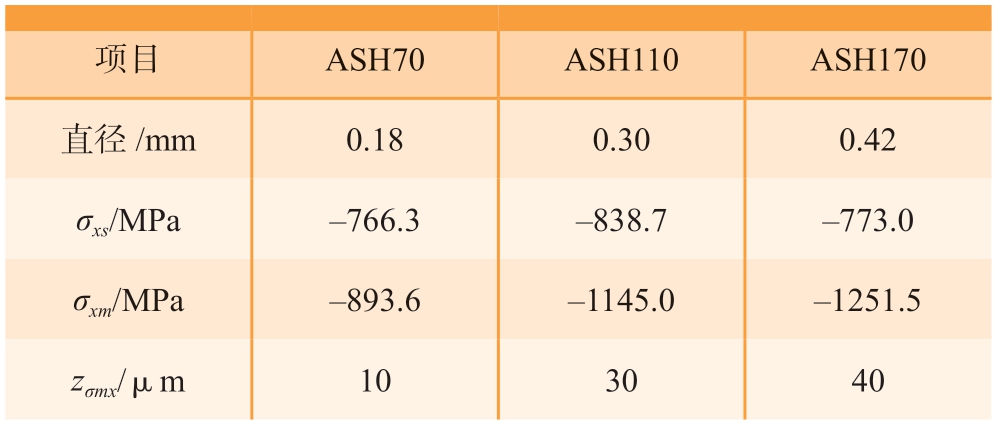
注：zσmx 为齿宽方向最大残余应力值所在深度。
项目ASH70ASH110ASH170直径/mm0.180.300.42 σxs/MPa–766.3–838.7–773.0 σxm/MPa–893.6–1145.0–1251.5 zσmx/μm103040
4 结论
本文基于离散元与有限元耦合的方法，建立AISI 9310 钢螺旋锥齿轮的喷丸工艺残余应力场仿真计算模型，探寻喷丸工艺参数与喷丸后齿面残余压应力的关联规律。
（1）本文所建立的仿真模型对齿面残余应力场的预测误差在10%以内，计算结果准确。
（2）当喷丸时间为72 s 时，弹丸冲击个数达到360个/mm2，靶板覆盖率达到满覆盖率。当喷丸时间继续增加时，靶板表面压应力逐渐稳定在–800 MPa 左右。
（3）喷丸工艺主要影响轮齿表面至50 μm 深度内的残余应力场，深度大于50 μm 时，残余应力场由喷丸前工艺确定。
（4）当喷丸覆盖率为200%时，弹丸直径和速度的改变对本文所用零件的表面残余压应力影响较小。
（5）当弹丸初始速度和直径提高时，靶板表面残余压应力值变化较小，靶板表层最大残余压应力值和最大残余压应力深度都得到明显提高，其中最大残余压应力值可提高到–1251.5 MPa，最大残余压应力深度可提高到40 μm。
[1] 罗诚,冯治恒,丁军鹏,等.工程机械螺旋锥齿轮喷丸强化工艺及试验研究[J].现代制造工程,2015(3): 7–10.
LUO Cheng,FENG Zhiheng,DING Junpeng,et al.Shot-peening process and experimental study of spiral bevel gear of construction machinery[J].Modern Manufacturing Engineering,2015(3): 7–10.
[2] 栾伟玲,涂善东.喷丸表面改性技术的研究进展[J].中国机械工程,2005,16(15): 1405–1409.
LUAN Weiling,TU Shandong.Recent trends on surface modification technology of shot peening[J].China Mechanical Engineering,2005,16(15): 1405–1409.
[3] 孙艳,罗宏亮.强化喷丸对渗碳齿轮表面接触疲劳裂纹形成与扩展的影响[J].汽车技术,2009(1): 56–58.
SUN Yan,LUO Hongliang.Influence of strengthening shot peening on formation and extension of fatigue crack in carburized gear surface[J].Automobile Technology,2009(1): 56–58.
[4] 朱鹏飞,严宏志,陈志,等.齿轮齿面喷丸强化研究现状与展望[J].表面技术,2020,49(4): 113–131,140.
ZHU Pengfei,YAN Hongzhi,CHEN Zhi,et al.Research status and prospect of shot peening of gear tooth flanks[J].Surface Technology,2020,49(4): 113–131,140.
[5] 王仁智.金属材料的喷丸强化原理及其强化机理综述[J].中国表面工程,2012,25(6): 1–9.
WANG Renzhi.Overview on the shot peening principle and its strengshening mechanisms for metallic materials[J].China Surface Engineering,2012,25(6): 1–9.
[6] 邹德志,李骏,徐卉,等.喷丸强化对齿轮材料弯曲疲劳性能的影响[J].汽车工艺与材料,2020(6): 47–52.
ZOU Dezhi,LI Jun,XU Hui,et al.Effect of shot peening strengthening on gear material bending fatigue performance[J].Automobile Technology & Material,2020(6): 47–52.
[7] 冯琴.喷丸强化提高渗碳齿轮疲劳强度[J].金属加工,2001(12): 32–33.
FENG Qin.Improving fatigue strength of carburized gear by shot peening[J].Metal Forming,2001(12): 32–33.
[8] 盖鹏涛,陈福龙,尚建勤,等.喷丸强化对表面完整性影响的研究现状与发展[J].航空制造技术,2016,59(20): 16–21.
GAI Pengtao,CHEN Fulong,SHANG Jianqin,et al.Recent situation and development trend of shot peening on surface integrity[J].Aeronautical Manufacturing Technology,2016,59(20): 16–21.
[9] MIAO H Y,LAROSE S,PERRON C,et al.On the potential applications of a 3D random finite element model for the simulation of shot peening[J].Advances in Engineering Software,2009,40(10): 1023–1038.
[10] 李源,雷丽萍,曾攀.弹丸束喷丸有限元模型数值模拟及试验研究[J].机械工程学报,2011,47(22): 43–48.
LI Yuan,LEI Liping,ZENG Pan.Shot stream finite element model for shot peening numerical simulation and its experiment study[J].Journal of Mechanical Engineering,2011,47(22): 43–48.
[11] BAGHERIFARD S,GHELICHI R,GUAGLIANO M.On the shot peening surface coverage and its assessment by means of finite element simulation: A critical review and some original developments[J].Applied Surface Science,2012,259: 186–194.
[12] MURUGARATNAM K,UTILI S,PETRINIC N.A combined DEM–FEM numerical method for shot peening parameter optimisation[J].Advances in Engineering Software,2015,79: 13–26.
[13] SHEN S P,ATLURI S N.An analytical model for shotpeening induced residual stresses[J].Computers,Materials and Continua,2006,4(2): 75–85.
[14] 蔡国梁,苗宝军,史雪荣.解析几何教程[M].镇江: 江苏大学出版社,2012.
CAI Guoliang,MIAO Baojun,SHI Xuerong.Analytic geometry tutorial[M].Zhenjiang: Jiangsu University Press,2012.
[15] KLEMENZ M,SCHULZE V,ROHR I,et al.Application of the FEM for the prediction of the surface layer characteristics after shot peening[J].Journal of Materials Processing Technology,2009,209(8):4093–4102.
[16] LIN Q J,LIU H J,ZHU C C,et al.Effects of different shot peening parameters on residual stress,surface roughness and cell size[J].Surface and Coatings Technology,2020,398: 126054.
[17] SCHWARZER J,SCHULZE V,VÖHRINGER O.Finite element simulation of shot peening—A method to evaluate the influence of peening parameters on surface characteristics[M].Weinheim: Wiley–VCH Verlag GmbH & Co.KGaA,2002.
[18] MEGUID S A,SHAGAL G,STRANART J C.3D FE analysis of peening of strain-rate sensitive materials using multiple impingement model[J].International Journal of Impact Engineering,2002,27(2): 119–134.
[19] KIM T,LEE H,HYUN H C,et al.Effects of Rayleigh damping,friction and rate-dependency on 3D residual stress simulation of angled shot peening[J].Materials & Design,2013,46: 26–37.
[20] 卢国鑫,王强,陆峰.300M 钢多弹丸喷丸强化的有限元模拟[J].材料保护,2014,47(1): 28–30,43.
LU Guoxin,WANG Qiang,LU Feng.Finite element simulation of multi-shots shot peening of 300M stainless steel[J].Materials Protection,2014,47(1): 28–30,43.
[21] NORDIN E,ALFREDSSON B.Measuring shot peening media velocity by indent size comparison[J].Journal of Materials Processing Technology,2016,235: 143–148.