SiC/SiC 复合材料因其低密度、高比强度、高比模量、耐高温、抗氧化等优异性能,成为目前公认的最具潜力的高温热结构材料之一,是航天航空、国防军工等重要领域中极具应用前景的理想材料[1–3]。单向SiC/SiC复合材料是结构最简单的SiC/SiC 复合材料,也是编织复合材料、叠层复合材料等复杂结构复合材料的基本组成结构。掌握单向SiC/SiC 复合材料在拉伸过程中的微观破坏机理和宏观拉伸行为,将对SiC/SiC 复合材料的工程应用具有实用价值。
对于单向SiC/SiC 复合材料的拉伸力学行为,国内外学者至今已经做了大量的试验研究,并取得了丰富的成果。Morscher 等[4]通过声发射技术检测了单向SiC/SiC 复合材料的拉伸过程,大量的声信号暗示材料在拉伸过程中存在一定程度的微观破坏,试验发现由于单向SiC/SiC 复合材料具有的非均质的结构和材料特点,试样在拉伸过程中可能产生多种微观破坏机制。Marshall等[5–6]在单向纤维增强SiC/SiC 复合材料的拉伸破坏过程中观测到了致密的基体裂纹以及纤维的断裂拔出现象,但并未认识到界面对拉伸破坏行为的影响机制。Barsoum[7]和Wang[8]等在研究单向纤维增强陶瓷基复合材料基体裂纹的开裂起始时,考虑到了界面对破坏过程的影响,认为基体裂纹扩展至界面会引起界面脱粘,随后在界面处扩展。由于这些微观破坏机理,单向SiC/SiC复合材料拉伸过程的力学响应曲线呈现明显的双线性特征[9]。Inghels 等[10]研究了SiC/SiC 复合材料和C/SiC 复合材料的拉伸损伤破坏行为,获得两种材料的拉伸力学曲线均有明显的非线性段特征。Kim 等[11]认为基体的首先开裂是拉伸力学响应曲线开始由线性段向非线性段过渡的原因。需要特别指出的是,在随后的众多有关单向纤维增强SiC/SiC 复合材料拉伸行为的研究中,学者们均在破坏试样的基体上发现了致密的裂纹,并且这些致密裂纹有趋向于均匀分布的特征,如图1所示[12–13]。

图1 基体裂纹SEM 图[12–13]
Fig.1 SEM images of matrix crack[12–13]
基于对SiC/SiC 复合材料微观破坏机理的理解,近年来学者们也提出了不同模型并用于计算和预测单向SiC/SiC 复合材料拉伸性能和行为。由于纤维丝强度分布的不均匀性,Coleman[14]于1958年提出了一种纤维强度统计模型,后经学者们不断完善,常用Monte Carlo方法按照某一概率分布来随机确定纤维的断裂位置或概率。Oh[15]最早采用Monte Carlo 方法结合基于经典断裂力学理论的剪滞模型[16]模拟研究了单向纤维增强复合材料的破坏过程,得到了与试验值吻合的结果,此后该方法一直被延用。针对基体,孙志刚等[17]基于Monte Carlo 思想,认为基体的开裂概率服从一个Weibull 分布形式函数,结合剪滞模型模拟了陶瓷基复合材料基体随机开裂的过程。李龙彪等[18]在有关单向陶瓷基复合材料单轴拉伸强度研究的剪滞模型中,不仅结合了基体随机开裂模型,同时引入了纤维的随机失效准则以及界面脱粘模型,纤维与基体的失效概率均服从Weibull 分布形式。Zhang 等[19]针对单向SiC/SiC 复合材料提出了一种基体失效模型,将基体裂纹产生的概率分布转化为基体单元强度的随机分布,基体单元的强度与未脱粘区域的长度有关,证实了该模型与试验结果更接近。Chen等[20]构建的二维单向纤维增强陶瓷基复合材料的细观有限元模型中,纤维与基体的损伤均是基于Monte Carlo方法,纤维与基体单元服从同一个Weibull 强度分布形式。Do–Won 等[21]提出了含有复杂微观结构的单向(UD)复合材料横向力学行为的预测模型。
尽管目前针对单向SiC/SiC 复合材料行为的理解已取得长足进展,但仍存在问题有待厘清。首先,基于强度分布的建模方法无法完全反映基体裂纹数量随拉伸过程增加且裂纹分布趋于均匀的物理特征;其次,大部分模型往往将出现裂纹后的基体刚度设置为0 或采用经验性公式模拟基体损伤规律,这些设定也缺乏足够的科学支撑。
本文将建立一个二维微观尺度有限元模型,针对基体裂纹随裂纹密度会趋向于均匀分布的特点,采用多尺度模拟的研究方法,建立基体裂纹的连续损伤模型;采用强度分布方法模拟纤维的随机断裂过程;采用内聚力模型模拟界面脱粘现象,阐释单向SiC/SiC 复合材料拉伸过程中的损伤破坏机制,然后通过参数化研究,探索不同微观破坏机理对复合材料性能的影响机制和它们之间的相互作用关系。
1 单向SiC/SiC 复合材料拉伸模型
1.1 有限元模型
将单向SiC/SiC 复合材料在微观尺度的结构简化为基体层、纤维层和界面层交替分布的二维平面结构。模型总长度设置为480 μm。根据纤维直径数据,纤维层厚度设定为14 μm。由于单向SiC/SiC 复合材料纤维体积分数接近60%,基体层厚度设置为10 μm。对纤维、基体和界面进行网格划分,在沿长度方向均划分40 个单元,沿厚度方向均仅划分1 个单元。纤维与基体的网格单元类型为平面应力四边形单元CPS4。界面层单元类型为4 节点二维内聚力单元COH2D4。
将10 根纤维之间的基体、界面组装成为单向SiC/SiC 复合材料结构。模型一侧施加位移作为边界条件;在另一端施加对称性边界条件,如图2所示。各组分实体之间采用绑定约束,使得各组分两侧的单元能够协调位移与应力。
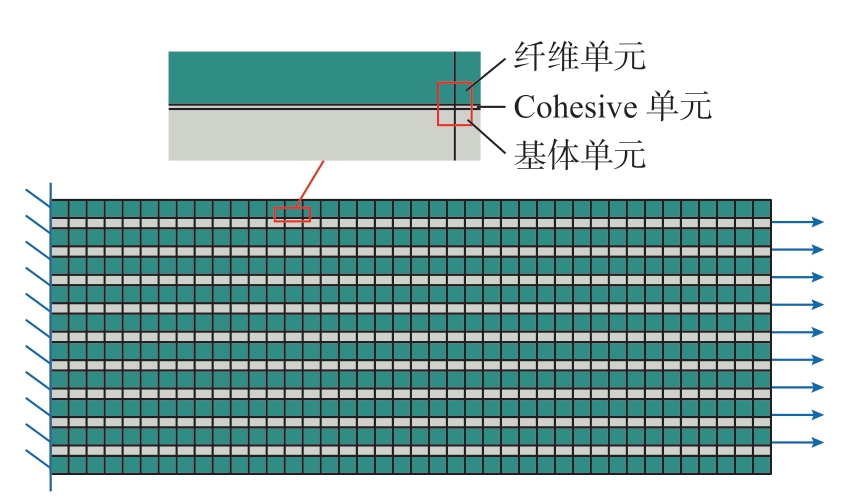
图2 有限元模型及边界条件
Fig.2 Finite element model and boundary conditions
1.2 纤维损伤理论模型
1.2.1 纤维强度分布
研究假设SiC 纤维的拉伸强度服从Weibull 分布[22]形式。
式中,F 为拉伸强度;mf 为Weibull 分布的形状参数;σ0为Weibull 分布的尺寸参数;L0 为模型总长度;L 为单元的长度;σ 为单根纤维强度。由上式反推可得纤维强度:
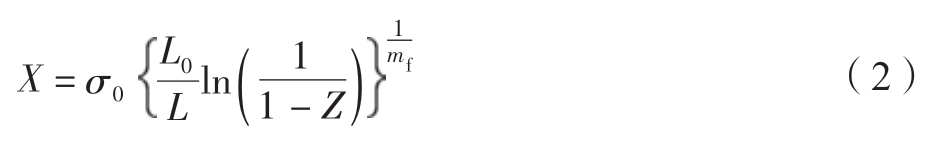
式中,X 为纤维单元的强度;Z 为单元失效概率,取均匀分布的[0,1]的随机数,由于Z 的随机性,纤维强度存在统计学上的意义,不是确定值。式(2)中关于Weibull分布模型中的参数是根据单丝拉伸的试验结果(图3)拟合获得。
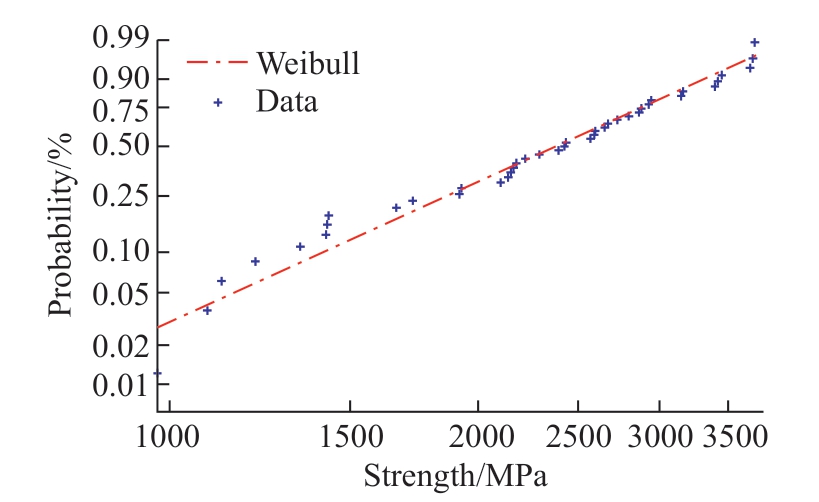
图3 纤维强度的Weibull 分布拟合结果
Fig.3 Fitting results of Weibull distribution of fibe strength
1.2.2 纤维失效准则
为了表达纤维在轴向上的脆性断裂现象,纤维的损伤失效理论被定义为

式中,E0 为SiC 纤维的杨氏模量;Ed 为SiC 纤维发生断裂后的杨氏模量;d 为损伤变量,用来表示因断裂导致的材料刚度损伤,其范围在0 到1 之间;σ 为纤维单元承受的应力;σf 为纤维单元的强度。该纤维损伤破坏规则的含义是当纤维单元所承受的应力达到其强度时发生断裂,纤维失效,刚度趋近于0;而在纤维单元未达到其强度之前,纤维单元完好,为线弹性性能。
1.2.3 纤维的相关力学性能参数
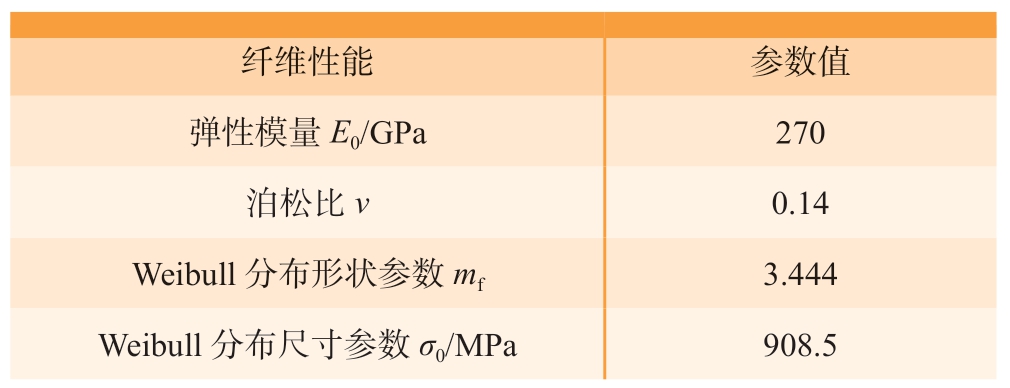
模型中SiC 纤维的相关基本性能参数如表1所示。
表1 SiC 纤维的相关性能参数
Table 1 Related performance parameters of SiC fibe
?纤维性能参数值弹性模量E0/GPa270泊松比ν0.14 Weibull 分布形状参数mf3.444 Weibull 分布尺寸参数σ0/MPa908.5
1.3 基体损伤理论模型
1.3.1 基于断裂能释放率的损伤法则
试验证明,SiC 基体会在单向拉伸过程中首先产生垂直于纤维方向的裂纹,且裂纹数量随着拉伸过程不断增加,最终趋向于均匀分布。因此假设SiC 基体裂纹呈周期性分布特征(图4),建立微观尺度上的两条裂纹间一个周期性单细胞(RVE)的有限元模型,基于均匀化理论[23],计算不同裂纹密度时材料在细观尺度上等效刚度的损伤。最终基于断裂能释放率,以连续介质损伤力学来建立SiC 基体的细观损伤准则。
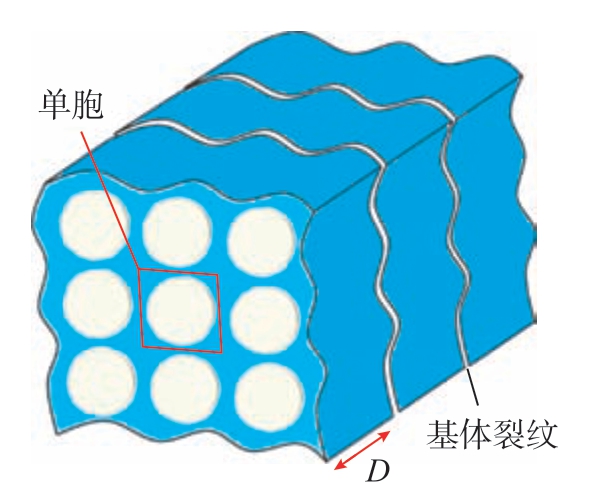
图4 周期性裂纹假设和周期性单胞示意图
Fig.4 Schematics of the periodic distribution of matrix cracks and RVE
断裂能释放率G 的计算公式为
式中,A 为裂纹总面积;Wp 为总势能,即裂纹扩展面积为A 时,弹性系统所释放的能量。系统中的总势能Wp、外力功U 和弹性应变能W 有如下关系:
由于外力功U 与弹性应变能存在U=2W 的关系,将式(5)代入式(4)中,可将式(4)表达为
式中,ρ 为裂纹密度,即裂纹间距(D)的倒数,也可认为是单位长度的裂纹数量。该公式中,![]() 可通过计算推导得出;
可通过计算推导得出;![]() 可通过多尺度模拟和均匀化方法获得;
可通过多尺度模拟和均匀化方法获得;![]() 可从几何角度分析获得。当断裂能释放率达到临界断裂能释放率Gc(即断裂韧性)时,基体组分开始产生裂纹,损伤开始演化。
可从几何角度分析获得。当断裂能释放率达到临界断裂能释放率Gc(即断裂韧性)时,基体组分开始产生裂纹,损伤开始演化。
1.3.2 ![]() 的计算推导
的计算推导
SiC 基体是各向同性的材料,其弹性应变能W 的计算公式为
式中,V 为破坏结构的体积;σ 为应力矩阵;S 为柔度矩阵,即刚度矩阵的逆矩阵。根据复合材料的结构特点及破坏形式,将刚度的损失引入到柔度矩阵中。考虑到单向SiC/SiC 复合材料拉伸行为的特点,在其剪切方向上的刚度损失很小,故而在本研究忽略不计。本文中只考虑材料在拉伸方向上的刚度损失,其应力矩阵及柔度矩阵如下。
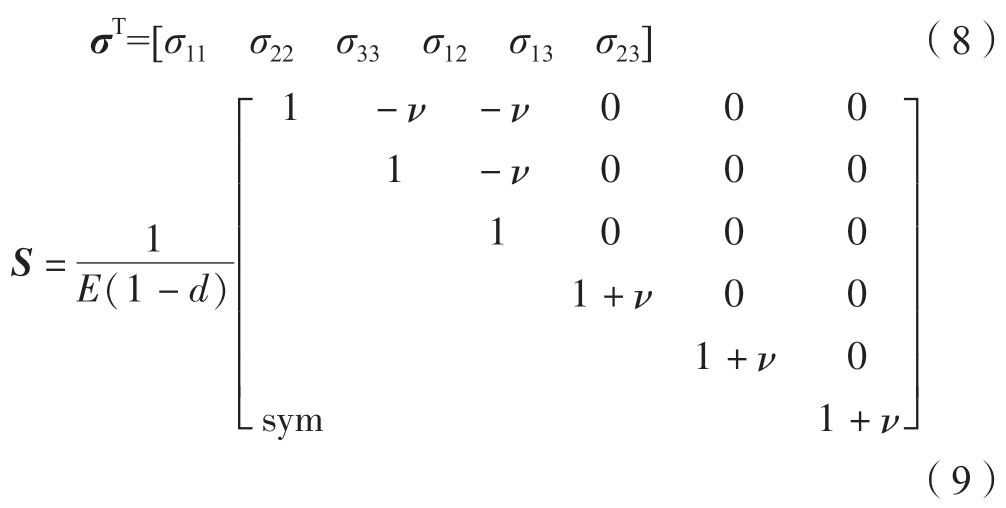
式中,σ11、σ22、σ33、σ12、σ13、σ23 为应力,下标1、2 和3 为性能方向,本文中拉伸方向为1;E0 为弹性模量;ν 为泊松比。本文中基体的弹性模量设定为190 GPa,泊松比为0.14。根据上述公式,可计算得到基体的弹性应变能W 是有关损伤变量d 的函数,由此可计算推导得到∂![]() 。
。
1.3.3 ![]() 的获得
的获得
为获得损伤变量d 与裂纹密度ρ 的关系,研究通过构建微观尺度周期性单胞模型,基于均匀化方法将基体裂纹转变为基体刚度的损伤。三维微观单胞几何模型及其网格划分如图5(a)所示,纤维直径为12 μm,占单胞总体积的60%,几何模型的长度为裂纹间距D,随所研究裂纹密度的变化而变化。使用8 节点的线性块体单元C3D8 对单胞进行划分。针对无裂纹单胞模型,对各外表面施加周期性边界条件;针对有裂纹单胞模型,对垂直于纤维方向的基体裂纹面不施加边界条件,以模拟裂纹出现后断裂面无约束的状态,其余外表面施加周期性边界条件。计算后对比两种单胞的应力状态可见,基体裂纹造成断裂面应力的释放,也使得有裂纹单胞拥有更低的应变能。
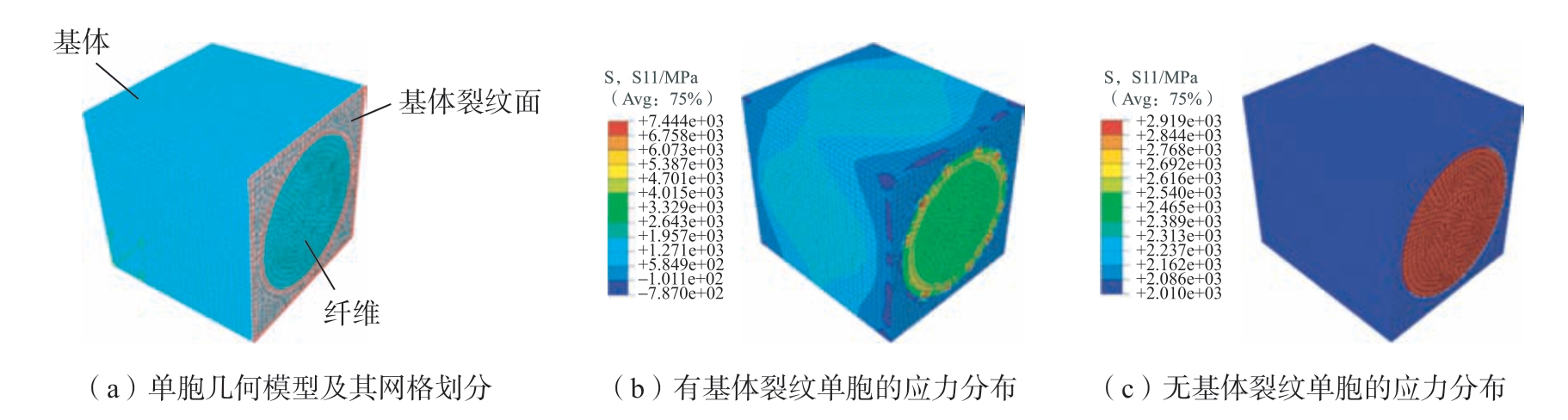
图5 单胞几何模型及其网格划分和有基体裂纹及无基体裂纹单胞的应力分布
Fig.5 RVE model,stress distribution of the RVE with and without matrix crack
通过比较无裂纹单胞模型(Wm0)和有裂纹单胞模型(Wmd)的应变能即可计算裂纹所导致应变能的消散,进一步推导出刚度损伤公式:
通过改变模型长度,可分别计算不同裂纹密度下材料损伤程度,并建立起损伤变量与裂纹密度间的关系(图6)。计算结果通过数值方法应用于式(6)中,也可以被拟合为函数(如本研究所使用的指数型函数)。
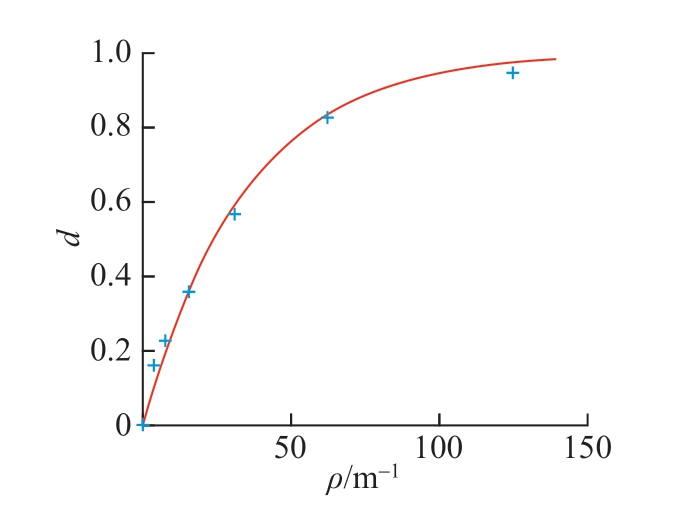
图6 损伤变量随裂纹密度变化规律
Fig.6 Variation of damage variable with crack density
式中,C 为常数系数。
1.3.4 ![]() 的计算
的计算
由于裂纹被假设呈周期性分布,![]() 可通过几何关系推导为如下形式。
可通过几何关系推导为如下形式。
式中,A0 表示单个基体裂纹的面积;D 为裂纹面积。
1.4 界面损伤理论模型
常见的SiC/SiC 复合材料的单层界面相成分主要有PyC、SiC 和BN,本文中的界面参考BN 界面的力学性能参数,弹性模量为10 GPa,泊松比为0.1[24]。界面的损伤理论是基于Traction-separation 方法[25]的双线性理论模型,如图7所示。应力随应变线性增大直至损伤起始,界面刚度开始衰减。
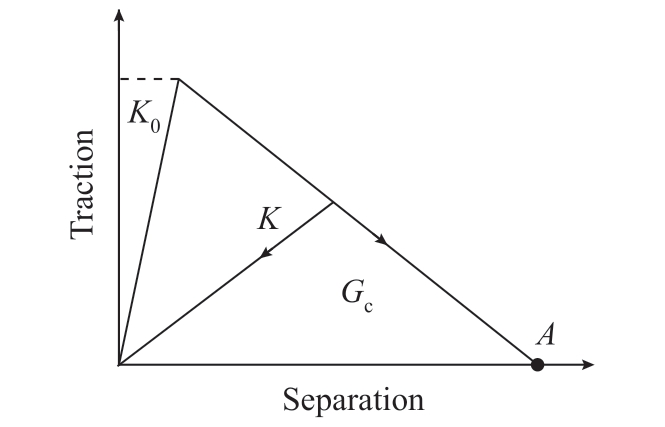
图7 界面损伤的双线性理论模型
Fig.7 Traction-separation law for interface model
界面的损伤起始采用最大名义应力准则,可表示为
式中,t 为应力;下标n 为主方向;下标s 为两个剪切方向;下标t 为应力的剪切方向;上标0 为极限强度。该式表达的是当任一方向上的应力达到其极限强度时界面开始损伤。本研究中3 个方向的界面强度分别设定为70 MPa、70 MPa、70 MPa[26]。
2 单向SiC/SiC 复合材料拉伸行为
2.1 单向SiC/SiC 复合材料拉伸破坏机理
模型计算得到的应力–应变曲线整体呈现出双线性的特征(图8),这一模拟结果与试验研究的单向SiC纤维增强复合材料的应力–应变曲线类似[27–28],在低应变区域(OA 段)应力随应变线性增加。随着应变的提高,个别纤维发生断裂(点A)。由于纤维断裂导致的应力集中效果使断裂纤维周围的基体和界面也开始损伤(图9(a))。随后应力–应变曲线于B 点出现明显拐点。导致这一现象的原因是基体的断裂能释放率达到临界值,基体裂纹现象开始出现,伴随基体刚度的整体衰减。随着拉伸过程的继续,更多的纤维开始产生破坏,并最终产生材料整体的失效,体现为C 点载荷的剧烈跌落。最终的失效图谱(图9(c))显示,在材料最终失效前,每根纤维仅断裂了1 次。裂纹在材料内发生偏转,沿界面方向拓展,通过失效的界面和基体被串联在一起。这一失效图谱对应试验研究中弱界面SiC/SiC 复合材料参差不齐的断裂面和纤维拔出现象[27]。
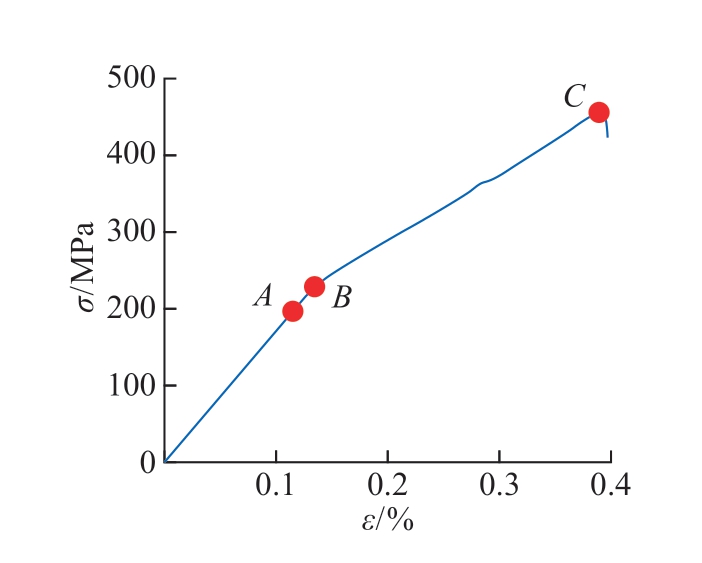
图8 单向SiC/SiC 复合材料拉伸的典型应力–应变曲线
Fig.8 Calculated stress–strain curve for the tensile process of unidirectional SiC/SiC composites
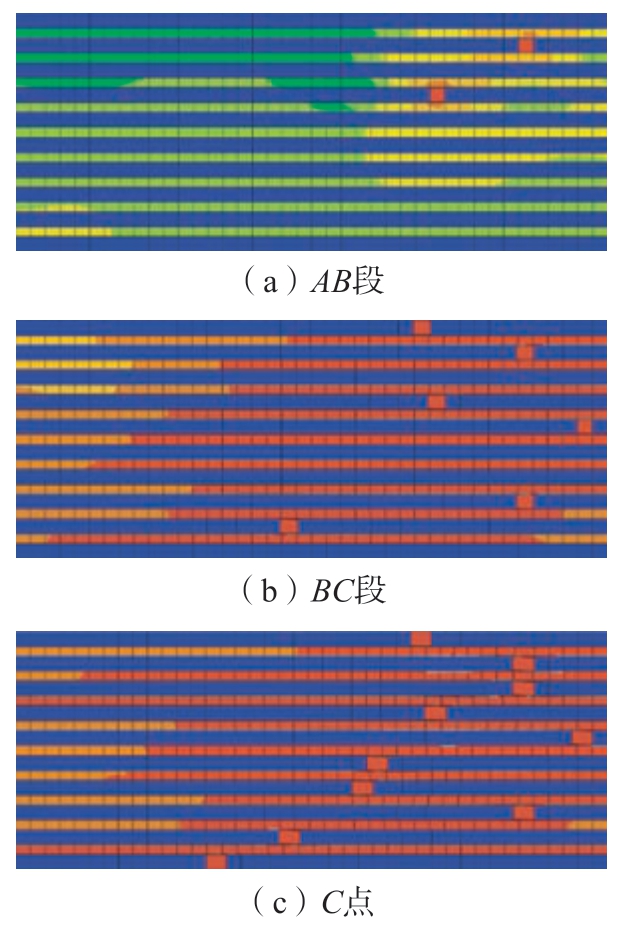
图9 界面剪切强度为70 MPa 时拉伸各阶段的单元失效状态图
Fig.9 Failure state figu e of the element at each tensile stage when the interfacial shear strength is 70 MPa
2.2 基体性能对单向SiC/SiC 复合材料拉伸行为的影响
通过改变基体的临界断裂能释放率,研究了基体性能对单向SiC/SiC 复合材料拉伸行为的影响(图10)。单向SiC/SiC 复合材料双线性的特征被证明主要受基体裂纹损伤的影响。随着临界断裂能释放率的降低,基体损伤更早出现,材料整体也更早迎来刚度的拐点。结果同时显示材料整体强度随临界断裂能释放率的提高而升高。图11为ε =0.37%时,不同基体性能试样的微观失效图谱,可解释出现这一现象的原因。弱基体单向SiC/SiC 复合材料的基体裂纹密度和损伤已达到饱和,损伤严重的基体无法承担起在纤维间传递和分散应力的作用,致使纤维的局部应力集中现象更加显著,最终导致更多纤维的提前断裂和材料整体破坏(图11(a))。对比可见相同应变下,强基体SiC/SiC 复合材料的基体损伤程度较低,因此尽管纤维的强度相同,强基体SiC/SiC 复合材料的断裂纤维更少,材料整体也可以拉伸至更高应变(图11(b))。
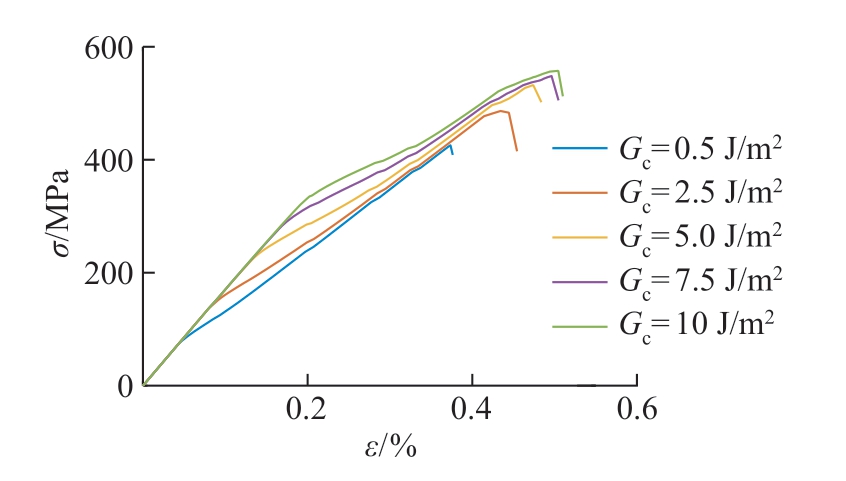
图10 不同基体性能试样的拉伸应力–应变曲线
Fig.10 Tensile stress–strain curves of samples with different matrix properties
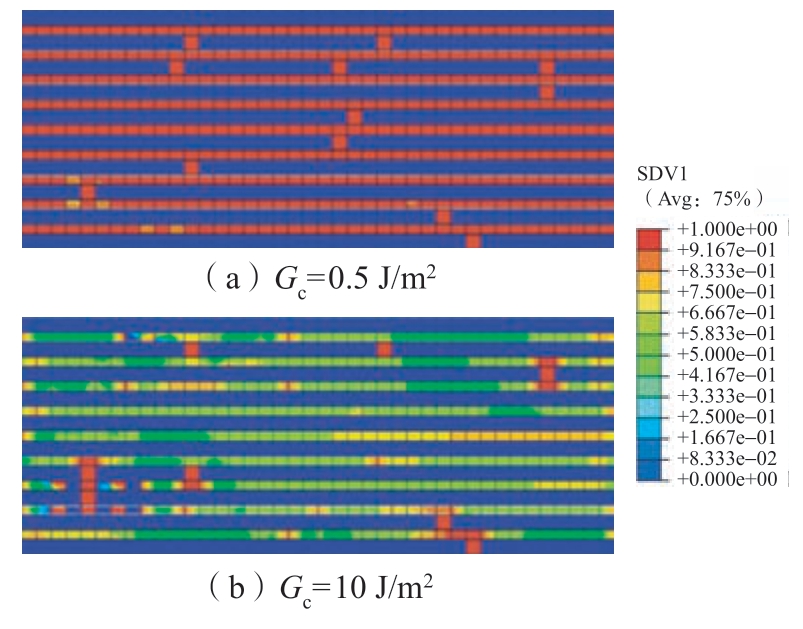
图11 ε =0.37%时不同基体性能试样的失效图谱
Fig.11 Failure patterns of samples with different matrix properties when ε =0.37%
2.3 纤维性能对单向SiC/SiC 复合材料拉伸行为的影响
通过改变Weibull 分布中的形状参数mf,研究了纤维强度分布情况对单向SiC/SiC 复合材料拉伸行为的影响。结果显示单向SiC/SiC 复合材料的拉伸强度随mf 的升高而升高(图12(a))。形成这一现象的原因可以通过纤维强度分布图谱得以解释(图12(b))。随着mf 的提高,纤维强度的分布更集中,离散更小。纤维的断裂会导致应力集中现象,与这一现象连锁产生的其他纤维、基体和界面局部破坏,才是导致材料整体失效的主要原因。尽管mf 较低的试样存在更多的高强度纤维段,但同时更多的低强度纤维段会在更低的应变时发生断裂,并导致材料最终破坏的提前出现。因此强度均匀的纤维更有利于复合材料性能潜力的完全发挥。计算得到的这一结论也可以在复合材料的研究中得到试验验证[29]。
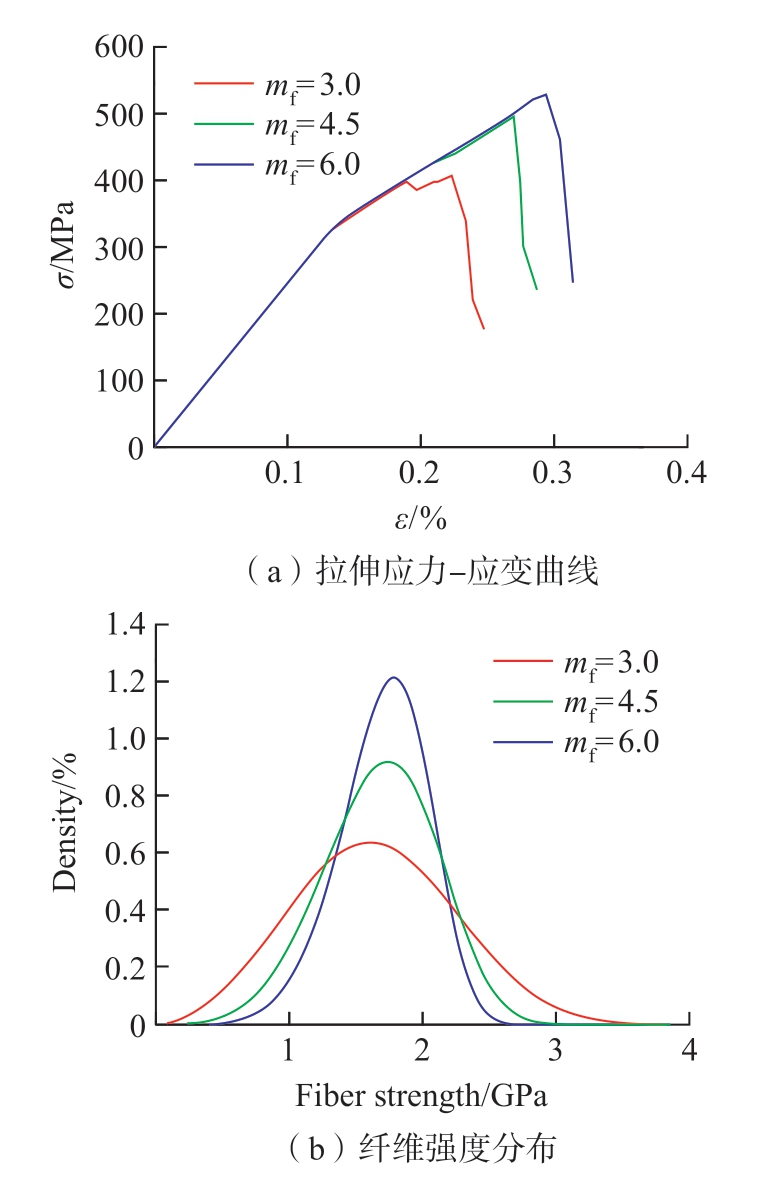
图12 不同形状参数值时试样的拉伸应力–应变曲线和纤维强度分布
Fig.12 Tensile stress–strain curves of samples and fibe strength distribution atlas with different shape parameters
2.4 界面性能对单向SiC/SiC 复合材料拉伸行为的影响
通过改变界面强度,本文进一步研究了界面性能对单向SiC/SiC 复合材料拉伸行为的影响,结果如图13所示。在一定界面强度内,单向SiC/SiC 复合材料的拉伸强度随着界面强度的增加而升高,但是增幅随界面强度的增加而减小,Lissart 等[13]在试验中也得到过类似结果。尽管不同界面强度的试样表现出相似的曲线特征,试样的最终破坏机理却不尽相同。图14为高界面剪切强度试样(τc=120 MPa)的失效图谱。在低应变区域,高界面剪切强度试样表现出与低界面剪切强度试样相似的行为,即个别纤维的破坏导致应力集中和基体的局部损伤,随后基体的损伤导致了材料应力–应变的拐点。然而在高应变区域,较高的界面强度保证了材料界面的完好,使零星的纤维断裂无法串联在一起形成材料整体的破坏。因此,材料整体可以拉伸至更高应变,单根纤维也可能断裂多次,直至断裂纤维导致的应力集中现象导致临近纤维的临近单元断裂,试样中出现一条直线型的断裂带,在宽度方向上贯穿了复合材料整体,最终导致材料完全失效。这一失效图谱对应试验研究中强界面SiC/SiC 复合材料的脆性断裂和平整的断裂面[27]。
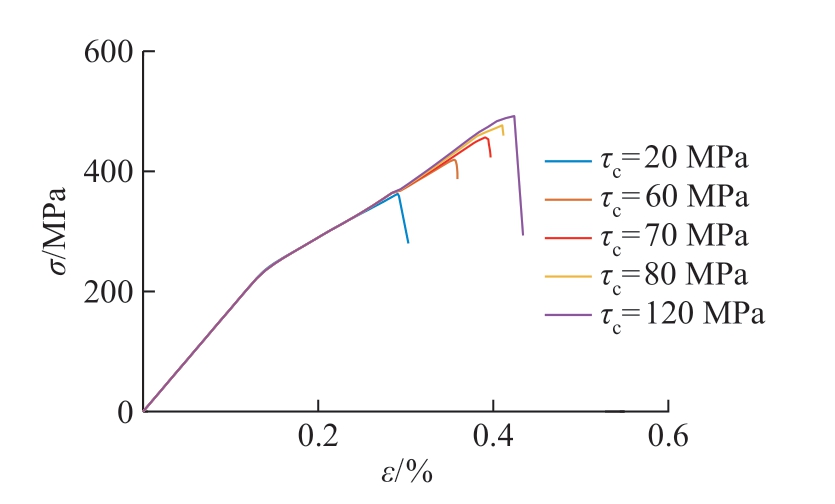
图13 不同界面剪切强度试样的拉伸应力–应变曲线
Fig.13 Tensile stress–strain curves of specimens with different interface shear strength
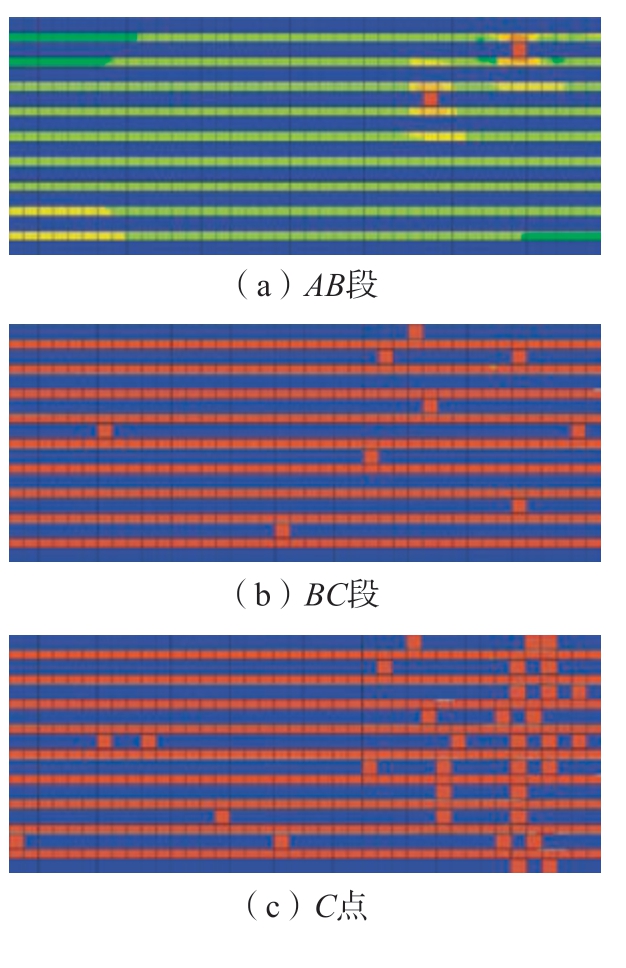
图14 界面剪切强度为120 MPa 时拉伸各阶段的单元失效状态图
Fig.14 Failure state figu e of the element at each tensile stage when the interfacial shear strength is 120 MPa
3 结论
本文针对单向SiC/SiC 复合材料的拉伸失效过程建立了一个二维微观有限元模型。模型以强度法则模拟了纤维断裂现象;以内聚力模型模拟了界面脱粘现象;通过均匀质方法,以连续损伤力学理论模拟了基体裂纹现象。通过该模型,成功模拟了单向SiC/SiC 复合材料在拉伸过程中应力应变曲线的双线性特征,阐释了单向SiC/SiC 复合材料在拉伸中的微观损伤破坏机制,比较研究了不同组分结构的性能对复合材料整体力学性能和微观破坏过程的影响,得到的结论如下。
(1)纤维的断裂将引起局部应力集中现象,诱发临近纤维、基体和界面的破坏,并最终导致材料的整体破坏。
(2)基体裂纹是材料应力–应变曲线呈现双线性特征的主要来源,含有强基体复合材料的损伤起始于更高的应力,也具有更高的整体强度。
(3)纤维强度的低离散则有助于发挥材料的性能潜力,复合材料整体可以拉伸至更高强度。
(4)界面性能对材料的最终破坏形貌有一定影响。在弱界面复合材料中,断裂纤维由界面脱粘串联在一起形成材料整体失效,体现为纤维拔出现象和粗糙的断裂面。强界面复合材料则会在拉伸过程中形成一条贯穿整个材料宽度的裂纹,并形成平齐的断裂面。
[1] AN Q L,CHEN J,MING W W,et al.Machining of SiC ceramic matrix composites: A review[J].Chinese Journal of Aeronautics,2021,34(4): 540–567.
[2] JONES R H.SiC/SiC composites for advanced nuclear applications[J].Ceramic Engineering and Science Proceedings,2008,24(4): 261–267.
[3] RIVERA K,MUTH T,RHOAT J,et al.Novel temperature sensors for SiC–SiC CMC engine components[J].Journal of Materials Research,2017,32(17): 3319–3325.
[4] MORSCHER G N.Modal acoustic emission of damage accumulation in a woven SiC/SiC composite[J].Composites Science and Technology,1999,59(5): 687–697.
[5] MARSHALL D B,COX B N,EVANS A G.The mechanics of matrix cracking in brittle-matrix fiber composites[J].Acta Metallurgica,1985,33(11): 2013–2021.
[6] MARSHALL D B,EVANS A G.Failure mechanisms in ceramic-fiber/ceramic-matrix composites[J].Journal of the American Ceramic Society,1985,68(5): 225–231.
[7] BARSOUM M W,KANGUTKAR P,WANG A S D.Matrix crack initiation in ceramic matrix composites Part I: Experiments and test results[J].Composites Science and Technology,1992,44(3): 257–269.
[8] WANG A S D,HUANG X G,BARSOUM M W.Matrix crack initiation in ceramic matrix composites Part II: Models and simulation results[J].Composites Science and Technology,1992,44(3): 271–282.
[9] PRYCE A W,SMITH P A.Behaviour of unidirectional and crossply ceramic matrix composites under quasi-static tensile loading[J].Journal of Materials Science,1992,27(10): 2695–2704.
[10] INGHELS E,LAMON J.An approach to the mechanical behaviour of SiC/SiC and C/SiC ceramic matrix composites[J].Journal of Materials Science,1991,26(20): 5411–5419.
[11] KIM R Y,PAGANO N J.Crack initiation in unidirectional brittle-matrix composites[J].Journal of the American Ceramic Society,1991,74(5): 1082–1090.
[12] BEYERLE D S,SPEARING S M,ZOK F W,et al.Damage and failure in unidirectional ceramic-matrix composites[J].Journal of the American Ceramic Society,1992,75(10): 2719–2725.
[13] LISSART N,LAMON J.Damage and failure in ceramic matrix minicomposites: Experimental study and model[J].Acta Materialia,1997,45(3): 1025–1044.
[14] COLEMAN B D.On the strength of classical fibres and fibre bundles[J].Journal of the Mechanics and Physics of Solids,1958,7:60–70.
[15] OH K P.A Monte Carlo study of the strength of unidirectional fiber-reinforced composites[J].Journal of Composite Materials,1979,13(4): 311–328.
[16] HEDGEPETH J M,VAN DYKE P.Local stress concentrations in imperfect filamentary composite materials[J].Journal of Composite Materials,1967,1(3): 294–309.
[17] 孙志刚,宋迎东,苗艳,等.陶瓷基复合材料基体随机开裂的损伤模拟[J].复合材料学报,2009,26(4): 130–135.
SUN Zhigang,SONG Yingdong,MIAO Yan,et al.Simulation of the matrix random cracking of ceramic matrix composite by Monte Carlo model[J].Acta Materiae Compositae Sinica,2009,26(4): 130–135.
[18] 李龙彪,宋迎东,孙志刚.单向陶瓷基复合材料单轴拉伸强度研究[J].航空动力学报,2010,25(10): 2177–2187.
LI Longbiao,SONG Yingdong,SUN Zhigang.Study on uniaxial tensile strength of unidirectional ceramic matrix composites[J].Journal of Aerospace Power,2010,25(10): 2177–2187.
[19] ZHANG S,GAO X G,CHEN J,et al.Strength model of the matrix element in SiC/SiC composites[J].Materials & Design,2016,101:66–71.
[20] CHEN T L,QIAO R,XIA Y M.A Monte Carlo simulation of damage and failure process with crack saturation for unidirectional fiber reinforced ceramic composites[J].Composites Science and Technology,2004,64(13–14): 2251–2260.
[21] DO–WON,K,HYOK L J,SEVNGCHUL L.Prediction and validation of the transverse mechanical behavior of unidirectional composites considering interfacial debonding through convolutional neural networks[J].Composites Part B: Engineering,2021,225: 109314.
[22] 卡恩,哈森,克雷默.复合材料的结构与性能[M].吴人洁,译.北京: 科学出版社,2001.
CAHN R,HAASEN P,KRAMER E,et al.Structure and properties of composites[M].WU Renjie,Trans.Beijing: Science Press,2001.
[23] OLLER S.Numerical simulation of mechanical behavior of composite materials[M].New Delhi: Springer,2014
[24] 方光武,高希光,宋迎东.多层界面相陶瓷基复合材料裂纹偏转机制模拟[J].航空动力学报,2019,34(8): 1805–1812.
FANG Guangwu,GAO Xiguang,SONG Yingdong.Simulation of the crack deflection mechanism for ceramic matrix composites with multilayer interphase[J].Journal of Aerospace Power,2019,34(8): 1805–1812.
[25] CANAL L P,GONIÁLEI C,SEGURADO J,et al.Intraply fracture of fiber-reinforced composites: Microscopic mechanisms and modeling[J].Composites Science and Technology,2012,72(11): 1223–1232.
[26] KRENKEL W.Ceramic matrix composites: Fiber reinforced ceramics and their applications[M].Hoboken: Wiley,2008.
[27] 何宗倍,张瑞谦,付道贵,等.不同界面SiC 纤维束复合材料的拉伸力学行为[J].材料工程,2019,47(4): 25–31.
HE Zongbei,ZHANG Ruiqian,FU Daogui,et al.Tensile mechanical behavior of SiC fiber bundle reinforced composites with different interfaces[J].Journal of Materials Engineering,2019,47(4): 25–31.
[28] 刘洋.SiC/SiC 陶瓷基复合材料损伤失效机理研究[D].哈尔滨: 哈尔滨工业大学,2019.
LIU Yang.Study on damage failure mechanism of SiC/SiC ceramic matrix composites[D].Harbin: Harbin Institute of Technology,2019.
[29] 杨永岗,李润民,贺福,等.用Weibull 模数表征炭纤维增强树脂基复合材料的力学性能[J].炭素技术,1996(5): 1–4.
YANG Yonggang,LI Runnin,HE Fu,et al.The mechanical properties of carbon fiber reinforced resin matrix composites were characterized by Weibull modulus[J].Carbon Techniques,1996(5): 1–4.