航空发动机高压转子由高压压气机(High pressure compressor,HPC)转子和高压涡轮(High pressure turbine,HPT)转子组成,如图1所示。同心度指标是高压转子最为关键的装配参数,直接影响转子不平衡量和整机振动水平。同心度是转子零件几何中心相对转子组件回转轴线的径向偏心矢量[1–2]。工程上,一般通过测量联合基准(前、后轴颈中心连线)下的高压压气机篦齿盘盘心孔径向跳动来表征高压转子组件的同心度指标。转子内腔狭长,结构高度复杂,实现高精度测量难度很大,特别是对于某型军用航空发动机,现有同心度测量手段非常有限,因为前轴颈被其他结构遮挡,测量工具只能同步测量篦齿盘盘心孔和后轴颈外圆跳动,无法同步测量前轴颈跳动,所以测量精度低、稳定性差,也需要人工旋转转子,导致劳动强度大、效率低[3]。因此需要开展对航空发动机高压转子装配同心度预测及装配相位优化的研究,提升同心度预测精度与预测效率,保证高压转子装配质量,提升一次装配成功率。

图1 航空发动机(F136)高压转子示意图
Fig.1 High pressure rotor of aero-engine (F136)
诺丁汉大学Hussain等[4]提出的连接装配模型(Connective assembly model,CAM)基于刚体假设,通过建立零件位姿矩阵描述其空间位姿关系以及几何误差在三维空间中传递过程,但并未考虑零件真实形状对装配误差传递的影响,并且零件空间装配关系的复杂度严重影响CAM的计算准确度和计算时间。孙岩辉等[5]针对回转特征零件装配,提出一种通过精密主轴的结构及零部件制造误差预测其几何精度的计算方法,并通过灵敏度分析获得对各零件公差对回转精度的贡献度大小,但该计算方法也是基于刚体假设,没有考虑装配变形对回转精度的影响。
对于航空发动机等回转特征零件来说,装配过程存在过盈配合,且为薄壁结构,装配过程零件变形对误差传递影响较大。因此,在传统装配问题中引入智能算法,使用数据探索难以准确描述的装配机理,弥补装配中依据经验装调的不足,对装配提供可靠指导,对于解决航空发动机装配误差预测与相位优化具有很好的应用前景和价值。Prabhaharan等[6]提出基于遗传算法的最优化公差分配方法。刘海博[7]提出基于粒子群算法的公差优化模型。曹衍龙等[8]提出基于人工神经网络方法的公差优化模型。王巍等[9]结合了BP神经网络法与评价函数法,研究了针对多个目标同时优化的公差优化和公差设计方法。然而,在航空发动机装配领域却鲜有将机理模型与智能算法等先进人工智能技术相结合来解决经验装配、试错装配等传统装配方法造成的装配合格率低、一次装配成功率低等问题。因此,为了提高航空发动机高压转子装配精度,亟须研究融合机理模型与智能算法的先进装配技术与方法。
本文首先对航空发动机高压转子关键装配参数进行分析,然后基于某发动机127台份装配数据提出了基于神经网络模型的同心度预测智能算法,并对比了直接基于实测数据和基于实测数据通过几何模型预测后修正两种方法的准确性,最后提出了装配相位优化方法,并与SP值匹配和轻重点匹配的装配方法进行对比,讨论了其对装配偏心的影响。
1 高压转子关键装配参数分析
在航空发动机高压转子装配中,HPC/HPT转子试车前的SP(Stack projection,SP)值以及高压转子装配体的SP值、篦齿盘盘心跳动等多项装配参数是进行装配几何误差评定的直接参数,该几何误差状态同样会对转子不平衡量的质量特性产生影响。
国内航空发动机制造企业采用了多台Taylor Hobson公司研制的Aerospect SPS系列航空发动机转子装配测试仪器,将当前被测转子的误差状态及其与所定义参考平面距离表达为被测零组件的SP值,并应用于装配相位优化中。但此检测技术为接触式测量,对零件姿态有较高要求,且只能测量单圈跳动,不能完整反映止口三维形貌。
HPC/HPT转子及高压转子组件的SP值为各单件单盘跳动参数对组件状态同心度影响量的矢量投影。以图2所示三级转子装配为例,一级转子的SP值(包含大小与方向)P1包含了一级转子的偏心、上端面倾斜及上级所有转子的高度和信息,与影响转子装配同轴度的影响因素一致,表征了一级转子偏心和倾斜误差对安装其上的多级转子装配同轴度的影响。需要说明的是,上述定义中以最上层转子上端面作为投影平面。

图2 一级转子偏心矢量投影
Fig.2 Eccentricity vector projection of stage 1
篦齿盘盘心跳动是HPC/HPT装配后进行几何误差评价的重要指标,与采用某一基准面进行评价不同,采用组件前后端面的联合基准作为评价基准。如图3所示,篦齿盘位于HPC/HPT中间装配位置,测量中以前后端面拟合圆心为联合基准,篦齿盘盘心相对于联合基准轴线的偏移P表征为篦齿盘盘心偏心,跳动值约为偏心的2倍。
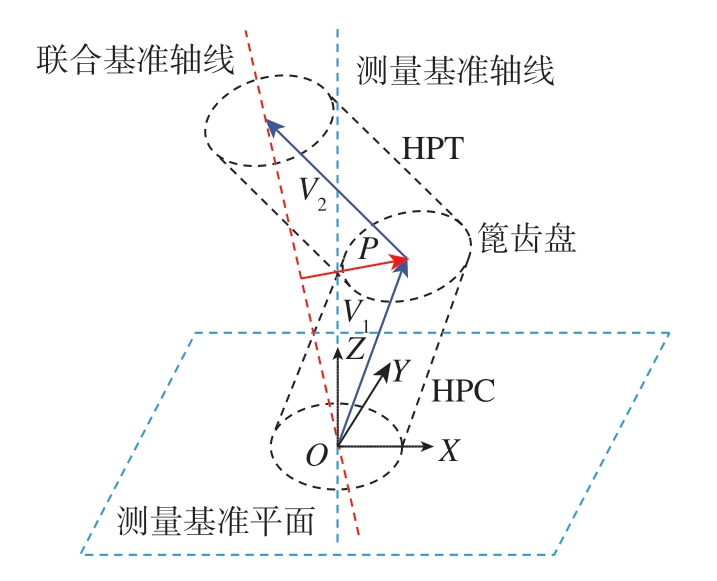
图3 篦齿盘心跳动
Fig.3 Runout of labyrinth disc center
2 高压转子关键装配参数预测
航空发动机高压转子是由高压压气机和高压涡轮转子根据一定安装相位堆叠装配而成。在装配前,需要对HPC/HPT转子的重要几何特征参数,比如同心度指标、关键截面跳动、几何尺寸等进行精密测量,以实现对装配后同心度的预测、评价与装配相位优化。
对于航空发动机包含几何误差的薄壁结构件装配,需要在装配误差分析预测中考虑形状误差、过盈量、螺栓连接等导致的零件变形,实现装配误差的准确预测[10]。通过构建航空发动机转子安装边有限元模型,将实测几何误差加入到模型中,并进行静力学分析,是实现考虑零件变形的装配误差预测的有效方法,其建模和计算时间较长,不能满足实际装配现场的节拍要求。因此,从数据驱动的角度考虑,通过大量历史测量样本数据的学习,采用机器学习的方法对HPC/HPT转子几何特征参数进行装配同轴度的预测。
2.1 基于神经网络的高压转子关键 装配参数预测技术
BP神经网络有着很强的非线性映射能力,可以快速拟合HPC/HPT转子几何特征参数和装配同轴度之间的非线性关系,适合用来进行航空发动机高压转子装配同轴度预测。在不忽略转子零件形状误差、考虑装配变形的条件下,快速高效地计算转子装配同心度。在BP神经网络模型构建中,一般认为隐含层层数越多,训练出的网络精度越高,但增加层数会使网络结构复杂,难以确定参数,增加程序调试难度,而且有可能出现过拟合现象。
在本研究中,通过HPC/HPT的SP实测值预测篦齿盘盘心跳动大小(表征装配同心度),现场采集样本数为127组,由于样本数不多且输入输出节点数少,因此采用80%的采集样本用作训练集,20%的采集样本用作测试集。为避免过拟合现象,采用单隐含层神经网络模型,隐含层神经元个数为10,如图4所示。
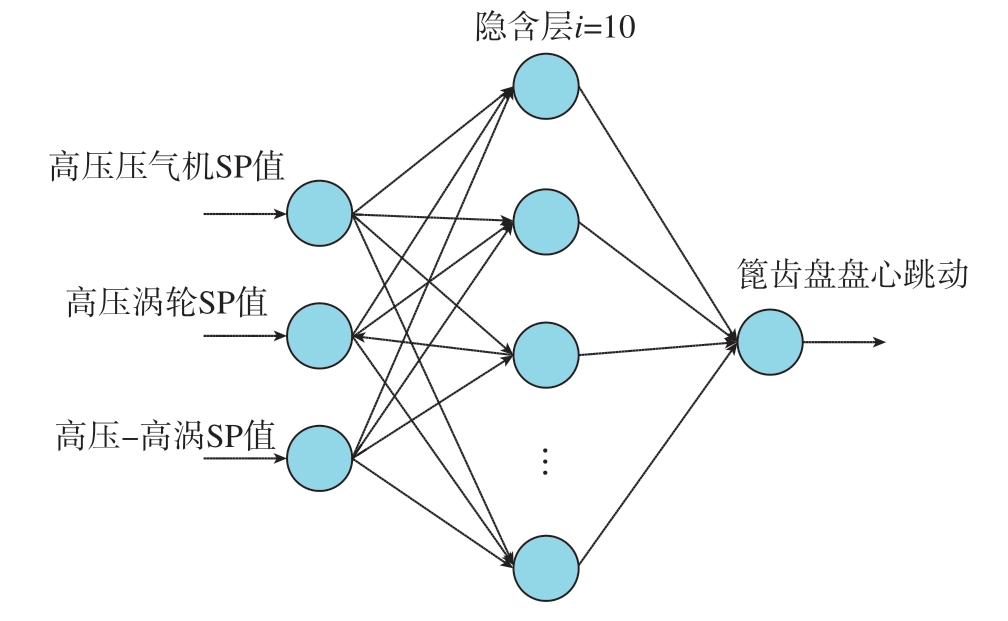
图4 篦齿盘盘心跳动预测的BP神经网络模型
Fig.4 BP neural network model for predicting runout of labyrinth disc center
上述为直接通过样本数据中测量得到的SP值进行篦齿盘盘心跳动。本文进一步讨论了利用修正值进行篦齿盘盘心跳动预测,其不同之处在于首先通过实测得到SP值,通过几何分析方法计算得到篦齿盘盘心跳动的理论分析结果,并将其与实测篦齿盘盘心跳动的偏差修正值作为样本输出进行神经网络模型构建与预测。
2.2 高压转子关键装配参数预测分析
基于127组HPC/HPT转子几何特征参数(SP值)和篦齿盘盘心跳动的实测值进行神经网络模型的训练和测试,其结果如图5所示,约70%样本的预测误差小于30%,且基于偏差修正值的神经网络模型相对于仅采用实测数据的方法,其预测精度更高。本文分别利用刚体堆叠理论[4]、两种智能预测方法对样本数据中20组测试集数据进行篦齿盘盘心跳动计算。图6为20组测试集试验测试、刚体堆叠和智能预测结果的对比,可以看出相比刚体堆叠理论方法,神经网络的智能预测算法的篦齿盘盘心跳动预测精度更高。
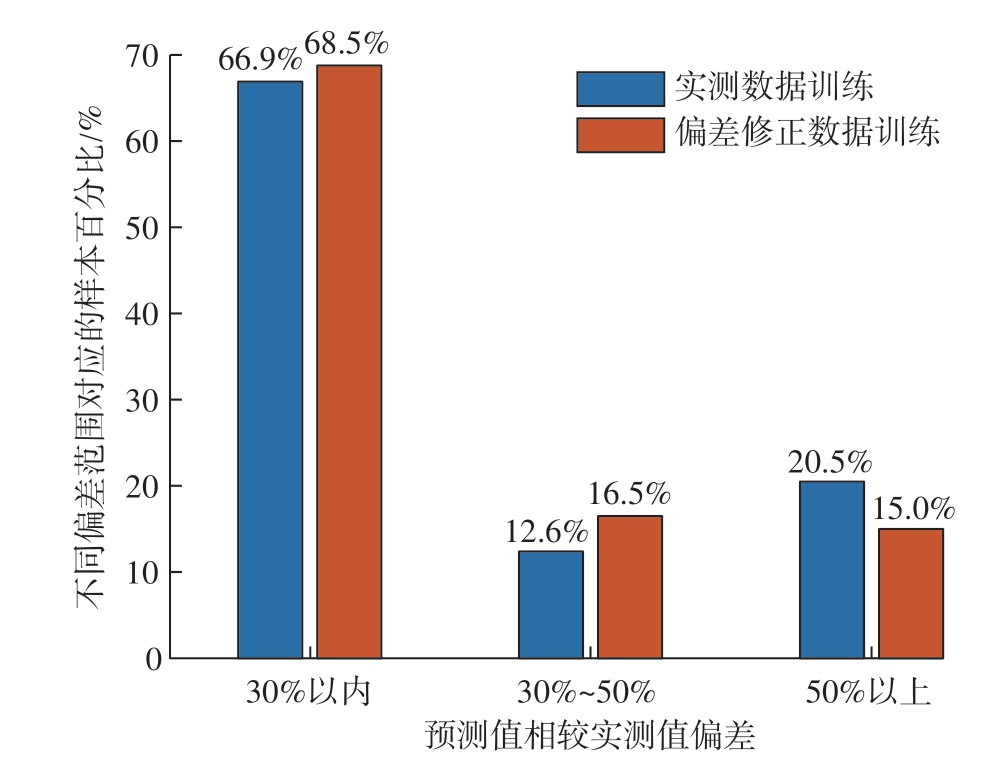
图5 基于神经网络模型篦齿盘盘心跳动预测
Fig.5 Prediction of runout of labyrinth disc center based on neural network model

图6 不同方法下篦齿盘盘心跳动测试集预测结果对比
Fig.6 Comparison of measured and predicted runout of labyrinth disc center using different methods
3 高压转子装配相位优化
根据工程经验和理论分析,HPC/HPT转子安装相位对高压转子最终同心度和振动响应影响较大。根据不同主机厂经验,高压转子装配相位确定有SP值匹配、高低点匹配和轻重点匹配方法。上述某发动机127台份装配数据中的HPC/HPT转子安装相位则是根据SP匹配方法确定的。然而以上装配相位的确定原则,实际上是在对转子几何误差特定的表征基础上(如SP值、高低点、轻重点等)基于逻辑判断直接匹配装配相位的方法,所以其几何误差表征不全面,造成装配相位优化中考虑因素较片面,无法得到最优的装配相位。在多级盘装配中,其误差将会累积增加,造成最终装配同心度难以满足要求[11]。
本文基于上述某主机厂127组的HPC转子和HPT转子的SP实测值,利用所提模型分别计算SP值匹配以及优化装配相位(以同心度最小为目标)后联合基准的同心度(篦齿盘盘心跳动)。由于本文分析案例中只有HPC与HPT装配,因此装配相位寻优采用枚举法,通过得到最小预测同心度进而获得最优装配相位。图7为高压组合转子两种装配方法(SP值匹配以及优化装配相位)篦齿盘盘心跳动预测对比。其中,为了便于对比各种装配方法的同心度,将所有数据按装配相位优化结果升序排列。可以看出,装配相位优化后篦齿盘盘心同心度整体均小于SP值匹配装配方法,说明通过装配相位优化可以有效减小高压组合转子篦齿盘盘心跳动数值。

图7 高压组合转子两种装配方法篦齿盘盘心跳动预测对比
Fig.7 Comparison of predicted runout of labyrinth disc center for high pressure rotor based on two assembly methods
本文进一步在某主机厂开展了3台份某型发动机高压组合转子优化装配对比试验。基于HPC转子和HPT转子的几何跳动数据,利用所提模型以篦齿盘盘心跳动最小为目标计算优化装配相位,并通过测量试验对比分析该主机厂现有轻重点匹配装配工艺方法和优化装配相位的装配结果。表1为高压组合转子两种装配方法(轻重点匹配以及优化装配相位)篦齿盘盘心跳动测量结果对比。可以看出,有两台份篦齿盘盘心跳动明显减小30%以上,有一台份盘心跳动与轻重点匹配方法接近。
表1 高压组合转子两种装配方法篦齿盘盘心跳动实测结果对比
Table 1 Comparison of measured runout of labyrinth disc center for high pressure rotor based on two assembly methods
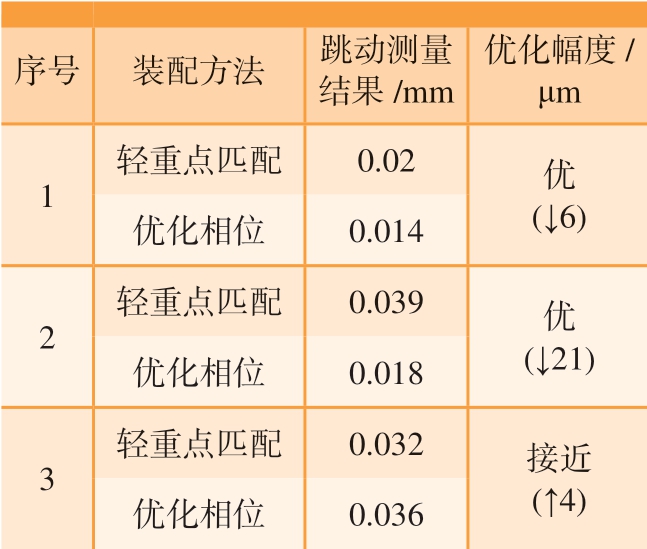
序号 装配方法 跳动测量结果/mm优化幅度/μm 1轻重点匹配 0.02 优(↓6)优化相位 0.014 2轻重点匹配 0.039 优(↓21)优化相位 0.018 3轻重点匹配 0.032 接近(↑4)优化相位 0.036
4 结论
针对某航空发动机高压转子同心度测量精度低、稳定性差的技术问题: (1)可以研发新型检测技术,特别是基于光学的自动化测量装备的应用,其是未来重要发展方向; (2)可以开发专用仿真模型,使用装配过程实测数据进行快速仿真计算同心度指标,减少对高精度测量的技术需求和依赖性。本文提出的智能堆叠仿真技术可以根据HPC/HPT转子几何特征参数实测值和安装相位快速计算高压转子同心度指标。使用HPC/HPT转子几何特征参数实测值,本文提出的相位优化方法可以使高压转子同心度指标进一步降低。
[1] 孙贵青, 吴法勇.航空发动机不同心度测试技术研究[C]//第六届中国航空学会青年科技论坛, 沈阳, 2014.
SUN Guiqing, WU Fayong.Study on test technology of aeroengine nonconcentricity[C]//The 6th Youth Science and Technology Forum of CSAA, Shenyang, 2014.
[2] 孙汕民, 周烁, 高鸽, 等.航空发动机装配仿真的关键技术问题[J].航空制造技术, 2018, 61(22): 98–103.
SUN Shanmin, ZHOU Shuo, GAO Ge, et al.Key technical issues on aero-engine assembly simulation[J].Aeronautical Manufacturing Technology, 2018, 61(22): 98–103.
[3] 刘君, 吴法勇, 王娟.航空发动机转子装配优化技术[J].航空发动机, 2014, 40(3): 75–78.
LIU Jun, WU Fayong, WANG Juan.Optimization technique of aeroengine rotor assembly[J].Aeroengine, 2014, 40(3): 75–78.
[4] HUSSAIN T, YANG Z, POPOV A A, et al.Straight-build assembly optimization: A method to minimize stage-by-stage eccentricity error in the assembly of axisymmetric rigid components (two-dimensional case study)[J].Journal of Manufacturing Science and Engineering, 2011, 133(3): 1–9.
[5] 孙岩辉, 洪军, 刘志刚, 等.考虑零部件制造误差的精密主轴几何回转精度计算方法[J].机械工程学报, 2017, 53(3): 173–182.
SUN Yanhui, HONG Jun, LIU Zhigang, et al.A calculating method for the geometric rotation accuracy of precision spindles considering the manufacturing errors of component parts[J].Journal of Mechanical Engineering, 2017, 53(3): 173–182.
[6] PRABHAHARAN G, RAMESH R, ASOKAN P.Concurrent optimization of assembly tolerances for quality with position control using scatter search approach[J].International Journal of Production Research, 2007, 45(21): 4959–4988.
[7] 刘海博.机械产品几何精度设计中的多目标公差优化技术[D].北京: 北京理工大学, 2015.
LIU Haibo.Multi-objective tolerance optimization in design of geometric precision for mechanical products[D].Beijing: Beijing Institute of Technology, 2015.
[8] 曹衍龙, 刘保军, 杨将新.基于模糊神经网络的公差–成本模型研究[J].工程设计学报, 2004, 11(2): 73–76.
CAO Yanlong, LIU Baojun, YANG Jiangxin.New cost-tolerance function based on fuzzy neural networks[J].Journal of Engineering Design, 2004, 11(2): 73–76.
[9] 王巍, 梁涛, 刘中文, 等.基于 BP 神经网络的装配容差多目标优化设计[J].中国科技纵横, 2012(16): 27.
WANG Wei, LIANG Tao, LIU Zhongwen, et al.Multi objective optimization design of assembly tolerance based on BP neural network[J].China Science & Technology Panorama Magazine, 2012(16): 27.
[10] SUN Y H, GUO J K, HONG J, et al.Modeling of rotation accuracy of multi-support rotating machinery considering geometric errors and part deformation[J].Assembly Automation, 2020, 40(5): 665–673.
[11] SUN Y H, GUO J K, HONG J, et al.Repair decision based on sensitivity analysis for aero-engine assembly[J].International Journal of Precision Engineering and Manufacturing, 2019, 20(3): 347–362.
