随着新一代信息与通信技术的快速普及,航空产品的设计和装配在加速走向数字化、智能化时代。飞机装配作为整个飞机制造过程中精度控制的重要保障环节,是决定飞机产品性能的核心[1]。但飞机装配过程多涉及大量设备,工序繁杂且人工参与较多,导致多个零件构成的部件与部件之间出现装配不协调问题[2–3]。特别是飞机舱门,其装配过程存在复杂的相互作用关系,因装配工艺、零件具体装配特征等不同,最终装配偏差呈现异同,使装配准确度难以达到预期。传统的装配偏差分析以理论三维数模为基础,难以反映制造、装配、调试多阶段相互作用影响下真实产品与理论模型之间的差异[4],无法满足验收时的检测精度要求。数字孪生作为物理实体的真实“映射”技术,以此为基础进行舱门装配过程偏差传递分析,可有效实现复杂产品装配精度预测。
目前,许多学者对此进行了广泛研究。在数字孪生模型构建方面,陶飞等[5–6]认为数字孪生具有实时同步、忠实映射、高保真度等特性,是实现虚实之间双向映射、动态交互、实时连接的关键途径,并提出统一数据和模型标准、共享数据与模型、服务创新、思想碰撞等方式,以促进数字孪生技术落地应用;Schleich等[7]基于皮肤模型对零件的形状偏差表达、装配关系进行了深入研究后,提出基于皮肤模型的产品数字孪生模型,并指出上述装配关系模型应用于其数字孪生模型的可行性;姜珊等[8]提出了一种基于有限状态机的工装数字孪生几何模型建模方法,通过实时数据采集与预处理、定义状态及其转移机制、参数化几何实体建模实现了实物工装在数字空间的动态映射,为基于数字孪生模型的虚拟仿真奠定基础。在偏差传递分析方面,刘伟东等[9]从偏差源入手,提出了偏差源正负累积性判定及评价方法,并基于偏差有向图,采用统一的多元统计偏差模型对某航天器装配精度进行了分析与计算。苏春等[10]给出零件内误差、配合面误差、主被动配合面以及装配精度可靠度的定义,基于位姿变换矩阵对某型号测量平台机架进行装配误差模型的构建,并对其进行公差优化分配,提高其装配精度。祝鹏等[11]提出基于复杂网络的自调节偏差传递网络建模方法与误差溯源方法,利用实测数据对模型进行赋权,研究了锥齿轮轴组件复杂的多段装配过程。在基于数字孪生的装配分析方面,陶飞等[12]提出了一套数字孪生模型构建准则与理论体系,将数字孪生三维结构模型创新性地扩展到五维,在此基础上提出6条应用的基本准则,搭建面向装配、车间的数字孪生模型装配理论体系,促进数字孪生模型装配技术发展。Wang等[13]提出了一种基于通用零件数字孪生模型的装配精度分析方法,构建了多源异构数据集成下的几何模型,将装配信息映射到几何特征上,实现了数字孪生装配技术下装配精度控制。Zhuang等[14]构建了基于数字孪生的复杂产品装配车间智能生产管理和控制方法框架,以卫星装配车间为例,通过物理数据实时获取、数字孪生体构建、数字孪生体和大数据驱动预测、生产管理和控制服务四大技术,为数字孪生装配车间落地应用提供了解决方案。可以看出,基于数字孪生理念构建产品高保真模型,以此为基础分析产品装配过程的偏差传递机理,可实现装配精度的提高。
因此,本研究以某型飞机舱门为研究对象,结合产品建模需求,开展数字孪生模型构建技术研究,在此模型基础上改进传统的偏差传递计算方法,研究民用飞机零部件装配过程中的偏差传递规律,以实现通过数字化手段预测装配偏差,保障飞机产品精度,提高产品交付率。
1 面向装配过程的某型舱门数字孪生模型构建
现有工作模式下,随着装配现场、装配工艺的不断变化,零件和工装的状态与理想状态偏差较大,产品理论模型难以反映真实状态,基于此类模型开展的数字化仿真结果与实际装配结果存在较大差异,难以实现“虚实相映”。数字孪生理念的诞生为解决此类问题给出精准方案,即以数字孪生技术为核心,构建高保真模型,配合后续仿真操作,实现复杂产品装配过程中的误差控制、精度预测。
1.1 数字孪生模型建模需求定义
某型飞机前服务门为半堵塞外开式舱门,由结构骨架、众多运动机构等构成。其主要功能为飞机上运送食品餐饮及清理机上垃圾等勤务工作的通道,在必要情况下作为机务人员和乘客的登机、离机通道。该型舱门装配过程如图1所示,通过工装定位蒙皮,按照蒙皮→边框Ⅰ→中间梁→边框Ⅱ→壁板→结构骨架进行安装;接着完成结构骨架→锁轴、外部把手→模式选择机构→插销机构→提升机构、内手柄→支臂组件→泄压口盖→导向滚轮、观察窗等步骤;最后,安装电气元件完成整个产品的安装过程。
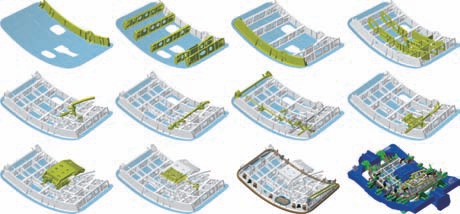
图1 某型飞机舱门装配过程
Fig.1 Assembly process of certain type of hatch
该型号舱门采用一套与舱门接头处对应配对的检验工装装置,充当机身上与舱门装配的部分,以模拟机体与舱门配合工况,通过检测舱门与验证工装对缝处的间隙和阶差是否满足相应的协调准确度,判断舱门各机构件功能是否符合要求。然而,该型号舱门产品交付时频繁出现让步接收现象。
经研究发现,由于零件存在尺寸公差与形位公差、接头类零件存在安装误差,不同批次的边框、梁、隔框等装配特征的位置不同,各机构组件尺寸、形状等不同,造成装配过程中偏差累积,舱门实际装配状态与理想状态不一致,实际运动时导向滚轮在滑槽处存在碰撞,导致舱门开启力超差。
1.2 数字孪生模型构建方法
随着装配现场、装配工艺的不断变化,零件和工装的状态与理想状态偏差较大,只含有设计参数的MBD模型无法反映真实状态。为满足实际装配现场需要,以MBD模型框架为基础,融合装配过程零件几何变化状态、装配工艺、特征配准约束等信息,构建面向装配过程的数字孪生模型。具体的建模思路为“点云数据重构理论模型+制造、装配、调试等多阶段衍生信息挂载”,如图2所示。
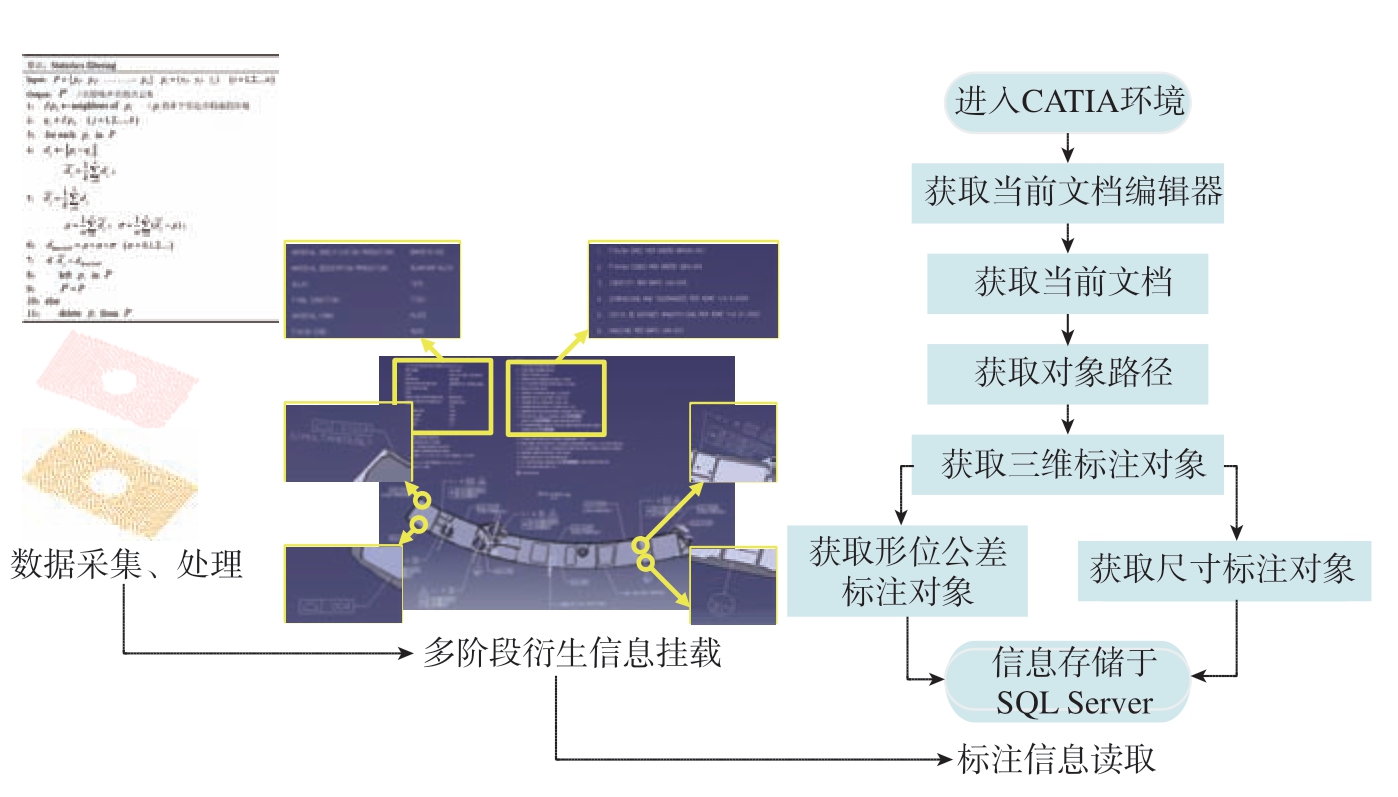
图2 面向装配过程的数字孪生模型建模思路
Fig.2 Modeling ideas for digital twins of assembly process
首先,通过高精度测量仪器获取装配过程中零件关键特征部位的实测数据,采用点云滤波、点云配准等算法进行点云处理,借助曲面重构软件进行特征曲面重构,驱动模型几何层的高保真构建;其次,在CATIA V5 R21建模环境中实现零件关键特征原表面与重构表面的更换、融合,定义几何信息与非几何信息挂载方式,即采用三维标注表达法或属性表达法进行信息表征,借助CAA实现模型信息读取功能;最后,基于信息挂载规则,以设计模型为载体,融合设计、制造、装配、检测等信息。下面以某型舱门零件边框Ⅰ为研究对象,给出数字孪生模型构建过程中关键技术的具体流程。
1.3 数字孪生模型实例
1.3.1 关键特征确定
按照装配顺序和尺寸链传递路线进行边框Ⅰ关键特征的确定。边框Ⅰ的装配过程为工装定位好蒙皮,然后将边框Ⅰ安装到蒙皮上,在与蒙皮通过预制定位销的位置实现定位,采用面面贴合定位方式。左右4个小孔为与锁头连接的配制孔,中间2个大孔为轴承安装孔,其大孔周围的几个小孔为轴承座安装的配制孔。综上,待测装配特征有2个: (1)边框Ⅰ中间的两个轴承安装孔; (2)边框Ⅰ的底端贴合面,如图3所示。
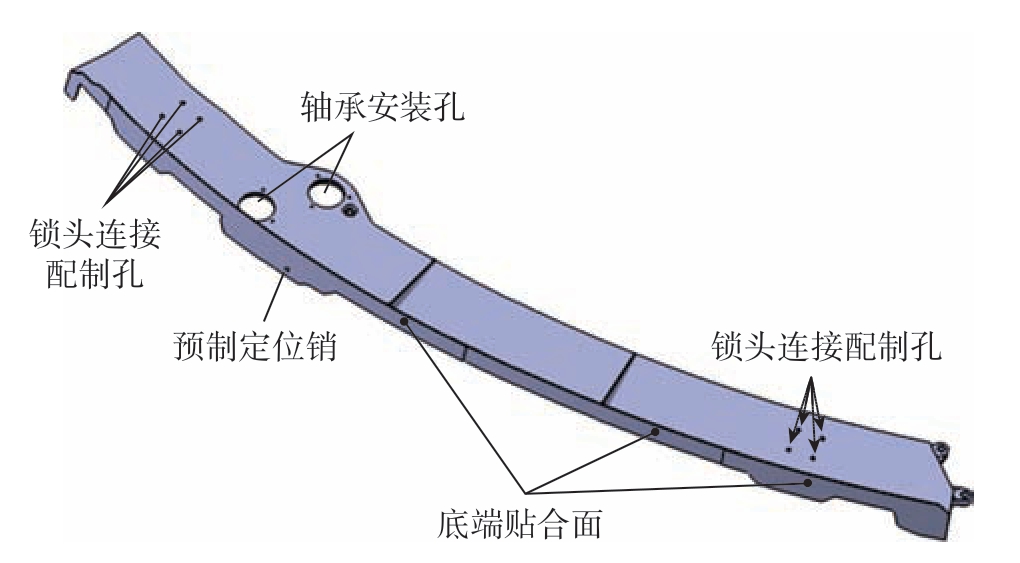
图3 某型舱门边框Ⅰ关键特征
Fig.3 Key features of a certain type of hatch frame Ⅰ
1.3.2 点云数据滤波
采用LEICA激光跟踪仪进行零件表面特征的数据采集工作,通过不断移动靶球进行扫描,扫描完毕后导出.txt格式的点云文件,如图4所示。

图4 待测特征现场采集
Fig.4 On site collection of characteristics to be tested
测量过程中,当技术人员多次平缓地扫描圆周,形成的环状点云带大多数已达到预期要求,但受环境及操作技术的影响,存在很多不必要的噪点,仅需将部分误差点剔除即可后续重构工作。基于“统计滤波算法”的原理在MATLAB R2019b中编写Pcdenoise子程序,运行程序获得统计滤波处理后的点云,安装孔圆柱面I,其点云离散点从653个降为496个,点云整体形状与规则圆柱面基本一致,如图5所示。
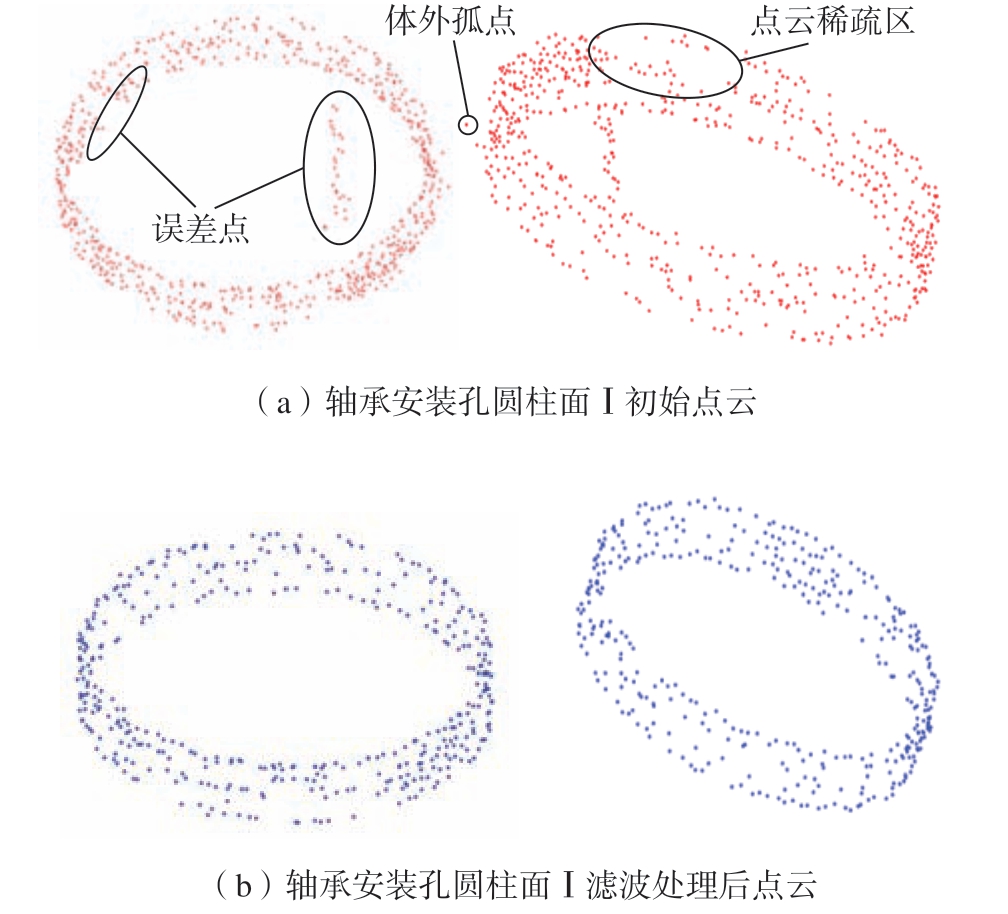
图5 关键特征点云滤波处理
Fig.5 Key feature point cloud filtering
1.3.3 特征曲面重构
在边框Ⅰ的定位安装过程中,主要采用面面贴合定位方式,为得到其关键特征的真实曲面,将处理过的点云导入Geomagic Studio软件,进行封装操作,对重构曲面中的空洞部位采用多边形界面填充孔功能进行基于曲率填充操作,查看封装好的模型并进行快速平滑处理、剔除边缘毛刺点。最终,用于去重构的三角网络曲面个数分别为916个、1296个和1378个。将Geomagic Studio软件重构的曲面以.stl格式导出,在CATIA的Digitized Shape Editor建模环境中导入,如图6所示。

图6 边框Ⅰ关键特征重构曲面
Fig.6 Reconstruction surface by frame Ⅰ key feature
1.3.4 孪生信息生成
在上述已经构建好的数字孪生模型中,获取重构曲面的中心位置数据,即在CATIA环境下直接利用指南针将全局坐标系移动至重构曲面中心,在点定义模块选取指南针方向进行点建立,从而生成局部坐标系,并进行信息挂载,如将零件尺寸、基准、公差等信息以三维标注的信息添加到设计模型上;将一系列非几何信息以文本、属性集的形式加载进去;将特征面的点云数据集通过Export操作添加到设计模型上,以便导出信息为后续操作奠定基础。对于重构曲面的中心坐标信息、非几何文本信息,通过CATIA中创建设计表,将其以.xlsx格式导出;对于以点云数据集挂载的孪生数据,直接以.wrl格式导出,后缀改成.txt即可查看点云信息;对于以三维标注挂载的公差信息,则通过CAA程序进行选取导出,如图7所示。
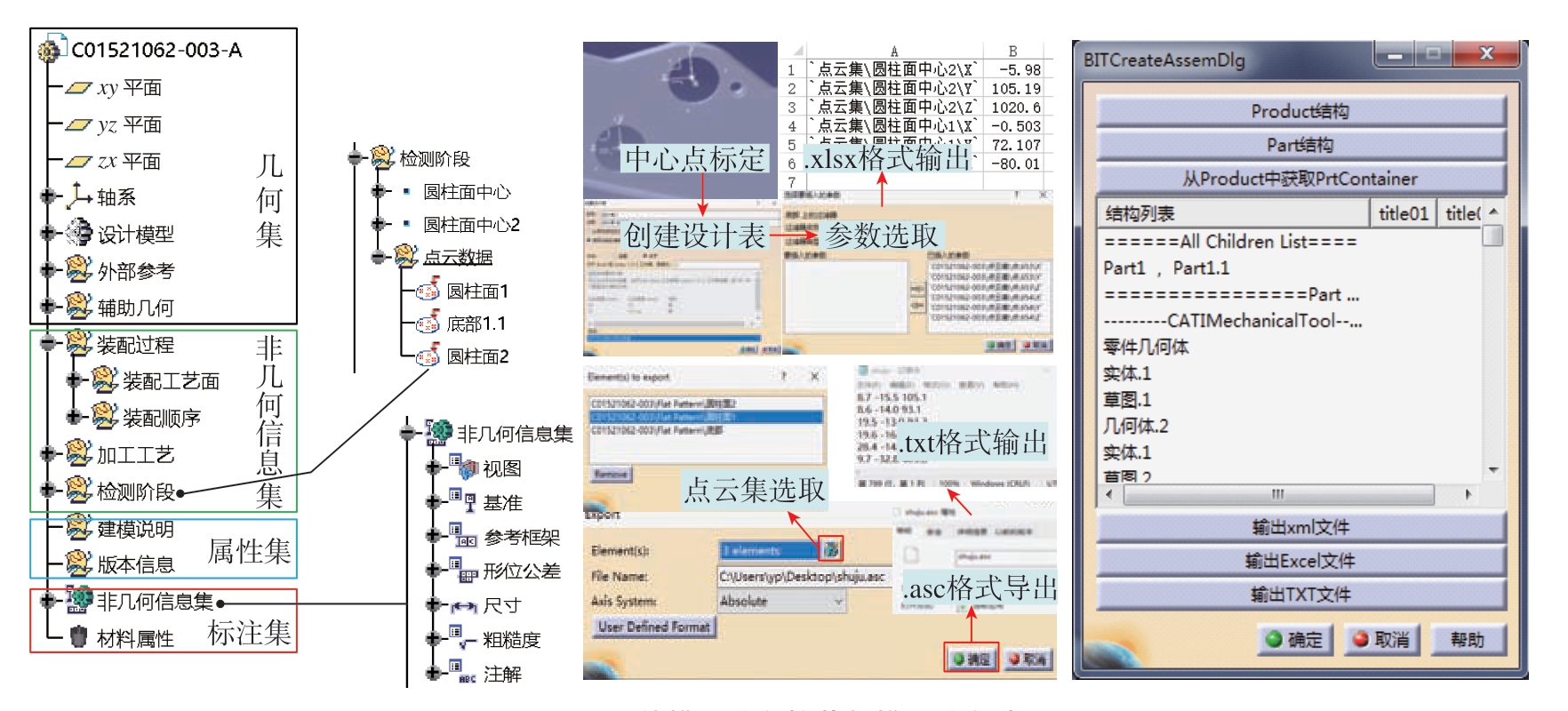
图7 零件模型信息挂载与模型信息读取
Fig.7 Part model information mounting and model information reading
1.3.5 模型效果展示
基于上述构建思路,对其余部分零件、工装开展建模工作,其模型效果对比如图8所示。

图8 各类零部件、工装数字孪生模型效果图
Fig.8 Effect drawings of digital twin model of various parts and tooling
2 基于数字孪生的偏差传递模型建立
飞机舱门因其复杂结构与机构的影响,导致装配过程中会引入大量偏差,如何有效表达装配过程中存在的偏差传递关系及累积效应,从而预测产品装配准确度是复杂产品精度控制的研究重点。传统研究方法以理论设计模型为基础开展偏差预测,忽略了零部件加工过程中的制造误差和真实配合关系,理论预测值往往与实际状况相差较大。因数字孪生模型可实现产品几何上的高保真建模,基于此模型开展装配偏差分析,可有效实现复杂产品装配精度预测。
2.1 基于数字孪生模型的偏差传递分析
目前,在偏差传递表达方面,常用雅克比矩阵模型表达零件之间的公差传递,小位移旋量(Small displacement torsors,SDT)模型描述公差域变动,结合两者的优点形成雅克比旋量模型,以此进行装配偏差分析,具体步骤如下。
步骤1:对装配过程进行分析,建立特征FEij的SDT模型。
步骤2:建立特征FEij的局部坐标系,求解特征FEij与FR之间的雅克比矩阵模型。
步骤3:建立FR的雅克比旋量模型,其数学表达式为


本质上,产品装配是由若干个零部件按照一定顺序将各装配特征进行重合而实现,而装配特征往往通过待装配零件上两两形状特征间的共扼配合关系来体现。采用上文所提出的数字孪生模型构建方法,即通过激光跟踪仪对零件关键特征的真实表面进行数据采集,基于采集的离散点云数据进行零件关键特征表面重构,从而反映最真实的几何接触表面。因受实际制造误差及测量误差的影响,构建出的数字孪生模型与理论模型相比,其零件特征的位置或形状难免存在偏差。实际装配过程中,当某个零件的特征发生变动时,与其他待装配零件将无法形成共扼配合关系,该变动伴随着装配关系一直传递并不断衍生出新的非共轭配合关系,最终将形成偏差累积效应,影响产品装配体关键特征点的几何准确度。
2.2 基于数字孪生的偏差传递计算方法
传统研究以理论设计模型为基础开展偏差传递分析,其基于理想配合面研究零件特征在装配关系、公差域约束作用下,对最终关键目标点FR的影响。但受加工技术、测量方法、夹具/刀具制造精度等条件影响,实际零件常与理想模型之间存在偏差,直接采用雅克比矩阵进行偏差传递分析,将导致理论计算值与实际不符。因此,需开展基于数字孪生模型的偏差传递分析,综合考虑制造误差作用下零件特征位置、形状的变动情况,结合真实配合关系,对原有雅克比矩阵进行修正,通过数学方式对零件特征与最终关键目标点FR的关系进行表征,具体修正过程详见下文。
2.2.1 雅克比矩阵模型修正

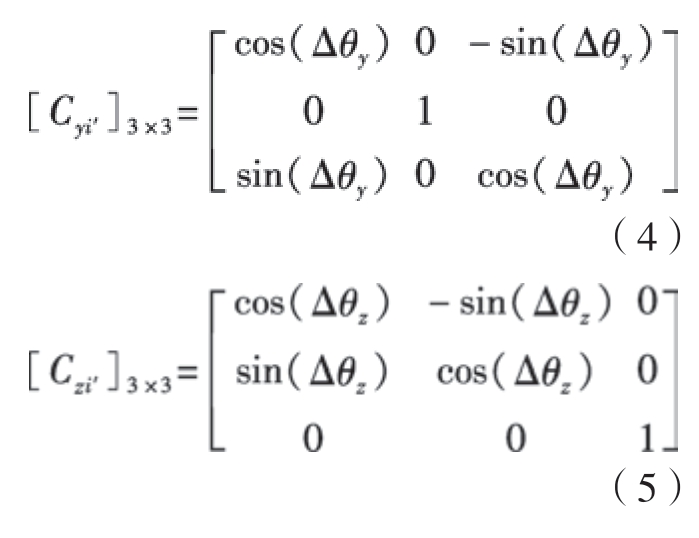
式中,[Cxi′]、[Cyi′]、[Czi′]代表特征FEi需要进行方位转换的坐标轴相对于全局坐标系(Oo – xo yo zo)中x、y、z三轴的变换矩阵。
(2)修正[Win]3×3。

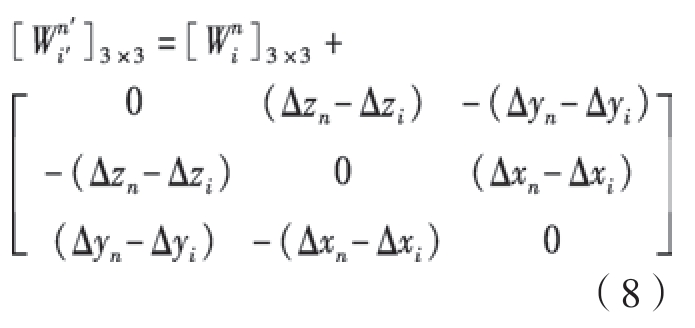
式 中,n为目标点;dxn′、dyn′、dzn′、dxi′、dyi′、dzi′分别为局部坐标系(On′– xn′yn′zn′)与(Oi′ – xi′yi′zi′)下各点在全局坐标系(Oo– xo yo zo)下的坐标值。
因特征参考坐标系方向是基于具体情况人为选取的,其方向不随特征变动而变动,故投影矩阵[RPti]3×3不变。综上,修正后的雅克比矩阵为
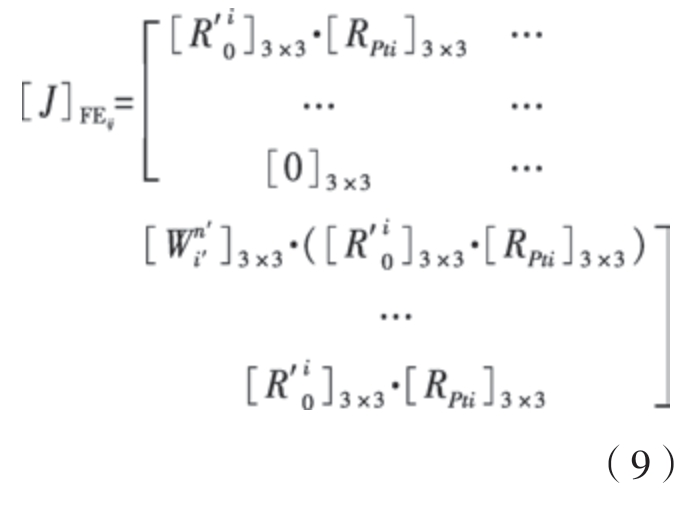
2.2.2 SDT模型修正
在装配过程中,受设计影响,两个零件可能存在多个配合特征,但采用现有模型开展偏差分析时,往往会忽略掉低优先级配合关系,导致大量公差信息丢失。下面以一种常见的局部并联结构为例,分析如何修改SDT模型,使局部并联结构能有效表达。
图9所示的局部并联结构,零件1、零件2上的主要几何特征FE1、FE2、FE3、FE4均为平面特征,由SDT模型的表达可知,平面特征包含了1个平动矢量和2个转动矢量。分析装配过程,取空间中任一观测点M,假设零件1固定、零件2浮动,仅考虑FE1、FE3配合时,若零件2绕X、Y轴转动或沿Z轴平动,则从M点看到的装配关系将发生变动,但沿X、Y轴平动或绕Z轴转动时,观测到的装配关系不会变化。事实上,该结构在FE1、FE3配合时,还受FE2、FE4的配合约束,其限制了FE1、FE3配合时零件2沿Y轴平动与绕Z轴转动,导致装配过程中仅当零件2沿X轴平动,M点的观测结果才不会变。因此,该结构的旋量等效于两个零件的旋量累加,称其为并操作,修正后的旋量模型如下。
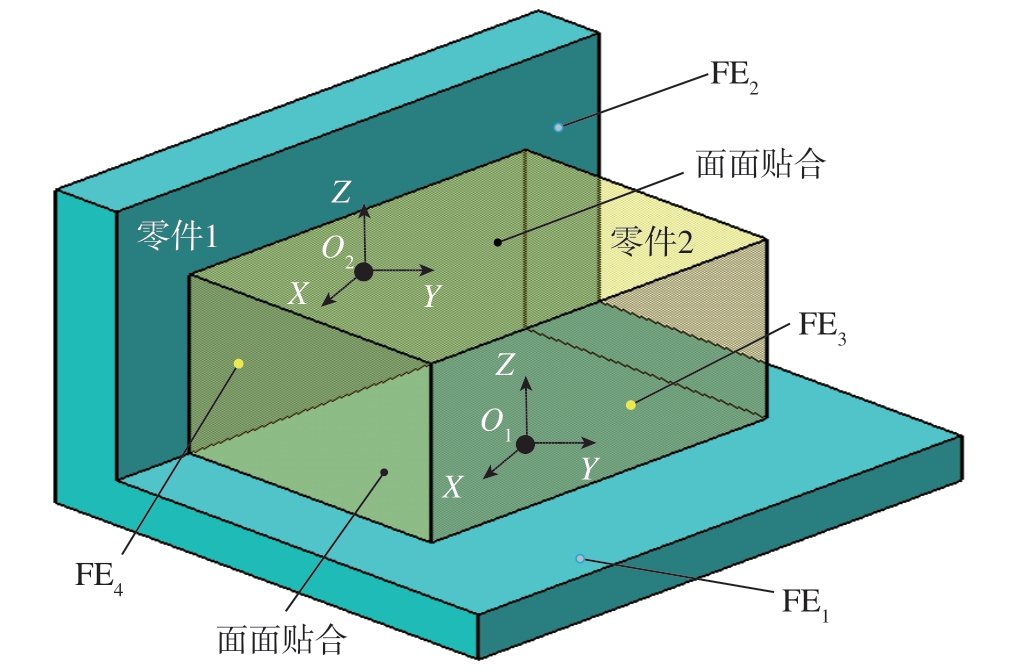
图9 平面与平面组成的局部并联结构示意图
Fig.9 Schematic diagram of local parallel structure composed of plane and plane
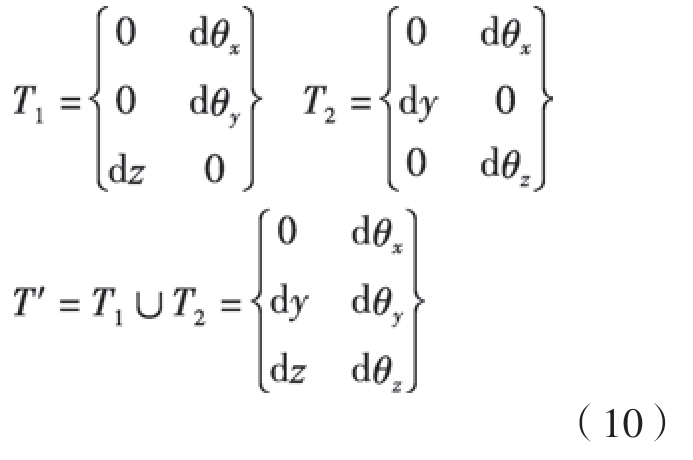
式中,T1为特征FE1对应的SDT模型;T2为特征FE2对应的SDT模型;T ′为特征FE1、FE2共同约束作用下对应的SDT模型。
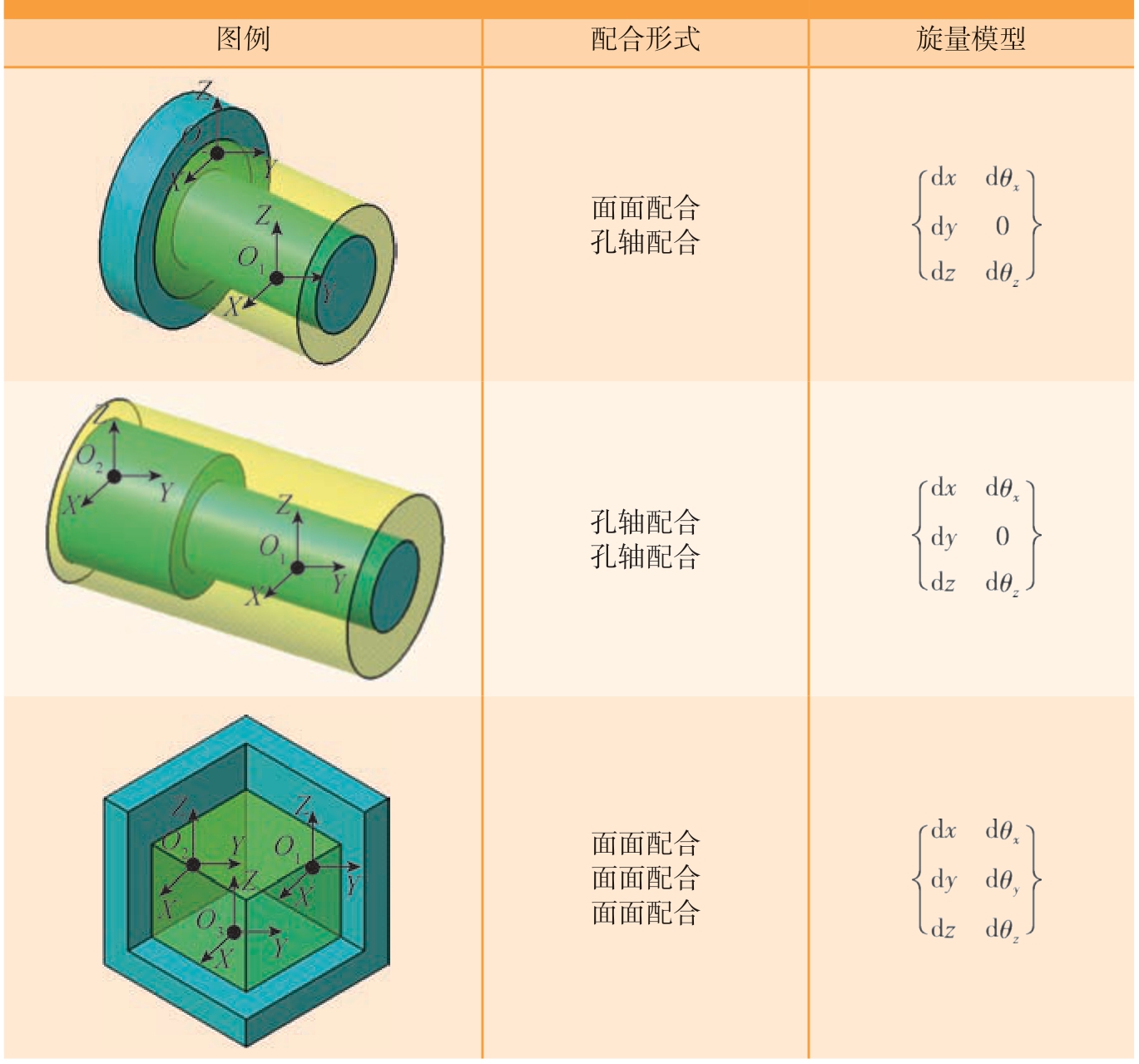
基于上述分析思路,可以推导任意一个形成局部并联结构的旋量表达形式,针对配合关系中常用的孔轴配合、面面配合,对其组合情况下的旋量模型进行描述,即两模型中无对应的矢量,则无重叠,若有对应的矢量,保留小的矢量,如表1所示。
表1 常见的并行连接结构的SDT模型
Table 1 SDT model of common parallel connection structure
图例 配合形式 旋量模型images/BZ_44_1061_1103_1423_1454.png面面配合孔轴配合images/BZ_44_2042_1210_2197_1354.pngimages/BZ_44_1000_1485_1485_1829.png孔轴配合孔轴配合images/BZ_44_2042_1583_2197_1727.pngimages/BZ_44_1070_1869_1415_2269.png面面配合面面配合面面配合images/BZ_44_2042_1995_2197_2144.png
3 基于数字孪生的某型舱门偏差传递模型实例分析
3.1 某型舱门偏差传递模型构建
本研究通过某型舱门部分运动机构对所提出的偏差传递模型建模方法进行研究,为便于建模分析及后续计算,将该产品结构中的部分组件视为一个整体,不考虑其内部偏差传递,以此开展偏差传递分析,图10为简化处理后的舱门某运动机构示意图。
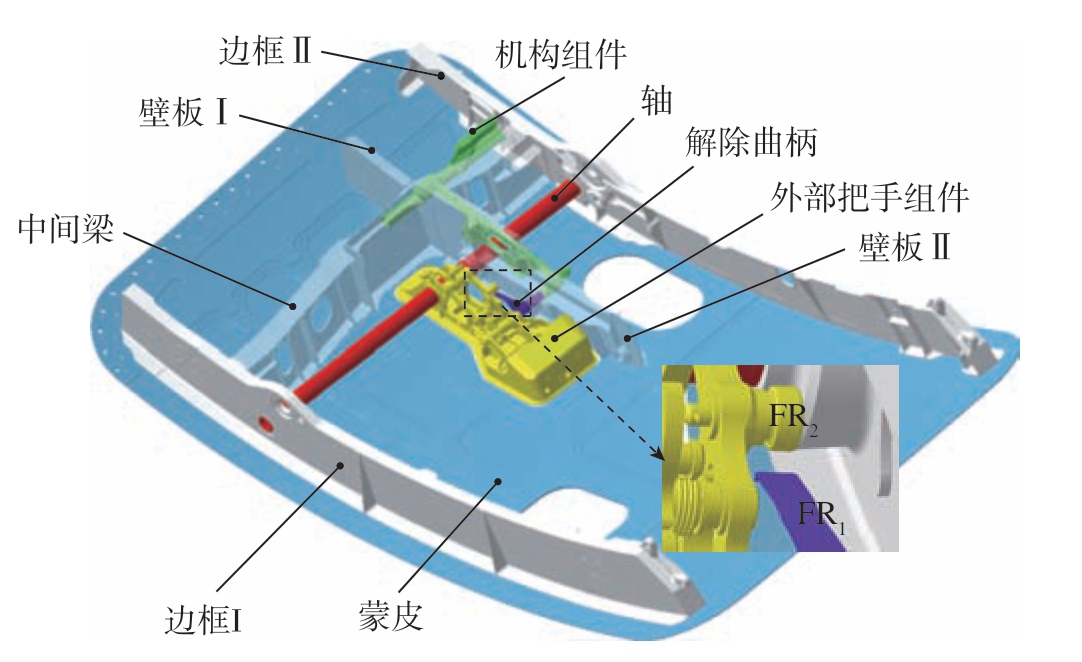
图10 舱门某运动机构简化示意图
Fig.10 Simplified schematic diagram of a moving mechanism of hatch
该舱门运动机构装配体由10个零件组成,基础定位部件蒙皮安装在舱门工装上,确保了安装准确度,在蒙皮上安装5个舱门骨架结构(边框Ⅰ、中间梁、壁板、边框Ⅱ、壁板Ⅱ),作为后续零件的安装支撑,轴提供外部把手组件的转动功能,机构组件实现舱门预位(Armed)与非预位(Disarmed)状态转换,解除曲柄实现该机构时序控制。该舱门运动机构装配体的装配定位步骤如下。
步骤1:通过舱门工装对蒙皮进行定位。
步骤2:通过舱门工装以及蒙皮预制定位孔对边框Ⅰ进行定位、连接。
步骤3:通过边框Ⅰ以及蒙皮预制定位孔对中间梁进行定位、连接。
步骤4:通过中间梁以及蒙皮预制定位孔对边框Ⅱ进行定位、连接。
步骤5:通过边框Ⅱ对机构组件进行定位,通过边框Ⅱ、机构组件对壁板I定位。
步骤6:通过机构组件对解除曲柄进行定位,通过机构组件、解除曲柄对壁板Ⅱ定位。
步骤7:通过边框Ⅰ对轴定位,通过轴定位外部把手组件。
在分析过程中,上述零件的公差注释如表2所示。
表2 舱门零部件模拟分析公差
Table 2 Simulation analysis and tolerance of hatch parts
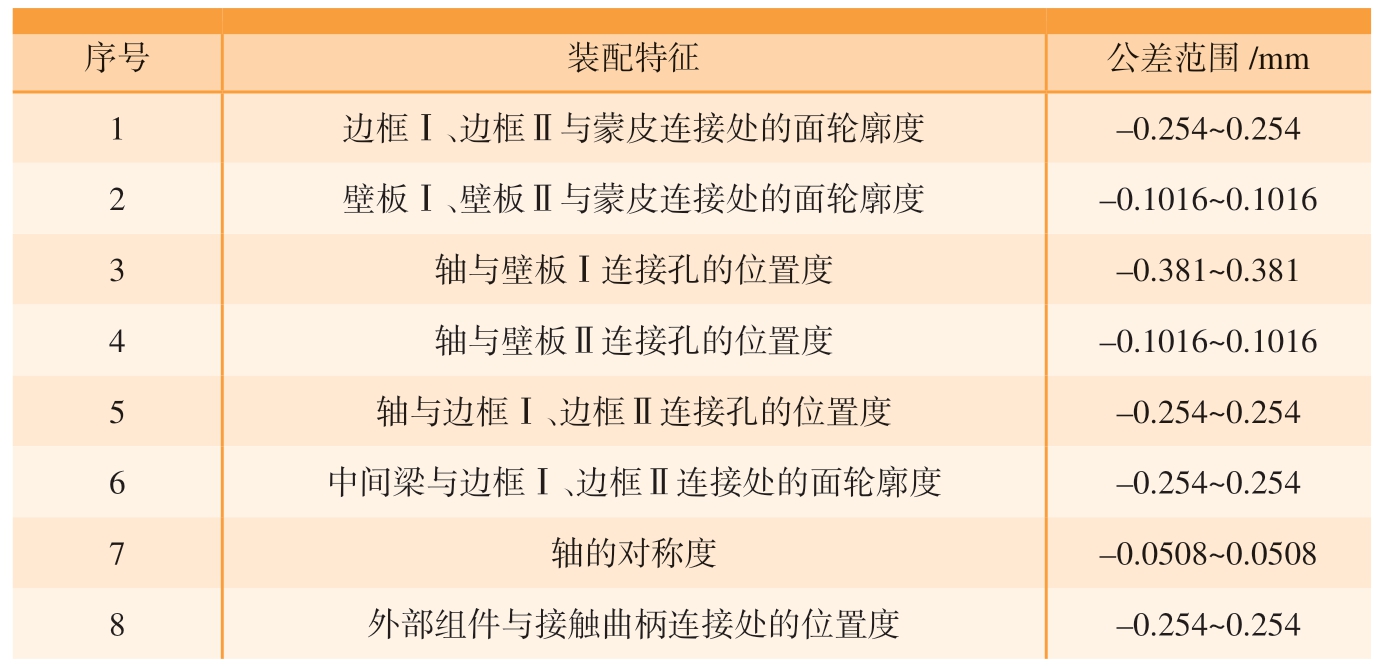
序号 装配特征 公差范围/mm 1边框Ⅰ、边框Ⅱ与蒙皮连接处的面轮廓度 –0.254~0.254 2壁板Ⅰ、壁板Ⅱ与蒙皮连接处的面轮廓度 –0.1016~0.1016 3轴与壁板Ⅰ连接孔的位置度 –0.381~0.381 4轴与壁板Ⅱ连接孔的位置度 –0.1016~0.1016 5轴与边框Ⅰ、边框Ⅱ连接孔的位置度 –0.254~0.254 6中间梁与边框Ⅰ、边框Ⅱ连接处的面轮廓度 –0.254~0.254 7轴的对称度 –0.0508~0.0508 8外部组件与接触曲柄连接处的位置度 –0.254~0.254
在建立偏差传递模型前,应对装配体中的每一个零件进行局部坐标系建立。因此,根据零件各自配合特征及全局坐标系方向,建立零件局部坐标系,如图11所示。
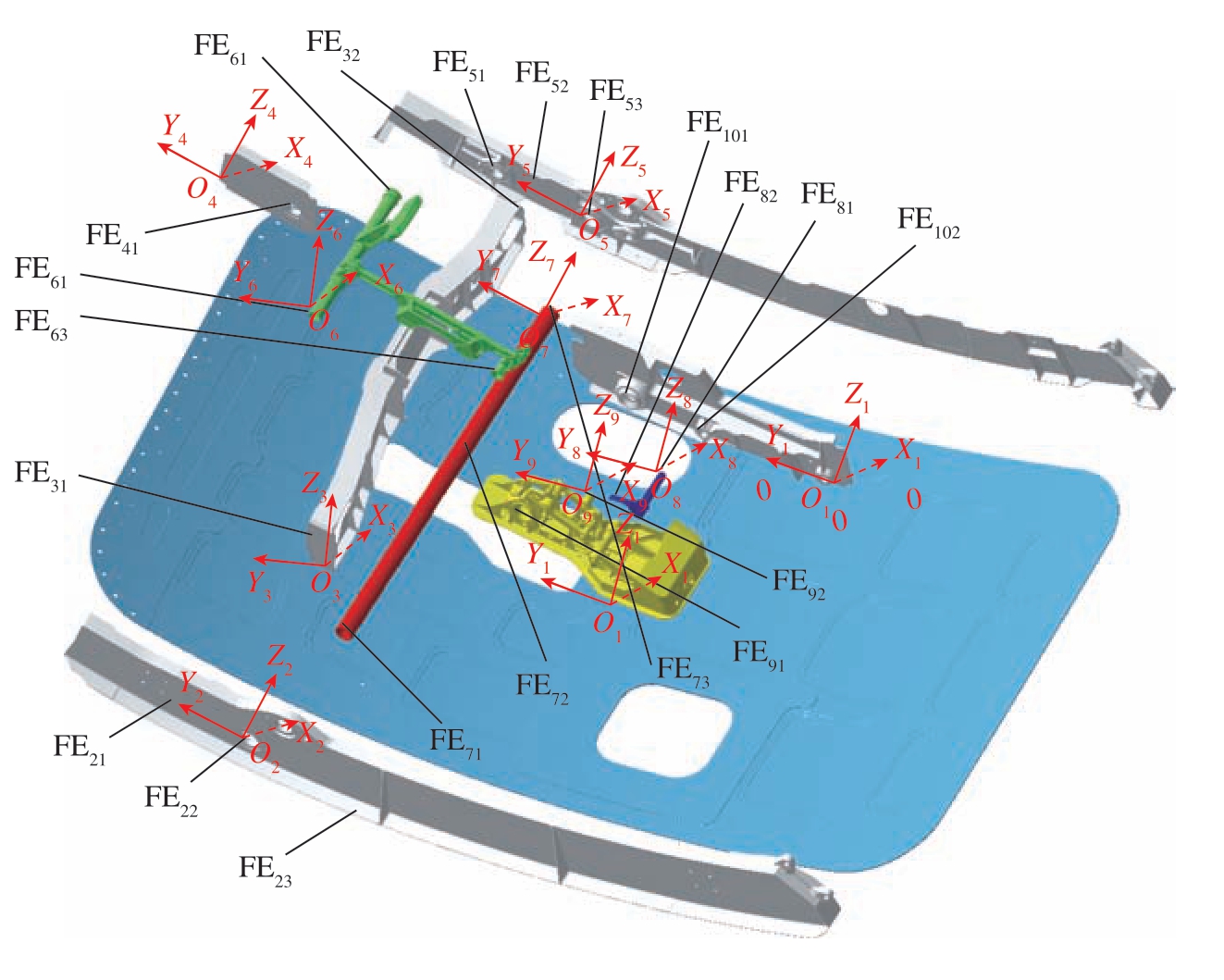
图11 舱门某运动机构局部坐标系及特征建立
Fig.11 Establishment of local coordinate system and characteristics of moving mechanism of hatch
为了便于后续分析,将全局坐标系(Oo – xo yo zo)与蒙皮所在的局部坐标系(O1 – x1 y1 z1)相重合,关键目标点FR为解除曲柄的特征FE82与外部把手组件的特征FE92之间Z方向的偏差,难以直接计算得到。因此,分别求解特征FE82、FE92各自Z方向的偏差FR1、FR2,然后计算FR。根据上述装配过程,建立该结构尺寸链传递关系图,如图12所示。
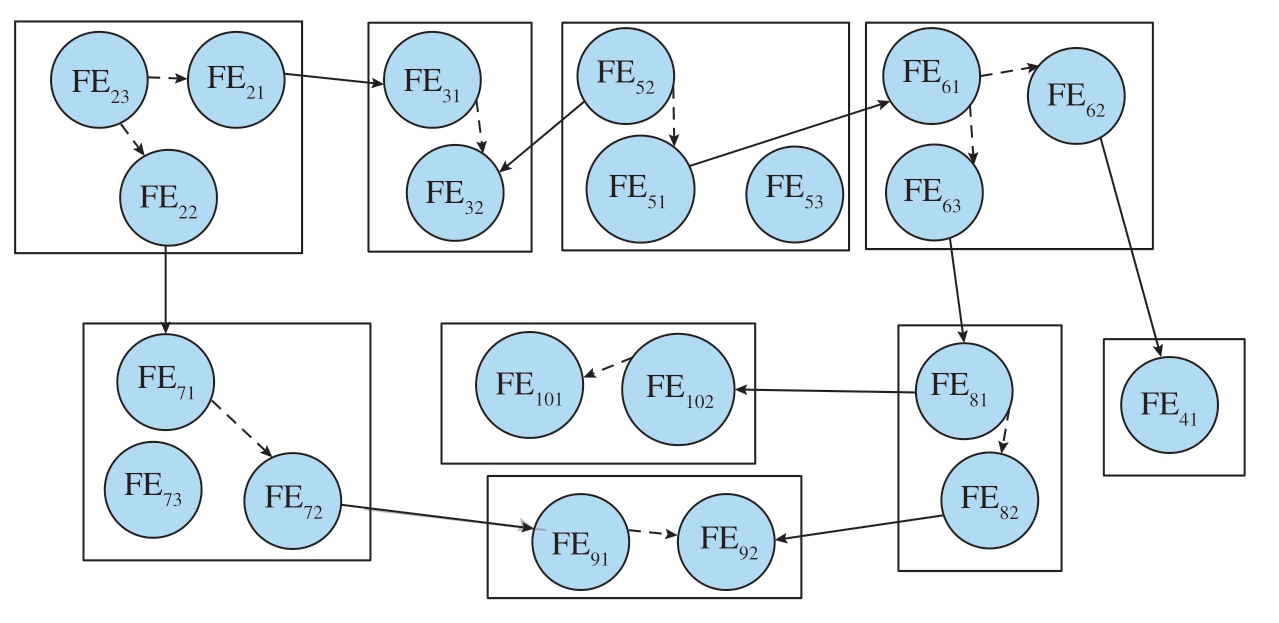
图12 尺寸链传递关系图
Fig.12 Dimension chain transfer diagram
结合上述分析,建立该舱门运动机构装配体的雅克比旋量模型。
(1)建立全局坐标系(Oo – xo yo zo)以及各零件特征处的局部坐标系(Oi – xi yi zi),本研究(Oo – xo yo zo)与局部坐标系(O1 – x1 y1 z1)重合,且各局部坐标系方向与全局坐标系方向相同。
(2)根据尺寸链传递关系图可知,该装配体中传递路线为
FE31–FE32–FE52–FE51–FE61–FE63–FE81–FE82
FE23–FE22–FE71–FE72–FE91–FE92
(3)建立待求解特征的雅可比矩阵和SDT模型。
3.2 雅克比矩阵与SDT模型求解
基于上文所提到的尺寸链传递关系,结合各零部件三维空间坐标信息,求解得到参与装配过程的各特征雅可比矩阵与SDT模型,如表3和4所示。
上述特征中FE51理想坐标为(11643.76,1487.222,5212.08),方向向量为(1,0,0),经点云拟合重构生成数字孪生模型后,其坐标变为(11643.763,1487.236,5216.02),对应的方向向量也有所变动,为(0.997,0.087,0.047);同理FE22经表面重构后,从原来的(10863.993,1481.392,5041.9)变为(10864.076,1481.701,5042.819),其方向向量(1,0,0)变为(0.999,0.043,0.008)。其对应的雅克比矩阵和SDT模型如表5和6所示。
将表3和4、表5和6中不变动/变动特征的雅克比矩阵、SDT模型带入求解,可得
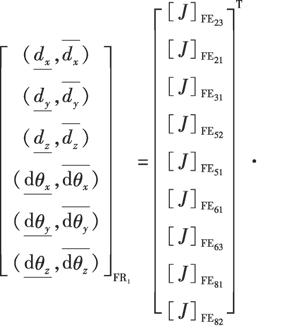
表3 特征对应的雅克比矩阵
Table 3 Jacobian matrix corresponding to feature
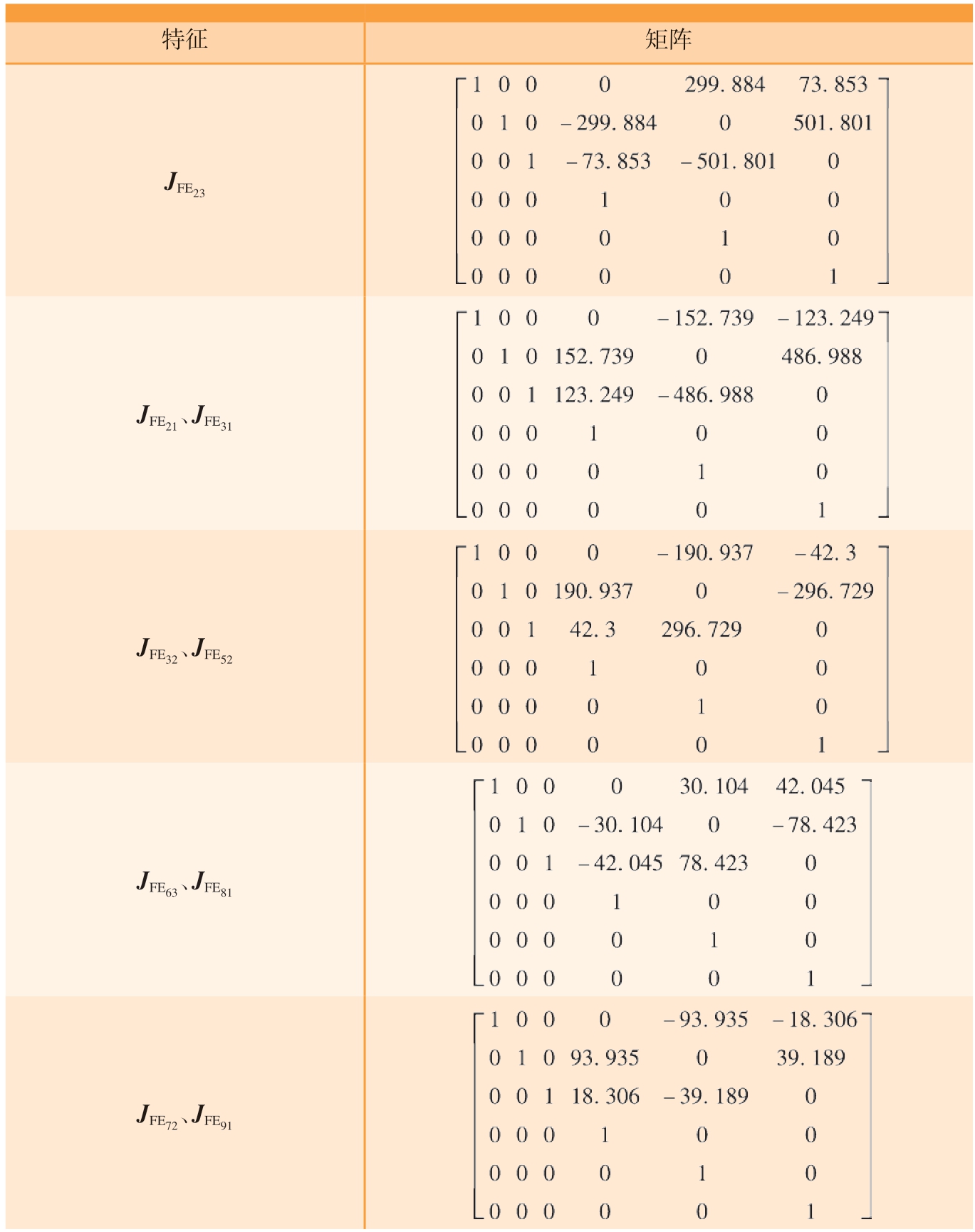
特征 矩阵JFE23images/BZ_46_1584_529_2191_821.pngJFE21、JFE31 images/BZ_46_1584_856_2191_1148.pngJFE32、JFE52images/BZ_46_1584_1187_2191_1479.pngJFE63、JFE81images/BZ_46_1608_1514_2166_1806.pngJFE72、JFE91images/BZ_46_1608_1841_2166_2133.png
表4 特征对应的SDT模型
Table 4 SDT model corresponding to feature

特征 模型FE23images/BZ_47_462_515_780_815.pngFE21images/BZ_47_478_824_764_1123.pngFE31images/BZ_47_478_1135_764_1434.pngFE32images/BZ_47_478_1449_764_1749.pngFE52images/BZ_47_478_1758_764_2058.pngFE63images/BZ_47_462_2069_780_2369.pngFE81images/BZ_47_462_2380_780_2680.pngFE72images/BZ_47_462_2691_780_2991.pngFE91{(0,0)(–0.127,0.127)(–0.127,0.127)(0,0)(–0.0041,0.0041)(–0.0041,0.0041)}T
表5 变动特征对应的雅克比矩阵
Table 5 Jacobian matrix corresponding to variable characteristics
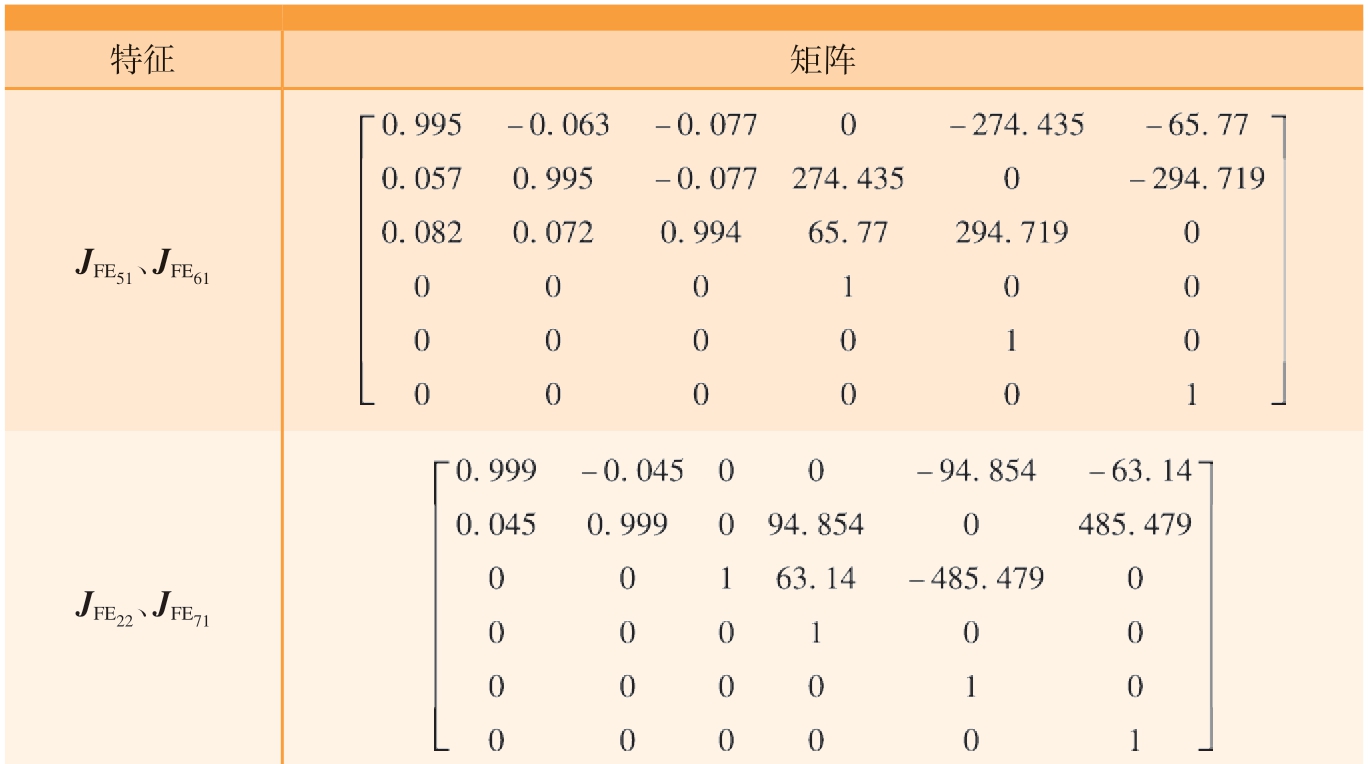
特征 矩阵JFE51、JFE61images/BZ_47_1307_532_2232_824.pngJFE22、JFE71images/BZ_47_1380_877_2159_1169.png
表6 变动特征对应的SDT模型
Table 6 SDT model corresponding to variation characteristics
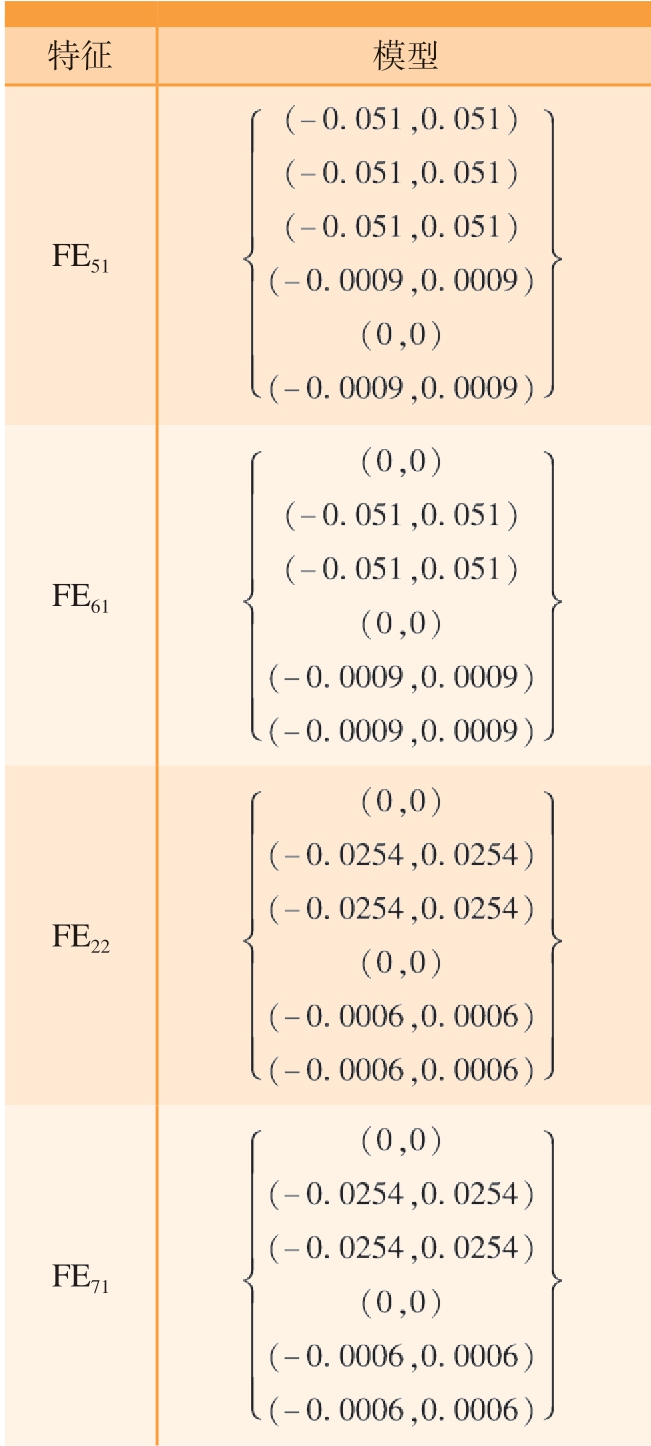
特征 模型images/BZ_47_1190_1500_1508_1800.pngFE51images/BZ_47_1190_1843_1508_2142.pngFE61 FE22images/BZ_47_1190_2182_1508_2482.pngFE71images/BZ_47_1190_2522_1508_2821.png

3.3 基于3DCS的装配偏差求解
采用上文所提出的数字孪生装配体偏差传递计算方法,可以计算出舱门其他零件在装配过程中的偏差累积值,本研究通过3DCS开展以数字孪生模型为输入的装配偏差求解,3DCS分析流程如图13所示。
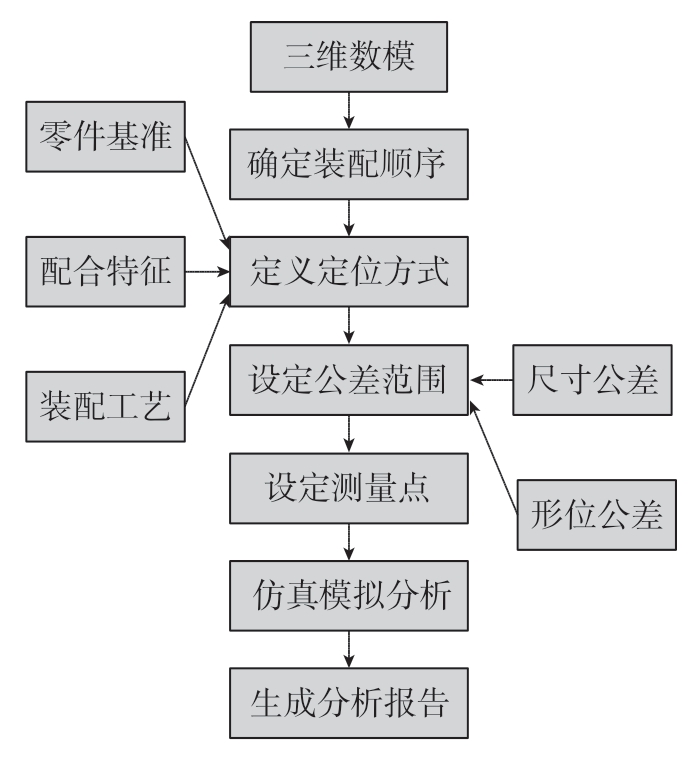
图13 3DCS分析流程示意图
Fig.13 Flow diagram of 3DCS analysis
(1)三维几何模型导入。三维几何模型的准确性决定了仿真模拟的精度,本研究将所构建的数字孪生模型以.CATPart格式导入3DCS软件,该模型包含了待装配零件的几何设计信息与几何装配特征信息。
(2)确定装配顺序。基于上文分析结果,按照蒙皮→边框Ⅰ→中间梁→边框Ⅱ→壁板→锁轴、外部把手→模式选择机构→插销机构→提升机构、内手柄→支臂组件→泄压口盖的顺序进行装配。
(3)确定定位方式。采用3DCS中的“Move”功能创建不同的装配定位约束方式,常用方式有3–2–1定位、“Three-Point”定位、“Step Plane”定位、“Six-Plane”定位方式等。本研究所分析模型的装配特征大多为曲面与曲面、平面与平面、孔与轴,根据模型自身结构特点,先通过移动操作将各零部件分开,然后将曲面与曲面的定位方式设置为“Step Plane”,平面与平面的定位方式设置为“Three-Point”定位或3–2–1定位,孔与轴的定位方式设置为“Three-Point”定位或“Step Plane”定位,如图14所示。

图14 3DCS待分析模型设置流程
Fig.14 3DCS model setting process to be analyzed
(4)设置公差范围。3DCS中公差方位的设定通过DCS GD&T模块与Update GD&T模块自动导入CATIA零件在FT&A模块标定的三维标注公差,如图15所示。
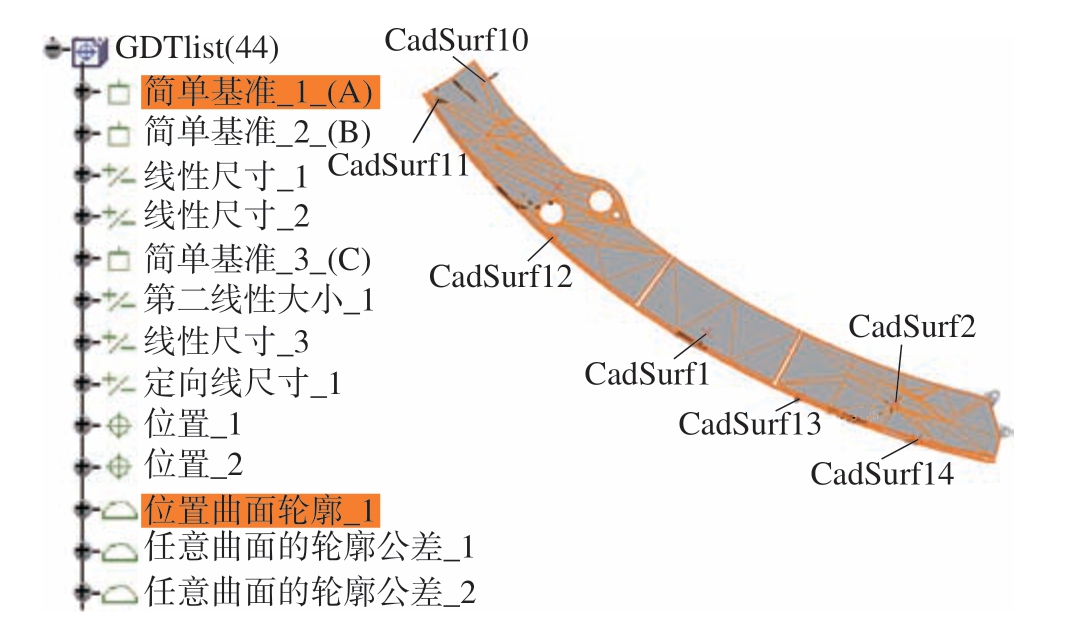
图15 3DCS设定公差
Fig.15 Set tolerance on 3DCS
(5)设置测量对象。本研究通过Define/Edit Measure模块设置所需测量的目标,主要测量两零件特征在Z方向的偏差。
最后,将零件模型导入,设置各装配特征的公差范围,模拟上述装配过程,测量最终关键目标点FR1、FR2各自在Z方向的偏差变动,其结果如图16所示。可知,3DCS模拟下FR1、FR2在Z方向变动范围分别为[–1.59,1.58]mm、[–0.55,0.55]mm,即Z方向偏差变动的绝对值分别为1.585mm、0.55mm;计算结果得出的FR1、FR2在Z方向变动范围为[–1.7665,1.7665]mm、[–0.5790,0.5790]mm,其Z方向偏差变动的绝对值分别为1.7665mm、0.5790mm,将3DCS的结果作为标准,两者对比可得,理论计算出来的FR1偏差率为11.45%,FR2偏差率为5.27%,表明所提出的数字孪生装配体偏差传递计算方法具有一定的可行性。

图16 3DCS仿真分析结果
Fig.16 3DCS simulation analysis results
4 结论
民用飞机零部件制造过程中质量检测与控制难、装配误差累积严重,传统以理论模型为基础,难以体现多阶段相互作用影响下真实产品与理论模型之间的差异,仿真结果难以实现“以虚控实”。数字孪生模型作为物理实体在数字空间的高保真映射模型,以此为基础开展偏差传递分析,可有效预测装配偏差。本研究研究内容与成果如下。
(1)以某型飞机舱门为研究对象,开展面向装配过程的数字孪生模型构建方法研究,提出“点云数据重构理论模型+制造、装配、调试等多阶段衍生信息挂载”的建模思路;从信息组成、数据处理、使用规则等方面研究并给出数字孪生模型关键构建技术;最后,通过舱门零件—边框Ⅰ的数字孪生模型构建实例,展示了本研究所提到的方法与技术。
(2)分析了雅可比旋量理论建模方法,结合数字孪生模型装配特点,综合考虑制造误差和真实配合关系等因素,对雅克比旋量模型进行修正,提出了基于数字孪生模型的偏差传递计算方法。最后,以某机构舱门组件中的两零件装配偏差为例进行计算,对比3DCS软件计算结果,结果表明两者分别相差11.45%和5.27%,验证了该方法的可行性。
[1] 郭飞燕, 刘检华, 邹方, 等.数字孪生驱动的装配工艺设计现状及关键实现技术研究[J].机械工程学报, 2019, 55(17): 110–132.
GUO Feiyan, LIU Jianhua, ZOU Fang, et al.Research on the state-of-art, connotation and key implementation technology of assembly process planning with digital twin[J].Journal of Mechanical Engineering, 2019, 55(17): 110–132.
[2] 岳胜, 代多兵, 安鲁陵.飞机结构装配间隙超差分析与对策[J].航空制造技术, 2013, 56(12): 81–84.
YUE Sheng, DAI Duobing, AN Luling.Analysis and countermeasure for out-oftolerance clearance in structural assembly of aircraft[J].Aeronautical Manufacturing Technology, 2013, 56(12): 81–84.
[3] 查艳妮.飞机装配不协调问题的原因分析及解决方法[J].科技创新导报, 2018, 15(5): 13–15.
ZHA Yanni.Cause analysis and solution of aircraft assembly disharmony problem[J].Science and Technology Innovation Herald, 2018, 15(5): 13–15.
[4] 樊心东.考虑零件变形的产品装配误差分析及选配技术[D].杭州: 浙江大学, 2020.
FAN Xindong.Product assembly error analysis and selective assembly technology considering part deformation[D].Hangzhou: Zhejiang University, 2020.
[5] TAO F, QI Q.Make more digital twins[J].Nature, 2019, 573(7775): 490–491.
[6] 陶飞, 刘蔚然, 张萌, 等.数字孪生五维模型及十大领域应用[J].计算机集成制造系统, 2019, 25(1): 1–18.
TAO Fei, LIU Weiran, ZHANG Meng, et al.Five-dimension digital twin model and its ten applications[J].Computer Integrated Manufacturing Systems, 2019, 25(1): 1–18.
[7] SCHLEICH B, ANWER N, MATHIEU L, et al.Shaping the digital twin for design and production engineering[J].CIRP Annals, 2017, 66(1): 141–144.
[8] 姜珊, 王仲奇, 夏松, 等.飞机柔性工装数字孪生几何模型构建方法[J/OL].航空制造技术, (2021–08–01)[2021–10–29].https://kns.cnki.net/kcms/detail/11.4387.v.20211028.1613.002.html.
JIANG Shan, WANG Zhongqi, XIA Song, et al.Construction Method of Digital Twin Geometry Model for Aircraft Flexible Tooling[J/OL].Aeronautical Manufacturing Technology, (2021–08–01)[2021–10–29].https://kns.cnki.net/kcms/detail/11.4387.v.20211028.1613.002.html.
[9] 刘伟东, 宁汝新, 刘检华, 等.机械装配偏差源及其偏差传递机理分析[J].机械工程学报, 2012, 48(1): 156–168.
LIU Weidong, NING Ruxin, LIU Jianhua, et al.Mechanism analysis of deviation sourcing and propagation for mechanical assembly[J].Journal of Mechanical Engineering, 2012, 48(1): 156–168.
[10] 苏春, 黄漪.装配误差传递建模及其精度可靠性评估[J].中国机械工程, 2017, 28(19): 2359–2364.
SU Chun, HUANG Yi.Modeling for assembly error propagations and assessments of assembly precision reliability[J].China Mechanical Engineering, 2017, 28(19): 2359–2364.
[11] 祝鹏, 余建波, 郑小云, 等.机械装配过程的偏差传递网络建模与误差溯源[J].浙江大学学报(工学版), 2019, 53(8): 1582–1593.
ZHU Peng, YU Jianbo, ZHENG Xiaoyun, et al.Variation propagation network-based modeling and error tracing in mechanical assembling process[J].Journal of Zhejiang University (Engineering Science), 2019, 53(8): 1582–1593.
[12] 陶飞, 刘蔚然, 刘检华, 等.数字孪生及其应用探索[J].计算机集成制造系统, 2018, 24(1): 1–18.
TAO Fei, LIU Weiran, LIU Jianhua, et al.Digital twin and its potential application exploration[J].Computer Integrated Manufacturing Systems, 2018, 24(1): 1–18.
[13] WANG K, LIU D X, LIU Z Y, et al.An assembly precision analysis method based on a general part digital twin model[J].Robotics and Computer-Integrated Manufacturing, 2021, 68: 102089.
[14] ZHUANG C B, LIU J H, XIONG H.Digital twin-based smart production management and control framework for the complex product assembly shop-floor[J].The International Journal of Advanced Manufacturing Technology, 2018, 96(1–4): 1149–1163.
