随着现代工业技术自动化、数字化、智能化飞速发展,航空发动机、高铁运载装备、智能化武器装备、燃气轮机组、风电机组等重大装备的可靠性、安全性备受关注,反映装备的4大质量指标(性能、可靠性、经济性、安全性)的可靠性指标成为衡量装备质量的重要指标,愈来愈凸显出极其重要的地位。由“制造大国”走向“智造强国”的瓶颈之一就是装备的可靠性不足。伴随着装备运行时间的不断延续,装备出现了越来越多的运行健康问题,其可靠性、安全性受到不同程度风险影响。为了在早期发现并排除装备可靠性、安全性隐患,保证装备的可靠运行,避免重大事故发生,需要对装备的功能部件进行可靠性适时评价,而实现由“定期维修”、“状态维修”到“预测维修”的转变,必须对装备在运行过程中的可靠性进行评估。传统的可靠性评价方法如故障模式影响分析[1]、故障树分析[2]、模糊集方法[3]、贝叶斯网络分析法[4–5]、响应面分析法[6]、矩法[7]、频率分析法[8]、动态与渐变耦合分析法[9]等此类静态或动态的评价方法不能很好地解决不确定性、随机性、适时性的可靠性评价问题。表1比较了这些可靠性评估的主要分析方法。
表1 可靠性分析方法的比较
Table 1 Comparison of reliability analysis methods
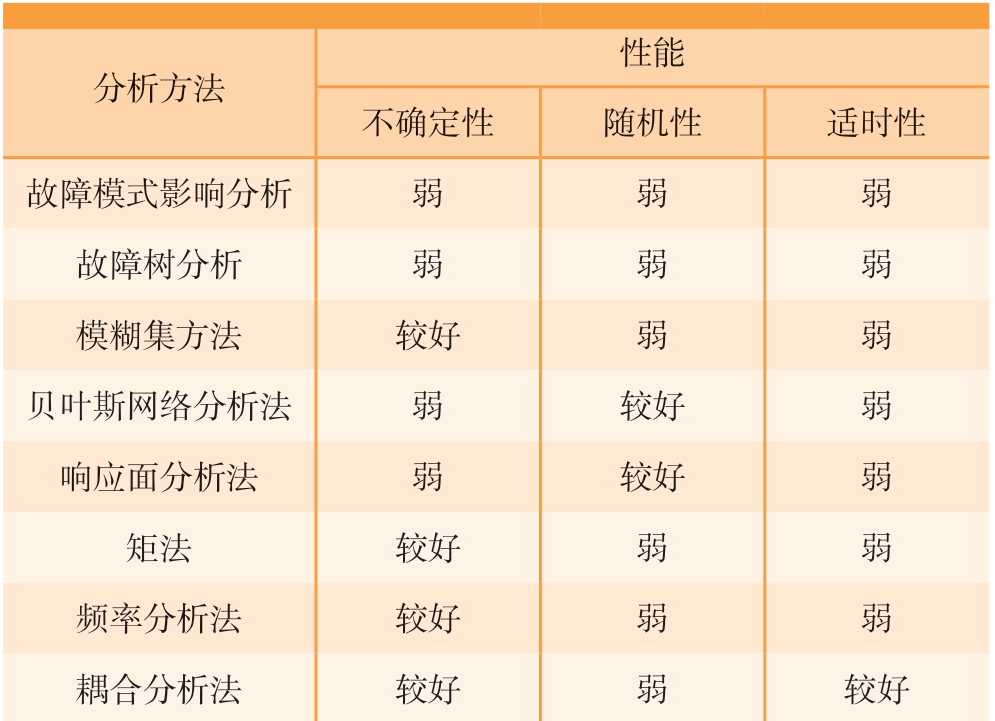
分析方法性能不确定性 随机性 适时性故障模式影响分析 弱 弱 弱故障树分析 弱 弱 弱模糊集方法 较好 弱 弱贝叶斯网络分析法 弱 较好 弱响应面分析法 弱 较好 弱矩法 较好 弱 弱频率分析法 较好 弱 弱耦合分析法 较好 弱 较好
装备的可靠性主要有固有可靠性和使用可靠性。其中,固有可靠性主要受装备设计环节、制造环节、检验环节等影响,而装备的使用可靠性即运行可靠性与装备运行时的使用条件、所处环境、使用时间、功能件衰退失效等因素有关,具有时变性、动态性和随机性。随着工业互联网、物联网、人工智能、大数据、自动监测技术和传感器技术的迅速发展,装备的大量系统运行监测数据的获取和处理成为必然。为了精准、有效地评估装备运行可靠性的确定性及适时性,亟须在现有可靠性评估基础上做出转变。因此,面向健康监测数据驱动的可靠性评估十分必要和迫切,并体现出前所未有的机遇。本研究分析监测信息可靠性评估的国内外研究现状与进展,揭示面向健康监测数据驱动下装备可靠性评估研究存在的挑战,并指出应对现有挑战的可能途径。
1 装备可靠性评估的国内外研究现状
历经近一个世纪的发展,以概率统计和故障物理为基础的传统可靠性理论方法尽管在处理随机不确定性信息方面能够确定设备的失效分布,从而获得一批同类设备共性总体的平均可靠性,然而,针对个体特定设备,通常在不同工况与状态下运行的可靠性评估难以获得个体的可靠性。英国O’connor[10]指出现有的可靠性研究依赖于传统的概率统计方法,阐明该可靠性方法在解决工程实际问题时,由于实际结构的复杂性和人为因素,传统可靠性研究方法容易产生误导。Lin[11]和Yong [12] 等在基于状态的可靠性评估和预测维修方面做了有益的尝试工作,提供了研究的新思路。意大利Zio[13]深刻洞察复杂系统可靠性分析是可靠性工程的新挑战,并提出利用状态监测来确保系统可靠的运行,以降低故障率、提高生产率。国内谢里阳[14]剖析当前机械可靠性理论、方法及模型方面存在的一些问题,指出可靠性是一门仍在发展之中的学科,简单移植或借用在不同领域或不同问题背景下发展起来的可靠性理论、方法或模型会引起各种各样的问题。
面向健康监测的装备可靠性评估包括如图1所示的几个环节: (1)装备运行状态信息获取; (2)可靠度映射模型构建; (3)可靠度计算。国内研究人员在这3个环节的诸多方面开展了大量的研究工作,本文未能详细列举所有相关文献,只挑选了近年来代表性的工作予以综述。
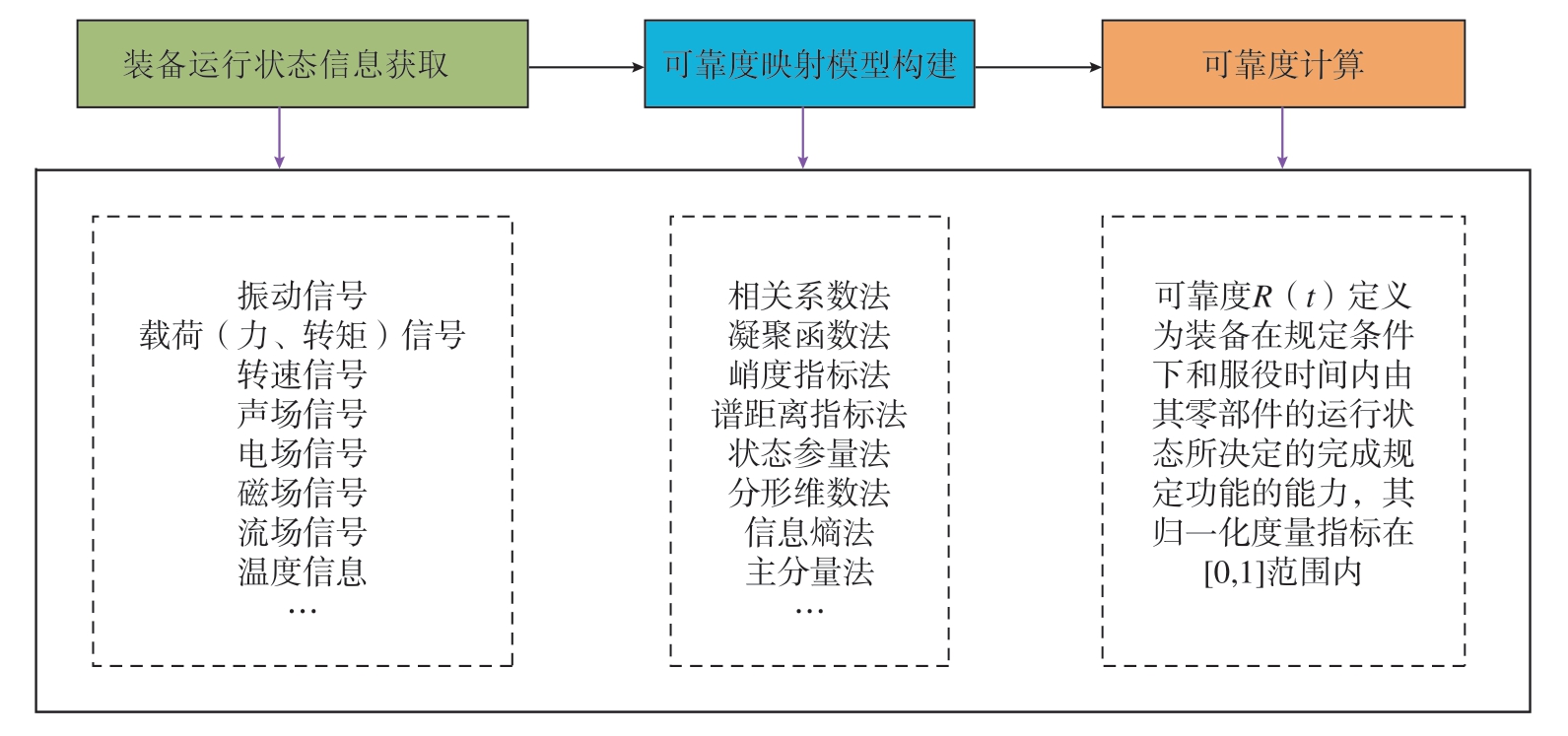
图1 面向健康监测的装备可靠性评估
Fig.1 Equipment reliability assessment based on health monitoring
1.1 基于监测信息的装备可靠性评估
针对传统的可靠性分析方法难以在线、实时、动态地评估运行可靠性问题,国内外学者开始进行实时、动态、基于监测信息的装备可靠性评估研究。Chinnam[15]研究了涉及多衰退信号的复杂系统可靠性在线评估。Lu等[16]提出一种具有线性趋势指数平滑的适应模型,预测独立单元的某一性能并评估基于状态的可靠性。Lu等[17]将状态空间方法结合卡尔曼滤波进行多元状态性能可靠性评估。这些方法在失效边界是已知的情况下对可靠性评估是十分有效的。Ahmad[18]提出一种新的基于状态监测数据的概率方法,用于考虑不确定性量化时风险因素对安全指标的影响,并对自主供电运行随机过程进行了在线可靠性评估。Liu等[19]深入研究了基于系统级监测数据的多状态系统动态可靠性评估,通过部件退化遵循齐次连续时间马尔可夫过程和非齐次连续时间马尔可夫过程两个案例验证了该方法的有效性和准确性。Soliman等[20]提出基于监测数据的铝合金舰船零件疲劳可靠性与寿命预测方法,根据累积疲劳损伤和疲劳可靠性,对不同运行条件下获得的结构健康监测数据进行量化。何正嘉等[21]综述了基于机械设备状态信息的运行可靠性评估的发展,并提出思考。丁锋等[22–25]提出设备状态振动特征的比例故障率模型可靠性评估新方法,建立主动监测机制的可靠性评估模型,提出基于监测信息的设备运行可靠性研究方法和基于比例风险模型的刀具磨损监测及其可靠性分析方法。陈保家等[26–27]提出基于车刀振动信号和磨损数据建立的Logistic可靠性评估模型,实现基于振动信号logistic回归模型的刀具可靠性评估。蔡改改等[28–29]提出基于状态监测信息的比例协变量模型,并用于刀具运行可靠性评估,提出利用设备响应状态信息的运行可靠性评估方法。
1.2 基于协变量的可靠性评估
自动监测技术和传感器技术的快速发展,使得数据驱动的可靠性评估中基于协变量的方法得到了广泛应用。根据系统运行环境中协变量数据的不同变化规律,将基于协变量方法的可靠性评估模型主要分为固定协变量模型、时变协变量模型和随机协变量模型3种类型[30]。
考虑协变量作用的寿命分析模型即比例风险模型(Proportional hazard model, PHM)自从Cox [31]提出以来,已经被广泛接受为一种半参数的模型,也是其中最有效的模型,可用于联合协变量的风险分析,最早应用于生物医学和经济学领域,在可靠性工程领域也得到了较多的应用[32–34]。由于比例风险模型所要求条件是不同协变量间失效率比值相等,这在实际系统中是比较难以达到的,因此,Kumar[35]和Hassan[36]等提出了分层比例风险模型 (Stratified proportional hazard model, SPHM),该模型只要求同一层协变量间的失效率比值相等,这与实际衰退化过程比较接近。上面所说的比例风险模型和分层比例风险模型主要应用于恒定协变量的状况,由于实际工程系统运行状态是时变的,协变量是变化的,即时变协变量数学模型,如Cox提出的比例强度模型 (Proportional intensities model, PIM);Sun等[37]提出比例协变量模型 (Proportional covariates model, PCM);Jardine等[38]采用基准分布为威布尔分布的比例风险模型,提出威布尔比例风险模型(Weibull proportional hazard model, WPHM);Compare等[39]建立衰退过程的贝叶斯三态Weibull回归模型,不仅考虑了这些协变量的影响,还估计具有相关不确定性的模型参数,对生物制药工业中使用的隔膜阀进行了可靠性评估;为了能同时考虑外部协变量与内部协变量对系统衰退的影响,Gorjian等[40]提出了显式风险模型 (Explicit hazard model, EHM);Disadi等[41]指出该模型能更好地评估系统的可靠性。针对不同的随机协变量,有泊松振动模型和Markov随机模型,其中泊松振动模型[42–44]是系统衰退由随机冲击引起的随机协变量模型,Markov随机模型[45–47]是受随机协变量影响的随机过程协变量模型,这2个随机协变量模型在工程上较多用于评估系统可靠性。
1.3 面向健康监测的可靠性评估
健康状态监测(Health condition monitoring, HCM)已被证明是提高装备可靠性和改善客户服务的一种经济有效的手段,而可靠性分析、评估是指导维护决策和数据驱动健康监测的非常有用的手段。面向监测健康状态的可靠性评估是智能运维和健康管理的更高要求。
飞行器健康管理专家卿新林教授指出,在未来很长的一段时间内,飞行器健康管理将是航空航天领域的一个重要发展方向,结构健康状态监测技术对于提高飞行器性能、可靠性及安全性意义重大[48]。Yue等[49]提出了基于导波的结构健康状态监测不确定性量化和可靠性评估的分层方法,为不确定性情况下不同结构提供了一种系统和实用的方法。Marcantonio等[50]提出了一种基于健康状态数据驱动HCM系统的新诊断方法,通过测量被测系统的关键参数,有效监测风力涡轮机的健康状况并检测其损伤,重点指出了在设计的早期阶段,可靠性分析如何成为指导维护决策和数据驱动CM有用且强大的手段。Zhang等[51]提出了一种基于健康状态监测和系统可靠性评估的架空线路维护策略,通过建立状态监测数据与架空线路故障率之间的定量关系,利用监测数据评估系统可靠性,从而提出能够以最低的维护成本和预算提供最大的可靠性改进策略。陈志为[52]基于健康状态监测数据建立运载装备与风荷载的概率模型,使用概率模型和蒙特卡洛模拟方法,对大跨多荷载桥梁的疲劳可靠度进行评估。郑蕊等[53]利用结构健康监测系统所记录的应变时程曲线,同时选取若干天的应变时程曲线,通过统计分析得到其标准样本,并且利用雨流计数法,得到标准样本的应力幅谱,最终对桥面的疲劳寿命作出可靠性的评估。Hu等[54]针对机电设备的3种状态的特点及获得监测数据的方式,对其可靠性寿命预测方法进行了系统研究和评述。肖鑫[55]提出的基于健康监测和随机车辆荷载模型的承载力可靠性评估方法具有较强的适用性。刘玉梅等[56]采用核密度估计法对采集数据统计处理,建立关键部件的威布尔失效率模型及Markov状态转移模型,基于实时故障率及维修率分析传动系可靠性的变化。李游等[57]依据实桥动应变监测数据,参考了雨流计数法及Palmgren-Miner线性损伤累积理论,基于均匀设计–径向基神经网络–重要蒙特卡罗法(UD–RBF–IMC)相结合的算法,运用线弹性断裂力学对 U 肋对接焊缝疲劳可靠性进行了评估,与此同时,也研究了交通量及轴重增长对疲劳可靠度的影响规律。陈世杰等[58]通过对运营地铁的结构健康监测数据进行压缩和重构,以提高获取的地铁健康相关数据的信息完备与可靠性,为隧道结构健康安全评价提供数据基础,构建运营地铁隧道安全风险指标评价体系,采用云推理综合评估运营地铁隧道的可靠程度,并找到影响其可靠性的关键风险。Okasha等[59]提出了一种在不确定性条件下基于向量自回归建模、利用结构健康监测数据进行高速舰船可靠性分析和损伤检测的方法。
2 面临的挑战与发展方向
随着大数据、人工智能、自动监测技术和嵌入式传感器技术的快速发展,目前面向健康监测数据驱动的可靠性评估方法获得了一定的数据支持,并且得到了较为广泛的应用,但是,面向健康监测数据驱动的可靠性评估方法还存在一定的问题与挑战。
(1) 目前的协变量处理模型在一定程度上混淆了协变量与失效率的因果关系,实际中,二者互相影响,一些协变量影响失效率,如外部协变量,但另一些协变量则受失效率的影响,如内部协变量。所以在研究协变量对系统衰退的影响时,应该对协变量类型进行有的放矢加以区分,并针对性建模,这是面向健康监测的可靠性评估进一步深入研究的方向。
(2)目前数据驱动的可靠性评估方法是针对衰退数据寻求单一零部件的失效规律,未充分考虑不同零部件之间相互影响及作用对装备整体衰退失效过程的影响。装备是由诸多零部件组合的有机统一体,单一零部件的性能衰退会影响其他零部件,从而引起整个装备的复合症兆,对整个装备可靠安全运行造成影响。所以,充分利用工业大数据资源实现整个装备可靠性评估是面向健康监测的可靠性评估的发展方向。
(3) 基于监测信息的装备运行可靠性评估,虽然能够在基于装备状态监测数据的基础上得到及时的更新,为装备的基于状态的预测维修提供支持,并且在装备运行可靠性评估方面有一定效果。但是,可靠性评估的精度、准确度仍依赖于样本的大小和运行状态与可靠性之间的关联映射模型。因此,通过装备状态信息建立可靠度时间序列,准确反映装备运行状态与可靠性之间的关联映射模型,这也是面向健康监测的可靠性评估的重点发展方向。
3 结论
随着人工智能、大数据、深度学习、智能运维等技术的迅速发展,面向健康监测的装备运行可靠性评估的研究更加精准化、定量化、智能化、科学化,但仍然有诸多问题有待研究。
(1) 针对具体装备健康监测的两个关键方面,即故障机理(故障物理)和状态信号特征提取,二者的交叉研究是进一步加强运行可靠性评估的重要基石。
(2) 利用装备运行状态监测信息建立个性化的准确可靠性模型,譬如进一步提高协变量模型在评估具体系统可靠性上的针对性,是对装备进行瞬时或稳态可靠度分析和运行可靠性评估的关键环节。
(3) 如何根据面向健康监测的可靠度分析和可靠性评估进行装备的故障预测和健康管理,从而进行装备的剩余寿命预测,是实现装备资产全周期管理和智能运维的最高追求。
(4) 综合可靠性数学、可靠性物理、可靠性工程、人工智能、信号处理、故障诊断、大数据、自动监测技术和嵌入式传感器技术等多个领域,展开交叉融合研究,并形成全方面的数字孪生系统是推进面向健康监测的运行可靠性评估理论和技术发展的有效途径。
[1] JOO B, KIM S, KIM S, et al.FMEA for the reliability of hydroformed flanged part for automotive application[J].Journal of Mechanical Science and Technology, 2013, 27(1): 63–67.
[2] FAZLOLLAHTABAR H, AKHAVAN NIAKI S T.Integration of fault tree analysis, reliability block diagram and hazard decision tree for industrial robot reliability evaluation[J].Industrial Robot, 2017, 44(6): 754–764.
[3] KABIR S, PAPADOPOULOS Y.A review of applications of fuzzy sets to safety and reliability engineering[J].International Journal of Approximate Reasoning, 2018, 100(9): 29–55.
[4] LEE D, CHOI D.Analysis of the reliability of a startergenerator using a dynamic Bayesian network[J].Reliability Engineering and System Safety, 2020, 195(3): 1–11.
[5] 李享, 黄洪钟, 黄鹏, 等.基于动态贝叶斯网络的电源系统可靠性分析与故障诊断[J].电子科技大学学报, 2021, 50(4): 603–608.
LI Xiang, HUANG Hongzhong, HUANG Peng, et al.Reliability analysis and fault diagnosis for power system via dynamic Bayesian network[J].Journal of University of Electronic Science and Technology of China, 2021, 50(4): 603–608.
[6] NEZHAD H B, MIRI M, GHASEMI M R.New neural network-based response surface method for reliability analysis of structures[J].Neural Computing and Applications, 2019, 31(3): 777–791.
[7] 童明娜, 卢朝辉, 赵衍刚, 等.基于矩法的CRTSⅡ型轨道板裂缝宽度可靠性研究[J].铁道学报, 2020, 42(11): 130–138.
TONG Mingna, LU Zhaohui, ZHAO Yangang, et al.Reliability evaluation of crack width of CRTSⅡ ballastless track slab using methods of moment[J].Journal of the China Railway Society, 2020, 42(11): 130–138.
[8] 张义民.机械动态与渐变可靠性理论与技术评述[J].机械工程学报, 2013, 49(20): 101–114.
ZHANG Yimin.Review of theory and technology of mechanical reliability for dynamic and gradual systems[J].Journal of Mechanical Engineering, 2013, 49(20): 101–114.
[9] 李常有, 张义民, 王跃武.线性连续系统的动态与渐变耦合可靠性分析[J].机械工程学报, 2012, 48(2): 23–29.
LI Changyou, ZHANG Yimin, WANG Yuewu.Dynamic and gradual coupling reliability analysis of linear and continuous system[J].Journal of Mechanical Engineering, 2012, 48(2): 23–29.
[10] O’CONNOR P D T.Commentary: Reliability-past, present, and future[J].IEEE Transactions on Reliability, 2000, 49(4): 335–341.
[11] LIN C C, TSENG H Y.A neural network application for reliability modelling and condition-based predictive maintenance[J].The International Journal of Advanced Manufacturing Technology, 2005, 25(1–2): 174–179.
[12] YONG S N, LIN M A, JOSEPH M, et al.Mechanical systems hazard estimation using condition monitoring[J].Mechanical Systems and Signal Processing, 2006, 20(5): 1189–1201.
[13] ZIO E.Reliability engineering: Old problems and new challenges[J].Reliability Engineering & System Safety, 2009, 94(2): 125–141.
[14] 谢里阳.机械可靠性理论、方法及模型中若干问题评述[J].机械工程学报, 2014, 50(14): 27–35.
XIE Liyang.Issues and commentary on mechanical reliability theories, methods and models[J].Journal of Mechanical Engineering, 2014, 50(14): 27–35.
[15] CHINNAM R B.On-line reliability estimation of individual components, using degradation signals[J].IEEE Transactions on Reliability, 1999, 48(4): 403–412.
[16] LU H, KOLARIK W J, LU S S.Real-time performance reliability prediction[J].IEEE Transactions on Reliability, 2001, 50(4): 353–357.
[17] LU S S, LU H, KOLARIK W J.Multivariate performance reliability prediction in real-time[J].Reliability Engineering & System Safety, 2001, 72(1): 39–45.
[18] AHMAD B T, FILIPPO D C, NICOLA P, et al.Bayesian regression based condition monitoring approach for effective reliability prediction of random processes in autonomous energy supply operation[J].Reliability Engineering and System Safety, 2020, 201(9): 921–934.
[19] LIU Y, ZUO M J, HUANG H Z.Dynamic reliability assessment for multi-state systems utilizing system-level inspection data[J].IEEE Transactions on Reliability, 2015, 64(4): 1287–1299.
[20] SOLIMAN M, BARONE G, FRANGOPOL D M.Fatigue reliability and service life prediction of aluminum naval ship details based on monitoring data[J].Structural Health Monitoring, 2015, 14(1): 3–19.
[21] 何正嘉, 曹宏瑞, 訾艳阳, 等.机械设备运行可靠性评估的发展与思考[J].机械工程学报, 2014, 50(2): 171–186.
HE Zhengjia, CAO Hongrui, ZI Yanyang, et al.Developments and thoughts on operational reliability assessment of mechanical equipment[J].Journal of Mechanical Engineering, 2014, 50(2): 171–186.
[22] 丁锋, 何正嘉, 訾艳阳, 等.基于设备状态振动特征的比例故障率模型可靠性评估[J].机械工程学报, 2009, 45(12): 89–94.
DING Feng, HE Zhengjia, ZI Yanyang, et al.Reliability assessment based on equipment condition vibration feature using proportional hazards model[J].Journal of Mechanical Engineering, 2009, 45(12): 89–94.
[23] DING F, RE Z J.Formalization of reliability model for assessment and prognosis using proactive monitoring mechanism[C]IEEE International Conference on Prognostics and Health Management Conference.Piscataya, 2010: 1–6.
[24] 丁锋.基于监测信息的设备运行可靠性研究[D].西安: 西安交通大学, 2010.
DING Feng.Research on equipment operation reliability based on monitoring information[D].Xi’an: Xi’an Jiaotong University, 2010.
[25] DING F, HE Z.Cutting tool wear monitoring for reliability analysis using proportional hazards model[J].The International Journal of Advanced Manufacturing Technology, 2011, 57(5–8): 565–574.
[26] 陈保家, 陈雪峰, 李兵, 等.Logistic回归模型在机床刀具可靠性评估中的应用[J].机械工程学报, 2011, 47(18): 158–164.
CHEN Baojia, CHEN Xuefeng, LI Bing, et al.Reliability estimation for cutting tool based on logistic regression model[J].Journal of Mechanical Engineering, 2011, 47(18): 158–164.
[27] CHEN B J, CHEN X F, LI B, et al.Reliability estimation for cutting tools based on logistic regression model using vibration signals[J].Mechanical Systems and Signal Processing, 2011, 25(7): 2526–2537.
[28] CAI G G, CHEN X F, LI B, et al.Operation reliability assessment for cutting tools by applying a proportional covariate model to condition monitoring information[J].Sensors, 2012, 12(10): 12964–12987.
[29] 蔡改改, 陈雪峰, 陈保家, 等.利用设备响应状态信息的运行可靠性评估[J].西安交通大学学报, 2012, 46(1): 108–113.
CAI Gaigai, CHEN Xuefeng, CHEN Baojia, et al.Operating reliability assessment by equipment response condition information[J].Journal of Xi’an Jiaotong University, 2012, 46(1): 108–113.
[30] 喻勇, 司小胜, 胡昌华, 等.数据驱动的可靠性评估与寿命预测研究进展: 基于协变量的方法[J].自动化学报, 2018, 44(2): 216–227.
YU Yong, SI Xiaosheng, HU Changhua, et al.Data driven reliability assessment and life-time prognostics: A review on covariate models[J].Acta Automatica Sinica, 2018, 44(2): 216–227.
[31] COX D R.Regression models and life-tables[J].Journal of the Royal Statistical Society: Series B (Methodological), 1972, 34(2): 187–202.
[32] LUGTIGHEID D, JARDINE A K S, JIANG X Y.Research optimizing the performance of a repairable system under a maintenance and repair contract[J].Quality and Reliability Engineering International, 2007, 23(5): 943–960.
[33] GASMI S, LOVE E C, KAHLE W.A general repair, proportional-hazards, framework to model complex repairable systems[J].IEEE Transactions on Reliability, 2003, 52(1): 26–32.
[34] SAMROUT M, CHÂTELET E, KOUTA R, et al.Optimization of maintenance policy using the proportional hazard model[J].Reliability Engineering & System Safety, 2009, 94(1): 44–52.
[35] KUMAR D, WESTBERG U.Some reliability models for analyzing the effect of operating conditions[J].International Journal of Reliability, Quality and Safety Engineering, 1996, 4(2): 133–148.
[36] HASSAN M, NEMATI, ANITA SANT’ANNA, et al.Reliability evaluation of power cables considering the restoration characteristic[J].International Journal of Electrical Power and Energy Systems, 2019, 105: 622–631.
[37] SUN Y, MA L, MATHEW J, et al.Mechanical systems hazard estimation using condition monitoring[J].Mechanical Systems and Signal Processing, 2006, 20(5): 1189–1201.
[38] JARDINE A K S, ANDERSON P M, MANN D S.Application of the Weibull proportional hazards model to aircraft and marine engine failure data[J].Quality and Reliability Engineering International, 1987, 3(2): 77–82.
[39] COMPARE M, BARALDI P, BANI I, et al.Industrial equipment reliability estimation: A Bayesian Weibull regression model with covariate selection[J].Reliability Engineering and System Safety, 2017, 166: 25–40.
[40] GORJIAN N, MA L, MITTINTY M, et al.The explicit hazard model-part 1: Theoretical development[C] IEEE Proceedings of the Prognostics & System Health Management Conference.Macao, 2010: 167–179.
[41] BISADI V, PADGETT J E.Explicit time-dependent multihazard cost analysis based on parameterized demand models for the optimum design of bridge structures[J].Computer-Aided Civil and Infrastructure Engineering, 2015, 30(7): 541–554.
[42] SHELDON M R.Generalized poisson shock models[J].The Annals of Probability, 1981, 9(5): 896–898.
[43] PANDEY A, MITRA M.Poisson shock models leading to new classes of non-monotonic aging life distributions[J].Microelectronics Reliability, 2011, 51(12): 2412–2415.
[44] JUNCA M, SANCHEZ-SILVA M.Optimal maintenance policy for a compound Poisson shock model[J].IEEE Transactions on Reliability, 2013, 62(1): 66–72.
[45] LISNIANSKI A, ELMAKIAS D, LAREDO D, et al.A multistate Markov model for a short-term reliability analysis of a power generating unit[J].Reliability Engineering & System Safety, 2012, 98(1): 1–6.
[46] GUILANI P P, SHARIFI M, ZARETALAB A.Reliability evaluation of non-reparable three-state systems using Markov model and its comparison with the UGF and the recursive methods[J].Reliability Engineering & System Safety, 2014, 129: 29–35.
[47] TOBON-MEJIA D A, MEDJAHER K, ZERHOUNI N, et al.A data-driven failure prognostics method based on mixture of Gaussians hidden Markov models[J].IEEE Transactions on Reliability, 2012, 61(2): 491–503.
[48] 李丹.结构健康监测技术提高飞行器性能——访飞行器健康管理专家卿新林教授[J].航空制造技术, 2016, 59(8): 22–24.
LI Dan.Structural health monitoring technology promotes the performance of aircraft[J].Aeronautical Manufacturing Technology, 2016, 59(8): 22–24.
[49] YUE N, ALIABADI M H.Hierarchical approach for uncertainty quantification and reliability assessment of guided wavebased structural health monitoring[J].Structural Health Monitoring, 2020, 19(8): 1–26.
[50] MARACNTONIO C, LORENZO C, DIEGO G, et al.Optimizing maintenance policies for a yaw system using reliabilitycentered maintenance and data-driven condition monitoring[J].IEEE Transactions on Instrumentation and Measurement, 2020, 69(9): 6241–6249.
[51] ZHANG D B, LI W Y, XIONG X F.Overhead line preventive maintenance strategy based on condition monitoring and system reliability assessment[J].IEEE Transactions on Power Systems, 2014, 29(4): 1839–1846.
[52] 陈志为.基于健康监测系统的大跨多荷载桥梁的疲劳可靠度评估[J].工程力学, 2014, 31(7): 99–105.
CHEN Zhiwei.Fatigue reliability assessment of multi-loading suspension bridges based on SHMS[J].Engineering Mechanics, 2014, 31(7): 99–105.
[53] 郑蕊, 李兆霞.基于结构健康监测系统的桥梁疲劳寿命可靠性评估[J].东南大学学报(自然科学版), 2001, 31(6): 71–73.
ZHENG Rui, LI Zhaoxia.Reliable evaluation of bridge fatigue life based on structural health monitoring system[J].Journal of Southeast Univwrsity (Natural Science Edition), 2001, 31(6): 71–73.
[54] HU C H, ZHOU Z J, ZHANG J X, et al.A survey on life prediction of equipment[J].Chinese Journal of Aeronautics, 2015, 28(1): 25–33.
[55] 肖鑫.基于健康监测的钢桁梁桥结构承载力可靠性评估[J].铁道标准设计, 2020, 64(5): 89–95.
XIAO Xin.Reliability assessment of bridge structural bearing capacity based on health monitoring[J].Railway Standard Design, 2020, 64(5): 89–95.
[56] 刘玉梅, 陈云, 赵聪聪, 等.基于KDE及Markov高速列车传动系振动评价及可靠性分析[J/OL].西南交通大学学报, (2020–08–10)[2020–12–02].https://kns.cnki.net/kcms/detail/51.1277.U.20201202.1202.002.html.
LIU Yumei, CHEN Yun, ZHAO Congcong, et al.Vibration evaluation and reliability analysis of high speed train transmission system based on KDE and Markov[J/OL].Journal of Southwest Jiaotong University, (2020–08–10)[2020–12–02].https://kns.cnki.net/kcms/detail/51.1277.U.20201202.1202.002.html.
[57] 李游, 李传习, 陈卓异, 等.基于监测数据的钢箱梁U肋细节疲劳可靠性分析[J].工程力学, 2020, 37(2): 111–123.
LI You, LI Chuanxi, CHEN Zhuoyi, et al.Fatigue reliability analysis of U-rib detail of steel box girder based on monitoring data[J].Engineering Mechanics, 2020, 37(2): 111–123.
[58] 陈世杰, 吴贤国, 姚春桥, 等.基于压缩感知隧道结构健康监测与可靠性评价[J].铁道标准设计, 2020, 63(11): 101–108.
CHEN Shijie, WU Xianguo, YAO Chunqiao, et al.Health monitoring and reliability evaluation of tunnel structure based on compressed sensing theory[J].Railway Standard Design, 2020, 63(11): 101–108.
[59] OKASHA N M, FRANGOPOL D M, SAYDAM D, et al.Reliability analysis and damage detection in high-speed naval craft based on structural health monitoring data[J].Structural Health Monitoring, 2011, 10(4): 361–379.