基于模型的定义（Model based definition，MBD）的数字化设计制造模式已广泛应用于航空航天研制过程，对于基于三维模型的设计制造起到了巨大的促进作用。然而基于理论模型的制造过程仿真无法真实反映出物理对象的几何时变特性，导致制造过程仿真结果往往偏离实际工况。随着数字孪生技术的兴起，数字孪生模型（Digital twin model，DTM）已被逐渐认为是一种可以在虚拟空间实现与产品物理实体数字化映射的仿真模型[1]，它是实物对象的虚拟表示，是一个随着物理对象状态、工作条件、产品几何结构和资源状态等的变化而不断更新和变化的活体模型（Living model，LM）[2]。基于数字孪生模型的制造过程仿真可有效提高仿真准确度。本文将这种由实测数据驱动创建、能够表达时变物理对象几何变化的模型称为数字孪生几何模型。
目前，国内外学者对孪生建模做了一些研究，Schleich等[3]提出一种基于肤面模型（Skin model shape，SMS）概念的综合参考模型充当物理产品的数字孪生模型，并研究了该模型在全生命周期的表征与应用。于勇等[4]引入实作模型（As-build model，ABM）的概念来描述加工工件的孪生模型，利用本体技术对实作模型进行管理。鲍劲松等[5]提出一种半实物虚拟装配模型（Quasiphysical virtual assembly model，QPVAM），融合了产品几何及装配特征的CAD数据，还集成了制造过程信息和关键尺寸点云数据，真实映射实物产品，其本质与孪生模型一致。上述建模方法均能形成接近实物产品的数字模型，但与产品不同，多点式飞机柔性工装几何上分散布置、联动控制、间歇运动，常处于时变状态，尚无相关的孪生建模研究。
上述柔性工装几何信息主要包括静态信息和动态信息两大类。前者包括定位表面的几何形貌、工装各零件的连接关系等；后者包括定位器联动规律、定位器受装配工艺和环境等影响产生的时变现象等。在紧凑的时间段内，柔性工装根据装配工艺处于并联运动状态；在工装整个生命周期中，受环境因素和装配任务等的影响，柔性工装各定位器的位置也会发生变化。由此可见，工装状态是连续的无限集合且具有不确定性。
实时性是数字孪生建模最重要的特性，对物理实体建模产生静态模型，在此基础上，融合实时数据进行模型驱动，动态跟踪物理实体的工作状态。有限状态机（Finite-state machine，FSM）是一种常见的动态系统描述方法，它通过对系统状态、触发条件以及系统状态间的跃迁能够有效描述一个动态系统的整个过程。由于用于装配仿真的工装孪生模型应是能够实现快速映射离散化的实体模型，故将柔性工装的整个生命周期按不同批次的装配任务划分为无限个单元，每个单元生成一个柔性工装数字孪生几何模型，每个动态模型的建模动作可按装配工艺离散为有限个状态，并基于FSM进行建模。
本文提出一种基于FSM理论对时变物理对象状态进行离散、利用CATIA的开发工具CAA进行参数化建模的飞机柔性工装数字孪生几何模型建模方法，利用控制对象与被控对象的依赖关系，将飞机部件6个维度的动作对应到工装的联动调整操作上，将抽象出的工装若干建模动作作为状态，结合装配工艺，得出每个状态下工装各定位器执行末端移动规律，并利用传感器获取相应定位器的实测位移值。将测量系统和运动控制系统统一集成到CATIA平台，通过数据接口来实现虚实融合，从而实现运用实物的数据来动态修正模型。
1 基于FSM的柔性工装数字孪生几何模型构建方法
FSM是一种时序电路，通过控制一个或多个输入信号，实现电路在预设的各种状态里进行转换。按是否有输入信号直接进入输出端，FSM分为米利（Mealy）型FSM和摩尔（Moore）型FSM[6]。在分析柔性工装数字孪生建模系统时，将其建模过程划分为几个确定的状态，通过事件的触发实现状态的跳转，同时将部分输入条件作为最终模型的驱动参数，故选用Mealy型FSM。可将其定义为一个六元组FSM=（S，s0，∑，Λ，δ，ω），其中有限状态集S是一个有穷集，S=（s0，s1，…，sn）；s0∈S是状态机的初始状态；∑=（σ1，σ2，…，σn）是输入的有穷集合；Λ=（λ1，λ2，…，λn）是输出的有穷集合；δ是状态转移函数，定义为δ：S×∑→S，δ（S1，σ）=S2表示S1状态下接受输入σ后将转移到状态S2；ω是动作输出函数，定义为ω：S×∑→Λ，该函数为每个状态和输入对指派特定输出动作。
由于柔性工装实物的分散性、联动性和不确定性，难以预设其有限个状态。考虑到工装作为控制对象显著影响被控对象的几何特征，故利用这种依赖关系，用产品的空间位姿变化描述工装多轴的联动调整动作，将抽象出的6个维度的动作当作FSM模型的有限个状态。通过测量关键产品特性（Key product characteristics，KPCs）和关键控制特性（Key control characteristics，KCCs）[7]完成产品状态和工装状态的监测。
首先，通过实测数据重构工装各定位件的初始位置，在三维模型上添加相应约束使其与真实的联动机构运动保持一致，继而实时获取飞机部件位姿变化的六维数据
通过阈值判断|Δd|≤ε（Δd分别为位姿变化向量的3个位移量和3个欧拉角）得到工装状态转移指令向量，用B=（Bx，By，Bz，Bα，Bβ，Bγ）（其中Bi=0 or 1）表示，输入至FSM。将抽象出的工装若干建模动作封装为有限个状态，用S=（s0，s1，…，sn）表示。同时，各个建模动作下的工装定位器各轴的位移实测值用
表示，输入至三维建模软件。由定位器联动规律确定不同调姿动作下需改变的驱动轴编号，基于CATIA CAA提供的接口，模型的位移约束窗口选择性读取
中对应编号轴的位移值，进行数模参数改变。将每个建模步骤的内部执行结果描述为基本转移条件，用x=（x1，x2，…，xm）表示，并输入至FSM。对已调整的动作，工装状态转移向量中对应维度数值将置0。状态（建模动作）是有限的，由基本条件x和指令集B构成的状态转移条件x∩B也是有限的，对于每一个确定状态s和状态转移条件x∩B，状态的转移输出是唯一确定的，即从sp→sm的转移条件为xp∩Bm（p= 0，1，2，…，n–1；m=1，2，…，n）。转移至末态，即完成工装数字孪生几何的构建。
综上，建模流程划分为3个步骤，分别为实时数据采集与预处理、状态及其转移机制的定义以及参数化几何实体建模。进一步的，柔性工装的数字孪生模型有如下表述。
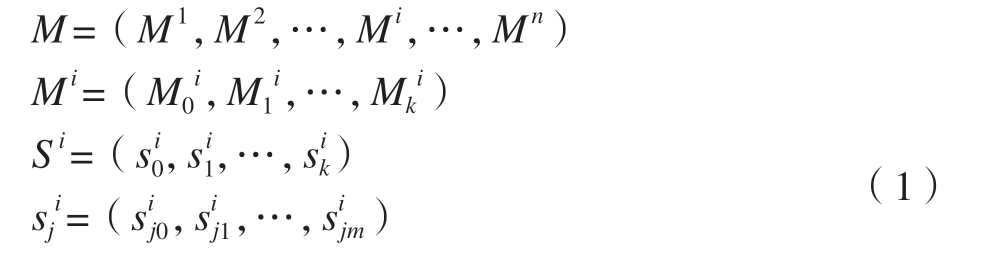
整个生命周期中工装数字孪生模型的个数是无限的，Mi为第i个工装孪生几何模型。每个工装数字孪生几何模型是一组有限的模型集合，均基于FSM方法构建，其个数和FSM模型中状态Si的数量k相同。面对不同时间段、不同批装配任务，初始状态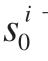
下所对应的柔性工装静态几何模型
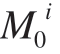也不尽相同。为简化模型数量，将m个相同类型的调整动作封装为一个状态。状态转移的过程即工装数字孪生几何建模过程，整体建模流程如图1所示。
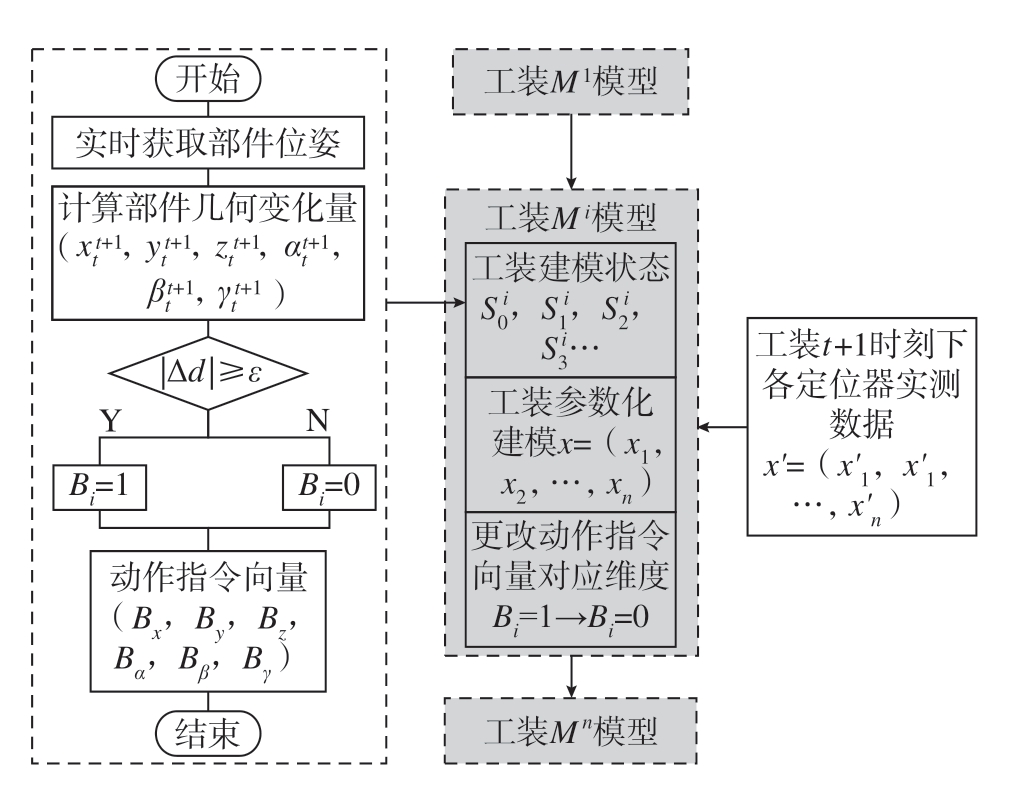
图1 基于FSM的柔性工装数字孪生几何模型构建流程
Fig.1 Construction process of digital twin geometric model of flexible tooling based on FSM
2 柔性工装的数字孪生几何模型构建
2.1 翼身对接试验平台
大部件对接调姿机构是一种典型的柔性工装，故以翼身对接试验平台为对象，建立调姿机构的数字孪生几何模型。孪生的翼身对接试验平台如图2所示，该平台由多点柔性工装、飞机翼身模拟件、控制系统、测量系统、工控主机等组成。中机身和机翼分别由4个和3个定位器支撑，并通过球铰与定位器相连接，控制软件协调多个定位器沿X、Y、Z向的直线运动来完成部件6个自由度方向上的运动。通过螺旋理论分析位置控制轴的选取合理性，运用速度椭球和刚度椭球考察机构的综合性能，确定位置控制轴的最佳选取策略[8]，如图3所示，各定位器附近标明了各轴的具体情况，实线表示驱动轴，虚线表示从动轴，且所有定位器Z向均为驱动轴。保持机身位置，通过调整机翼位置完成对接。
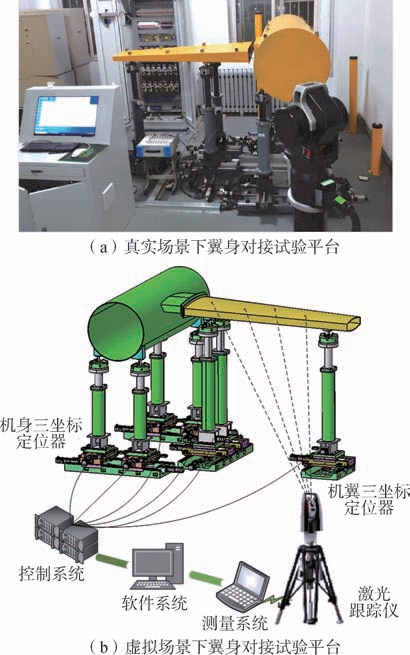
图2 孪生翼身对接试验平台
Fig.2 Digital twins of wing and fuselage docking platform
图3 翼身对接柔性工装布置示意图
Fig.3 Layout diagram of wing and fuselage flexible docking tooling
2.2 实时数据采集与预处理
将实时测量数据分为两类：一类为用来判断物理对象是否发生状态转移的状态测量项；另一类用于建模的几何参数项。
利用机翼位姿变化判断工装模型是否需要进行调整的策略，基于激光跟踪仪进行机翼部件位姿测量[9]，基于奇异值分解法（SVD） 计算机翼空间位姿[10]，如图4所示。
图4 基于激光跟踪仪的机翼部件位姿测量流程
Fig.4 Pose measurement process of wing parts based on laser tracker
飞机部件姿态计算即找到一组变换{R，t}，使一组点集坐标Xi=（xi，yi，zi）T，i=1，2，…，n，经过变换后，与另一组点集
，i=1，2，…，n相匹配。SVD法是研究两个场相互关系的有效方法，其实质是计算点集的质心在两个坐标系中的坐标，假设它们存在
的坐标转换关系，再实现所有的点在两个坐标系的最小偏差拟合。一般选部件上的5～10个不共线的测量点，SVD算法思路为以下4个步骤。
（1）分别计算质心在全局坐标系和局部坐标系中的坐标M′和N′。
（2）计算协方差矩阵H=
，其中qi=Xi–μ，
（3）对H进行奇异值分解H=UDVT，其中D是对角矩阵，V和U是正交矩阵。
（4）计算旋转矩阵R=VUT，并求其行列式。若det（R）= +1，则R就是所需要计算得到的解；若det（R）= –1，则R是一个反射变换。此时，令V′=[v1，v2，–v3]，则R=V′UT就是所求的旋转矩阵。平移矩阵T=μ′–Rμ。
在翼身对接调姿过程中，考虑到部件间可能发生碰撞，通常将调姿对接分解成以下3个阶段进行[11]。首先，完成部件姿态3个欧拉角（α，β，γ）调整；其次，完成（0，y，z）方向位置调整；最后，完成（x，0，0）方向上对合过程。表1中第2～7列数据记录相邻时刻机翼在6个维度上的位姿变化量，每行为1个六维向量，计算相邻时刻下机翼位姿变化向量（Δx，Δy，Δz，Δα，Δβ，Δγ），针对每一维数据给一个阈值，两者相较，超过阈值的维度可视为进行该维度的平动或转动。
表1 T0～T6时刻机翼位姿数据
Table 1 Wing pose data at T0–T6
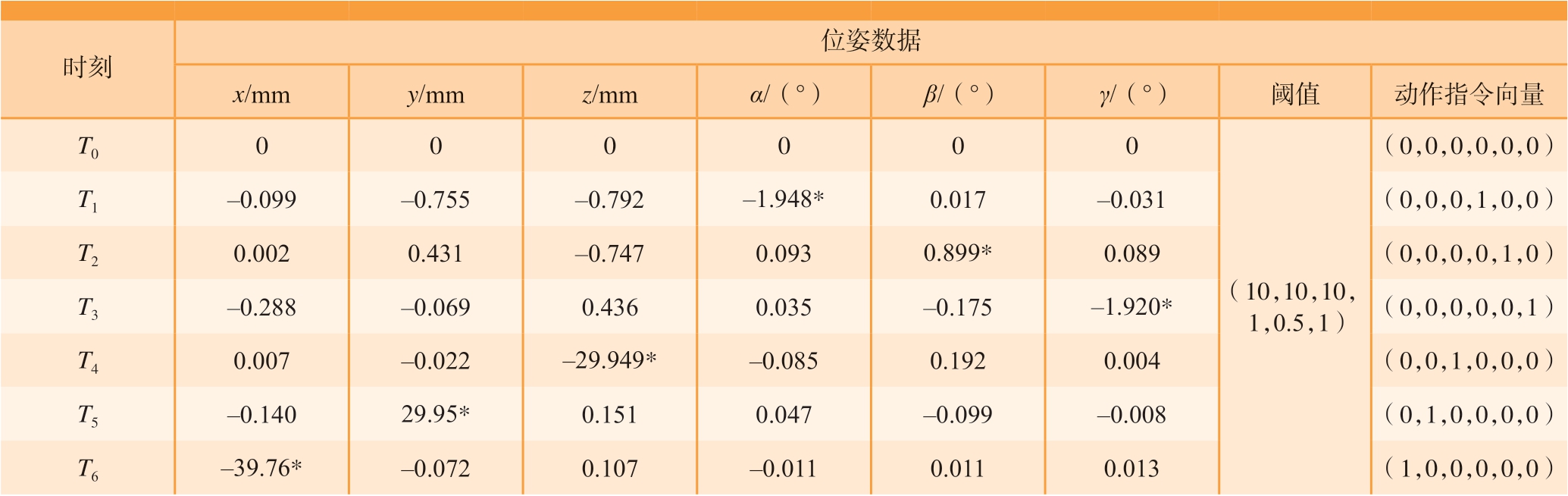
*注：根据表1中标星号数值，即得到动作指令向量；阈值根据试验数据、精度要求、调姿幅度等选取。
时刻位姿数据x/mm y/mm z/mm α/（°） β/（°） γ/（°） 阈值 动作指令向量T0 0 0 0 0 0 0（0，0，0，0，0，0）T1 –0.099 –0.755 –0.792 –1.948* 0.017 –0.031 （0，0，0，1，0，0）T2 0.002 0.431 –0.747 0.093 0.899* 0.089 （0，0，0，0，1，0）T3 –0.288 –0.069 0.436 0.035 –0.175 –1.920* （0，0，0，0，0，1）T4 0.007 –0.022 –29.949* –0.085 0.192 0.004 （0，0，1，0，0，0）T5 –0.140 29.95* 0.151 0.047 –0.099 –0.008 （0，1，0，0，0，0）T6 –39.76* –0.072 0.107 –0.011 0.011 0.013 （1，0，0，0，0，0）（10，10，10，1，0.5，1）
为实现机翼空间六自由度的运动，需使3个定位器联动，共9根轴进行并联运动，而在进行参数化建模时只需传入不同调姿动作下特定几个驱动轴的实测位移值即可。为了验证模型与实物运动的一致性，将其他3根从动轴作为参照量，若不同时刻下模型上9根轴的位移值均与实测数据相近，即可证明建模方法的有效性。所有工装定位器各轴上均安装拉线式位移传感器，通过配套的信号测试分析系统实现同步采样、同步传输、实时显示和实时存盘。本文选用TZT3828EN系列信号测试分析系统。
现场采集的各点位定位器在X、Y、Z方向上的位移原始数据会由于驱动装置或传感装置、现场信号干扰等原因，出现在一段时间内缺失，或在一段时间内恒定在某个很大或很小的固定值的现象，如图5所示。针对数值空缺，利用其前后数据进行插值处理；针对异常值采用局部加权回归散点平滑法进行处理。处理后得到的位移变化曲线如图6所示。
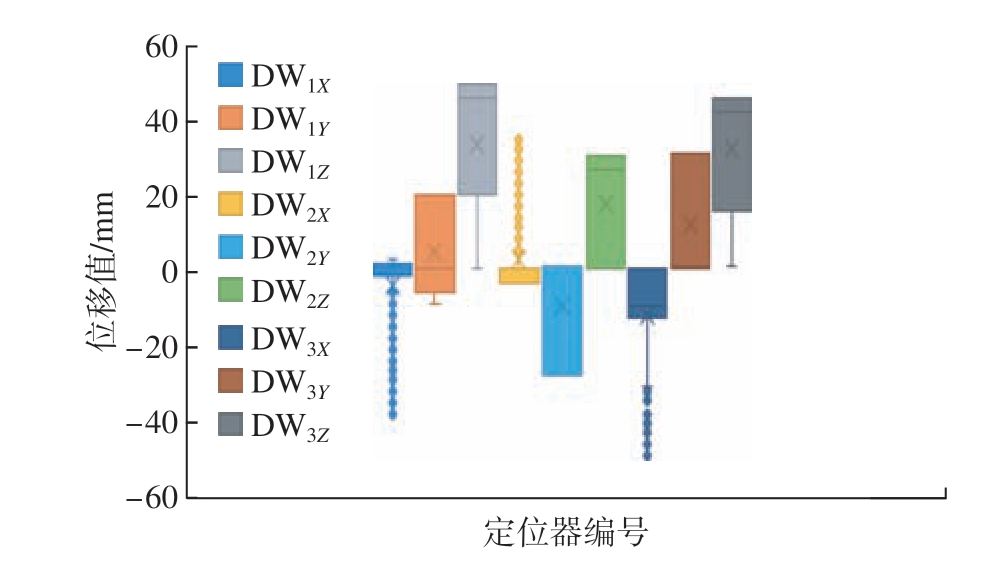
图5 定位器位置数据箱线图
Fig.5 Box-plot of locator position data
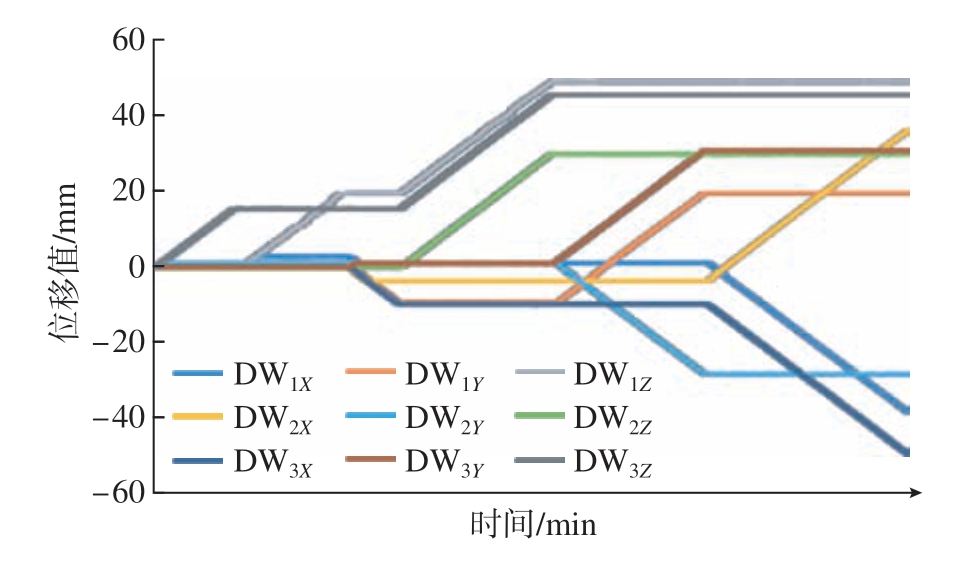
图6 定位器数据处理结果
Fig.6 Processing result of locator data
与机翼位姿数据相对应，T0～T6时刻定位器数据见表2。其中，特征命名中包含“DW1Z”的表示机翼定位器1沿Z方向的位移。
表2 T0～T6时刻定位器测量数据
Table 2 Positioner measurement data at T0–T6
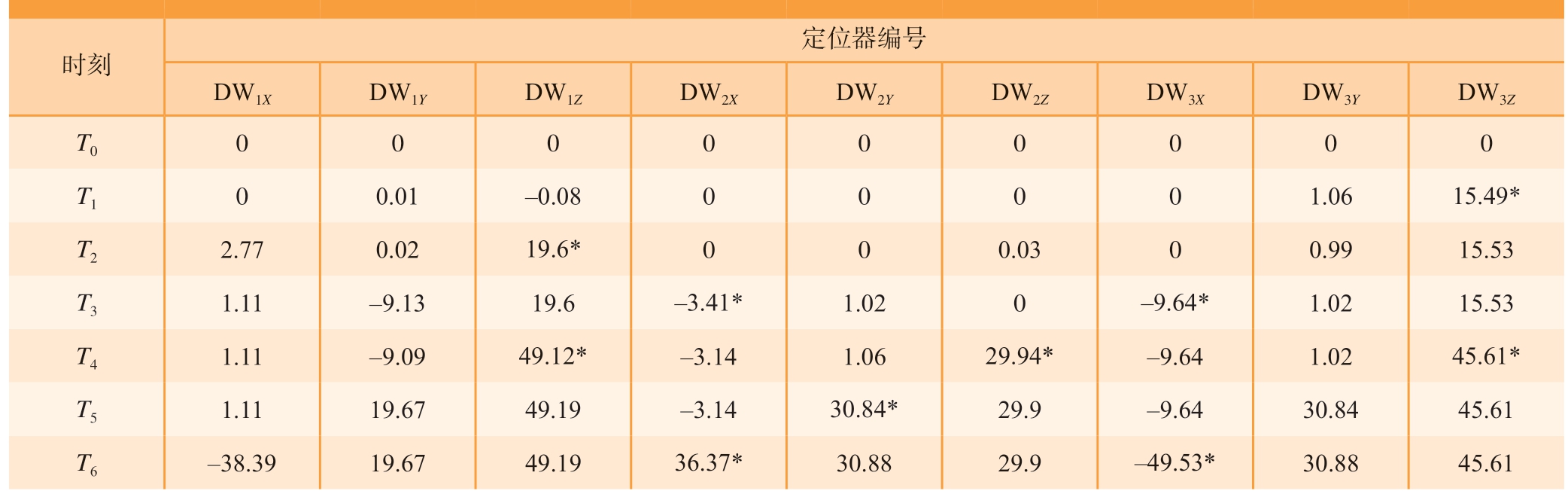
*注：标星号数值对应的纵坐标代表当前调姿动作结束时的时刻，对应的横坐标代表当前调姿动作下产生位移的驱动器编号，该值即为该时刻该驱动器的实测位移值，这些数据是用于调姿机构孪生建模的几何参数项。
?
2.3 状态及其转移机制的定义
根据机翼调姿对接流程，以调姿机构完成的机翼调整动作作为状态，以由机翼位姿变化得到的工装动作指令集和工装定位器各轴的位移量作为输入信号，建立机翼调姿下工装建模过程与Mealy型有限状态机的映射关系，如表3所示。
表3 工装调姿过程与有限状态机的映射关系
Table 3 Mapping relationship between tooling posture adjustment process and finite state machine
模型参数 机翼调姿对接过程S=（s0，s1，s2，s3）由对接调姿机构完成的调整动作组成的状态集合，其中，s0为静置状态；s1为转动调整状态；s2为沿Y或Z轴平动调整状态；s3为沿X轴对合调整状态（末态）调姿机构静置状态，初始状态下所对应的调姿机构三维几何模型为基于实测数据进行过表面层、约束层和联动层建模的工装实体模型∑=（σ1，σ2） 由工装动作指令集和定位器各轴位移数据集组成的输入信号集合s0 δ：S×∑→S状态转移函数，用于判断是否发生状态转移，当si状态下基本转移条件和sj状态下工装动作转移指令同时满足时，调姿机构可由状态si转移至状态sj ω：S×∑→Λ动作输出函数，用于确定状态转移时哪些驱动轴发生位移变化，由定位器联动规律确定不同状态、不同调姿动作下需改变的驱动轴编号Λ=（λ1，λ2，…，λn）输出信号集合,根据动作输出函数，输出对应驱动轴实时位移移值，由接口至CATIA三维建模软件
根据有限状态机原理，可将工装模型调整动作抽象封装为4个状态，每个状态下对应若干调姿动作。依次提取输入的工装动作指令集中元素[Bα，Bβ，Bγ]、[By，Bz]和[Bx]，分别对应状态s1，s2，s3。CATIA位移约束窗口选择性读取对应编号轴的位移值并更新，返回完成信号至FSM，此时工装动作指令向量相应维度数值置0。当si状态下工装动作转移指令平方和F=∑Bi2为0且在si+1状态下不为0时，可由状态si转移至状态sj，三维模型也由Mi变为Mi+1。图7给出了状态转移流程图并结合六维工装动作指令向量设置了状态转移的条件。
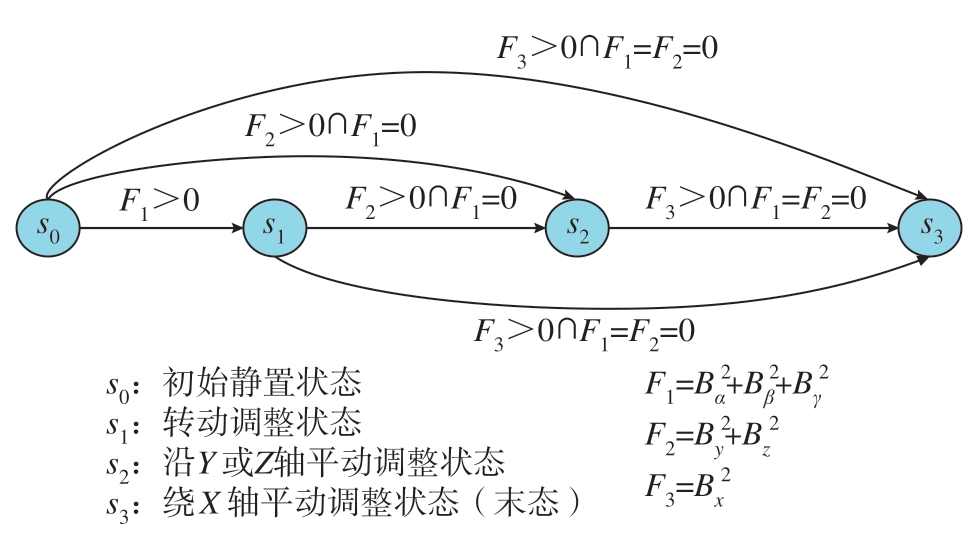
图7 工装建模状态转移图
Fig.7 State transition diagram of tool modeling
2.4 参数化几何实体建模
首先，在明晰了实际工装并联机构基于螺旋理论和速度椭球的设计原理和运动规律的基础上，在CATIA建模软件中，需要对零部件组进行合理划分，并在装配设计界面添加相合、位移、固定、垂直等约束，保证驱动轴与实际情况一致，并能够实现与柔性工装实物相同的联动控制，如图8所示。
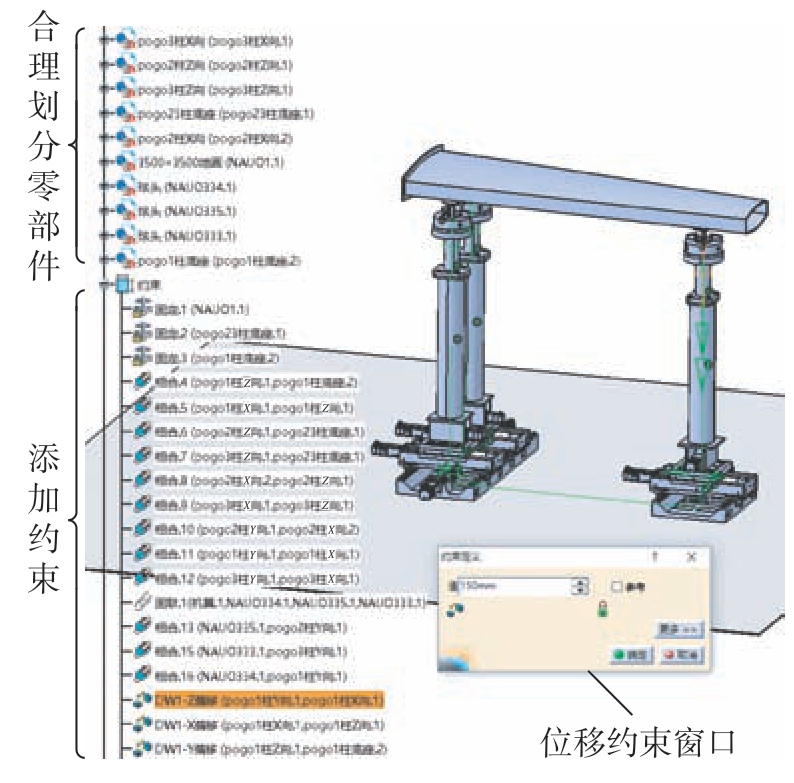
图8 调姿机构零部件划分及约束处理
Fig.8 Part division and constraint treatment of posture adjustment mechanism
然后，建立现场测量系统、定位器运动控制系统和建模软件系统之间的网络连接。基于FSM进行调姿机构的可视化建模，如图9所示。其中Mi为当前状态下的工装孪生几何模型；
分别为工装静置状态、转动调整状态、沿Y或Z轴平动调整状态、绕X轴对合调整状态。每个状态下对应若干调姿动作，其中
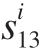分别为绕X、Y、Z轴转动
分别为沿Y、Z轴平动。状态转移的过程即工装数字孪生几何建模过程。
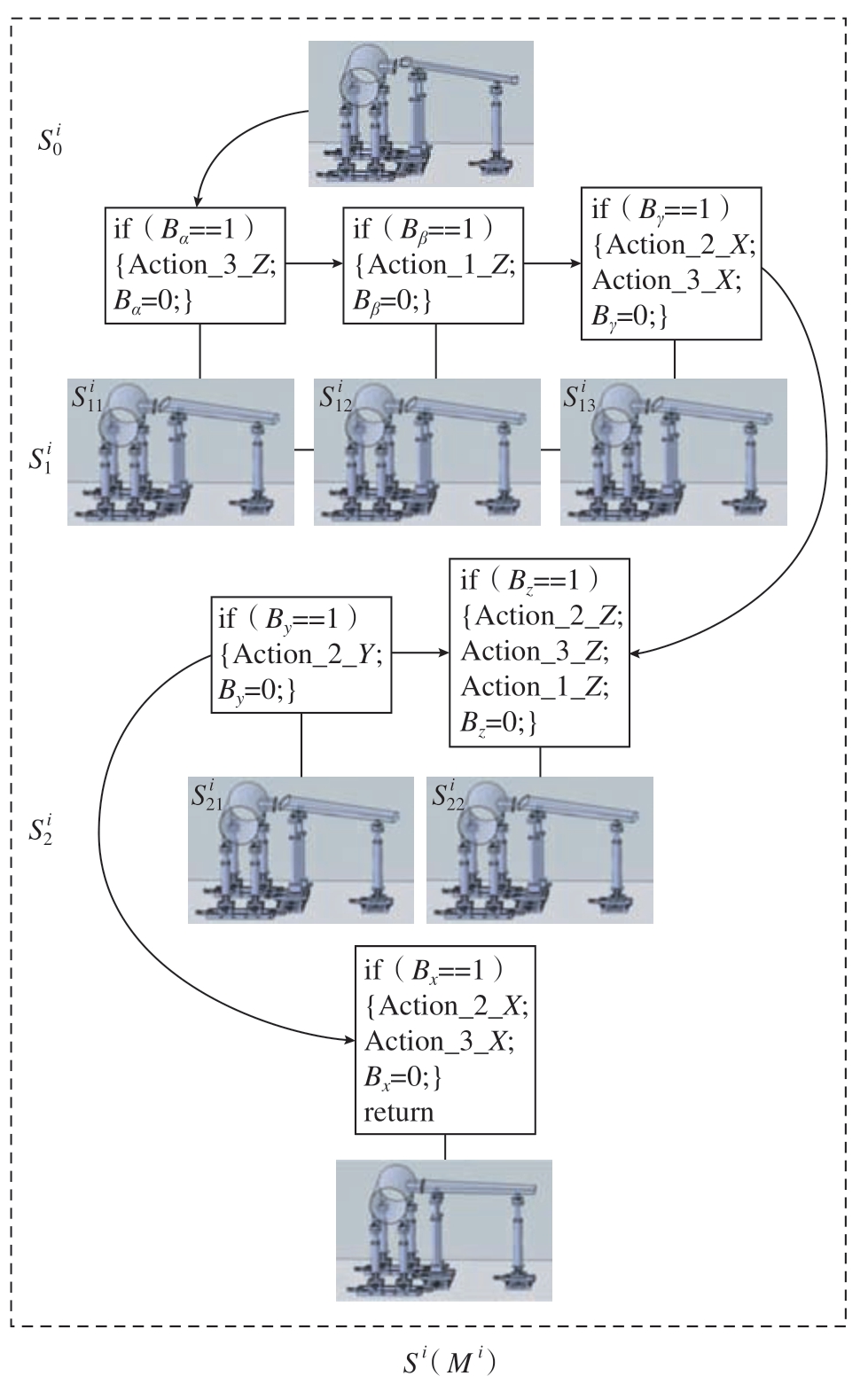
图9 对接调姿机构数字孪生几何模型可视化表达
Fig.9 Visual expression of digital twin geometric model of docking attitude adjustment mechanism
最终，模型能够随实物进行动态转换，工装模型上定位器各轴的位移与实际工装各轴的位移方向一致，数值相近。证明了基于FSM对工装进行实测数据驱动的参数化动态建模方法的可行性。同时也证明了从几何尺寸、约束关系、驱动轴设置、联动机构运动规律、几何时变特性等全面映射柔性工装实物，构建的工装数字孪生几何模型可以有效用于后续的装配仿真，具有较强的拟实性。
3 结论
从无限的柔性工装状态中提取出有限的可离散的工装状态建模步骤，提出基于FSM对柔性工装几何时变特性进行动态建模的方法。FSM这一概念新颖且使得数字孪生建模过程更加简洁。数字孪生模型内涵丰富，本文仅从几何方面入手，所建孪生模型能基本映射物理实物，未来还可考虑实物的物理属性、受力变形等特性，构建拟实性更高的数字孪生模型。
[1] TALKHESTANI B A, WEYRICH M.Digital twin of manufacturing systems: A case study on increasing the efficiency of reconfiguration[J].At-Automatisierungstechnik, 2020, 68(6): 435–444.
[2] LU Y Q, LIU C, WANG I K, et al.Digital twin-driven smart manufacturing: Connotation, reference model, applications and research issues[J].Robotics and Computer-Integrated Manufacturing, 2019, 61: 101837.
[3] SCHLEICH B, ANWER N, MATHIEU L, et al.Shaping the digital twin for design and production engineering[J].CIRP Annals-Manufacturing Technology, 2017, 66(1): 141–144.
[4] 于勇, 胡德雨, 戴晟, 等.数字孪生在工艺设计中的应用探讨[J].航空制造技术, 2018, 61(18): 26–33.
YU Yong, HU Deyu, DAI Sheng, et al.Study on application of digital twin in process planning[J].Aeronautical Manufacturing Technology, 2018, 61(18): 26–33.
[5] 鲍劲松, 李志强, 项前, 等.半实物虚拟装配的建模、演化与应用[J].机械工程学报, 2018, 54(11): 61–69.
BAO Jinsong, LI Zhiqiang, XIANG Qian, et al.The modeling, evolutionary and application of quasi-physical virtual assembly[J].Journal of Mechanical Engineering, 2018, 54(11): 61–69.
[6] PETER Minns, LAN Elliott.基于FSM和Verilog HDL的数字电路设计[M].姚世扬, 译.北京: 机械工业出版社, 2016.
PETER Minns, LAN Elliott.FSM based digital design using Verilog HDL[M].YAO Shiyang, Tran.Beijing: China Machine Press, 2016.
[7] 陈哲涵, 杜福洲, 唐晓青.基于关键测量特性的飞机装配检测数据建模研究[J].航空学报, 2012, 33(11): 2143–2152.
CHEN Zhehan, DU Fuzhou, TANG Xiaoqing.Key measurement characteristics based inspection data modeling for aircraft assembly[J].Acta Aeronautica et Astronautica Sinica, 2012, 33(11):2143–2152.
[8] 罗中海.调姿机构力/位置混合控制系统设计[D].杭州: 浙江大学, 2014.
LUO Zhonghai.Hybrid force position control system design of posture alignment[D].Hangzhou: Zhejiang University, 2014.
[9] 冯祝雷, 李明, 丁海东.激光跟踪仪高精度测量运动物体位姿的研究[J].激光技术, 2016, 40(3): 436–440.
FENG Zhulei, LI Ming, DING Haidong.High precision measurement of position and posture of kinetic objects with laser trackers[J].Laser Technology, 2016, 40(3): 436–440.
[10] 罗芳, 邹方, 周万勇.飞机大部件对接中的位姿计算方法[J].航空制造技术, 2011, 54(3): 91–94.
LUO Fang, ZOU Fang, ZHOU Wanyong.Posture calculating algorithm in large aircraft component butt[J].Aeronautical Manufacturing Technology, 2011, 54(3): 91–94.
[11] 徐源, 沈建新.机翼调姿对接运动仿真技术研究[J].机械制造与自动化, 2018, 47(2): 110–113.
XU Yuan, SHEN Jianxin.research on kinematic simulation of aircraft wing adjustment-docking[J].Machine Building & Automation, 2018, 47(2): 110–113.