20世纪60年代,我国开始对电主轴进行研究及应用,其最早应用于机械领域的磨床上,由于优异的性能得到了飞快发展,又被广泛地应用在加工制造中。作为数控加工中心机床的关键部件,高速电主轴的出现使我国高速加工技术达到了一个新的高度[1]。
高速电主轴是机床主轴与电机融为一体而产生的新技术,以内置电机直接驱动的方式代替了传统的带传动或链传动,该驱动方式将数控加工主传动链的长度缩短为0,从而使传动过程中的能量损耗基本减为0。由于电机直接安装在主轴外壳内,工作时相当于热源位于一个密闭空间中,导致其散热能力较差,内部的零件会因自身不同的热膨胀系数产生不同程度的热伸长而改变各个零件间的配合情况,因此,需要采取相应的控制方法来降低电主轴的整体静动态刚度和工作安全系数。大量研究表明,有60%~80%的加工精度误差来源于机械制造中各部分的发热变形,因此如何降低电主轴热变形所造成的影响是提高数控机床加工表现的重点和一个亟须解决的课题[2]。
近年来,随着我国工业化发展进程的加快和智能数控机床的普及,电主轴的关键技术也得到了巨大的发展,包括动静压轴承、磁悬浮轴承、流体动力轴承的出现;Cronidur30、陶瓷、碳纤维等新型材料的使用;油雾润滑、油气润滑、永久脂润滑在某些电主轴上的应用;热管等新型冷却方式的发明;以同步电动机代替传统的异步电动机等研究,这些均是在设计阶段提高了电主轴的热态性能,这类方法对于技术水平和经济水平要求很高[3–6]。而电主轴热误差的补偿技术是在电主轴的运行阶段减小了主轴的热误差,这类方法不需要改变电主轴自身的结构、材料等物理特性,仅需要很少的经济投入便可以获得设计阶段难以达到的精度水平。它通过提前预知电主轴产生的热误差大小,使用补偿的手段控制热误差,从而提高高速电主轴的加工精度,是最为经济有效的方法。
电主轴热误差补偿技术的主要原理就是通过智能算法建立能够预测主轴热位移的数学模型,根据模型计算得到的补偿值整体调整轴系的相对位置,以此来减小热误差的大小。由该技术的内容流程可知,首先热误差补偿以电主轴数据检测技术为基础,其次热误差补偿的关键在于电主轴温度测点优化技术,而热误差补偿结果的好坏则与电主轴热误差建模技术的鲁棒性与精确度直接相关,三者不可或缺[7–8]。
1 电主轴数据检测技术的研究
电主轴温度和热位移数据作为热误差模型的输入和检验数据,其采集需要极高的准确度。精确的温度数据输入值可以改良主轴热误差预测模型的预测结果;优异的热位移数据在与模型输出的补偿值进行比较时更具有权威性。
为了采集到高精度的电主轴温度及热位移数据,国内外学者及专家为此进行了大量的研究,主要可以分为数字仿真法和热试验法。其中,数字仿真法可以通过有限元仿真手段深入了解主轴内部温度场分布情况,但边界条件的计算问题限制了此方法的上限。同时,由于电主轴复杂的结构及运行特点,热试验法使用的检测系统难以获得主轴内部的温度数据,高速电主轴的结构见图1。如果只测量主轴外部壳体的温度,进行内部温度的推算,将造成一定的误差。因此,以数字仿真法为理论指导,结合热试验法进行电主轴温度及热位移数据的采集才是精确获悉电主轴内外部温度的最佳方案。
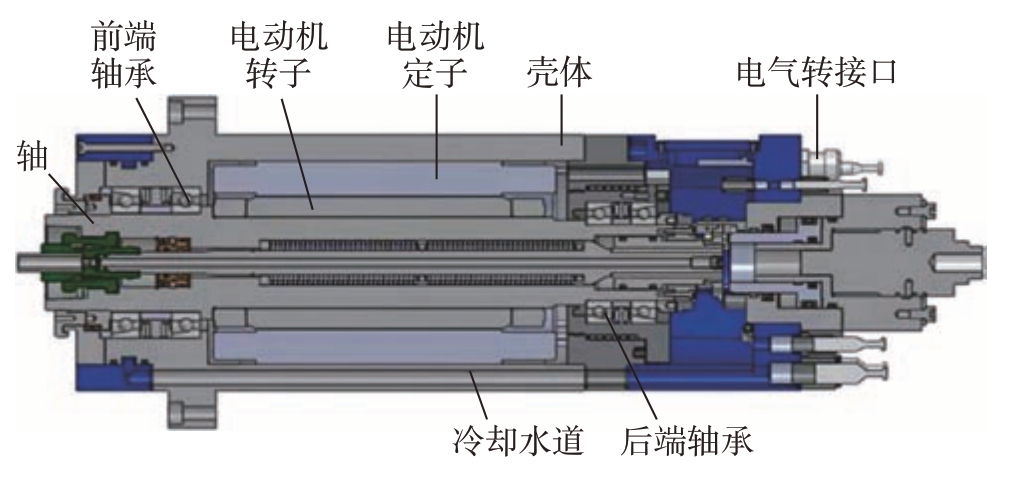
图1 高速电主轴内部构成图
Fig.1 Inner structure diagram of high-speed motorized spindle
1.1 数字仿真法的原理
数字仿真法即通过计算机软件来研究电主轴内部温度场分布情况,它是解决数据采集问题的首要条件。据统计,随着计算机技术的发展,国内外大多数研究人员都选用了有限元分析软件作为温度场分析的工具。
高速电主轴系统中许多零部件在工作时会产生巨大的热量,它们以各自的传热方式,如热传导、热辐射、热对流等方式互相影响,其中热传导和热对流是其内部的主要传热方式。所以,电主轴系统内的同一个零部件的温度可能是两种或两种以上传热方式共同造成的结果,具有发热不确定性。利用传热学理论知识对高速电主轴系统进行热分析时,应该提炼次要因素,抓住主要矛盾。
电主轴系统内部的主要热源为电机和轴承。其中,以热传导和热对流为主要热传递方式的是存在于电动机周围的热量,电机定子受到自身生热以及电机转子热传导的复合影响,其余转子的一部分热量将以热对流传递给主轴轴系和周围空气。轴承的滚动体与滚道之间的摩擦热主要通过两者的接触面进行热传导;而轴承外圈和跟其装配的主轴外壳之间的热传导路径主要是各个零件气隙间的热对流[9–10]。
根据传热机理,进行电主轴系统与流体的对流换热分析、电机定子与转子间隙气体的对流换热分析、定子与冷却水套的对流换热分析、前后支撑轴承与压缩空气的对流换热分析、电主轴与周围空气的对流换热分析等,这些是得到主轴系统内部温度场分布情况的必需条件。
对于数控加工仿真技术的发展与改革,国内许多学者已经进行了总结。关于仿真技术具体分类及其相关内容见表1。
表1 仿真技术的分类及主要内容
Table 1 Classification and main content of simulation technology
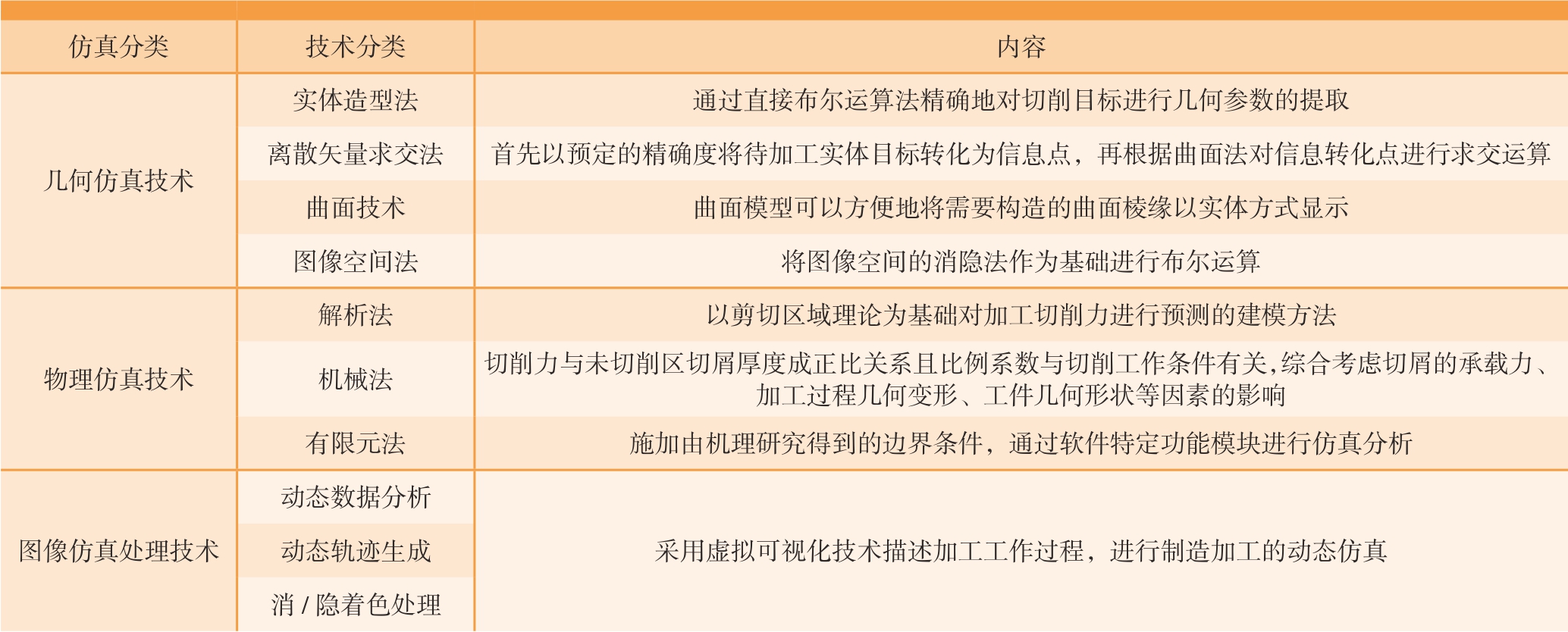
仿真分类 技术分类 内容几何仿真技术实体造型法 通过直接布尔运算法精确地对切削目标进行几何参数的提取离散矢量求交法 首先以预定的精确度将待加工实体目标转化为信息点,再根据曲面法对信息转化点进行求交运算曲面技术 曲面模型可以方便地将需要构造的曲面棱缘以实体方式显示图像空间法 将图像空间的消隐法作为基础进行布尔运算物理仿真技术解析法 以剪切区域理论为基础对加工切削力进行预测的建模方法机械法 切削力与未切削区切屑厚度成正比关系且比例系数与切削工作条件有关,综合考虑切屑的承载力、加工过程几何变形、工件几何形状等因素的影响有限元法 施加由机理研究得到的边界条件,通过软件特定功能模块进行仿真分析图像仿真处理技术动态数据分析采用虚拟可视化技术描述加工工作过程,进行制造加工的动态仿真动态轨迹生成消/隐着色处理
1.2 热试验法的研究
热试验法是在数字分析法获取的电主轴内部温度场分布情况的基础上,在主轴外壳上合理设置附加传感器的试验仪器,直接读取到电主轴温度及热位移数据。由此方法测量的试验结果可以与上文数字仿真法的分析结果进行比较,根据两种方法的优势达到各自优化的目的。电主轴数据检测主要采集主轴温度和热位移两个物理量。
对电主轴进行温度数据的采集主要有两种方法。第1种方法是通过选用热电偶、铂热电阻等基础元件连接相应的数据采集卡及软件进行数据的获取。20世纪末,国外学者Attia等[11]就使用热电偶测量了电主轴外壳温度的诸多影响因素。近年,戴野等[12]自主设计了一款C01型变压预紧电主轴,其变压预紧结构见图2,之后将PT100温度传感器和32路模块采集器配套使用进行了电主轴表面温度数据的采集,且他们设计的C01型电主轴在生产制造阶段就在主轴中安装了PT1000温度传感器,所以主轴内部前后轴承的温度也可以通过高精度数字监视器监测得到。第2种方法通过红外热成像仪拍摄热成像图片并使用先进的图像温度提取处理算法,获得对应位置的温度数据。传统红外成像仪的工作原理见图3。清华大学罗勇等[13]采用红外热成像仪结合相关分析算法获得了机床主轴温度数据并输入到线性回归模型中,取得了良好的效果。
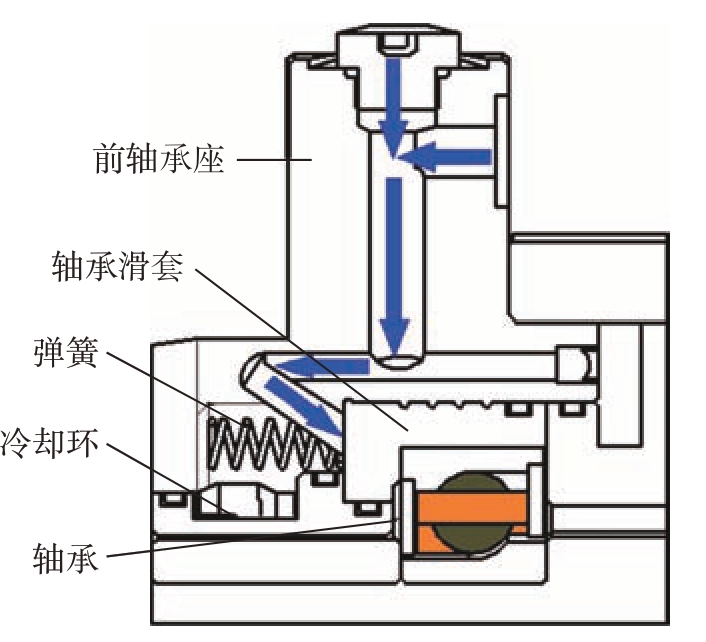
图2 电主轴变压预紧结构图[12]
Fig.2 Variable pressure preload structure drawing of motorized spindle[12]

图3 红外成像仪工作原理图
Fig.3 Working principle diagram of infrared imager
根据检测的原理来讲,热位移检测法主要有两种,分别是直接检测法和间接检测法。采用位移、激光传感器或电子水准仪设备,对相关数据进行测量的方法称为直接检测法,其优点为简单、便利等,但电子水准仪不能测量绕着重力方向的转动误差,直接测量常用于测量中小型机床,在大型机床的测量中应用较少[14–15]。由于电主轴系统具有难以描述的传热特性,通常研究人员使用三点检测法、五点检测法等方法进行主轴热位移的检测。其中,将在数控加工中心机床坐标系的3个轴线方向分别安装位移传感器的同时由计算机数据处理中心提取、显示工作过程中主轴在3个轴线方向的热位移大小的方法称为三点检测法。Sarhan[16]由某加工中心机床坐标系3个轴线方向上的电涡流位移数据传感器测得了主轴的多自由度热位移数据。李宝伟[17]搭建了数据检测试验平台,见图4,使用LK–H020光点式高精度CMOS激光位移传感器结合DH5922–1多通道数据采集仪及LK–Navigator2计算机软件对电主轴位移数据进行检测及保存。2007年,使用五点检测法测量机床热误差的方法、设备、注意事项等出现在国际标准化组织最新颁布的ISO 230—3的内容中的同时,国内学者根据国外之前的研究经验,积极进行了多点检测方法的使用。同年,新疆大学满蛟[18]和西安交通大学Yang[19]等通过五点检测法对机床主轴进行了测量,获取了主轴在3个轴线方向上的热漂移以及X、Y方向的旋转误差。常添渊等[20]使用电涡流传感器和标准芯棒测量了主轴3个方向上的热变形,包括芯棒前端和后端水平方向的形变值、芯棒前端和后端竖直方向的形变值以及芯棒前端轴向形变值。利用此方法采集的数据进行试验发现,模型热误差补偿能力高达98.4%。

图4 电主轴位移数据检测平台[17]
Fig.4 Displacement data detection platform of motorized spindle[17]
与直接检测法不同,使用球杆仪等为代表的需要从初步测量得到的综合误差中提取热位移数据的方法称为间接检测法。早在1982年,美国学者Bryan通过球杆仪测量了主轴的运动轨迹,提出了对比分析标准圆形轨迹和测量所得的主轴运动,观察两者形状差异,从而评估主轴产生的热位移误差大小的测量方法。在此基础上,国内外学者陆续开展了对球杆仪应用的研究。Srinivasa等[21]使用球杆仪检测机床主轴的运动误差,通过对主轴进行连续三边检测,得到了主轴两个方向的热位移数据。项四通等[22]通过球杆仪切向、径向、轴向大的测量模式,低成本、高精度地给出了20项综合误差的辨识解析解。西北工业大学的马锡琪教授[23]发明了双球杆测量仪,详细介绍了双球杆测量仪的结构及测量系统的组成,为我国误差检测技术提供了新的方法。虞敏等[24]提出了一种利用球杆仪高效地测量、分离及提取几何误差和热误差的方法,成功提取出主轴5项高精度热误差元素。
目前,国内外专家和学者大多采用直接检测法进行电主轴温度的检测,且需要对电主轴进行多点的温度检测才能描述主轴的发热情况。对于主轴热位移的测量多使用电涡流式、电容式和激光式等可直接进行测量的位移传感器,仅有少部分有高精度测量需求的工作才使用间接测量的方法。同时间接测量法为了获取多方向、多位置的误差需要多次更换安装位置参数,且自身存在不可避免的安装误差,一般只能用在数控机床等具有运动控制装置的设备上。
2 电主轴温度测点优化技术的研究
通过上文对电主轴数据检测技术的研究可知,一般对电主轴系统进行数据采集需要设置较多的测温点才能全面描述主轴系统的发热情况,且每一个测温点都会带有一定的误差。这些数据点虽然可以全方面地概括电主轴系统各个部分的发热情况,但过多的测量数据会造成电主轴热误差模型输入数据的冗余性,降低模型计算速度的同时也会降低模型的拟合效果和准确度。所以,电主轴温度测点的优化是必须进行的工作。通过减少相关度高以及共线性明显的数据,获得最优质的一部分数据,达到提高热误差补偿效果的作用。国内外学者对此做出了大量的研究。
20世纪末,Veldhuis[25]利用相关系数法将主轴的23个测温点去除了9个,达到了一定的温度测点优化效果,且所建立的热误差模型精度并没有因测温点减少而降低,这为电主轴温度测点优化技术的研究打下了基础。
21世纪初,各国学者对电主轴温度测点优化技术开展了广泛的研究。Lee等[26]首先提出了使用独立成分分析的方法在电主轴温度数据中进行热源的提取,然后使用OBS(Optimal brain surgeon)算法对特征不明显的温度变量进行简化处理,最后利用此方法进行实际补偿试验,证明了该方法可补偿微米级的热误差。Wang等[27]摒弃了现有的建模方法,使用隐性变量建模方法确定了最佳温度敏感点,最后通过试验验证了此方法的可行性。直接判据法和间接分组法都是合成的灰色关联度模型,Yan等[28]在结合了两种方法的基础上建立了电主轴多元回归分析模型,同时给出了4个温度传感器的最优组合方式。厦门大学的朱睿等[29]以机械结构热变形原理和热环境下机床主轴模态变化原则为理论基础通过最优分割法选取温度敏感点,将初始的16个温度测点淘汰掉13个并由试验结果证明了温度测点优化的必要性。Ouafi等[30]通过田口正交表设计试验并计算贡献度值,将主轴的16个温度变量减少到4个,且验证得到主轴的建模精度提高了大约5%。王秀山等[31]结合小波压缩技术和遗传算法最终获取了4个电主轴最优敏感点热源的位置。王续林等[32]采用粒子群优化算法优化的K均值聚类算法对温度测点进行了优化。清华大学的李逢春等[33]分别在稳健回归热误差模型和人工神经网络模型中提出了选择温度传感器的方法,通过分别使用基于相关系数分析的模糊C均值 (FCM)聚类算法,将传感器数量减少到原来的1/6,很大程度上达到了降低数据冗余性的效果。苗恩铭等[34]考虑了温度敏感点动态特性对结果造成的影响,采用主回归分析的方法对温度测点进行优化,结果表明使用主回归分析优化后的温度数据点建立的模型鲁棒性更好。Fan等[35]采用逐步回归分析方法对电主轴进行温度测点优化,最终确定5个最优温度变量,消除了温度变量的冗余性。Li等[36]基于传统逆导热理论和有限元仿真分析的结果,研究了一种平均冲击值的新方法来选择主轴系统中的热敏感点,该方法从13个温度点中提取出4个主要的热敏感点,在基于热敏感点在内的多变量热误差建模结果中表明热敏感点的选择结果效果较好。华中科技大学的张捷等[37]结合模糊聚类法和灰色关联度分析方法对测温点进行了优化,考虑了温度变量之间的复共线性和测温点温度与热误差数据之间的相关性,使主轴测温点数量从8个减至3个,所建立的预测模型可决系数更大,预测残差更小。上海交通大学刘璞凌等[38]探究了热误差对工件尺寸及加工能力指数Cpk的影响规律,提出了一种基于Cpk指数的热敏感点选择方法,利用测温点数据与工件内径尺寸数据构建了预测模型D(T),其中热敏感点的选择流程如图5所示,此方法成功选出了3个敏感点,为温度测点优化技术提供了一个新方法。
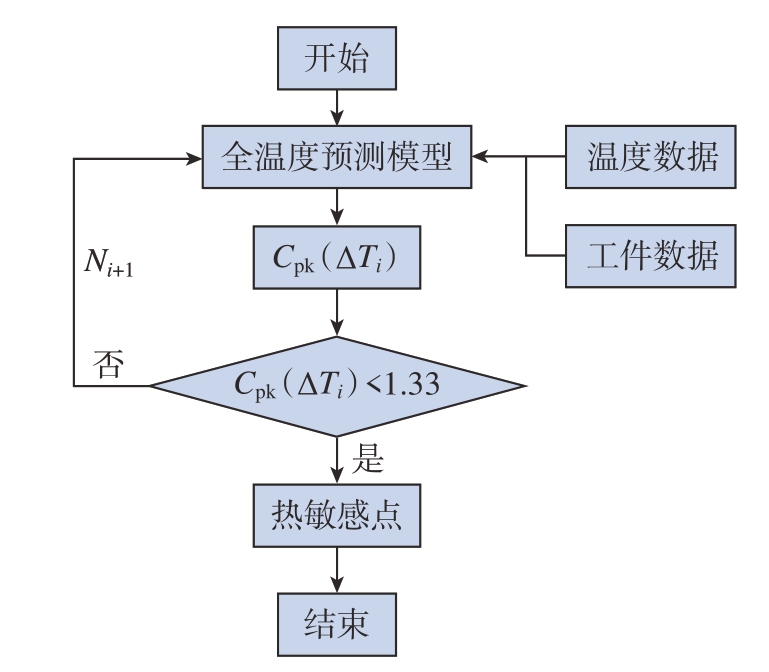
图5 基于Cpk指数的热敏感点选择流程示意图[38]
Fig.5 Schematic diagram of thermal sensitive point selection process based on Cpk index[38]
综上所述,国际上关于电主轴温度测点的优化方法已经发展得较为成熟。目前的条件,可以根据不同应用条件选取不同的优化方法,对需要摒弃的温度点进行数据处理,提取其中较有价值的部分进行保留,达到较好的优化结果。
3 电主轴热误差建模技术的研究
建立电主轴热误差预测模型是热误差补偿中最为关键的一步,此模型的准确度和鲁棒性决定了热误差补偿的最终效果。经过几十年的发展,国内外的研究人员已经在电主轴热误差建模领域取得了丰硕的成果,主要可分为理论热误差建模方法和经验热误差建模方法。
理论热误差建模方法主要是指通过对热量、温度、位移之间关系的探究建立相应的约束方程,从而获取主轴温度场和位移场,按照所建立模型的离散度不同,可分为集中质量法和有限元法。其中,集中质量法需要将零部件简化为由热阻进行连接的质量点,并建立能量守恒方程;有限元法则对物理模型进行离散的网格化划分,进行混合单元建模分析。在主轴热变形过程中,其温度场与结构场会互相影响,使温度场的边界条件发生变化,此类方法的求解过程相比于经验模型更加复杂,一般需要循环迭代,且存在不收敛的情况,很难对电主轴复杂的内部传热特性进行处理,所以其建立的热误差预测模型的误差较大,发展也相对较慢[39]。
经验热误差建模法根据实际测得的试验数据,考虑输入数据与输出数据间的数学关系,建立热误差预测模型,一般具有较高的预测精度,包括最小二乘法、回归分析模型、灰色模型、神经网络模型、支持向量机模型等[40–42]。
最小二乘法原理相对比较简单,由仿真分析得到电主轴温度场分布情况,便可确定试验数据的最佳拟合线,是热误差建模中应用最早的方法之一。由于这种方法建立的热误差模型预测效果较差,通常与其他方法配合使用。Tan等[43]以某机床主轴为研究对象,采用最小二乘支持向量机 (LS–SVM)的混合模型对主轴进行建模,对比传统的灰色模型 (GM)和多元线性回归(MLR)模型,LS–SVM模型的预测精度比GM模型和MLR模型分别提高了74.6%和54.3%。
回归分析由于本身的特型比最小二乘法更适合用于复杂的电主轴系统热误差的建模。Han等[44]对某机床主轴的温度变量和热误差变量进行了稳健回归分析,在验证试验中满足了补偿要求。兰州理工大学雷春丽等[45]以热位移作为自变量,基于多元自回归模型对电主轴热误差建模与预测进行了研究,图6为此方法的预测结果,由于自回归模型的阶数在主轴运行初始阶段较小,所以在此阶段并未获取到模型的预测值。随着运行时间增长,与热位移有关的解释变量累计增多,预测值才能拟合成预测曲线,所以此方法在电主轴早期热误差的预测中表现较差。西安交通大学杜宏洋等[46]从理论角度推导出一种主轴轴向热误差一阶自回归建模方法,克服了目前机床主轴热误差经验建模法普遍缺乏物理意义、建模精度和稳健性受热变形伪滞后效应影响较大等问题,此方法将主轴简化为一维杆件,指出自回归模型系数与主轴物理特性、自回归时间间隔、热源条件的关系,通过进行有限元仿真,并在海德曼T65车床上进行试验验证,发现此方法可以在特定转速下将主轴Z向热误差控制在10μm内,满足实际使用需求,证明了一阶自回归模型的有效性。
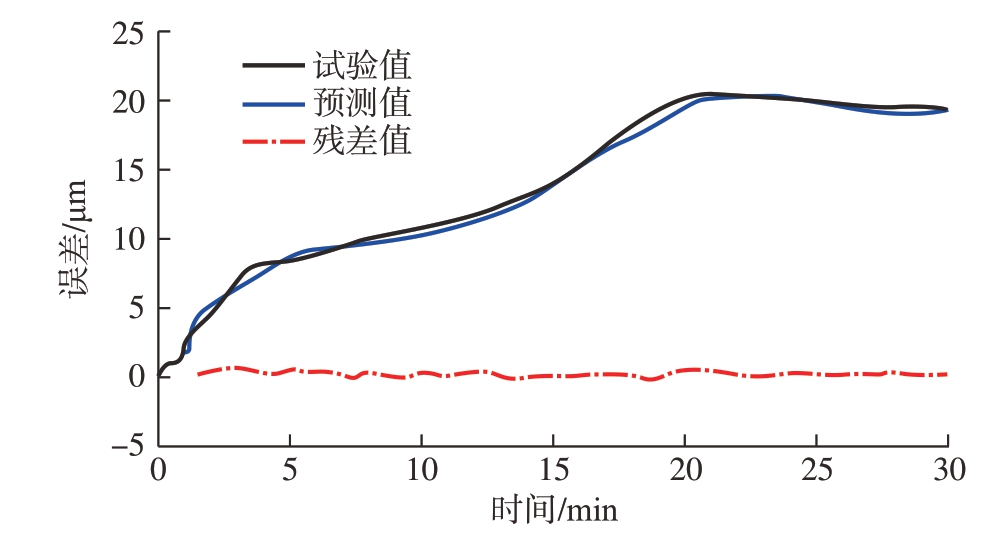
图6 电主轴热误差试验值与预测值对比[45]
Fig.6 Comparison of experimental and predicted thermal error of motorized spindle[45]
1982年,中国学者邓聚龙[47]创立了灰色系统理论,该理论可以通过生成、挖掘和提取有用的小样本信息实现对处理信息不完整、数据不准确的复杂系统进行分析。Wang等[48]的研究结果表明,利用灰色系统理论构建预测模型可以将主轴热误差残值降低到10%左右。余文利等[49]利用混沌粒子群对灰色系统模型进行优化,且基于混沌粒子群的灰色系统模型 (GM–ICPSO)表现出优于人工神经网络模型的数据处理能力,对机床主轴热位移预测问题的处理可以满足实际需求,为高速电主轴热误差建模提供了一种新的方法。
与回归模型和灰色系统理论原理不同,神经网络由多层结构组成,层与层之间通过节点相互连接,应用于复杂变量之间关系的经验建模。因此,为了有效降低建模分析的困难性,在模型的选择上,可以采用具有多个输出层的神经网络来处理电主轴多个方向存在的热误差。早在20世纪末Chen[50]就尝试使用人工神经网络(Artificial neural network)方法对机床热误差建模进行了研究,但受限于当时计算机的计算能力,该模型的预测精度较低。BP神经网络模型作为使用最为广泛的神经网络模型,虽然可以对主轴热误差进行映射和预测,但因其不好确定的阈值及权值,收敛速度较慢,预测效果不是很理想,神经元数目、阈值和权值的大小这3个变量当中一个变量达到峰值时,其他两者通常不能都达到峰值,这就是BP神经网络模型的不足之处,RBF径向基神经网络的基本功能就可以解决掉BP神经网络峰值不同步的问题[51–54]。上海交通大学杜正春等[55]剖析了传统BP神经网络模型的缺陷,将理论与实践结合,利用径向基函数的理论建立了基于RBF神经网络的数控机床热误差预测模型,通过对比RBF神经网络和最小二乘线性模型预测结果的评价指标发现RBF神经网络具有更好的拟合精度及补偿效果。天津大学崔良玉[56]首先通过小波转换方法对电主轴温度数据和热位移数据进行了降噪处理,降低了试验数据的误差,并分别对多元回归分析方法、BP神经网络方法和RBF神经网络方法建立的电主轴热误差模型进行了对比分析,验证了RBF神经网络在电主轴热误差建模领域的优越性。
基于以上的研究,戴野等[57]通过自适应神经模糊推理系统 (ANFIS)进行了电主轴热误差建模,具体建模流程见图7,并将9000r/min转速下ANFIS与传统的人工神经网络模型预测精度进行对比,结果表明ANFIS作为一种新型的混合智能系统模型是预测高速电主轴热误差的良好模型选择。谭峰等[58]提出了一种基于LSTM循环神经网络的热误差建模方法,此模型的优势在于可以将各个时刻的温度数据进行总结分析并用于热误差补偿,通过试验对不同工况下的不同预测模型进行对比分析,发现此模型的预测精度较其他模型提高了52%,为提高数控机床精度提供了一种可靠的方法。
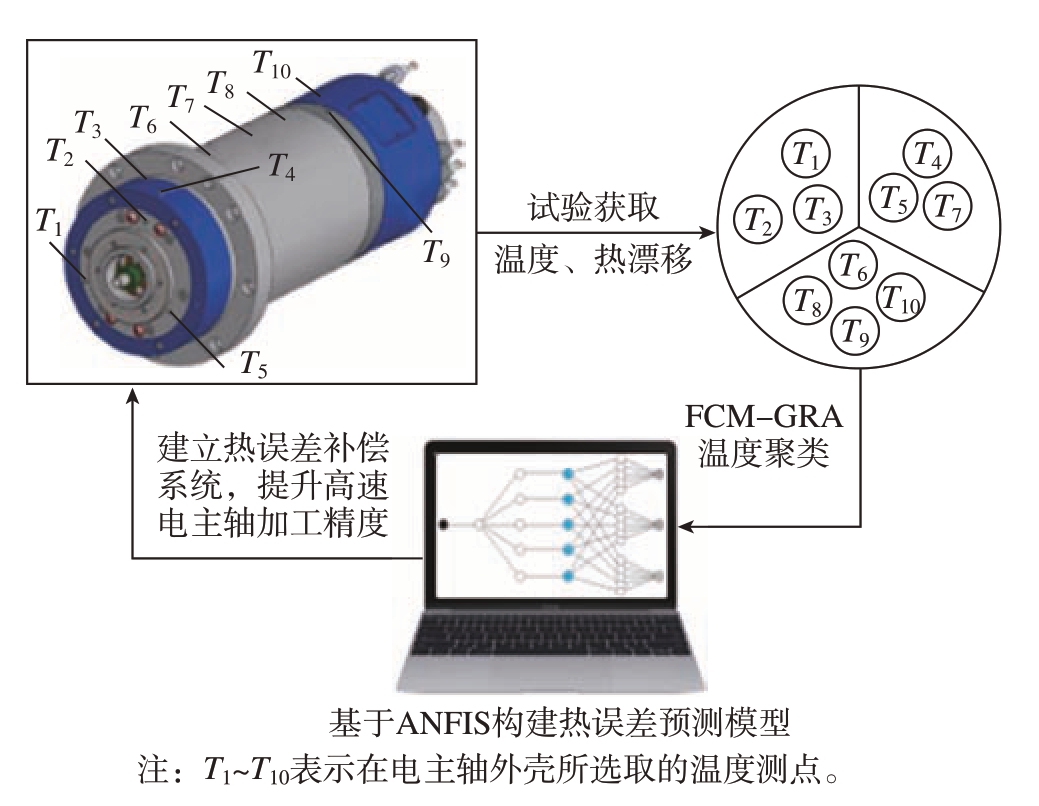
图7 热误差建模流程图[57]
Fig.7 Flow diagram of thermal error modeling[57]
近年来还有一种受关注度很高的机器学习方法,即支持向量机 (SVM)建模方法,SVM建模方法以SRM原理为基础,考虑目标的结构特性,使结构风险误差的上限值降低,从而达到解决问题的目的[59]。Miao等[60]通过多组试验测得主轴在不同工况下的温度以及与之相对热误差大小,发现在建模数据的总量很小的情况下,MRA模型与多元回归模型的预测结果精度低,鲁棒性差。相比之下,SVM模型具有预测精度不会因工况条件的改变而降低的特性。李高强等[61]提出一种基于遗传算法 (GA)的LS–SVM热误差建模方法,并与未经过优化的LS–SVM模型和经典BP神经网络模型进行补偿结果对比分析,发现此模型通过遗传算法的优化选择具有较低的补偿残差且拟合效果得到了很大程度的提升。陈卓等[62]考虑了季节因素对机床热误差的影响,将主轴进行了冬夏两季内外关键测点的划分并把温度数据输入到基于神经网络(SOM)及SVM的模型中,成功地使主轴拟合残差控制在5μm内,验证了此模型在不同季节的复杂工况下热误差建模和预测的适用性,在热误差建模季节性预分类领域中踏出了第一步。
目前,随着热误差建模方法的不断完善,一些功能更为强大的热误差补偿方法层出不穷。西安交通大学的颜宗卓等[63]提出了一种电主轴系统热特性的卷积建模方法,通过热源测点温度变化量与响应函数的卷积来近似推算各部分温度,将热源温度代入优化后的卷积模型获得热误差预测值,与线性拟合结果相比,电主轴在运行前50min和前100min的拟合精度分别提升了23.03%和26.4%,证明卷积模型在热特性较为复杂的开机阶段和升降温拐点处具有更加强大的处理能力,为电主轴热误差补偿提供了一种新的解决思路。赵家黎等[64]将统计模型的回归系数当作状态向量,统计模型当作观测方程,以线性最小方差估计为原理,提出了一种基于卡尔曼滤波的机床主轴热误差建模新方法,试验表明此方法构建的热误差预测模型相比于最小二乘法 (LS)和LS–SVM的补偿效果分别提升了10.5%和1.8%,建模时间分别减少了0.9%和6.8%。Xiang等[65]克服了传统模型的主轴热误差预测 (MBP)方法存在的3个严重矛盾,即未建模的动力学与鲁棒性、模型精度与模型复杂度、部分线性化与整体复杂度,并将一种新的数据驱动预测 (DDP)方法应用到了主轴热误差动态线性化建模中。在该模型中,利用伪偏导数使模型具有动态的自适应特性,选取前轴承上的4个关键温度点作为DDP模型的输入,不需要物理机理的信息,进行了不同速度谱和初始温度下与MBP的3次对比试验,充分地验证了DDP模型在精度和鲁棒性方面明显优于传统的MBP方法。
4 电主轴热误差补偿方法的研究
电主轴热误差补偿方法即在尽量不改变机床本身结构和工作条件的情况下,人为地引入热误差模型的预测值以修正主轴的工作位置,从而抵消因主轴热变形引起的热误差,使机床综合加工误差大大减小,这种方法建立在大量测试数据和快速检测、反馈和执行系统基础上[66]。
早期的电主轴热误差补偿方法研究主要集中于修改CAM模型、CAD模型以及NC数据等方面,这些方法具有相同的特点,即需要在加工前就将主轴热误差值加以修改,无法解决机床在工作时需要面临的突发状况[67]。自20世纪30年代发现机床热变形影响定位精度,进而造成加工误差后,人们开始有针对性地对机床热变形进行被动控制,进而发展到进行热误差补偿的主动控制技术和方法[68]。
基于热误差补偿原理,常用的主轴热误差补偿方法主要可分为反馈中断补偿法和原点偏移补偿法。原点偏移法由美国密西根大学的吴贤铭制造研究中心 (S.M.Wu,Manufacturing Research Center)首先提出,其通过I/O接口将补偿量输入到CNC控制器中,利用数控系统的外置机械坐标系原点平移功能实现补偿,这种方法不会对加工编程及操作造成任何影响,具有更好的实时性,对误差模型的优化也更加灵活,其原理如图8所示。杨建国[69]利用所建立的热误差数学模型将检测获取的实时主轴位置坐标及其对应的温度数据进行处理得到所需的误差补偿值,CNC控制器根据补偿信号平移控制系统的参考原点并加到伺服环的控制信号中以实现热误差实时补偿,从而使机床误差降低了60%以上。任永强等[70]基于FANUC数控系统,通过修改其中的PLC程序,将主轴的热误差量读入数控系统,利用外部主轴坐标系的偏移实现热误差的实时补偿。刘明敏[71]在三轴立式数控加工中心Leaderway V–450上完成了主轴温度敏感点的筛选、模型的建立及热误差的补偿,通过补偿卡将多元回归分析模型的补偿值传送至控制器中,发送控制指令后对机床原点进行平移,消除了由温度引起的热变形误差。童文利[72]绘制了主轴温升与热变形的误差曲线,再根据误差曲线编制数控系统可执行的PMC热补偿程序,利用FANUC机械原点偏移功能的实时生效特性,纠正刀具与工件的相对位置偏差,有效减小主轴热变形引起的误差。林志杭等[73]提出了主轴热误差的几何与热综合误差数学模型,并使用西门子840D数控系统内置的补偿接口将误差补偿模型嵌入PLC中,并通过改变运动轴位置的方式实现误差实时补偿,补偿后主轴x、y、z向的热误差分别减小了63.32%、55.53%和66.02%。原点偏移补偿技术综合了电子硬件与软件技术的优点,充分发挥了机床CNC控制器的I/O接口补偿作用,保证了机床坐标值和执行程序不会受到影响,但需要改变CNC控制器中的PLC单元,以便在CNC端可以接收补偿值。
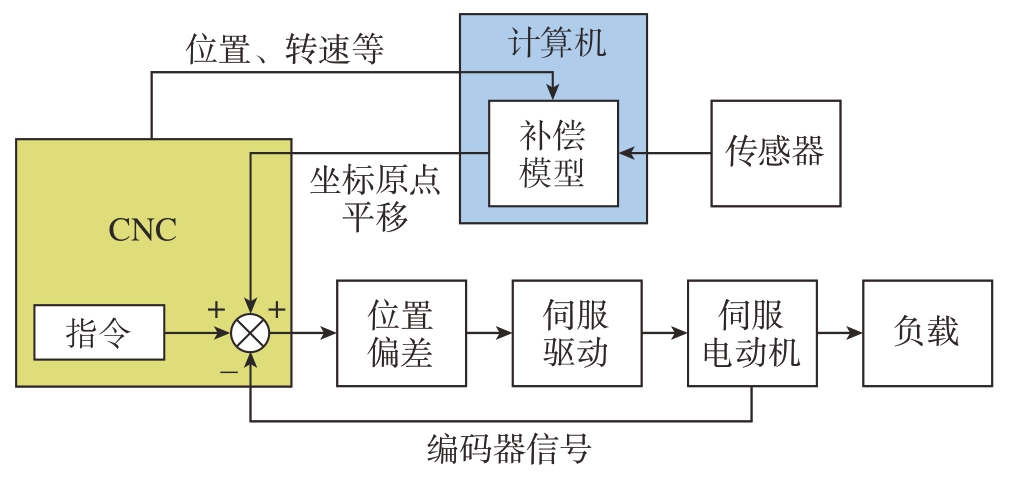
图8 原点偏移法补偿原理图
Fig.8 Compensation principle diagram of origin migration method
反馈中断法同时进行编码器反馈信号的获取和主轴热误差值的计算,伺服系统就可根据热误差信号与编码器信号的差值实时调节系统坐标的位置,其原理如图9所示。高玉平[74]以反馈中断补偿原理为依据,开发了以PLC单片机为控制核心的补偿电路,深度剖析了反馈信号的特点,掌握了准确控制补偿的时机,实现了较好的热误差在线补偿效果。合肥工业大学计昌柱[75]开发设计了一套主轴热误差补偿卡,分别以多元线性回归模型和分布滞后模型进行补偿,均有效地将热误差控制在10μm以内,满足了实际使用要求。南京航空航天大学柏衡[76]对反馈截断法的最佳应用场合进行了说明分析,设计了基于反馈截断法的热误差补偿系统并对软硬件各模块进行了测试验证。湖南大学吕洪杰[77]应用自研制的补偿装置及FANUC 31i–B数控系统的直线度补偿功能对TH6926B重型数控落地铣镗加工中心的镗轴的移动误差和热变形进行了补偿,使镗轴产生的最大热误差从0.62mm降至0.1mm。武汉理工大学胡建民[78]反馈中断法的最小补偿间隔小于原点偏移法,具有更高的实时性,因此基于FANUC数控系统设计了一套基于反馈中断法的嵌入式补偿系统,并对其进行了4种定向运动补偿测试。哈尔滨工业大学的崔岗卫[79]改进了西门子840D数控系统扩展的手轮偏置功能,将模型预测值附加到机床进给轴上,实现了热误差补偿功能。反馈中断补偿法属于电子硬件补偿法,无需改变CNC控制软件,适用于任何机床,但需要特殊的电子装置将相位信号小心地添加到伺服系统中,以免补偿信号与机床自身的反馈信号相干涉。该技术需要特定的外部装置将相位信号添加到伺服环中,且补偿信号与机床本身的反馈信号容易发生干涉,实施难度较大。
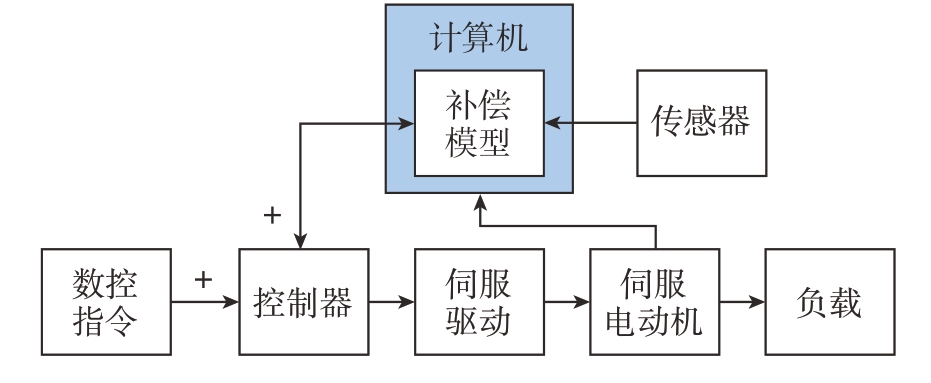
图9 反馈中断法补偿原理图
Fig.9 Schematic diagram of feedback interruption compensation
5 结论
本文通过总结国内外专家和学者的研究成果,主要从电主轴热误差补偿技术的3个关键阶段开展介绍,其中每一个阶段的工作效果都会对最终补偿结果产生重大的影响。目前,我国的电主轴热误差补偿技术与国外仍有很大差距,为了满足实际应用的需求,对高速电主轴热误差控制技术提出更高的要求,我国电主轴热误差补偿技术未来的发展方向主要有以下5方面:
(1)在数据采集技术方面,现有的方法一般是在电主轴外壳表面附加传感器从而获取主轴的相关数据,此方法测量的数据具有一定的误差,应该在满足主轴刚度要求的条件下,附加内部传感器,保证采集到的数据与真实数据具有较高的相近度;
(2)在电主轴温度测点优化技术方面,对于现有使用的聚类优化算法来讲,需要建立统一标准的聚类数目、提升同一算法在不同工况条件下的泛化性;
(3)在电主轴热误差建模技术方面,应该深度剖析电主轴温度数据和位移数据的时序特点,使用性质匹配融洽的深度学习等新兴算法代替传统算法建立满足不同工况条件、可以保证长期预测效果的混合模型;
(4)考虑将主轴理论建模过程中进行机理分析所得到的某些规律作为理论基础,指导经验模型的选型及参数辨识过程,对经验热误差模型进行补充和修正,结合两种建模方法的优点,从而提高热误差模型的预测精度及稳定性;
(5)目前,主轴热误差补偿方法采用外置补偿器进行热误差的补偿,对于热误差信息的获取与补偿反馈存在一定的迟滞性,应对如何把热误差的补偿模块嵌入到数控系统的内核任务调度中实现直接补偿进行研究。
[1] 齐男.数控机床电主轴的发展研究[J].山东工业技术,2018(9): 45.
QI Nan.Research on the development of CNC machine tool spindle[J].Shandong Industrial Technology, 2018(9): 45.
[2] 杨传启.数控机床电主轴系统结构特性分析[J].现代制造技术与装备, 2020, 56(8): 158–159.
YANG Chuanqi.Analysis on the structural characteristics of motorized spindle system of CNC machine tools[J].Modern Manufacturing Technology and Equipment, 2020, 56(8): 158–159.
[3] 郑良钢, 陈铮, 周志科.数控机床高速电主轴技术要点分析[J].中国设备工程, 2021(9): 203–204.
ZHENG Lianggang, CHEN Zheng, ZHOU Zhike.Analysis of the key points of high-speed motorized spindle technology for CNC machine tools [J].China Plant Engineering, 2021(9): 203–204.
[4] BLASER P, PAVLIČEK F, MORI K, et al.Adaptive learning control for thermal error compensation of 5-axis machine tools[J].Journal of Manufacturing Systems, 2017, 44: 302–309.
[5] BERNSTEIN P, NOUDEM J.Superconducting magnetic levitation: Principle, materials, physics and models[J].Superconductor Science and Technology, 2020, 33(3): 033001.
[6] 郭力, 张华.高效精密磨床动静压主轴回转精度的测试研究[J].航空制造技术, 2020, 63(5): 20–24.
GUO Li, ZHANG Hua.Test research on rotation accuracy of hybrid spindle of high-efficiency precision grinding machine[J].Aeronautical Manufacturing Technology, 2020, 63(5): 20–24.
[7] 刘阔, 韩伟, 王永青, 等.数控机床进给轴热误差补偿技术研究综述[J].机械工程学报, 2021, 57(3): 156–173.
LIU Kuo, HAN Wei, WANG Yongqing, et al.Review on thermal error compensation for feed axes of CNC machine tools[J].Journal of Mechanical Engineering, 2021, 57(3): 156–173.
[8] 刘宏伟, 杨锐, 向华, 等.数控机床空心丝杠进给轴热误差补偿研究[J].组合机床与自动化加工技术, 2019(3): 124–125, 142.
LIU Hongwei, YANG Rui, XIANG Hua, et al.Research on thermal error compensation for the feed-axis of CNC machine tool hollow screw[J].Modular Machine Tool & Automatic Manufacturing Technique,2019(3): 124–125, 142.
[9] 朱振学, 杨林.电主轴热特性研究[J].机械工程与自动化,2020(4): 62–63.
ZHU Zhenxue, YANG Lin.Study on thermal characteristics of motorized spindle[J].Mechanical Engineering & Automation, 2020(4):62–63.
[10] DENKENA B, BERGMANN B, KLEMME H.Cooling of motor spindles—A review[J].The International Journal of Advanced Manufacturing Technology, 2020, 110(11–12): 3273–3294.
[11] ATTIA M H, FRASER S.A generalized modelling methodology for optimized real-time compensation of thermal deformation of machine tools and CMM structures[J].International Journal of Machine Tools and Manufacture, 1999, 39(6): 1001–1016.
[12] 戴野, 战士强, 王建辉, 等.基于键合图的变压预紧力电主轴热误差建模研究[J].仪器仪表学报, 2021, 42(5): 42–48.
DAI Ye, ZHAN Shiqiang, WANG Jianhui, et al.Thermal error modeling of motorized spindle under variable pressure preload based on the bonding graph method[J].Chinese Journal of Scientific Instrument,2021, 42(5): 42–48.
[13] 罗勇, 邵珠峰, 王立平, 等.NL201HA数控卧式车床X轴热误差建模及补偿[J].清华大学学报(自然科学版), 2021, 61(1):28–35.
LUO Yong, SHAO Zhufeng, WANG Liping, et al.X-axis thermal error modeling and compensation for an NL201HA CNC horizontal lathe[J].Journal of Tsinghua University (Science and Technology), 2021,61(1): 28–35.
[14] 王建臣, 林思琦, 沈雨欣, 等.数控机床主轴热误差测点优化及建模技术研究[J].航空制造技术, 2019, 62(6): 41–46, 59.
WANG Jianchen, LIN Siqi, SHEN Yuxin, et al.Measurement point optimization and modeling techniques of spindle thermal error for CNC machine tool[J].Aeronautical Manufacturing Technology, 2019, 62(6):41–46, 59.
[15] 项四通, 杜正春, 杨建国.数控机床几何与热误差测量和建模研究新进展[J].机械设计与研究, 2019, 35(6): 52–57.
XIANG Sitong, DU Zhengchun, YANG Jianguo.Recent advances in measurement and modeling of geometric and thermal error of CNC machine tools[J].Machine Design & Research, 2019, 35(6): 52–57.
[16] SARHAN A A D.Investigate the spindle errors motions from thermal change for high-precision CNC machining capability[J].The International Journal of Advanced Manufacturing Technology, 2014,70(5–8): 957–963.
[17] 李宝伟.高速电主轴热误差试验分析及预测模型的建立[D].哈尔滨: 哈尔滨理工大学, 2021.
LI Baowei.Experimental analysis on thermal error of high-speed electric spindle and establishment of prediction model[D].Harbin: Harbin University of Science and Technology, 2021.
[18] 满蛟, 王新, 穆塔里夫·阿赫迈德, 等.利用偏最小二乘回归法对主轴热误差数值建模的研究[J].组合机床与自动化加工技术,2005(11): 17–19.
MAN Jiao, WANG Xin, MUTELLIP Ahmat, et al.Numerical modeling research for thermal error for the spindle by partial leastsquares regression method[J].Modular Machine Tool & Automatic Manufacturing Technique, 2005(11): 17–19.
[19] YANG J, SHI H, FENG B, et al.Applying neural network based on fuzzy cluster pre-processing to thermal error modeling for coordinate boring machine[J].Procedia CIRP, 2014, 17: 698–703.
[20] 常添渊, 黄晓华.基于IA-PSO-BP模型的电主轴热误差预测方法[J].机械与电子, 2020, 38(10): 52–56.
CHANG Tianyuan, HUANG Xiaohua.A thermal error prediction method of electric spindle based on IA-PSO-BP model[J].Machinery &Electronics, 2020, 38(10): 52–56.
[21] SRINIVASA N, ZIEGERT J C, MIZE C D.Spindle thermal drift measurement using the laser ball bar[J].Precision Engineering,1996, 18(2–3): 118–128.
[22] 项四通, 杨建国, ALTINTAS Yusuf, 等.五轴数控机床空间误差测量、建模与补偿技术研究[J].机械工程学报, 2018, 54(4):108.
XIANG Sitong, YANG Jianguo, ALTINTAS Yusuf, et al.Research on spatial error measurement, modeling and compensation technology of five axis NC machine tool [J].Journal of Mechanical Engineering, 2018, 54(4):108.
[23] 马锡琪.数控机床运动误差的测试装置——双球规测量仪[J].计量与测试技术, 1996, 23(4): 3–5.
MA Xiqi.Testing device for motion error of NC machine tool—Double ball gauge measuring instrument [J].Metrlogy and Measurement Technique, 1996, 23(4): 3–5.
[24] 虞敏, 赵建华, 邱明勇, 等.基于球杆仪的主轴热误差检测及识别方法[J].机械制造, 2015, 53(11): 86–88, 92.
YU Min, ZHAO Jianhua, QIU Mingyong, et al.Spindle thermal error detection and identification method based on ball and club instrument [J].Machinery , 2015, 53(11): 86–88, 92.
[25] VELDHUIS S C, ELBESTAWI M A.A strategy for the compensation of errors in five-axis machining[J].CIRP Annals, 1995,44(1): 373–377.
[26] LEE D S, CHOI J Y, CHOI D H.ICA based thermal source extraction and thermal distortion compensation method for a machine tool[J].International Journal of Machine Tools and Manufacture, 2003,43(6): 589–597.
[27] WANG H, HUANG Q, YANG H.In-line statistical monitoring of machine tool thermal error through latent variable modeling[J].Journal of Manufacturing Systems, 2006, 25(4): 279–292.
[28] YAN J Y, YANG J G.Application of synthetic grey correlation theory on thermal point optimization for machine tool thermal error compensation[J].The International Journal of Advanced Manufacturing Technology, 2009, 43(11–12): 1124–1132.
[29] 朱睿, 朱永炉, 陈真, 等.基于最优分割和逐步回归方法的机床热误差建模方法研究[J].厦门大学学报(自然科学版), 2010,49(1): 52–56.
ZHU Rui, ZHU Yonglu, CHEN Zhen, et al.Optimal partition method& stepwise regression based thermal error modeling for a machine tool[J].Journal of Xiamen University (Natural Science), 2010, 49(1): 52–56.
[30] OUAFI A, GUILLOT M, BARKA N.An integrated modeling approach for ANN-based real-time thermal error compensation on a CNC turning center[J].Advanced Materials Research, 2013, 664: 907–915.
[31] 王秀山, 李智广, 陈静, 等.基于遗传算法的五轴机床最优敏感热源点优化[J].制造业自动化, 2015, 37(21): 93–95, 117.
WANG Xiushan, LI Zhiguang, CHEN Jing, et al.Optimal thermal sensitive point optimization of five axis machine tool based on genetic algorithm[J].Manufacturing Automation, 2015, 37(21): 93–95, 117.
[32] 王续林, 顾群英, 杨昌祥, 等.基于PSO聚类和ELM神经网络机床主轴热误差建模[J].组合机床与自动化加工技术, 2015(7):69–73.
WANG Xulin, GU Qunying, YANG Changxiang, et al.Modeling for machine tool thermal error based on PSO clustering algorithm and ELM model preprocessing neural network[J].Modular Machine Tool &Automatic Manufacturing Technique, 2015(7): 69–73.
[33] 李逢春, 王海同, 李铁民.重型数控机床热误差建模及预测方法的研究[J].机械工程学报, 2016, 52(11): 154–160.
LI Fengchun, WANG Haitong, LI Tiemin.Research on thermal error modeling and prediction of heavy CNC machine tools[J].Journal of Mechanical Engineering, 2016, 52(11): 154–160.
[34] 苗恩铭, 刘义, 高增汉, 等.数控机床温度敏感点变动性及其影响[J].中国机械工程, 2016, 27(3): 285–289, 322.
MIAO Enming, LIU Yi, GAO Zenghan, et al.Variability of temperature-sensitive points and its influences for CNC machine tools[J].China Mechanical Engineering, 2016, 27(3): 285–289, 322.
[35] FAN S, GUO Q J.Study on temperature measurement point optimization and thermal error modeling of NC machine tools[J].The Open Mechanical Engineering Journal, 2017, 11(1): 37–43.
[36] LI Y, ZHAO W H, WU W W, et al.Boundary conditions optimization of spindle thermal error analysis and thermal key points selection based on inverse heat conduction[J].The International Journal of Advanced Manufacturing Technology, 2017, 90(9–12): 2803–2812.
[37] 张捷, 李岳, 王书亭, 等.基于遗传RBF神经网络的高速电主轴热误差建模[J].华中科技大学学报(自然科学版), 2018, 46(7):73–77.
ZHANG Jie, LI Yue, WANG Shuting, et al.High-speed motorized spindle thermal error modeling based on genetic RBF neural network[J].Journal of Huazhong University of Science and Technology (Natural Science Edition), 2018, 46(7): 73–77.
[38] 刘璞凌, 杜正春, 冯晓冰, 等.基于工件尺寸的数控机床热误差建模与补偿[J].机械设计与研究, 2020, 36(5): 122–125, 131.
LIU Puling, DU Zhengchun, FENG Xiaobing, et al.Comprehensive thermal error modeling and compensation based on workpiece data for CNC machine tool[J].Machine Design & Research, 2020, 36(5): 122–125, 131.
[39] 王海同, 李铁民, 王立平, 等.机床热误差建模研究综述[J].机械工程学报, 2015, 51(9): 119–128.
WANG Haitong, LI Tiemin, WANG Liping, et al.Review on thermal error modeling of machine tools[J].Journal of Mechanical Engineering, 2015, 51(9): 119–128.
[40] 公维晶, 张丽秀, 李金鹏, 等.电主轴热变形预测模型的综述[J].机电产品开发与创新, 2016, 29(3): 125–128.
GONG Weijing, ZHANG Lixiu, LI Jinpeng, et al.Summary of prediction model for thermal deformation of motorized spindle[J].Development & Innovation of Machinery & Electrical Products, 2016,29(3): 125–128.
[41] 刘阔, 孙名佳, 吴玉亮, 等.无温度传感器的数控机床进给轴热误差补偿[J].机械工程学报, 2016, 52(15): 162–169.
LIU Kuo, SUN Mingjia, WU Yuliang, et al.Thermal error compensation without temperature sensors for CNC machine tools' feed drive system[J].Journal of Mechanical Engineering, 2016, 52(15): 162–169.
[42] 赵万芹, 刘昊栋, 施虎.机床热误差的检测与建模方法[J].科学技术与工程, 2021, 21(16): 6546–6555.
ZHAO Wanqin, LIU Haodong, SHI Hu.Detection and modeling for thermal error of machine tools[J].Science Technology and Engineering,2021, 21(16): 6546–6555.
[43] TAN F, YIN M, WANG L, et al.Spindle thermal error robust modeling using LASSO and LS–SVM[J].The International Journal of Advanced Manufacturing Technology, 2018, 94(5–8): 2861–2874.
[44] HAN J, WANG L P, CHENG N B, et al.Thermal error modeling of machine tool based on fuzzy C-means cluster analysis and minimal-resource allocating networks[J].The International Journal of Advanced Manufacturing Technology, 2012, 60(5–8): 463–472.
[45] 雷春丽, 芮执元.基于多元自回归模型的电主轴热误差建模与预测[J].机械科学与技术, 2012, 31(9): 1526–1529.
LEI Chunli, RUI Zhiyuan.Thermal error modeling and forecasting based on multivariate autoregressive model for motorized spindle[J].Mechanical Science and Technology for Aerospace Engineering, 2012,31(9): 1526–1529.
[46] 杜宏洋, 陶涛, 侯瑞生, 等.机床主轴轴向热误差一阶自回归建模方法[J].哈尔滨工业大学学报, 2021, 53(7): 60–67.
DU Hongyang, TAO Tao, HOU Ruisheng, et al.First-order autoregressive modeling method for axial thermal error of machine tool spindle[J].Journal of Harbin Institute of Technology, 2021, 53(7): 60–67.
[47] 邓聚龙.灰色系统基本方法[M].武汉: 华中工学院出版社,1987.
DENG Julong.Basic method of grey system [M].Wuhan: Huazhong Institute of Technology Press, 1987.
[48] WANG Y D, ZHANG G X, MOON K S, et al.Compensation for the thermal error of a multi-axis machining center[J].Journal of Materials Processing Technology, 1998, 75(1–3): 45–53.
[49] 余文利, 姚鑫骅.改进混沌粒子群优化的灰色系统模型在机床热误差建模中的应用[J].现代制造工程, 2018(6): 101–107, 22.
YU Wenli, YAO Xinhua.Application of improved chaotic particle swarm optimization grey system model to thermal error modeling of machine tools[J].Modern Manufacturing Engineering, 2018(6): 101–107, 22.
[50] CHEN J S.A study of thermally induced machine tool errors in real cutting conditions[J].International Journal of Machine Tools and Manufacture, 1996, 36(12): 1401–1411.
[51] 苏宇锋, 袁文信, 刘德平, 等.基于BP神经网络的电主轴热误差补偿模型[J].组合机床与自动化加工技术, 2013(1): 36–38, 41.
SU Yufeng, YUAN Wenxin, LIU Deping, et al.A thermal errors compensation model for high-speed motorized spindle based on BP neural network[J].Modular Machine Tool & Automatic Manufacturing Technique, 2013(1): 36–38, 41.
[52] 谢杰, 黄筱调, 方成刚, 等.MEA优化BP神经网络的电主轴热误差分析研究[J].组合机床与自动化加工技术, 2017(6): 1–4.
XIE Jie, HUANG Xiaodiao, FANG Chenggang, et al.Thermal error analysis based on MEA optimized BP neural network for motorized spindle[J].Modular Machine Tool & Automatic Manufacturing Technique, 2017(6): 1–4.
[53] 万正海, 李锻能, 潘岳健.GMDH神经网络在电主轴热位移建模中的应用[J].组合机床与自动化加工技术, 2019(6): 9–11, 16.
WAN Zhenghai, LI Duanneng, PAN Yuejian.Application of GMDH neural network in thermal displacement modeling of moterized spindle[J].Modular Machine Tool & Automatic Manufacturing Technique, 2019(6):9–11, 16.
[54] 魏文强.高速电主轴温度测点优化及热误差建模研究[D].哈尔滨: 哈尔滨理工大学, 2020.
WEI Wenqiang.Research on temperature measuring point optimization and thermal error modeling of high speed motorized spindle[D].Harbin: Harbin University of Science and Technology, 2020.
[55] 杜正春, 杨建国, 窦小龙, 等.基于RBF神经网络的数控车床热误差建模[J].上海交通大学学报, 2003, 37(1): 26–29.
DU Zhengchun, YANG Jianguo, DOU Xiaolong, et al.Thermal error modeling of CNC turning center using radial basis function neural network[J].Journal of Shanghai Jiao Tong University, 2003, 37(1): 26–29.
[56] 崔良玉.高速电主轴热误差测试与建模方法[D].天津: 天津大学, 2010.
CUI Liangyu.Thermal error measurement and modeling of highspeed motorized spindle[D].Tianjin: Tianjin University, 2010.
[57] 戴野, 尹相茗, 魏文强, 等.基于ANFIS的高速电主轴热误差建模研究[J].仪器仪表学报, 2020, 41(6): 50–58.
DAI Ye, YIN Xiangming, WEI Wenqiang, et al.Thermal error modeling of high-speed motorized spindle based on ANFIS[J].Chinese Journal of Scientific Instrument, 2020, 41(6): 50-58.
[58] 谭峰, 李成南, 萧红, 等.基于LSTM循环神经网络的数控机床热误差预测方法[J].仪器仪表学报, 2020, 41(9): 79–87.
TAN Feng, LI Chengnan, XIAO Hong, et al.A thermal error prediction method for CNC machine tool based on LSTM recurrent neural network[J].Chinese Journal of Scientific Instrument, 2020, 41(9): 79-87.
[59] 王一鹏, 陈学振, 李连玉.基于小波包混合特征和支持向量机的机床主轴轴承故障诊断研究[J].电子测量与仪器学报, 2021,35(2): 59–64.
WANG Yipeng, CHEN Xuezhen, LI Lianyu.Research on fault diagnosis of machine spindle bearing based on wavelet packet mixing feature and SVM[J].Journal of Electronic Measurement and Instrumentation, 2021, 35(2): 59–64.
[60] MIAO E M, GONG Y Y, NIU P C, et al.Robustness of thermal error compensation modeling models of CNC machine tools[J].The International Journal of Advanced Manufacturing Technology, 2013, 69(9–12): 2593–2603.
[61] 李高强, 张宇, 李鸣.基于GA-LSSVM的数控机床热误差建模方法研究[J].机床与液压, 2021, 49(2): 26–30.
LI Gaoqiang, ZHANG Yu, LI Ming.Study on thermal error modeling method for CNC machine tool based on GA-LSSVM[J].Machine Tool & Hydraulics, 2021, 49(2): 26–30.
[62] 陈卓, 李自汉, 杨建国, 等.基于SOM神经网络聚类以及支持向量机的数控机床热误差建模方法的研究[J].组合机床与自动化加工技术, 2016(11): 68–72.
CHEN Zhuo, LI Zihan, YANG Jianguo, et al.Modeling for thermal error of machine tool based on SOM neural network and support vector regression machine[J].Modular Machine Tool & Automatic Manufacturing Technique, 2016(11): 68–72.
[63] 颜宗卓, 陶涛, 侯瑞生, 等.机床电主轴热特性卷积建模研究[J].西安交通大学学报, 2019, 53(6): 1–8.
YAN Zongzhuo, TAO Tao, HOU Ruisheng, et al.Convolution modeling for thermal properties of motorized spindle in machine tools[J].Journal of Xi’an Jiaotong University, 2019, 53(6): 1–8.
[64] 赵家黎, 黄利康, 李桥林.基于卡尔曼滤波的数控机床主轴热误差建模研究[J].现代制造工程, 2018(7): 23–26, 64.
ZHAO Jiali, HUANG Likang, LI Qiaolin.Modeling research on machine tool spindle thermal error based on Kalman filter method[J].Modern Manufacturing Engineering, 2018(7): 23–26, 64.
[65] XIANG S T, YAO X D, DU Z C, et al.Dynamic linearization modeling approach for spindle thermal errors of machine tools[J].Mechatronics, 2018, 53: 215–228.
[66] 刘容.车削中心电主轴系统热误差控制和补偿技术研究[D].长沙: 湖南大学, 2016.
LIU Rong.Thermal error control and compensation of motorized spindle system of turning center[D].Changsha: Hunan University, 2016.
[67] 牛鹏程.数控机床热误差建模理论技术研究[D].合肥: 合肥工业大学, 2014.
NIU Pengcheng.Research on thermal error modeling theory and technology of CNC machine tool[D].Hefei: Hefei University of Technology,2014.
[68] 周宝仓.大型数控成形磨齿机几何误差理论及补偿方法研究[D].重庆: 重庆大学, 2017.
ZHOU Baocang.Research on geometric error theory and compensation method for large CNC gear profile grinding machine tools[D].Chongqing: Chongqing University, 2017.
[69] 杨建国.数控机床误差综合补偿技术及应用[D].上海: 上海交通大学, 1998.
YANG Jianguo.Error synthetic compensation technique and application for NC machine tools[D].Shanghai: Shanghai Jiao Tong University, 1998.
[70] 任永强, 杨建国, 罗磊, 等.基于外部机床坐标系偏移的热误差实时补偿[J].中国机械工程, 2003, 14(14): 1243–1245.
REN Yongqiang, YANG Jianguo, LUO Lei, et al.Real-time thermal error compensation based on shift of external machine coordinate system[J].China Mechanical Engineering, 2003, 14(14): 1243–1245.
[71] 刘明敏.基于机械原点偏移原理的数控机床热误差补偿技术应用[J].电子技术与软件工程, 2019(23): 115–116.
LIU Mingmin.Application of thermal error compensation technology for CNC machine tools based on mechanical origin migration principle[J].Electronic Technology & Software Engineering, 2019(23):115–116.
[72] 童文利.基于FANUC 31i的主轴热变形补偿方法[J].制造技术与机床, 2020(2): 191–194.
TONG Wenli.Based on FANUC 31i spindle thermal deformation compensation method[J].Manufacturing Technology & Machine Tool,2020(2): 191–194.
[73] 林志杭, 李殿新, 冯平法, 等.一种龙门铣床误差实时补偿方法[J].机械科学与技术, 2020, 39(7): 1035–1039.
LIN Zhihang, LI Dianxin, FENG Pingfa, et al.Real-time error compensation method for gantry milling machine[J].Mechanical Science and Technology for Aerospace Engineering, 2020, 39(7): 1035–1039.
[74] 高玉平.数控机床热误差的反馈截断式补偿研究[M].大连: 大连理工大学, 2009.
GAO Yuping.Research on feedback truncated compensation for thermal error of CNC machine tools[M].Dalian: Dalian University of Technology, 2009.
[75] 计昌柱.数控机床热误差补偿系统研究[D].合肥: 合肥工业大学, 2014.
JI Changzhu.The research of CNC thermal error compensation system[D].Hefei: Hefei University of Technology, 2014.
[76] 柏衡.面向机身大部件复合加工机床的误差补偿技术研究[D].南京: 南京航空航天大学, 2016.
BAI Heng.Research on error compensation technology of fuselage components compound machine tool[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2016.
[77] 吕洪杰.TH6926B落地铣镗加工中心几何误差补偿技术及实现[D].长沙: 湖南大学, 2016.
LÜ Hongjie.The technology and realize of geometric error compensation for the TH6926B floor boring and milling machine center[D].Changsha: Hunan University, 2016.
[78] 胡建民.嵌入式数控机床热误差实时补偿控制器的设计与实现[D].武汉: 武汉理工大学, 2014.
HU Jianmin.Design and implementation of real-time thermal error compensation controller on CNC tools based on embedded[D].Wuhan:Wuhan University of Technology, 2014.
[79] 崔岗卫.重型数控落地铣镗床误差建模及补偿技术研究[D].哈尔滨: 哈尔滨工业大学, 2012.
CUI Gangwei.Research on error modeling and compensation for heavy-duty CNC floor-typed boring and milling machine tool[D].Harbin:Harbin Institute of Technology, 2012.