航空航天构件装配需要进行大量的制孔加工。孔轴线相较于工件表面的垂直度对构件的连接质量和疲劳寿命有很大的影响。美国波音公司通过单剪搭接形式对钛合金螺栓进行了试验验证，发现当紧固件沿外载荷作用方向倾斜大于2°时，疲劳寿命会降低约47%；倾斜大于5°时，疲劳寿命会降低约95%[1]。因此为保证装配质量，航空航天构件装配制孔时，通常要求装配孔的法向垂直度偏差不超过0.5°[2]。
为了保证制孔效率，航空航天制造业大量使用机器人等自动化制孔形式。而在自动制孔过程中，受工件形状误差、工件定位误差、机器人运动误差等因素的影响，难以有效保证制孔垂直度。为此需要在制孔设备末端安装专用的法向测量装置，对每个加工孔的法向进行在位测量。
国内外针对工件表面的法向测量进行了大量的研究，Hasegawa 等[3]利用向量叉积法进行工件表面法向量的求解。薛汉杰等[4]利用安装在压脚上的4 台接触式直线位移传感器对钻孔法向进行了测量，使刀具法向实时调整精度达到了0.1°。公茂震等[5]利用3 个激光测距传感器测量出钻孔点周围3 个特征点的坐标，通过向量叉积的原理计算出钻孔点的法向量及与钻头中心轴线的夹角，并通过二元角度调节法调节钻头角度来保证钻孔的垂直度。段曙凯[6]利用机器视觉的方式进行飞机蒙皮的法矢检测，基于改进3 次B 样条拟合算法进行法矢的求解。Gao 等[7]提出一种将4 个激光位移传感器布置成菱形进行法向测量的新方法，并针对该方法提出了一种计算测量精度的方法，试验表明，该测量方式对不同工件的测量精度分别达到了±0.15°和±0.3°。冯昌源等[8]在4 台点激光位移传感器测量的基础上，利用离线仿真环境预测出以拟合平面法矢替代曲面法矢而引入的固有理论误差，并进行调姿补偿，通过试验证明了该方法可将制孔垂直精度控制在0.4°以内。
利用机器人对航空航天构件进行制孔加工时，通常将接触式位移传感器或者点激光位移传感器集成到压脚中，待压脚压紧工件后再进行法向测量。这种压紧条件下的法向测量方式，充分考虑了由压脚的压紧力引起的工件变形，适用于某些薄壁弱刚度蒙皮的制孔加工。我国目前正在研制的小型无人机、高超音速飞行器等航空航天设备，具有体积小、结构复杂的特点，不仅存在大量的大曲率表面，而且一部分大曲率构件还具有较大的刚度。上述采用接触式位移传感器和点激光传感器进行法向测量的方法，由于采集数据量少，不能有效反映工件的表面特征，因此不适用于大曲率工件表面的法向测量。同时由于压紧力使此类工件产生的变形很小，因此也无须压紧后再进行测量。
线激光传感器具有体积小、测量精度高、受环境影响小、易于集成等诸多优点。基于线激光传感器搭配直线运动机构对工件表面制孔位置所在区域进行非压紧条件下的直线扫描，可以获得工件局部表面的点云数据。点云数据包含了丰富的信息，能够更好地反映工件的局部表面特征。因此，利用点云数据进行法向量求解，可以更好地适应大曲率工件表面法向测量的需求。
本文提出了一种基于点云数据的大曲率工件表面法向计算方法，通过选取工件表面制孔位置处的局部点云数据进行平面拟合，利用拟合平面的法向代替曲面上制孔位置的法向。选取几种典型曲率，通过仿真生成曲面点云数据，探究了该方法中点云数据的选取范围对不同曲率的表面法向拟合精度的影响规律。通过对实际圆柱试验件的测量试验，验证了该方法的有效性。
1 大曲率表面法向计算方法
1.1 大曲率表面点云数据获取
线激光传感器采用激光三角法测量原理，通过柱面物镜将激光扩散为线激光后投射在目标物表面形成漫反射，使反射光通过传感器采集窗口，在CMOS 单元上成像，通过检测成像的位置变化测量高度信息。
利用直线运动机构带动线激光传感器做直线扫描，实现了对大曲率工件表面的三维测量，具体过程如图1所示。首先，搭载线激光测量模块的自动制孔设备到达制孔工位；然后，直线运动机构带动传感器对工件表面进行局部直线扫描，扫描过程中通过设置线激光传感器的测量频率和直线运动机构的运动距离，可以获得工件表面一定区域内的点云数据。由于线激光传感器每条激光线上的采集点分布密集，激光线间的测量间隔也可以设置得很小，因此所获得的点云数据十分密集，能够有效反映大曲率工件表面局部区域的详细信息。
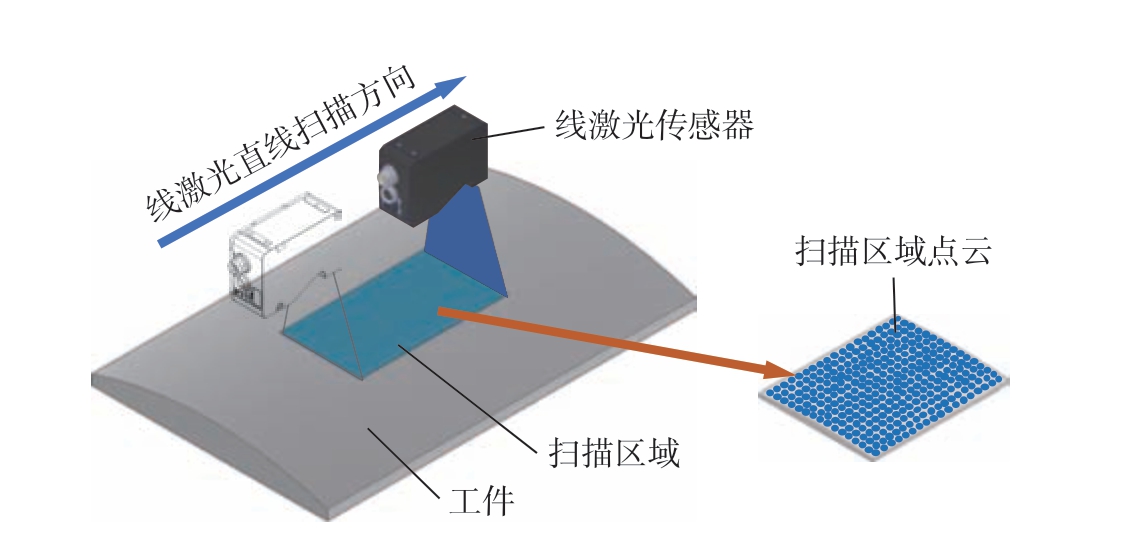
图1 线激光直线扫描测量过程
Fig.1 Line laser line scanning measurement process
1.2 点云数据平面拟合方法
由于工件表面曲率的存在，每条激光线的两端实际分辨率减小，点的密集程度降低。因此在获得大曲率工件表面局部区域的点云数据之后，首先需要对点云数据进行选取，然后再对得到的数据进行处理分析。如图2 所示，本文选取以大曲率工件制孔位置为中心的圆形区域内的点云数据进行处理，利用主成分分析（Principal component analysis，PCA）算法对点云数据进行平面拟合，用拟合平面的法向代替工件制孔位置处的法向。
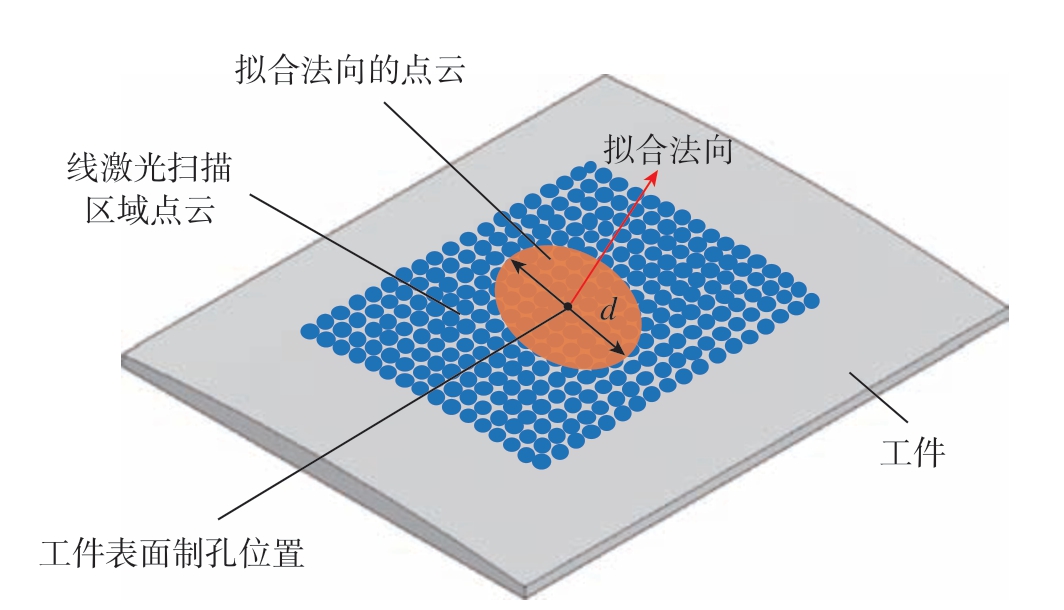
图2 利用点云拟合工件表面法向
Fig.2 Using point cloud to fit workpiece surface normal
PCA 作为一种多元统计技术，最早由美国统计学家Pearson 在1901 年的生物学理论研究中引入。PCA 基于统计特征进行多维的正交线性变换，变换后的原始数据在各维度上线性无关，可用于提取数据的主要特征分量，常用于高维数据的降维。PCA 基于数据本身的相关性，在降维的同时尽量降低信息损失，即运用统计分析原理与方法提取少数几个彼此不相关的综合性指标而保持其原指标所提供的大量信息，力求通过原来变量的少数几个线性组合来解释原来变量绝大多数的信息，从而简化问题。目前，PCA 已经广泛地应用于图像识别、管理决策、回归分析、模式识别、时间序列预测等各个领域[9–10]。
采用PCA 进行平面拟合的步骤如下。
（1） 假设用于拟合的原始点云数据总共有m 条，pi =（xi，yi，zi）T 是其中一条数据，按列组成一个3×m的矩阵X。
（2） 将X 的每一行进行零均值化，即减去这一行的均值。
（3） 求出协方差矩阵：
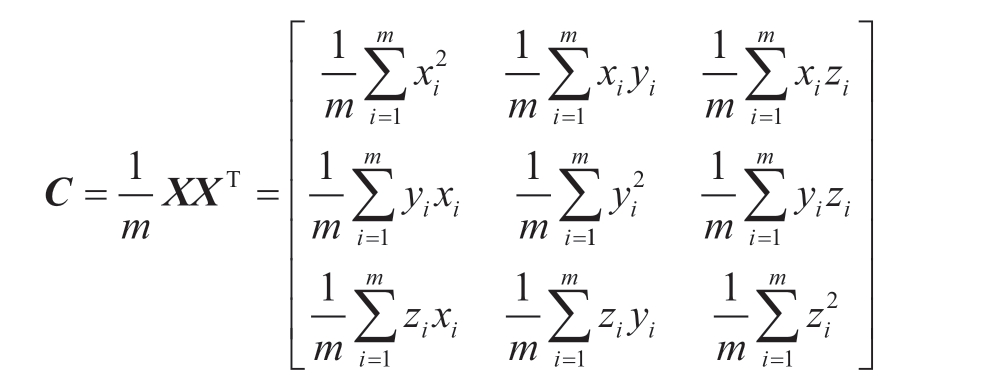
计算出协方差矩阵的特征值及对应的特征向量，C = UΣV T。其中，Σ 为对角阵，其对角元素为C 的特征值；U 为C 的3 组特征向量组成的三阶的特征矩阵。在U中按对应特征值由大到小取前2 组特征向量作为拟合的点云平面的一组基底，最小的特征值对应的特征向量即为所拟合平面的法向量。
2 大曲率表面法向计算误差分析
2.1 误差分析过程
选取直径为d 的圆形区域内的点云数据进行平面拟合时，理论上所选区域越小，其拟合平面法向越逼近工件表面制孔位置的实际法向。但在实际应用中，区域选择过小时用于拟合平面的点云数据减少，测量时产生的噪声点对拟合法向的影响增大，使得法向拟合精度降低。原则上在保证精度的前提下，点云的选择范围应大于要加工的孔径。
另外，在实际应用中，受工件形状误差、定位误差及制孔设备运动误差的影响，线激光传感器在做直线扫描时并不能保证完全对正待测表面，由此产生测量角度的偏差也会影响工件表面制孔位置处的法向拟合精度。
航空航天构件的高斯曲率大多为0，而平均曲率较大。以机身壁板工件为例，通常在一个方向上曲率要更大[2]，故而可以近似认为是半径一定的柱面。因此针对不同曲率大小的工件，研究其法向拟合误差随点云选择范围的变化规律时，选取若干典型曲率，通过仿真生成柱面点云进行分析。利用线激光对柱面进行测量时的具体情况如图3 所示。
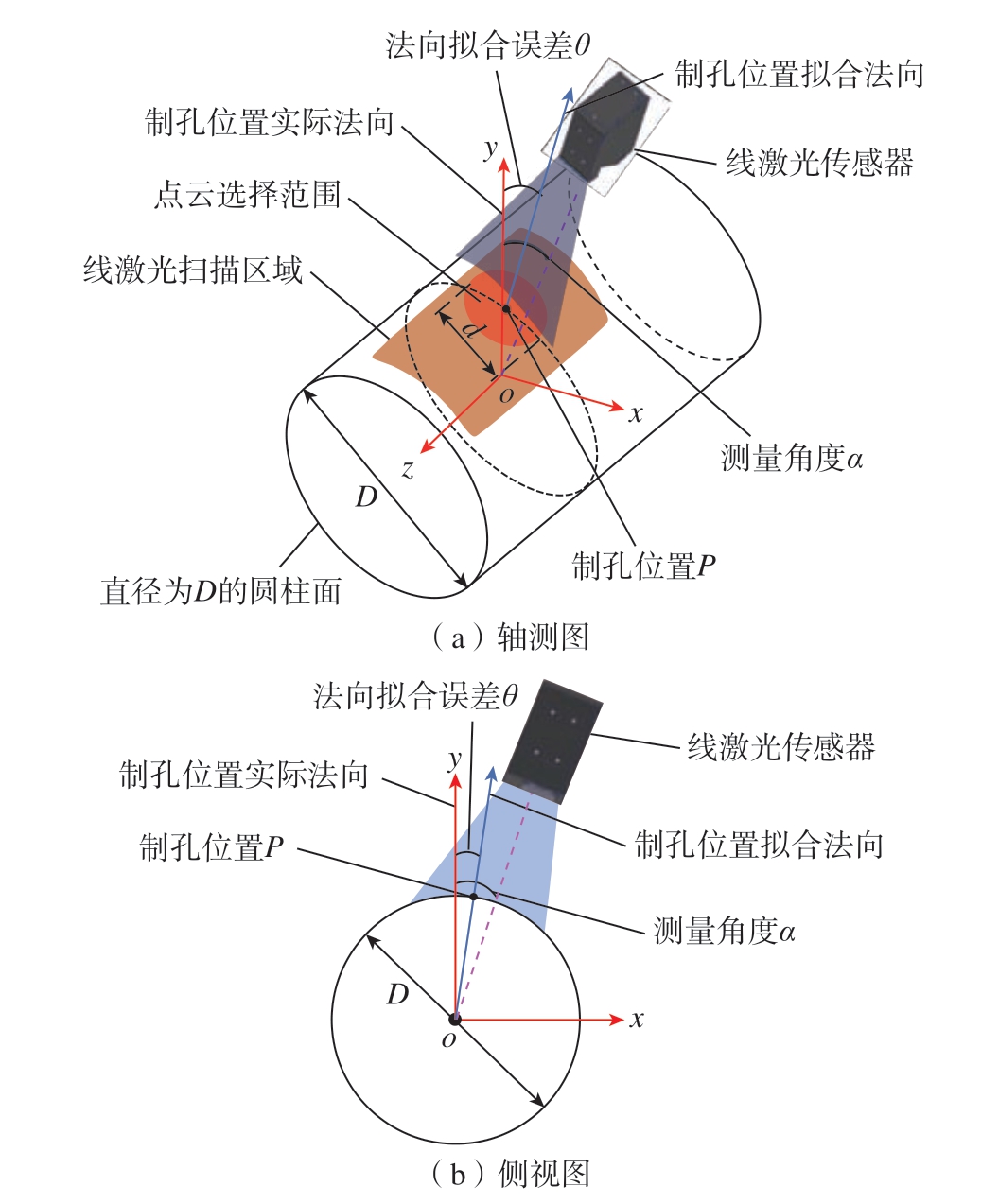
图3 线激光传感器测量圆柱面示意图
Fig.3 Schematic diagram of line laser sensor measuring cylindrical surface
首先确定圆柱面的直径D（50 mm、100 mm、200 mm、400 mm），利用CloudCompare 软件得到该圆柱面的点云数据，点云密度为10000 个/cm2。然后在圆柱面上选择一点P 作为制孔位置，并根据柱面方程计算P点的实际法向。为计算方便，本文选择坐标系y 轴与圆柱母线的交点作为P 点，其实际法向为 （0，1，0）。接着确定测量角度α（2°、3.5°、5°）。在不同的测量角度α下以P 为中心，选择直径为d 的圆形区域内点云数据进行平面拟合，得到拟合法向并计算与实际法向的拟合误差，不断改变d 的大小就可以得到1 组法向拟合误差数据。其具体流程如图4 所示。
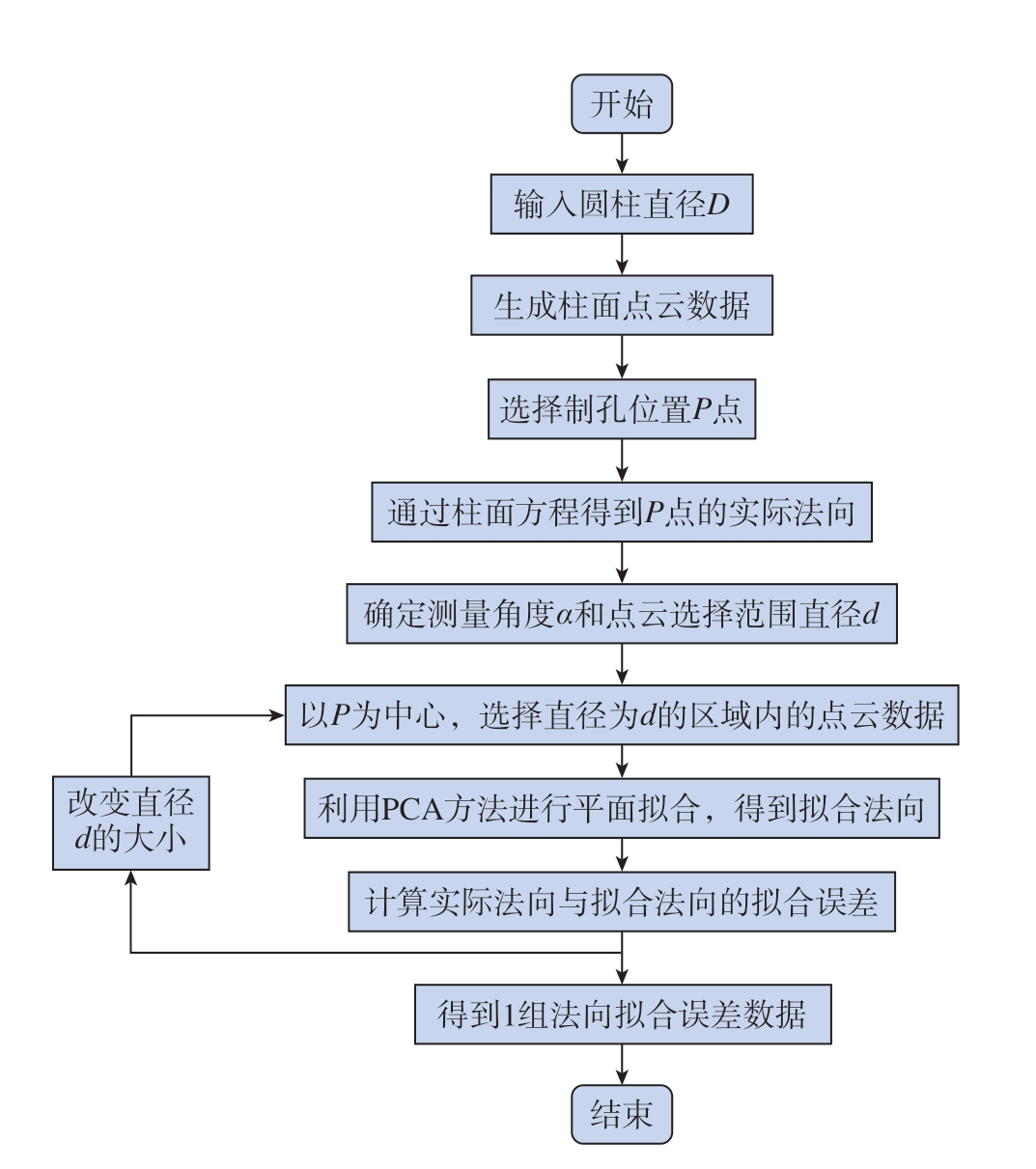
图4 点云选择范围对法向拟合误差影响规律探究过程
Fig.4 Process of exploring the influence of point cloud selection range on normal fitting error
2.2 结果与分析
对所得到的数据整理分析，结果如图5 所示。可以看出，当曲率和测量角度一定时，法向拟合误差随着点云选择范围的增大而增大，且这种增长趋势呈非线性。对同一圆柱面，当点云选择范围较小时，由于选择的点云数据所在的区域十分接近平面，曲率的影响可以忽略不计，相邻范围内的法向拟合误差变化趋势较小；当点云选择范围增大到一定值之后，相邻范围内的法向拟合误差变化趋势显著变大，这是因为随着范围的增大，所选择的点云数据增多，受曲率影响拟合的法向与实际法向的偏差增大。
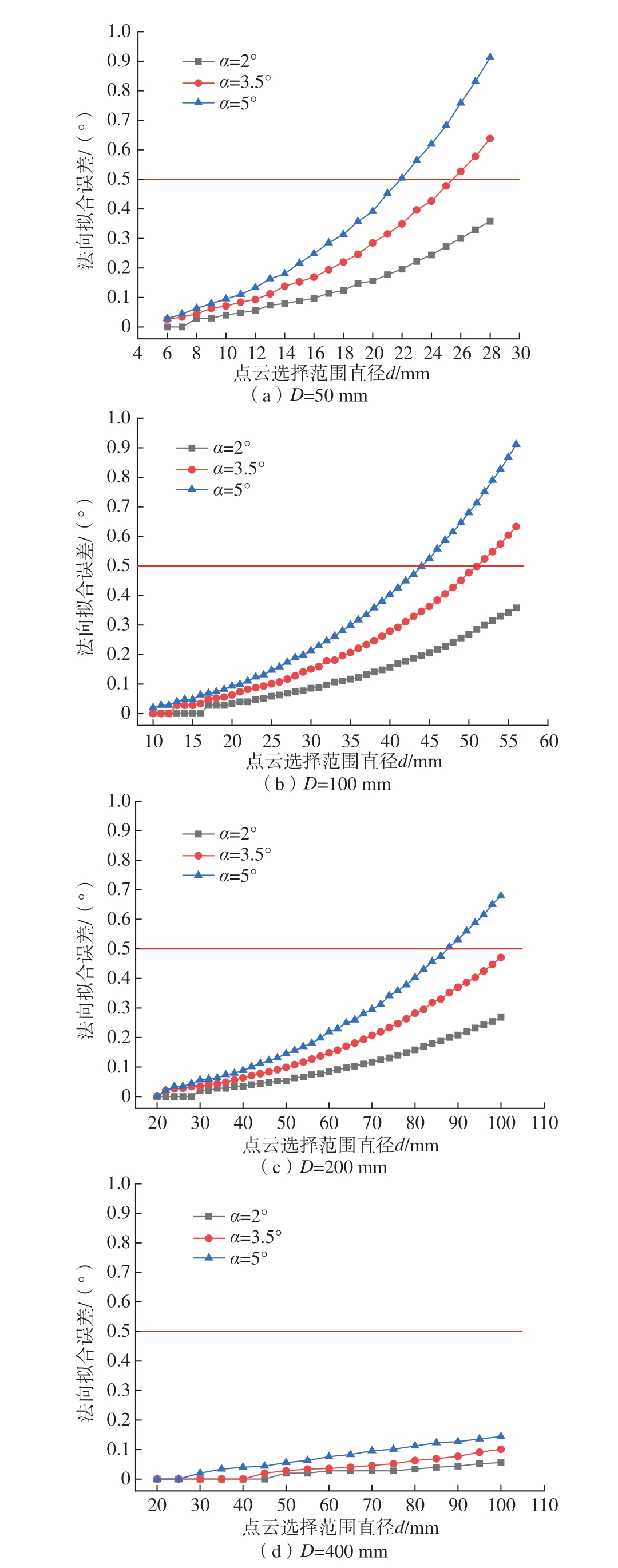
图5 点云选择范围对法向量拟合误差的影响
Fig.5 Influence of point cloud selection range on normal vector fitting error
当点云选择范围较小时，不同测量角度下的法向拟合误差差别很小，这是因为范围越小，所选取的点云数据越趋近制孔位置，并且受测量角度的影响也越小，拟合的法向越接近实际法向。当点云选择范围超过某一临界值后，随着测量角度增大，法向拟合精度显著变差。这是因为当点云选择范围相同时，测量角度增大会使得实际选择的点云相对于制孔位置P 所在母线的不对称程度加大，对拟合法向产生较大的影响。对于D 为100 mm 的圆柱面，当d 为10 mm 时，α 为5°的法向拟合误差比α 为2°的法向拟合误差大0.020°，而当d 为30 mm 时，两者之间的差距达0.127°。
当α 和点云选择范围一定时，曲率越小，法向拟合误差越小 （以d = 30 mm 为例，其法向拟合误差如图6所示），这是因为在相同的点云选择范围下，曲率越小，用于拟合法向的点云所在的区域越接近平面，拟合法向与实际法向之间的偏差越小。注意到当D =400 mm 时，点云选择范围d 在100 mm 以下时均能获得较高的法向拟合精度 （图5（d））。因此，当工件的曲率较大时，为保证法向拟合精度应选择较小区域内的点云数据进行平面拟合；当工件的曲率较小时，可适当扩大用于拟合平面的点云数据的选择范围。但考虑到线激光传感器测量线宽的限制和点云数据增多后带来的处理时间变长的问题，点云数据的选择范围也不应过大。
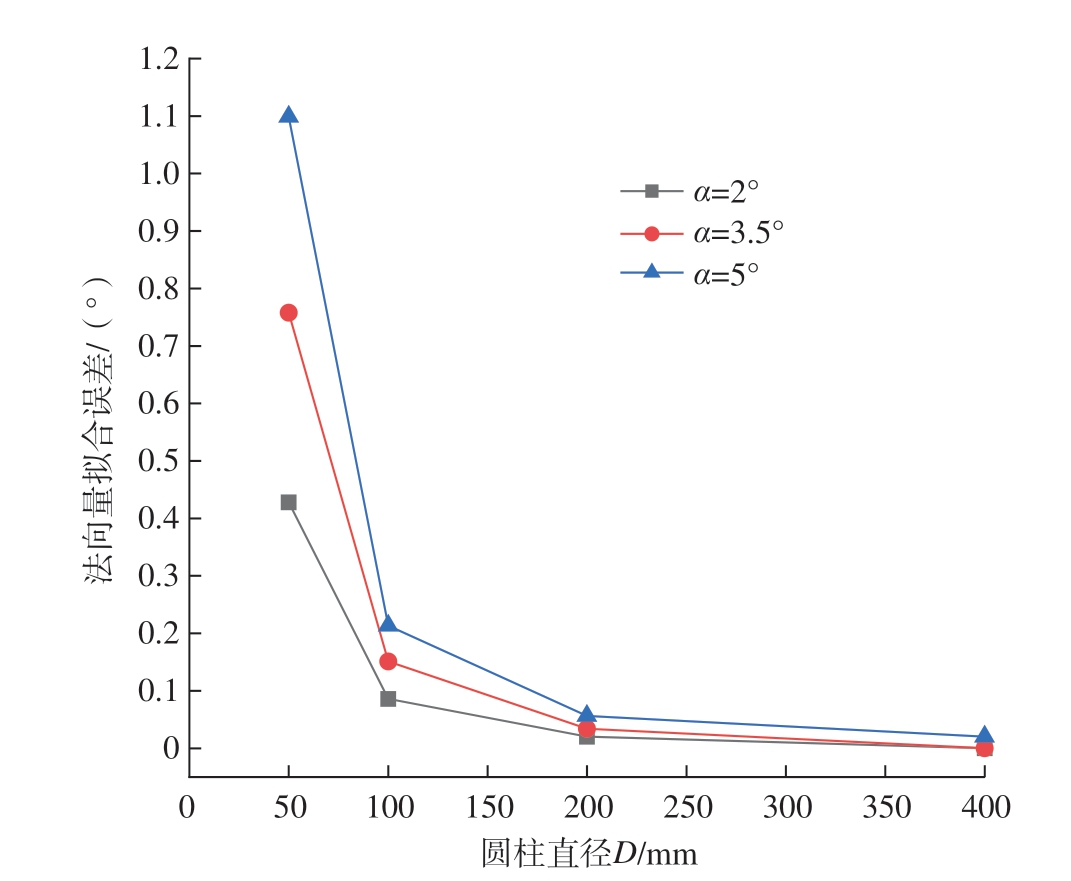
图6 曲率对法向拟合误差的影响 （d=30 mm）
Fig.6 Effect of curvature on normal fitting error (d=30 mm)
3 试验验证
试验利用D =50 mm 的铝合金圆柱试验件，通过线激光传感器采集其表面点云数据并进行法向拟合来验证本文算法。试验所用线激光传感器Gocator 2530 为加拿大LMI Technologies 公司生产，具体参数如表1 所示。
表1 线激光传感器Gocator 2530 参数
Table 1 Parameters of line laser sensor Gocator 2530
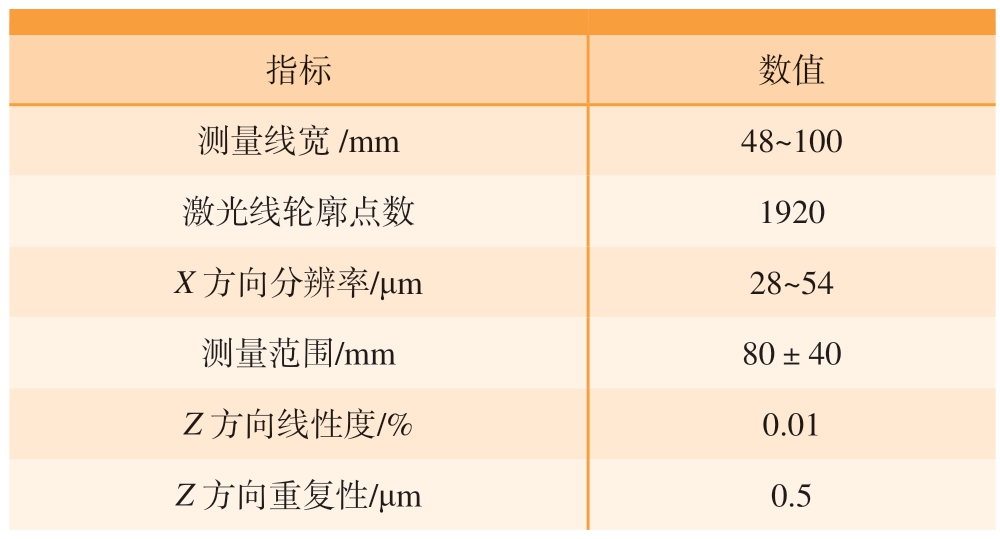
指标数值测量线宽/mm48～100激光线轮廓点数1920 X 方向分辨率/μm28～54测量范围/mm80±40 Z 方向线性度/%0.01 Z 方向重复性/μm0.5
试验首先将线激光传感器安装在机床主轴上，通过机床的直线运动带动线激光传感器完成直线扫描，试验件利用V 型块进行定位，试验平台如图7 所示。试验过程中机床的直线运动速度为120 mm/min，线激光传感器的测量频率为16 Hz，测量得到试验件的点云 （预处理后）如图8 所示。
图7 试验平台
Fig.7 Test bed
图8 试验件测量点云（预处理后）
Fig.8 Point cloud of test piece (after pre-treatment)
将试验件最靠近线激光传感器的母线定义为上母线，在其上选择一点P 作为参考点。由于试验过程中线激光传感器相对于试验件的测量姿态没有改变，为了模拟仿真试验中的传感器在不同α 下的情况，将与P 点位于同一径向截面圆上的P'点作为点云选择范围的中心，
所对应的圆心角为α，如图9 所示。数据处理过程：首先选择上母线上一点P（xP，yP，zP），分别在不同的圆心角α（2°，3.5°，5°）下得到P'（xP'，yP'，zP'），然后以P'为圆心依次得到不同直径大小的圆形区域内的点云。但由于测量过程中V 型块的安装不可避免地存在误差，使得试验件的轴向与传感器坐标系的y 轴方向不重合，存在夹角φ。因此，在求解P'坐标时，需考虑夹角φ 的影响。
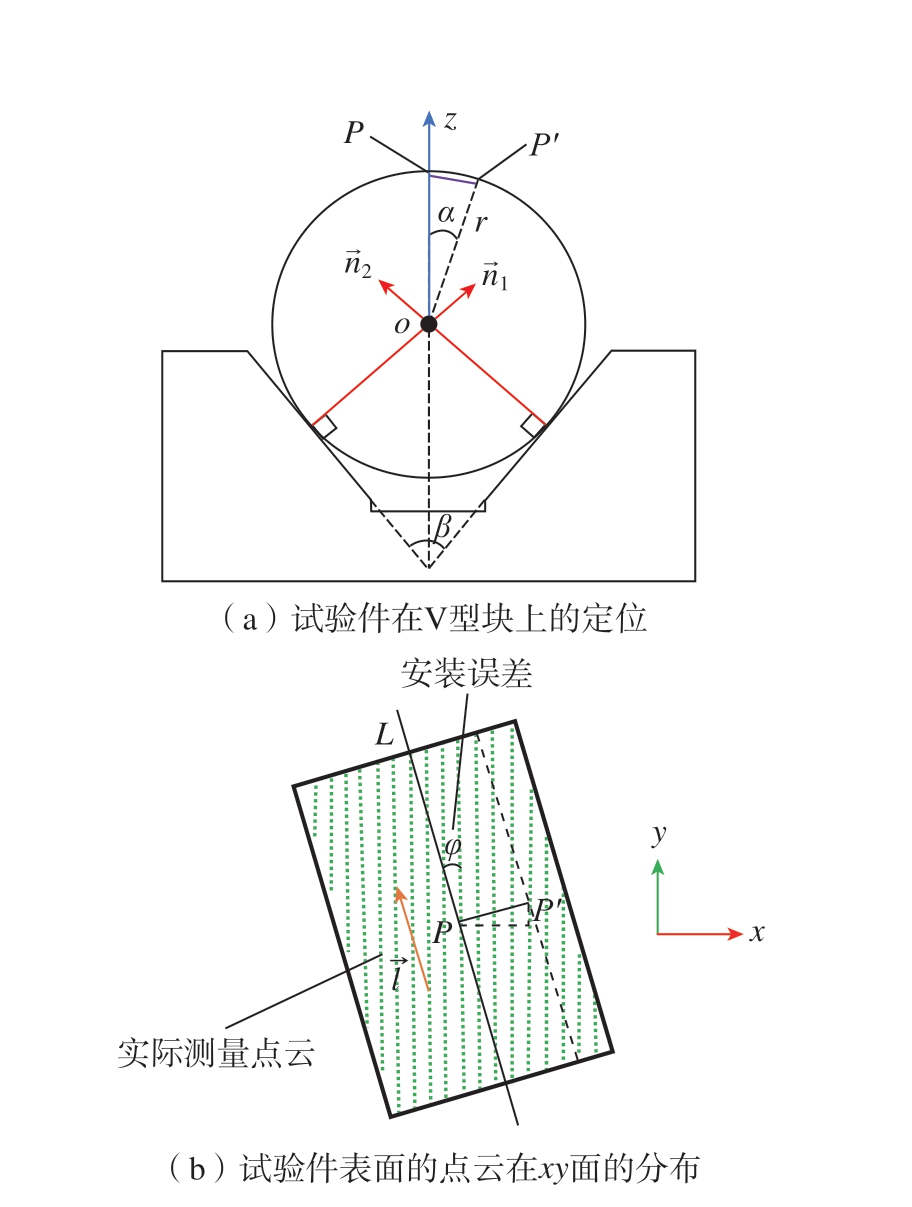
图9 V 型块安装误差示意图
Fig.9 V-block installation error diagram
试验过程中同时会得到V 型块两定位面的部分点云数据，分别对其进行平面拟合得到两定位面的法向量
，试验件轴线的方向向量
通过式 （1）求得。将试验件点云投影到xy坐标平面内，如图9所示。试验件轴向与传感器坐标系y 方向的夹角φ 可由式（2）确定；
的投影长度|PP'|在△OPP'中由式 （3）确定；P'点的横、纵坐标可由式（4）求得。
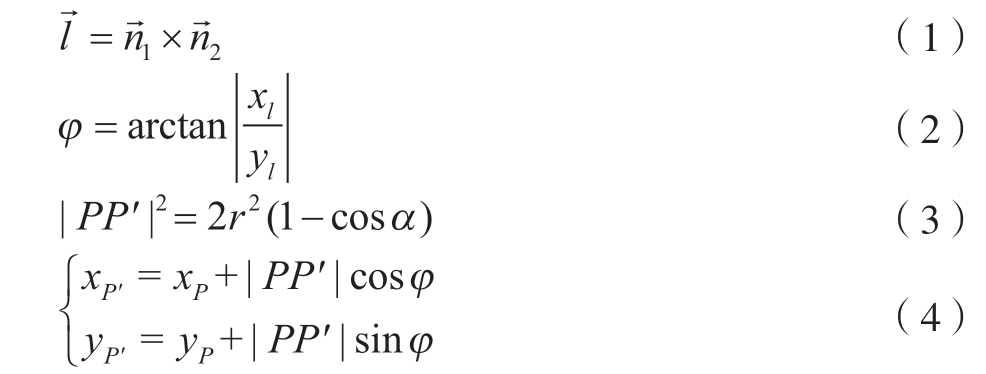
分别在不同的角度下选择4 种不同直径d 大小 （8 mm、12 mm、16 mm、20 mm）区域内的点云数据进行验证。图10 为圆形区域内点云的选取情况，然后利用本文算法处理得到法向拟合误差，结果如表2 所示。
表2 试验结果对比（D=50 mm）
Table 2 Comparison of test results (D=50 mm)
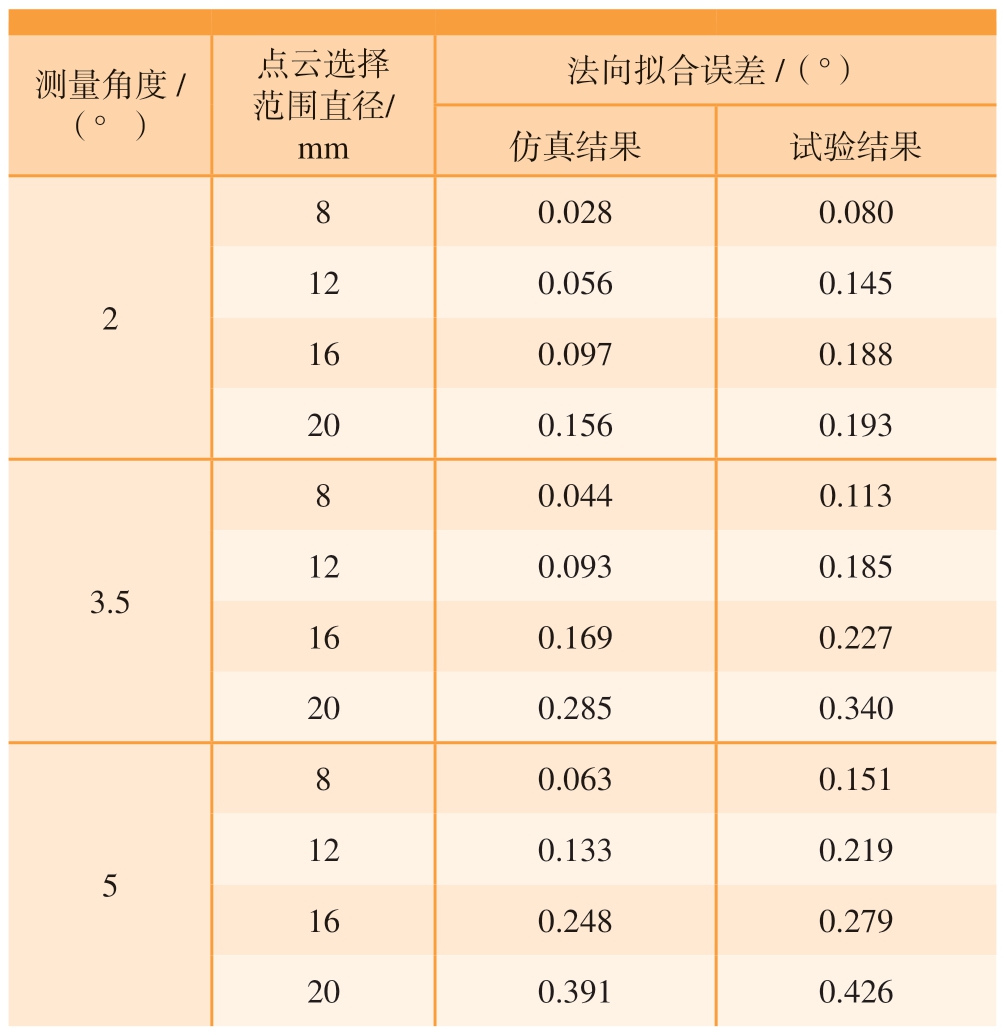
测量角度/（°）点云选择范围直径/mm法向拟合误差/（°）仿真结果试验结果2 8 0.028 0.080 120.056 0.145 160.097 0.188 200.156 0.193 3.5 8 0.044 0.113 120.093 0.185 160.169 0.227 200.285 0.340 5 8 0.063 0.151 120.133 0.219 160.248 0.279 200.391 0.426
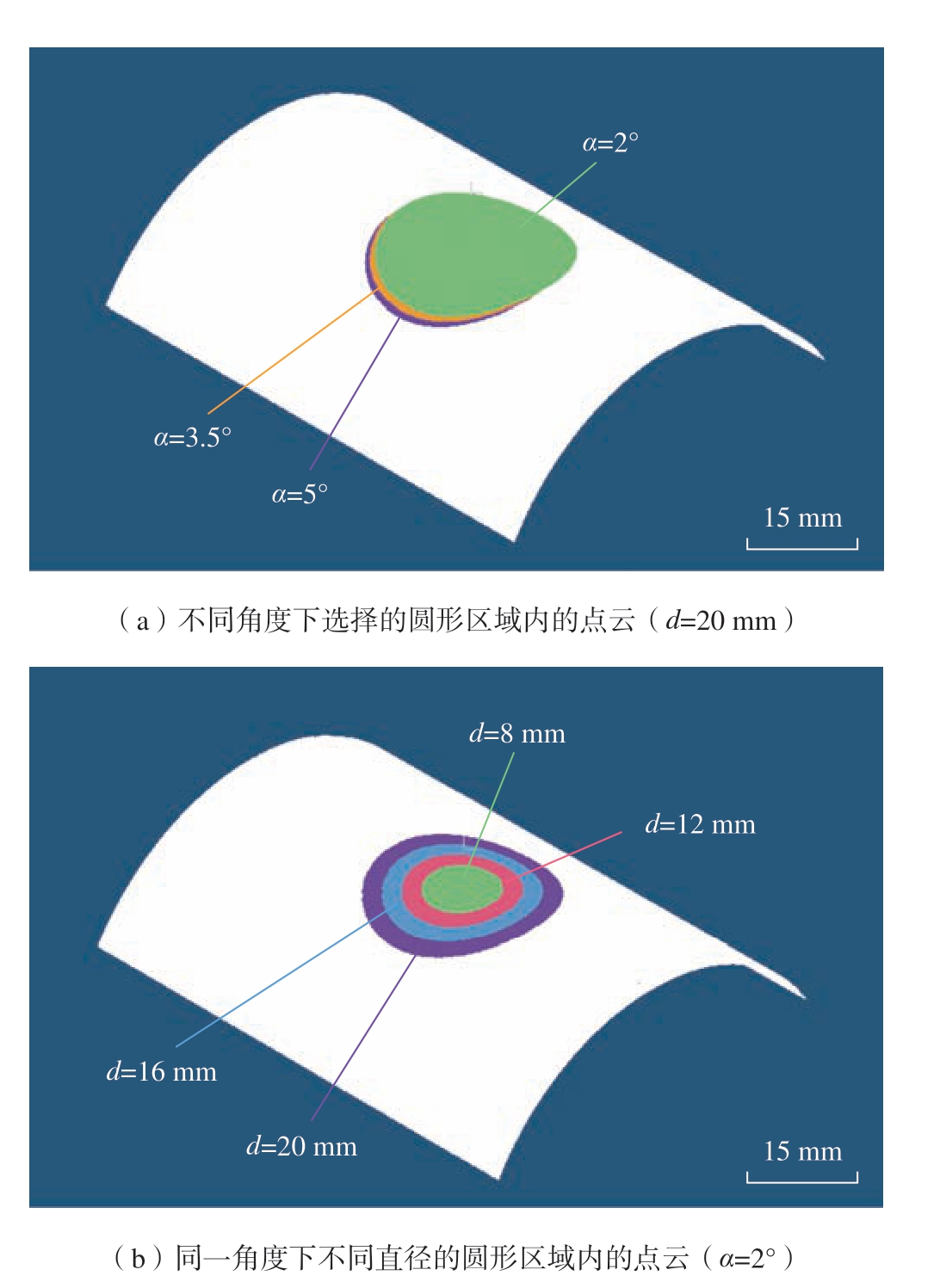
图10 圆形区域内的点云选取
Fig.10 Selected point cloud in circular area
可以发现，在同一测量角度下法向拟合误差的试验结果随点云选择范围的变化趋势与仿真结果基本一致，但在相同的测量角度和点云选择范围下，试验测得的法向拟合误差均比仿真得到的大。考虑到试验件的尺寸误差、圆柱度误差、定位误差、安装误差，以及线激光传感器的测量误差等诸多因素均不可避免地会对法向拟合误差产生影响，所以实际的法向拟合误差大于仿真得到的法向拟合误差。从试验结果可以看出，实际计算时只要选择合适范围内的点云数据，就能保证法向拟合精度满足航空航天制造业对制孔垂直精度的工艺要求，这也证明了本文方法的有效性。
4 结论
（1）通过线激光直线扫描的方式对大曲率工件表面进行测量，能够获得大量包含大曲率工件表面局部区域详细信息的点云数据，利用所得到的点云数据进行平面拟合，可用拟合平面的法向代替工件表面制孔位置处的实际法向。在进行平面拟合时，点云的选择范围对大曲率工件表面的法向拟合误差有很大的影响。
（2）仿真试验结果表明，对于直径为50 mm 的圆柱面，当点云选择范围在12 mm 以下时，法向拟合误差可以保证在0.133°以下。
（3）对于直径为50 mm 的圆柱试验件，当点云选择范围在12 mm 以下时，实际测得的法向误差可以保证在0.219°以下。
（4）在实际的应用中，首先应根据工件的数模得出各制孔位置处的曲率，并根据曲率的大小和实际的测量精度要求选择合适范围内的点云数据进行法向拟合。若制孔位置处的曲率大于直径为50 mm 的圆柱面的曲率，则点云选择范围在12 mm 以下可获得较高的法向拟合精度；若制孔位置处的曲率较小，则点云选择范围可适当扩大，但应兼顾传感器的测量线宽以及数据的处理速度。
（5）传感器测量角度作为测量时的随机误差，对法向拟合误差的影响较大。实际测量中，在直线扫描时应保证线激光传感器对正工件待测表面，减小测量角度对法向拟合误差的影响。
[1] 袁红璇. 飞机结构件连接孔制造技术[J]. 航空制造技术,2007, 50(1): 96–99.
YUAN Hongxuan. Manufacturing technology of connecting hole in aircraft structures[J]. Aeronautical Manufacturing Technology, 2007,50(1):96–99.
[2] 宋尧, 姚振强, 薛雷, 等. 飞机制孔末端执行器法向检测方法及误差分析[J]. 机械设计与研究, 2017, 33(4): 117–122.
SONG Yao, YAO Zhenqiang, XUE Lei, et al. Development and error analysis of the normal vector detection of end effector for aircraft component drilling[J]. Machine Design & Research, 2017, 33(4): 117–122.
[3] HASEGAWA N, OKADA T, SHIMIZU T. Measurement of surface-normal using a range sensor with a pair of wedge-prisms[C]//2005 IEEE Instrumentationand Measurement Technology Conference Proceedings. Ottawa, 2006: 1744–1749.
[4] 薛汉杰, 张敬佩. 蒙皮类部件钻孔法向的测量和调整[J]. 航空制造技术, 2010, 53(23): 60–62, 66.
XUE Hanjie, ZHANG Jingpei. Measurement and adjustment of drilling normal direction of skin parts[J]. Aeronautical Manufacturing Technology, 2010, 53(23): 60–62, 66.
[5] 公茂震, 袁培江, 王田苗, 等. 航空制孔机器人末端垂直度智能调节方法[J]. 北京航空航天大学学报, 2012, 38(10): 1400–1404.
GONG Maozhen, YUAN Peijiang, WANG Tianmiao, et al.Intelligent verticality-adjustment method of end-effector in aeronautical drilling robot[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(10): 1400–1404.
[6] 段曙凯. 飞机蒙皮法矢的视觉检测技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.
DUAN Shukai. Research on visual detection technology of normal vector of aircraft skin[D]. Harbin: Harbin Institute of Technology, 2013.
[7] GAO Y H, WU D, NAN C G, et al. Normal direction measurement in robotic drilling and precision calculation[J]. The International Journal of Advanced Manufacturing Technology, 2015,76(5–8): 1311–1318.
[8] 冯昌源, 田威, 胡俊山, 等. 面向变曲率曲面的自动钻铆垂直精度补偿技术[J]. 机械制造与自动化, 2021, 50(1):33–35, 44.
FENG Changyuan, TIAN Wei, HU Junshan, et al. Automatic precision riveting vertical accuracy compensation technology for variable curvature surface[J]. Machine Building & Automation, 2021, 50(1):33–35, 44.
[9] 陈佩. 主成分分析法研究及其在特征提取中的应用[D]. 西安: 陕西师范大学, 2014.
CHEN Pei. Research on principal component analysis and its application in feature extraction[D]. Xi’an: Shaanxi Normal University,2014.
[10] 浮丹丹, 周绍光, 徐洋, 等. 基于主成分分析的点云平面拟合技术研究[J]. 测绘工程, 2014, 23(4): 20–23.
FU Dandan, ZHOU Shaoguang, XU Yang, et al. Point cloud plane fitting technology based on principal component analysis[J]. Engineering of Surveying and Mapping, 2014, 23(4): 20–23.