目前,高端工业装备正朝着轻量化、高性能、长寿命的方向发展,这对材料综合力学性能提出了更高的要求。颗粒增强复合材料在比强度、比刚度、耐磨性及抗疲劳方面性能优异,而且有较好的耐高温性、热膨胀性和尺寸稳定性,具有广阔的发展前景。国内外学者采用解析建模、试验研究及计算机模拟等方法对颗粒增强复合材料进行了广泛研究,但至今没有完善的理论结果。因其试验研究成本高、准备周期长,只能获得宏观力学物理状态,且很难获得试件中温度、应力、应变变化。早期的颗粒增强复合材料切削加工有限元模拟主要是针对二维切削加工过程开展研究,但由于与真实颗粒的三维结构差异较大,导致对实际加工的指导作用有限。鉴于此,众多学者开始致力于颗粒增强复合材料切削加工三维有限元模拟的研究,但在贴近真实情况的几何建模和材料模型等关键技术研究方面还需进一步深入探讨。因此,本文对颗粒增强复合材料切削加工的三维有限元模拟研究进展进行了综述,介绍了几何模型、界面模型和本构模型的建立,以及网格划分和边界条件处理方面的最新研究进展,并探讨了存在的问题和发展方向。
1 几何模型的建立
对于颗粒增强复合材料,增强颗粒的分布是随机的,因此对其进行切削加工有限元模拟研究时,需要建立颗粒随机分布几何模型,以便更接近材料真实的微观结构。为了建模方便,随机分布可以简化为多颗粒均匀分布,而均匀分布几何模型可以进一步简化为单颗粒几何模型。因此,颗粒增强复合材料切削加工三维有限元模拟的几何建模主要针对单颗粒几何模型和多颗粒随机分布几何模型开展研究。
1.1 单颗粒几何模型
在颗粒增强复合材料切削加工模拟研究时,通过单颗粒仿真,可以研究界面层对颗粒切削及强化性能的影响。郑阳升等[1]假定复合材料由无数个内含单个增强颗粒的六棱柱单胞组成,在建模时将六棱柱单胞简化为圆柱体单胞,因为圆柱体具有轴对称性,分析时可以将三维问题简化为二维问题,而且只需要对其中的1/4 进行研究。图1[1]为二维单胞模型的转化过程。
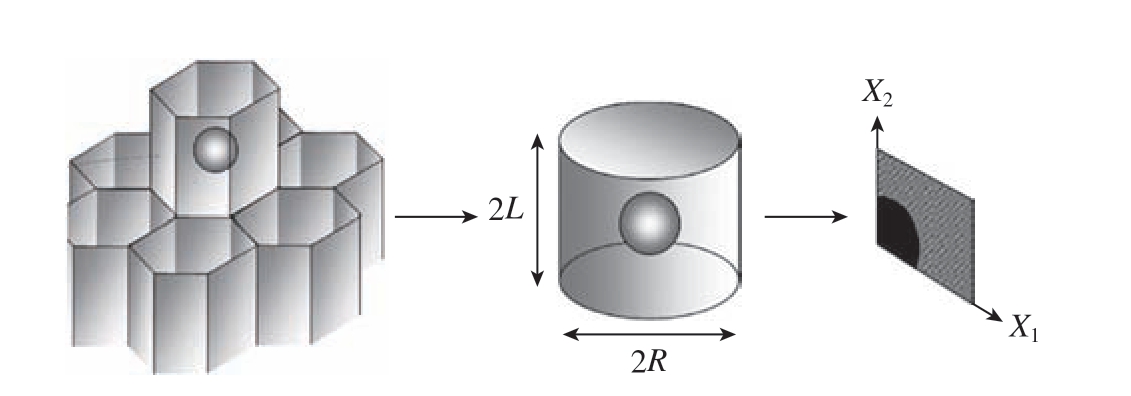
图1 二维单胞模型转化过程[1]
Fig.1 Transformation process of two-dimensional cell model[1]
单颗粒轴对称单胞模型是一种理想模型,其实质是对增强颗粒均匀分布的简化,无法反映颗粒间的相互影响。尽管单颗粒立方单胞模型也不考虑颗粒间的相互作用,但比二维单颗粒轴对称单胞模型更接近实际情况,因此模拟结果的可靠性更高。Qi 等[2]采用局部分析方法对增强体规则排列复合材料开展了单颗粒立方单胞建模研究,在单轴拉伸、压缩模拟时只需要对模型的1/8 进行分析,如图2(a)所示。齐小乐[3]通过抽取正方体基体进行研究,将SiC 颗粒简化为球体,并假设颗粒位于基体材料中心,建立了颗粒增强复合材料的三维球体单颗粒几何模型,如图2(b)所示。
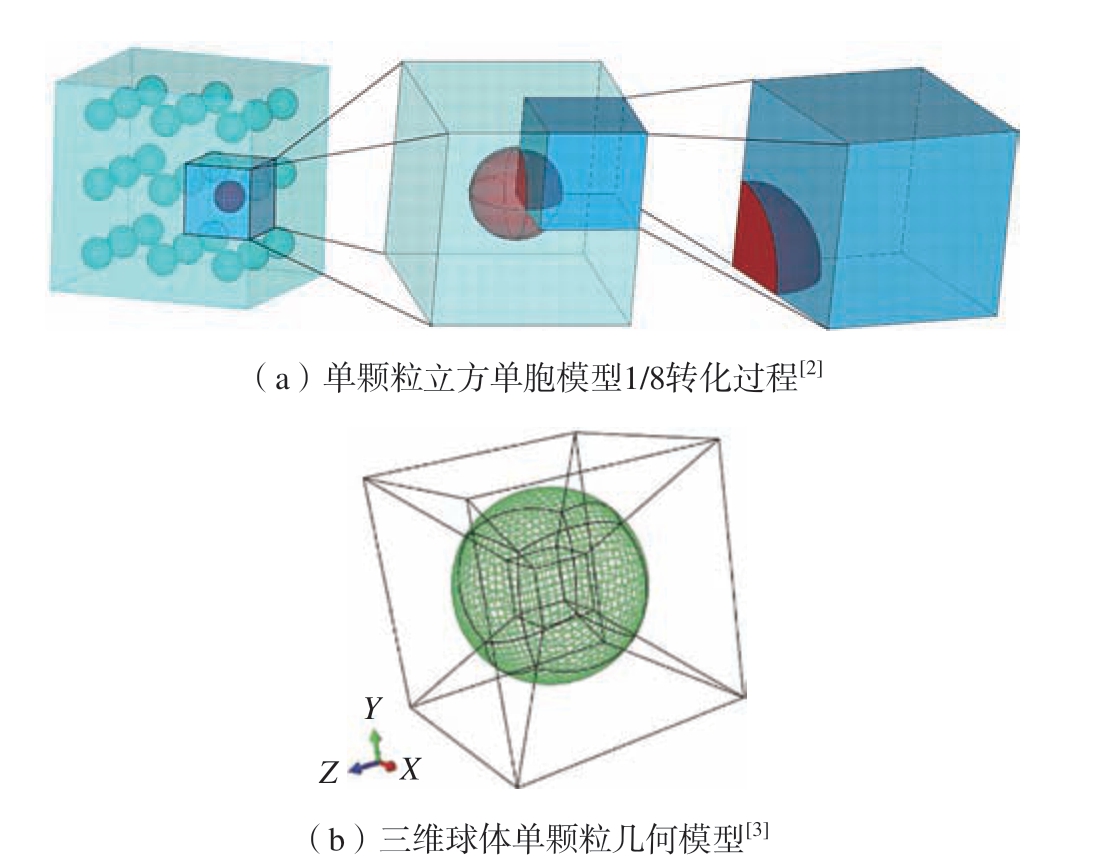
图2 球体单颗粒立方单胞几何模型
Fig.2 Geometric model of cubic cell of spherical single particle
耿昆等[4]采用Camisizer XT 多功能粒径分析仪对SiC 颗粒的真实几何形貌进行了统计分析,得到了颗粒尺寸大小和颗粒分布情况。根据真实几何形貌统计,首先简化得到三角形和四边形基本形状,然后进行拉伸得到初步的三维多面体,再对多面体进行切除,最终获得较为真实的SiC 颗粒三维结构模型,如图3 所示[4]。
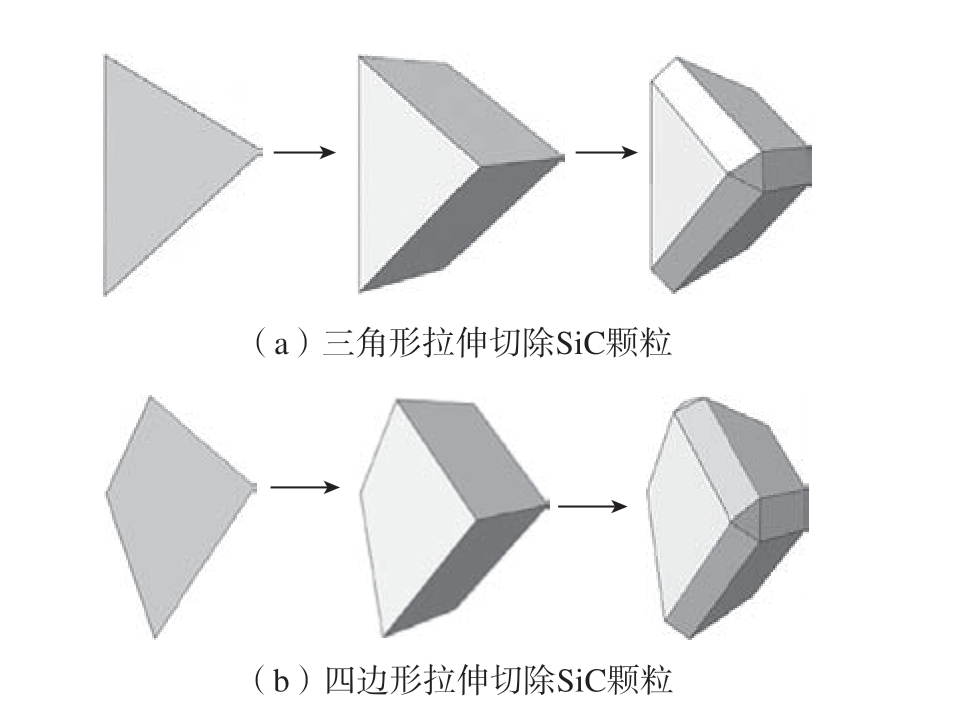
图3 复杂几何形貌SiC 颗粒三维结构建模[4]
Fig.3 Three-dimensional structure modeling of SiC particles with complex geometry[4]
1.2 多颗粒几何模型
三维多颗粒几何模型比单颗粒几何模型更能真实地反映复合材料的结构。多颗粒几何模型可以分为均匀分布几何模型和随机分布几何模型,其中随机分布几何模型更能体现复合材料的非均质特点,因此学者对多颗粒随机分布建模研究较多。
1.2.1 多颗粒均匀分布几何模型
Gao 等[5]为了研究网状结构的强化效果,建立了在网状结构内均匀分布的SiC 颗粒壁,如图4 所示,首先建立Al 基体和网状结构模型,然后将SiC 颗粒在网状结构模型中均匀分布,最后将SiC 颗粒、网状结构模型和Al 基体装配得到完整的几何模型,通过仿真分析验证了连续网状结构金属基复合材料具有更高刚度和强度的试验结论。
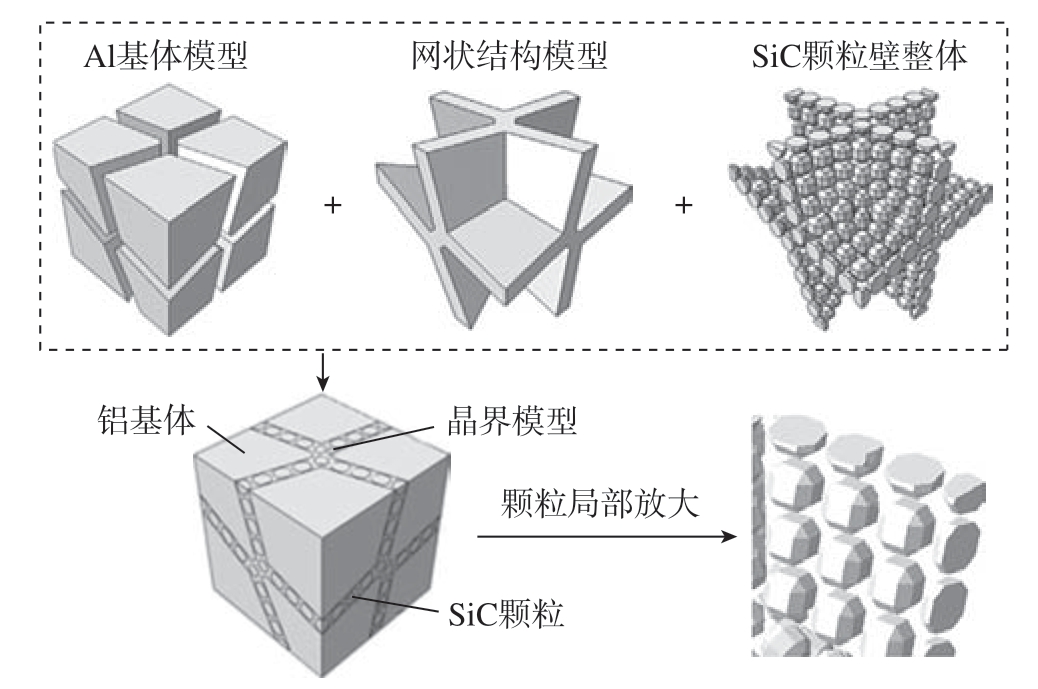
图4 网状结构模型、SiC 颗粒和Al 基体装配图[5]
Fig.4 Network structure model, SiC particles and Al matrix assembly diagram[5]
Wang 等[6]为了研究刀具和SiC 颗粒的相对位置对切削机理的影响,将SiC 颗粒简化为球体,建立了颗粒直径为40 μm 的均匀分布三维有限元模型 (图5)。通过对比不同切削深度下的加工表面形貌,分析颗粒相对位置对表面形貌的影响,发现颗粒的相对位置和切削路径不同,颗粒断裂行为不同,模拟结果与精密车削试验数据吻合,验证了均匀分布三维有限元模型的有效性。
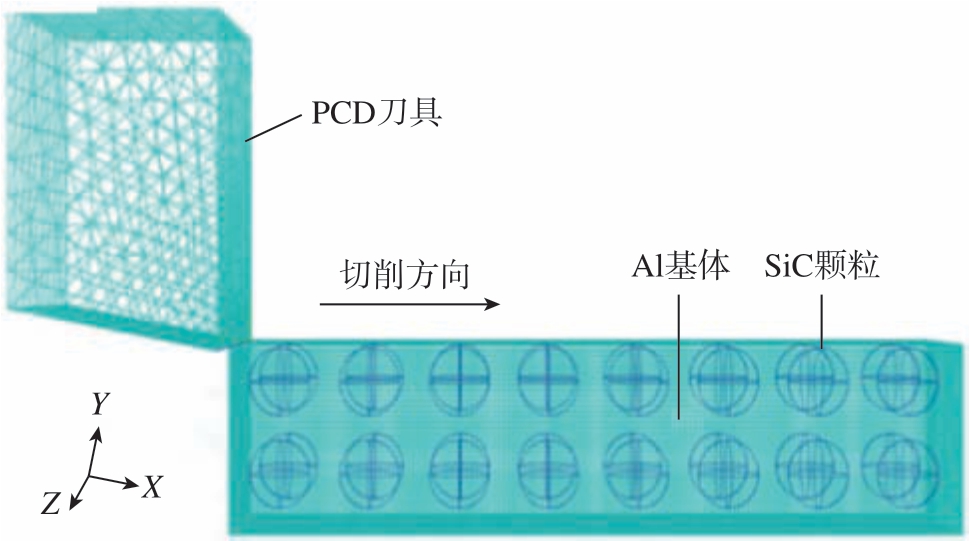
图5 SiC 颗粒均匀分布三维几何模型[6]
Fig.5 Three-dimensional geometric model of uniform distribution of SiC particles[6]
Setia 等[7]建立了多颗粒均匀分布二维切削仿真模型,通过改变切削速度和切削深度,分析切削力、切削温度的变化规律后发现,随着切削速度的增加,切削力减小,切削温度升高;切削深度增加使切削力和切削温度呈上升趋势,模拟结果与试验结果吻合,验证了有限元模型的有效性。王进峰等[8]为了研究不同切削速度和切削深度对切削力的影响及应力场分布情况,建立了二维多颗粒均匀分布有限元仿真模型,仿真结果发现,切削力变化和形成机制与试验结果一致。Chen 等[9]为了比较均匀分布相同尺寸颗粒和随机分布非等尺寸颗粒SiC/Al 复合材料切削机理的差异,建立了二维颗粒均匀分布和非均匀分布有限元模型,通过模拟仿真发现,颗粒均匀分布有限元模型的切屑连续性好,切削力波动小,模拟结果和试验结果有良好的相关性。Zheng 等[10]为了研究SiC 颗粒增强复合材料的去除机理,以及刀具、SiC 颗粒、Al 基体和界面之间的相互作用,建立了均匀分布二维细观力学模型,如图6 所示,发现刀具与SiC 颗粒的相对位置不同时,其去除模式不同,仿真结果与试验结果吻合较好。
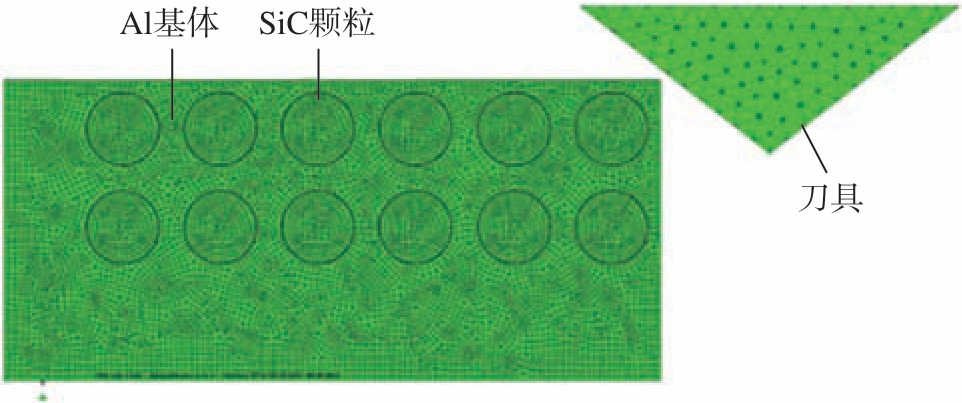
图6 均匀分布二维细观力学模型[10]
Fig.6 Uniformly distributed two-dimensional mesomechanical model[10]
1.2.2 多颗粒随机分布几何模型
(1)随机序列吸附法建模。
随机序列吸附法 (Random sequential absorption,RSA)是在基体中逐个加入随机位置和取向的增强颗粒,每次加入新颗粒后都要判断与已存在的颗粒是否相交。如果不相交,则保留;如果相交,则舍弃并重新加入位置和取向随机的增强颗粒。重复按照上述方法添加增强颗粒,达到相应体积分数时停止加入。RSA 的缺点是难以生成高体积分数增强颗粒模型,当颗粒达到一定的数量,基体中的空隙无法加入完整的增强体颗粒,而已存在的颗粒位置已经固定,因此容易达到饱和状态。与球形颗粒相比,圆柱体颗粒由于长径比较大,更容易达到饱和。
大部分学者将颗粒形貌简化为规则形状,如球体、正方体、圆柱体和椭球体。Mishnaevsky 等[11]建立了球形SiC 颗粒增强铝基复合材料的多颗粒立方单胞模型,分析了颗粒体积分数对复合材料流动应力的影响,结果表明,颗粒含量较高时,复合材料的流动应力较高。Abedini 等[12]将颗粒简化为球体,建立了3 种不同的多颗粒立方单胞模型,将单轴拉伸试验结果和模拟结果进行对比,结果表明,颗粒的聚集增加了基体中塑性应变的累积,提高了加工硬化速率。Dandekar 等[13]在建立SiCp /Al 复合材料三维微观模型时,通过RSA 实现了球形颗粒的随机分布,研究发现,模拟切削力和亚表面损伤与实际测量结果相差不大。Llorca 等[14]首先建立了颗粒形状为球体的单粒子圆柱体单元模型,通过模拟分析获得拉伸的应力–应变曲线,再利用RSA 方法得到30 个球体随机分布的多粒子单元模型,进行三维有限元分析,模拟得到多粒子单元模型的拉伸应力–应变曲线,发现与单粒子轴对称单元模型模拟结果基本一致。球形多颗粒周期立方单元模型如图7 所示。
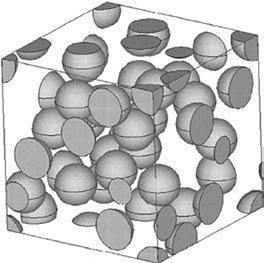
图7 球形多颗粒周期立方单元模型[14]
Fig.7 Spherical multi-particle periodic cubic element model[14]
齐小乐[3]在建立三维单颗粒几何模型的基础上,建立了SiCp /Al 颗粒增强复合材料的三维多相模型。采用Python 语言编写脚本文件,实现了三维模型中正方体颗粒和球体颗粒的随机分布,如图8 所示。
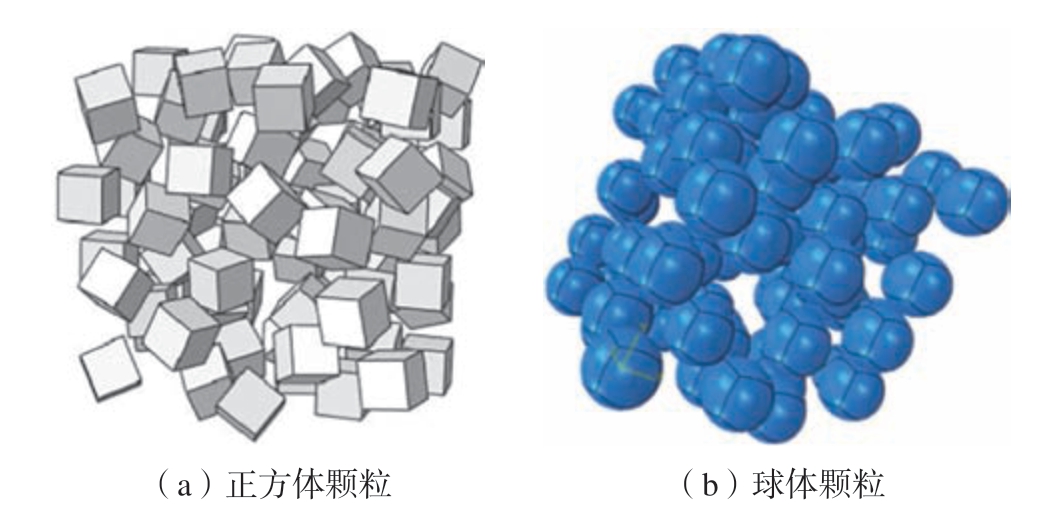
图8 正方体颗粒和球体颗粒随机分布三维几何模型[3]
Fig.8 Three-dimensional geometric model of random distribution of square and spherical particles[3]
金泉等[15]运用RSA 方法将球形颗粒和短纤维混合增强复合材料单胞建模,进行纤维状TiB 和球形颗粒状TiC 增强Ti6242 合金的有限元分析。模型设定为边长20 μm 的正方体,模型中含有5 个半径为1.7 μm 的TiC 颗粒和25 根半径0.77 μm、长10.77 μm 的TiB 纤维,构成增强体的体积分数为8%,如图9 所示。
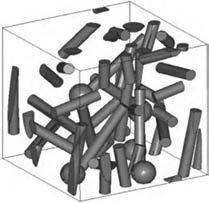
图9 纤维和颗粒混合增强复合材料的三维模型[15]
Fig.9 Three-dimensional model of fiber and particle reinforced composites[15]
为了更灵活控制颗粒的形状,还有学者根据RSA方法的基本思想,通过编程得到不同体积分数增强颗粒的复合材料几何模型。根据概率函数生成椭球或其他形状颗粒的尺寸参数,将颗粒进行投放并判断是否与已存在的颗粒接触或相交,如果不相交则保留,相交则舍弃,重新生成新的颗粒进行投放和判断,达到相应体积分数时停止。李友云等[16]将颗粒简化为椭球形状,以体积为标度并设定椭球之间不相交或不相互包含,提出三维随机骨料投放算法:首先设定边长参数建立矩形模型,其次设定椭球生成相关参数的概率分布及终止条件,达到相应体积分数后停止运行,图10 为体积分数分别为15%和25%时的几何模型。关振群等[17]建立了几何模型自动算法,通过控制参数生成相应体积分数的几何模型,为模拟复合材料的宏观力学性能奠定基础。
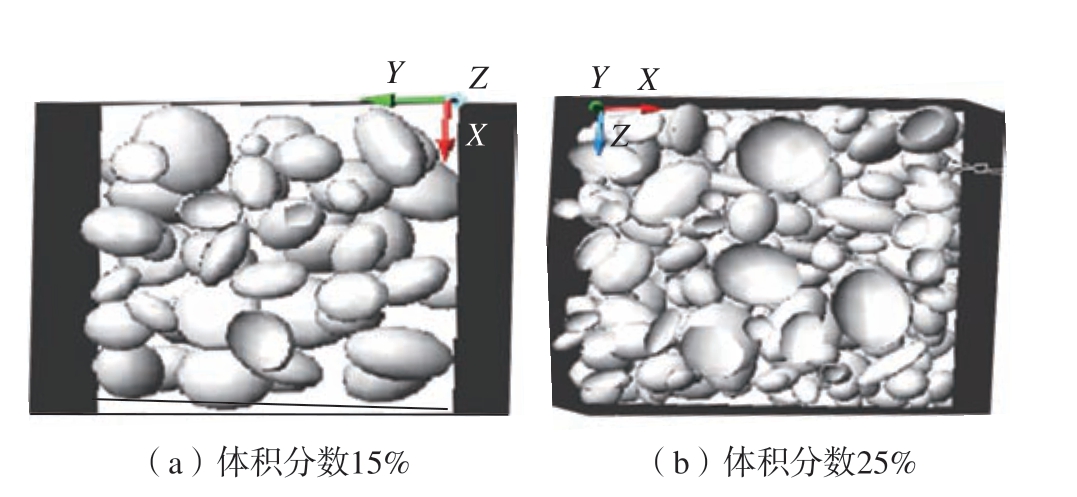
图10 不同体积分数复合材料椭球颗粒随机分布几何模型[16]
Fig.10 Geometric model of random distribution of ellipsoidal particles in composites with different volume fractions[16]
为了建立高体积分数椭球颗粒增强复合材料的几何模型,陈云等[18]基于紧凑和舍选算法,提出了一种高体积分数增强颗粒建模方法,依次在x、y、z 方向生成几何模型,使椭球在单胞区域内紧凑分布,最后根据舍选算法随机舍弃部分椭球,使其达到相应的体积分数,图11为第1 层椭球分布模型。
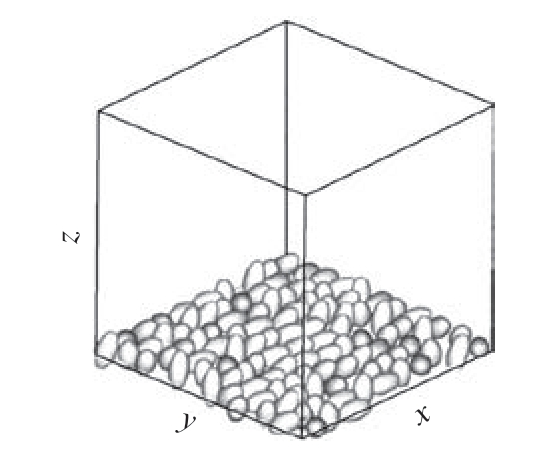
图11 第1 层椭球分布模型[18]
Fig.11 First layer ellipsoid distribution model[18]
还有部分学者根据颗粒的真实形貌,建立了不规则多面体SiC 颗粒模型。耿昆等[4]运用RSA 方法建立了低体积分数SiC 颗粒模型,并进一步进行了SiCp /Al 复合材料建模;具体建模流程及结果如图12 所示,首先获取模型的各项参数 (如SiC 颗粒尺寸大小、相应的SiC颗粒体积分数),然后建立单颗粒三维图形,插入该图形并运行Python 随机分布脚本,确保SiC 颗粒不相交,当SiC 颗粒体积分数到达设定值时停止插入,最后根据颗粒几何形状,采用内聚力单元进行界面层建模,完成SiCp /Al复合材料的微细观三维有限元建模。Zhang等[19]采用三维代表性体积元进行建模,模拟复合材料微观结构,SiC 颗粒的形貌为多面体,程序控制碳化硅颗粒的尺寸、形状、位置和体积分数等几何参数,可用于根据实际几何信息复制任意形状的SiC 颗粒增强材料。
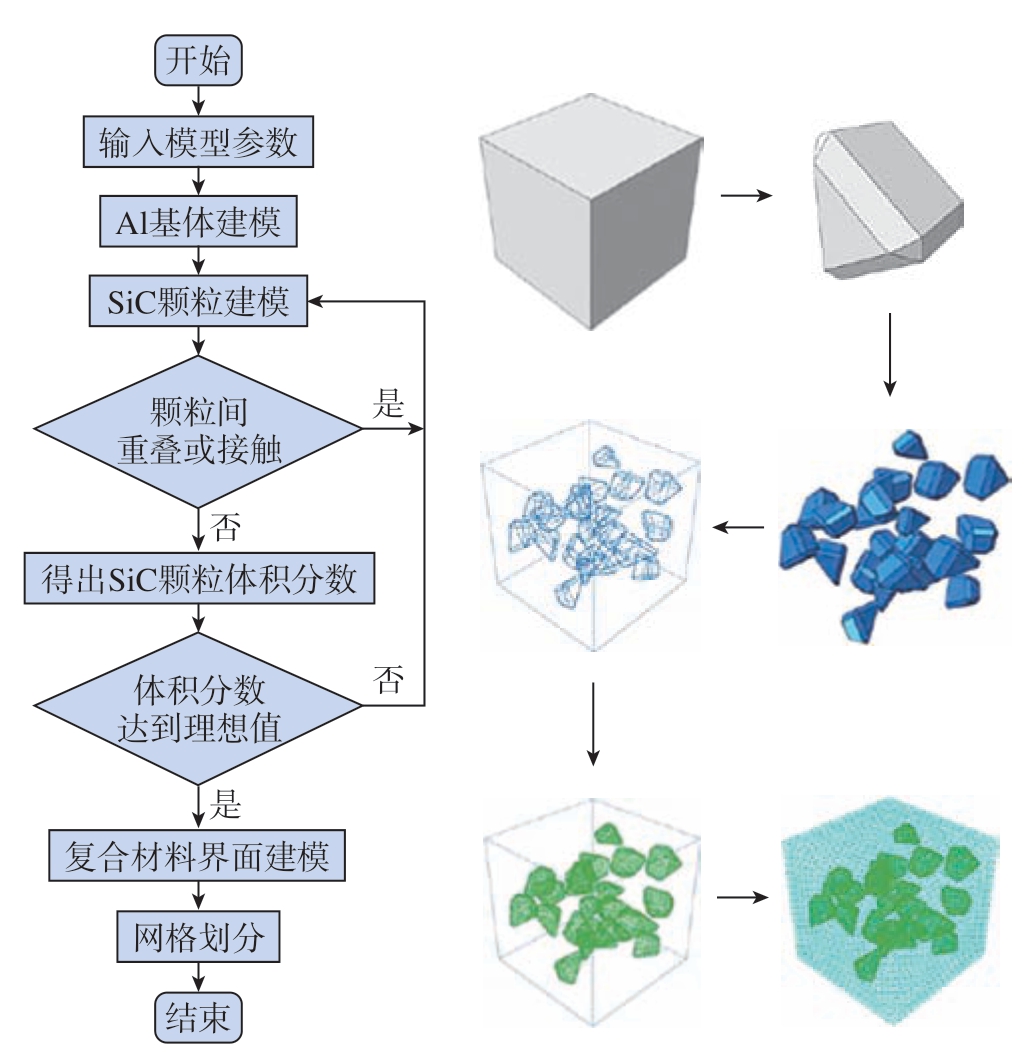
图12 SiCp /Al 复合材料三维建模流程[4]
Fig.12 Three-dimensional modeling process of SiCp /Al composites[4]
Su 等[20–21]根据对SiC 颗粒的物理观察和统计分析,得到了SiC/Al 复合材料的实际微观结构,对四面体进行边缘切除,得到不同形状的多面体SiC 颗粒;通过Python 编写颗粒随机分布脚本,生成SiC 颗粒三维几何模型;通过对脚本修改可以生成不同体积分数SiC 颗粒的三维几何模型,如图13 所示。
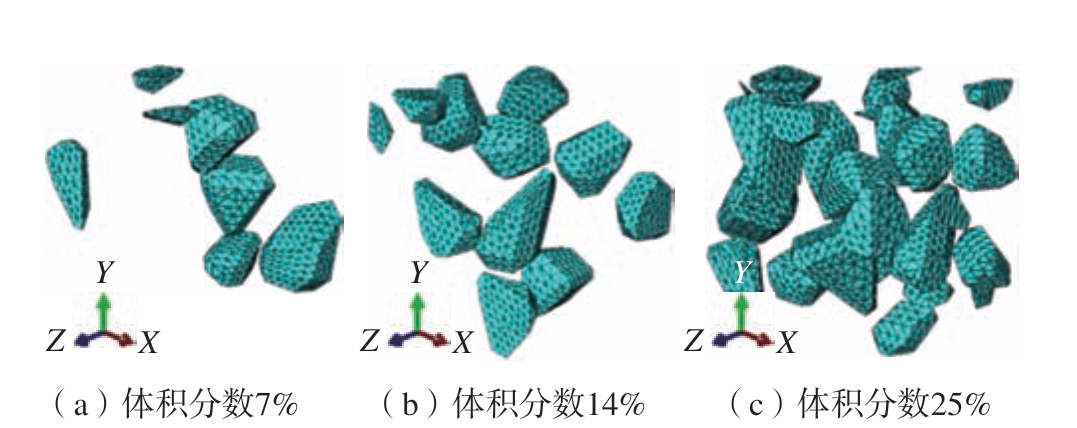
图13 不同体积分数SiC 颗粒三维几何模型[20]
Fig.13 Three-dimensional geometric models of SiC particles with different volume fractions[20]
(2)三维重构法建模。
三维重构法是将复合材料进行抛光,然后在显微镜下观察拍照,通过对不同抛光深度下的照片进行三维重构得到其三维结构。Sidhu 等[22]采用维氏压痕法对试样表面进行循环抛光和拍照,生成一系列微观结构截面;将分割后的微观结构进行堆叠,并采用矢量软件重建粒子的三维形态,具体流程如图14 所示。
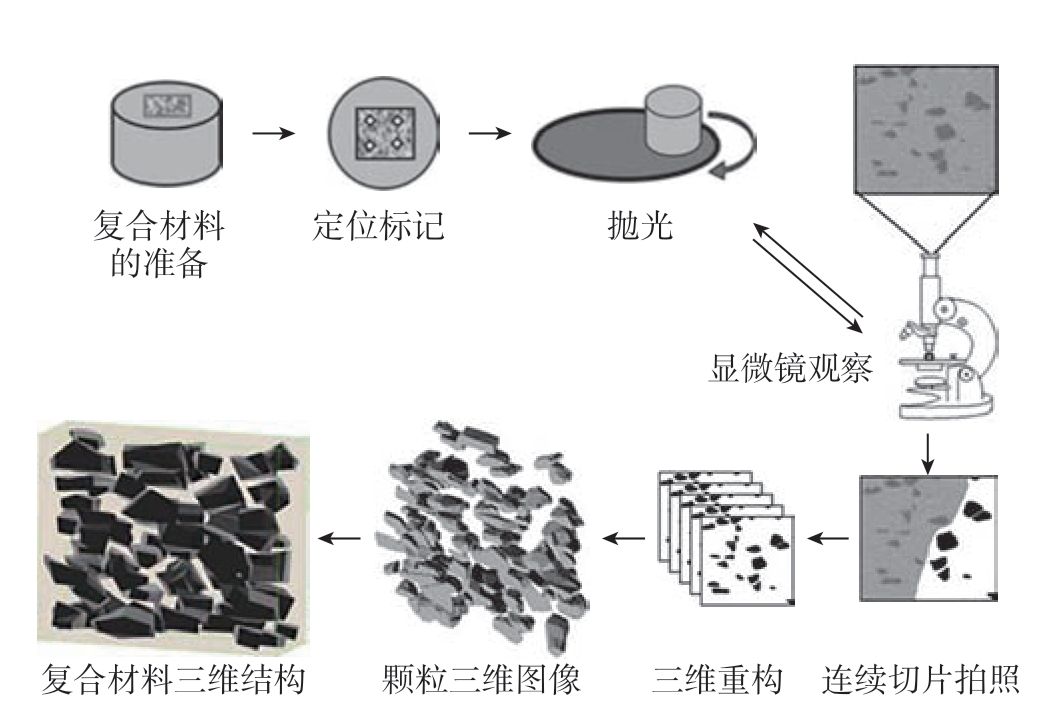
图14 维氏压痕法抛光测量流程[22]
Fig.14 Polishing measurement process of Vickers indentation method[22]
为了对复合材料进行细观力学研究,必须建立合理的分析模型,这种模型从复合材料中选取典型体积单元,保证取出的典型单元必须小到足以表示材料的细观结构特征,而且又要大到足以表征复合材料的全部物理力学性能,这种简化的单元体称为代表性体积单元(RVE)。雷书宾等[23]根据典型颗粒形貌,采用三维混合画法进行CAD 矢量图重构,针对4 种不同形状的颗粒,采用随机分布算法,将4 种不同形状重构颗粒 (图15(a))均匀地插入Al 基体中,建立了含有不同SiC 尺寸、形貌、分布和体积分数的RVE 模型(图15(b))。
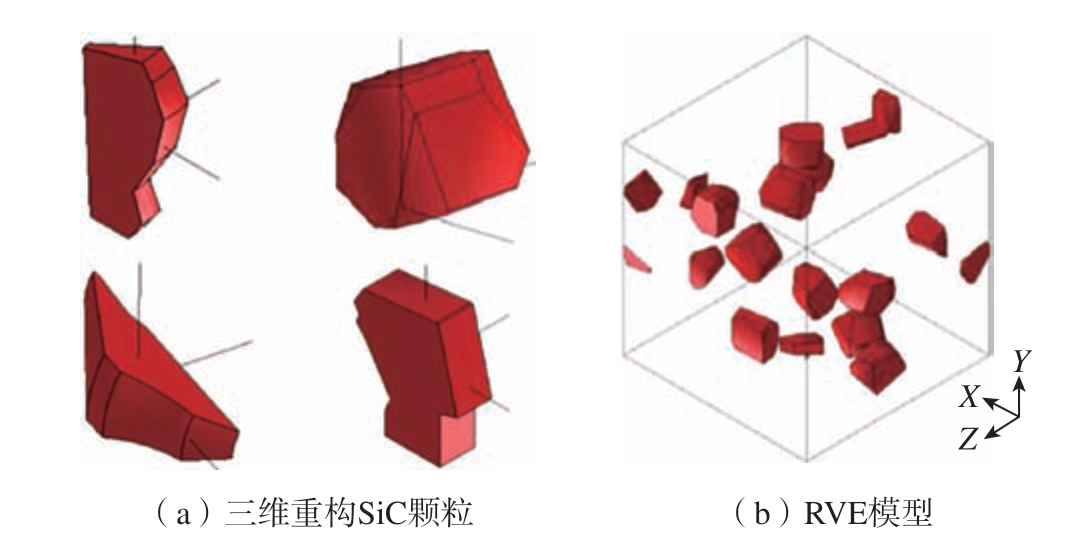
图15 三维重构SiC 颗粒及RVE 模型[23]
Fig.15 Three-dimensional reconstruction of SiC particles and RVE model[23]
1.3 界面模型的建立方法
1.3.1 直接绑定约束
颗粒增强复合材料三维有限元建模时,界面建模最简单的方法为直接绑定,就是用绑定约束将颗粒和基体约束为一个整体。薛锡国[24]首先建立两个部分 (SiC颗粒和Al 基体),然后采用绑定方式将两者约束起来,如图16 所示。

图16 直接绑定约束界面三维模型[24]
Fig.16 Three-dimensional model of direct binding constraint interface[24]
1.3.2 内聚力模型
相比于传统断裂力学模型,建立在弹塑性断裂力学基础上的内聚力模型对复合材料界面开裂行为的研究更为有效。内聚力是指物质内部相互作用力,包括原子力和分子力。采用内聚力模型表征颗粒–基体界面层材料的力学行为,需要将基体和颗粒界面设置为内聚力单元。界面层建模采用内聚力模型具有两个优点:一是能克服裂纹萌生预测的困难,对界面裂纹的萌生、扩展和失效进行统一描述;二是当断裂表征参数的尺度与材料或结构的特征尺度接近时仍然有效。
建立内聚力界面模型有零厚度界面层和有厚度界面层两种方式。零厚度界面层采用颗粒–基体两侧界面共用节点的方式,通过内聚力单元传递应力;有厚度界面层则是赋予内聚力单元并通过绑定约束将其与颗粒和基体进行装配。
徐春光[25]在SiCp /Al 复合材料振动切削界面层损伤机理仿真研究中,介绍了界面层建模的两种方法:(1)在同一个部件中直接划分出基体、颗粒及界面层(图17(a)),内聚力单元通过共用节点方式在颗粒–基体之间传递应力,采用此方法时基体、颗粒及界面始终是在一个部件内,避免了不同部件之间的装配、接触和约束等定义,但网格划分较为复杂; (2)对颗粒、基体和界面分别建立部件 (图17(b)),三者之间通绑定约束绑定在一起,用约束传递应力与位移,采用该方法时,颗粒、基体、界面可以独立划分网格,但三者的装配、接触及约束较为烦琐。
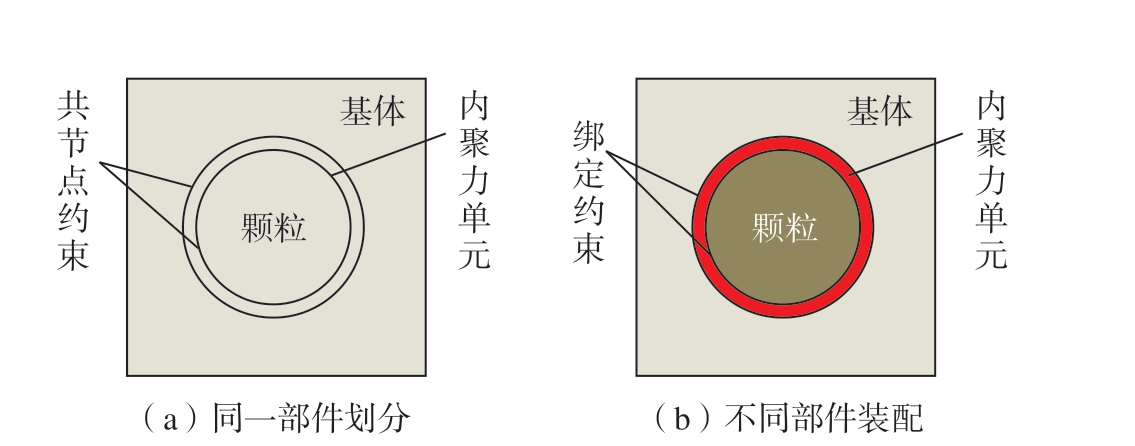
图17 界面层建模方法[25]
Fig.17 Interface layer modeling method[25]
大多数学者采用零厚度的内聚力单元建立界面模型。Zhang等[19]为了模拟裂纹的产生和拓展,采用零厚度内聚力单元,发现裂纹引起的孔洞降低了复合材料的承载能力,加速了损伤累积。Ghandehariun等[26–28]为了验证内聚力模型的正确性,采用零厚度的内聚力单元对界面进行约束和模拟,模拟结果和试验数据吻合较好,使得在切削加工中模拟颗粒脱黏和断裂成为可能。Dandekar 等[29]对颗粒和基体之间界面的建模也通过零厚度内聚力单元实现,预测了颗粒–基体界面的脱黏,研究表明,亚表面损伤和切削力的模拟结果和试验测量结果基本一致。Yuan 等[30]通过零厚度界面层来研究颗粒增强复合材料的界面失效机理,发现长径比大且垂直于拉伸载荷方向的颗粒容易开裂,而长径比小的颗粒则容易从颗粒极点处发生界面脱黏。Williams等[31]采用零厚度的内聚力单元描述两种不同形状的SiC 颗粒–基体界面脱黏现象,模拟发现椭球颗粒表面在脱黏过程中未发生松弛,验证了椭球模型颗粒增强复合材料对脱黏缺乏敏感性的结论。Yuan等[32]采用内聚力零厚度单元模型对界面裂纹扩展进行建模,分析界面性能对材料应力应变状态的影响,研究表明,界面断裂韧性在5~60 J/m2 时,界面断裂韧性的增加将导致流动应力增加;当界面断裂韧性超过60 J/m2 时,随着界面断裂韧性的增加流动应力反而减小。Umer等[33]采用零厚度内聚力单元对增强颗粒–铝基体的界面行为进行研究,通过定义界面力和裂纹张开位移之间的关系来表征界面行为,裂缝区由两个相同的内聚面组成,模拟发现内聚单元的刚度随着分离度的增加而降低。
少数学者采用有厚度的内聚力单元建立界面模型。齐小乐[3]为了分析不同界面模型的优缺点,建立了零厚度界面层和有厚度界面层两种界面模型,通过对采用两种不同界面模型的SiCp /Al 复合材料切削仿真模型的模拟,发现采用有厚度界面模型时,切削过程中材料失效会在颗粒周围造成较大缝隙,对仿真结果有一定影响,零厚度界面模型的模拟结果较好。薛锡国[24]将有厚度内聚力单元加入到颗粒和基体之间,三者采用绑定约束方式形成一个整体,如图18 所示。Yu 等[34]选用有厚度内聚力单元研究复合材料的切削加工去除机理和损伤行为,发现颗粒聚集处切屑容易分离,颗粒边角处应力集中现象严重。
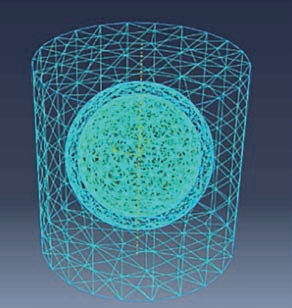
图18 有厚度内聚单元模型[24]
Fig.18 Thickness cohesive element model[24]
2 本构模型
建立的本构模型是否能够准确描述颗粒增强复合材料切削过程的动态力学行为,直接影响切削加工模拟的准确性。因此,本构模型是颗粒增强复合材料切削加工有限元建模的重要内容。
2.1 等效均质本构模型
等效均质本构模型将复合材料等效为均质材料,通过准静态压缩试验和动态力学性能试验来获取均质本构模型参数。薛锡国[24]进行了准静态压缩试验和分离式霍普金森压杆试验,获取Johnson–Cook 本构模型参数,应变率范围为0.01~8500 s–1,温度范围为50~400 ℃;对体积分数15%的SiCp /Al 复合材料的静态和动态力学性能进行研究,得到其Johnson–Cook 本构方程参数。Johnson–Cook 本构模型的表达式为
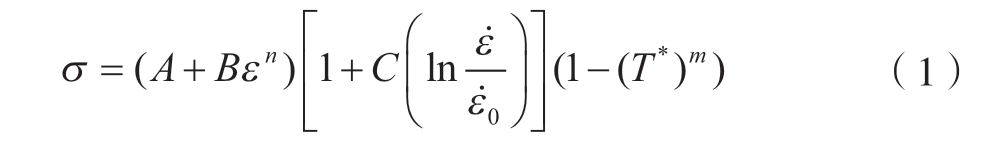
式中,σ 为等效流动应力;ε 为等效塑性应变;A、B、n、C和m 为模型常数;ε.为等效塑性应变率;ε.0 为参考应变率;无量纲温度T *=(T – Troom) /(Tmelt – Troom),T 为切削温度;Troom为参考温度;Tmelt 为材料熔点。
具体求解过程:通过准静态压缩试验得到应力–应变曲线,再经过线性拟合求出A、B、n 的值。由于试验应变率较低,温升可以忽略,此时Johnson–Cook 本构模型可转化为
通过不同温度和应变率下的霍普金森压杆试验得到真实的应力–应变曲线,再经过线性拟合得到参数C和m。在霍普金森压杆试验中,试验过程短暂,因此温度对材料强度的影响忽略不计。因此式(2)转化为
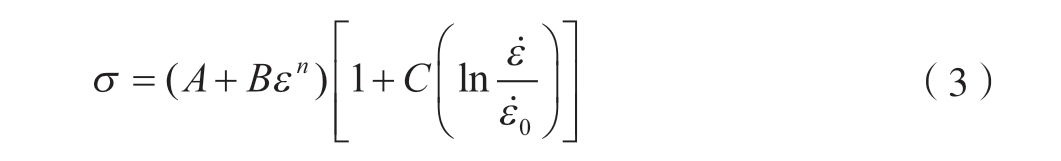
取同一塑性应变,不同应变速率下的应力值,拟合获取C 值,对其计算平均值得到最终结果。取同一应变和应变率,不同温度下的材料塑性应变和应力值代入式(1)中来获取m 值。
Chen 等[35]采用了上述本构模型参数建立了SiCp /Al6063 复合材料三维槽铣有限元模型,将仿真结果和试验结果进行对比,结果表明,不同进给速度和转速条件下的铣削力模拟值与试验值基本吻合,预测的铣削力和切屑形状与试验结果相差不大,误差控制在20%以内。
杨嘉[36]对SiCp /Al6063 复合材料进行不同温度和应变率试验,获取其Johnson–Cook 本构参数,并使用Advantage 软件进行了铣削仿真。通过仿真应力场结果的分析发现,在铣削过程中应力从刀尖向后逐渐降低,应力最大值位于刀尖处,其次进行温度场分析,获取了不同铣刀的温度分布云图,发现铣削过程中大量切削热被切屑带走。
孙素杰等[37]通过准静态压缩试验和霍普金森压杆试验获取SiCp /Al6063 复合材料的Johnson–Cook 本构参数,结合泰勒位错理论和微细切削理论得到修正后的材料本构模型及参数,进行模拟仿真获得轴向力、扭矩随进给速度和主轴转速变化的结果,发现扭矩受主轴转速的影响较大,而轴向力受进给速度的影响较大。
Sun 等[38]通过电子万能试验机和霍普金森压杆试验得到Al2024 的应力–应变曲线,拟合得到Al 基体的Johnson – Cook 本构参数,结合Weibull 统计分布、Eshelby 等效夹杂理论和高斯函数,并考虑颗粒损伤和热软化,得到SiCp /Al 复合材料的修正动态塑性本构模型,通过理论分析和试验进行了验证,结果表明,该动态本构模型能够准确预测颗粒增强复合材料的动态压缩行为,颗粒的强化作用随着颗粒损伤概率的增加而降低,随着温度的升高,基体的流动性逐渐增强,使得复合材料的动态压缩力学特性与韧性基体材料逐渐接近。
等效均质材料模型计算效率较优异,因此上述学者在建模时,将复合材料视为均质模型,进行一系列力学试验或者理论公式计算获得均质模型的本构参数(表1)。
表1 SiCp /Al 复合材料的Johnson–Cook 本构参数
Table 1 Johnson–Cook constitutive parameters of SiCp /Al composites
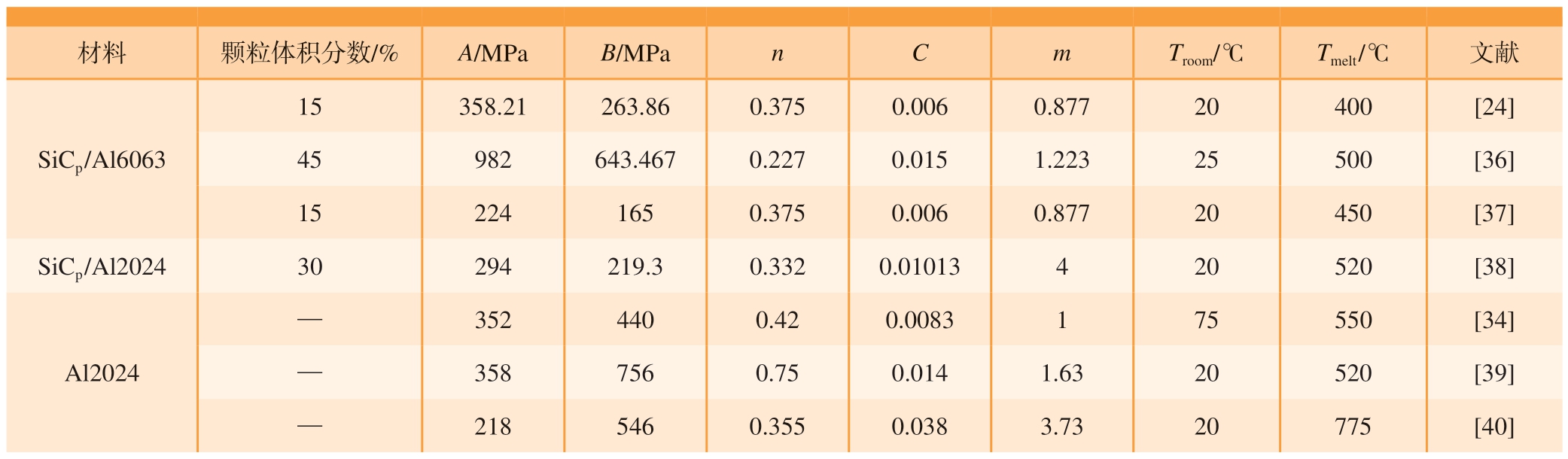
材料颗粒体积分数/%A/MPaB/MPanCmTroom/℃Tmelt /℃文献SiCp /Al6063 15358.21263.860.3750.0060.87720400[24]45982643.4670.2270.0151.22325500[36]152241650.3750.0060.87720450[37]SiCp /Al202430294219.30.3320.01013420520[38]Al2024—3524400.420.0083175550[34]—3587560.750.0141.6320520[39]—2185460.3550.0383.7320775[40]
2.2 非均质本构模型
等效均质模型假设复合材料均质且各向同性,与材料的真实情况差异较大,不能准确预测材料的变形和失效。因此学者对基体、颗粒和界面分别赋予本构模型,从而构建非均质本构模型,进而对颗粒增强复合材料进行三维切削有限元分析。
2.2.1 基体本构模型
Yu 等[34]建立考虑颗粒损伤的颗粒增强金属基复合材料切削有限元模型,研究其在加工过程中损伤行为,采用Johnson – Cook 本构描述Al2024 基体的材料特性,并添加Johnson – Cook 损伤模型来定义初始损伤,其表达式为
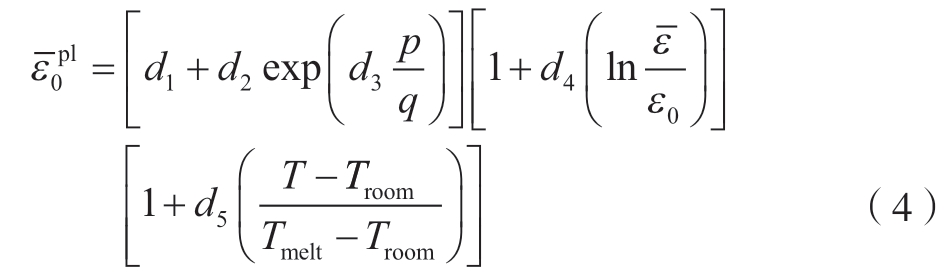
式中,d1~ d5为失效模型系数;p为平均主应力,即静水压力;q为流动应力;![]() 为塑性应变率;
为塑性应变率;![]() 为参考应变率;
为参考应变率;![]() 为失效时的等效应变。通过模拟仿真发现,在颗粒聚集处,切屑很容易分离,颗粒边角处应力集中严重,切削力和表面损伤随切削深度的增加而增加,与试验结果相吻合,验证了有限元方法的可靠性。
为失效时的等效应变。通过模拟仿真发现,在颗粒聚集处,切屑很容易分离,颗粒边角处应力集中严重,切削力和表面损伤随切削深度的增加而增加,与试验结果相吻合,验证了有限元方法的可靠性。
Fan 等[39]通过压缩试验和分离式霍普金森压杆试验,获得了Al2024 的Johnson – Cook 模型参数 (表1),采用的应变率范围为3000 ~ 8500 s–1,温度范围为20 ~520 ℃;结合应变梯度与主剪切变形区长度的关系,获得修正后的Johnson – Cook 本构模型,采用修正后的本构模型进行仿真,模拟结果和试验结果基本一致,验证了修正本构模型的有效性,进而研究温度对几何必须位错密度的影响,结果表明,在切削过程中,高温促进了位错的剧烈运动,加速了位错的扩散速率,使几何必须位错密度减小。
郑伟[40]通过准静态和动态压缩试验得到Al 基体的Johnson – Cook 本构参数,进行了SiCp /Al 复合材料的非均质微观建模,对刻划过程中复合材料表面缺陷的形成进行了研究,结果表明,磨削过程中SiC 颗粒出现应力集中现象,由于磨粒的相对位置不同而出现翻滚压入、局部破碎断裂、完全破碎断裂和脱黏拔出现象,仿真结果与刻划试验结果符合较好,验证了模型的正确性。
2.2.2 增强颗粒本构模型
颗粒脆性断裂在复合材料切削加工过程中时有发生,为了在仿真中考虑颗粒的断裂,通常采用以下两种途径进行研究: (1)通过引入脆性断裂准则,实现对颗粒断裂的仿真; (2)省略其材料模型中的脆性断裂属性,分析颗粒受力情况,预测其断裂的可能性。第2 种途径较为简单,文献[41]表明,当颗粒发生断裂时其抗拉强度的临界值大约为1500 MPa。SiC 颗粒发生断裂后,可以采取断裂能准则表征其失效演化行为[42]。裂纹开始位移un0 可以通过式 (5)计算。
式中,![]() 为材料的I 型断裂能;
为材料的I 型断裂能;![]() 为I 型裂纹形成时的失效应力。
为I 型裂纹形成时的失效应力。
通过剪切应力模型描述SiC 颗粒失效演化过程中剪切应力的影响。此时剪切模量Gs 为
式中,G为材料失效前的剪切模量;![]() 为材料的剪切保留因子,其计算公式为
为材料的剪切保留因子,其计算公式为
式中,![]() 为SiC 颗粒的开裂应变;P 和
为SiC 颗粒的开裂应变;P 和![]() 为材料参数。
为材料参数。
Liu 等[43]通过碳化硅的脆性断裂模型研究了切削速度和刀具–颗粒相互作用位置对微细加工过程中颗粒行为和表面形成的影响,发现刀具切削路径在颗粒上部区域时,SiC 颗粒去除形式以破碎为主,而表面缺陷的深度随着切削速度的增加而减小。王涛[44]通过包含颗粒脆性断裂准则的简化圆形和多边形颗粒微观形貌模型,模拟了SiCp /Al 复合材料切削加工时,SiC 颗粒的破损、剪断和剥离现象。武永祥[45]在对SiCp /Al 复合材料进行切削仿真建模时也采用了脆性开裂模型。以上3 位学者采用了相同的断裂参数 (表2)。
表2 SiC 颗粒脆性断裂模型参数
Table 2 Parameters of SiC particle brittle fracture model

σI tu /MPaGf I/(J·m–2)Pεck max 15003010.001
2.2.3 颗粒–基体界面本构模型
复合材料的界面层是在材料制备时,基体材料与增强相材料相互作用生成的不同于这两相材料的第三相材料。近年来,随着界面层相关理论的完善和计算机技术的发展,关于包含界面层的颗粒增强复合材料力学性能的研究开始引起研究人员的广泛兴趣,主要以内聚力模型为主。
内聚力模型通过界面层张应力与张开位移的关系进行表示,可以采用双线性、指数、梯形等形式,其中双线性形式应用最多,如图19 所示。界面失效过程分为两个阶段: (1)OA 段为线弹性阶段,随着界面位移的增加、材料刚度线性增大; (2)AB 段为线性软化阶段,达到应力最大值后,材料刚度随着张开位移的增加而减小。可以看出,内聚力单元的应力–位移曲线可以由界面强度 (图19 中三角形的高)、界面完全失效时的最大位移 (图19 中三角形的底边长度)和界面断裂能 (图19中三角形的面积)中的任意两个确定。界面断裂能和完全失效最大位移的关系为
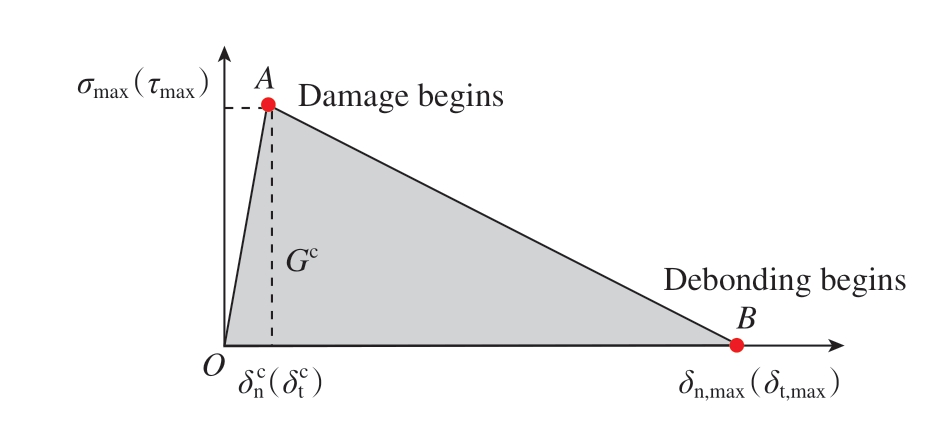
图19 内聚力单元的应力–位移关系[44]
Fig.19 Stress–displacement relationship of cohesive element[44]
式中,Gc为界面断裂能;σmax为模型中界面强度;δn,max为界面完全失效时的最大位移。
部分学者[13,34,40]使用内聚力单元建立界面模型,内聚单元本构关系可以表达为
式中,σmax为内聚单元强度,GPa;ξ为内聚力单元损伤值。
内聚力单元损伤断裂准则如式 (10)所示,当内聚力单元损伤值为1 时,单元失效去除。
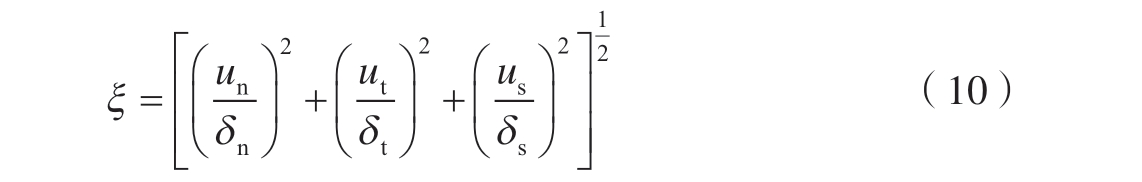
式中,ut、us为内聚力单元切向分离位移;un为内聚力单元法向分离位移;δt、δs为内聚力单元切向分离位移阈值;δn为内聚单元法向分离位移阈值。
目前在SiCp /Al 复合材料切削有限元模拟时,多数学者采用内聚力模型进行界面层建模,表3[13,34,46]给出了部分学者采用的模型参数。
表3 界面层内聚力模型参数
Table 3 Parameters of cohesive model in interface layer
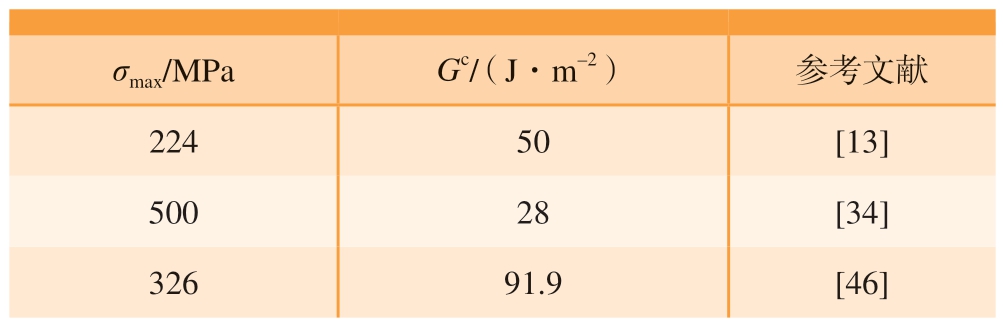
σmax/MPaGc/(J·m–2)参考文献22450[13]50028[34]32691.9[46]
3 网格划分及边界条件处理
3.1 网格划分
在有限元分析中,颗粒增强复合材料三维建模较为复杂,使得许多学者在颗粒增强复合材料三维模型网格划分中进行分块划分,即分别对基体、增强颗粒和界面进行网格划分。
齐小乐[3]选用六面体网格划分方法,其中Al 基体和SiC 颗粒为八节点的六面体单元,界面为八节点的三维内聚力单元。金泉等[15]采用四面体单元进行网格划分并对增强体附近区域进行局部网格加密。关振群等[17]采用改进的推进波前法 (Advancing front technique,AFT)分别对基体的内外边界、基体和增强颗粒进行网格划分,最后进行装配,基于AFT 的网格生成及装配步骤如图20 所示。Zhang 等[19]采用线性三维实体单元对基体和SiC 颗粒进行网格划分,使用细网格 (SiC 颗粒和基体网格尺寸分别为0.5 mm 和0.8 mm)对几何模型离散,单元类型采用六节点和八节点的三维内聚力单元。Su等[21]建立了RVE 模型,Al 基体和SiC 颗粒采用四面体单元网格自动划分方法,对界面模型沿厚度方向进行扫掠划分网格。薛锡国[24]对Al 基体采用C3D4 单元进行网格划分,采用小于Al 基体的SiC 颗粒和界面的网格尺寸以提高计算精度。

图20 基于AFT 的网格生成及装配步骤[17]
Fig.20 Grid generation and assembly steps based on AFT[17]
3.2 边界条件处理
颗粒增强复合材料有限元模拟中对边界条件的处理大致分为两种:对RVE 模型采用周期性边界条件;对宏观切削模型采用切削边界条件。
在RVE 模型的周期性边界条件设置方面,Zhang等[19]采用位移边界条件,一方面对所有模型施加10 mm 的位移,加载方向为拉伸方向;另一方面,位移加载时 (仅固定面和RVE 加载面)节点的旋转自由度在三轴方向均受到约束。雷书宾等[23]对RVE 模型采用周期性边界条件,沿X 轴方向施加2%应变的单向加载。高翔[47]采用拉伸边界条件,先对模型进行约束,再对加载点施加X 方向的拉伸位移载荷,模型约束流程如下:先固定模型的左表面 (X = 0)并施加约束,使左表面节点不能在X 轴方向移动;其次对上下表面进行约束,保证上下表面平行X – Z 平面;同理,对前后表面进行约束;最后约束右表面,保证该面始终与Y – Z 平面平行,如图21 所示。
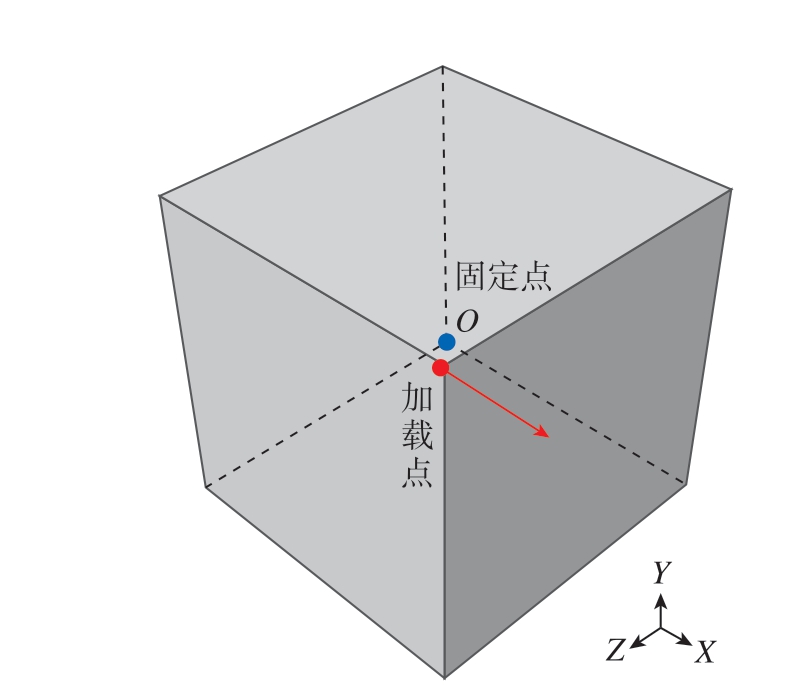
图21 RVE 模型边界处理[47]
Fig.21 Boundary processing of RVE model[47]
在对切削边界条件进行设置时,二维模型和三维模型在本质上没有区别。武永祥[45]建立了颗粒增强复合材料二维切削有限元模型,对工件模型切削层下方的左右两侧和底部进行固定约束,而在切削层和刀具之间建立面面接触,施加的边界条件如图22 所示。
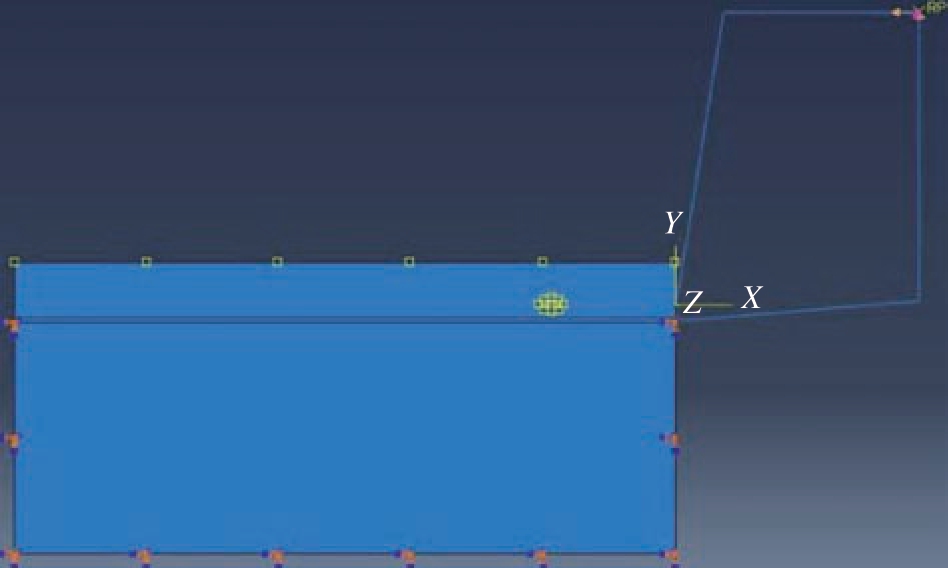
图22 切削有限元模型边界处理[45]
Fig.22 Boundary treatment of cutting finite element model[45]
4 存在的问题和发展方向
由上述研究可以看出,随着有限元仿真技术的发展,颗粒增强复合材料切削加工的三维有限元模拟已经取得一定的进展,但还需要进一步完善和改进,主要包括以下6 个方面。
(1)颗粒合理简化模型的建立。在对增强颗粒建模时,规则模型 (如圆球体、椭球体、正方体)和不规则模型 (根据对颗粒真实微观结构的观测和统计分析建立)都有涉及,但是缺乏对不同模型模拟结果的对比研究。应进一步研究不同模型对仿真结果的影响,以便在颗粒增强复合材料切削加工三维有限元模拟时进行合理简化,既能保证模拟结果的有效性,又能降低建模难度。
(2)多颗粒几何模型的建立。当前对于颗粒规则分布模型的微观研究,通常采用单颗粒模型进行分析。这种方法虽然能够较好地分析颗粒与基体的相互作用,但是难以体现颗粒之间的相互影响和变形协调效应,而这些随着颗粒增强复合材料体积分数的增大将会变得显著。因此,应进一步建立双颗粒模型,开展对增强颗粒相互影响及变形协调效应的研究。
(3)高体积分数颗粒增强复合材料几何模型的建立。在当前的颗粒增强复合材料切削加工仿真中,对多颗粒均匀分布和随机分布模型都有研究。随机序列吸附算法和微观重构建模方法都得到了较好的应用。但是随机序列吸附算法在高体积分数颗粒增强复合材料的建模时存在困难,微观重构建模方法不仅过程烦琐,而且从统计角度来看,对模拟结果的有效性提升作用有限。因此开展高体积分数颗粒增强复合材料有限元仿真几何建模的研究仍是将来的一个重点方向,而基于Python 编程的建模方法仍是主流,紧凑算法和随机舍选算法是较好的选择。
(4)界面模型的建立。目前在界面建模时,采用内聚力单元是主流方法,但是零厚度和有厚度内聚力单元都有采用。有必要开展对比研究,确定合理界面模型的建立原则,同时考虑界面层材料与基体及颗粒的界面效应。
(5)合理本构模型的建立。在本构模型方面,等效均质本构模型和非均质本构模型都有成功应用。但还应进一步考虑各自的适用范围并进行合理选择。进行切削力、切削形态和切削温度等宏观物理量模拟时,可以采用等效均质模型,建模简单且本构模型易于获取。而在研究颗粒挤压、SiC 颗粒脱黏、颗粒断裂和裂纹等微观现象时,则应采用非均质本构模型。而在非均质本构建模时,应保证基体材料力学性能试验时,其试件与颗粒增强复合材料的基体在微观组织上保持一致,以此保证基体本构模型的有效性。同时界面内聚力模型参数的确定还有较大的随意性,应进一步通过对非均质模型的RVE 仿真反求确定。
(6)网格畸变的有效处理。在颗粒增强复合材料切削加工的三维有限元仿真中,网格畸变的问题将更加突出。简化有利于减小网格畸变的颗粒及界面模型、分区网格划分及结合Hypermesh 进行网格优化等都是需要进一步深入研究的内容。
5 结论
有限元仿真作为颗粒增强复合材料切削加工机理研究的一个主要手段,在节省成本、获得应力、应变、温度分布及微观机理研究方面体现出较好的优越性。目前对颗粒增强复合材料切削加工三维有限元模拟方面的研究不仅较少,还存在诸多问题,如缺乏对不同颗粒简化模型模拟结果的对比研究,单颗粒模型难以体现颗粒之间的相互影响和变形协调效应,随机序列吸附算法在高体积分数颗粒增强复合材料的建模方面存在困难等。将来应进一步开展的研究有:高体积分数颗粒增强复合材料切削有限元仿真几何建模的研究;零厚度和有厚度内聚力单元的对比研究;非均质本构建模时基体本构模型的有效性研究;内聚力模型参数的确定方法研究;颗粒及界面模型简化、分区网格划分以及网格优化研究。
[1] 郑阳升, 杨伟苓, 郑顺奇, 等. 颗粒增强复合材料结构的有限元建模研究现状[J]. 兵器材料科学与工程, 2018, 41(4): 97–102.
ZHENG Yangsheng, YANG Weiling, ZHENG Shunqi, et al. Research status of finite element modeling of particle reinforced composites structure[J]. Ordnance Material Science and Engineering, 2018, 41(4):97–102.
[2] QI F G, DING H M, WANG X L, et al. The stress and strain field distribution around the reinforced particles in Al/TiC composites: A finite element modeling study[J]. Computational Materials Science, 2017,137: 297–305.
[3] 齐小乐. SiCp /Al 颗粒增强复合材料切削加工有限元模拟及实验研究[D]. 天津: 天津职业技术师范大学, 2020.
QI Xiaole. Research of experimental and finite element simulation on cutting of SiCp /Al particle reinforced composites[D]. Tianjin: Tianjin University of Technology and Education, 2020.
[4] 耿昆, 张杰, 张荻. 使役条件下SiCp /Al 复合材料的建模拟实[J]. 航空制造技术, 2017, 60(17): 66–74.
GENG Kun, ZHANG Jie, ZHANG Di. Modeling and simulation of SiCp /Al composite under working conditions[J]. Aeronautical Manufacturing Technology, 2017, 60(17): 66–74.
[5] GAO X, ZHANG X X, GENG L. Strengthening and fracture behaviors in SiCp /Al composites with network particle distribution architecture[J]. Materials Science and Engineering: A, 2019, 740–741: 353–362.
[6] WANG Y F, LIAO W H, YANG K, et al. Simulation and experimental investigation on the cutting mechanism and surface generation in machining SiCp /Al MMCs[J]. The International Journal of Advanced Manufacturing Technology, 2019, 100(5–8): 1393–1404.
[7] SETIA S, CHAUHAN S R. Comparative analysis and optimization of FEM and RSM based regression model with experimental results for the dry turning of SiCp –Al7075 composite[J]. Silicon, 2021,13(12): 4681–4701.
[8] 王进峰, 储开宇, 赵久兰, 等. SiCp /Al 复合材料切削仿真及实验研究[J]. 人工晶体学报, 2016, 45(7): 1756–1764.
WANG Jinfeng, CHU Kaiyu, ZHAO Jiulan, et al. Study on cutting simulation and experiment of SiCp /Al composites[J]. Journal of Synthetic Crystals, 2016, 45(7): 1756–1764.
[9] CHEN Y F, ZHANG X. Study on the cutting mechanism of SiCp /Al considering particle size and distribution[J]. The International Journal of Advanced Manufacturing Technology, 2021, 115(4): 1211–1225.
[10] ZHENG W, DA QU, QIAO G C. Multi-phase modeling of SiC particle removal mechanism in ultrasonic vibration–assisted scratching of SiCp /Al composites[J]. The International Journal of Advanced Manufacturing Technology, 2021, 113(1–2): 535–551.
[11] MISHNAEVSKY L L Jr. Three-dimensional numerical testing of microstructures of particle reinforced composites[J]. Acta Materialia,2004, 52(14): 4177–4188.
[12] ABEDINI A, BUTCHER C, CHEN Z T. Numerical simulation of the influence of particle clustering on tensile behavior of particlereinforced composites[J]. Computational Materials Science, 2013, 73: 15–23.
[13] DANDEKAR C R, SHIN Y C. Multi-scale modeling to predict sub-surface damage applied to laser-assisted machining of a particulate reinforced metal matrix composite[J]. Journal of Materials Processing Technology, 2013, 213(2): 153–160.
[14] LLORCA J, SEGURADO J. Three-dimensional multiparticle cell simulations of deformation and damage in sphere-reinforced composites[J].Materials Science and Engineering: A, 2004, 365(1–2): 267–274.
[15] 金泉, 覃继宁, 张荻, 等. 颗粒和纤维混杂增强复合材料力学性能的三维有限元模拟[J]. 复合材料学报, 2006, 23(2): 14–20.
JIN Quan, QIN Jining, ZHANG Di, et al. 3D FEM simulation of mechanical property of composites reinforced by both particles and fibers[J].Acta Materiae Compositae Sinica, 2006, 23(2): 14–20.
[16] 李友云, 崔俊芝. 具有大量椭圆颗粒/孔洞随机分布区域的计算机模拟及其改进三角形自动网格生成算法[J]. 计算力学学报,2004, 21(5): 540–545.
LI Youyun, CUI Junzhi. Computer simulation method for the domain with large numbers of random ellipse grains/cavities and the improving automatic triangle mesh generation algorithm[J]. Chinese Journal of Computational Mechanics, 2004, 21(5): 540–545.
[17] 关振群, 高巧红, 顾元宪, 等. 复合材料细观结构三维有限元网格模型的建立[J]. 工程力学, 2005, 22(S1): 67–72.
GUAN Zhenqun, GAO Qiaohong, GU Yuanxian, et al. The construction of three-dimensional finite element mesh for microstructure of multiphase composites[J]. Engineering Mechanics, 2005, 22(S1): 67–72.
[18] 陈云, 于艳. 颗粒随机分布复合材料的细观构造对有效热传导系数的影响[J]. 复合材料学报, 2012, 29(2): 145–149.
CHEN Yun, YU Yan. Micro-structure of composites with randomly distributed particles on the impact of the effective thermal conductivity parameters[J]. Acta Materiae Compositae Sinica, 2012, 29(2): 145–149.
[19] ZHANG J, OUYANG Q B, GUO Q, et al. 3D Microstructurebased finite element modeling of deformation and fracture of SiCp /Al composites[J]. Composites Science and Technology, 2016, 123: 1–9.
[20] SU Y S, OUYANG Q B, ZHANG W L, et al. Composite structure modeling and mechanical behavior of particle reinforced metal matrix composites[J]. Materials Science and Engineering: A, 2014, 597:359–369.
[21] SU Y S, LI Z, YU Y, et al. Composite structural modeling and tensile mechanical behavior of graphene reinforced metal matrix composites[J]. Science China Materials, 2018, 61(1): 112–124.
[22] SIDHU R S, CHAWLA N. Three-dimensional(3D) visualization and microstructure-based modeling of deformation in a Sn-rich solder[J].Scripta Materialia, 2006, 54(9): 1627–1631.
[23] 雷书宾, 李建平, 郭永春, 等. SiCp/Al 复合材料的三维微观结构建模与力学行为模拟[J]. 热加工工艺, 2017, 46(10): 121–125, 135.
LEI Shubin, LI Jianping, GUO Yongchun, et al. 3D microstructure modeling and mechanical behavior simulation of SiCp/Al composite[J].Hot Working Technology, 2017, 46(10): 121–125, 135.
[24] 薛锡国. SiCp/Al 复合材料三维铣削仿真基础问题研究[D].北京: 北京理工大学, 2015.
XUE Xiguo. Study on 3D milling simulation of SiCp/Al composites[D].Beijing: Beijing Institute of Technology, 2015.
[25] 徐春光. SiCp/Al 材料振动切削界面层损伤机理仿真与实验研究[D]. 大连: 大连交通大学, 2020.
XU Chunguang. Simulation and experimental research on the damage mechanism of interface layer in SiCp/Al materials during vibration cutting[D].Dalian: Dalian Jiaotong University, 2020.
[26] GHANDEHARIUN A, KISHAWY H A, UMER U, et al. On tool–workpiece interactions during machining metal matrix composites:Investigation of the effect of cutting speed[J]. The International Journal of Advanced Manufacturing Technology, 2016, 84(9–12): 2423–2435.
[27] GHANDEHARIUN A, KISHAWY H A, UMER U, et al. Analysis of tool-particle interactions during cutting process of metal matrix composites[J]. The International Journal of Advanced Manufacturing Technology, 2016, 82(1–4): 143–152.
[28] GHANDEHARIUN A, NAZZAL M, KISHAWY H A, et al.On modeling the deformations and tool–workpiece interactions during machining metal matrix composites[J]. The International Journal of Advanced Manufacturing Technology, 2017, 91(5–8): 1507–1516.
[29] DANDEKAR C R, SHIN Y C. Multi-step 3-D finite element modeling of subsurface damage in machining particulate reinforced metal matrix composites[J]. Composites Part A: Applied Science and Manufacturing, 2009, 40(8): 1231–1239.
[30] YUAN Z W, LI F G, XUE F M, et al. Analysis of the stress states and interface damage in a particle reinforced composite based on a micromodel using cohesive elements[J]. Materials Science and Engineering:A, 2014, 589: 288–302.
[31] WILLIAMS J J, SEGURADO J, LLORCA J, et al. Three dimensional (3D) microstructure-based modeling of interfacial decohesion in particle reinforced metal matrix composites[J]. Materials Science and Engineering: A, 2012, 557: 113–118.
[32] YUAN M N, YANG Y Q, LI C, et al. Numerical analysis of the stress–strain distributions in the particle reinforced metal matrix composite SiC/6064Al[J]. Materials & Design, 2012, 38: 1–6.
[33] UMER U, ASHFAQ M, QUDEIRI J A, et al. Modeling machining of particle-reinforced aluminum-based metal matrix composites using cohesive zone elements[J]. The International Journal of Advanced Manufacturing Technology, 2015, 78(5–8): 1171–1179.
[34] YU W W, CHEN J, MING W W, et al. Experimental and FEM study of cutting mechanism and damage behavior of ceramic particles in orthogonal cutting SiCp/Al composites[J]. Ceramics International, 2021,47(5): 7183–7194.
[35] CHEN X L, XIE L J, XUE X G, et al. Research on 3D milling simulation of SiCp/Al composite based on a phenomenological model[J].The International Journal of Advanced Manufacturing Technology, 2017,92(5–8): 2715–2723.
[36] 杨嘉. 铝基碳化硅精密铣削过程有限元仿真及实验研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
YANG Jia. Finite element simulation of precision milling SiCp/Al and experimental study[D]. Harbin: Harbin Institute of Technology, 2012.
[37] 孙素杰, 董志国, 轧刚, 等. 基于ABAQUS/Explicit 的SiCp/Al 复合材料三维微孔钻削有限元仿真[J]. 工具技术, 2018, 52(3): 56–59.
SUN Sujie, DONG Zhiguo, YA Gang, et al. Finite element simulation of 3D micro drilling of SiCp/Al composites based on ABAQUS/Explicit[J].Tool Engineering, 2018, 52(3): 56–59.
[38] SUN W, DUAN C Z, YIN W D. Development of a dynamic constitutive model with particle damage and thermal softening for Al/SiCp composites[J]. Composite Structures, 2020, 236: 111856.
[39] FAN Y H, XU Y S, HAO Z P, et al. Cutting deformation mechanism of SiCp/Al composites based on strain gradient theory[J]. Journal of Materials Processing Technology, 2022, 299: 117345.
[40] 郑伟. SiCp/Al 复合材料超声振动磨削材料去除及表面质量研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
ZHENG Wei. Research on material removal and surface finish in ultrasonic vibration grinding of SiCp/Al composites[D]. Harbin: Harbin Institute of Technology, 2017.
[41] LIU J W, CHENG K, DING H, et al. An investigation of surface defect formation in micro milling the 45% SiCp/Al composite[J]. Procedia CIRP, 2016, 45: 211–214.
[42] WU Q, XU W X, ZHANG L C. A micromechanics analysis of the material removal mechanisms in the cutting of ceramic particle reinforced metal matrix composites[J]. Machining Science and Technology, 2018, 22(4): 638–651.
[43] LIU J W, CHENG K, DING H, et al. Simulation study of the influence of cutting speed and tool–particle interaction location on surface formation mechanism in micromachining SiCp/Al composites[J].Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2018, 232(11): 2044–2056.
[44] 王涛. 高体积分数SiCp/Al 复合材料高速铣削基础研究[D].北京: 北京理工大学, 2015.
WANG Tao. Fundamental study on high speed milling of high volume fraction SiCp/Al composite[D]. Beijing: Beijing Institute of Technology,2015.
[45] 武永祥. SiCp/Al 复合材料切削仿真研究与实验验证[D]. 哈尔滨: 哈尔滨工业大学, 2017.
WU Yongxiang. Research on the cutting simulation of SiCp/Al composite and experimental verification[D]. Harbin: Harbin Institute of Technology, 2017.
[46] SEGURADO J, LLORCA J. A new three-dimensional interface finite element to simulate fracture in composites[J]. International Journal of Solids and Structures, 2004, 41(11–12): 2977–2993.
[47] 高翔. 增强体网状分布对SiCp/Al 复合材料力学性能影响的有限元模拟[D]. 哈尔滨: 哈尔滨工业大学, 2019.
GAO Xiang. Effects of reinforcement network distribution on mechanical properties of SiCp/Al composites via finite element method[D].Harbin: Harbin Institute of Technology, 2019.