光学三维测量技术是指运用光学方法获取物体表面三维坐标的技术。其中,结构光三维测量技术凭借其精度高、非接触、装置简易等优点[1],在工业检测、生物医学、法医刑侦、虚拟现实、逆向工程等领域得到广泛应用[2]。条纹投影轮廓术(Fringe projection profilometry,FPP)通常由频域法或者相移法计算测量所需相位信息,由于其高测量精度、灵活性以及简单的硬件配置而成为最受欢迎的三维测量技术之一[3]。频域法可依据单帧光栅条纹计算相位,但是较难保持待测物体边界、复杂面型等细节信息[4];相移法依据至少3 帧以上相移光栅条纹,时域内计算得到相位信息,能较好地保持待测物体细节[5]。但在复杂介质下,相机捕获条纹振幅降低,受到噪声干扰,从而产生相位误差,降低FPP 三维重建精度。
现今大多数关于FPP 的研究集中在以空气为介质的3D 测量中,而当场景和光源所处的介质对光线存在吸收与散射时,FPP 在相位计算过程中会产生不可忽略的相位误差,导致三维重建精度降低。因此,在复杂探测场景中完成高精度重建是当下关于FPP 的需要攻克的难关之一。航空工业中为了适应航空产品减轻重量、提高使用性能的要求,绝大多数航空金属零件要在高温炉内进行热处理,以获得高的比强度和良好的综合性能。航空零件的热处理工艺繁杂,但大致分为退火、正火、淬火、回火4 种基本工艺,决定了零件的内在质量,直接影响零件的加工性和使用性[6]。在这样的加工工艺和车间环境下,易产生烟雾、水汽,三维探测效果在工件制造与检测过程中受到严重干扰。另外,对飞行器尾翼等硬脆性工件进行水下激光加工[7]可减少切割工艺对材料造成的热损伤,完成高效、高质量切割,应用前景广阔,相关的水下高精度在线三维检测已成为必要。除了工业制造与检测,在雾霾、烟雨等复杂大气环境下的航空摄影重建与无人机测绘,在江河湖海中的考古重建与生物监测等[8]复杂环境下的实际应用中,FPP 都面临着严峻考验。
为模拟水下加工制造与监测环境,表征存在烟雾和水汽等复杂介质的检测场景,本文以浑浊水体为例进行问题分析与方案验证。在浊水环境下,由于水下光的吸收与散射,相机捕获的条纹振幅大大衰减[9],图像细节模糊,噪声严重干扰相位计算,由此产生的相位误差导致FPP 三维测量精度欠佳。
由此可见,对于传统FPP,有效、准确降低相位误差具有重要意义。近些年来,随着计算机领域的不断发展,深度学习也得到了广泛关注,在计算机视觉、语音识别、自然语言理解等领域成果斐然[10]。与此同时,研究者们也开始将深度学习运用到水下图像增强中去。基于深度学习的水下图像增强主要划分为两类:一类结合了物理模型,将成像模型和数据驱动结合,实现了图像的复原;另一类是没有结合物理模型,仅仅依靠数据驱动对图像进行恢复[11]。物理模型法中,Hou 等[12]提出了水下残差卷积神经网络模型(Underwater residual convolutional neural neworks,URCNN)用于水下图像复原,其模型结构包括了用于 TM 估计的数据驱动残差架构和用于水下照明平衡的知识驱动场景残差公式。Li 等[13]提出了一种单目水下图像颜色校正生成对抗模型(Water generative advsarial net works,Water–GAN),应用于水下岩石资源图片的颜色处理。Water–GAN 的生成器具有3 个主要阶段:衰减(G–I)、散射(G–II)、相机模型(G–III),每个阶段都是依据水下图像的物理形成过程进行建模。通过生成器生成相应的合成水下图像作为输出。然后,将合成的水下图像和水下图像样本都输入到颜色校正网络中对图像色彩进行恢复。Chen 等[14]提出一种结合深度学习方法与物理成像模型的水下图像增强算法,对背景散射光和直接传输光两个模块进行估计,最后根据水下成像的物理模型公式,对退化图像进行重构,得到质量增强后的图像。
当深度学习与物理模型相结合时,会受到物理模型的约束,降低其适应性,非物理模型的深度学习方法则在适应性方面具有较好的表现[11]。Liu 等[15]提出了一种基于深度残差模型的水下图像增强解决方法,与其他基于深度学习的增强方法不同,该方法专注于生成对抗网络与弱监督学习网络之间的合作,旨在建立更深的网络并改善水下图像增强的性能。Farhadifard 等[16]提出了一种减少水下色偏和模糊的图像增强方法,首先,应用颜色校正算法来校正色偏,生成海底图像的自然外观;其次,应用一对基于稀疏表示的学习字典对图像进行锐化和细节增强;最终有效地增强水下图像。Mello 等[17]提出一种端到端的无监督深度学习算法,在损失函数的约束下运用编码解码器完成水下成像模型的训练,可恢复较为真实的水下场景图像。
基于深度学习的水下图像增强工作多已落地于海底探测识别等领域,由此可见,使用深度学习改善水下图像质量已然可行。因此,基于深度学习改善FPP 条纹图质量以提升水下三维重建精度是本文研究的目的和意义。鉴于结合水下成像模型以完成图像增强对参数估计的精度要求较高,而不同水体环境对应的模型参数大相径庭,通过网络模型估计出的物理模型参数误差在三维重建阶段易被加以放大,本文采用一种端到端的图像增强算法,运用条纹图像增强卷积神经网络(Fringe pattern enhancement convolutional neural network,FPENet),无需对浑浊水体中的目标物体进行额外的图像采集,可直接对已有的条纹图进行快速优化,实现水下FPP 条纹对比度提升及去噪,以降低相位误差,获得更高精度的三维重建结果。在高浑浊度水体中,经FPENet 增强的条纹图像所得相位误差可减小50%左右,三维重建精度提升显著。
1 方法
1.1 条纹投影轮廓术
在FPP 中,投影仪将一组相移正弦条纹图案投射到物体上,相机拍摄到从物体表面反射的这些图案,相机像素点和与其具有相同相位的投影仪像素点一一对应。以实际白色玩具为例,传统的FPP 测量示意图如图1所示。
假设条纹图像的光强符合标准的正弦分布,其光强分布函数[5]可表示为
式中,N为相位步长;u = 1,2,…,U和v = 1,2,…,V,(其中,u×v为投影仪分辨率);a 和b 分别是投影条纹图的背景和振幅;φ = 2πfu为待求解的相位;f为空间频率。本文采用三步相移条纹投影,相机获取的三帧相移图像如图1(a)所示。相机所捕获的条纹图的光强[5]为
式中,A 和B 分别为条纹背景强度和调制度。条纹调制度[18]可以表示为
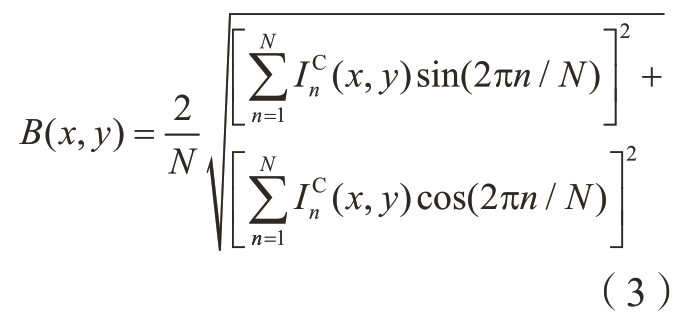
图1(b)为采用相移算法得到的真实包裹相位。包裹相位φ 可用最小二乘法求得[3],即
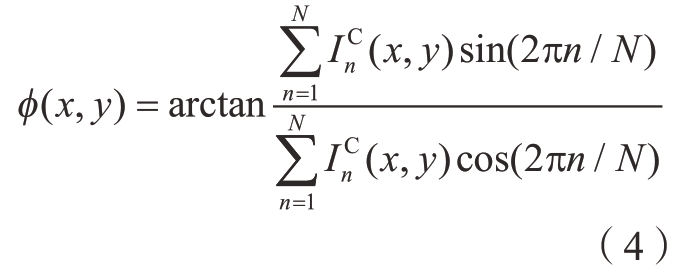
经反正切函数运算所得的相位结果φ(x,y)包裹在(–π,π]主值区间内,因此需要一种相位展开算法来获取连续的相位分布,即绝对相位[19]。
式中,K为包裹相位对应的周期级次。相位展开算法分为时域法和空域法,如图1(c)所示,本文采用时域编码中的格雷码编码法来展开包裹相位,获取相移条纹的级次信息,如图1(d)所示。每个相机像素点对应的投影仪像素坐标可由式(6)获得[20]。
最后,根据系统标定参数从绝对相位中恢复目标物体的三维信息,如图1(f)所示。
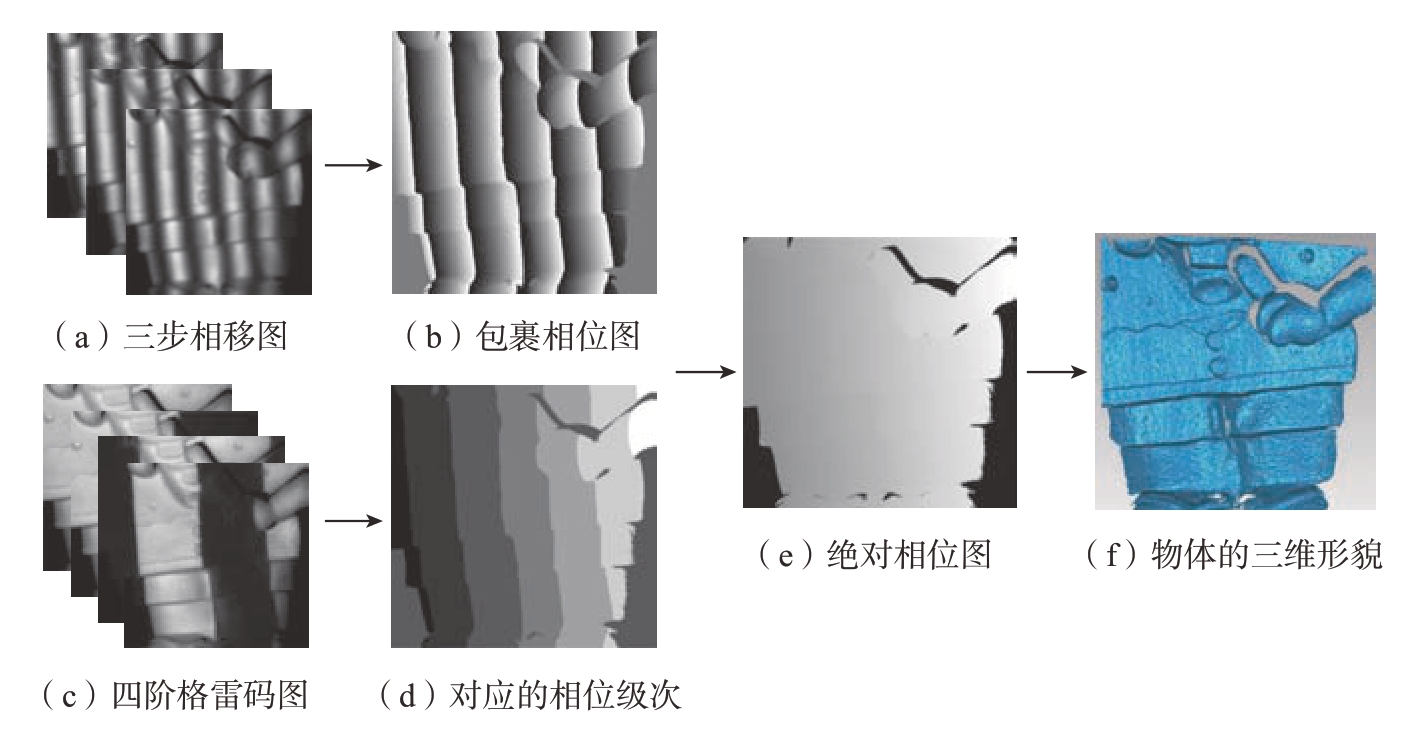
图1 传统条纹投影三维测量示意图
Fig.1 Schematic diagram of traditional fringe projection 3-D measurement
1.2 水下FPP 误差分析
相机接收的水下目标响应光包括直接光、前向散射光和后向散射光[21–23],如图2所示。直接光是从物体表面反射的光,相较于入射光,其光强由于水下光的吸收而产生衰减,算法为[9]
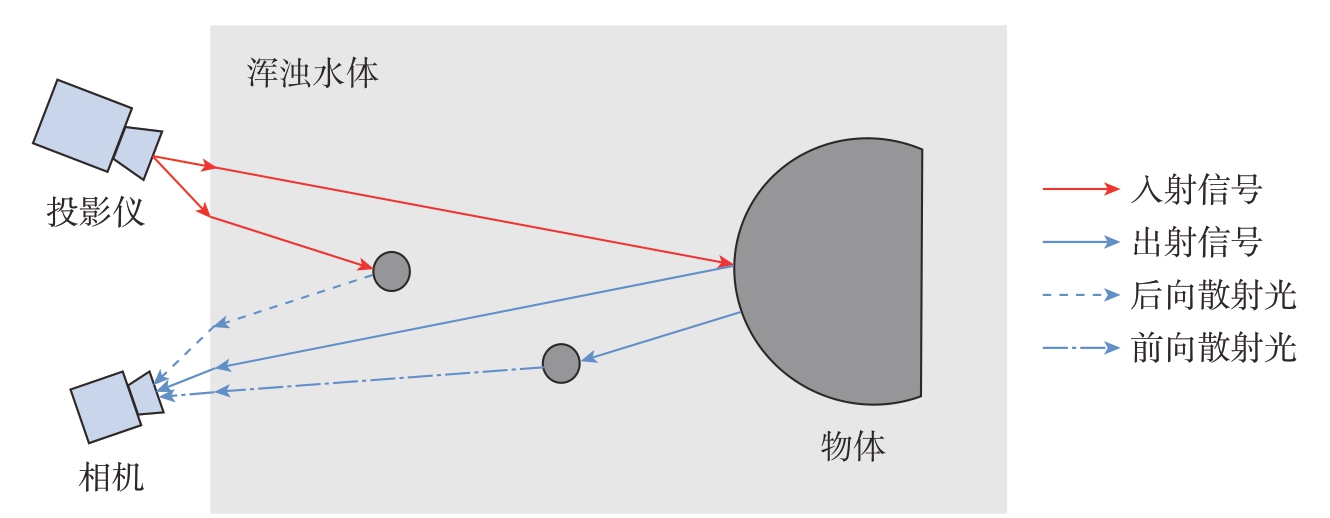
图2 水下光线传输示意图
Fig.2 Schematic diagram of underwater light transmission
式中,(x,y)为相机平面像素坐标;T1(x,y)为介质传输系数;![]() 和
和![]() 分别为第n 步相移条纹的出射光强和直接光强。
分别为第n 步相移条纹的出射光强和直接光强。
前向散射光是指被相机捕获之前经物体反射又被水中悬浮颗粒散射的光[21],对直接光产生模糊效应,使水下图像的细节清晰度变差。前向散射光强计算方式为[9]
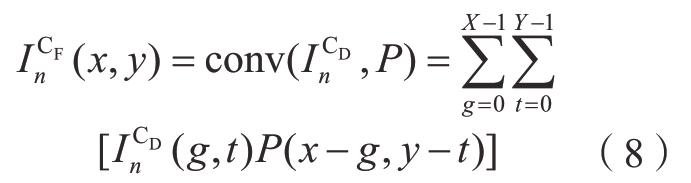
式中,X×Y为相机分辨率;P(x,y)为水下点扩散函数(Point spread function,PSF)。
PSF 被水下悬浮颗粒影响,其模型一般用几个经验常数来表示,如式(9)所示[22–23]。
式中,T = T2–T1(T2 > T1),T2为经验常数;Q为一个与水浊度相关的阻尼系数;F –1为傅里叶逆变换;ω为相机捕获图像的空间频率[23]。
后向散射光是指到达目标物体表面之前就被水中悬浮颗粒散射的光,造成水下图像对比度下降,为直接光和前向散射光增加了特定的强相关噪声。后向散射光强为[9]
式中,Gn 表示均值为0,方差为σ2 的白噪声。
综上,相机拍摄的条纹光强![]() y)为直接光、前向散射光和后向散射光之和。
y)为直接光、前向散射光和后向散射光之和。
浊水中,除了光的吸收造成的光强衰减问题,散射现象带来的误差不容小觑。在低浑浊度水体中,条纹质量主要受后向散射影响,相位误差表现为符合高斯分布的随机噪声。而在高浑浊度水体中,除后向散射的影响外,前向散射导致图像细节清晰度不佳,也对相位计算的准确性产生不利影响。
综上,水下光的吸收和散射造成光信号强度衰减,带来条纹图像对比度和细节模糊问题,引入大量噪声。随着水体浑浊程度增强,条纹质量下降,导致FPP 计算出的相位误差严重,三维重建效果不佳。
1.3 水下条纹图像增强算法
为将深度学习融入传统的FPP测量流程,本文提出基于FPENet网络模型的条纹图像增强算法,在FPP 的一系列运算之前,优化所采集的条纹图质量,以削弱浑浊水体吸收与散射引入的测量误差。所提方法中使用深度学习实现高质量相移条纹图获取和相位计算的流程如图3所示。
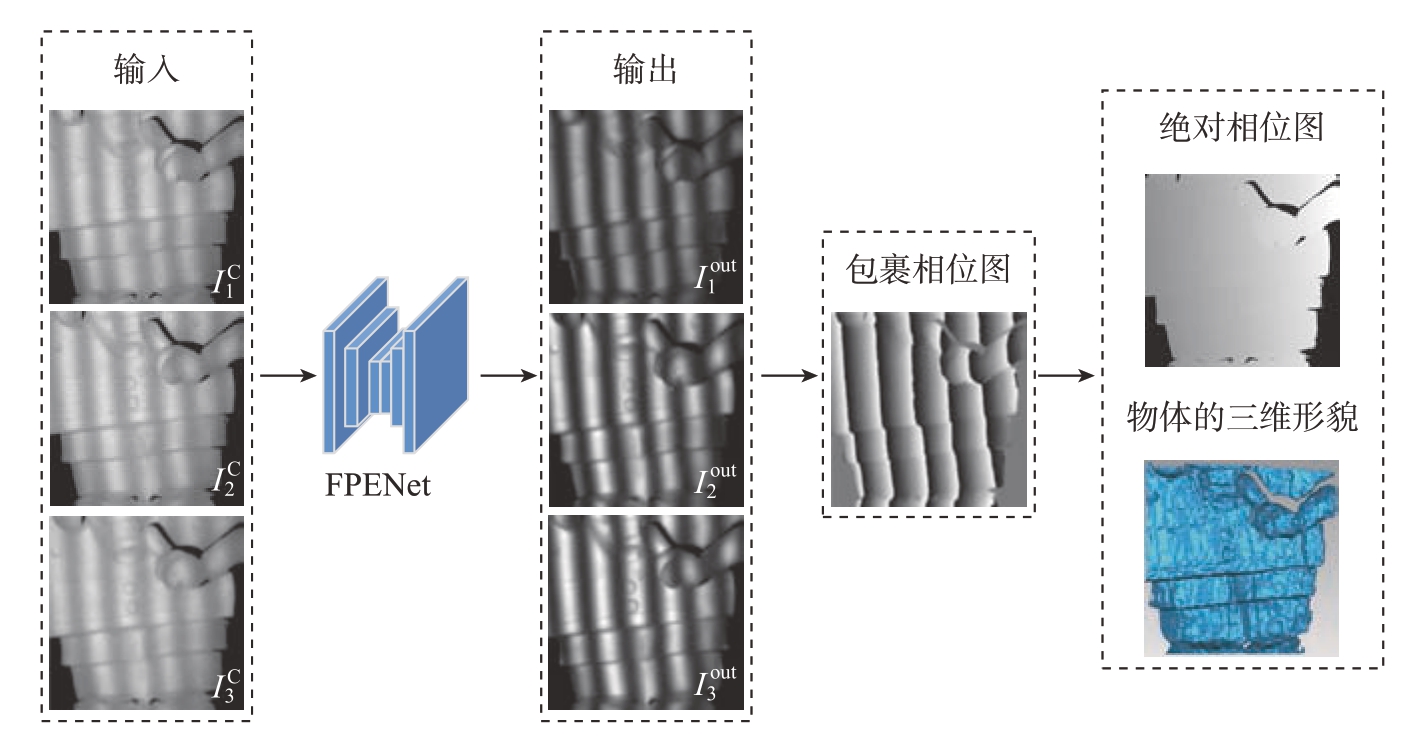
图3 基于FPENet 的传统条纹投影三维测量示意图
Fig.3 Schematic diagram of traditional fringe projection 3-D measurement based on FPENet
引入的FPENet 网络构建出含噪声条纹图I C 到理想条纹真值图(清水中条纹图)的端到端方式训练模型,网络训练过程中输出的优化条纹图I out 与条纹真值图I 进行残差学习并返回误差值至网络中,促使网络不断迭代而得到最优参数,使网络模型对不同程度的噪声和不同目标物体都具有较好的去噪鲁棒性。误差函数公式如式(12)所示。
式中,I out为经FPENet 训练算出的条纹图灰度值;I为理想条纹图;m为条纹灰度图中有效像素个数。最终,训练完成后所得到的ERFNet 训练模型可输出对不同水浊度下不同物体进行去噪优化的条纹图I out,以获取精度较高的包裹相位,完成较精确的三维重建。
FPENet 网络在效率和准确性之间取得了显著的权衡[24]。如图4所示,该网络与其他高效的卷积神经网络(如ENet[25]或SegNet[26])一样,具有端到端的编码器–解码器结构,编码器对原始输入数据下采样,输出小分辨率的特征图,随后通过解码器对其进行上采样到初始分辨率后输出。FPENet 通过使用一维卷积,在保证精度的前提下,减少了计算量,提升了运行速度。
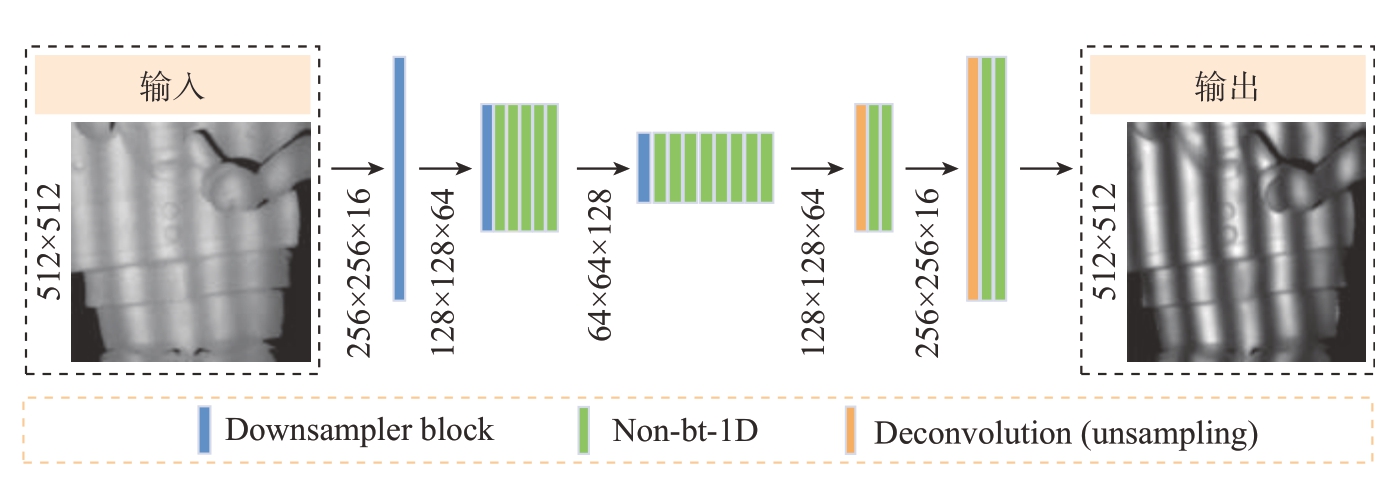
图4 FPENet 的结构
Fig.4 Structure of FPENet
本网络模型采用单通道的输入和输出,输入和输出图像分辨率为512×512。网络模型主要包括下采样模块(Downsampler block)、弱瓶颈模块(Non-bt-1D)和上采样模块(Deconvolution(upsampling))。
本网络模型共23 层。其中,1~16层为编码器模块,17~23 层为解码器模块。编码器模块包括3 个下采样层和卷积层[24],旨在获取输入图像并将它们编码为深层特征,这一步是产生良好分类结果的关键。解码器模块包括上采样层和卷积层,旨在对编码的特征进行预处理,最终恢复出与输入图像相同尺寸的目标输出图。网络主要模块及参数见表1。
表1 FPENet 主要模块及参数
Table 1 Main modules and parameters of ERFNet
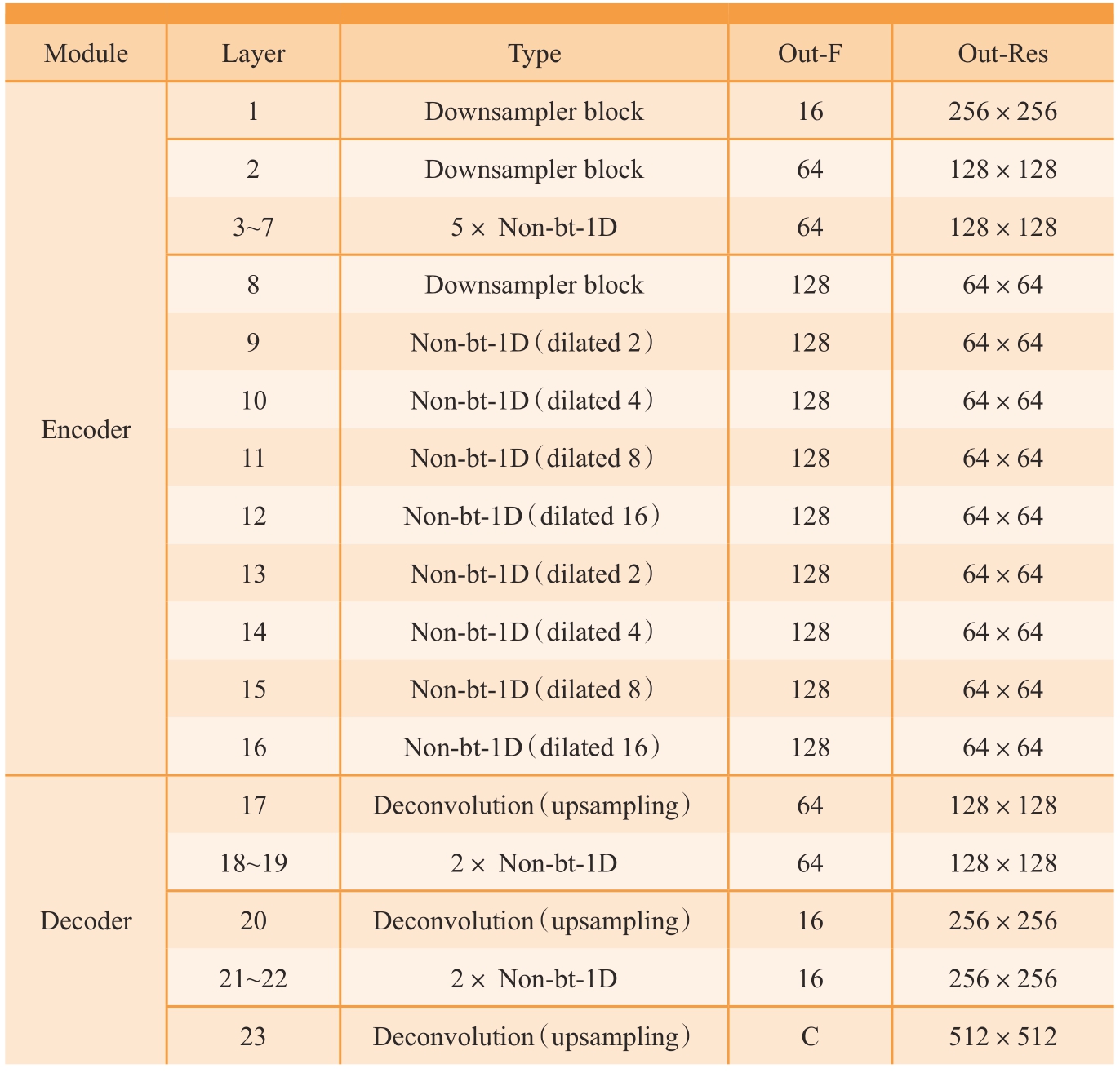
ModuleLayerTypeOut-FOut-Res Encoder 1 Downsampler block16256×256 2 Downsampler block64128×128 3~75× Non-bt-1D64128×128 8 Downsampler block12864×64 9 Non-bt-1D(dilated 2)12864×64 10Non-bt-1D(dilated 4)12864×64 11Non-bt-1D(dilated 8)12864×64 12Non-bt-1D(dilated 16)12864×64 13Non-bt-1D(dilated 2)12864×64 14Non-bt-1D(dilated 4)12864×64 15Non-bt-1D(dilated 8)12864×64 16Non-bt-1D(dilated 16)12864×64 Decoder 17Deconvolution(upsampling)64128×128 18~192× Non-bt-1D64128×128 20Deconvolution(upsampling)16256×256 21~222× Non-bt-1D16256×256 23Deconvolution(upsampling)C512×512
第1、2、8 层作为下采样层,经过3×3 卷积(步长为2)和2×2 最大池化操作后得到输出。下采样处理一方面有助于扩大卷积层感受野而丰富上下文信息,另一方面有利于降低特征图分辨率,减少信息冗余,提升网络效率与实时性。
第3~7 层、第9~16 层、第18~19层和第21~22 层作为弱瓶颈模块(Non-bt-1D),也称残差连接模块,由一维滤波器构成,包括两层卷积核大小3×1 的卷积层和两层卷积核大小1×3 的卷积层,在感受野相同的时候大大减少计算量,同时也减少了参数量,在精度损失较小的情况下大大提升了网络运算速度。其中,第9~16层中使用了不同扩张系数下的扩张卷积(Dilated convolution),也称空洞卷积,旨在防止图像信息丢失的同时增大网络局部感受野[27],从而提升网络性能。
第17、20 层作为上采样层,使用步长为2 的转置卷积(Transposed convolution),同时实现图像的上采样和卷积操作,得到与初始图像尺寸相同的恢复图像。
2 试验结果
2.1 试验配置与数据集
本研究使用 PyTorch 1.2.0 深度学习框架实现所提出的条纹图像增强网络模型,在 Ubuntu 16.04 下搭建系统环境。硬件设备有英特尔酷睿i9–7900X CPU(3.30 GHz),32 GB 内存和GeForce GTX Titan RTX(NVIDIA)。本研究运用条纹投影轮廓术获取数据集,称之为Water3D,简称W3D 数据集。采集过程中,使用投影仪(DLP4500,Texas Instruments)投射相移步数N = 3、频率f = 1/15 的三步相移条纹图以及对应频率的4 阶格雷码图。使用CMOS 相机(Basler acA800–510 um,分辨率为800×600,焦距12 mm)采集由物体表面反射的光和散射的光,选取512×512 大小的图像区域作为数据集。本试验的系统结构如图5所示,被测物体被放置在一个尺寸为0.48 m×0.22 m×0.28 m 的水箱中,测量系统被放置在水箱外,距离物体约0.35 m。

图5 试验系统结构
Fig.5 Experimental system structure
本研究用照度表征水体浑浊程度,在图像采集前,先将照度计放于待测玩具处,投影仪投射白光,测得当前采样环境下的照度值。首先把水箱里装满清水,完成投影,获取照度值与真值图像;然后把牛奶倒进水箱里,构造浑浊的水体环境;向水缸中逐步累加牛奶,产生由低到高4个浓度的水体环境,分别为浊度1、浊度2、浊度3、浊度4;采集相应照度与输入图像数据集。水浊度与照度对应关系见表2。
表2 水浊度及相应照度
Table 2 Water turbidity and corresponding illuminance lx

清水浊度1浊度2浊度3浊度4 919552498443434
本数据集共包含70 个不同目标物体在清水和在4 个不同水体浑浊度下的图像数据(数据样本不重复、结构多样性复杂性高[8])。同一浑浊度下的目标物体图像作为一组数据,每一组数据中前50 个目标物体的图像数据作为训练集,剩余的20 个目标物体的图像数据作为测试集。训练集和测试集分别用于训练网络和评估最终网络的性能。本研究所有试验结果均由测试集提供。为突出采样环境对目标物体信号调制的影响,本文呈现的条纹图、相位图与三维重建效果,皆滤除目标之外的背景信息,仅展示有效区域信息。
2.2 传统FPP 与基于FPENet 的FPP三维测量试验
完成系统标定后,根据式(1),使用相应的相移条纹图和格雷码图进行编码投影,相机端同时完成图像采集。根据式(2),运用最小二乘法计算包裹相位。运用时域编码中的格雷码编码法获取相位级次,根据式(5),对包裹相位进行相位展开,得到绝对相位。最后,根据系统标定参数获取目标物体准确的深度值,完成传统FPP 的三维重建。
本次试验选取不同的玩具模型作为目标物体完成三维重建,运用FPENet 网络模型对上述FPP 法在浑浊水体中采集的三步相移条纹图进行优化,清水下的条纹图如图6(a)所示,由低到高4 种浊度下去噪前后的效果如图6(b)和(c)所示。

图6 第三步相移条纹图
Fig.6 Fringe diagram of phase shift in the third step
表3 列出了4 种浊度下FPENet网络优化前后的条纹对比度,其中输入条纹和输出条纹的对比度分别用contrastin 和contrastout 表示。因为相机捕获的条纹图中不同像素可能具有不同的条纹对比度,因此计算整个图像的条纹对比度均值来体现FPENet 对条纹对比度的增强效果。输入的4 组条纹对比度范围为0.134 ~ 0.304,输出的4 组条纹对比度在0.59 以上,清水中真值图的条纹对比度为0.641。
表3 4 种浊度下的条纹对比度
Table 3 Contrast of fringe under 4 types of turbidity

方法浊度1浊度2浊度3浊度4 contrastin0.3040.2000.1510.134 contrastout0.6530.6520.5920.610
总体而言,FPENet 在不同浊度下去噪效果显著,可以有效提升条纹对比度,完成条纹质量提升,高效、快速地降低浊水环境下的相位误差。
2.3 传统FPP 与基于FPENet 的FPP三维测量试验误差分析
为研究传统FPP 和基于FPENet的FPP 在不同浊度条件下的性能,本文使用有效区域内的包裹相位误差来评估测量精度。采用最小二乘算法,根据等式计算包裹相位。清水环境下算得的包裹相位作为真值,在浊水条件下得到的包裹相位与真值相减,计算出相位误差,本文将测试集玩具在深度学习前后的包裹相位平均绝对误差(Mean absolute error,MAE)累加后平均,以此作为不同水浊度下的网络性能指标。以测试集中的一个玩具为例,其在4 种不同的水浊度下的包裹相位以及相位误差分布如图7所示。根据误差值分布可得,经FPENet 优化的包裹相位误差主要集中于目标物体边缘和细节处,但整体上去噪效果明显。

图7 4 种不同的水浊度下的包裹相位以及包裹相位误差
Fig.7 Wrapping phase and wrapping phase error under 4 types of turbidity
如表4所示,通过计算去噪前后的相位MAE 数值(测试集20 个玩具的相位MAE 平均值)可知,在由低到高4 种浊度下,基于FPENet 的FPP均表现优异,有明显的降噪功能。最低浊度(浊度1)下,相位MAE 数值由0.091 rad 降到0.069 rad;最高浊度(浊度4)下,相位MAE 数值由0.414 rad 降到0.237 rad。
表4 4 种浊度下所有玩具包裹相位MAE
Table 4 MAE values of all toys wrapping phase errors under 4 types of turbidity rad

方法浊度1浊度2浊度3浊度4 FPP 0.0910.1890.2740.414 FPENet-based FPP0.0690.1060.1130.237
为进一步验证FPENet 的条纹优化效果,本文对使用该方法处理前后的三维重建效果进行了比较。以本试验中的简单玩具为例,4 种浊度下的包裹相位误差和三维欧式距离标准偏差见表5 和6。由此可见,相位精度与三维重建精度成正比。本文提出的条纹图像增强算法在提升三维重建精度方面效果显著。
表5 4 种浊度下简单玩具包裹相位MAE
Table 5 MAE values of simple toys wrapping phase errors under 4 types of turbidity rad

方法浓度1浓度2浓度3浓度4 FPP0.0840.1770.3160.413 FPENet-based FPP0.0590.0840.1220.129
传统FPP 受水下噪声干扰较大,重建结果表面平滑度极差,难以恢复物体细节。而本文提出的方法去噪效果明显,可基本恢复物体形态并在一定程度上恢复目标细节。因此,本文提出的方法与传统FPP 在目标重建视觉效果对比上优势明显。
此处以测试集中的两个目标为例。玩具1(称为简单形貌物体),深度变化较小,表面纹理细节较少,如图8(a)所示;玩具2(称为复杂形貌物体),深度变化较大,表面纹理细节较多,如图8(b)所示。玩具1 在浓度1~ 4 去噪前相位MAE 值分别为0.084 rad、0.177 rad、0.316 rad、0.413 rad,去噪后分别为0.059 rad、0.084 rad、0.122 rad、0.128 rad,重建效果对比见图8(c);玩具2 去噪前相位MAE 值分别为0.134 rad、0.337 rad、0.474 rad、0.740 rad,去噪后分别为0.0740 rad、0.140 rad、0.135 rad、0.337rad。重建效果对比见图8(d)。
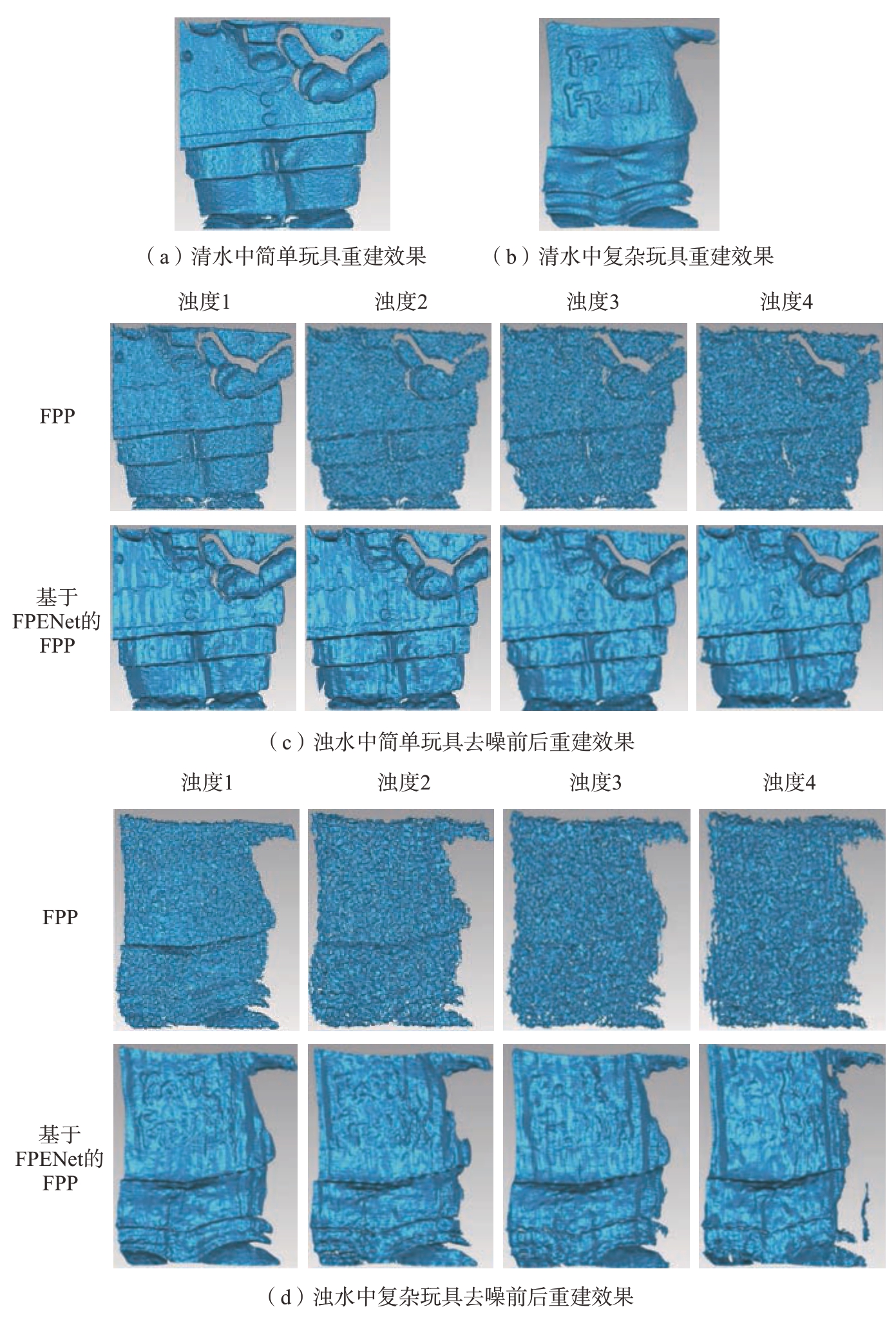
图8 不同采样条件下不同玩具的重建效果
Fig.8 Reconstruction effect of different toys under different sampling conditions
由图9 可知,复杂玩具相对简单玩具,在不同采样环境下的误差整体偏高,但FPENet 对二者兼有较好的去噪效果。由此可见,在同样的采样环境下,物体形貌复杂度对重建误差存在影响,FPENet 在高浊度下对目标物体边缘与细节的恢复能力仍有待提升。
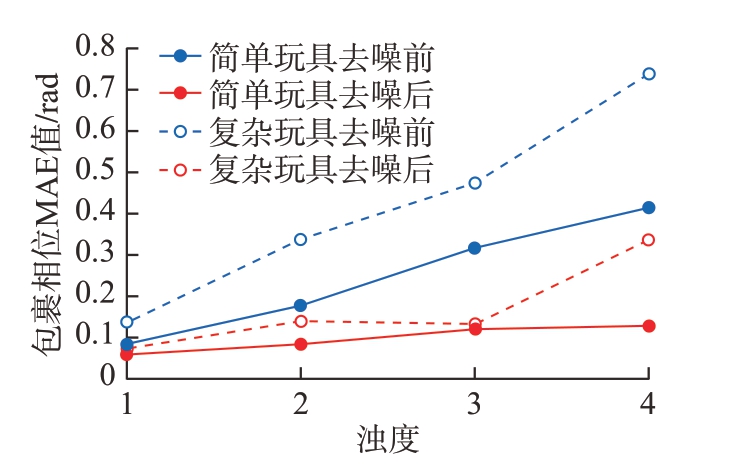
图9 简单玩具与复杂玩具在不同浊度下的相位误差MAE 值
Fig.9 MAE values of phase error between simple and complex toys at different turbidity
表6 4 种浊度下三维欧式距离标准偏差
Table 6 3-D Euclidean distance standard deviation under 4 types of turbidity mm

方法浓度1浓度2浓度3浓度4 FPP0.9401.7992.6503.049 FPENet-based FPP0.5910.8061.0811.124
图10所示为对水浊度4 下重建细节进行分析。图10(b)和(c)所示的深度阶跃区域属于细节部分,本文使用的FPENet基于编码解码结构,在编码过程中进行下采样,导致部分细节信息丢失;在解码过程中进行上采样,但难以恢复全部细节[10]。此外,本文是对条纹图而非相位进行处理,网络模型对条纹正弦性的恢复能力直接影响重建三维形貌的平滑度。由FPENet 恢复的条纹图进行重建,目标的平滑度差,降噪水平仍有待提升,如图10(d)所示。
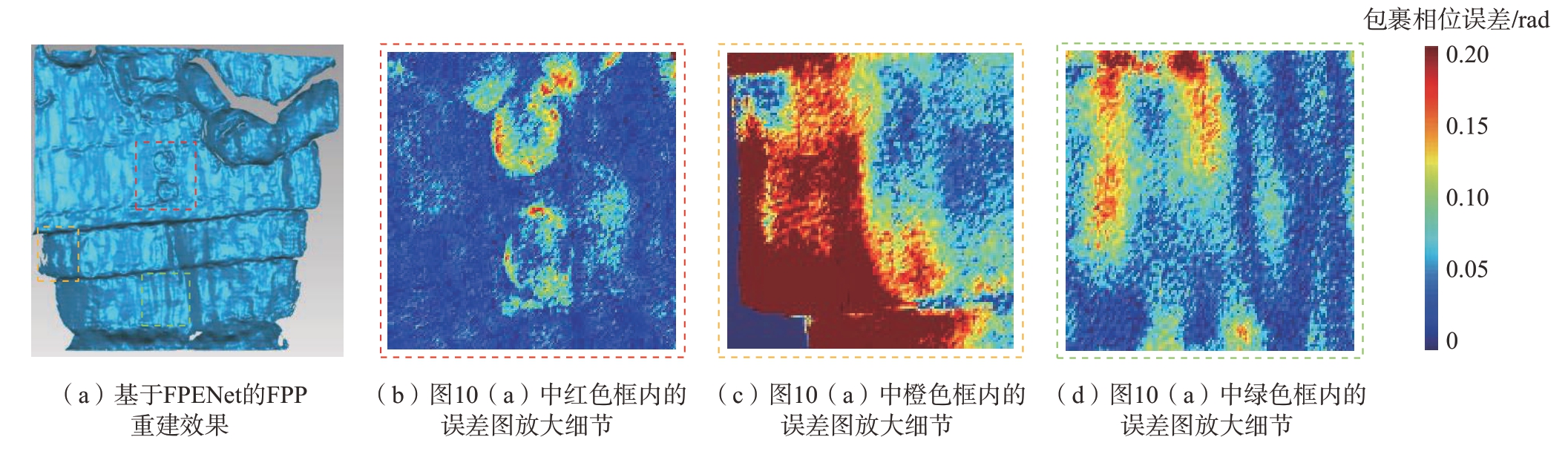
图10 浊度4 下基于重建细节分析
Fig.10 FPP reconstruction effect based on FPENet at turbidity 4
综上,相比传统的FPP 算法,基于FPENet 的FPP 算法具备较强的抗噪性,针对复杂水下环境中光强衰减,条纹对比度下降和图像细节模糊带来的噪声干扰问题具有显著优势,可实现较精确的三维测量。
3 结论
本文通过运用FPENet 条纹图像增强卷积神经网络模型,提出一种端到端的图像增强算法,利用FPENet对浑浊水体中低对比度高噪声的条纹图进行对比度增强和去噪。此方法可直接对低质量的条纹图进行优化处理,无需增加采样次数即可完成条纹图增强,可快速高效地降低相位误差。在4 个不同浑浊度的水体环境中,基于 FPENet 的 FPP 与传统FPP 相比,相位误差均明显降低,浊度1 下相位误差由0.091 rad 降低至0.069 rad,浊度2 下相位误差由0.189 rad 降低至0.106 rad,浊度3 下相位误差由0.274 rad 降低至0.113 rad,浊度4 下相位误差由0.414 rad 降低至0.237 rad,相位 MAE 值平均降低43%左右,尤其在浓度3 下可将相位误差减少59%。但该方法仍在一定程度上受前向散射和编解码结构影响,恢复条纹正弦性和信息完备性仍有待提升。此外,FPENet 的提出验证了使用深度学习优化条纹投影三维测量效果的可行性,后续可寻找更为高效的网络模型,加强图像细节恢复,优化损失函数,提升水下FPP 的抗散射能力,将条纹投影测量技术推向更广泛的应用场景。
[1]WU Z,ZUO C,GUO W,et al.Highspeed three-dimensional shape measurement based on cyclic complementary Gray-code light[J].Optics Express,2019,27(2):1283–1297.
[2]CARLSSON T E.Ultrashort-pulse interferometric sensors for optical shape and deformation measurement[C]//Proc SPIE 4398,Optical Measurement Systems for Industrial Inspection II:Application in Industrial Design,2001,4398:1–13.
[3]ZHANG S.High-speed 3D shape measurement with structured light methods:A review[J].Optics and Lasers in Engineering,2018,106:119–131.
[4]SU X Y,CHEN W J.Fourier transform profilometry:A review[J].Optics and Lasers in Engineering,2001,35(5):263–284.
[5]ZUO C,FENG S J,HUANG L,et al.Phase shifting algorithms for fringe projection profilometry:A review[J].Optics and Lasers in Engineering,2018,109:23–59.
[6]张守辉,杨敏洁.航空工业中热处理过程质量控制[C]//第十六届沈阳科学学术年会.沈阳,2019.ZHANG Shouhui,YANG Minjie.Quality control of heat treatment processes in the aviation industry[C]//The 16th Shenyang Science Annual Conference.Shenyang,2019.
[7]季画,柴明霞,赵鑫,等.一种高速飞行器尾翼水下激光加工装置:CN20191024 0807.5[P].2019–06–14.JI Hua,CHAI Mingxia,ZHAO Xin,et al.An underwater laser processing device for the tail wing of high speed aircraft:CN201910240807.5[P].2019–06–14.
[8]NURTANTIO ANDONO P,MULYANTO YUNIARNO E,HARIADI M,et al.3D reconstruction of under water coral reef images using low cost multi-view cameras[C]//2012 International Conference on Multimedia Computing and Systems.Tangiers:IEEE,2012.
[9]LYU N Q,YU H T,HAN J,et al.Structured light-based underwater 3-D reconstruction techniques:A comparative study[J].Optics and Lasers in Engineering,2023,161:107344.
[10]ZHANG Z,HAN B W,YU H T,et al.Multi-stage deep learning based single-frame fringe projection 3D measurement method[J].Infrared and Laser Engineering,2020,49(6):20200023.
[11]彭小红,梁子祥,张军,等.深度学习驱动的水下图像预处理研究进展综述[J].计算机工程与应用,2021,57(13):43–54.PENG Xiaohong,LIANG Zixiang,ZHANG Jun,et al.Review of underwater image preprocessing based on deep learning[J].Computer Engineering and Applications,2021,57(13):43–54.
[12]HOU M J,LIU R S,FAN X,et al.Joint residual learning for underwater image enhancement[C]//2018 25th IEEE International Conference on Image Processing.Athens:IEEE,2018.
[13]LI J,SKINNER K A,EUSTICE R M,et al.WaterGAN:Unsupervised generative network to enable real-time color correction of monocular underwater images[J].IEEE Robotics and Automation Letters,2018,3(1):387–394.
[14]CHEN X L,ZHANG P,QUAN L W,et al.Underwater image enhancement based on deep learning and image formation model[EB/OL].(2021–01–07)[2022–10–29].https://arxiv.org/abs/2101.00991.
[15]LIU P,WANG G Y,QI H,et al.Underwater image enhancement with a deep residual framework[J].IEEE Access,2019,7:94614–94629.
[16]FARHADIFARD F,ZHOU Z L,VON LUKAS U F.Learning-based underwater image enhancement with adaptive color mapping[C]//2015 9th International Symposium on Image and Signal Processing and Analysis (ISPA).Zagreb:IEEE,2015.
[17]MELLO C D,MOREIRA B U,DREWS P L J,et al.Alternative underwater image restoration based on unsupervised learning and autoencoder with degradation block[C]//2020 Latin American Robotics Symposium (LARS),2020 Brazilian Symposium on Robotics (SBR) and 2020 Workshop on Robotics in Education (WRE).Natal:IEEE,2020.
[18]YU H,ZHENG D,FU J,et al.Deep learning-based fringe modulationenhancing method for accurate fringe projection profilometry[J].Optics Express,2020,28(15):21692–21703.
[19]ZUO C,CHEN Q,GU G,et al.Highspeed three-dimensional profilometry for multiple objects with complex shapes[J].Optics Express,2012,20(17):19493–19510.
[20]SRINIVASAN V,LIU H C,HALIOUA M.Automated phase-measuring profilometry of 3-D diffuse objects[J].Applied Optics,1984,23(18):3105.
[21]SCHECHNER Y Y,KARPEL N.Clear underwater vision[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington:IEEE,2004.
[22]JAFFE J S.Computer modeling and the design of optimal underwater imaging systems[J].IEEE Journal of Oceanic Engineering,1990,15(2):101–111.
[23]MCGLAMERY B L.A computer model for underwater camera systems[C]//Proceedings of the Society of Photo-Optical Instrumentation Engineers.Monterey,1979.
[24]SÁEZ Á,BERGASA L M,LÓPEZ-GUILLÉN E,et al.Real-time semantic segmentation for fisheye urban driving images based on ERFNet[J].Sensors (Basel,Switzerland),2019,19(3):E503.
[25]PASZKE A,CHAURASIA A,KIM S,et al.ENet:A deep neural network architecture for real-time semantic segmentation[EB/OL].(2016–01–05)[2022–10–29].https://arxiv.org/abs/1606.02147.
[26]BADRINARAYANAN V,HANDA A,CIPOLLA R,et al.Segnet,a deep convolutional encoder-decoder architecture for robust semantic pixel-wise labelling[J].Computer Science,2015.DOI:10.48550/arXiv.1505.07293.
[27]ZHAO Y,FU J,YU H T,et al.Defocus projection three-dimensional measurement based on deep learning accurate phase acquisition[J].Infrared and Laser Engineering,2020,49(7):20200012.
