在航空制造领域,通常需要对零部件进行外形尺寸测量实现零部件实际制造外形与理论设计外形之间的差异检测。零部件外形尺寸测量依赖于深度估计,进而获取三维点云数据来实现不同要素的测量任务。目前,常用的方法主要有飞行时间[1–2]、雷达技术[3]、结构光[4]、激光扫描[5]以及视觉技术[6–7]。其中,视觉技术不需要向待测量物体主动投射光源,仅需要依赖环境光便可实现深度估计,具有结构简单、应用范围广泛等特点。
光场成像[8]作为一种新颖的三维视觉技术,能通过同时记录光线的方向和强度信息来实现深度估计,具有单次曝光获取场景三维信息的特点。因此,研究者们提出了许多算法来恢复光场成像中的三维信息,有效地促进了该领域的发展。Jeon 等[9]运用傅里叶域中的相移定理来解决光场相机中的短基线匹配问题,并结合迭代优化方法对获取的结果进行优化,获得短基线光场相机的精确结果。Strecke 等[10]提出使用部分光场重聚焦序列图像的对称性来解决光场成像三维信息恢复的遮挡问题,该方法分别将中心视角上、下、左、右方向上的偏移子孔径图像进行累加来生成不同的重聚焦序列,进而解决遮挡问题。Sheng 等[11]通过理论分析发现光场成像中存在倾斜方向上的极平面图像(Epipolar-plane image,EPI)。该方法在 Zhang 等[12]的基础上获取水平、垂直以及两个倾斜EPI 中的直线斜率,进而构建4 个代价体积。同时,该方法也发现在遮挡区域与非遮挡区域不同EPI 中的深度值具有不同的特性,并利用该特征获取遮挡边缘来解决遮挡问题。Williem 等[13]利用信息熵度量角度域图像中的像素与其中心像素之间的距离,以此构建约束的角度熵代价体积。同时,该方法将角度熵代价体与自适应重聚焦代价体融进马尔可夫随机场(Markov random field,MRF)优化框架,以此提升算法抗遮挡与抗噪声能力。Wang 等[14]通过理论分析发现光场角度域图像中的遮挡边界与空域中保持一致。该方法利用这种特性将空域中的分割结果映射到角度域图像中,以此处理遮挡问题。尽管上述方法能有效解决光场深度估计中所面临的不同问题,并获得具有竞争力的试验结果,但是这些方法仅能获取相对深度,即视差,不能得到绝对深度来实现三维测量。针对光场视差与绝对深度之间的数值转换关系问题,本文对微透镜阵列光场相机的成像原理进行理论分析,建立了光场视差与绝对深度之间的数值转换关系。首先,该方法结合EPI 对光场成像中的视差原理进行了理论分析,并通过使用双平面的形式表达EPI 来获取等效基线;其次,该方法对微透镜阵列光场相机的成像原理进行分析,并结合几何光学与高斯物象公式获得到等效基线与光场相机结构参数之间的关系式;最后,试验结果表明,本文提出的光场视差与绝对深度之间的转换关系能准确地实现绝对深度测量。
1 提出的方法
四维光场可以使用双平面对其进行参数化,如图1所示。同参数平面不平行的光线分别与相机平面(平面1)相交于点(u,v),与成像平面(平面2)相交于点(x,y)。光场成像便可通过上述两个平面记录光线的方向信息。因此,光场可以简单地表示为L(u,v,x,y)(其中,(u,v)表示角度坐标,(x,y)表示空间坐标)。固定光场L(u,v,x,y)中的不同变量能得到3 个主要的光场特征,即子孔径图、角度域图像以及EPI。这些光场特征与光场成像所蕴含的三维信息具有内在关系。下面将通过EPI 分析光场视差与等效基线之间的关系,进而推导光场视差与绝对深度之间的数值转换关系。
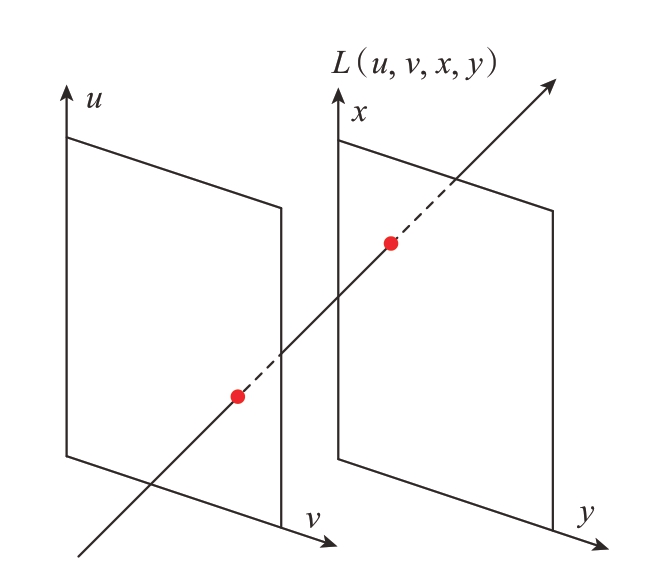
图1 四维光场参数化
Fig.1 Four-dimensional light field parameterization
1.1 光场视差原理
光场EPI 蕴含着丰富的三维场景信息,即不同视角下的物点在极平面图上构成一条倾斜的直线。该直线的斜率与物点所在空间中的深度存在联系。因此,固定光场L(u,v,x,y)中的(u,x)或者(v,y)能得到水平或者垂直方向上的EPI,即
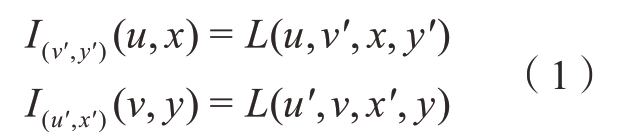
式中,I(v′,y′)(u,x)表示水平方向EPI,具体获取过程如图2所示。光场原始图像[15]解码成为子孔径阵列图像如图2(a)和(b)所示。其中,(x,y)表示空间坐标,索引每个像素值;(u,v)表示角度坐标,索引不同视角。在获取I(v′,y′)(u,x)过程中,固定变量v表示提取子孔径阵列图像(图2(b))中的第v′行图像,并按照原有的顺序进行堆叠,如图2(c)所示。固定变量y 表示将图2(c)中每张子孔径图像的第y′行像素提取出来进行排布,进而形成EPI,如图2(d)所示。EPI 中存在线特征,如图2(d)中的红、绿、蓝3 条线。这些线上的像素点均来自不同子孔径图像中同一坐标位置的像素点,如图2(a)中1 位置的像素点在图2(d)中直线上。这些直线的斜率直接反映了同一像素点在不同子孔径图像中的位置差,即视差。因此,为了进一步分析光场视差与等效基线的关系,光场EPI 可利用双平面表示,如图3所示。来自物点p 不同方向的光线与双平面相交。物点p 到u–v 平面的距离为Z。两个平面之间的距离为l。固定两个参数平面上的变量v 与变量y 可得到EPI 在双平面中的表达形式,如图3中的蓝色线所示。此时,具有以下几何关系。
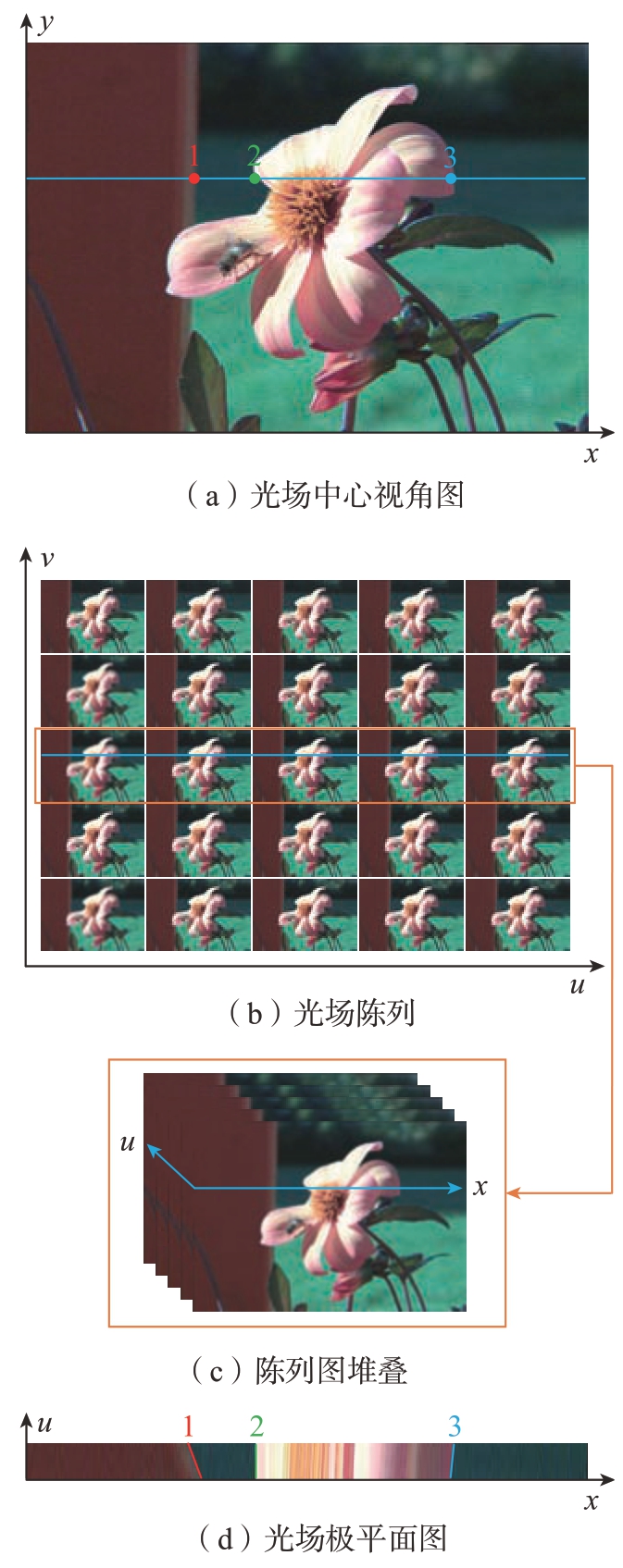
图2 光场极平面图获取过程
Fig.2 Process of acquiring the epipolar plane image
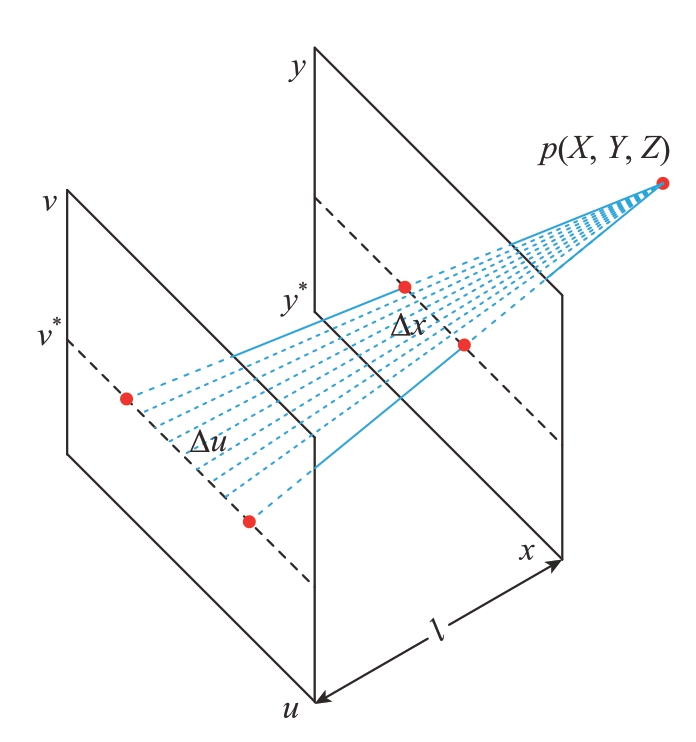
图3 光场双平面参数模型
Fig.3 Light field two plane parameterizatio model
式(2)反映了视差Δx 与等效基线Δu 之间的关系。令Z = αl,α为比例因子,则式(2)可变形为
1.2 光场视差与深度的数值关系
上一节主要介绍了光场视差与等效基线之间的关系。下面将通过等效基线推导光场视差与绝对深度之间的数值转换关系。固定四维光场L (u,v,x,y)中的(u,v)变量即可得到子孔径图像。由于u–v为主透镜所在平面,那么固定四维光场L (u,v,x,y)中的(u,v)变量相当于在主透镜上获取一个视点。因此,子孔径图像可看作是通过该视点的所有光线形成的图像,如图4(a)中的绿色点所示。那么,光场相机主透镜可以被分为多个等效子镜,并且这些等效子镜的焦距同主镜头的一致。等效子镜的数量与每个微透镜所覆盖的像素数保持一致。当微透镜阵列所在的平面与空间中的焦平面满足高斯物像关系时,该焦平面为初始对焦平面。初始对焦平面上的物点向不同方向发出的光线通过各等效子镜后将被同一个微透镜下所覆盖的像元记录,如图4(a)中的蓝色、黄色以及红色线所示。当通过相邻等效子镜的光线被微透镜所覆盖的像元记录时,记录这些光线的像元通常仅差1 个像素。那么,这些等效子镜的等效基线可以通过相似三角形关系计算,即
式中,fm 表示微透镜阵列所在平面与图像传感器之间的距离;l 表示主透镜与微透镜阵列所在平面的距离,即两平面距离;q0 表示图像传感器像元大小;b 表示等效基线。当物点位于初始对焦平面前后的平面时,该平面上的物点向不同方向发出的光线通过各等效子镜后将会被不同微透镜下的像元记录,如图4(b)所示。由于通过相邻等效子镜的光线被不同微透镜下的像元记录,相邻的子孔径图像将产生视差。那么,式(3)可以通过被重写来表示视差d 与等效基线之间的关系。
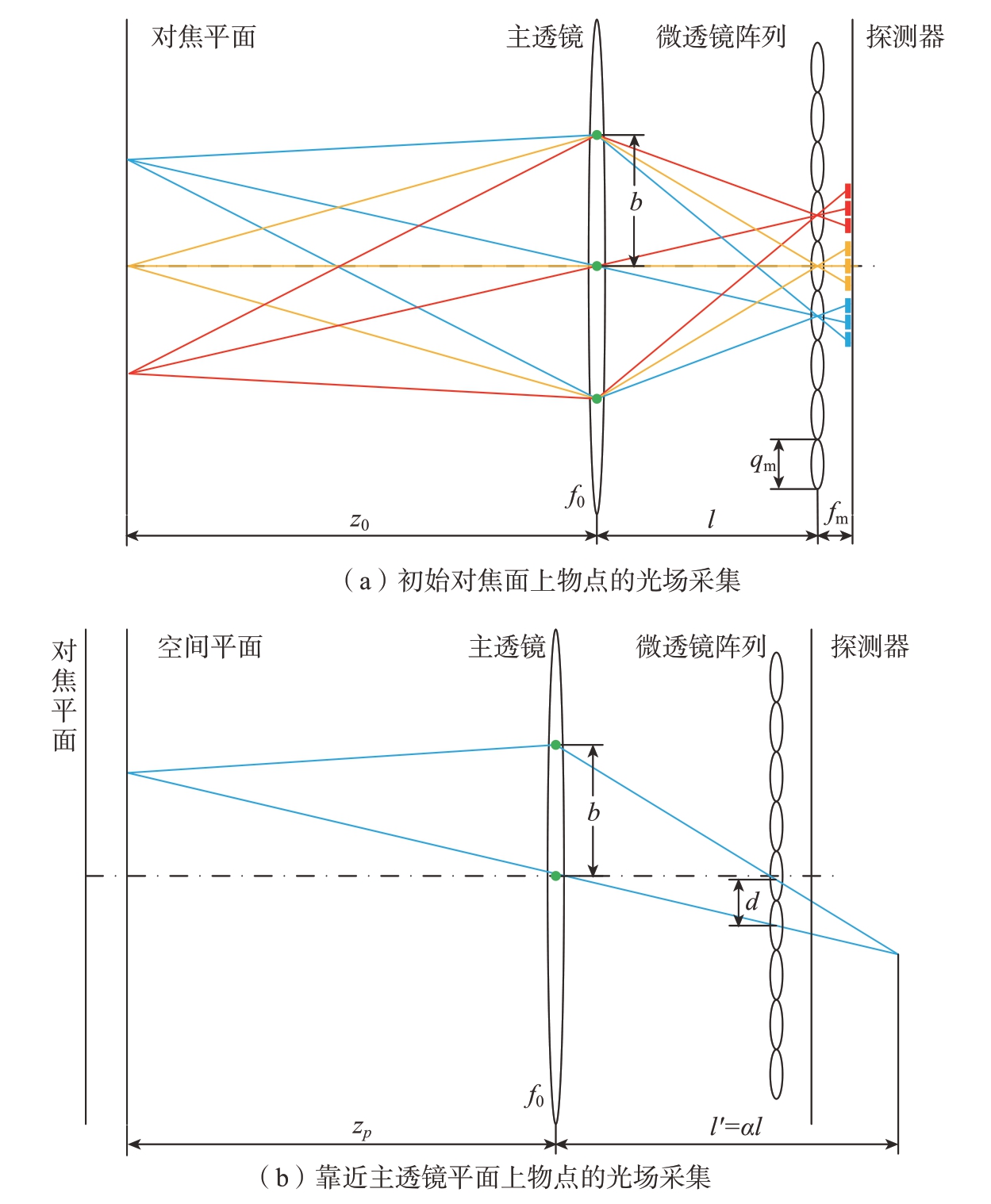
图4 微透镜阵列光场相机等效基线示意图
Fig.4 Schematic diagram of the equivalent baseline of lenslet array light field camer
同时,根据高斯物像关系有

式中,f0 表示主透镜焦距;zp 表示物点在物方空间的距离,即绝对深度;l′ = αl。结合式(4)~(6)即可得到光场视差与绝对深度之间的数值转换关系。
式中,![]() Z0 表示初始焦平面在物方空间的距离。视差通常以像素为单位。那么式(7)可重写为
Z0 表示初始焦平面在物方空间的距离。视差通常以像素为单位。那么式(7)可重写为
式中,qm为微透镜直径;ds为以像素为单位的视差。因此,式(8)给出了光场视差与绝对深度之间的数值转换关系。光场视差与绝对深度的倒数呈线性关系。式中的其他参数为光场相机的结构参数,可以通过光场相机标定算法获取。本文采用Bok等[16]提出的方法对光场相机的结构参数进行标定。同时,对式(8)求关于深度的微分可得光场视差精度与深度精度之间的关系,即
式中,Zq 表示相机光心到空间物点的深度;fm、qm、q0、l为光场相机结构参数,仅与设备有关。从式(9)可发现在视差精度一定的情况下,深度精度随着测量距离的增加而不断降低。这与视觉测量的基本原理也相吻合。下面试验也进一步验证了随着测量距离增加深度测量精度而不断降低。另外,光场相机的结构参数标定误差也会降低深度估计精度。通常情况下,光场相机结构参数误差被视为系统或固定误差。
2 试验结果
上一节主要推导了光场视差与绝对深度之间的数值转换关系,并分析了深度测量精度的影响因素。本小节将搭建相应的试验系统,并结合现有的视差估计方法验证提出方法的有效性。
2.1 试验系统
试验系统包含光场数据采集设备与补光设备,如图5(a)所示。补光设备用于补充环境光,防止因图像过暗而引起视差估计算法失效。光场相机采用一款商用的Lytro Illum 光场相机,如图5(b)所示。该相机搭载一块分辨率为7728×5368 的CMOS图像传感器。图像传感器的有效尺寸为10.82 mm×7.52 mm。同时,光场相机在主镜头与图像传感器之间放置了一块微透镜阵列,实现光场数据采集功能。每个微透镜覆盖的像元数量大约为15。绝对深度测量试验测量一块定制铝材料标准件的外形尺寸,如图6所示。由于铝材料标准件表面光滑且缺乏纹理信息,因此标准件表面被贴上一层富有纹理信息的贴纸。标准件具有3 级台阶面,相邻台阶面之间的距离为50 mm。试验系统采集标准件的光场数据如图7所示。光场相机与标准件之间的距离大概为450 mm。

图5 试验系统
Fig.5 Test system

图6 标准件尺寸
Fig.6 Dimension of standard part

图7 深度测量数据采集
Fig.7 Capturing depth estimation light field dat
2.2 绝对深度测量试验
本文采用现有的视差估计方法计算标准件场景的视差图,如图8所示。视差图分别来自于马帅等[17] 的方法(图8(a))、Wang 等[14]的方法(图8(b))、Jeon 等[9]的方法(图8(c))以及Williem 等[13]的方法(图8(d))。由于光场相机的光心难以确定,因此光场相机到标准件之间的实际距离难以确定。试验将测量标准件两个台阶面之间的距离作为绝对深度测量结果,即图8 中①与②、②与③之间的距离。其中,标准件相邻两个台阶面之间的真实距离为50 mm。在试验过程中,用提出的方法将图8 中不同方法的视差转换为绝对深度,并将红色框中深度值的平均值作为光场相机到该台阶面的距离。标准件3 个台阶面上的红色框的范围分别为(260∶330,90∶150)、(260∶330,200∶260)、(260∶330,300∶360)。将光场相机到相邻台阶面之间的距离差作为深度测量结果,如表1所示。可知,提出的方法能有效地将不同方法的视差结果转换为绝对深度,进一步验证了光场视差与绝对深度之间数值转换关系的有效性。本文提出的方法能将马帅[17]、Jeon[9]及Williem[13]等的视差结果转换为绝对深度,且深度测量结果与真实值的差异较小。从图8(a)、(c)、(d)中可以看出,这3 种方法获得的视差图具有较少噪声与不连续区域。因此,视差误差对最终的绝对深度测量误差影响较小。从表1 中可以发现,本研究提出的方法利用马帅[17]、Jeon[9]及Williem[13]等的视差结果实现了标准件②与③台阶面距离的高精度测量,其测量误差在2 mm 以内。同时,利用马帅等[17]的视差结果所获得标准件②与③台阶面距离的误差在1 mm 以内,进一步验证了本研究提出的光场视差与绝对深度之间数值转换关系的准确性。然而,提出的方法将Wang 等[14]的视差结果转换为绝对深度时,其深度测量结果与真实深度差异较大,测量误差在7 mm 以上。测量精度较低的主要原因在于该方法获得了较差的视差结果,如图8(b)所示。可以看出,该方法的视差图存在较多噪声以及视差值不连续的区域。因此,这些噪声以及视差不连续区域直接影响绝对深度测量精度。另外,光场相机的结构参数标定误差也将直接影响绝对深度测量精度。同时,从表1 中还可以发现①—②台阶面的深度测量精度均低于②—③的。主要原因在于①—②台阶面的测量距离大于②—③台阶面的测量距离,进一步验证了上述的深度精度分析。

图8 视差图
Fig.8 Disparity map
表1 绝对深度测量结果
Table 1 Results of absolute depth measurement mm

台阶面真实值马帅等[17]Wang 等[14]Jeon 等[9]Williem 等[13]①—②50.056.840.548.153.5②—③50.050.842.548.948.6
3 结论
(1)本研究结合EPI 对光场视差原理进行了理论分析,并通过双平面表达EPI 得到光场视差与等效基线之间的关系。
(2)通过对微透镜阵列光场相机的三维成像原理进行理论分析,并结合几何光学原理建立了等效基线与光场相机结构参数之间的关系。通过上述关系推导出光场视差与绝对深度之间的数值转换关系。
(3)通过搭建试验平台以及结合现有的视差估计算法验证了本文提出的光场视差与绝对深度之间数值转换关系的有效性,并获得了高精度的深度估计结果。
[1]MAY S,DROESCHEL D,FUCHS S,et al.Robust 3D-mapping with time-offlight cameras[C]//2009 IEEE/RSJ International Conference on Intelligent Robots and Systems.Louis:IEEE,2009:1673–1678.
[2]任禹,罗一涵,徐少雄,等.非视域定位中光子飞行时间提取方法对比研究[J].光电工程,2021,48(1):84–93.REN Yu,LUO Yihan,XU Shaoxiong,et al.A comparative study of time of flight extraction methods in non-line-of-sight location[J].Opto-Electronic Engineering,2021,48(1):84–93.
[3]SCHWALBE E,MAAS H,SEIDEL F.3D building model generation from airborne laser scanner data using 2D GIS data and orthogonal point cloud projections[J].International Archives of Photogrammetry and Remote Sensing,2004,35(3):249–254.
[4]龙玺,钟约先,李仁举,等.结构光三维扫描测量的三维拼接技术[J].清华大学学报(自然科学版),2002,42(4):477–480.LONG Xi,ZHONG Yuexian,LI Renju,et al.3-D surface integration in structured light 3-D scanning[J].Journal of Tsinghua University(Science and Technology),2002,42(4):477–480.
[5]李清泉,李必军,陈静.激光雷达测量技术及其应用研究[J].武汉测绘科技大学学报,2000,25(5):387–392.LI Qingquan,LI Bijun,CHEN Jing.Research on laser range scanning and its application[J].Journal of Wuhan Technical University of Surveying and Mapping,2000,25(5):387–392.
[6]MAYER N,ILG E,HÄUSSER P,et al.A large dataset to train convolutional networks for disparity,optical flow,and scene flow estimation[C]//2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).Las Vegas:IEEE,2016:4040–4048.
[7]YAO Y,LUO Z X,LI S W,et al.Recurrent MVSNet for high-resolution multiview stereo depth inference[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR).Long Beach:IEEE,2020:5520–5529.
[8]LEVOY M,HANRAHAN P.Light field rendering[C]//Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques.New York:1996:31–42.
[9]JEON H G,PARK J,CHOE G,et al.Accurate depth map estimation from a lenslet light field camera[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).Boston:IEEE,2015:1547–1555.
[10]STRECKE M,ALPEROVICH A,GOLDLUECKE B.Accurate depth and normal maps from occlusion-aware focal stack symmetry[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).Honolulu:IEEE,2017:2529–2537.
[11]SHENG H,ZHAO P,ZHANG S,et al.Occlusion-aware depth estimation for light field using multi-orientation EPIs[J].Pattern Recognition,2018,74:587–599.
[12]ZHANG S,SHENG H,LI C,et al.Robust depth estimation for light field via spinning parallelogram operator[J].Computer Vision and Image Understanding,2016,145:148–159.
[13]WILLIEM,PARK I K,LEE K M.Robust light field depth estimation using occlusionnoise aware data costs[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2018,40(10):2484–2497.
[14]WANG T C,EFROS A A,RAMAMOORTHI R.Depth estimation with occlusion modeling using light-field cameras[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2016,38(11):2170–2181.
[15]MATYSIAK P,GROGAN M,LE PENDU M,et al.A pipeline for lenslet light field quality enhancement[C]//2018 25th IEEE International Conference on Image Processing(ICIP).Athens:IEEE,2018:639–643.
[16]BOK Y,JEON H G,KWEON I S.Geometric calibration of micro-lens-based light field cameras using line features[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2017,39(2):287–300.
[17]马帅,王宁,朱里程,等.基于边框加权角相关的光场深度估计算法[J].光电工程,2021,48(12):58–69.MA Shuai,WANG Ning,ZHU Licheng,et al.Light field depth estimation using weighted side window angular coherence[J].Opto-Electronic Engineering,2021,48(12):58–69.
