随着卫星星座的大规模部署与应用，对我国卫星批量化生产的能力提出了更高的要求。而传统卫星装配以人工作业为主，单颗卫星总装、测试周期为2 ～ 3 个月，所需操作人员10 ～ 15 名，极大地制约了卫星的生产能力[1]。卫星总装阶段为卫星主框架与舱板的装配，卫星尺寸跨度大（1 m×1 m×1 m ～ 5 m×2 m×1 m），舱板内侧安装有大量传感器与结构件，导致待装配舱板重量大（10 ～ 500 kg），且要求主框架与舱板的装配精度优于0.2 mm，装配干涉力不大于50 N，使得人工作业模式无法满足卫星总装的装配效率与装配精度，亟须开展自动化、批量化、智能化的卫星生产新模式[2]。随着工业机器人的不断发展，其承载能力、定位精度、可靠性等得到了进一步提升，广泛应用于搬运码垛、汽车与电子装配等领域[3]。基于多机器人的卫星装配可以替代人工作业方式，实现对不同尺寸、不同重量、不同类型卫星的自动化、批量化装配。基于多机器人的卫星装配需要主机器人通过夹爪与工装完成对舱板的夹取，由于工业机器人存在一定的定位误差[4]，同时主框架与舱板在工装固定过程中存在一定的安装误差，导致采用示教重复装配模式下卫星主框架与舱板的装配精度变差，且装配完成后舱板与主框架之间存在较大干涉力，严重制约了卫星装配自动化、批量化新模式的发展。
在视觉研究方面，根据相机数量的不同，可以分为单目[5]、双目[6]与多目视觉系统[7]；根据相机安装位置与机器人的相对位置关系不同，分为“眼在手上”和“眼在手外”两种方式[8–9]；根据系统视觉伺服控制方式的不同，分为基于位置的视觉伺服[10]、基于图像的视觉伺服和混合视觉伺服等[11–12]。在视觉装配领域，王斌等[13]提出了面向机器人精密装配的高精度圆片位姿视觉检测，通过单目相机实现了对目标的精确检测，快速、准确地引导机械臂进行待装配圆片和孔的对中操作；杜福洲等[14]针对大尺度部件对接过程中的相对位姿测量需求，采用单目视觉采集合作靶标图像，实时解算大部段间的相对位姿，用于辅助大尺度部件的装配。在卫星装配领域，胡瑞钦等[15]采用红外相机结合自制合作靶标，将待装配部件引导至销钉的锥面导向范围；季旭全等[16]提出了基于机器人与视觉引导的星载设备智能装配方法，利用双目相机采集视觉靶标与视觉探针，实现了装配路径的规划与校正。
在力觉研究方面，研究者们利用安装在机器人上的力传感器来实现机器人外力感知[17–18]，通过对机器人末端负载的重力补偿[19]可以测量得到末端外力的大小与方向。胡瑞钦等[20]提出了一种基于力/位控制的机器人柔顺控制方法，实现了航天器大部件机器人柔顺装配。罗威等 [21]提出了一种基于力–位图像学习的柔顺装配方法，将装配过程中的位姿和接触力信息转化为力–位图像，然后通过对力–位图像的分类学习获得不同初始位姿情况下的柔顺装配动作策略，从而控制机器人实现柔顺装配。
将视觉与力觉控制应用在卫星装配领域存在装配精度有待进一步提高、误差补偿方法有待研究、舱板与主框架位姿测量难、装配干涉力大等问题。根据实际卫星装配特点与需求分析，待装配卫星舱板与主框架的装配面均有对应销孔、螺纹孔及沉头孔等特征孔，为了得到卫星舱板与主框架的位姿，需要测量特征孔的三维坐标，因此可以采用双目视觉系统测量舱板与主框架对应特征孔，实现对舱板与主框架的位姿测量。同时，为满足双目视觉系统对不同尺寸、不同型号卫星的测量范围全覆盖，采用“眼在手上”的形式，将两组双目视觉系统分别安装在两台辅助工业机器人法兰盘末端，从而实现对测量范围的扩展。由于装配误差的影响，卫星舱板与主框架装配完成后仍存在较大装配干涉力。因此，在卫星舱板与主框架装配过程中引入力觉控制，实时测量装配干涉力信息，进而实现对装配干涉力的控制。
针对本文卫星装配的特点与要求，拟采用视觉装配误差测量与力觉装配干涉力测量相结合的方式，实现卫星舱板与主框架的高精度装配。主机器人通过夹爪夹持带舱板的工装，两台辅助机器人分别携带双目视觉检测系统完成对卫星主框架与舱板位姿的测量，计算主框架与舱板装配位姿误差，进而求解装配误差补偿的主机器人运动参数，直至装配精度满足要求，最后采用力觉实时测量装配干涉力信息，从而实现舱板与主框架装配面的贴合。
所采用的方案具有以下优点：
（1）采用两台辅助机器人与两套双目视觉检测系统相结合的方式，实现了对不同尺寸卫星舱板和主框架装配误差的精确测量；
（2）建立了卫星舱板与主框架装配误差补偿机制，实现了高精度装配；
（3）采用视觉与力觉相结合的方式，通过视觉测量保证卫星舱板与主框架装配精度，利用力觉测量控制卫星舱板与主框架贴合装配干涉力；
（4）此方案不需要设计特制靶标，通过视觉检测卫星舱板与主框架特征孔实现其位姿精确测量，无需人工干预。
1 系统组成及工作原理
1.1 系统组成
融合视觉与力觉的卫星装配误差在线测量与补偿系统由视觉检测装置和力觉检测装置等共同组成。视觉检测装置由两台小视场双目视觉检测装置和1 台大视场双目视觉检测装置构成。为了扩展对卫星舱板与主框架测量范围，两台小视场双目视觉检测装置分别固定安装在两台辅助机器人法兰盘末端，用于测量卫星舱板与主框架的特征孔并求解位姿；大视场双目视觉检测装置安装固定在装配系统正上方，可以实现对配套靶标点的三维坐标测量，用于建立主机器人基坐标系和标定各坐标系之间的转换矩阵。力觉检测装置采用六维力传感器，并安装在主机器人法兰盘末端，用于测量舱板与主框架贴合装配过程中的干涉力信息。
1.2 系统工作原理
图1为卫星模拟验证件装配效果以及舱板与主框架特征孔示意图。
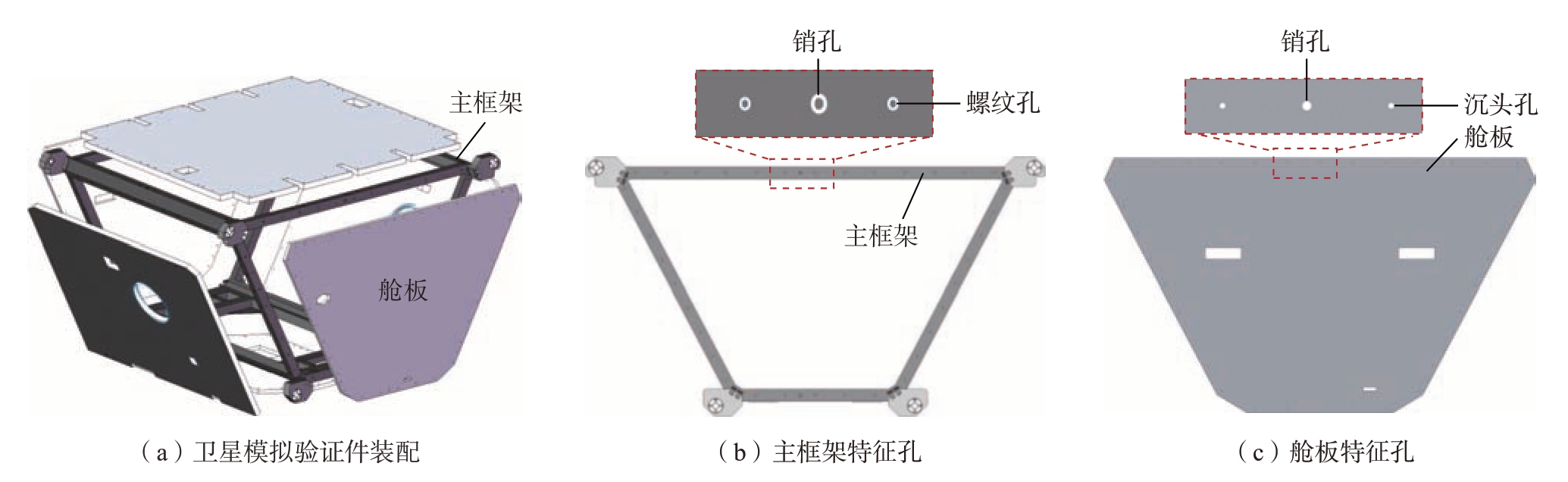
图1 卫星模拟验证件装配及特征孔示意图
Fig.1 Schematic diagram of satellite simulation verification part assembly and characteristic hol
根据卫星装配需求，应用该系统配合卫星装配系统进行装配作业的主要步骤如下：
（1）小视场双目视觉检测装置标定与机器人手眼标定，舱板与主机器人法兰盘相对位姿标定；
（2）规划主机器人与两台辅助机器人运动路径，确定两台双目视觉检测装置测量舱板与主框架时的位姿与机器人运动位置；
（3）两台小视场双目视觉检测装置测量主框架特征孔，确定主框架在小视场双目视觉检测装置Ⅰ坐标系下的位姿；
（4）两台小视场双目视觉检测装置测量待装配舱板特征孔，并将小视场双目视觉检测装置Ⅱ坐标系下测量的特征孔坐标转换至小视场双目视觉检测装置Ⅰ坐标系下，确定舱板在小视场双目视觉检测装置Ⅰ坐标系下的位姿，并求解舱板坐标系与主机器人法兰盘坐标系间的转换矩阵；
（5）计算舱板装配时主机器人运动参数，并进行预装配，即根据位姿测量结果进行第1 次装配作业；
（6）执行融合视觉与力觉的卫星装配误差在线测量与补偿过程，直至完成装配。
2 系统关键算法
2.1 系统标定方法
2.1.1 双目标定
双目标定主要是为了得到相机的内参矩阵、畸变系数和左右相机的相对位置关系。其中相机内参矩阵表征相机坐标系到像素坐标系的转换关系；畸变系数用于矫正相机光学系统制造和安装误差导致的实际成像与理想成像不符；左右相机标定的目的是得到右相机相对于左相机的平移向量与旋转矩阵，从而实现三维测量。
2.1.2 机器人手眼标定
机器人手眼标定主要分为大视场双目视觉检测装置坐标系与主机器人基坐标系间的矩阵转换关系标定，两台小视场双目视觉检测装置坐标系分别与主机器人基坐标系间的矩阵转换关系标定、两台小视场双目视觉检测装置坐标系间的矩阵转换关系标定。
图2为大视场双目视觉检测装置坐标系与主机器人基坐标系间的矩阵转换关系标定示意图。定义主机器人基坐标系为OB–XBYBZB，大视场双目视觉检测装置坐标系为OC–XCYCZC。在主机器人机械臂末端粘贴靶标点，分别旋转主机器人A1 轴与A2 轴，并采集靶标点在OC–XCYCZC 坐标系下的三维坐标。根据主机器人D–H 参数，在OC–XCYCZC 坐标系下建立OB–XBYBZB 坐标系，得到OC–XCYCZC坐标系与OB–XBYBZB 坐标系间的矩阵转换关系
。
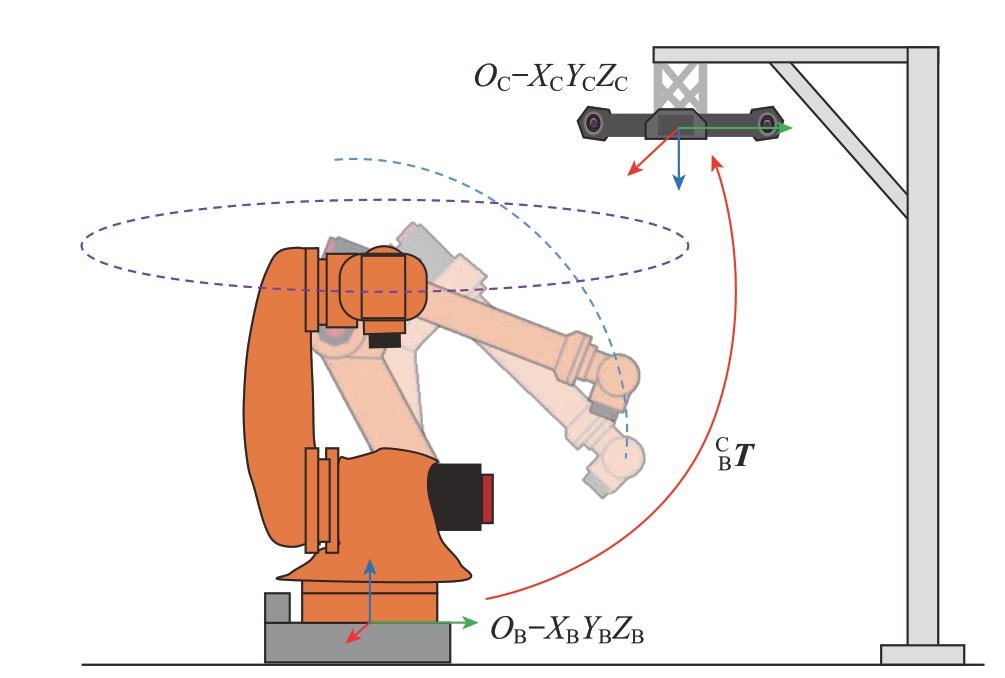
图2 OC–XCYCZC 坐标系与OB–XBYBZB 坐标系标定示意图
Fig.2 Calibration diagram of OC–XCYCZC coordinate system and OB–XBYBZB coordinate system
靶标点标定板由标定板与粘贴在标定板平面上的若干靶标点组成。定义小视场双目视觉检测装置Ⅰ坐标系为OCI–XCIYCIZCI，小视场双目视觉检测装置Ⅱ坐标系为OCⅡ–XCⅡYCⅡZCⅡ，靶标点标定板坐标系为OP–XPYPZP。图3为OCI–XCIYCIZCI 坐标系、OCⅡ–XCⅡYCⅡZCⅡ坐标系与OB–XBYBZB 坐标系的矩阵转换关系标定示意图。
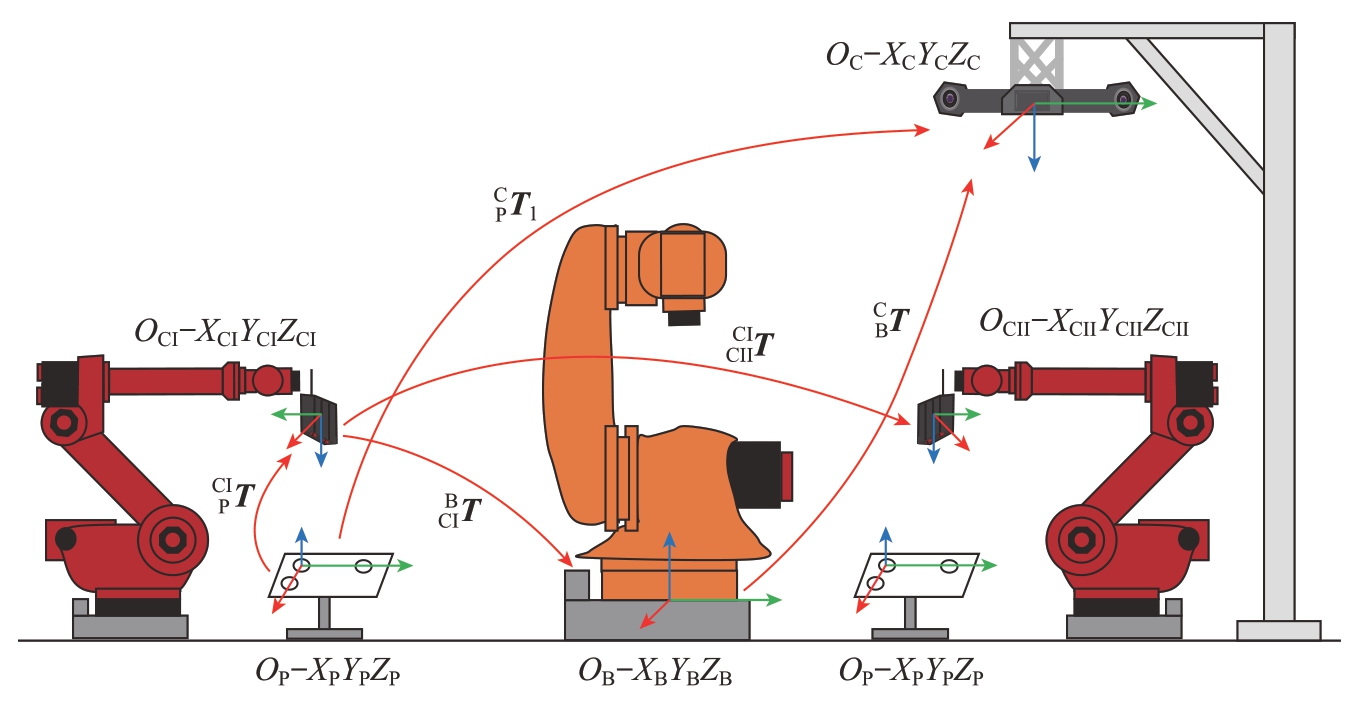
图3 坐标系标定示意图
Fig.3 Diagram of coordinate system calibration
通过小视场双目视觉检测装置与大视场双目视觉检测装置分别对靶标点标定板进行靶标点三维测量，并利用测量的靶标点三维坐标分别在OCI–XCIYCIZCI 坐标系与OC–XCYCZC坐标系下建立OP–XPYPZP 坐标系，求解得到OP–XPYPZP 坐标系分别与OCI–XCIYCIZCI 坐标系、OC–XCYCZC 坐标系间的矩阵转换关系
同理，在移动靶标点标定板至小视场双目视觉检测装置视野范围内，求解得到OP–XPYPZP 坐标系分别与OCⅡ–XCⅡYCⅡZCⅡ坐标系、OC–XCYCZC 坐标系间的转换关系
。
根据坐标系间的矩阵转换关系，OCI–XCIYCIZCI 坐标系相对于OB–XBYBZB坐标系的矩阵转换关系
为
同理，OCⅡ–XCⅡYCⅡZCⅡ坐标系相对于OB–XBYBZB 坐标系的矩阵转换关系为
因此，OCⅡ–XCⅡYCⅡZCⅡ坐标系相对于OCI–XCIYCIZCI 坐标系的矩阵转换关系
为
2.1.3 舱板与主机器人法兰盘标定
主机器人通过夹爪夹取舱板，受装夹误差的影响，主机器人法兰盘与舱板的相对位姿不确定。因此，每次舱板装配前均需要对舱板与主机器人法兰盘相对位姿进行测量与标定。
定义主机器人法兰盘坐标系为OF–XFYFZF，舱板坐标系为OD–XDYDZD，图4为OF–XFYFZF 坐标系与OD–XDYDZD坐标系间矩阵转换关系标定示意图。
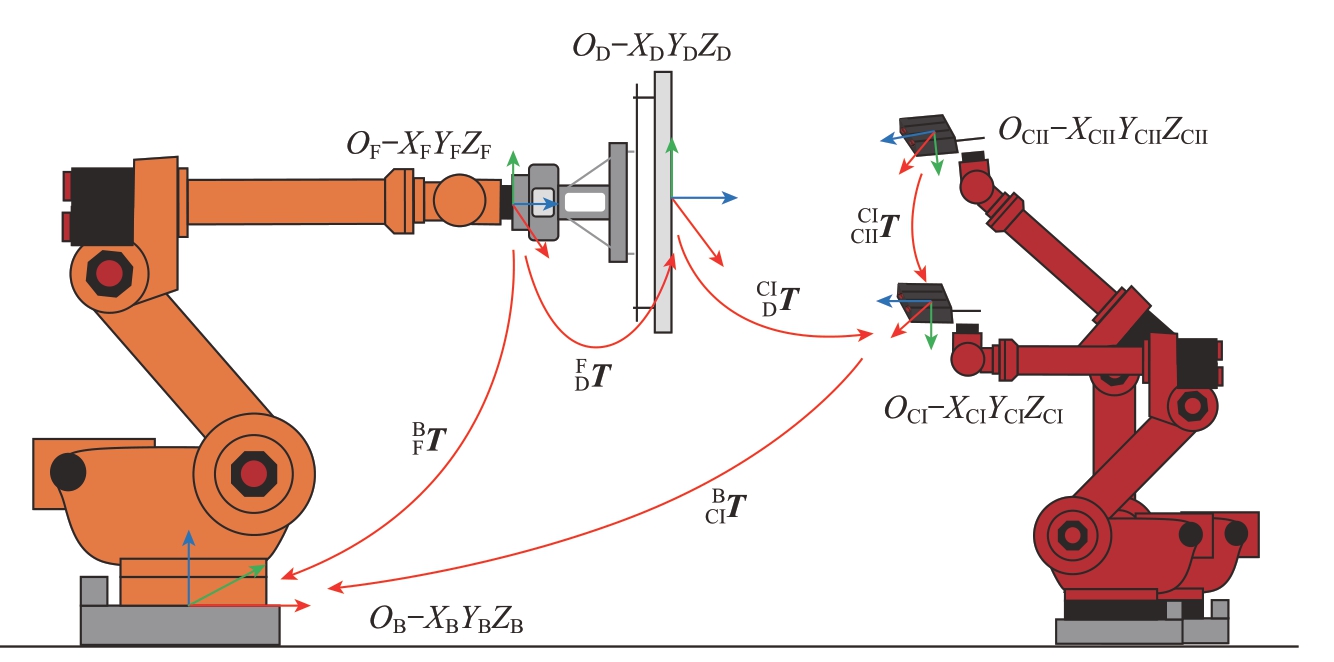
图4 OF–XFYFZF 坐标系与OD–XDYDZD 坐标系标定示意图
Fig.4 Calibration diagram of OF–XFYFZF coordinate system and OD–XDYDZD coordinate system
利用两台小视场双目视觉检测装置测量舱板特征孔，在OCI–XCIYCIZCI 坐标系下建立OD–XDYDZD 坐标系，得到OD–XDYDZD 坐标系相对于OCI–XCIYCIZCI 坐标系的矩阵转换关系CIDT。记录当前OF–XFYFZF 坐标系相对于OB–XBYBZB 坐标系的矩阵转换关系BFT。根据坐标系间的矩阵转换关系，OD–XDYDZD 坐标系相对于OF–XFYFZF 坐标系的转换关系矩阵
为
2.2 卫星装配误差求解方法
2.2.1 主框架位姿求解
图5为两台小视场双目视觉检测装置测量主框架特征孔（销孔、螺纹孔）示意图。每台小视场双目视觉检测装置均测量1 个销孔与周围2 个螺纹孔。
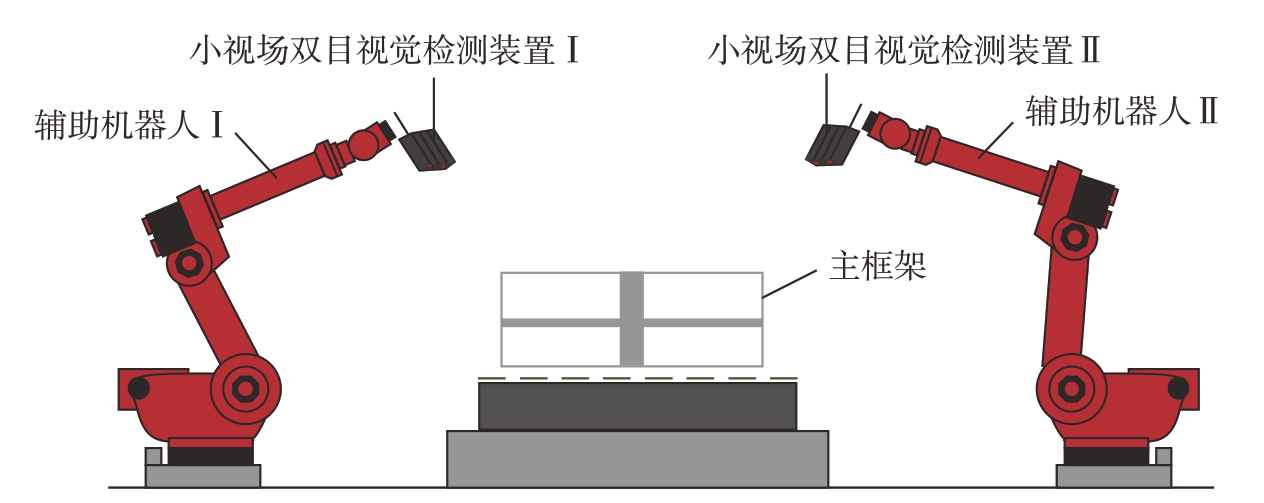
图5 卫星主框架位姿测量示意图
Fig.5 Diagram of satellite main frame position and attitude measurement
如图6所示，小视场双目视觉检测装置采集主框架特征孔图像，对原始图像进行如下图像处理步骤。
图6 卫星主框架特征孔图像
Fig.6 Satellite main frame feature hole image
（1）滤波处理：去除图像部分噪声；
（2）边缘检测：采用Canny 边缘检测方法，提取特征孔轮廓边缘特征；
（3）椭圆拟合：根据最小二乘法原理，将特征孔轮廓点云进行椭圆拟合，得到椭圆中心点像素坐标；
（4）椭圆筛选：根据拟合椭圆的面积、周长等参数，去除误拟合的非特征孔椭圆。
通过左右相机标定关系，分别得到3 个特征孔中心在OCI–XCIYCIZCI坐标系下的三维坐标P1（x1，y1，z1）、P2（x2，y2，z2）、P3（x3，y3，z3）和其余3 个特征孔中心在OCⅡ–XCⅡYCⅡZCⅡ坐标系下的三维坐标P4（x4，y4，z4）、P5（x5，y5，z5）、P6（x6，y6，z6）。根据OCI–XCIYCIZCI 坐标系与OCⅡ–XCⅡYCⅡZCⅡ坐标系的矩阵转换关系，求解点P4、P5 与P6 在OCI–XCIYCIZCI 坐标系下的三维坐标，得P′4、P′5 与P′6。
定义主框架坐标系为OM–XMYMZM。根据最小二乘法原理，利用点
拟合平面N1，将所有点投影至平面N1，得到投影点
以
位置为原点，
与
连线方向为
轴，平面N1 的法线方向为
轴，Y′M轴通过右手定则确定，在OCI–XCIYCIZCI坐标系下建立
坐标系。根据建立的
坐标系与主框架理论坐标系位姿关系，将
坐标系变换至主框架理论坐标系处，得到OM–XMYMZM 坐标系。求解OM–XMYMZM 坐标系相对于OCI–XCIYCIZCI 坐标系的矩阵转换关系
，则主框架在OCI–XCIYCIZCI坐标系下的位姿采用欧拉角表示为
，且后续位姿均采用欧拉角表示。
2.2.2 主机器人预装配参数求解
图7为舱板位姿测量示意图。根据主框架位姿求解方法，得到OD–XDYDZD坐标系相对于OCI–XCIYCIZCI 坐标系的转换关系矩阵
。记录当前OF–XFYFZF 坐标系相对于OB–XBYBZB坐标系的转换关系矩阵
。根据式（4）得出OD–XDYDZD 坐标系相对于OF–XFYFZF 坐标系的矩阵转换关系
。
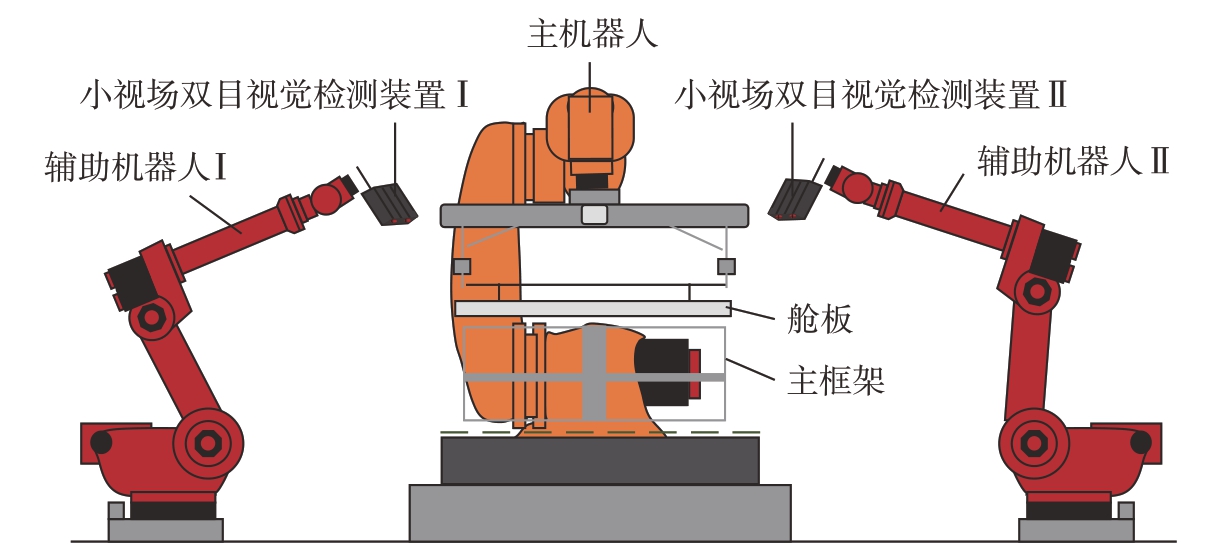
图7 卫星舱板位姿测量示意图
Fig.7 Diagram of satellite deck position and attitude measurement
根据舱板与主框架数模装配位姿关系，当舱板与主框架装配完成，且间隔固定安全贴合距离时，理论上OD–XDYDZD 坐标系相对于OM–XMYMZM 坐标系的转换关系矩阵为
。则舱板在OM–XMYMZM 坐标系下的位姿为
，且存在
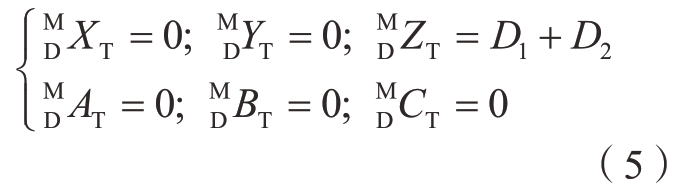
式中，D1为舱板厚度；D2为安全贴合距离。
因此，可得在理论位置时OD–XDYDZD 坐标系相对于OCI–XCIYCIZCI坐标系的转换关系矩阵为
。
计算舱板预装配时OF–XFYFZF坐标系相对于OB–XBYBZB 坐标系的矩阵转换关系
为
整理得出
通过转换关系矩阵
即得到舱板预装配时主机器人运动位姿参数为
。
2.2.3 装配误差求解
在主机器人运动至位姿参数
时，舱板到达预装配位置。小视场双目特征检测装置对舱板位姿进行测量，得到此时OD–XDYDZD 坐标系相对于OCI–XCIYCIZCI 坐标系的矩阵转换关系 ，根据矩阵转换关系，得出OD–XDYDZD 坐标系相对于OM–XMYMZM 坐标系的转换关系矩阵为
。
整理得出即得到舱板在OM–XMYMZM 坐标系下的位姿为
。
计算此时舱板与主框架装配误差为[ΔX1，ΔY1，ΔZ1，ΔA1，ΔB1，ΔC1]。
2.3 卫星装配位姿误差补偿方法
卫星装配位姿误差补偿方法是通过测量舱板与主框架的位姿与偏差后，控制主机器人运动实现对舱板位姿的调整，进而保证卫星舱板与主框架装配位姿精度。
图8为卫星装配位姿误差补偿流程图。
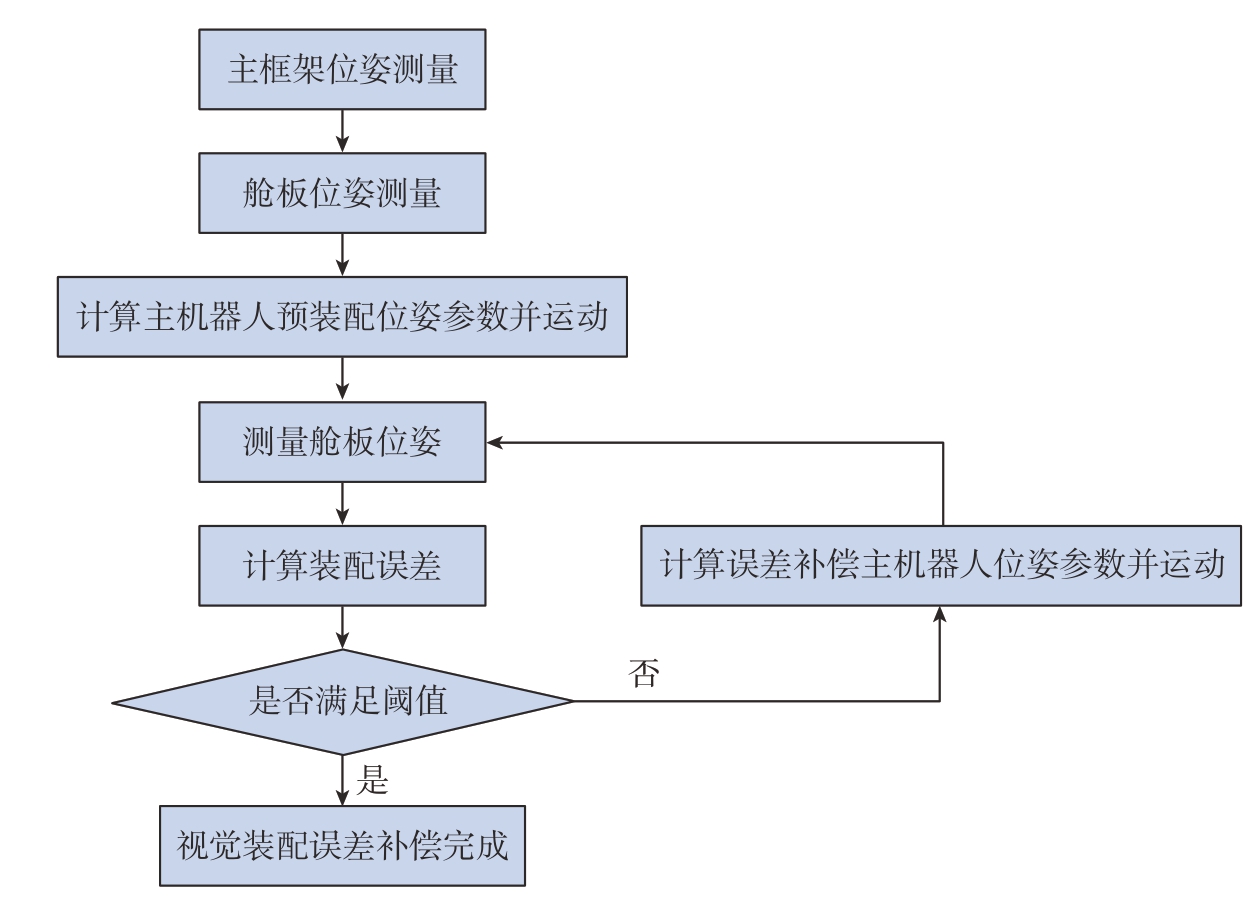
图8 卫星装配位姿误差补偿流程图
Fig.8 Flow chart of satellite assembly position and attitude error compensation
根据舱板与主框架装配误差，定义误差补偿舱板在OM–XMYMZM 坐标系下的位姿参数为
。
根据式（10），定义误差补偿OD–XDYDZD 坐标系相对于OM–XMYMZM坐标系的矩阵转换关系为
。
根据式（7），计算误差补偿OF–XFYFZF 坐标系相对于OB–XBYBZB 坐标系的矩阵转换关系
为
根据矩阵转换关系 ，得到第1次卫星装配误差补偿时主机器人运动位姿参数为
，并控制主机器人进行误差补偿运动。
根据式（9）和（10），对第1 次误差补偿完成后的舱板再次进行位姿测量与装配误差计算，得到OD–XDYDZD 坐标系相对于OM–XMYMZM坐标系的矩阵转换关系
，舱板在OM–XMYMZM坐标系下的位姿为
得到舱板与主框架装配误差为[ΔX2，ΔY2，ΔZ2，ΔA2，ΔB2，ΔC2]。
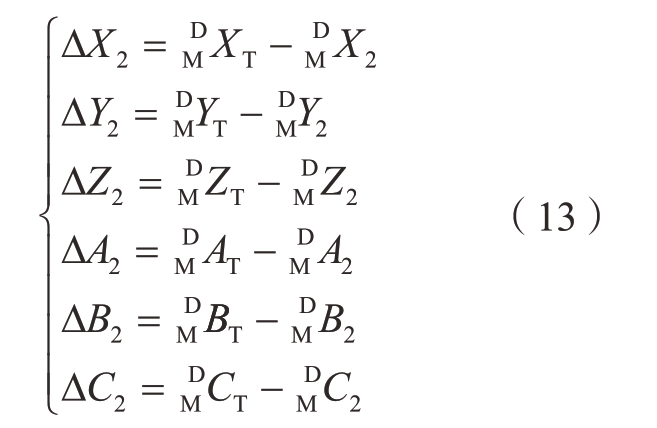
根据舱板与主框架第2 次装配误差测量结果，定义第2 次误差补偿舱板在OM–XMYMZM 坐标系下的位姿参数，输入
为
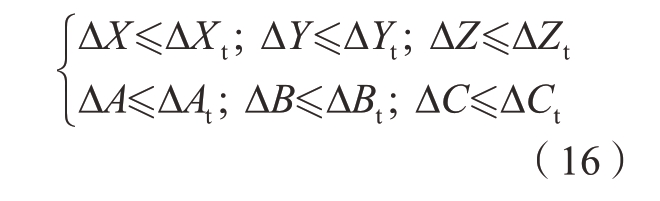
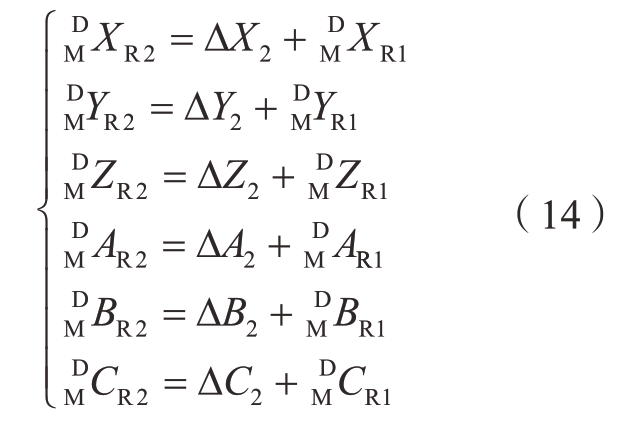
根据式（10），定义第2 次误差补偿OD–XDYDZD 坐标系相对于OM–XMYMZM 坐标系的矩阵转换关系
。
根据式（7），计算第2 次误差补偿OF–XFYFZF 坐标系相对于OB–XBYBZB 坐标系的矩阵转换关系
。
根据矩阵转换关系BFTR2，得到第2 次卫星装配误差补偿时主机器人运动位姿参数
，并控制主机器人进行误差补偿运动。
重复上述卫星装配误差检测与补偿步骤，直至舱板与主框架装配误差[ΔX，ΔY，ΔZ，ΔA，ΔB，ΔC]小于所设阈值[ΔXt，ΔYt，ΔZt，ΔAt，ΔBt，ΔCt]，即
当满足式（16），则说明基于视觉的卫星舱板与主框架装配位姿误差在线测量与补偿完成。
2.4 力觉感知装配方法
2.4.1 重力补偿
图9（a）所示为主机器人与六维力传感器、夹爪、舱板等之间的相对安装位置示意图。由于重力作用（仅考虑静态或低速运动情况）六维力传感器采集的力信息受到夹爪、舱板等重力和重心位置的影响，不能完全反映末端装配干涉力情况。因此为了准确反映舱板与主框架装配干涉力，需要进行末端重力补偿。
如图9（b）所示，主机器人携带夹爪夹持舱板工装，通过变换主机器人位姿，记录六维力传感器的力信息，采用重力补偿辨识方法，完成对末端负载的重力补偿[22]。
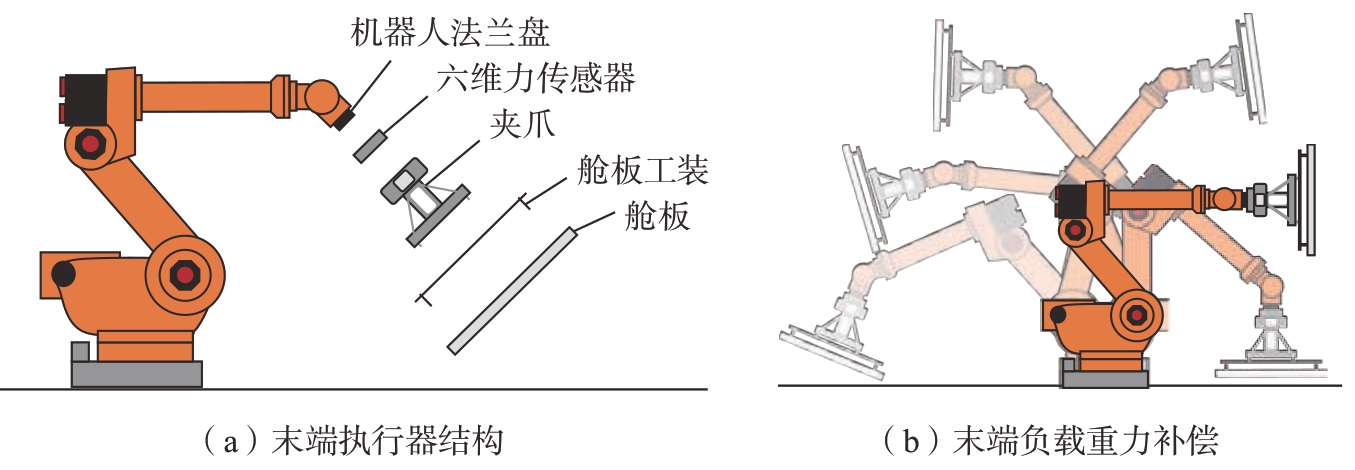
图9 主机器人末端执行器结构与末端负载重力补偿示意图
Fig.9 Diagram of main robot end actuator structure and end load gravity compensation
2.4.2 力觉控制装配
在基于视觉的卫星装配误差在线测量与补偿完成后，需完成舱板与框架的装配贴合，即舱板沿着当前OD–XDYDZD 坐标系的ZD 轴方向移动，直至轴方向装配干涉力FZD 满足所设阈值Ft，即FZD≥Ft。
为保证舱板沿着当前OD–XDYDZD坐标系的ZD 轴方向平移，且装配干涉力FZD 达到预设阈值Ft，需给定舱板平移的目标值与主机器人移动的贴合目标值为
。
假设最后一次误差补偿完成后，舱板在OM–XMYMZM 坐标系下的位姿参数为
，则舱板平移的贴合目标值为
。
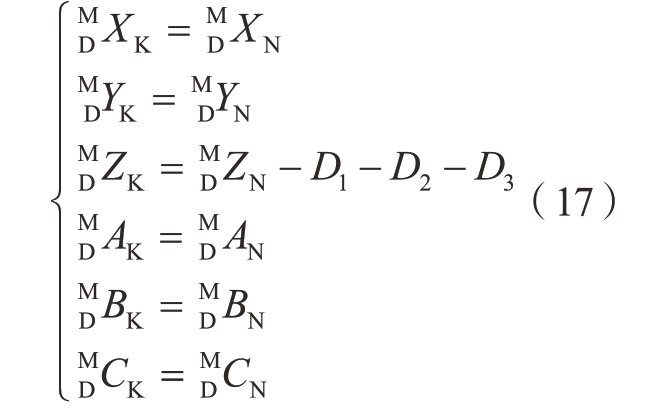
式中，D3为过贴合距离。
得到舱板平移目标值时OD–XDYDZD 坐标系相对于OM–XMYMZM坐标系的转换关系矩阵为
。
根据式（7），得到舱板平移目标值时OF–XFYFZF 坐标系相对于OB–XBYBZB 坐标系的矩阵转换关系
为
即可计算得到主机器人移动的贴合目标值
。
根据上述计算得到的主机器人移动贴合目标值
控制主机器人运动。同时，采用力觉检测装置实时采集并计算ZD 轴方向装配干涉力，并与所设阈值Ft 做比较，直至满足条件FZD≥Ft，则控制主机器人停止向贴合目标值
运动，即贴合装配完成。
3 装配试验与分析
3.1 试验条件
试验系统平台如图10所示，主机器人为SIASUN 公司生产的SR500A，两台辅助机器人为SIASUN公司生产的T90A–30 机器人。主机器人法兰盘末端安装有SRI 公司生产的M4347K 六维力传感器，两台辅助机器人法兰盘末端分别安装有RVBUST 公司生产的RVC–P5330 小视场双目视觉检测装置，此装置由左相机L 和右相机R 组成。试验系统平台正上方固定安装有SCANTECH公司生产的大视场双目视觉检测装置E-Track。
图10 卫星装配试验系统平台
Fig.10 Satellite assembly experiment system platform
试验中使用的模拟卫星主框架重约100 kg，模拟卫星舱板重约50 kg，安装面尺寸为500 mm×1000 mm，舱板与主框架四周边缘分别设有φ5 mm沉头孔与M5 螺纹孔，安装面边缘设有两个φ6 mm 销孔，用于检测舱板与主框架装配精度。试验中D1、D2、D3参数分别取15 mm、10 mm、10 mm。
3.2 装配试验结果与分析
两台辅助机器人分别携带小视场双目视觉检测装置在不同位姿下拍摄相机标定板，并进行相机标定，其标定结果见表1。
表1 相机标定参数
Table 1 Camera calibration parameters
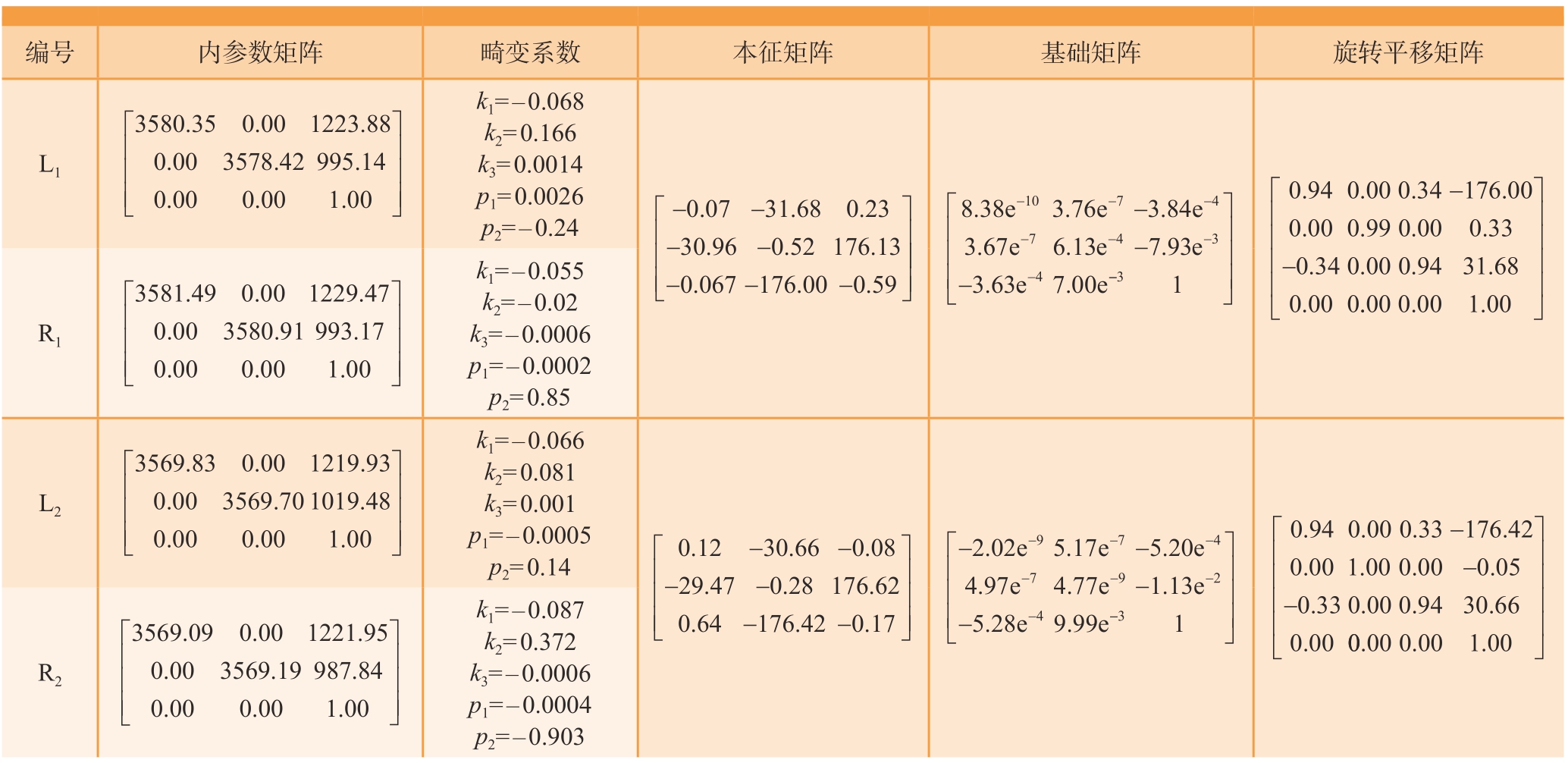
编号内L1 3580 35 0 00 3..■■■参数矩阵畸变系数本征矩阵基础矩阵旋转平移矩阵0 00 1223 88 578 42 995 14 0 000 001 00.......■■■■■■■k1=–0.068 k2= 0.166 k3= 0.0014 p1= 0.0026 p2=–0.24-------■■■■■■■■0 07 31 68 0 23 30 96 0 52 176 13 0 067 176 00 0 59.........■■8 383 763 84 3 676 137 93 3 63 7 00-1074 7 4 3........eee eee ee------4--■■■■■-■■■■■-31 0 94 0 00 0 34 0 00 0 99 0 00 0 33 0 34 0 00 0 94 31 68 0 00 0...............--176.00 00 0 00 1 00■■■■■■■■■■■■R1 3581 49 0 00 1229 47 0 00 3580 91 993 17 0 000 001 00.........■■■■■■■■■■k1=–0.055 k2=–0.02 k3=–0.0006 p1=–0.0002 p2= 0.85 L2 3569 83 0 00 1219 93 0 00 3569 70 1019 48 0 000 001 00.........■■■■■■■■■■k1=–0.066 k2= 0.081 k3= 0.001 p1=–0.0005 p2= 0.140 1230 66 0 08 29 47 0 28 176 62 0 64 176 42 0 17.........------■■■■■■■■■■---9-7-4-7-9-2-4-2 02 5 175 20 4 974 77 9 99......eee ee1.13e 5.28ee■■■■■-■■■■■-31 0 94 0 00 0 33 176 42 0 00 1 00 0 00 0 05 0 33 0 00 0 94 30 66 0 00.............---0 00 0 00 1 00...■■■■■■■■■■■■R2 3569 09 0 00 1221 95 0 00 3569 19 987 84 0 000 001 00.........■■■■■■■■■■k1=–0.087 k2= 0.372 k3=–0.0006 p1=–0.0004 p2=–0.903
采用上述机器人手眼标定方法完成OC–XCYCZC 坐标系与OB–XBYBZB 坐标系间的转换关系标定，OCI–XCIYCIZCI 坐标系、OCⅡ–XCⅡYCⅡZCⅡ坐标系分别与OB–XBYBZB 坐标系间的转换关系标定，OCI–XCIYCIZCI 坐标系与OCⅡ–XCⅡYCⅡZCⅡ坐标系间的转换关系标定。采用上述舱板与主机器人法兰盘标定方法，完成OD–XDYDZD坐标系相对于OF–XFYFZF 坐标系的转换关系标定。其标定结果见表2。
表2 坐标系标定
Table 2 Coordinate system calibration
C BTCI BTCII BTCII CITF DT--------------86 16 0 00 0 00 0 00 1 00 0 97 0 15 0 16 177 29 0 07 0 89 0 43 247 18 0 21 0 41 0 88 59...........■■....■■-----..0 30 0 94 0 18 2310 82 0 94 0 33 0 12 1732 98 0 17 0 13 0 98 17 0.99 0.12 0.02 1276.00 0.120.02 664.42 0.02 0.01 0.99 112.90-...........-■■■■■■■■■■■■....■■....0 97 0 17■■■■-38 29 0 00 0 00 0 00 1 00■■■■.0.192095.04 0.97 0.21 0.14 306.38 0.17 0.14 0.98 171■■■■■■■■■■■■.....3.23 0 00 0 00 0 00 1 00■■■■---0.99-0 00 0 00 0 00 1 00■■■■■■■■■■■■0 01 0 99 0 04 34 21 0 99 0 02 0 06 12 92 0 06 0 04 0 99 501 99 0 00.............0 00 0 00 1 00...■■■■■■
两台小视场双目视觉检测装置检测主框架位姿与舱板当前位姿，计算得到主机器人预装配位姿参数，控制主机器人运动至预装配位置。小视场双目视觉检测装置对舱板位姿进行测量，求解装配误差。根据卫星装配误差计算误差补偿主机器人运动参数，并控制主机器人进行装配误差补偿运动。重复上述操作，直至舱板与主框架装配误差小于所设阈值，试验中设置的阈值为ΔX阈=ΔY阈=ΔZ 阈= ± 0.05 mm、ΔA阈=ΔB阈=ΔC阈=± 0.005°。采用基于视觉的卫星装配误差测量与补偿，单次试验的卫星装配位姿误差变化过程如图11所示。从数据变化情况得出，采用上述方法可以实现对卫星装配误差的补偿，并且逐步达到所设阈值。
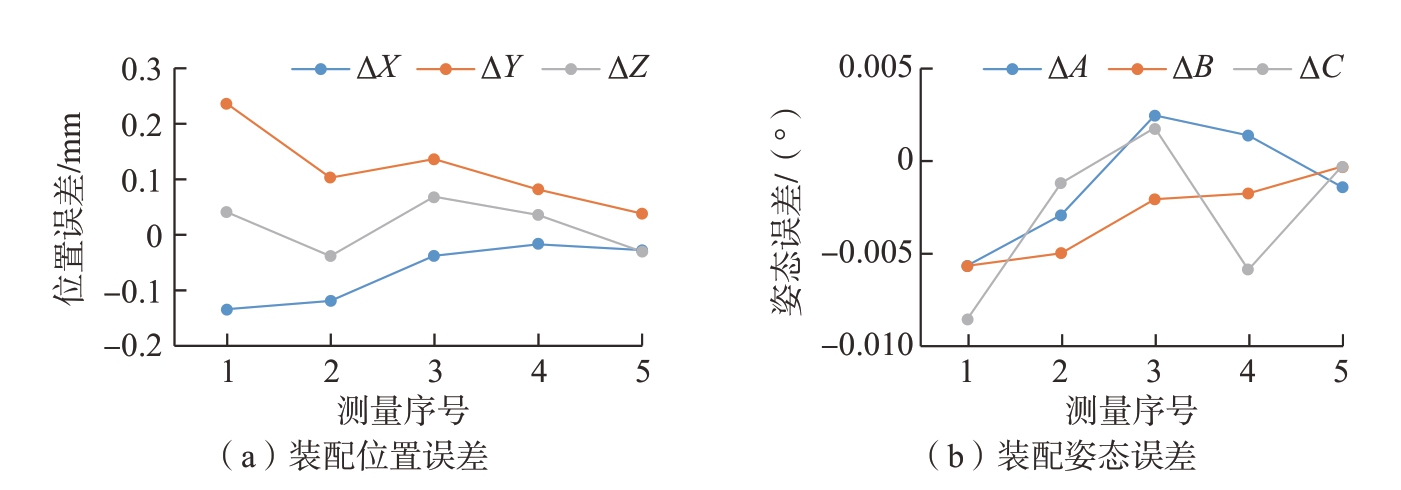
图11 卫星装配位姿误差补偿过程误差变化
Fig.11 Error variation in satellite assembly position and attitude error compensation process
在视觉装配误差补偿后，控制主机器人沿OD–XDYDZD 坐标系的ZD轴方向平移，六维力传感器实时采集装配干涉力FZD，当FZD 达到设定的阈值Ft 后，控制主机器人停止向贴合目标运动，其中力控中的干涉力阈值为35 N。装配完成后通过六维力传感器测量装配干涉力，其部分试验测量结果如图12所示。可以得出，采用上述方法可以实现对卫星装配干涉力的控制，保证装配干涉力低于50 N。
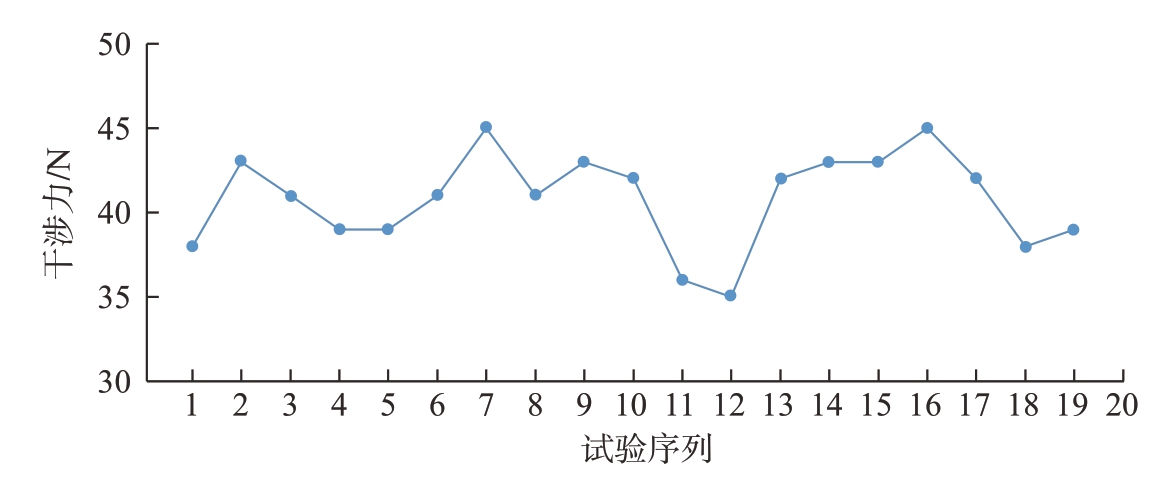
图12 装配干涉力测量结果
Fig.12 Measurement results of assembly interference force
图13所示为卫星装配完成后，采用柱式塞规对舱板与主框架的装配结果进行插销精度测量。由于销孔直径为6.00 mm，因此选用塞规直径为5.80～6.00 mm，间隔0.01 mm，塞规直径精度为0.001 mm。
图13 卫星装配误差补偿试验精度测量过程
Fig.13 Precision measurement process of satellite assembly error compensation experiment
图14为卫星装配误差补偿测量结果。可以得出，采用本文所述方法进行卫星舱板与主框架装配误差检测与补偿可以保证装配精度优于0.2 mm，满足实际卫星装配精度要求。
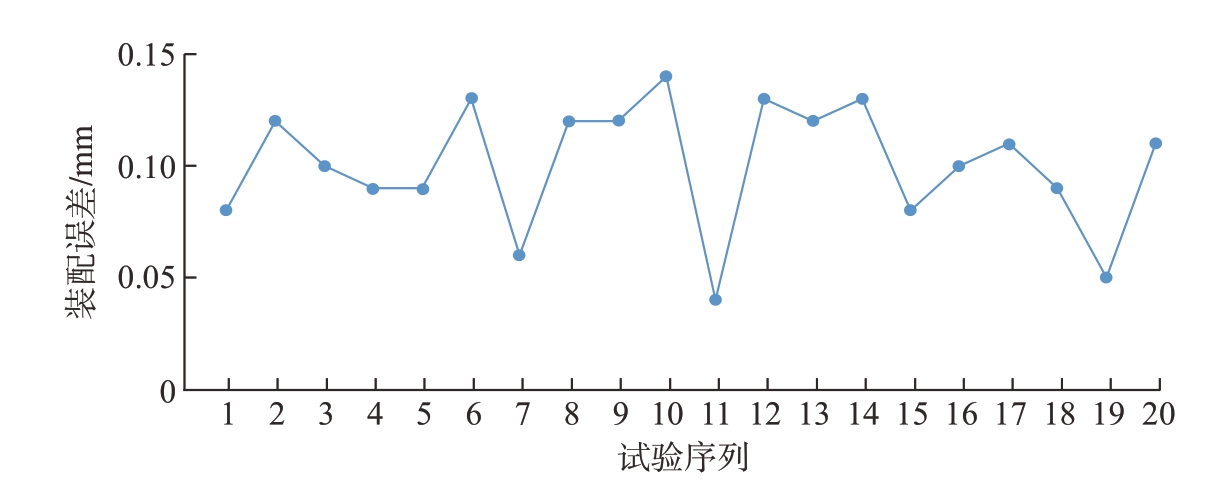
图14 卫星装配误差补偿试验精度测量结果
Fig.14 Precision measurement results of satellite assembly error compensation experiment
4 结论
本文针对卫星总装阶段舱板与主框架装配精度低、装配干涉力过大的问题，提出了一种融合视觉与力觉的卫星装配误差在线测量与补偿方法：通过视觉检测装置在线测量舱板与主框架装配过程误差，并建立舱板与主框架装配误差补偿机制，实现了卫星舱板与主框架高精度装配；同时通过力觉检测装置实时测量舱板与主框架装配过程干涉力，实现了对装配干涉力的控制。本文介绍了融合视觉与力觉的卫星装配误差在线测量与补偿系统组成及工作原理，提出了系统坐标系标定、装配误差测量、装配误差补偿、力觉控制装配干涉力等关键内容及算法，最后对试验平台与测试数据进行了说明分析。卫星装配试验表明，采用视觉与力觉相结合的卫星装配误差在线测量与补偿方法，可以保证卫星舱板与主框架装配误差在0.2 mm 以内，且装配干涉力小于50 N。所采用的方法可以满足实际卫星装配的精度需求与技术要求。
[1]王洪雨,胡溶溶,喻懋林.装配仿真技术在卫星装配中的应用[J].航空制造技术,2015,58(21):56–58.WANG Hongyu,HU Rongrong,YU Maolin.Application of assembly simulation technology in satellite assembly[J].Aeronautical Manufacturing Technology,2015,58(21):56–58.
[2]张名毅,邱增帅,马双庆,等.小卫星总装技术发展历程与展望[J].航天器工程,2021,30(6):106–112.ZHANG Mingyi,QIU Zengshuai,MA Shuangqing,et al.Development review and prospect of small satellite assembly technology[J].Spacecraft Engineering,2021,30(6):106–112.
[3]曾远帆.基于空间相似性的工业机器人定位精度补偿技术研究[D].南京:南京航空航天大学,2017.ZENG Yuanfan.Positional error compensation technology for industrial robot based on spatial similarity[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2017.
[4]廖文和,田威,李波,等.机器人精度补偿技术与应用进展[J].航空学报,2022,43(5):627142.LIAO Wenhe,TIAN Wei,LI Bo,et al.Error compensation technology and its application progress of an industrial robot[J].Acta Aeronautica et Astronautica Sinica,2022,43(5):627142.
[5]LUO H,ZHANG K,SU Y,et al.Monocular vision pose determination-based large rigid-body docking method[J].Measurement,2022,204:112049.
[6]QIAO T Z,CHEN L L,PANG Y S,et al.Integrative binocular vision detection method based on infrared and visible light fusion for conveyor belts longitudinal tear[J].Measurement,2017,110:192–201.
[7]KONG J,LI Q,YIN Y,et al.Research on the bolt positioning system based on multieye vision industrial robots[J].Shock and Vibration,2022,2022:1–11.
[8]LIU X J,MADHUSUDANAN H,CHEN W Y,et al.Fast eye-in-hand 3-D scannerrobot calibration for low stitching errors[J].IEEE Transactions on Industrial Electronics,2021,68(9):8422–8432.
[9]TARYUDI,WANG M S.Eye to hand calibration using ANFIS for stereo vision-based object manipulation system[J].Microsystem Technologies,2018,24(1):305–317.
[10]SHARMA R S,SHUKLA S,BEHERA L,et al.Position-based visual servoing of a mobile robot with an automatic extrinsic calibration scheme[J].Robotica,2020,38(5):831–844.
[11]KARRAS G C,FOURLAS G K,NIKOU A,et al.Image based visual servoing for floating base mobile manipulator systems with prescribed performance under operational constraints[J].Machines,2022,10(7):547.
[12]李玮.机器人同时移动与作业的运动规划研究[D].杭州:浙江大学,2020.LI Wei.Study on motion planning of simultaneous mobile and manipulation of robot[D].Hangzhou:Zhejiang University,2020.
[13]王斌,吴丹,盖宇航.面向机器人精密装配的高精度圆片位姿视觉检测[J/OL].机械工程学报,[2023–02–06].http://kns.cnki.net/kcms/detail/11.2187.TH.20220805.1736.058.html.WANG Bin,WU Dan,GAI Yuhang.Highprecision wafer pose visual detection for robot precise assembly[J].Journal of Mechanical Engineering,[2023–02–06].http://kns.cnki.net/kcms/detail/11.2187.TH.20220805.1736.058.html.
[14]杜福洲,叶晗鸣.基于视觉的大尺度部件相对位姿实时测量方法研究[J].航空制造技术,2021,64(6):34–40,47.DU Fuzhou,YE Hanming.Research on realtime relative pose measurement method of largescale components based on vision[J].Aeronautical Manufacturing Technology,2021,64(6):34–40,47.
[15]胡瑞钦,隆昌宇,张立建.视觉与力觉结合的卫星部件机器人装配[J].光学精密工程,2018,26(10):2504–2515.HU Ruiqin,LONG Changyu,ZHANG Lijian.Robotic assembly technology for satellite components based on visual and force information[J].Optics and Precision Engineering,2018,26(10):2504–2515.
[16]季旭全,王君臣,赵江地,等.基于机器人与视觉引导的星载设备智能装配方法[J].机械工程学报,2018,54(23):63–72.JI Xuquan,WANG Junchen,ZHAO Jiangdi,et al.Intelligent robotic assembly method of spaceborne equipment based on visual guidance[J].Journal of Mechanical Engineering,2018,54(23):63–72.
[17]KIM B,CHOI M,SON S W,et al.Vision-force guided precise robotic assembly for 2.5D components in a semi structured environment[J].Assembly Automation,2021,41(2):200–207.
[18]MA Y Q,DU K,ZHOU D F,et al.Automatic precision robot assembly system with micro-scopic vision and force sensor[J].International Journal of Advanced Robotic Systems,2019,16(3):172988141985161.
[19]DUAN J J,LIU Z C,BIN Y M,et al.Payload identification and gravity/inertial compensation for six-dimensional force/torque sensor with a fast and robust trajectory design approach[J].Sensors (Basel,Switzerland),2022,22(2):439.
[20]胡瑞钦,张立建,孟少华,等.基于柔顺控制的航天器大部件机器人装配技术[J].机械工程学报,2018,54(11):85–93.HU Ruiqin,ZHANG Lijian,MENG Shaohua,et al.Robotic assembly technology for heavy component of spacecraft based on compliance control[J].Journal of Mechanical Engineering,2018,54(11):85–93.
[21]罗威,李明富,赵文权,等.基于力–位图像学习的工业机器人柔顺装配方法研究[J].机械工程学报,2022,58(21):69–77.LUO Wei,LI Mingfu,ZHAO Wenquan,et al.Research on flexible assembly method of industrial robot based on force-pose-image learning[J].Journal of Mechanical Engineering,2022,58(21):69–77.
[22]李根.飞机襟翼机器人辅助装配柔顺控制技术[D].南京:南京航空航天大学,2021.LI Gen.Robot aided assembly compliance control technology for aircraft flap[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2021.
