航空制造技术涉及多个领域，飞机部件的安全性和可靠性一直被广泛关注和研究[1]。在飞机零部件生产制造过程中，复合材料内部会产生缺陷，为保证飞行安全，需要对复合材料机翼蒙皮进行无损检测[2–3]。随着复合材料制造技术的不断发展，对无损检测的完整性和可追溯性的要求不断提高。无损检测通常由技术人员进行手动操作，在工件轮廓表面上适当移动探头进行检测，这个方法会导致大型蒙皮的检查过程非常缓慢，且容易检测冗余。传统的人工检测方式已不能满足现代化精细、高效的检测要求，亟须开发可靠的自动化检测生产线。机器人具有柔性化，智能化的特点，广泛应用于航空航天领域，其为复合材料无损检测生产线提供了全新的思路，能够有效提升无损检测环节的效率。
机翼蒙皮具有外形复杂、尺寸大、易回弹等特点，无损检测对位姿精度要求高，现阶段大型机翼蒙皮的无损检测存在着很多挑战，蒙皮检测的路径一直是工业界的难题。为满足无损检测的精度要求，首先采用线扫描仪对蒙皮进行初始表面扫描，对蒙皮进行曲面重建。随后对扫描路径进行规划，扫描路径决定了扫描的质量、效率以及安全性。超声探头相对于扫描点的高度以及倾斜角度会影响扫描质量与安全性；扫描路径的总长度以及位姿调整时间决定了扫描的效率。
Mineo等[4–6]提出了一种新的复合材料航空组件机器人超声扫描系统，将路径规划与超声相控阵扫描系统同步，该方法没有考虑复合材料的回弹特性，造成测量时偏差较大。Riise等[7]采用了超声回波扫描调整机器人扫描路径的方法，来提高无损检测的质量，没有对扫描路径进行优化。艾小祥[8]采用传统的遗传算法对机翼连续曲面扫描路径进行优化，但效率较低。上述方法都没有考虑到整体的优化，无法将效率及精度最大化。
基于上述问题，本文提出了一种机翼蒙皮无损检测生产线中扫描路径优化方法，采用双机器人搭载无损检测设备对复合材料进行检测；对大型蒙皮进行总体扫描路径规划，同时对整体路径以及单道路径进行优化。首先，采用平行于桁条的行切法对总体扫描路径进行优化；其次，采用混合遗传LM算法对单道路径进行优化；最后，在RoboDK中进行仿真来验证该方法的有效性和实用性，通过机器人搭载线激光扫描仪验证该方法的精度。
1 大型机翼蒙皮无损检测方法
1.1 复合材料无损检测生产线原理
对于复合材料的无损检测，本文提出了一种新型的复合材料无损检测生产线系统，该系统采用双工业机器人搭载超声C扫描末端对复合材料机翼蒙皮进行透射超声处理。超声C扫描简称C扫描，即特定深度扫描模式 （Constant depth mode），采用2D的方式显示，波幅高度通过不同的颜色显示出来，厚度信息通过平面图层的宽度显示。在双工业机器人末端分别搭载超声C扫描信号输出端与信号接收端。两端垂直于蒙皮表面，喷出耦合剂使得超声波能够传导入复合材料内部，其检测过程如图1所示。
图1 透射式超声检测生产线示意图
Fig.1 Schematic diagram of transmission ultrasonic testing production line
当复合材料中有缺陷时，缺陷会反射出部分超声波，接收端的信号将会衰减。为了将组件界面处折射的影响和各向异性降至最低，在整个检查过程中，超声波探头必须与表面保持垂直。由于复合材料具有回弹特性，使得实际位置与理论位置出现了偏差，需要对检测点进行校正，来提高无损检测的质量。因此采用两次扫描的方法。第1次采用激光测距，采集出理论位置与实际位置的偏差，对检测点校准，来提高无损检测的精度。第2次进行透射式超声C扫描对复合材料进行无损检测，其原理如图2所示。
如图2（a）和 （b）所示，线激光扫描仪采用的是直射式激光三角测距法，由激光发射器的激光垂直射入被测物体表面，AB表示激光器中心与电荷耦合元件的距离，BF表示透镜的焦距，O表示蒙皮上被扫描的其中一个点，EF表示光斑在光敏单元上偏移的距离，记为x，则探头与蒙皮表面的距离可以表示为AO，由光路图中的几何关系可知ΔABO ～ ΔBFE，则有边长关系：
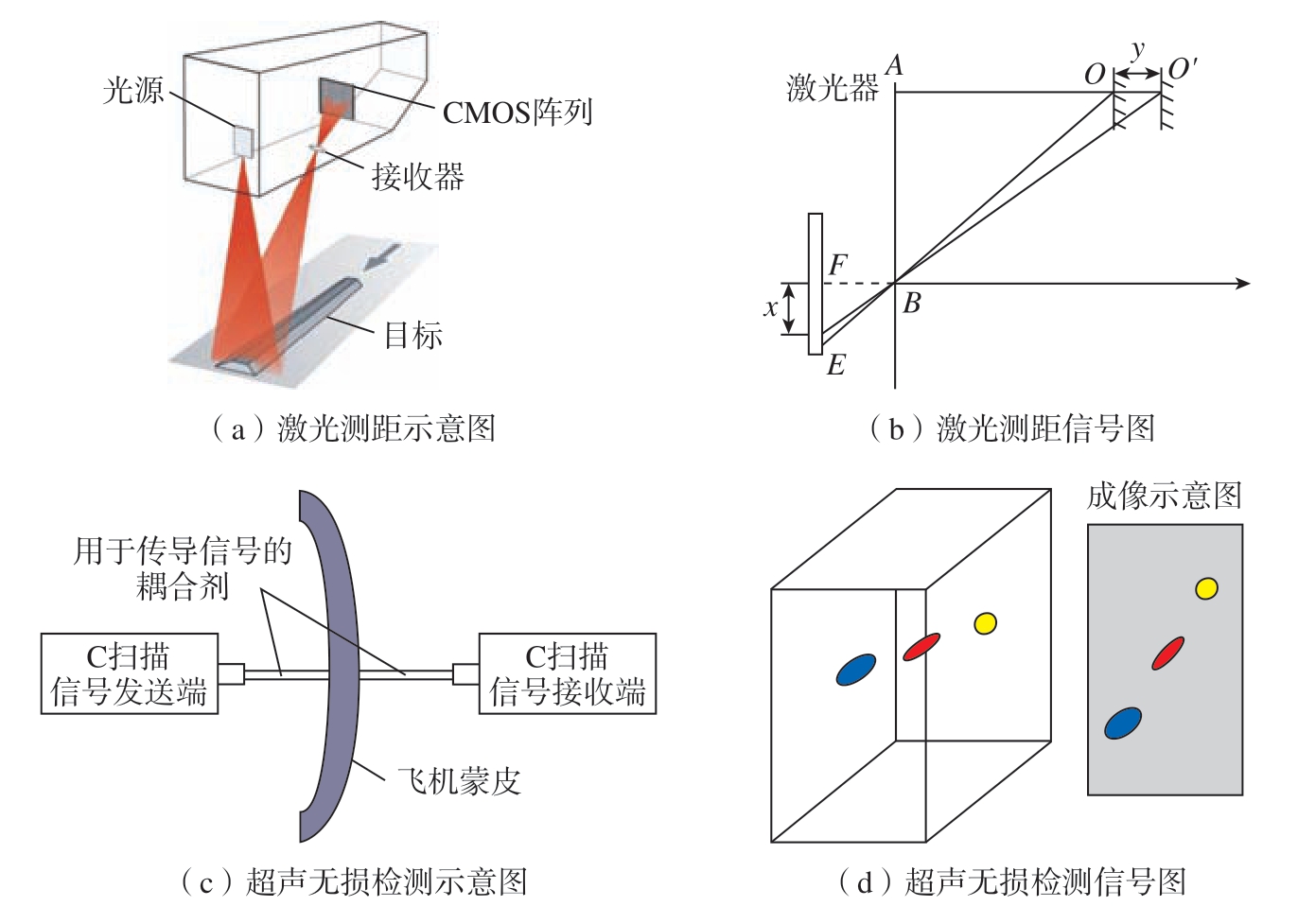
图2 扫描原理图
Fig.2 Scanning schematic diagram
易知AO = BF ·AB/EF，即可得到被测物体距离。
如图2（c）和 （d）所示，超声C扫描采用一收一发两个超声探头，采用透射法检测较大尺寸航空构件，避免反射法可能形成多次回波信号，且检测存在盲区等问题，并且可以直接显示内部缺陷的图像，根据图像可以识别缺陷的面积长度等，减小了缺陷识别的难度，避免了人工进行相应缺陷的分析和判断。
机翼蒙皮为大型复杂曲面，超声扫描对象的特征范围大、空间分散、扫描点数目多，因此需要对总体扫描路径进行规划，使得总距离最短、扫描时间最少，满足检测精度要求与安全性，有效提升生产线效率及安全要求。
1.2 超声扫描路径的总体策略
复合材料机翼蒙皮的外形总体接近于不规则梯形，由蒙皮和桁条构成，其形状如图3所示。
图3 机翼壁板蒙皮示意图
Fig.3 Schematic diagram of wing panel skin
行切法跟环切法是数控机床加工中的常见形式。同理，在生产线中，无损检测扫描方式主要是行切法。观察蒙皮的形状，如果扫描路径反复经过桁条，则会增加扫描距离，并且调姿复杂，容易发生碰撞，因此，本文采用一种平行于桁条的行切方法来实现对总检测面的扫描覆盖。由于蒙皮尺寸过大，超声扫描仪的扫描宽度较小，需要反复几十次的检测过程，如图4所示。总体路径策略采用“提取扫描面→生成扫描路径→离散扫描路径点→生成扫描法线→计算与输出路径→优化路径”的方式生成扫描参数，其具体步骤为：
图4 平行于桁条的行切检测路径
Fig.4 Line cutting detection path parallel to stringer
（1）扫描面的提取。将大型蒙皮曲面模型导入到CATIA中，按检测面积将其分为几个部分，每部分满足双机器人无损检测的范围。
（2）生成扫描路径。曲面扫描采用平行于桁条的行切法，因此扫描路径通过等距离的平行平面截取曲面获得。平面的距离与阵列式超声扫描仪的扫描宽度有关，程序将截取面与曲面求交线获得扫描路径。
（3）离散路径。将扫描路径等距离离散为扫描点，选择距离是扫描水柱横截面的直径。
（4）生成法线。超声扫描仪输出端过扫描点垂直于蒙皮曲面，根据超声扫描仪的工艺需求，在法向上一定距离处生成相应的法向点。
（5）路径计算与输出。通过计算得出机器人扫描所需的位姿参数，将每组参数依次输出。
（6）初始扫描路径生成。为提高扫描效率，将需要扫描的曲面简化为一组平面，从而缩短扫描路径，减少点位的个数。为满足时间最优的目的，首先采用最小二乘法拟合平面，取第一组扫描面P0作为示例进行分析，此组样点总数为N。如图5所示曲面简化为平面。
图5 曲面简化为平面示意图
Fig.5 Simplifying the surface into a plane diagram
采用最小二乘法拟合平面，其原理为：以系数a，b，c表示空间平面，所求系数a，b，c应使偏离扫描点的平方和E为最小，设所求平面方程为
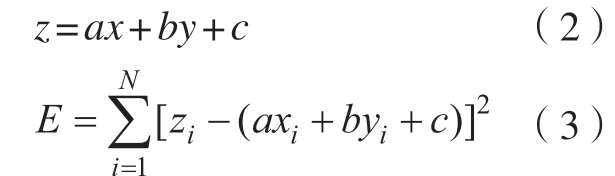
当
时，E取得最小值，此时可得系数a，b，c。以最小二乘法为基础，对初始点集进行分组，依据曲率的不同会对蒙皮进行自适应分组。曲率较大时，拟合的平面路径较短；曲率较小时，拟合的平面路径较长。为满足无损检测要求，其约束条件为：
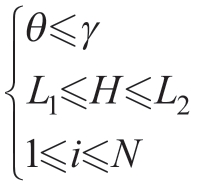
式中，θ为与平面垂线与法线的偏转角；γ为最大偏转角；H为超声扫描耦合剂的高度；L1为最小检测高度；L2为最大检测高度。此时问题转化为单目标多元函数在约束条件下最优解的数学问题，其流程如图6所示。
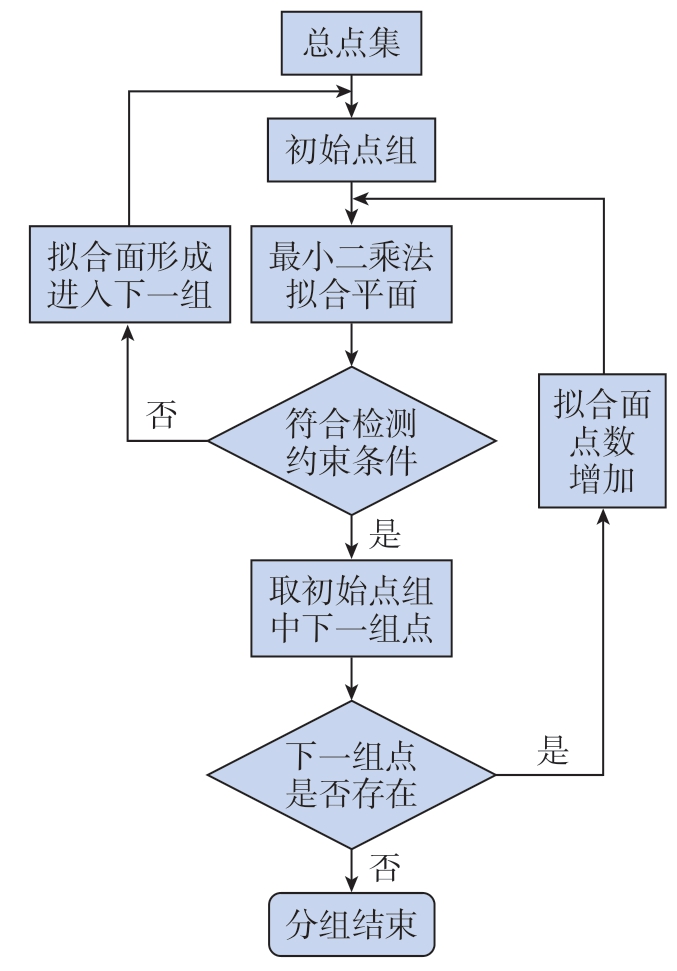
图6 自适应分组流程图
Fig.6 Adaptive grouping flow chart
解决此类问题的传统方法是基于梯度信息的搜索法，如拉格朗日法、最小梯度法、内点法、可行方向法等[9]。这些方法对初值点及梯度信息要求高，并且只能解决部分问题。而遗传算法在单目标多元函数问题时表现优越，在此基础上采用改进遗传算法以及LM算法相结合的方式来寻求优化路径。此时优化的平面虽然在满足约束的条件下缩短了扫描路径，但并不能达到最优，因此本文使用一种混合遗传LM算法的路径优化策略来解决总体扫描路径最优解问题。
2 基于混合遗传LM算法的扫描路径优化
为求得服从于总体最优平面P，将单条扫描路径分解为若干个平面，扫描一个平面所需要的时间为t1，调整姿态所需要的时间为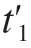
，则扫描此平面所需要的总时间为T1 = t1 +
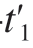，此条路径所需要的总时间为Tsum = T1 + T2 + T3 + …+ TN，令x = [a b c]，则目标函数为
2.1 基于改进遗传算法的路径优化
自然界生物在周而复始的繁衍中，基因发生重组、变异等，使其不断具有新的性状，以适应复杂多变的环境，从而实现进化[10]。遗传算法精简了这种复杂的遗传过程而抽象出一套数学模型，用较为简单的编码方式来表现复杂的现象，能够进行启发式搜索，大概率能找到全局最优解，与生俱来地支持并行计算，不依赖梯度信息，因此对于求解非线性多约束问题非常有效[11]。
在大型机翼蒙皮连续曲面路径规划模型中，模型精度要求高，因此有效数字的位数长，若采用传统的二进制编码，其二进制串的长度过长，使得遗传、杂交、变异等操作，以及解码和编码的过程占用计算机较多算力，并且缺乏明确的物理意义。本文采用一种改进的实数编码遗传方法，无须转化数制和数据类型，便于理解，能够节省遗传操作时间，并且实数、示数范围大，精度高，能够有效优化该模型[12]。其运算过程为：
步骤1，设置种群的规模N，变异概率Pm，交叉概率Pc，迭代次数或终止条件。与传统的遗传算法相同，对种群进行初始化。
步骤2，计算种群中每代个体的适应度，利用适应度函数评价每个个体的好坏。
步骤3，种群进化包括选择、交叉、变异等步骤。具体为 （1）选择，采用合适的算法从父代中选择出部分个体组成中间代Xs（t）； （2）交叉，按照概率Pc对中间代Xs（t）中的部分个体执行交叉运算，得到中间代Xc（t）； （3）变异，按照概率Pm对中间代Xc（t）中的部分个体执行变异运算，得到中间代Xm（t）。
步骤4，判断是否满足设定的终止条件，若符合终止条件，执行步骤五，否则回到步骤2。
步骤5，进化完成后，将适应度最高的个体输出，该个体即为最优解，其具体流程如图7所示。
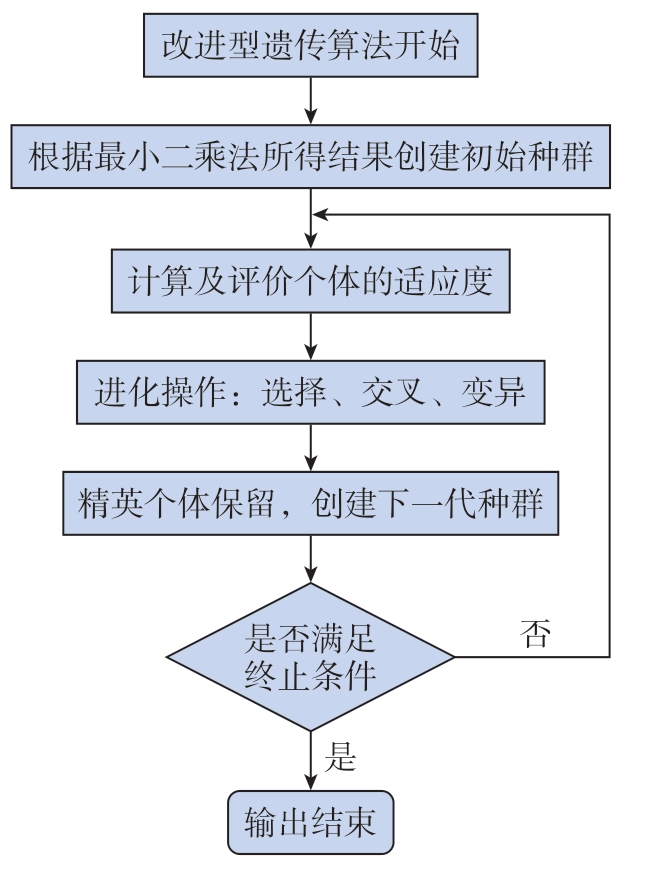
图7 实数型改进遗传算法流程图
Fig.7 Flow chart of real-number improved genetic algorithm
最小二乘法的作用是得到各组平面方程参数的初始值，优化的目标是求得各组平面方程参数的最优值，使总扫描路径长度值最小，求解的详细过程为：
（1）设计染色体。本文采用的是改进型实数编码的遗传算法，由实数组成染色体的基因。实数的个数决定染色体的长度，例如： （5.849，–3.189，7.393，1.136）表示的是长度为4的染色体。实数编码避免了二进制编码所引起的精度以及效率问题，对单目标多约束问题进行自然描述。为了加快算法的效率，因此只在a，b，c附近寻优，如a的取值范围为[0.7a，1.3a]。
（2）初始化。种群规模大小N =100，染色体变异概率Pm = 0.06，染色体交叉概率Pc = 1，最大迭代次数tmax = 200，调用遗传算法工具箱中的函数crtpc（）创建随机种群。
（3）计算适应度。本文采用的是可行性法则，需要计算每个个体违反约束的程度，并把结果保存在种群类的CV矩阵中。CV矩阵的每一行对应一个个体，每一列对应一个约束条件，CV矩阵中元素小于或等于0，表示对应个体满足对应的约束条件，否则是违反对应的约束条件，大于0的值越大，表示违反约束的程度越高。
可根据无损扫描仪的扫描高度、扫描角度等构造CV矩阵，越满足约束条件，则适应度越高。根据扫描高度建立CV矩阵：
根据扫描角度建立CV矩阵：
（4）选择、交叉及变异。选择算法采用锦标赛法与精英个体保存法相结合，在保证算法收敛性的同时，又能保障全局最优解。锦标赛法是从种群中等概率随机选择个体构成组，选择个体适应度最高的进入子代，重复该操作，直到子代种群数量等于父代。而精英个体保存策略是指选出父代中最优良的个体，不进行后续交叉和变异操作，重插入到经过选择、交叉、变异的子代种群，替换适应度最低的个体。
交叉为遗传算法的主要动力，起着全局搜索的作用，对于实数型遗传算法，采用以下公式来构建交叉算子：
变异为辅助动力，能够提高种群的多样性，降低算法陷入局部最优解的可能性，完成局部搜索，两者相互配合，完成待求解问题的优化过程。
在本步骤中，交叉算子对两个个体的基因结构进行分离重组，剧烈改变个体结构。在进化到达末期之后，改进型遗传算法已经锁定了最优解的所在范围，然而该算法对于局部搜索可能比较困难，这时可以利用局部优化的方法对该区域内的“山峰”进行局部搜索[5]，由近似最优解转变成最优解。
2.2 基于LM算法的路径优化
局部优化算法主要有梯度下降法、牛顿法、高斯牛顿法、LM算法等[13]。梯度下降法采用负梯度下降，收敛速度较慢；牛顿法保留一阶和二阶项，能够进行二次收敛，收敛速度较快，但是需要计算黑塞矩阵，计算较为复杂；采用高斯牛顿法，用雅克比矩阵近似代替黑塞矩阵，能够提高计算效率，但黑塞矩阵不满秩则无法迭代。LM（Levenberg-Marquardt）算法则能解决以上问题，作为一种阻尼最小二乘解法，兼具高斯牛顿法的局部收敛特性以及梯度下降法的全局特性，算法为
式中，Jk是雅克比矩阵，采用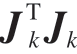
来代替黑塞矩阵降低计算难度；I是单位矩阵；μ是阻尼因子；gk是负梯度方向。当μ较小时和高斯牛顿法类似，μ较大时与梯度下降法相似。本文采用LM算法拟合平面，将μ取较大值，快速求得最优解。
2.3 混合遗传LM算法
结合上文中的改进型遗传算法以及LM算法，本文采用混合LM算法对路径进行优化。首先采用改进型遗传算法对路径进行全局寻优，避免了陷入局部最优解；第2步采用高效率的局部优化算法LM进行局部寻优，将改进型遗传算法的结果作为LM算法的初始值，结合两种算法的优点，进而得到全局最优解[13–15]。
3 优化结果分析与试验验证
为了验证混合遗传LM算法的性能，在Python中进行优化仿真，并在RoboDK中进行仿真分析，最后采用KR210搭载线激光扫描仪进行试验验证。
3.1 优化结果分析
大型机翼蒙皮扫描生产线检测路径规划总体流程如图8所示。
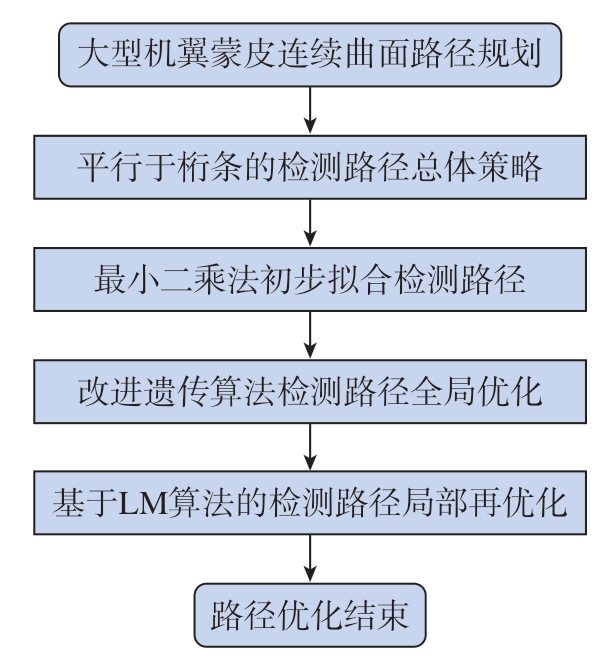
图8 大型机翼蒙皮路径规划总体流程图
Fig.8 General flow chart of large wing skin path planning
本文采用的阵列式超声扫描仪，扫描宽度为60 mm，扫描高度在60 ～ 80 mm之间，扫描点的法线与耦合剂之间的夹角在5°以内检测效果最佳。生产线的检测要求范围长5000 mm、宽3000 mm、高2000 mm。综合考虑计算量和无损扫描仪参数，将平行平面之间的距离设为20 mm，每组取3个平面与蒙皮相交，即扫描宽度为60 mm，初始扫描高度设置为70 mm。
为满足复杂曲面的检测要求，选用CATIA软件并结合VB进行二次开发，对检测点进行批量处理。选取其中一条检测路径，得到549个样点，通过自适应分组程序对路径进行分组，将曲面分解为一组平面，其分解路径如图9 所示。将扫描路径分解为5个平面，之后采用混合遗传LM算法对平面参数进行优化，选取其中一个平面，其遗传迭代种群如图10所示。
图9 平面扫描路径图
Fig.9 Schematic diagram of plane scanning path
图10 改进遗传算法种群值
Fig.10 Improved genetic algorithm population value
选取图4中的5条路径，进行混合遗传LM算法优化，得到优化路径，路径长度对比如表1所示。
表1 超声扫描路径长度
Table 1 Ultrasonic scanning path length mm
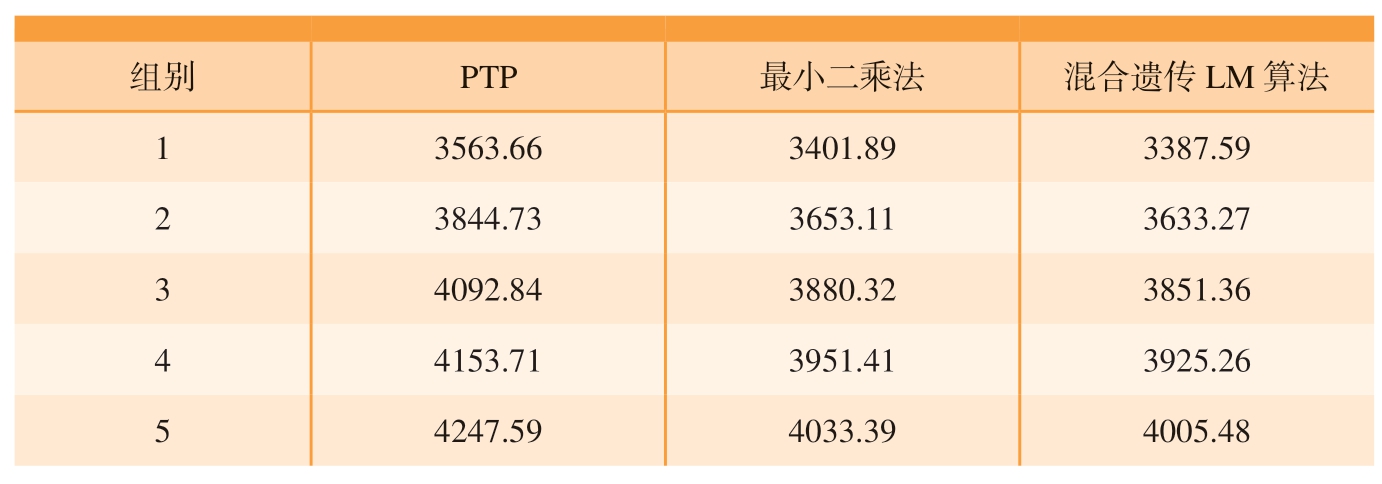
组别 PTP 最小二乘法 混合遗传LM算法1 3563.66 3401.89 3387.59 2 3844.73 3653.11 3633.27 3 4092.84 3880.32 3851.36 4 4153.71 3951.41 3925.26 5 4247.59 4033.39 4005.48
3.2 仿真试验
为验证该算法的优化效率以及实用性，首先在RoboDK中进行仿真试验。该软件是为机器人应用离线编程打造的虚拟仿真软件，支持库卡、发那科、安川、ABB和川崎等机器人品牌的离线仿真，能够便捷地导入工作站三维数模，还具有创建和编辑仿真程序、碰撞检测和生成离线程序等功能。采用KUKA KR210搭载超声扫描仪。为满足超声扫描要求，需提高扫描仪末端的平稳性与连续性，设置末端的移动速度为0.1 m/s，加速度a = 0.5 m/s2，其扫描时间主要由末端移动时间、达到扫描速度时间以及调姿时间构成，仿真过程如图11所示。
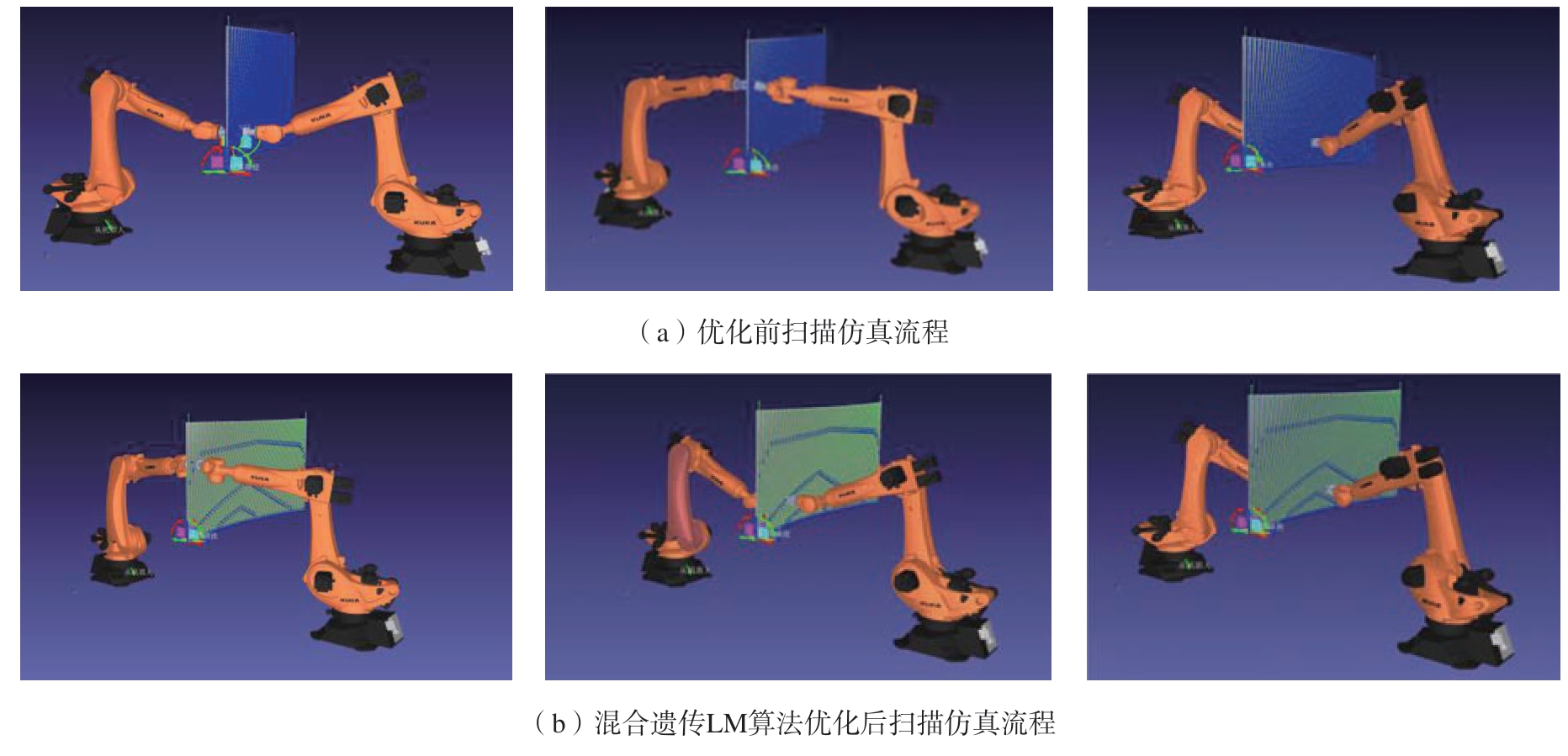
图11 双机器人无损检测仿真过程流程图
Fig.11 Flow chart of simulation process of double robot nondestructive testing
图11（b）表示优化后的仿真路径，相较于优化前的仿真路径图11（a），该路径点位信息简约，且路径长度较短，所需要的检测时间较少。仿真结果得到每组检测路径所需要的总时间如表2所示。
表2 不同模型超声扫描总时间对比
Table 2 Total ultrasonic scanning time of different models s
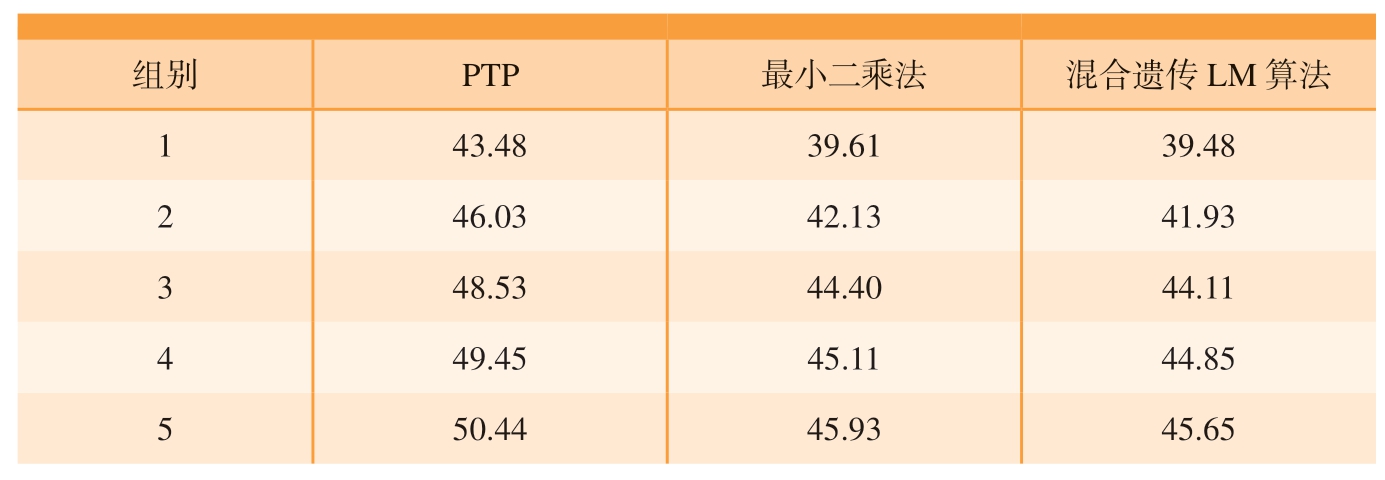
组别 PTP 最小二乘法 混合遗传LM算法1 43.48 39.61 39.48 2 46.03 42.13 41.93 3 48.53 44.40 44.11 4 49.45 45.11 44.85 5 50.44 45.93 45.65
由仿真结果可知，超声检测末端未与机翼蒙皮发生碰撞，路径满足检测的高度与角度约束条件，能够有效完成蒙皮路径的优化，采用本文混合LM算法相较于传统的PTP方法平均扫描时间减少了9.2%，提高了检测效率，提升了生产线吞吐量。
3.3 路径精度试验验证
线激光扫描仪具有精度高、成本低的特性，为了便于将机器人的TCP点位信息与传感器信息快速、精确结合，得到蒙皮工件表面的实际位置，采用线激光扫描仪验证混合遗传LM算法优化路径的准确性，搭建如图12所示的试验平台。
图12 试验平台
Fig.12 Experimental platform
在KUKA KR210末端执行器上安装线激光扫描仪，其型号为米铱scanCONTROL2900–25。根据扫描仪的型号以及夹具的尺寸，将线激光扫描仪的中心设为机器人TCP。所选线激光扫描仪根据三角测量法扫描距离，检测宽度为23.2 ～ 29.3 mm，精度为2 μm，传输速度为300 Hz。
选取复合材料异形件进行试验，首先采用线激光扫描仪按照原数模生成的路径进行测距，得到理论位置与实际位置的偏差，之后对修正的路径采用混合LM算法进行优化，在试验平台上进行精度验证，其试验过程如图13所示。
图13 混合遗传LM算法优化试验流程
Fig.13 Flow chart of experimental process of double robot nondestructive testing
将异形复合材料零件置于扫描台上，用底部吸盘固定，选取零件中间部分进行试验，选取其中15条路径，其扫描结果如图14所示。最大偏差为9.83 mm，其偏差主要来源于：（1）为提高扫描效率、优化扫描路径造成的误差，其最大偏移量为9.5 mm；（2）机器人自身的误差，机器人采用基于空间相似度的误差补偿方法，误差在0.3 mm以内。综上所述，该路径最大偏差满足阵列式超声C扫描仪要求。
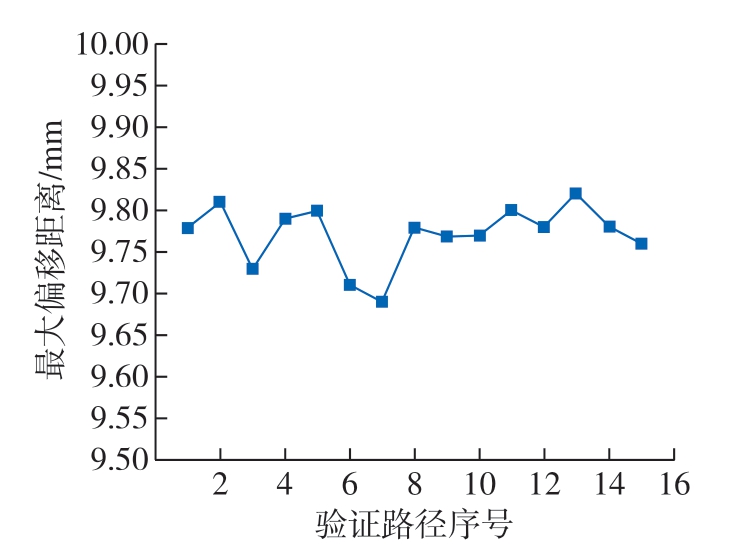
图14 混合遗传LM算法偏移距离
Fig.14 Offset distance of hybrid genetic LM algorithm
4 结论
对于大型复合材料机翼蒙皮无损检测生产线，采用两次检测的策略，第一次扫描对复合材料曲面进行重建，提高第二次透射式无损检测的精度。相对于传统的直线式蒙皮扫描路径规划方法，采用本文所述的混合遗传LM算法，完成整个扫描过程的时间减少，且曲率变化越大时效果越明显，改进内容如下。
（1）按照扫描约束条件对点集进行分类，采用最小二乘法对扫描路径进行平面拟合，得到平面参数初值：曲率较大路径，所含扫描点少；曲率较小路径，所含扫描点多，对总体扫描路径进行自适应划分。
（2）采用混合遗传LM算法以效率为目标对其进行优化，首先采用实数型改进遗传算法对路径进行启发式全局优化，之后用LM算法对其进行确定性局部优化，找到最优路径，在满足检测约束条件下，扫描效率相较于传统方法提高了9.2%。
[1] 沈桂鹏, 王从庆, 王琪.双框架飞机蒙皮检测机器人切换运动控制方法[J].航空学报, 2015, 36(6): 2064–2073.
SHEN Guipeng, WANG Congqing, WANG Qi.Switching motion control of an aircraft skin detection robot with double frames[J].Acta Aeronautica et Astronautica Sinica, 2015, 36(6):2064–2073.
[2] 邹智慧.金属材料超声无损检测技术应用研究[J].中国金属通报, 2018(8):114–115.
ZOU Zhihui.Research on application of ultrasonic nondestructive testing technology for metal materials[J].China Metal Bulletin, 2018(8):114–115.
[3] 冯华山, 秦现生, 王润孝.航空航天制造领域工业机器人发展趋势[J].航空制造技术, 2013, 56(19): 32–37.
FENG Huashan, QIN Xiansheng, WANG Runxiao.Developing trend of industrial robot in aerospace manufacturing industry[J].Aeronautical Manufacturing Technology, 2013, 56(19): 32–37.
[4] MINEO C, PIERCE S G, WRIGHT B, et al.Robotic path planning for non-destructive testing of complex shaped surfaces[J].AIP Conference Proceedings, 2015, 1650: 1977–1987.
[5] MINEO C, MACLEOD C,MOROZOV M, et al.Flexible integration of robotics, ultrasonics and metrology for the inspection of aerospace components[J].AIP Conference Proceedings, 2017, 1806: 020026.
[6] MINEO C, PIERCE S G,NICHOLSON P I, et al.Robotic path planning for non-destructive testing—A custom MATLAB toolbox approach[J].Robotics and Computer-Integrated Manufacturing, 2016, 37: 1–12.
[7] RIISE J, MINEO C, PIERCE S G, et al.Adapting robot paths for automated NDT of complex structures using ultrasonic alignment[J].AIP Conference Proceedings, 2019, 2102: 040006.
[8] 艾小祥.飞机机翼装配中的扫描路径规划研究[D].杭州: 浙江大学, 2014.
AI Xiaoxiang.Research on path planning of scanning in aircraft wing assembly[D].Hangzhou:Zhejiang University, 2014.
[9] 柯艺芬.非线性方程组迭代解法[M].北京: 电子工业出版社, 2021.
HE Yifen.Nonliner equations iterative method[M].Beijing: Publishing House of Electronics Industry, 2021.
[10] 丛明煜, 王丽萍.智能化遗传算法[J].高技术通讯, 2003, 13(4): 43–48.
CONG Mingyu, WANG Liping.An intelligentizing genetic algorithm[J].High Technology Letters, 2003, 13(4):43–48.
[11] 韩瑞锋.遗传算法原理与应用实例[M].北京: 兵器工业出版社, 2010.
HAN Ruifeng.Principle and application examples of genetic algorithm[M].Beijing: The Publishing House of Ordnance Industry, 2010.
[12] QING-DAO-ER-JI R, WANG Y P.A new hybrid genetic algorithm for job shop scheduling problem[J].Computers & Operations Research, 2012, 39(10): 2291–2299.
[13] 万超.一种混合遗传LM算法求解非线性最小二乘问题[J].长江信息通信, 2021,34(12): 52–54.
WAN Chao.A hybrid genetic LM algorithm for solving nonlinear least squares problem[J].Changjiang Information & Communications,2021, 34(12): 52–54.
[14] 吴思源.曲面工件超声自动检测中若干关键技术研究[D].杭州: 浙江大学, 2006.
WU Siyuan.Study on key techniques of ultrasonic automated inspection for curved surface parts[D].Hangzhou: Zhejiang University, 2006.
[15] MITRA S, MITRA A.A genetic algorithms based technique for computing the nonlinear least squares estimates of the parameters of sum of exponentials model[J].Expert Systems With Applications, 2012, 39(7): 6370–6379.
