金属间化合物Ti2AlNb具有高比强度、较高的断裂韧性和突出的耐高温性能，有望部分替代镍基高温合金，成为制造航空发动机热端部件的理想材料[1–3]。然而，Ti2AlNb优异的高温力学性能使其成为典型的难加工材料，切削加工时变形剧烈且易产生表面缺陷[4–5]。研究Ti2AlNb切削切屑形成过程中的材料变形和损伤演化规律对于优化加工工艺并实现Ti2AlNb高效率高质量加工具有重要意义[6]。
近年来，已有针对Ti2AlNb切削切屑形成过程的相关研究。如周恺等[7]开展正交试验，研究了Ti2AlNb在不同切削条件下的切屑形貌和刀具磨损，结果表明Ti2AlNb车削时切屑主要呈带状，刀具前刀面发生粘结磨损和出现月牙洼；铣削时切屑呈扭曲节状，刀具磨损集中在切削刃口附近区域。He等[6]应用改进Zerilli-Armstrong模型计算了不同切削参数下Ti2AlNb应变率硬化效应和热软化效应及其对流动应力的影响，证明流动应力对切屑形成过程的决定作用。Yuan等[8]将超声振动辅助铣削应用于Ti2AlNb加工，研究发现超声振幅增大或振动维度增加有助于提高材料去除效率。苏云玲等[9]通过开展Ti2AlNb深细孔加工试验，研究了工艺参数对切屑形态的影响规律，发现随主轴转速或进给速度增大，切屑形态分别呈单元切屑、崩碎切屑和连续切屑。然而，上述研究主要关注切削参数对Ti2AlNb切屑形态的影响规律，鲜有针对Ti2AlNb 切削切屑形成过程中材料变形和损伤演化机理的相关报道。
切削加工数值仿真是研究切屑形成过程的重要手段[10]。基于连续介质力学理论的切削加工数值仿真方法，如有限元法[11–12]、有限差分法[13]等在求解切削变形区域裂纹扩展与断裂破坏等问题时，裂纹尖端位移场的不连续易造成结果奇异性，计算时需要根据裂纹扩展路径重新划分网格，导致计算结果对网格依赖性强，且需要引入额外裂纹扩展准则指导裂纹的萌生和扩展，计算精度和计算效率低[14]。Belytschko等[15]提出的扩展有限元法克服了有限元法的网格依赖性，已成功应用于断裂问题，但其仍需引入额外的裂纹扩展准则，在切削变形区等复杂区域或多裂纹扩展区域的计算不够精确。基于非局部理论的分子动力学方法也已应用于切削过程模拟，但因计算量大而局限于微纳米尺度切削仿真，与实际加工过程的裂纹成核及扩展行为存在差别。
区别于连续性假设和空间微分求解方法的连续介质理论，近场动力学理论将连续体离散为空间域内一系列包含物性信息的物质点，通过求解空间积分方程描述物质点运动，其结果同时包含连续解和不连续解，裂纹能够自然萌生、扩展和分支[16–18]。根据物质点对点的作用力形式差异，近场动力学理论分为键基[16]、常规态基[19]和非常规态基[20]近场动力学理论。Shang等[21]利用键基近场动力学模型模拟了单向碳纤维增强高分子材料的直角切削加工，预测了切削过程切屑形态和表面损伤形成。Zhan等[22]将基于分子动力学的Al–SiC界面本构模型应用于键基近场动力学模拟，预测了金属基复合材料准静态单轴拉伸和冲击加载下的失效模式。然而，键基近场动力学模型简化了物质点对点力之间的相互作用，且受泊松比限制，难以描述金属材料在高应变率加载下的复杂力学行为[23]。Wu等[24]提出一种基于非常规态基的近场动力学改进模型并应用于纯铝切削仿真，通过使用混合局部/非局部梯度近似技术定义切削建模中的接触和边界条件，研究了物质点离散精细度和近场半径对计算结果的影响。然而，非常规态基材料模型易受零能振荡模式影响[25–26]，导致位移场计算不稳定。谷新保等[27]将常规态基线弹性本构模型应用于平面裂纹的扩展和连接过程，结果表明常规态基近场动力学方法无需借助额外裂纹扩展准则即可准确模拟裂纹扩展和分叉现象，且突破了传统键基模型泊松比的限制。
本文基于常规态基近场动力学理论构建Ti2AlNb合金的弹塑性本构模型，引入材料损伤准则和接触准则，通过Verlet-Velocity差分方法对Ti2AlNb直角切削进行仿真模拟，分析Ti2AlNb切削加工被切除层材料的力学响应特性，探讨Ti2AlNb切屑形成过程中的材料变形和损伤演化规律。
1 常规态基弹塑性近场动力学模型
1.1 近场动力学基本运动方程
近场动力学是在连续介质理论基础上，基于不连续性和长程力作用假设对受力体进行重构[16]，如图1所示。通过将宏观连续体R （即工件）离散成一定体积和质量的物质点，在某一时刻t时物质点x与其近场半径δ区域内的其他物质点x′通过键ξ产生相互作用力，根据牛顿第二定律，其运动方程为
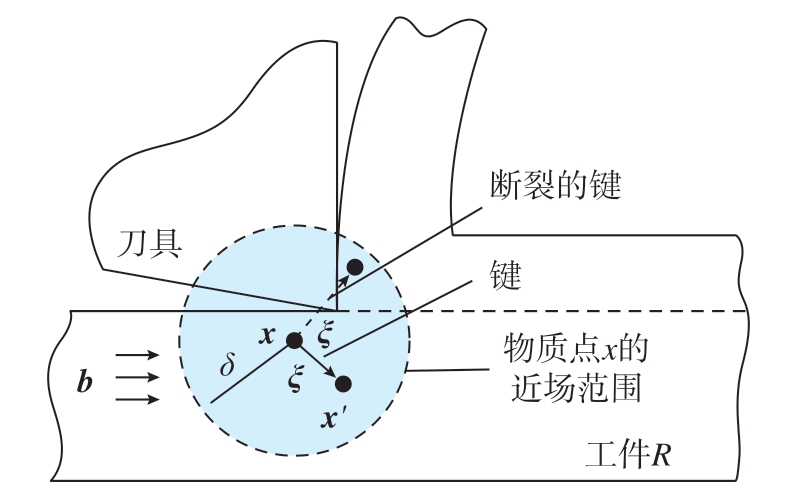
图1 切削过程中工件物质点间的非局部作用示意图
Fig.1 Nonlocal interactions between workpiece material particles in cutting process
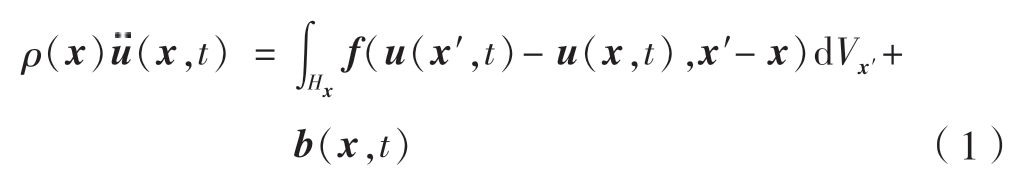
式中，ρ为物质点密度；u为物质点位移；）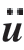
（为u的二次导数，表示物质点的加速度；t为时刻；Hx为物质点x的近场范围，其定义为Hx = {0<|x′–x|<δ}；x′为近场范围内其余物质点；f为物质点x与x′之间的相互作用力函数；b为外载荷密度，表示单位体积物质所受的外载荷。参考构型中两粒子的相对位置态
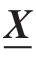〈ξ〉=ξ = x′–x，相对位移η = u（x′，t）–u（x，t）。
如图2所示，在态基近场动力学理论中，键的变形由键端点近场范围内所有键的变形决定[19]，由变形矢量态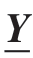
表示，即
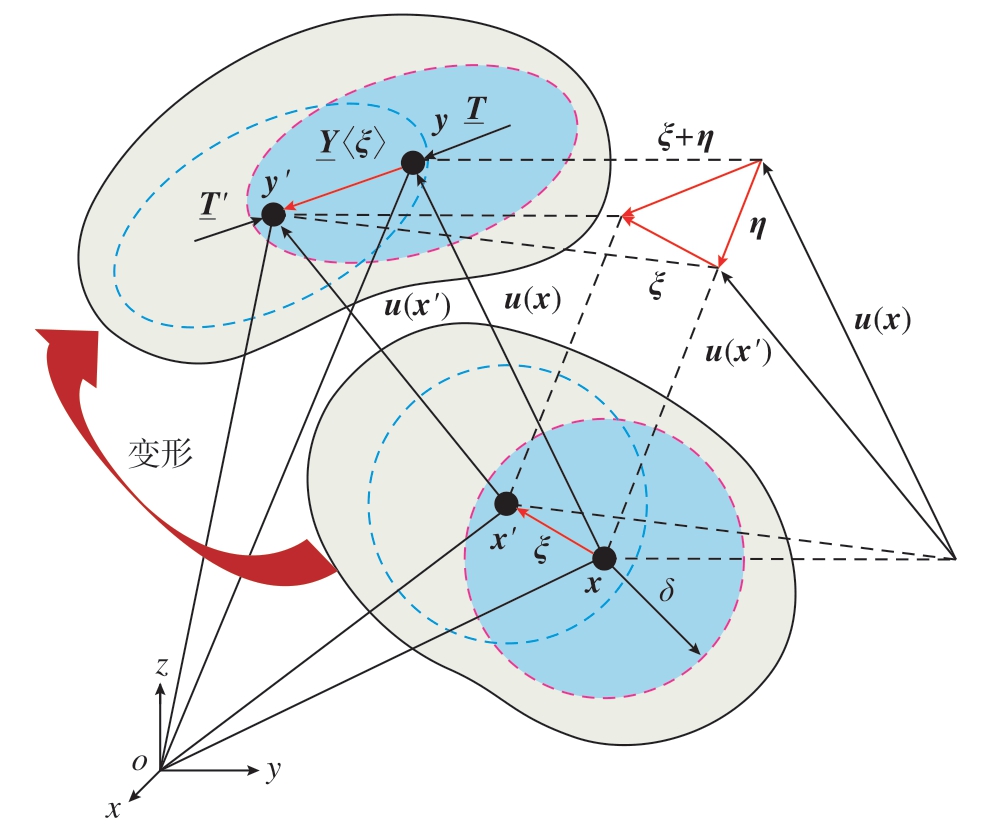
图2 常规态基近场动力学模型材料质点x和x′之间的非局部相互作用
Fig.2 Nonlocal interactions between material particles x and x′ in ordinary state-based peridynamics model
因此，式（1）可表达为
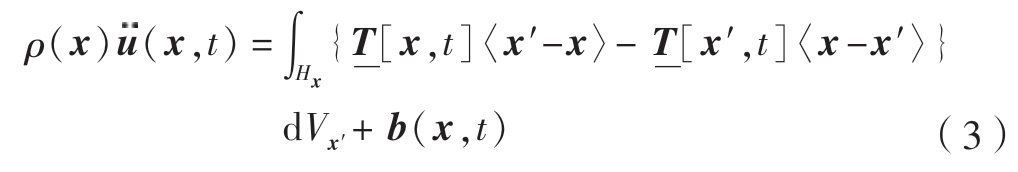
式中，
[x，t]为力矢量态，表示时刻t时物质点之间的相互作用。
由式（3）可知，构建材料本构模型的关键是确定力矢量态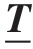
。对于常规金属材料，其力矢量状态[19，28]为
式中，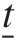
为标量力态；
表示单位状态值函数，即沿变形键方向的单位矢量。式（4）表明力矢量与键方向始终共线。
体积膨胀θ的标量值函数定义为
式中，
为扩展标量态，表示变形前后键长变化量，
表示初始构型中键的长度，加权体积标量
，其中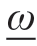
为影响函数。
扩展标量态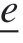
的体积膨胀部分和偏斜部分分别定义为
1.2 非局部近场动力学弹塑性模型
对于线弹性各向同性材料的非局部模拟，Silling等[19]提出近场动力学线性固体材料模型，该模型中材料弹性性质由体积模量、剪切模量以及近场半径表示，其标量力态表示为
式中，K为体积模量；系数+α与剪切模量G存在联系，α=15G/m。
常规态基近场动力学在处理塑性问题时的关键思想是将键的伸长标量态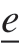
分解为体积膨胀部分
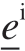和偏斜部分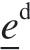
，并将键的偏斜部分
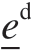加性分解为弹性部分
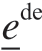和塑性部分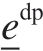
[29]：
假设各项同性延性金属材料的塑性变形与压力无关，则式（7）可以表达为
式中，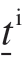
和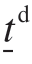
分别为体积力态和偏量力态。为方便利用弹性本构关系进行塑性计算，定义一标量函数f，称之为屈服函数；基于屈服函数定义允许的标量偏斜力态集合为
式中，ψ0为随材料变形变化的正变量，其与等效塑性应变相关并代表材料的屈服点；ψ为标量状态空间Sd的函数，Sd由式（11）定义的集合为
参考连续介质力学理论，基于屈服函数的弗雷歇导数[19]得出塑性流动准则，即
式中，Δdψ为函数ψ的弗雷歇导数；λ为一致性参数。
1.3 失效准则
在弹塑性材料模型中融合失效准则，以模拟变形体中键的自发断裂行为和损伤演化。引入键伸长率sc，可表达为
式中，s0为给定材料中键的临界伸长率，当键伸长率sc超过临界伸长率s0时发生破坏，此时该键连接的物质点不再存在相互作用，且破坏不可逆。通过式（14）定义的历史相关函数μ（t，t,§））描述所有键的断裂情况为
定义物质点x的局部损伤为与该点有关的断裂键数和键总数之比，即
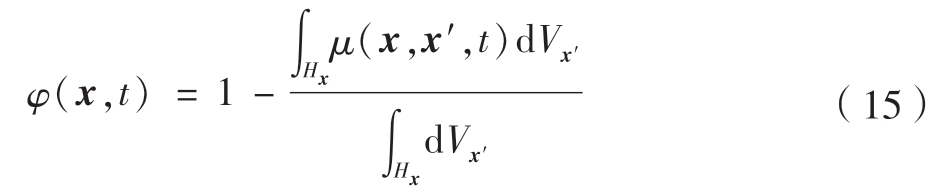
式中，φ的大小反映了局部损伤程度。当φ=0时，表明物质点没有损伤；而φ=1时，表明物质点近场范围内的键全部断裂。
材料变形时的破坏行为取决于临界伸长率s0，根据断裂能等效准则[30]，s0可由式（16）获得。
式中，G0为临界能量释放率。利用上述断裂失效准则，可以准确描述工件材料在切削变形时的损伤演化过程。
1.4 接触模型
在近场动力学理论中，物质点之间仅通过键产生相互作用。切削过程中刀具与工件的初始距离远大于近场半径，两者物质点之间不存在键连接[16]。如图3（a）所示，在刀具接触工件之前，工件处于静止状态且各物质点合力为0；当刀具切入工件时，由于刀具与工件材料之间不存在键及相互作用力，从而产生如图3（b）所示的物质点渗透现象。本研究采用Macek等[17]提出的短程力模型，以描述非键合物质点之间的相互作用关系，防止多体接触时物质点之间出现渗透现象。
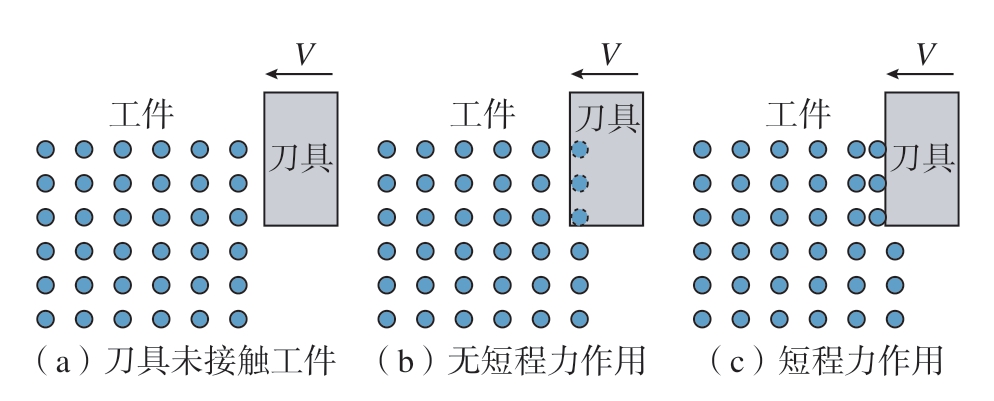
图3 刀具与工件接触时物质点位置变化示意图
Fig.3 Movement of material particles induced by tool-workpiece interaction
在短程力模型中，接触力不依赖于变形前各物质点间距离，而仅取决于当前位置中物质点P和i的相对位置，对物质点i，短程力fs可由式（17）获得。
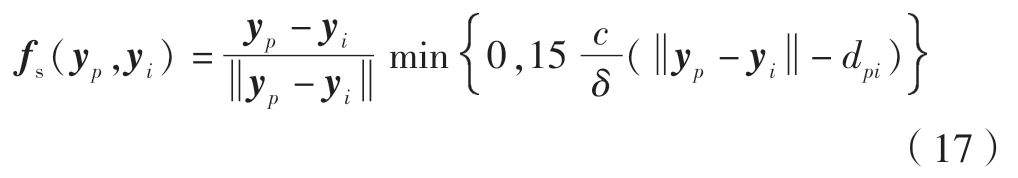
式中，yp和yi分别为物质点p和i的位置，正系数c=18K/πδ4，dpi为物质点p和i之间开始产生短程力作用的临界距离，其值由式（18）确定。短程力为排斥力，仅在工件受压时产生作用，如图3（c）所示。
2 切削过程近场动力学数值计算方法
将工件和刀具材料均匀离散为具有体积和密度信息的物质点，离散间距为Δx，对基本运动方程（即式（3））在时间和空间上离散化处理，形式如式（19）所示。
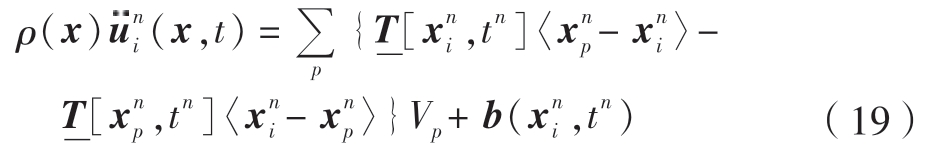
式中，n为时间步长；Vp=|Δ x|3为物质点xp的体积。
利用式（20）中的Verlet-Velocity显式差分方法[18]对式（19）进行求解获得物质点xi在t n+1时刻的位移。
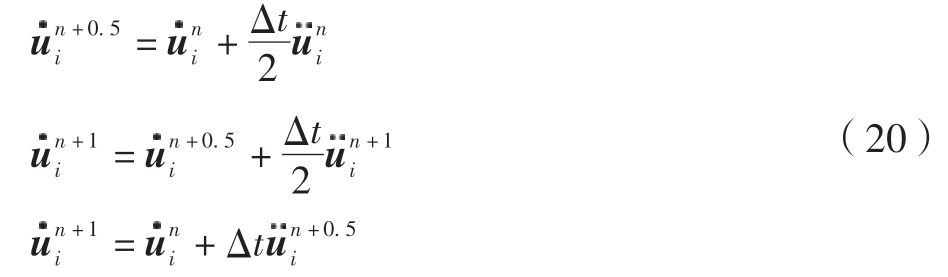
式中，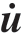
和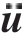
分别为物质点xi的速度和加速度；Δt为时间步长。
所建立近场动力学模型的数值实现过程如图4所示。首先输入离散几何模型信息和刀具工件材料参数，其次初始化边界条件，固定工件边界层部分，并设定切削速度；然后根据输入参数确定时间步长以及时间步数；利用Verlet-Velocity差分方法计算物质点xi的位置及速度信息，进而计算该物质点的对点力和变形态，判断物质点键的断裂情况，并更新物质点位置和损伤情况；当达到规定时间步时，输出物质点损伤及位移结果，计算结束。
图4 切削加工近场动力学模型数值计算流程
Fig.4 Flowchart of numerical implementation for peridynamics model of cutting process
3 Ti2AlNb直角切削数值仿真算例
图5为Ti2AlNb直角切削几何模型及其物质点离散分布情况，定义蓝色标记的物质点区域为边界层，并限制边界层物质点的x、y方向位移为0；定义黄色标记的物质点所在区域为工件切削区域；矩形工件试样尺寸为1.5 mm×0.5 mm；材料密度ρ = 5310 kg/m3，体积模量K=128.123 GPa，剪切模量G=45.9 GPa，屈服应力σs=1130 MPa。将刀具设置为刚体，切削速度V=60 m/min，切削深度ap=0.2 mm。工件被均匀离散为500×2000个物质点，物质点间距Δx=0.01 mm，近场半径δ取3倍物质点间距为0.03 mm，每个物质点的体积分数为Vi = 2.7×10–5 mm3。假定工件材料Ti2AlNb为各向同性的弹塑性材料，键临界伸长率为0.108，迭代时间步长取Δt =1.138×10–9 s，本算例模拟的切削长度为1 mm，计算时间步数为878758步。
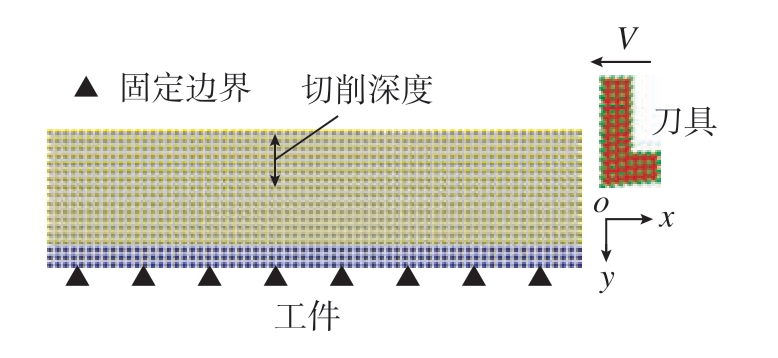
图5 Ti2AlNb直角切削几何模型及其物质点离散分布
Fig.5 Geometric model for orthogonal cutting of Ti2AlNb and associated mass particles discretization
图6为Ti2AlNb直角切削试验原位成像测试装置，搭建的在位测试系统包括刀具、工件、单色强光源和高速相机等主要部件，利用专用夹具将Ti2AlNb工件试样固定于直线滑轨上。试验采用肯纳NG3189R无涂层硬质合金刀具，其前角为0°，后角为6°，高速相机型号为Phantom v2012（配备5倍光学镜头），在768 pixel×576 pixel分辨率下以25000帧/s进行拍摄。试验采用同轴光源，最大功率为60 W。
图6 Ti2AlNb直角切削原位成像测试装置
Fig.6 In-situ imaging device for orthogonal cutting of Ti2AlNb
图7为Ti2AlNb直角切削切屑形成数值仿真与试验结果对比，可见在试验切削条件下切屑形态呈现锯齿状，利用近场动力学模型仿真预测的剪切角为40.23°，与直角切削试验测得的切角38.89°相比，误差仅为3.45%。表1为Ti2AlNb锯齿状切屑的形成过程，可见一个完整锯齿分节切屑的形成包括4个阶段，即挤压变形、剪切带启动、剪切带扩展、锯齿分节形成。表1数值仿真结果中锯齿分节形成的时间间隔共为16800时间步长；试验结果为高速相机拍摄的Ti2AlNb直角切削切屑形成过程在位测试图像，在切屑锯齿分节形成的4个阶段中分别选取典型图像与切屑形成数值仿真结果进行对比；切屑形成图示为Ti2AlNb锯齿状切屑形成过程示意图。
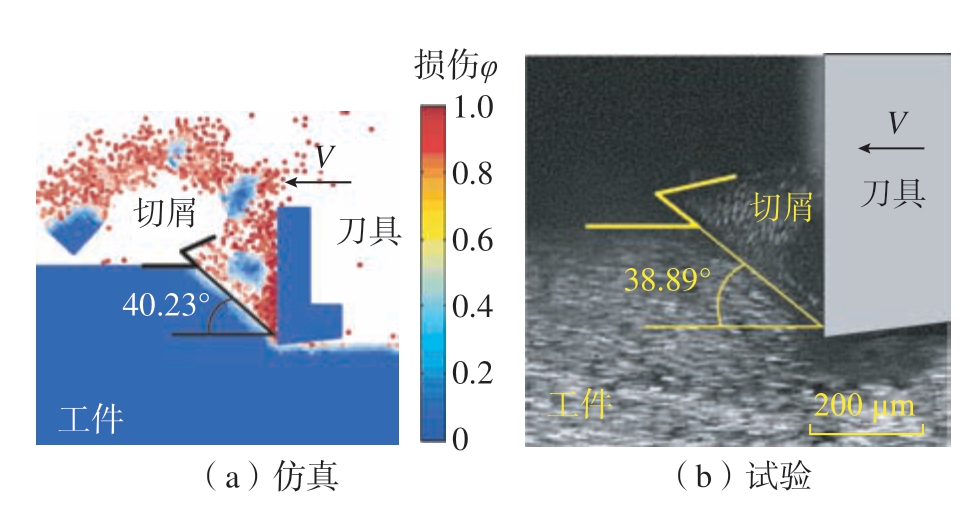
图7 Ti2AlNb切屑形成数值仿真结果与试验结果对比
Fig.7 Comparison between simulation and experimental results for chip formation of Ti2AlNb
如表1所示，锯齿状切屑形成的阶段1中刀具与待形成锯齿分节开始接触并产生挤压变形，此时被切除层表面受刀具挤压作用而轻微隆起；阶段2为剪切带启动阶段，在刀具持续运动和挤压作用下，切屑第1变形区发生累积塑性变形，在刀尖部位形成局部化剪切带；阶段3为剪切带扩展阶段，在切屑第1变形区塑性变形累积作用下，切屑自由表面形成微裂纹并向刀尖部位扩展，同时刀尖部位形成的剪切带向切屑自由表面扩展；阶段4为切屑锯齿分节的形成阶段，此时由刀尖部位形成的局部化剪切带与切屑自由表面向刀尖部位扩展的微裂纹相遇，形成完整的锯齿切屑分节，并在刀具运动作用下开始形成新的锯齿分节。
表1 Ti2AlNb锯齿状切屑形成过程
Table 1 Sawtooth chip formation process of Ti2AlNb
切屑形成阶段 数值仿真结果 试验结果 切屑形成过程示意图损伤φ时间步：661500images/BZ_75_733_655_1078_973.pngV阶段1：挤压变形刀具images/BZ_75_1101_685_1130_954.png1.0 0.8 0.6 0.4 0.2 0images/BZ_75_1298_615_1673_989.png工件时间步：665350images/BZ_75_732_1106_1078_1422.png损伤φ V阶段2：剪切带启动刀具images/BZ_75_1099_1144_1128_1414.png1.0 0.8 0.6 0.4 0.2 0images/BZ_75_1293_1075_1667_1448.png工件损伤φ时间步：673400images/BZ_75_736_1561_1081_1879.png阶段3：剪切带扩展V刀具images/BZ_75_1104_1596_1133_1866.png1.0 0.8 0.6 0.4 0.2 0images/BZ_75_1297_1526_1673_1899.png 工件时间步：678300images/BZ_75_732_2032_1078_2349.png损伤φ 阶段4：锯齿分节形成V images/BZ_75_1098_2070_1127_2339.png1.0 0.8 0.6 0.4 0.2 0images/BZ_75_1292_1982_1668_2355.png刀具 工件
为进一步揭示Ti2AlNb材料切除时的损伤演化行为，在切削厚度方向均匀设置6个损伤测量点，如图8所示，自下而上依次编号为No.1、No.2、No.3、No.4、No.5、No.6，各测试点之间间隔两个离散点，分析其损伤行为在锯齿状切屑形成过程中的时间演化以及空间分布规律。上述测量点损伤的时间演化结果如图9所示，在切屑锯齿分节单元形成的4个阶段中，阶段1为刀具和切屑新锯齿分节开始接触时刻，此时锯齿分节发生轻微变形，工件自由表面附近的No.6测试点受刀具挤压作用而产生轻微损伤；阶段2中刀尖部位切屑材料形成局部化剪切带，因No.1测试点位于剪切带处物质点的近场范围外，在该锯齿分节形成过程中未发生损伤，其余测试点损伤值均因剪切带扩展而增大；阶段3和阶段4是切屑剪切带的扩展阶段，由于应力局部化导致测量点处损伤剧烈增加，No.4测试点处于剪切带中心而损伤值最大，达到0.807。
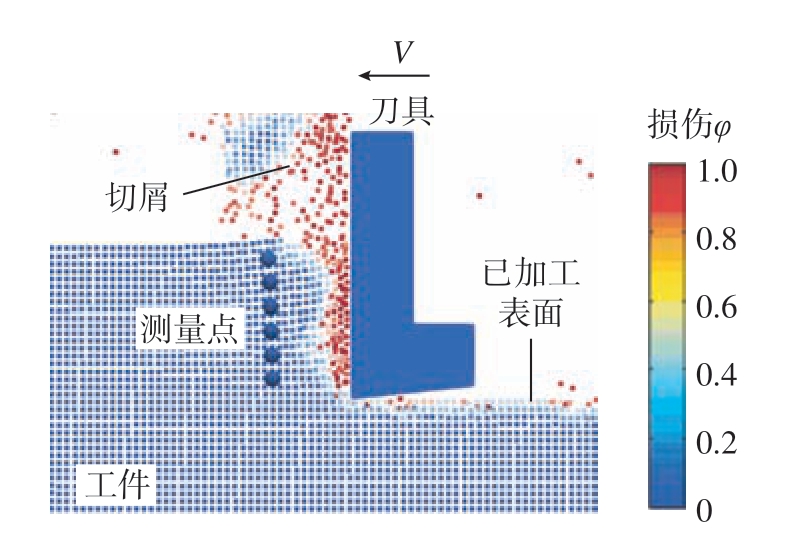
图8 材料切除过程损伤测量点分布图示
Fig.8 Diagram of damage measurement points
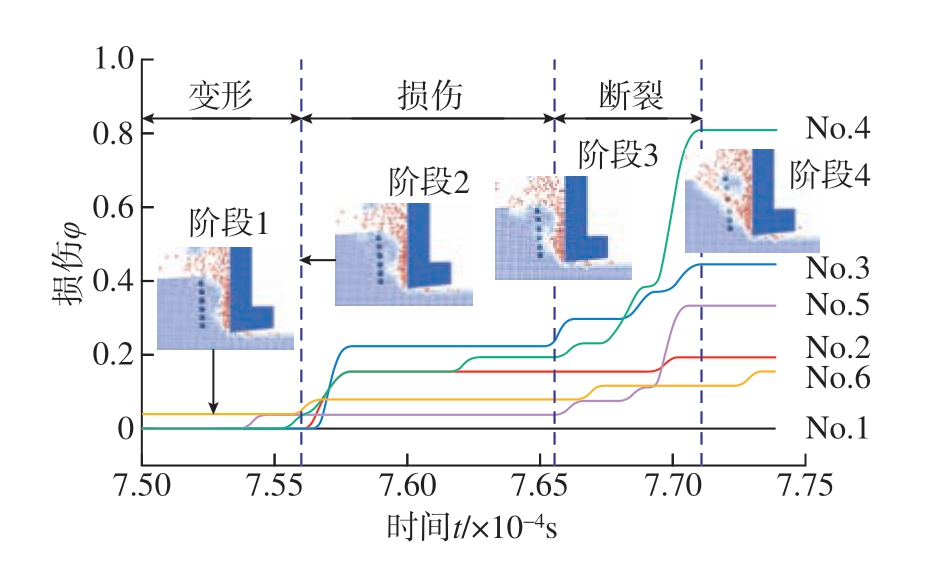
图9 材料切除过程物质点的损伤演化规律
Fig.9 Damage evolution of material points during material removal process
各测量点构成的空间损伤分布结果如图10（a）所示。在锯齿分节形成的4个阶段内，测量点损伤值在沿切削厚度方向整体呈现中间高两端低的分布趋势。结合No.6测试点位置，可以发现切屑损伤主要发生在局部化剪切变形区，锯齿分节内部损伤较小。本研究采用锯齿分节完全形成时（阶段4）空间损伤分布曲线的半峰宽值（FWHM）表征第1变形区宽度，并忽略宏观变形导致的离散点间距微小变化。使用该方法预测的第1变形区宽度约为60 μm，与试验测得的第1变形区宽度56.28 μm相比（图10（b）），预测误差值为6.6%。
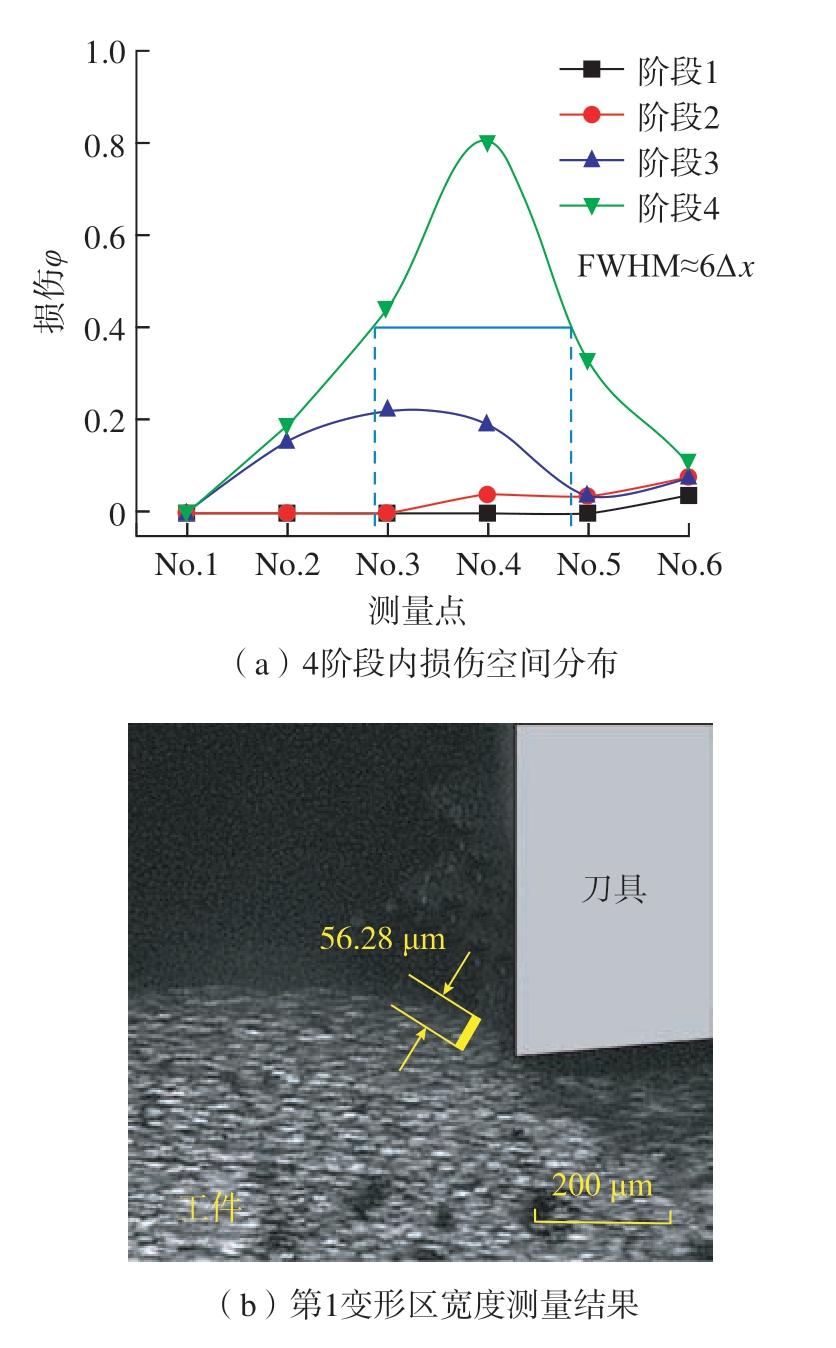
图10 Ti2AlNb切削切屑锯齿分节形成的4阶段内损伤空间分布及第1变形区宽度测量结果
Fig.10 Spatial distribution of damage envolutoin within the four stages of serrated chip formation and experimental measurement of primary shear zone width for Ti2AlNb
4 结论
本文基于近场动力学方法建立了常规态基近场动力学切削加工仿真模型，实现了Ti2AlNb切削切屑形成过程的态型近场动力学数值模拟。分析了Ti2AlNb被切除层材料力学响应特性，揭示了Ti2AlNb切屑形成过程中材料变形和损伤演化规律。本文主要结论如下。
（1）研究提出的近场动力学数值仿真方法能够准确模拟Ti2AlNb锯齿状切屑形成过程，通过Ti2AlNb直角切削仿真模拟和试验研究对比，证明本研究数值仿真获得的剪切角40.23°与试验结果38.89°吻合度高，误差值为3.45%。
（2）Ti2AlNb锯齿状切屑的形成过程可划分为4个阶段，即挤压变形、剪切带启动、剪切带扩展、锯齿分节形成。定量分析了单个锯齿节切屑形成过程中工件材料损伤时间演化和空间分布规律，结果表明，阶段4锯齿分节形成时，剪切带位置损伤演化最为剧烈，损伤值达到0.807。
（3）定义了损伤空间分布的半峰宽值（FWHM）为切削第1变形区宽度，忽略变形引起的离散点间距变化，在阶段4中切削第1变形区宽度约为0.06 mm，预测误差值小于7%。
本文验证了将近场动力学理论用于模拟研究金属切削加工的可行性，为分析切屑形成过程中的材料变形和损伤演化机理提供了一种新方法。
[1] 师昌绪, 仲增墉. 我国高温合金的发展与创新[J]. 金属学报, 2010, 46(11): 1281–1288.
SHI Changxu, ZHONG Zengyong. Development and innovation of superalloy in China[J]. Acta Metallurgica Sinica, 2010, 46(11): 1281–1288.
[2] POLOZOV I, GRACHEVA A, POPOVICH A. Processing,microstructure, and mechanical properties of laser additive manufactured Ti2AlNb-based alloy with carbon, boron, and yttrium microalloying[J].Metals, 2022, 12(8): 1304.
[3] 徐磊, 姚利盼, 卢正冠, 等. 粉末冶金Ti2AlNb合金研究进展[J]. 航空制造技术, 2019, 62(22): 14–20.
XU Lei, YAO Lipan, LU Zhengguan, et al. Development of powder metallurgy Ti2AlNb alloys[J]. Aeronautical Manufacturing Technology,2019, 62(22): 14–20.
[4] HE Linjiang, SU Honghua, XU Jiuhua, et al. Experiment on machinability of Ti2AlNb intermetallic alloy[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2017(5): 487–495.
[5] ATTAR H, EHTEMAM-HAGHIGHI S, KENT D, et al. Recent developments and opportunities in additive manufacturing of titaniumbased matrix composites: A review[J]. International Journal of Machine Tools and Manufacture, 2018, 133: 85–102.
[6] HE L J, SU H H, XU J H, et al. Study on dynamic chip formation mechanisms of Ti2AlNb intermetallic alloy[J]. The International Journal of Advanced Manufacturing Technology, 2017, 92(9–12): 4415–4428.
[7] 周恺, 刘月萍, 刘志兵. 叶轮轻量化用Ti2AlNb基合金的切削加工性研究[J]. 战术导弹技术, 2013(6): 74–78.
ZHOU Kai, LIU Yueping, LIU Zhibing. Research on machinability of Ti2AlNb based alloy for lightweight of impeller[J]. Tactical Missile Technology, 2013(6): 74–78.
[8] YUAN Z J, GAO G F, WANG Y, et al. Correction to:Experimental study on a two-dimensional ultrasonic vibration platform and milling of Ti2AlNb intermetallic alloy[J]. The International Journal of Advanced Manufacturing Technology, 2022, 122(5–6): 4187–4208.
[9] 苏云玲, 周贺, 刘月萍, 等. Ti2AlNb合金深细孔的高效切削加工工艺技术研究[J]. 航天制造技术, 2017(1): 30–33.
SU Yunling, ZHOU He, LIU Yueping, et al. Efficient machining technology research of deep pores in Ti2AlNb alloys[J]. Aerospace Manufacturing Technology, 2017(1): 30–33.
[10] 徐锦泱, 黄祥辉, 陈明, 等. 刀具磨损形态对Ti6Al4V切削过程影响的有限元仿真研究[J]. 航空制造技术, 2020, 63(3): 14–21.
XU Jinyang, HUANG Xianghui, CHEN Ming, et al. Finite element study on effects of tool wear patterns on the machining process of Ti6Al4V[J]. Aeronautical Manufacturing Technology, 2020, 63(3): 14–21.
[11] CALAMAZ M, COUPARD D, GIROT F. A new material model for 2D numerical simulation of serrated chip formation when machining titanium alloy Ti–6Al–4V[J]. International Journal of Machine Tools and Manufacture, 2008, 48(3–4): 275–288.
[12] UMBRELLO D. Finite element simulation of conventional and high speed machining of Ti6Al4V alloy[J]. Journal of Materials Processing Technology, 2008, 196(1–3): 79–87.
[13] LAZOGLU I, ALTINTAS Y. Prediction of tool and chip temperature in continuous and interrupted machining[J]. International Journal of Machine Tools and Manufacture, 2002, 42(9): 1011–1022.
[14] 黄丹, 章青, 乔丕忠, 等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40(4): 448–459.
HUANG Dan, ZHANG Qing, QIAO Pizhong, et al. A review on peridynamics(PD) method and its applications[J]. Advances in Mechanics, 2010, 40(4): 448–459.
[15] BELYTSCHKO T, BLACK T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal for Numerical Methods in Engineering, 1999, 45(5): 601–620.
[16] SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175–209.
[17] MACEK R W, SILLING S A. Peridynamics via finite element analysis[J]. Finite Elements in Analysis and Design, 2007, 43(15): 1169–1178.
[18] SILLING S A, ASKARI E. A meshfree method based on the peridynamic model of solid mechanics[J]. Computers & Structures, 2005,83(17–18): 1526–1535.
[19] SILLING S A, EPTON M, WECKNER O, et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity, 2007, 88(2):151–184.
[20] BREITENFELD M S, GEUBELLE P H, WECKNER O, et al. Non-ordinary state-based peridynamic analysis of stationary crack problems[J]. Computer Methods in Applied Mechanics and Engineering,2014, 272: 233–250.
[21] SHANG S, QIN X D, LI S P, et al. A bond-based peridynamic modeling of machining of unidirectional carbon fiber reinforced polymer material[J]. The International Journal of Advanced Manufacturing Technology, 2019, 102(9–12): 4199–4211.
[22] ZHAN J M, YAO X H, HAN F. An approach of peridynamic modeling associated with molecular dynamics for fracture simulation of particle reinforced metal matrix composites[J]. Composite Structures,2020, 250: 112613.
[23] WANG H, XU Y P, HUANG D. A non-ordinary statebased peridynamic formulation for thermo-visco-plastic deformation and impact fracture[J]. International Journal of Mechanical Sciences, 2019,159: 336–344.
[24] WU C T, REN B. A stabilized non-ordinary statebased peridynamics for the nonlocal ductile material failure analysis in metal machining process[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 291: 197–215.
[25] LI P, HAO Z M, ZHEN W Q. A stabilized non-ordinary state-based peridynamic model[J]. Computer Methods in Applied Mechanics and Engineering, 2018, 339: 262–280.
[26] 李潘, 郝志明, 甄文强. 一种近场动力学非普通状态理论零能模式控制方法[J]. 力学学报, 2018, 50(2): 329–338.
LI Pan, HAO Zhiming, ZHEN Wenqiang. A zero-energy mode control method of non-ordinary state-based peridynamics[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(2): 329–338.
[27] 谷新保, 周小平. 裂纹扩展和连接过程的近场动力学数值模拟[J]. 岩土力学, 2017, 38(2): 610–616.
GU Xinbao, ZHOU Xiaoping. Numerical simulation of propagation and coalescence of cracks using peridynamic theory[J]. Rock and Soil Mechanics, 2017, 38(2): 610–616.
[28] SILLING S A. Linearized theory of peridynamic states[J].Journal of Elasticity, 2010, 99(1): 85–111.
[29] MITCHELL J. A nonlocal, ordinary, state-based plasticity model for peridynamics[R]. Sandia National Laboratories (SNL),Albuquerque, NM, and Livermore, CA (United States), 2011.
[30] FOSTER J, SILLING S A, CHEN W N. An energy based failure criterion for use with peridynamic states[J]. International Journal for Multiscale Computational Engineering, 2011, 9(6): 675–688.