机器人砂带磨削是一种高效、高质量的加工方式，与砂轮或切削加工方式不同，砂带与弹性接触轮形成的加工工具是柔性的，这赋予其加工复杂曲面工件的独特优势[1–2]，但也给砂带磨削过程的控形、控性带来困难[3]。一方面，砂带磨削中的滑擦作用明显[4]，大多数磨削能在磨削区转变为热量[5]，柔性的接触状态使热量的分布不均匀，给磨削温度预测及控制带来困难，进而导致接触区受力大的部位可能出现高温损伤。另一方面，磨削去除量受局部接触状态的影响，然而目前缺少快速获取局部接触状态的方法。
砂带磨削中磨具与工件间的接触一般认为是弹性接触方式[6–8]，解决弹性接触的方法可分为解析法、数值法与数据驱动的方法。解析法是将接触问题归纳为Hertz接触[9]问题或Signorini[10]、Lurie等[11]接触问题。在砂带的抛光加工中，砂带与工件表面之间具有小的接触压力与摩擦力，有学者将其看作是Hertz接触问题并求解接触区的压力分布[12–14]，即
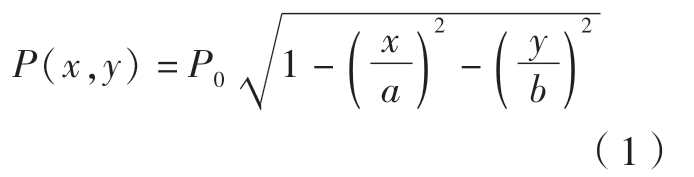
式中，P0为椭球体压力分布中心的压力；a为椭球体长半轴；b为椭球体短半轴。考虑到磨削过程中接触区材料不断被去除，导致接触压力的变化，Wang等[14]进一步提出了停留时间变化下的接触区压力分布，计算公式为
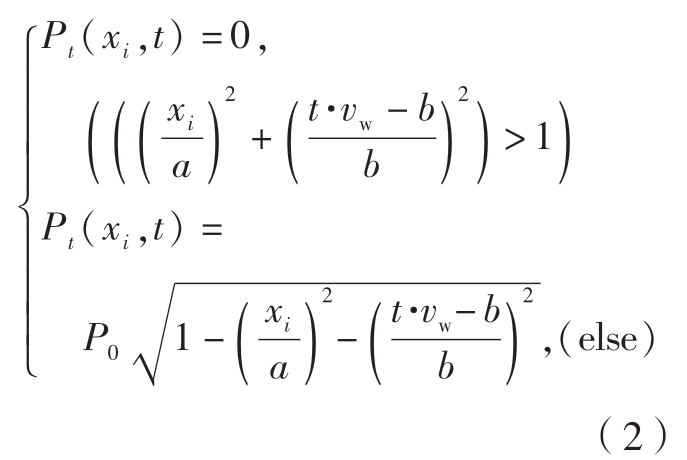
式中，xi为平行长于半轴a的x轴上的点；Pt为接触压力；t为停留时间；vw为工件移动速度。Wang等[15]同样将接触轮的变形简化为Hertz接触问题，平板磨削试验结果表明准确率不低于96.9%。
Signorini接触问题致力于解决弹性–刚性体之间的接触状态问题，与砂带磨削中的磨具–工件接触情形类似。然而，使用积分法对以上两种模型求解仍然是比较困难的，同时将接触问题简化为简单的二维接触问题，对于工件表面轮廓复杂的砂带磨削加工来说，难以满足实际生产中精确控形的需求。
有限元法（Finite element method，FEM）是将连续的方程离散化进而解决复杂的工程问题[16]。在解决多体接触问题上，商业有限元软件多以节点到表面（Node-to-Surface）形式处理物体间的接触问题。对FEM来说，离散化的程度一般决定了最终的计算精度，同时也是计算耗时多少的主要因素。在忽略时间成本的前提下，FEM在解决静态、准静态接触问题上具有比较高的准确度。Schröder等[17]通过改进FEM解决了具有Tresca摩擦现象的Signorini接触问题，砂带磨削水龙头试验结果证明考虑摩擦现象计算得到的接触状态更加准确，虽然FEM能够比较准确地计算三维、任意形状工件的接触状态，但是时间成本较高，一次接触状态仿真计算短则数分钟，长则数小时乃至数天。为解决FEM计算效率问题，Weinert等[18]引入误差自主控制的有限元思想，即在接触区自主划分高密度网格，而非接触区划分粗网格，以此提高计算效率。Blum[19]和Suttmeier[20]等同样引入自适应网格划分技术来提高FEM计算接触状态的效率。但优化后的FEM仍然需要较长的时间来获取接触状态计算结果。考虑到接触状态分析中已有研究只对工件表面的受力状态感兴趣，而内部的应力状态则不是计算目标，采用边界元法（Boundary element method，BEM）则能体现出这种优势[21]，只需要划分、求解工件表面网格节点，极大缩减计算量。BEM需要利用格林公式与基本解建立变形网格与外部力的积分方程，边界条件为在边界处的网格受外力为0，但是接触边界仍然需要迭代的方式计算得到，因此许多研究工作致力于提高迭代的效率或缩减迭代步骤。
考虑到FEM和BEM在快速获得接触状态方面的不足，有学者提出采用数据驱动的技术将繁琐耗时的计算过程采用机器学习模型进行代替[22–23]，仿真得到的接触状态结果用来训练机器学习模型。Zhang等[24–25]将获取接触问题看作是由磨具与工件间的距离信息到接触状态的回归问题，采用SVR建立预测模型，模型的输入为特别选择的接触体间的距离信息。模型的预测误差不超过5%，一次接触状态的预测时间为1 s左右，远高于数值法计算效率（15 min左右）。Lipiński等[26]同样提出了一个基于改进的神经网络模型进行接触状态预测的方法，测试结果表明该方法在预测磨削接触状态上表现优异。
综上，目前国内外在求解砂带磨削中接触状态时，广泛采用简化接触模型并结合数值法通过迭代计算得到结果，此种方法效率低，过度的简化难以满足高精度磨削加工要求；引入机器学习算法建立工件轮廓与接触状态映射模型是一种高效率的得到接触状态的方法，然而可能的接触范围难以界定，容易陷入局部最优。获取大量的、可靠的训练数据集也是建立机器学习模型预测接触状态的难点。此外，未考虑到磨具弹性参数的方法在计算接触状态时，实用性难以保证。因此，为了高效准确地计算砂带磨削接触状态，本研究引入视觉获得接触区域宽度，结合BEM快速计算得到接触状态。
1 基于数值法的接触状态计算
1.1 基于FEM的接触状态计算
要想获得磨削复杂曲面工件的高精度接触状态，需要建立磨具与工件的三维模型。考虑到工件轮廓的复杂性，无法将模型简化为二维进行数值求解，在ABAQUS有限元分析软件平台建立三维模型并求解。模型如图1所示，工件与磨具的接触姿态通过调整工件的角度确定。磨具由多孔PU轮与砂带组成，可以看作为具有确定力学参数的弹性体，力学参数通过简单试验对比FEM模型得到。最终得到的FEM设置参数如表1所示。
表1 有限元模型参数
Table 1 Parameters of finite element model
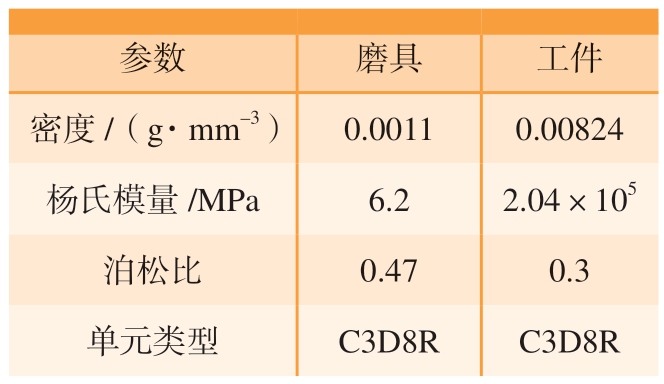
参数 磨具 工件密度/（g·mm–3） 0.0011 0.00824杨氏模量/MPa 6.2 2.04×105泊松比 0.47 0.3单元类型 C3D8R C3D8R
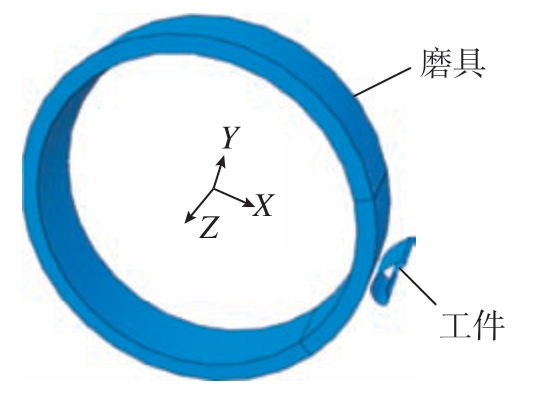
图1 有限元模型
Fig.1 Finite element model
1.2 基于BEM的接触状态计算
磨削过程中的接触是动态的、时变的，对计算的速度要求很高，FEM难以满足加工过程中接触状态快速获取的要求。在FEM的基础上，BEM被发展起来。与FEM不同的是，BEM仅需要将物体表面离散化，内部无网格、无节点，因此极大缩减了计算量。忽略摩擦力与切向应力，如图2所示，Love等[27]分析了均匀法向压力下，范围为–a≤x≤a，–b≤y≤b平面内任意一点p（x，y，z）在z方向上的位移与点A、B、C、D的关系为
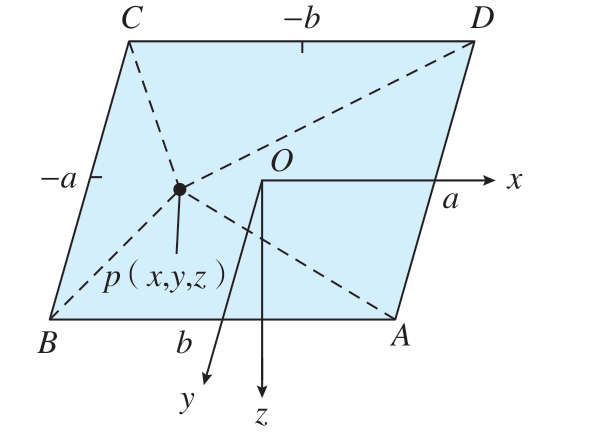
图2 均匀分布法向压力下矩形内点法向位移
Fig.2 Normal displacement of point in rectangular under uniform normal pressure
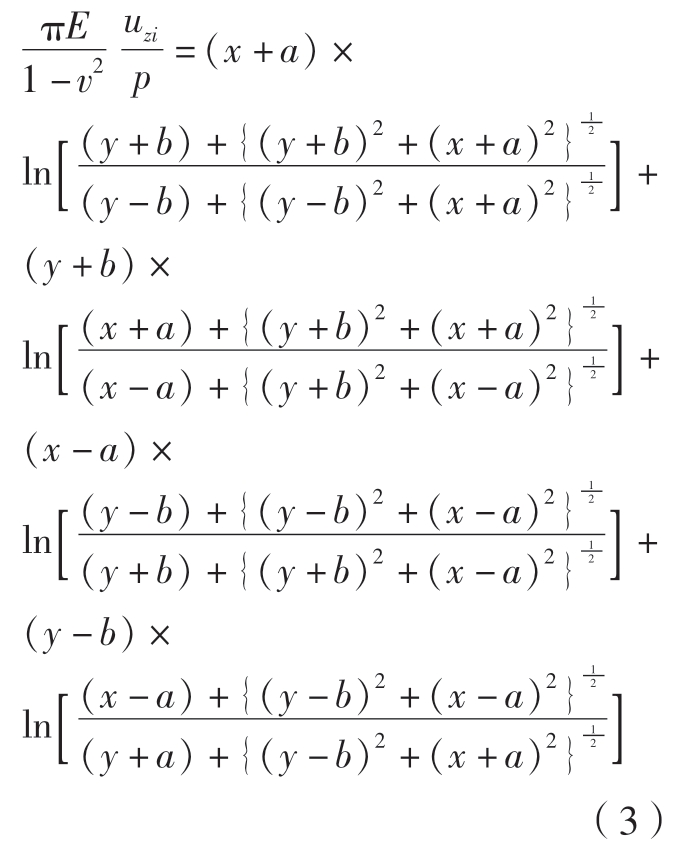
当上述结论推广到三维曲面时，如图3所示，在点（i，j）处的变形受到点1～4的影响，同时点1～4又受到其周围点的影响。因此对于砂带表面接触区域，变形的表面是一个整体，某点的变形服从于整体曲面变形的平衡。基于此，将曲面划分为宽度为c，大小为m×n的网格区域。由式（3）可得，应变与应力的矩阵表达式[28]为
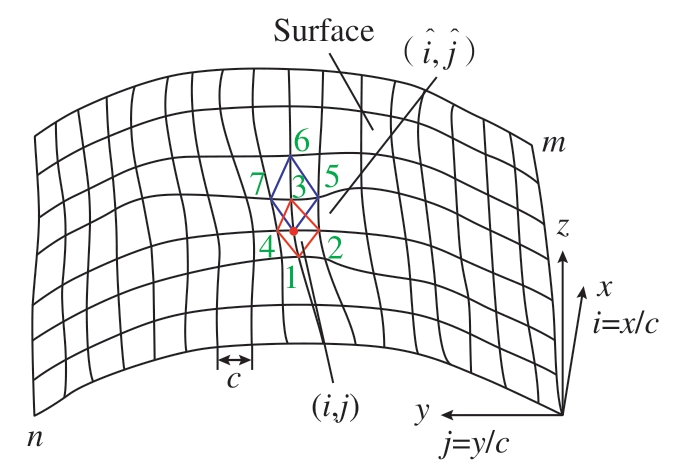
图3 离散曲面示意图
Fig.3 Diagram of discreted surface
式中，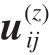
为点（i，j）处的法向位移；pij为点（i，j）的应力；
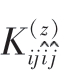为参考点为（i，j）时的全局影响系数，由式（3）可知
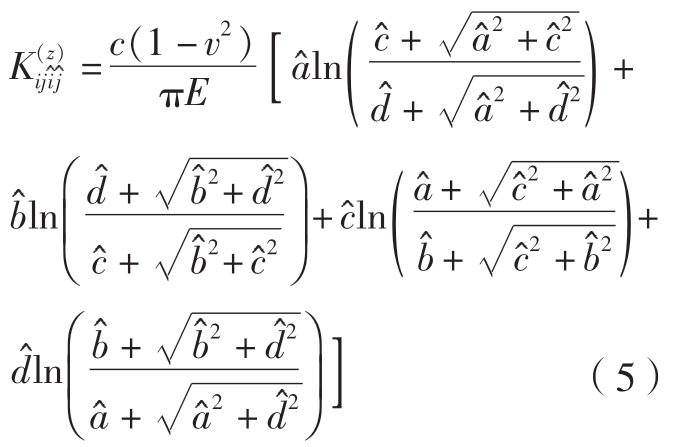
式中，
式（4）写成矩阵形式为
式中，A为（m×n）×（m×n）影响系数矩阵。
在实际接触问题中，砂带表面接触区域是未知的，即m、n未知，接触问题的解需要通过不断迭代来满足边界条件。在接触区域两物体接触间距为0（即在接触区，弹性体变形是已知的，服从于刚体表面轮廓）。在两物体接触区以外，压应力为0，而弹性体的位移，一般来说不为0。在开始迭代前，需要假设一个可能的砂带表面接触区域，应力与位移可以分为接触区内应力pi与接触区内位移ui，接触区外应力po与接触区外位移uo。若此状态成立，则ui已知，且po = 0。依据式（6），则有
进一步的，
接触状态pi最终可由式（8）得到。同时，砂带表面接触区外的弹性体变形可通过式（9）计算得到。通常，在第1次迭代时可能在接触区域内产生一个负的压应力（即拉应力），同时在接触区域外产生一个不合理的负分离距离。第2次迭代选择新的接触区域，使所有产生拉应力的接触点被消除，同时产生负分离的点被考虑为接触点。重复第2步直到迭代至一个合理的接触状态（没有受拉应力的点，没有负距离的点）。若没有给定接触区域范围的参考，上述迭代将是一个计算量很大且耗时的过程。
2 基于视觉的接触状态快速获取
与FEM相比，尽管BEM缩减了网格数量，但在精度要求高的计算过程中仍要求解大量的非线性方程组，迭代过程将成倍地增加计算时间。为进一步提高BEM计算接触状态效率，本研究提出采用基于视觉的方式得到接触区宽度b作为BEM的边界条件，即b+BEM方法，减少迭代求解大量非线性方程组计算量，一次计算得到整个接触区的接触状态。
2.1 试验设置
接触区域与磨削中的其他特征不同，其大小难以用声音、磨削力来映射。工件在与砂带接触过程中的接触区域也难以使用相机直接拍摄。但是参与磨削的磨粒顶部会裸露出光亮面，基于此特点，可采用磨削前对砂带进行着色+磨削后对砂带磨痕抓拍的方式得到实时的接触区宽度。
工件为3D激光选区熔覆成形的复杂曲面Inconel 718工件，如图4（a）所示，采用KEYENCE，LJ–7200线激光扫描仪获取扫描面点云数据，将点云数据作为曲面工件离散数据，扫描密度为0.2 mm。实时获取接触区宽度试验设置如图4（b）所示，工业相机+辅助超亮LED光源保证相机在50 μs的曝光时间下能够采集到运行中砂带的清晰图像。工业相机型号为Basler acA4112–8gc，曝光时间最小为30 μs，传感器为CMOS，分辨率不低于4112×3008，可采集彩色或黑白图像，采样率设置为4帧/s。其中砂带被黑色涂料粉刷，涂料为水溶性颜料，不会造成砂带空隙堵塞。粉刷位置为整条砂带的表面，可使磨削后磨痕清晰。需要特别说明的是，实际磨削过程中磨削宽度是时变的、没有规律的，新的磨削痕迹可能被前面磨削道次痕迹所覆盖，需要在相机与磨削区之间增加喷涂装置实时涂敷掉前面磨削痕迹。本试验为了简化试验装置，通过试验参数的特别设置，保证随着磨削的进行试验中接触区域是逐渐增大的，因此在本试验中识别到的最大砂带表面接触区宽度即为当前工件接触区宽度，不受前面磨削过程产生的痕迹影响。
图4 获得接触区宽度试验设置
Fig.4 Experimental setup to obtain contact width
2.2 基于图像的接触区域获取
基于图像在线获取接触区宽度流程如图5所示。图像尺寸标定是为了获得相机视场下的实际尺寸，参照物为已知宽度的砂带，如图6（a）所示。图6（b）为50 μs曝光时间下采集到的磨削过程中砂带图像，可以看出参与磨削的磨粒在图像中呈明显的光亮色，而未参与磨削的区域在黑色涂料染色下为黑色。图6（c）为对图6（b）进行二值化处理，二值化阈值设置为0.3。砂带表面接触区域外的少量噪点是由反光现象造成的，噪点随机分布且噪点之间相隔较远，因此对采集到的原始图像进行聚类去噪，k参数设置为4。为方便得出磨削区域宽度b，对去噪后的图片进行线性膨胀形态学处理，线性膨胀方向为砂带运行方向。经过上述步骤处理后结果如图6（d）所示，其中的磨削区域更加清晰，在选取宽度内测量白色区域平均宽度，得到实际的工件接触区宽度。
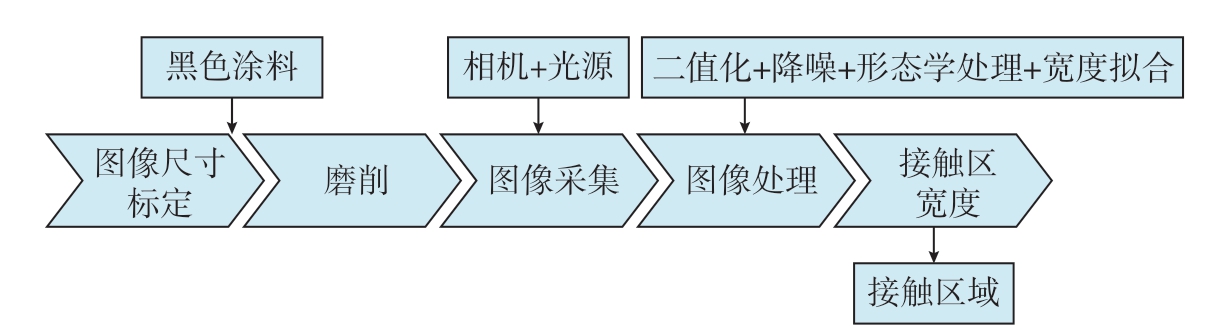
图5 实时获取接触区流程
Fig.5 Procedures to obtain contact area online
图6 基于图像处理获取接触区宽度
Fig.6 Procedures to obtain contact area based on image processing
因为砂带在与接触轮配合形成磨具时受到一定的张紧力，同时自身强度较高，因此忽略因转动和切向摩擦力带来的切向应力导致的接触状态变化。如图7所示，在已知工件与磨具接触姿态的条件下，由轮廓数据可得二者在点pij处的法向距离信息为
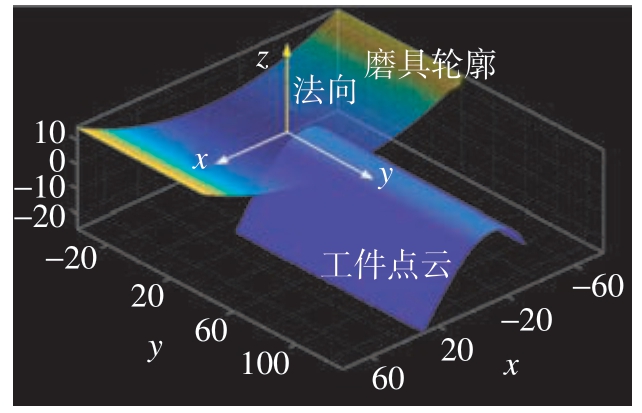
图7 磨具与工件接触姿态示意图（mm）
Fig.7 Diagram of contact posture between grinding tool and workpiece (mm)
式中，R为磨具半径。
如图8（a）所示，总的可能接触区域内磨具与工件的法向距离集合为
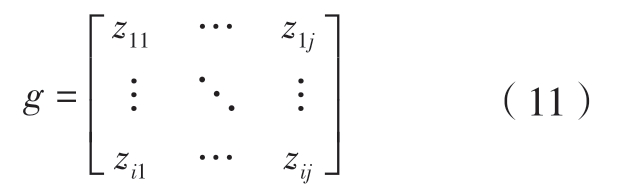
若接触区域宽度b已知，则可通过等高点数据寻优与最近邻搜索获得具体接触区域，寻优算法采用BADS（Bayesian adaptive direct search）。由接触区宽度获得接触区域的伪代码如下。
第1步：由工件轮廓、磨具轮廓和接触姿态确定可能的接触区域间距，确定可能的接触区间g。
第2步：由图像信息已知接触区宽度。
第3步：寻优。
BADS（@targetfun，hmin）：
targetfun：
搜索集合g内距离范围为hmin–0.1～hmin+0.1的点集合g1；
搜索g1集合内y轴数值最小的点ymin；
搜索g1集合内y轴数值最大的点ymax；
可能的接触区宽度Dis=|ymax–ymin|；
返回与真实接触区宽度b的差方D=（b–Dis）2
结束；
判断D是否满足优化准则；
是则返回hmin；
否则重复第3步；
结束。
第4步：输出接触区域集合g1。
其中，hmin为工件接触区域边缘在初始状态下的接触体法向距离；等高线宽度范围设置为0.1 mm；由于BADS在快速寻优问题中的优势，将其作为获得hmin的优化算法。假设b=20 mm，最终得到的工件接触区域如图8（b）所示。
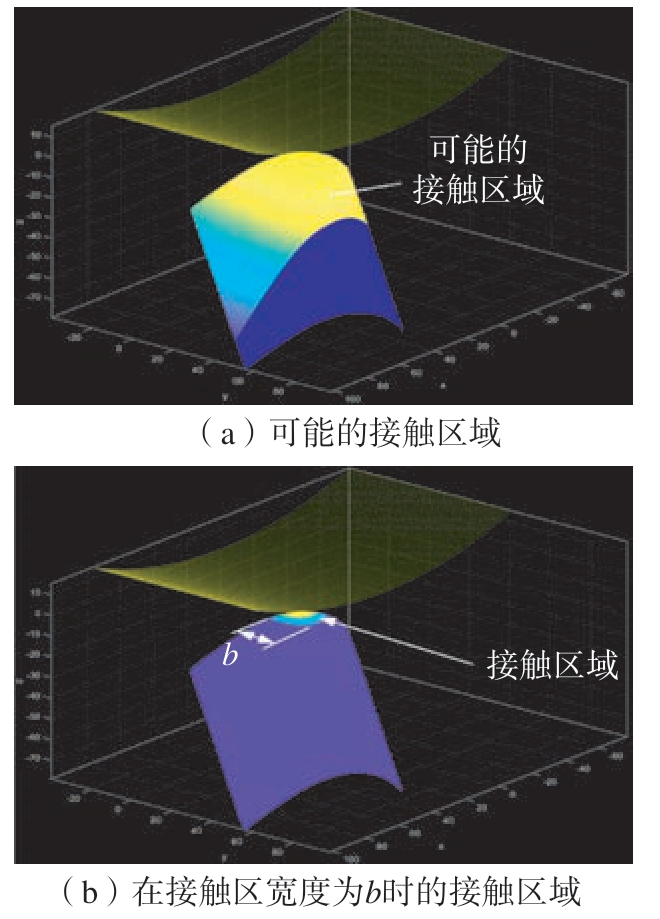
图8 接触区域示意图
Fig.8 Diagram of contact area
3 计算与验证
在已知工件接触区与轮廓离散点云的基础上，由式（8）可计算得到接触状态，将所得结果与磨削试验结果和FEM结果对比，验证本研究提出的接触状态获取方法的准确性与效率。在进行接触磨削试验前对工件表面涂色，以便清晰地看出工件接触区域。接触磨削试验参数如表2所示，为保证工件表面接触区域上的涂色在被去除的同时不会磨削过多的母材导致接触区域的变化，设置一个非常低的砂带速度。为模仿实际磨削的复杂工况，接触姿态在x、y、z轴方向分别进行了–5°、–15°和–20°的旋转。
表2 获取磨削接触状态试验设置
Table 2 Experimental settings to obtain grinding contact status
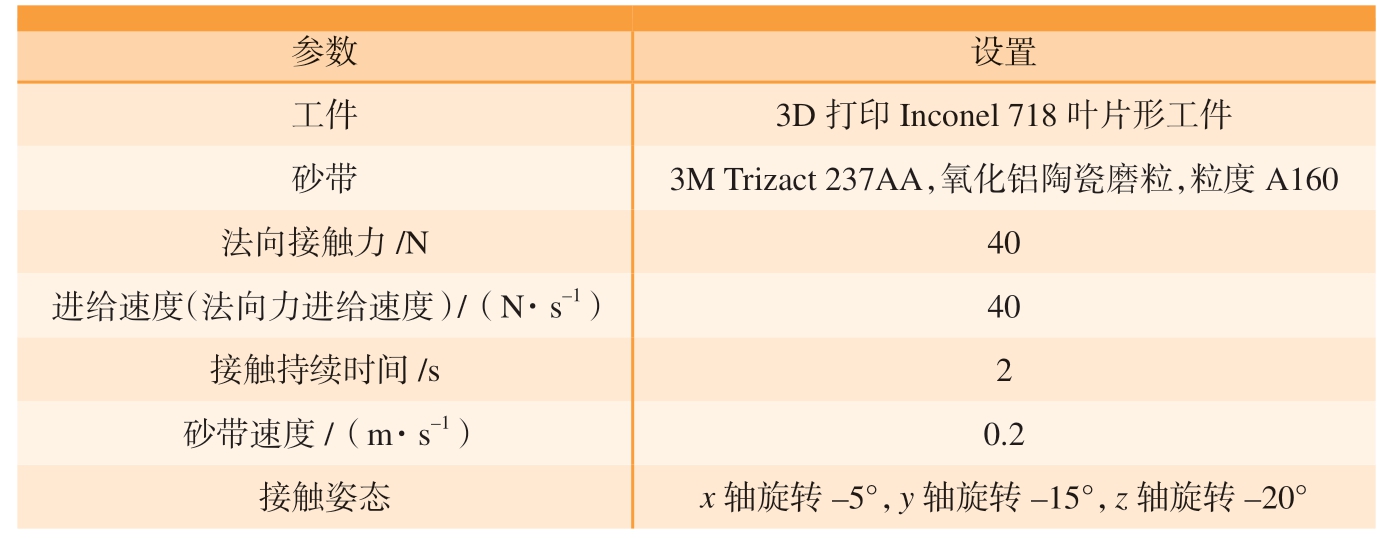
参数 设置工件 3D打印Inconel 718叶片形工件砂带 3M Trizact 237AA，氧化铝陶瓷磨粒，粒度A160法向接触力/N 40进给速度（法向力进给速度）/（N·s–1） 40接触持续时间/s 2砂带速度/（m·s–1） 0.2接触姿态 x轴旋转–5°，y轴旋转–15°，z轴旋转–20°
磨削试验结果、FEM计算结果与b+BEM获得的接触状态结果如图9所示。图9（a）为接触磨削试验结果，被磨掉的涂色部分为接触区域，其中沿y轴的磨削区宽度b可由垂直划痕的磨削区域最宽处测得，约为12 mm。图9（b）为FEM模型获得的接触状态，接触区宽度为11.23 mm，与接触磨削试验结果基本吻合，说明FEM模型合理，接触区最大压力为3.05 MPa。图9（c）为b+BEM获得的接触状态示意图，其中接触区宽度由接触磨削试验获得，b=12 mm，接触区最大压力为3.22 MPa。对比接触区域形状，FEM与b+BEM获得的接触区域和磨削试验获得的接触区域相似。
图9 不同方法获得接触状态
Fig.9 Contact status obtained by different methods
对比数据如表3所示，FEM获得的接触状态作为对照组，b+BEM获得接触状态为试验组。所有数据处理与仿真试验在个人电脑（CPU i5 7400，RAM 16G）上完成。FEM获得接触状态在ABAQUS软件中完成，接触区域附近网格尺寸精度最高为0.5 mm，接触状态的一次计算时间约为25 min。由于b+BEM的离散基于点云数据，因此网格尺寸精度与点云数据密度相关，都为0.2 mm。在采用b+BEM计算接触状态时，每次接触状态的计算约需要8 s，优于FEM计算效率，但是还达不到实时要求。造成b+BEM计算效率过低的原因是工件点云中与磨具接触的点需要一个寻优的步骤获得，当点云范围很大时，寻优的步骤增多，增加了计算成本。选取可能的接触区域点云集合，缩减感兴趣点云数据量，可以达到提高计算效率的目的。选取规则为以最邻近磨具的点为中心，宽度±（b+5），垂直于y轴的矩形带内的点云数据，选取结果如9（c）所示。在进行数据量缩减后，b+BEM计算一次接触状态的时间缩短到1 s内。
表3 不同方法获得接触状态对比
Table 3 Comparisons of different methods to obtain contact status
试验组 精度（网格尺寸）/mm 时间 最大压力 接触面积对照组 FEM ≥0.5 ≈25 min 3.05 MPa 98.6 mm2验证组 b+BEM 0.2 ≤1 s 3.22 MPa 93.12 mm2偏差 — — — 5.6% 5.6%
在最大接触压力与接触面积方面，b+BEM获得的接触状态与FEM结果吻合度较好，接触区最大压力与接触面积偏差都没有超过5.6%，一方面是因为接触区宽度由实际试验得到，保证了接触区域的准确性；另一方面是因为BEM在计算接触状态时将接触区看作一个整体，每个点的压力计算都会将其他接触点的影响计算在内，最终得到比较准确的接触状态。
综上，在已知材料参数的条件下，FEM获得的接触状态准确度较高，但计算成本也很高，难以满足实际生产活动中对于后续局部材料去除量与热流分布快速获取的需求，但可将其作为参照组来验证其他可行的获取接触状态的方法。b+BEM获取接触状态的方法需要额外的辅助得到接触区宽度，但得到的结果可信度高，采用选取可能接触区域，缩减点云数据量的方式提高计算效率，能够快速计算局部接触状态。未来，可通过升级计算机硬件、优化网格密度、改进寻优算法等手段进一步提高计算效率。因此，采用b+BEM获取接触状态的方法在磨削应用中具有明显的优势。
4 结论
本研究首先分析了FEM与BEM在接触状态获取方面的应用，提出了基于视觉获取接触区宽度并结合BEM，即b+BEM方法，实现了基于点云轮廓的局部接触状态快速计算。与数值法相比，该方法可计算复杂曲面工件接触状态，效率与适用性更高；与机器学习模型相比，该方法具有明确的物理意义，不会陷入局部最优且不需要额外的训练样本。计算结果与FEM仿真结果对比，b+BEM计算获得接触状态的误差不超过5.6%，而且在计算效率上远高于FEM。结合点云数据量缩减规则，该方法能够在1 s内获得18 mm×18 mm，精度0.2 mm区域内的接触状态，为后续计算局部材料去除量与热流分布奠定基础。
[1] 黄云, 黄智. 现代砂带磨削技术及工程应用[M]. 重庆：重庆大学出版社, 2009.
HUANG Yun, HUANG Zhi. Modern abrasive belt grinding technology and engineering application[M]. Chongqing:Chongqing University Press, 2009.
[2] 黄小康, 任绪凯, 陈华斌, 等. 高温合金机器人柔性磨削表面完整性研究进展[J].航空制造技术, 2021, 64(7): 38–52.
HUANG Xiaokang, REN Xukai, CHEN Huabin, et al. Research progress of surface integrity in robotic compliant grinding of superalloys[J]. Aeronautical Manufacturing Technology, 2021, 64(7): 38–52.
[3] PARK J W, CHO H U, CHUNG C W, et al. Modeling and grinding large sculptured surface by robotic digitization[J]. Journal of Mechanical Science and Technology, 2012,26(7): 2087–2091.
[4] ZHU D H, LUO S Y, YANG L, et al.On energetic assessment of cutting mechanisms in robot-assisted belt grinding of titanium alloys[J]. Tribology International, 2015, 90:55–59.
[5] SURESH G, VASU V, RAGHAVENDRA G. Optimization of input parameters on erosion wear rate of PTFE/HNT filled nanocomposites[J]. Materials Today:Proceedings, 2018, 5(1): 1462–1469.
[6] POPOV V L, HESS M. Method of dimensionality reduction in contact mechanics and friction[M]. Beiing: Tsinghua University Press, 2016.
[7] 齐俊德, 陈冰. 考虑单磨粒作用的砂带磨削机理模型[J]. 金刚石与磨料磨具工程, 2020, 40(3): 13–20.
QI Junde, CHEN Bing. Mechanism model of belt grinding considering single abrasive action[J]. Diamond & Abrasives Engineering,2020, 40(3): 13–20.
[8] 刘斐, 王伟, 王雷, 等. 接触轮变形对机器人砂带磨削深度的影响[J]. 机械工程学报, 2017, 53(5): 86–92.
LIU Fei, WANG Wei, WANG Lei, et al.Effect of contact wheel’s deformation on cutting depth for robotic belt grinding[J]. Journal of Mechanical Engineering, 2017, 53(5): 86–92.
[9] 李建勇, 程继发, 樊文刚, 等. 砂带磨削静态接触理论建模与有限元仿真[J]. 北京交通大学学报, 2018, 42(6): 125–130.
LI Jianyong, CHENG Jifa, FAN Wengang,et al. Theory modeling and finite element simulation of belt grinding static contact[J].Journal of Beijing Jiaotong University, 2018,42(6): 125–130.
[10] SIGNORINI A. Trasformazioni termoelastiche finite[J]. Annali Di Matematica Pura Ed Applicata, 1955, 39(1): 147–201.
[11] LURIE A I. Theory of elasticity[M].Berlin: Springer Science & Business Media,2010.
[12] WANG Y J, HUANG Y, CHEN Y X,et al. Model of an abrasive belt grinding surface removal contour and its application[J].The International Journal of Advanced Manufacturing Technology, 2016, 82(9–12):2113–2122.
[13] LI D Q, ZHANG L, YANG X, et al.Research on the double-sided grinding and polishing machine tool system[C]//The 2010 IEEE International Conference on Information and Automation. Harbin, 2010.
[14] WANG Y J, HUANG Y, CHEN Y X,et al. Model of an abrasive belt grinding surface removal contour and its application[J]. The International Journal of Advanced Manufacturing Technology, 2016, 82: 2113–2122.
[15] WANG W, LIU F, LIU Z H, et al.Prediction of depth of cut for robotic belt grinding[J]. The International Journal of Advanced Manufacturing Technology, 2017,91(1–4): 699–708.
[16] 岳彩旭, 王彦武, 高海宁, 等. 凸曲面拼接模具铣削过程三维有限元仿真研究[J]. 航空制造技术, 2018, 61(16): 34–42.
YUE Caixu, WANG Yanwu, GAO Haining, et al. FEM simulation research on convex surface splicing mold milling process[J].Aeronautical Manufacturing Technology, 2018,61(16): 34–42.
[17] SCHRÖDER A, BLUM H,RADEMACHER A, et al. Mixed fem of higher order for contact problems with friction[J].International Journal of Numerical Analysis &Modeling, 2011, 8(2): 302–323.
[18] WEINERT K,BLUM H,KUHLENKÖTTER B, et al. New methods for calculating the force distribution within belt grinding processes[J]. Production Engineering,2007, 1(3): 285–289.
[19] BLUM H, SUTTMEIER F T. An adaptive finite element discretisation for a simplified Signorini problem[J]. Calcolo, 2000,37(2): 65–77.
[20] SUTTMEIER F T. Error bounds for Finite Element solutions of elliptic variational inequalities of second kind[J]. Professorial Dissertation, 2001, 9(4): 307–313.
[21] 张伟, 姚玲, 赵帆, 等. 基于等几何–边界元法的热弹性力学问题分析[J]. 信阳师范学院学报(自然科学版), 2021, 34(4):661–666.
ZHANG Wei, YAO Ling, ZHAO Fan, et al. Thermoelastic mechanics analysis based on isogeometric boundary element method[J].Journal of Xinyang Normal University (Natural Science Edition), 2021, 34(4): 661–666.
[22] 赵亮, 李书. 基于MLPG混合配点法的接触问题形状优化[J]. 北京航空航天大学学报, 2010, 36(6): 745–748.
ZHAO Liang, LI Shu. Shape optimization for contact problem based on MLPG mixed collocation method[J]. Journal of Beijing University of Aeronautics and Astronautics,2010, 36(6): 745–748.
[23] 吴秀壮, 周焕林, 陈豪龙. 基于布谷鸟搜索算法的弹性力学边界条件识别[J].重庆大学学报, 2020, 43(6): 40–49.
WU Xiuzhuang, ZHOU Huanlin, CHEN Haolong. Identification of elasticity boundary conditions based on cuckoo search algorithm[J].Journal of Chongqing University, 2020, 43(6):40–49.
[24] ZHANG X, KUHLENKÖTTER B,KNEUPNER K. An efficient method for solving the Signorini problem in the simulation of freeform surfaces produced by belt grinding[J].International Journal of Machine Tools and Manufacture, 2005, 45(6): 641–648.
[25] ZHANG X, KNEUPNER K,KUHLENKÖTTER B. A new force distribution calculation model for high-quality production processes[J]. The International Journal of Advanced Manufacturing Technology, 2006,27(7–8): 726–732.
[26] LIPIŃSKI D, BAŁASZ B,RYPINA Ł. Modelling of surface roughness and grinding forces using artificial neural networks with assessment of the ability to data generalisation[J]. The International Journal of Advanced Manufacturing Technology, 2018,94(1–4): 1335–1347.
[27] LOVE A E H I X. The stress produced in a semi-infinite solid by pressure on part of the boundary[J]. Philosophical Transactions of the Royal Society of London Series A, Containing Papers of a Mathematical or Physical Character,1929, 228(659–669): 377–420.
[28] SHAO N, LIU J H, DING X Y.Effects of contact behaviors on tolerance analysis of mechanism based on skin model shapes and a boundary element method[J].Procedia CIRP, 2020, 92: 15–20.
