航空制造中主要的连接方式为铆接和螺栓连接，因此航空零件上存在大量孔径不一且呈空间分布的机加圆孔。目前对圆孔的数字化检测手段主要包括使用三坐标测量机[1]或点云扫描仪[2]等，然而，这些方法存在明显的局限性。例如，三坐标测量机难以测量直径较小的圆孔，而点云扫描得到的数据由于圆孔边缘的非连续性，很难在点云处理阶段快速有效分离出圆孔的真实边缘信息。随着工业环境对圆孔检测设备的通用性、快速性和高精度要求的提高，现有的圆孔高精度测量设备无法满足上述需求，而基于圆孔图像的定位和检测系统为机加圆孔的测量提供了创新的解决思路[3]。
机加圆孔的三维定位技术涉及相应圆孔图像的识别、椭圆提取技术和空间圆重建及优化技术等。由于加工质量和表面纹理等因素影响，圆孔图像边缘呈现出多条轮廓，因此通过Canny 算子提取轮廓后，直接拟合椭圆的方法往往失效。对这类图像椭圆提取算法的研究集中在弧链方面。这类图像椭圆提取算法包含了弧线段分割、弧线段匹配和弧线段聚合3 个步骤。Prasad等[4]研究了椭圆弧段和直线段检测算法 （ELSD）以实现对高噪声和多种假象中图像椭圆的精确识别和提取。Meng 等[5]提出了基于相邻弧线段及邻接矩阵的快速椭圆识别优化算法 （Arc adjacency matrix-based fast ellipse detection，AAMED），用于椭圆边缘检测。然而，现有的算法对边缘不连续的加工圆孔存在识别率不高等情况，因此需要一种自适应的椭圆提取算法以应对这类缺陷椭圆的图像。
对于两视图空间圆的重建算法，已有单视锥法以及两视锥求交法等算法。在此前的研究中，Safaee-Rad等[6]在已知空间圆真实半径的情况下，提出单目单视锥求解空间圆中心点和法矢量信息，然而计算的空间圆存在双解；Chen 等[7]通过基于圆心图像投影弦的几何方法找到图像上的点与实际圆上点的对应关系；Zheng 等[8]基于此形成了一个圆的投影方程，进而提出一个闭合形式的解决方案来估计圆的姿态。然而这些空间圆位姿估计的算法并未考虑到空间圆重建的二元性，魏振忠等[9]使用两条与空间圆共面的线之间的角度约束来消除歧义；Miao 等[10]使用从参考点到圆心的距离的欧几里得不变性作为约束来解决姿态歧义。然而上述方法存在问题，需要提前通过高精度的测量获得机加圆孔的半径信息，而Quan[11]在两个视角相对位置已知的情况下，重建对应的圆锥体并进行两视锥求交，就能解算空间圆的位姿信息的算法，无需圆孔的半径信息，但该方法仅仅依靠两视图解算圆的空间信息，受噪声干扰较大，因此需要进一步优化空间圆的位姿参数。
基于多视图几何的三维重建技术是一种通过增加图像提高重建精度的有效方法，可从不同角度拍摄到的多幅二维图像中恢复出三维结构。根据图像添加顺序的拓扑结构可分为增量式三维重建[12]、全局式三维重建[13]和混合式三维重建[14] 3 种。其中增量式三维重建能有效剔除外点且具有鲁棒性较强的特点，在工业摄影测量技术中被广泛使用。
本文针对航空制造中对空间分布圆孔的三维数字化质量检测的需求，基于视觉测量技术，系统探讨了机加圆孔的空间定位与三维重建方法。针对机加圆孔对应图像椭圆，采用了一种基于弧段分组技术的圆孔图像提取方法，并提出一种有效的筛选机制，利用该筛选机制，可以显著提升图像椭圆的准确识别率，为后续机加圆孔对应空间圆的重建提供了可靠的基础。利用两视锥的重建与交集，采用两椭圆锥求交法对空间圆的位姿进行粗估计，提出基于多视图几何的空间圆位姿优化的算法，并通过试验验证了本文方法的有效性和精确性。
1 方法概述
如图1 所示，机加圆孔定位及重建的技术路线包括（1）对图像的预处理； （2）基于弧链级图像椭圆提取算法的轮廓识别； （3）通过椭圆锥求交法对空间圆的位姿进行粗估计； （4）确定最佳视角图像作为多视图空间圆位姿优化的根据，利用本文提出的多视图下空间圆位姿优化算法对空间圆位姿进行精确估计。
图1 机加圆孔定位及重建总体技术路线
Fig.1 Overall technical route for machining circular hole localization and reconstruction
预处理包括图像降噪和边缘提取的过程，图像降噪采用高斯滤波、均值滤波、Canny 边缘提取等技术，而椭圆轮廓提取则采用基于相邻弧线段及邻接矩阵的快速椭圆识别优化算法 （AAMED）算法对椭圆轮廓进行提取并筛选。椭圆锥求交需要预先获取各图像对应相机的投影矩阵与对应图像椭圆，用于两视锥重建与求交；然后，利用多视角图像对空间圆的位姿进行优化，可以更准确地估计机加圆孔在空间中的位置和法矢量方向。
2 椭圆轮廓提取技术研究
在复杂工业场景下，由于传统的Canny 边缘检测算法对噪声敏感，以及难以处理不连续边缘的问题，不能直接有效地应用于椭圆轮廓的提取。因此，本研究首先对图像进行预处理，然后采用AAMED 算法来实现更精确的椭圆轮廓提取。AAMED 算法通过分割、匹配和聚合弧线段，能够较好地识别出图像中的椭圆轮廓。然而，在实际应用中，由于机加圆孔边缘的非连续性和噪声干扰，该算法仍然会产生一些错误的椭圆识别结果。为此，本文提出了一种有效的筛选机制，以进一步提高椭圆轮廓提取的准确性，为后续的空间圆重建提供更加可靠的数据基础。
2.1 图像预处理
图像预处理用来识别椭圆图像边缘的同时降低所在图像的噪声。传统的图像边缘轮廓提取方法可以采用 Sobel 算子，Canny 算子等。常规椭圆图像的提取步骤通常包括高斯滤波、各向异性扩散滤波、自适应二值化、形态学开闭运算、Canny 边缘检测，如图2 所示。通过以上步骤可以有效提取椭圆图像的边缘并能够进行鲁棒性拟合。图像预处理后，需要对Canny 算子检测到的轮廓进一步处理，包括弧段的分割、弧段的组合和弧段的聚合等操作。
图2 图像预处理流程图
Fig.2 Flowchart of image preprocessing
2.2 AAMED 算法
由于噪声干扰，工业圆孔轮廓被分成很多小段，凭借传统Canny 算子提取的图像轮廓非连续性较强，且存在不规则特征，这使得直接采用最小二乘法拟合图像椭圆存在困难且识别准确率较低。采用弧段级图像椭圆算法，例如AAMED 算法，却能达到识别的精度要求。本文采用AAMED 算法提取椭圆轮廓的过程如图3 所示。本研究机加螺纹圆孔原图由于倒角等边缘的干扰，无法直接提取真实螺纹孔椭圆，通过调整AAMED 算法的参数，剔除干扰弧段，最终成功提取螺纹孔真实椭圆轮廓。
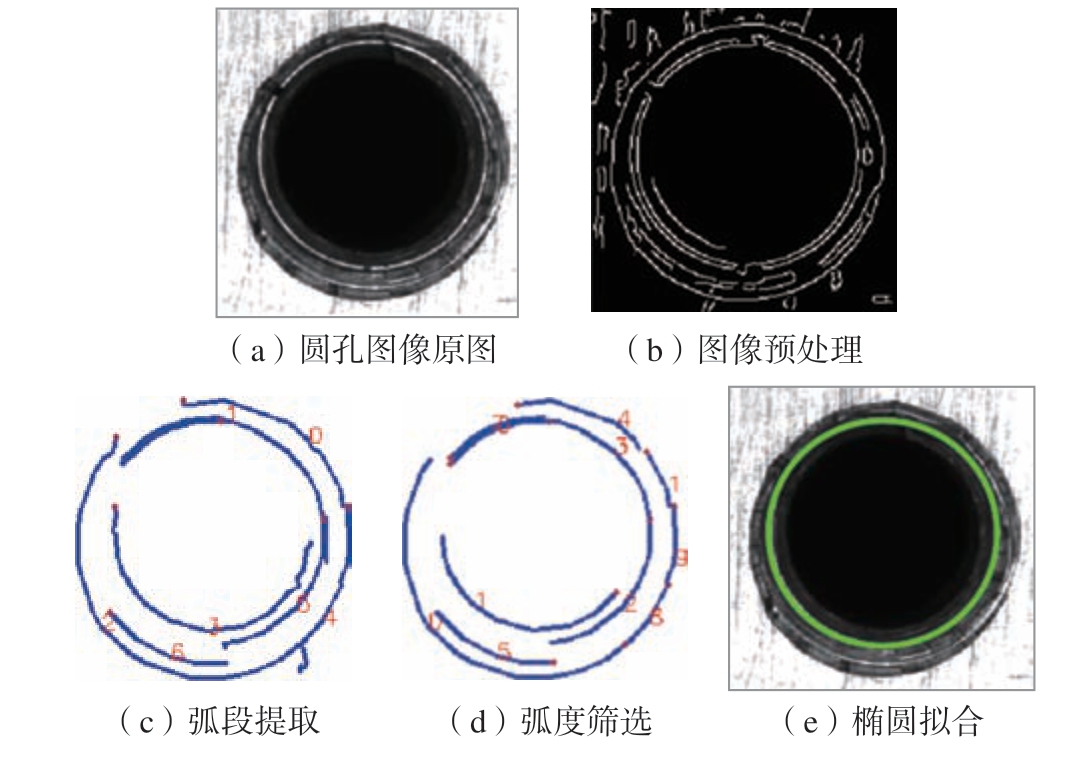
图3 AAMED 算法提取椭圆轮廓的过程
Fig.3 Process of extracting ellipse contour by AAMED algorithm
基于AAMED 的算法主要包括以下步骤。（1）通过图像边缘加粗查找边缘轮廓的首末点和弧段分割；（2）采用Douglas-Poike 算法[15]进行弧段分割和弧段索引的存储； （3）确定弧段的搜索范围并建立邻接矩阵，以便进行弧段聚类和弧段组合； （4）完成弧段组合和椭圆拟合后，采用综合评价指标Pscore 进行椭圆验证。具体流程如图4 所示。
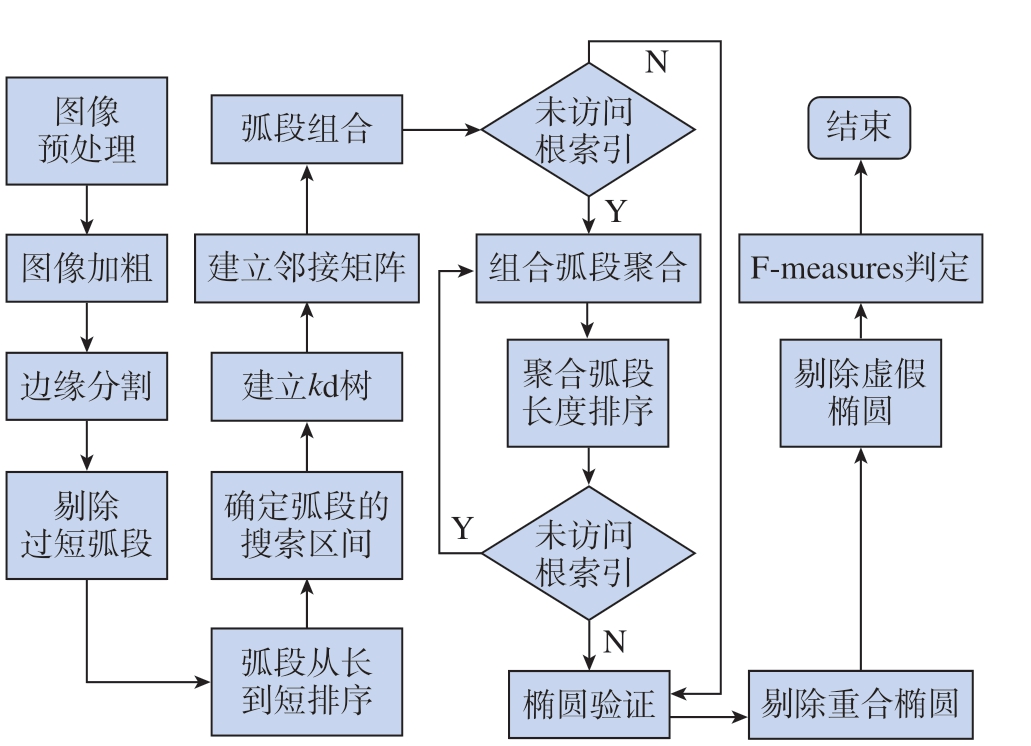
图4 AAMED 算法流程图
Fig.4 Flowchart of the AAMED algorithm
2.3 筛选机制
直接使用AAMED 算法对机加圆孔对应图像进行椭圆提取时，容易存在同一区域内有多个椭圆解释，使椭圆图像识别的准确性难以保证，即椭圆图像的二义性问题，见图5（a）。同时，AAMED 算法中对于不满足弧链提取的边缘轮廓，直接进行最小二乘法拟合容易增加虚假椭圆提取的数量，见图5（b）。因此，需要一定的筛选机制剔除这些错误提取结果。
图5 AAMED 算法的缺陷
Fig.5 Defects of the AAMED algorithm
设定经过综合评价指标Pscore 验证的椭圆图像集，表示为A={ei | i=1，2，…，Nd}，其中 ei 表示椭圆图像集中第i 个椭圆图像，Nd 为经过验证的椭圆图像的数量。对于第i 个椭圆ei，判断是否存在重叠的椭圆ej，其中j=1，2，…，Nd 且j≠i。假设，ei 的长半轴为ai，短半轴为bi，圆心为ci；ej 的长轴为aj，短半轴为bj，圆心为cj，则有
式中，dis（·）为两点之间的距离；max（·）为两值中的较大值；δ 为控制阈值，用以消除重叠椭圆的影响；δ1和δ2 也为控制阈值，用以消除其他圆形外轮廓的影响。
查找所有重叠椭圆集的集合C。对于第s 个重叠椭圆集Cs ={Ek | k =1，2，…，τ}，其中 Ek 为Cs 中的重叠椭圆，τ 为Cs 中重叠椭圆的数目。查找重叠椭圆集合Cs中的最大面积图像椭圆Emk，其中mk =1，2，…，τ。假设椭圆Emk 长半轴与短半轴的比值在给定范围内，则将Cs改为{Emk}，否则将Cs 设置为 。
同时采用F-measures[16]来评估衡量图像椭圆识别的准确程度。通过使用F-measures 对筛选后椭圆图像进行评估，即
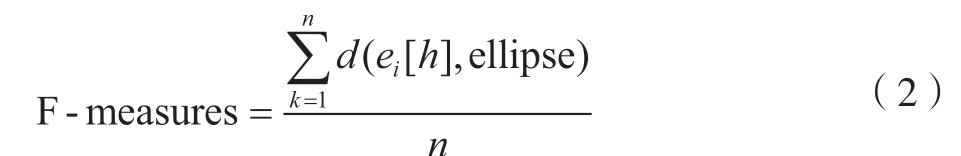
式中，ei[h]为边缘提取得到的第i 个轮廓ei 的第h 个边缘像素点；ellipse 是通过对轮廓ei 进行子弧段拟合后得到的边缘点的集合；n 为ei 轮廓上边缘像素点的数量；d（·）决定Canny 算法提取的图像轮廓ei 上的点h 是否靠近最后拟合出的轮廓ellipse。如果点k 到椭圆ellipse上点的距离小于THlen3，则d（ei[h]，ellipse）取1，反之则取0。THlen3为控制阈值，与椭圆图像的短轴b 像素长度有关。统计轮廓ei 上符合上述条件的点的数量，将满足条件的轮廓点的数量除以ei 轮廓边缘点的总数量n，即为F-measures 的值。对AAMED 算法的提取结果采用筛选机制后，其效果如图6 和7 所示。
图6 剔除重叠椭圆效果
Fig.6 Effect of removing overlapping ellipses
图7 剔除虚假椭圆效果
Fig.7 Effect of eliminating false ellipses
3 空间圆位姿粗–精估计
在空间圆位姿的初步估计过程中，本研究采用了基于对极几何约束的两视图椭圆匹配方法结合两视锥求交法。首先，通过分析两幅图像中椭圆的对应关系，利用对极几何约束筛选和匹配这些椭圆，确定可能的空间圆位置；接着，基于匹配的椭圆信息构建两个椭圆锥，并通过求解两椭圆锥的交集来获得空间圆的中心点和法矢量方向，从而实现对空间圆位姿的粗略估计。这种方法操作简便，且无需预先测量机加圆孔的实际半径信息，为进一步的优化奠定了基础；随后，通过基于多视图几何的增量式三维重建方法，对粗估计结果进行精确优化。多视图重建技术利用多个视角的图像数据，进一步优化空间圆的位姿参数，提高了空间圆位置与法矢量方向的估计精度，从而满足高精度测量的要求。图8 展示了空间圆重建的流程图。
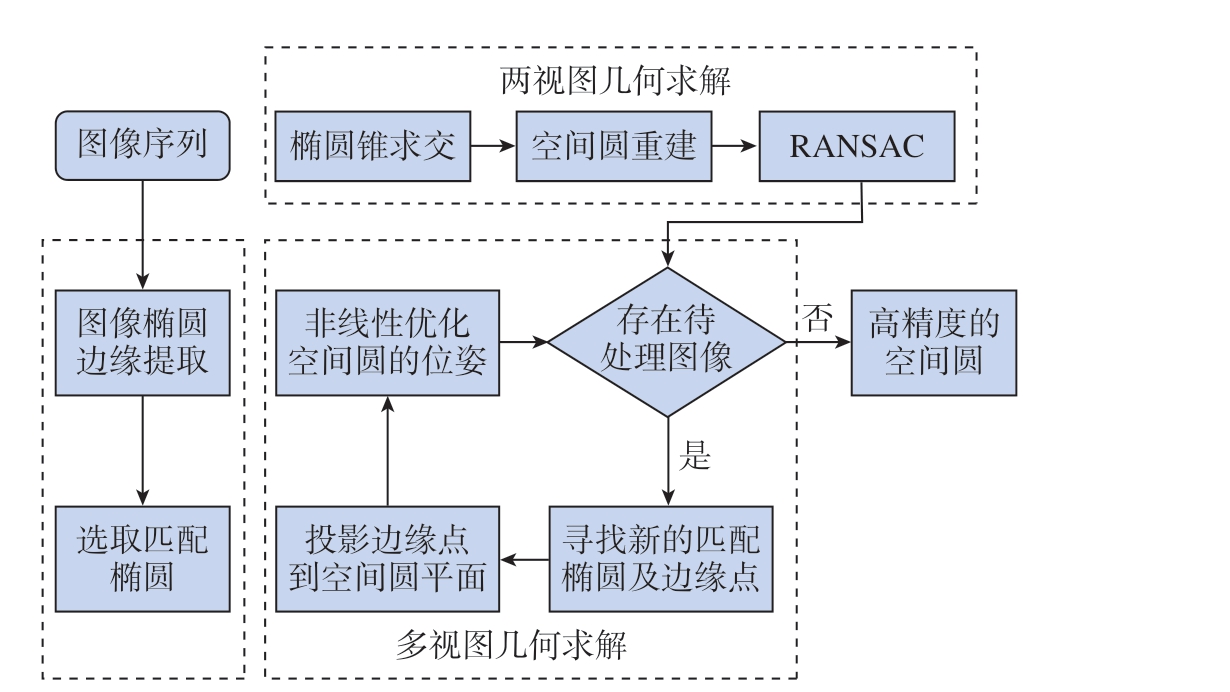
图8 空间圆重建流程图
Fig.8 Flowchart of spatial circle reconstruction
3.1 椭圆对的匹配
在进行双锥椭圆求交前，需要先在两视图中获得同名椭圆对。
本文采用对极几何约束的原理来进行同名椭圆对匹配[17]，假设视图I1 中椭圆图像ei 的中心点坐标表示为Pi = [xi，yi]T，对应视图I2 上的对极线li2 为
式中，F 为两视图间的基础矩阵。根据对极几何原理，视图I2 上同名椭圆的中心将落在对极线上，如果视图I2存在图像椭圆的中心与对极线距离小于阈值δ，则添加进入对应候选椭圆的集合Vi，其中i 为对应候选椭圆的数量。
随后，如图9 所示，在椭圆图像ei 边缘任取N 个边缘点Piq，其中q = 1，2，…，N，查找在集合Vi 中与对极线交点最多的图像椭圆，将其定义为匹配椭圆en。
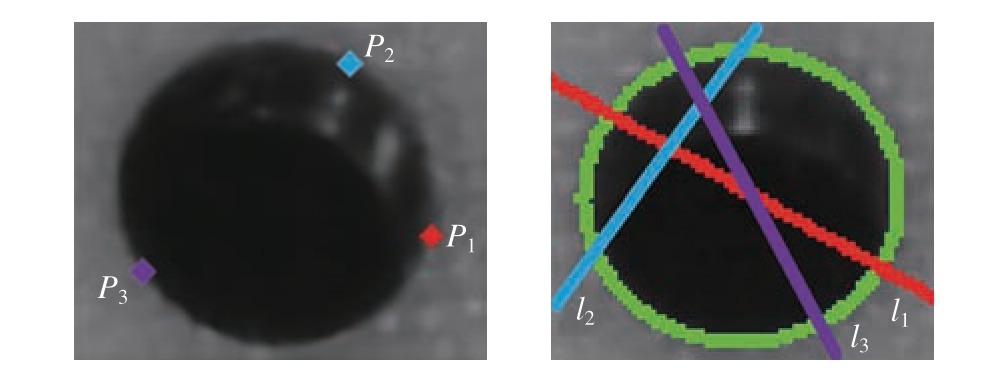
图9 匹配椭圆对的选取
Fig.9 Selection of matching ellipse pairs
3.2 基于双锥椭圆求交法的粗估计
基于椭圆图像的一般式及视图I1 和I2 下相机的投影矩阵P 和P'，Quan[11]详细阐述了椭圆锥求交的基本原理。根据该研究，两椭圆锥体在理论上通过其求交的平面会产生双解[9]，如图10 所示，即可以推导出两个不同的平面为piTx = 0，i =1，2，表示为[9]
图10 两视图下相机光心O1 和O2 之间的平面对pi
Fig.10 Plane pairs pi between camera optical centers O1 and O2 under both views
式中，μ1 > 0，μ2 < 0，v1 和v2 均为4×1 的向量，且μ1、μ2、v1 和v2 均与两视图下对应图像椭圆的一般式以及相机的投影矩阵P 和P'相关。
3.3 基于多视图的空间圆位姿优化
在增量式运动恢复结构 （Structure from motion，SFM）方法中，可以采用OpenMVG 框架获得准确的三维重建框架[18]。该框架可以提供多视图几何输出、内参优化结果、两两匹配及对极几何。环形编码点被用作特征点，通过跟踪环形编码点在视图中位置以及多视图下环形编码点的位置优化技术，估计相机的内参矩阵K 和外参矩阵T = [R | t]。而标尺提供了一个已知尺度的参考，从而计算出尺度因子以恢复场景的绝对尺度。
拟合椭圆Ei 平面pi 为Ai x + Bi y + Ci z + Di = 0，Ai、Bi、Ci、Di 的值为
假设有m 张图像 （m≥2），除去I1、I2 剩余 （m – 2）张图像。对于这 （m – 2）张图像，选择将与空间圆拟合圆对应的边缘点全部加进来，那么整体代价函数e3 变为
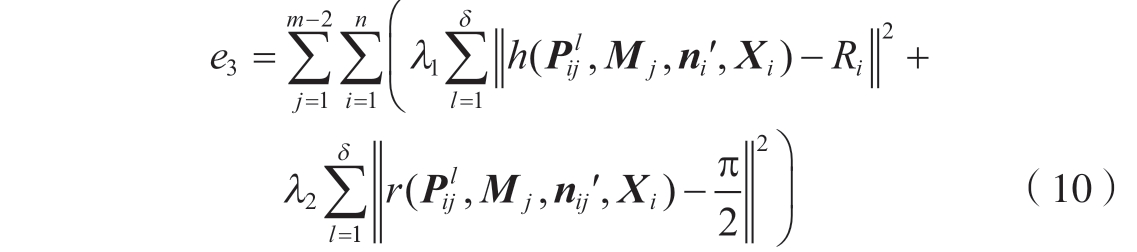
式中，n'为视图I1 和I2 通过三角化重建所得到的空间圆的数量；λ1 和λ2 为拉格朗日乘子，正则化参数λ1≤λ2时，误差方程λ2e2 起主要作用，正则化参数λ1 较大时λ1e1 起主要作用，在这两种情况下，Levenberg-Marquardt（LM）算法均接近于高斯牛顿法。
通常，基于LM 空间圆位姿优化可以转换为对两个参数块的优化。第一个参数块用于存储拟合圆Ei 的半径信息Ri，法矢量ni 的x 坐标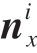
和y 坐标ni y，另一法矢量n'ij 的x 坐标
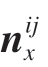和y 坐标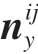
。
4 试验结果及分析
本文试验主要将圆形目标的识别、提取和重建技术应用于评估机加圆孔的加工精度，如零件中的圆孔、飞机蒙皮上的铆钉孔。这种方法不仅可以用于加工精度评价，还可以在机器人定位、装配关系建立等领域发挥作用。通过对圆形目标的重建和分析，可以更准确地评估机加圆孔的几何特征和精度，为生产过程的优化提供重要的数据支持。
4.1 试验设置
试验中，采用Nikon D7200 相机 （焦距为24 mm，其影像传感器的尺寸为23.5 mm×15.6 mm，图像尺寸为6000 px×4000 px）拍摄多个带有圆孔的样件并构建包含500 张图像的数据集，其中每张均有机加圆孔对应的椭圆图像。图11 展示了这些图像中的3 组，定义为工件1、工件2 与工件3，详见图6（a）～（c）。样件上各类圆孔均来源于实际加工现场，通过高精度机床加工以确保本文方法精度验证试验的有效性，且样件上可以集中体现出不同孔径 （2～8 mm）和空间分布。
图11 3 个包含机加圆孔的工件
Fig.11 Three workpieces containing machined round holes
4.2 有效椭圆轮廓提取及筛选试验
采用本文方法对工业现场机加圆孔进行提取，效果如图12 所示。图12（a）为金属标定板通孔的椭圆提取效果，用于后续工业机器人的高精度手眼标定，图12（b）为航空制造装配现场螺纹孔提取效果。由于螺纹孔受倒角和螺牙等干扰因素的影响，一般提取方法很难准确识别真实的螺纹孔边缘，而本文方法可以有效提取真实的螺纹孔边缘。
图12 标定板通孔和装配现场螺纹孔的提取
Fig.12 Extraction of calibration plate through-hole and assembly site threaded hole
采用筛选机制前后识别的机加圆孔对应图像椭圆边缘的结果见图13。图13（a）中仅采用AAMED 算法，对机加圆孔对应图像椭圆边缘的准确识别率仅为76.2%，而图13（b）采用筛选机制，对机加圆孔对应图像椭圆边缘的准确识别率则为96.8%，证明了本文提出的筛选机制的有效性。
图13 AAMED 算法直接提取结果和筛选错误椭圆结果
Fig.13 Direct extraction results of AAMED algorithm and results of screening error ellipse
4.3 多视图重建优化试验
完成图像椭圆的边缘提取后，利用两视图两椭圆锥求交算法获得空间圆位姿的初始估计。然后利用多视图重建的方法，对机加圆孔对应空间圆的位姿进行精优化。工件1 对应机加圆孔的试验，共计7×9 个机加圆孔。选取机加圆孔对应空间圆Xuv，其中u 表示空间圆的排数，v 表示空间圆的列数，测试两视锥重建粗估计和多视图重建优化后的半径误差，如图14 所示。试验结果显示，在工件1 的9 个机加圆孔中，经过多视图重建优化的空间圆半径精度均优于双锥重建粗估计的结果。
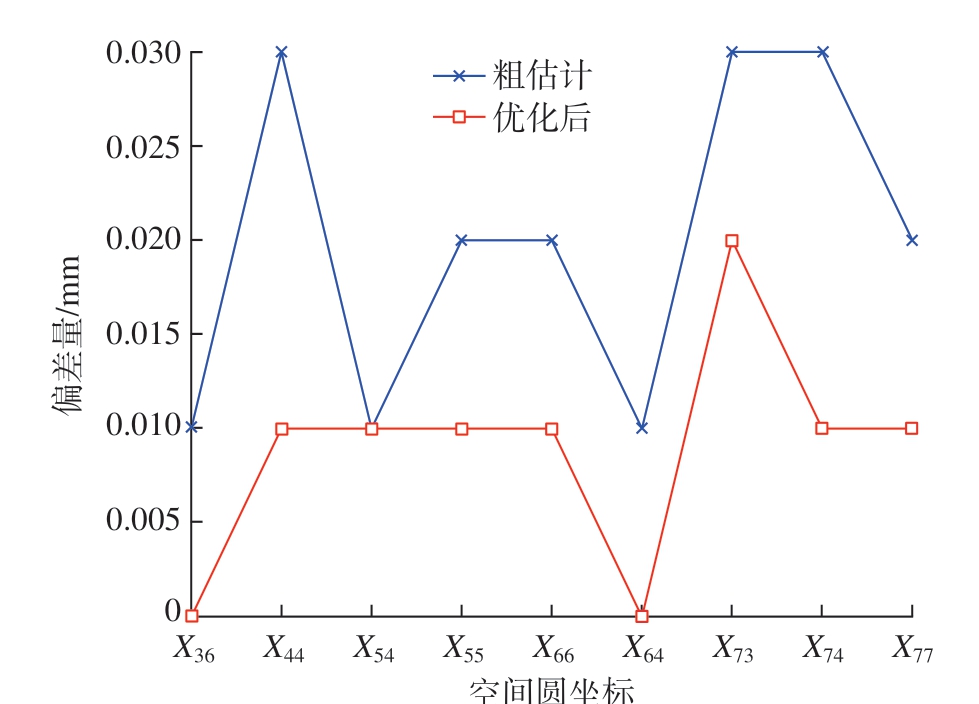
图14 优化前后试验结果对比
Fig.14 Comparison of experimental results before and after optimization
4.4 空间圆重建结果的综合试验验证
运用本文提出的多视图下空间圆位姿优化的算法，对3 个工件空间圆的位姿进行精确估计。图15 展示了工件1 对应的空间圆位姿精确估计后边缘离散点的信息。图16 为工件1 对应数模，用来对空间圆边缘离散点进行误差分析。通过在Geomagic Qualify 软件[20]中将数模与重建空间圆对齐，然后任意选取重建空间圆边缘上3 个点 （3 个点可以确定一个空间圆）与数模进行对比来评估重建的位置精度。
图15 工件1 对应的空间圆离散点三维显示
Fig.15 3D display of discrete points of spatial circle corresponding to workpiece 1
图16 工件1 对应数模三维模型
Fig.16 3D model of corresponding numerical mold for workpiece 1
图17 为空间圆离散点与工件1 部分圆孔重建的误差分析，结果显示最大偏差不超过0.200/- 0.199 mm，平均偏差为0.112/– 0.100 mm，标准差为0.119 mm。工件1 对应空间圆边缘点的误差分析的统计结果如图18 所示，工件1 重建的空间圆离散点与对应数模的误差分布总体呈正态分布。在工件1 重建的空间圆离散点中，有72 个点与该数模的误差在[- 0.040，0.040]范围内，占所有点数的16.744%，且占比最大。
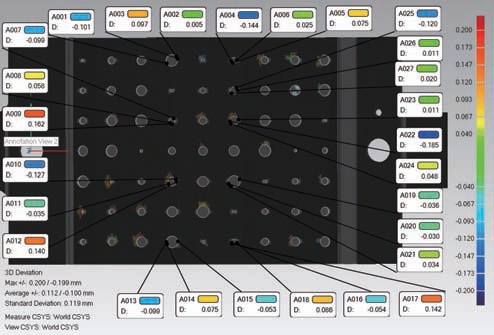
图17 工件1 部分圆孔的误差分析
Fig.17 Error analysis of partial holes in workpiece 1
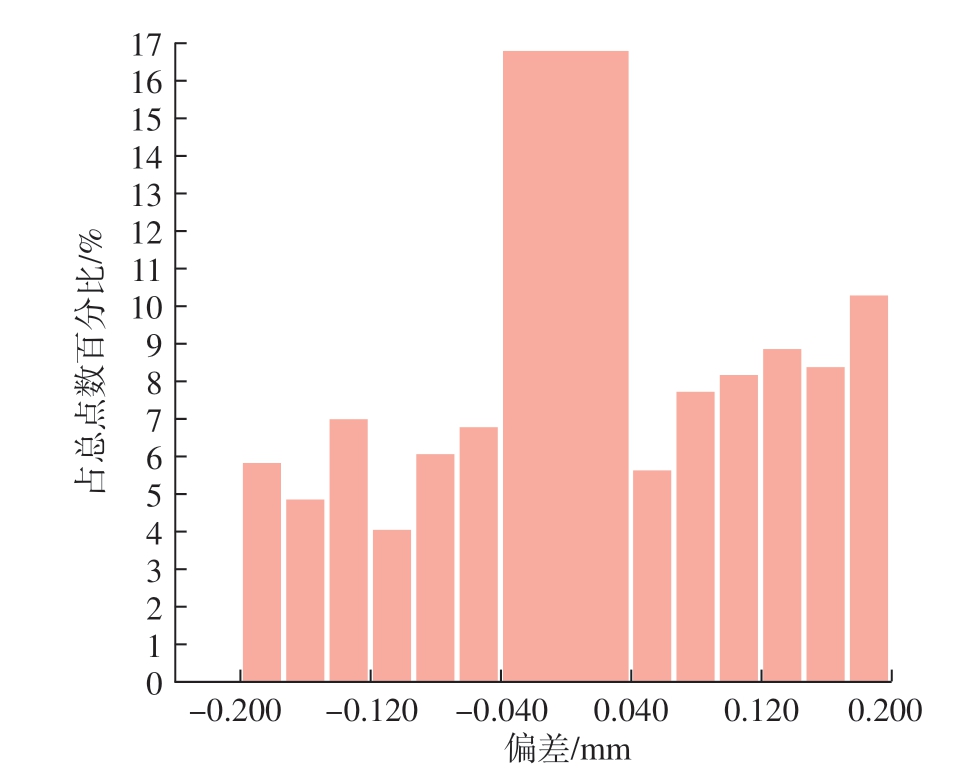
图18 工件1 空间圆的三维误差分布
Fig.18 3D error distribution of spatial circle of workpiece 1
工件2 对应重建空间圆的离散点三维显示 （图19）和对应数模的三维模型 （图20）具有一致性。图21 为空间圆离散点与工件2 部分圆孔的误差分析，最大偏差不超过0.198/- 0.200 mm，平均偏差为0.089/- 0.098 mm，标准差为0.108 mm。图22 中统计结果显示，工件2 重建的空间圆离散点中，72 个点与该数模的误差在[– 0.036，0.036]范围内，占所有点数的21.597%且占比最大。
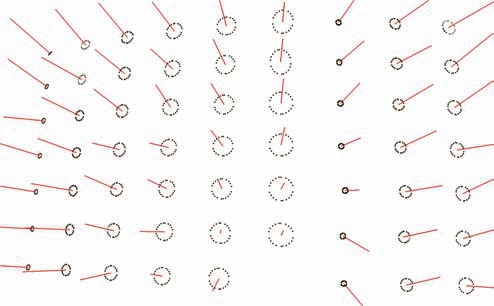
图19 工件2 对应空间圆的离散点三维显示
Fig.19 3D display of discrete points of space circle corresponding to workpiece 2
图20 工件2 对应数模三维模型
Fig.20 3D model of corresponding numerical mold for workpiece 2
图21 工件2 部分圆孔的误差分析
Fig.21 Error analysis of partial holes in workpiece 2
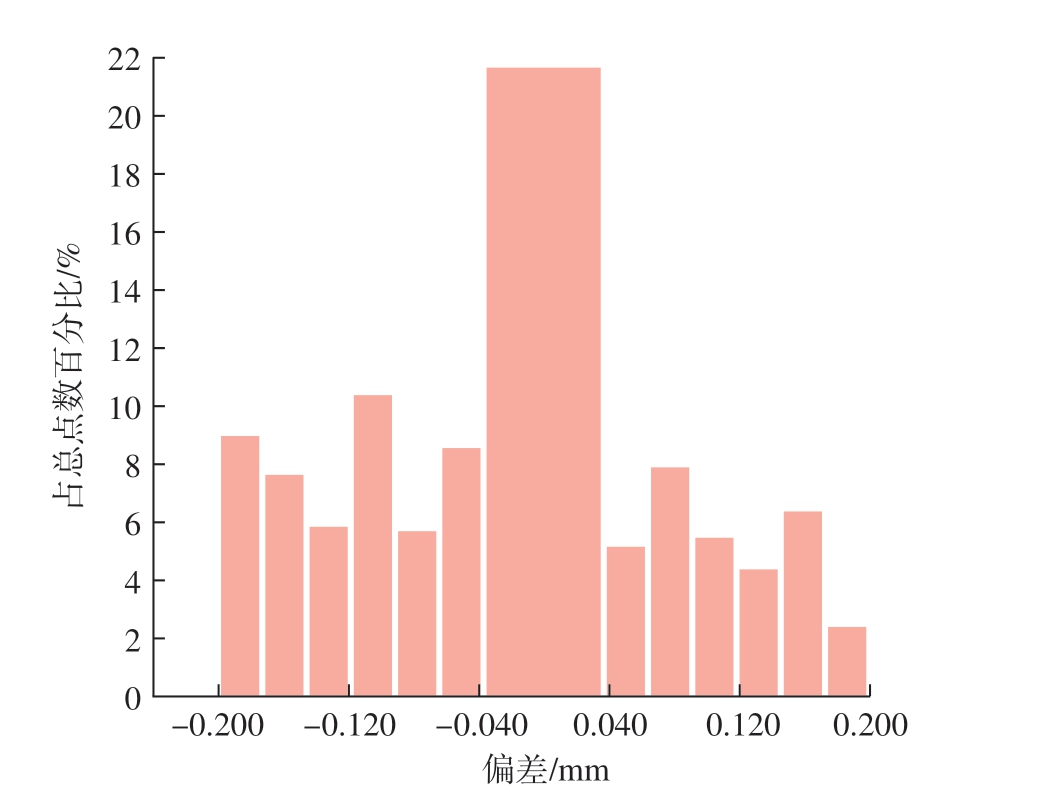
图22 工件2 空间圆的三维误差分布
Fig.22 3D error distribution of spatial circle of workpiece 2
工件3 对应空间圆的离散点三维显示 （图23）和对应数模的三维模型 （图24），两者也具有一致性。图25为空间圆离散点与工件3 部分圆孔的误差分析，最大偏差不超过0.200/- 0.194 mm，平均偏差为0.098/- 0.095 mm，标准差为0.110 mm。图26 显示，空间圆的离散点有54 个点与该数模误差在[– 0.036，0.036]范围内，占所有点数的18.947%，且占比最大。
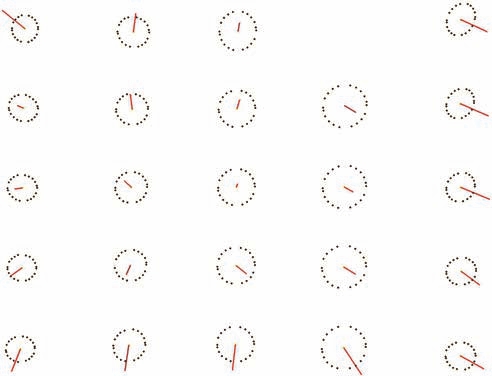
图23 工件3 对应空间圆的离散点三维显示
Fig.23 3D display of discrete points of space circle corresponding to workpiece 3
图24 工件3 对应数模三维模型
Fig.24 3D model of corresponding numerical mold for workpiece 3
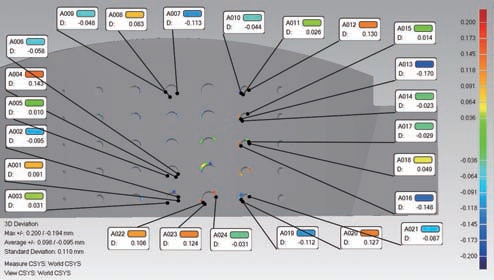
图25 工件3 部分圆孔的误差分析
Fig.25 Error analysis of partial holes in workpiece 3
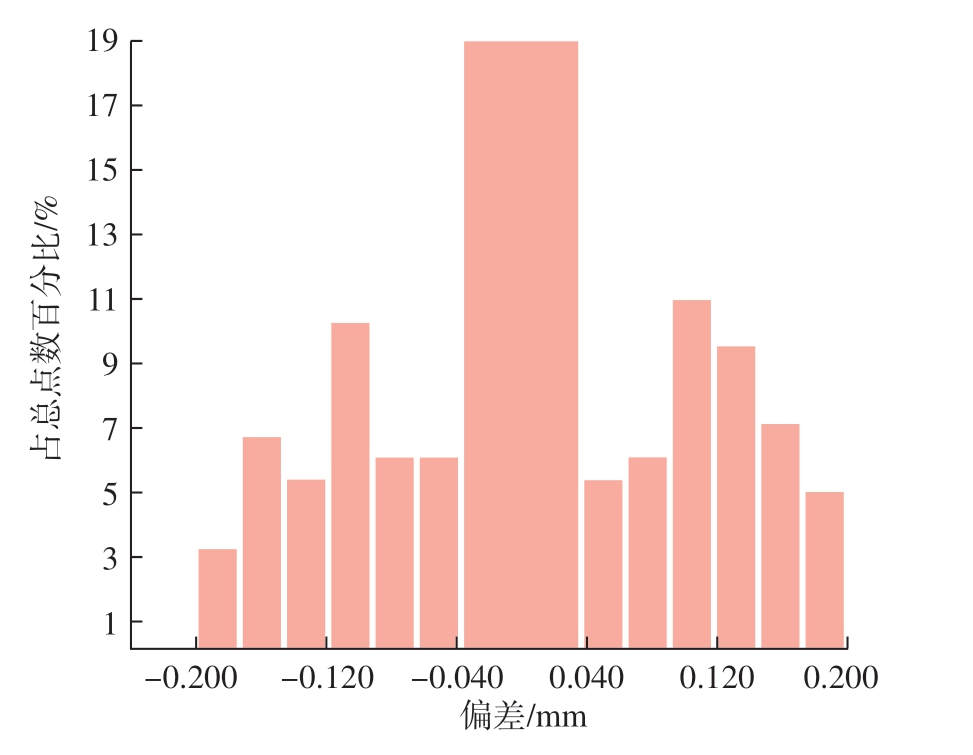
图26 工件3 空间圆的三维误差分布
Fig.26 3D error distribution of spatial circle of workpiece 3
5 结论
本文提出了一套完整的机加圆孔空间定位及三维重建技术路线，主要贡献在于： （1）提出一种改进的椭圆提取与筛选机制，显著提升了椭圆图像的识别精度； （2）利用两视锥求交法对空间圆的位姿进行初步估计，并通过多视图几何优化进一步提高定位精度； （3）试验证明，该方法能够在复杂工业环境下实现高精度的机加圆孔三维重建，对多个含有机加圆孔的工件试验测量时，重建空间圆与数模的最大上下偏差均不超过0.200/– 0.200 mm，其中3 个样件的平均偏差分别为0.112/– 0.100 mm、0.089/- 0.098 mm、0.098/- 0.095 mm，为航空制造等高精度要求的测量任务提供了有效的技术支持。
[1]CAPPETTI N, NADDEO A, VILLECCO F.Fuzzy approach to measures correction on coordinate measuring machines: The case of holediameter verification[J].Measurement, 2016, 93: 41-47.
[2]TABIB R A, JADHAV Y V, TEGGINKERI S, et al.Learningbased hole detection in 3D point cloud towards hole filling[J].Procedia Computer Science, 2020, 171: 475-482.
[3]勾江洋, 陈雪梅, 叶南, 等.飞机零部件连接孔在机视觉检测系统开发[J].航空制造技术, 2018, 61(5): 37-43, 50.GOU Jiangyang, CHEN Xuemei, YE Nan, et al.Development of on-machine vision inspection system for connection holes on aircraft parts[J].Aeronautical Manufacturing Technology, 2018, 61(5): 37-43, 50.
[4]PRASAD D K, LEUNG M K H, CHO S Y.Edge curvature and convexity based ellipse detection method[J].Pattern Recognition, 2012,45(9): 3204-3221.
[5]MENG C, LI Z X, BAI X Z, et al.Arc adjacency matrix-based fast ellipse detection[J].IEEE Transactions on Image Processing, 2020,29: 4406 - 4420.
[6]SAFAEE-RAD R, TCHOUKANOV I, SMITH K C, et al.Three-dimensional location estimation of circular features for machine vision[J].IEEE Transactions on Robotics and Automation, 1992, 8(5):624-640.
[7]CHEN Z, HUANG J B.A vision-based method for the circle pose determination with a direct geometric interpretation[J].IEEE Transactions on Robotics and Automation, 1999, 15(6): 1135-1140.
[8]ZHENG Y Q, MA W J, LIU Y C.Another way of looking at monocular circle pose estimation[C]//2008 15th IEEE International Conference on Image Processing.Piscataway, NJ: IEEE, 2008: 861-864.
[9]魏振忠, 赵征, 张广军.空间圆姿态识别二义性的角度约束消除[J].光学 精密工程, 2010, 18(3): 685-691.WEI Zhenzhong, ZHAO Zheng, ZHANG Guangjun.Solution of duality in pose estimation of single circle using Euclidean angular constraint[J].Optics and Precision Engineering, 2010, 18(3): 685-691.
[10]MIAO X K, ZHU F, DING Q H, et al.Monocular vision pose measurement based on docking ring component[J].Acta Optica Sinica,2013, 33(4): 0412006.
[11]QUAN L.Conic reconstruction and correspondence from two views[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1996, 18(2): 151-160.
[12]MOULON P, MONASSE P, MARLET R.Adaptive structure from motion with a contrario model estimation[M]//Computer Vision –ACCV 2012.Berlin, Heidelberg: Springer Berlin Heidelberg, 2013: 257-270.
[13]MOULON P, MONASSE P, MARLET R.Global fusion of relative motions for robust, accurate and scalable structure from motion[C]//2013 IEEE International Conference on Computer Vision.Piscataway, NJ: IEEE, 2013:3248-3255.
[14]HUTTON B F, KYME A, LAU Y H, et al.A hybrid 3D reconstruction/registration algorithm for correction of head motion in emission tomography[C]//2000 IEEE Nuclear Science Symposium.Piscataway, NJ: IEEE, 2000: 15/36-15/40.
[15]RADOUX J, DEFOURNY P.Accuracy assessment of forest stand delineation using very high spatial resolution satellite images[J].ForestSat 2005, 2005: 84.
[16]MAALEK R, LICHTI D D.Robust detection of non-overlapping ellipses from points with applications to circular target extraction in images and cylinder detection in point clouds[J].ISPRS Journal of Photogrammetry and Remote Sensing, 2021, 176: 83-108.
[17]LONGUET-HIGGINS H C.A computer algorithm for reconstructing a scene from two projections[J].Nature, 1981, 293: 133-135.
[18]MOULON P, MONASSE P, PERROT R, et al.OpenMVG: open multiple view geometry[M]//Reproducible Research in Pattern Recognition.Cham: Springer International Publishing, 2017: 60-74.
[19]史传飞, 张丽艳, 严俊, 等.面向大型装备的工业摄影测量技术及实现[J].航空制造技术, 2018, 61(19): 24-30.SHI Chuanfei, ZHANG Liyan, YAN Jun, et al.Industrial photogrammetry technology and its implementation for large-scale equipment[J].Aeronautical Manufacturing Technology, 2018, 61(19): 24-30.
[20]GAO D Q, MA J F, LIN H, et al.Precision analysis of the surface model based on geomagic qualify[J].Applied Mechanics and Materials,2014, 490-491: 649-653.