铣削作为一种高效的机械加工方法，具有加工精度高、材料去除率大和加工成本低等优点。在铣削过程中，主要存在的振动形式有自由振动、受迫振动和自激振动，其中自激振动中的再生颤振是引起加工过程不稳定的主要因素[1–2]。铣削颤振通常会导致加工零件表面质量差、刀具磨损加剧以及数控机床寿命降低等问题[3]。此外，考虑再生颤振的铣削动力学模型可以近似描述为时滞微分方程，通过求解时滞微分方程可以获得稳定性叶瓣图，达到铣削稳定性预测的目的[4]。因此，如何快速精确地获取变齿距铣削稳定性叶瓣图显得尤其重要。
Altintas 等[5]提出了一种零阶半解析法来预测铣削过程中的稳定性，但该方法无法预测小径向切深下的稳定切削区域。Merdol 等[6]提出了一种考虑高次谐波影响的多频率稳定性预测方法，该方法能满足小径向切深时的预测精度，但是计算效率相对较低。Insperger 等[7]首先提出了具有高精度的时域数值稳定性预测方法，该方法仅对时滞项进行离散处理。基于直接积分思想，Ding 等[8]提出了一种全离散法稳定性预测方法，全离散法利用线性插值同时逼近时滞微分方程中的状态项和时滞项，极大地提高了该方法的计算效率。张伟等[9]将变齿距铣刀铣削作为颤振的抑制策略，通过试验验证变齿距铣刀具有较好的铣削颤振控制能力。Wan 等[10]提出了由于变齿距引发的多时滞铣削稳定性预测模型，并基于半离散法求解变齿距铣削的稳定性边界。Zhang等[11]提出了一种改进的全离散来求解由变齿距引起的多时滞问题的铣削稳定性叶瓣图，并指出铣削过程中刀具跳动会影响铣削稳定性边界。Jin 等[12]提出了一种考虑螺旋角的变齿距铣削改进半离散法，并研究了不同变齿距铣刀对铣削颤振稳定性的影响。刘宽等[13]利用AdvantEdge 有限元仿真和Matlab 软件进行了铣削力建模和分析，验证了变齿距铣刀具有降低振幅和减小切削力的效果。Jin 等[14]建立了变齿距和变主轴转速的时滞微分运动方程并运用改进半离散法求解，获得了铣削稳定性叶瓣图。
针对目前变齿距铣削稳定性预测算法计算效率低且通用性差的问题，在不降低预测精度的情况下，本文提出了一种基于精细积分的变齿距铣削稳定性预测的全离散法，以快速精确地获得变齿距铣削系统的稳定性叶瓣图。
1 数学模型
如图1所示，铣削过程可以简化为两自由度振动“质量–弹簧–阻尼”模型。假定刀具相对于工件是弹性体。根据牛顿运动定律，铣削运动方程可表示为
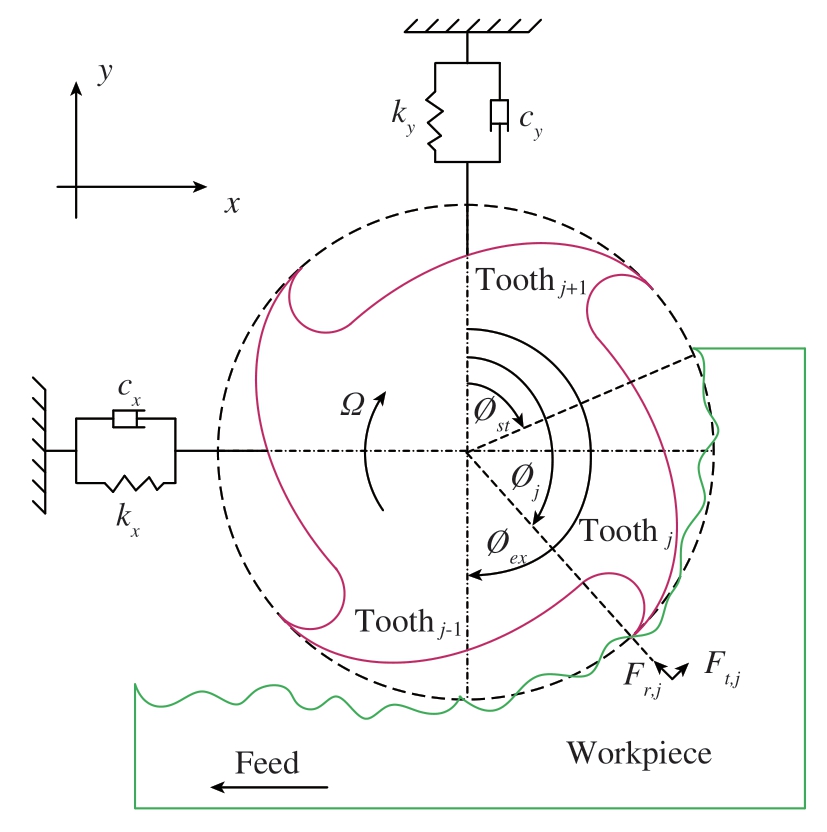
图1 两自由度铣削系统示意图
Fig.1 Schematic diagram of two-degree-of-freedom milling system
式中，M、C 和K 分别为模态质量、阻尼和刚度矩阵；q(t)=[ x(t) y(t)]T 是位移向量；F (t)=[ Fx (t) Fy (t)]T是切削力向量。
由于刀具考虑螺旋角效应，实际参与切削的刀齿的高度时刻发生变化。如图2所示，第j 齿在微单元高度dz 上沿切向和法向所受到的微元切削力表示为
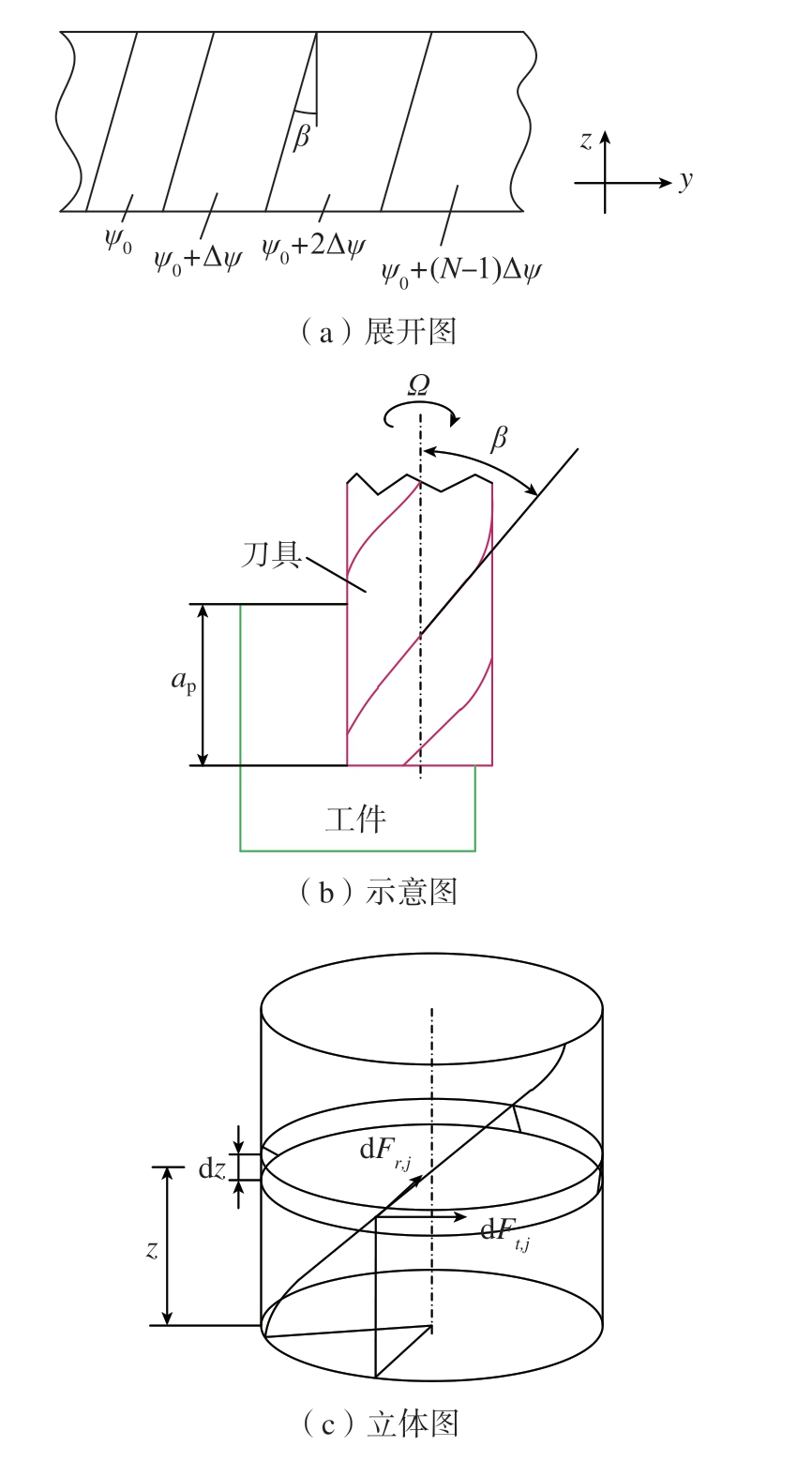
图2 变齿距螺旋刀具几何图
Fig.2 Geometry of variable pitch spiral cutter
式中，Kt 和Kr 是切向和法向切削力系数；hj（t,z）是动态切削厚度，可定义为
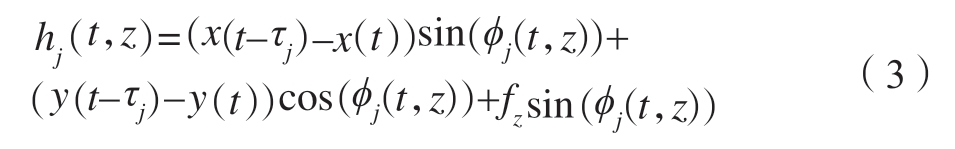
式中，τj 是时滞；fz 是进给量；ϕj（t,z）是第 j 齿随时间变化的角度位置，定义为
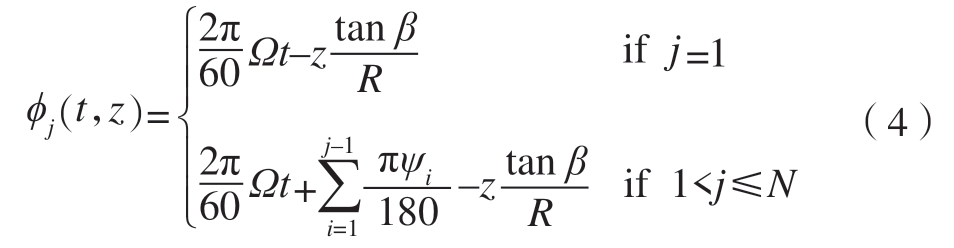
式中，Ω、β 和R 分别是主轴转速、刀具螺旋角和半径；ψi 是第j 齿和j–1 齿之间的齿距角。
在t 时刻，第j 齿在x 和y 方向的切削力为
则刀具作用在x 和y 方向上总切削力为
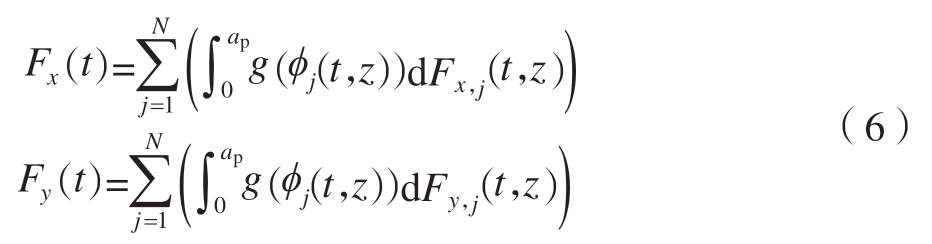
式中，窗函数g（ϕj（t,z））为
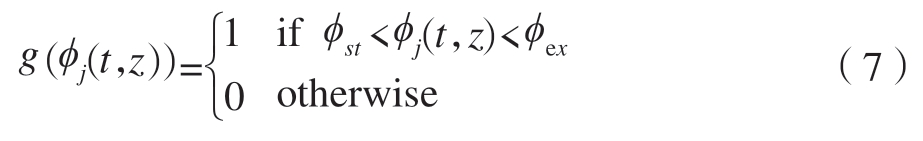
式中，ϕst 和ϕcx 是切入和切出角。
联立式（2）、（3）、（5）和（6），则可以得到式（1）切削力向量表达式
将式（8）带入式（1），可得到考虑螺旋角的变齿距铣削动力学方程为
式中，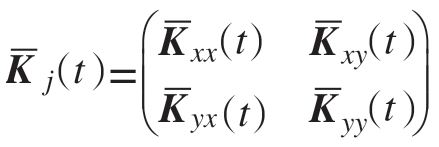
为切削力系数矩阵。
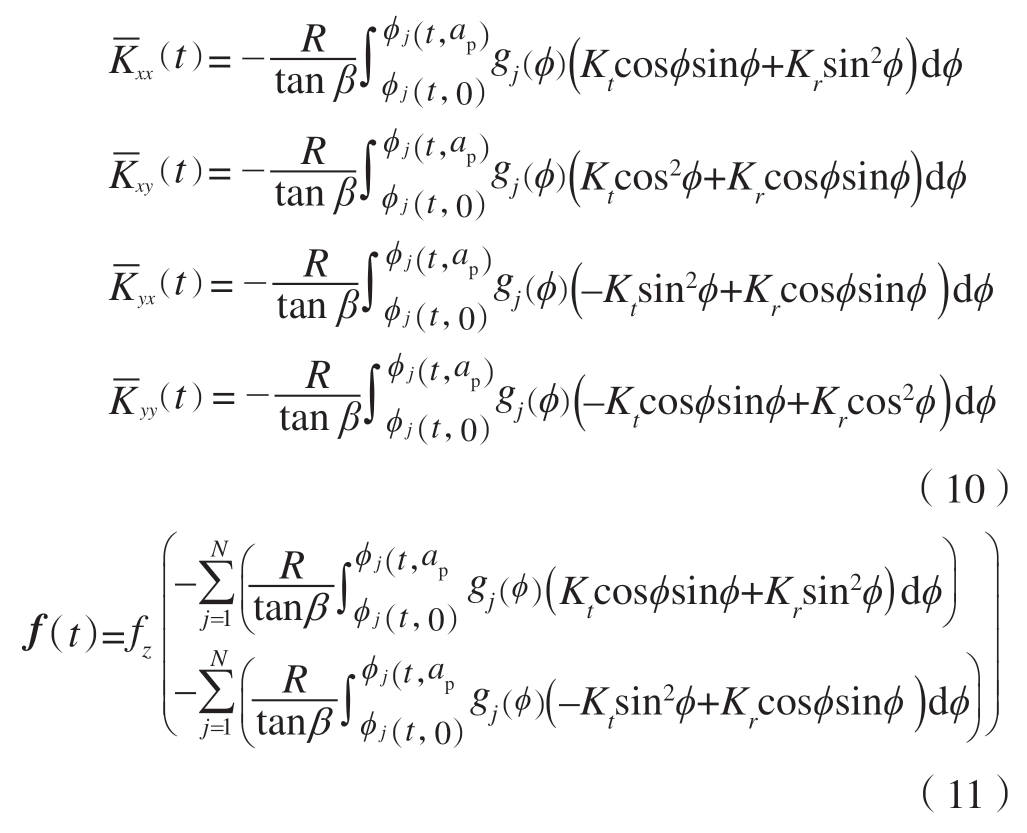
2 精细积分全离散法
令x(t)=[q (t),M q (t)+
(t)/2]，略去对铣削稳定性无影响的静态切削力部分，通过矩阵变换，则式（9）可改写为状态空间表达形式，即
式中
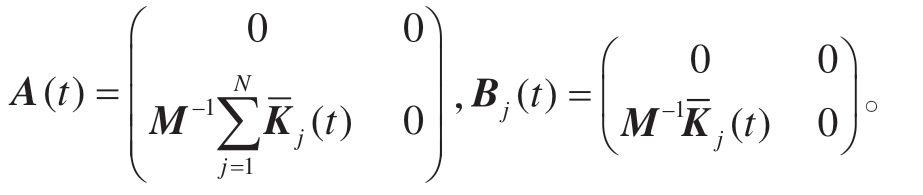
将主轴旋转周期T 分为m 等份，时间步长记为Δt=T/m，则第 j–1 齿与j 齿之间的时滞τj 所对应的离散间隔数mj 可近似表示为[12,14]
式中，int(*) 是将正数四舍五入到0 的函数，比如int（3.76）=3。为了简化运算，令v（t）=A（t）x（t）和θj（t–τj）=Bj（t）x（t–τj）。在时间间隔[kτ,（k+1）τ]（k=0，1，…，m），对式（12）进行常微分方程求解，初始条件为xk=x（tk），得到 xk+1 表达式为
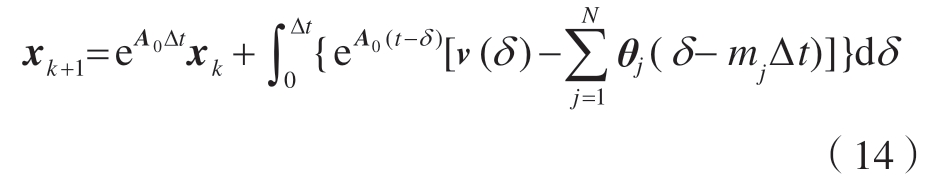
式中，δ=ξ–kΔt，δ ∈[0，Δt]。
其次，求解式（14）的积分项。在间隔[kτ,（k+1）Δt]中，式（14）状态项v（δ）和时滞项θj（δ–τj（t））都利用线性插值多项式来近似表示，即
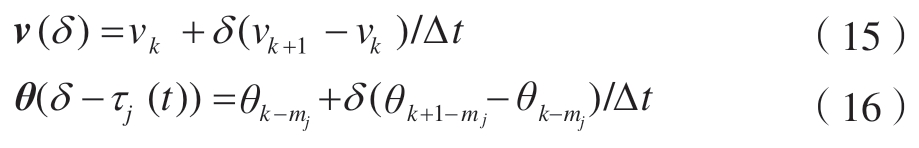
将式（15）和（16）代入式（14），得到
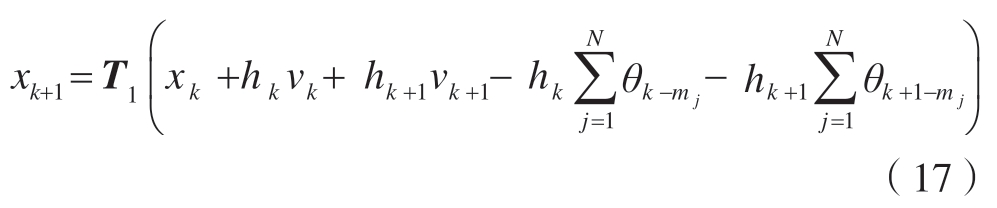
式中，
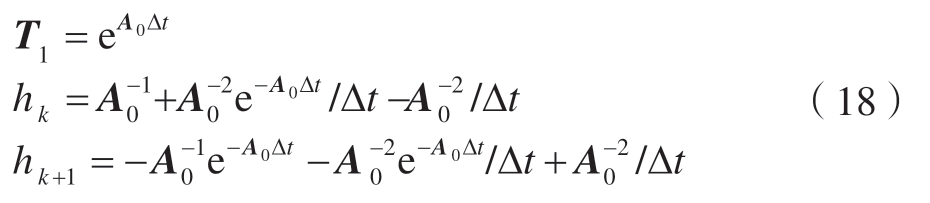
基于矩阵指数的加法定理，矩阵指数T1 可写为
式中，dt=Δt/2n。为了提高计算精度，一般取n=20，精细区段dt 就已经为非常小的区段了[15]。当dt 非常小时，可采用Taylor 级数展开近似矩阵指数，即
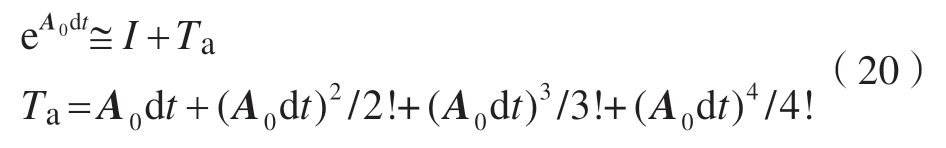
将式（20）代入式（19），矩阵指数T1 近似解为
执行以下运算
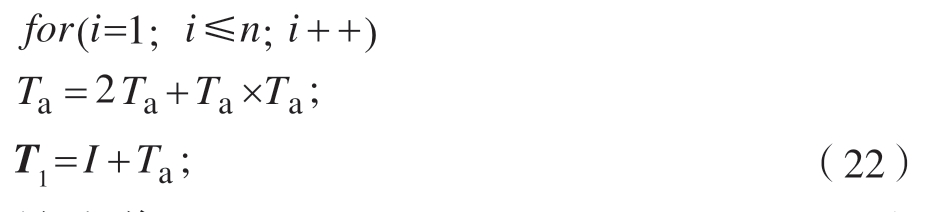
最后，将vk=Akxk，vk+1=Ak+1xk+1，θk–mj=Bj，k+1xk+1–mj 和θk+1–mj=Bj，k+1xk+1–mj 代入式（17），得
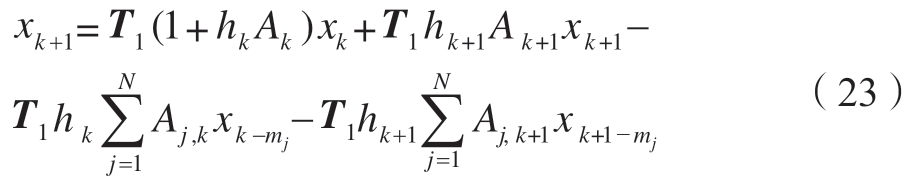
式（23）可获得原方程的离散映射形式为
其中，
这里Zk+1=（I–T1hk+1Ak+1）–1。近似求得系统的状态传递矩阵为 Φ=Dm -1，D m-2，…，D0。
依据Floquet 理论，假如传递矩阵Φ 特征值的模小于1，系统稳定；否则，系统不稳定。
3 数值仿真结果分析
对于考虑螺旋角的变齿距铣刀铣削，采用文献[12]提出的改进半离散法对文中提出的方法开展理论验证研究。本文中数值模拟所有采用的仿真参数见表1[12]。所有运算均基于Matlab9.2 平台并在同一台电脑上（Inter(R) Core(TM) i5-7400 CPU，8GB）完成。
在不同的径向切深率（a/D）下，文中方法和改进半离散法在表1所示切削条件下所获得的稳定性预测结果对比如图3所示[12]。可知，本文方法与文献[12]中所提的改进半离散法所预测结果基本吻合。由于改进半离散法的计算结果得到了很好的试验验证，也间接地验证了本文方法预测考虑螺旋角变齿距稳定性预测的准确性。本文方法在4 种不同的径向切深的计算时间约为35s，而改进半离散法约为320s，本文方法计算效率提高约90%。由此可知，本文方法具有更高的计算效率。
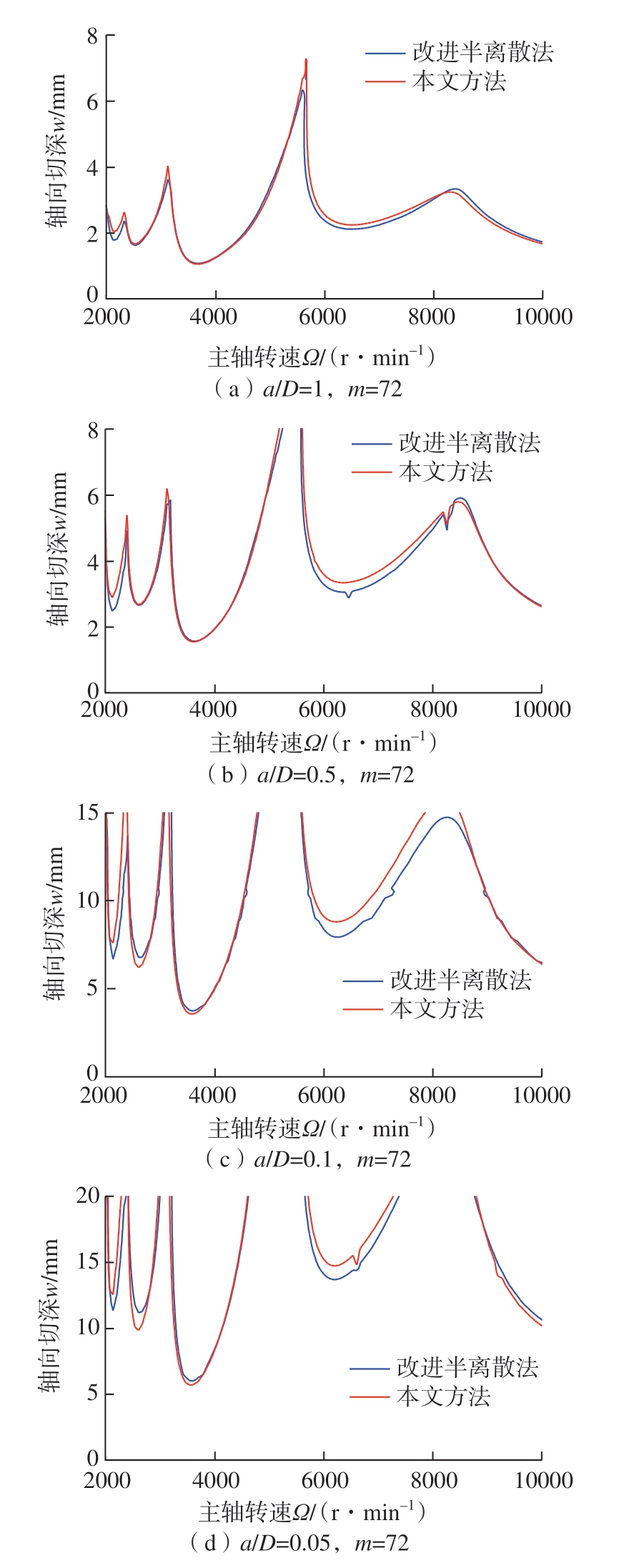
图3 本文方法与改进半离散法的叶瓣图[12]
Fig.3 Stability lobe diagrams of proposed method and updated semi-discretization method[12]
本文方法效率提升的原因：（1）当铣削稳定性预测时，式（19）中的矩阵T1 只与主轴转速有关，而与轴向切深无关，因此，在通过扫描轴向切深时，确定式（25）中转移传递矩阵Dk 的过程中，无须在不同的切削深度计算矩阵指数。然而，对于改进半离散法，在扫秒轴向切深时，矩阵指数的计算是必需的，并且是计算4 个类似矩阵指数。如果将主轴转速和切削深度组成的参数平面分为Ns×Nd 网格点，通过改进半离散法获得稳定性叶瓣图所需要的矩阵指数计算次数为Ns×Nd×k×4，但是用本文方法，该次数只为Ns次，因此计算效率极大提高。（2）本文方法通过精细积分计算矩阵指数，以替代改进半离散法中通过迭代公式计算矩阵指数，并且避免了求解矩阵指数时的求逆运算，从而有效地减少了计算消耗时间。
4 时域仿真
时域仿真可以预测铣削过程中刀具切削力和位移，广泛应用于铣削稳定性预测和模型验证。本节使用一种考虑跳刀情况下的变齿距铣削的时域仿真来验证所提出的算法[16]。所采用的仿真参数如表1所示[12]。通过绘制每转一次采样数据 （“+”符号）来研究模拟响应的稳定性。
表1 刀具和系统模态参数[12]
Table 1 Parameters of tool and system modal[12]
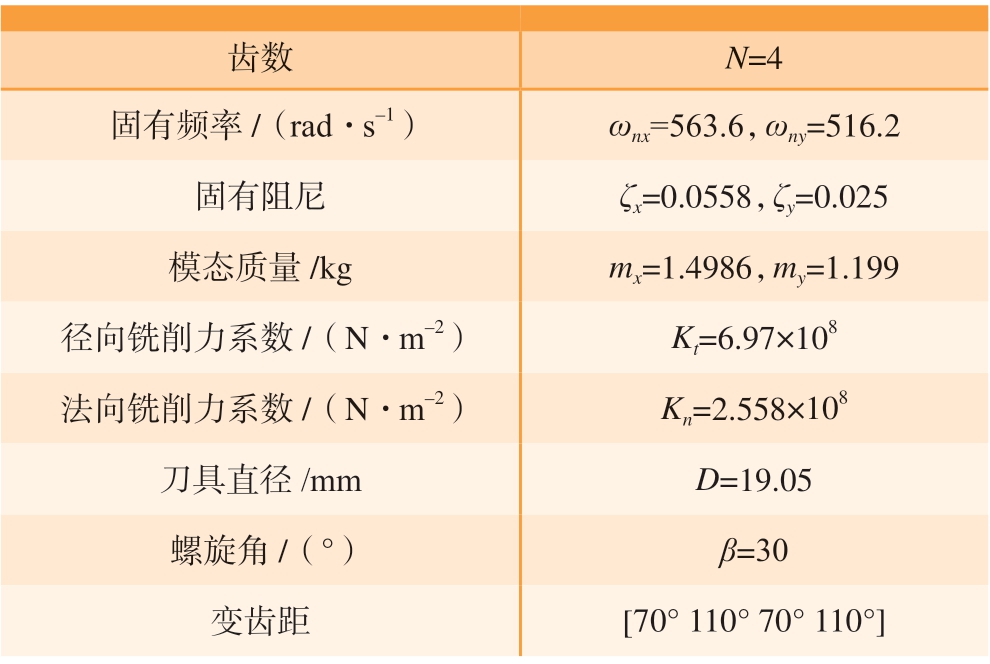
齿数 N=4固有频率/（rad·s–1）ωnx=563.6，ωny=516.2固有阻尼 ζx=0.0558，ζy=0.025模态质量/kg mx=1.4986，my=1.199径向铣削力系数/（N·m–2）Kt=6.97×108法向铣削力系数/（N·m–2）Kn=2.558×108刀具直径/mm D=19.05螺旋角/（°）β=30变齿距 [70° 110° 70° 110°]
图4[12]为文中提出方法和改进半离散法[12]在径向切深率a/D=0.5 和离散间隔数m=72 铣削条件下获得的稳定性叶瓣图。可以看出，文中提出方法与文献[12]中的改进半离散法所得预测结果有一定差异。因此，为了验证哪一种方法预测结果更加精确，选取图4中A（6500r/min，3mm）和B（8500r/min，5.8mm）2 个点进一步研究。从图5和6 可以看出，A 点处于稳定铣削状态，因为每转一次采样数据接近一个固定点值。相反，点B处于不稳定的铣削过程（图7），因为同步采样的数据分布在x 和y 方向的位移图中（图8）。因此本文方法具有更高的铣削稳定性预测精度。
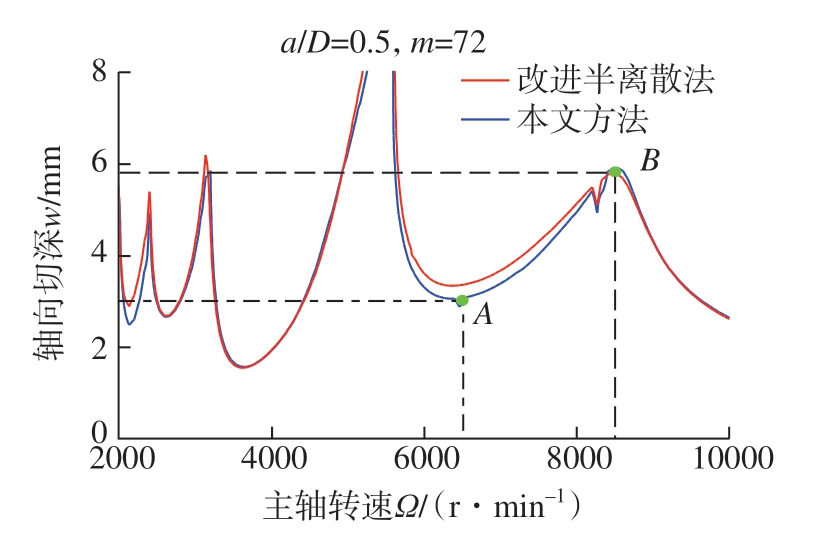
图4 本文方法与改进半离散法预测结果比较[12]
Fig.4 Stability lobe diagrams of proposed method and updated semi-discretization method[12]
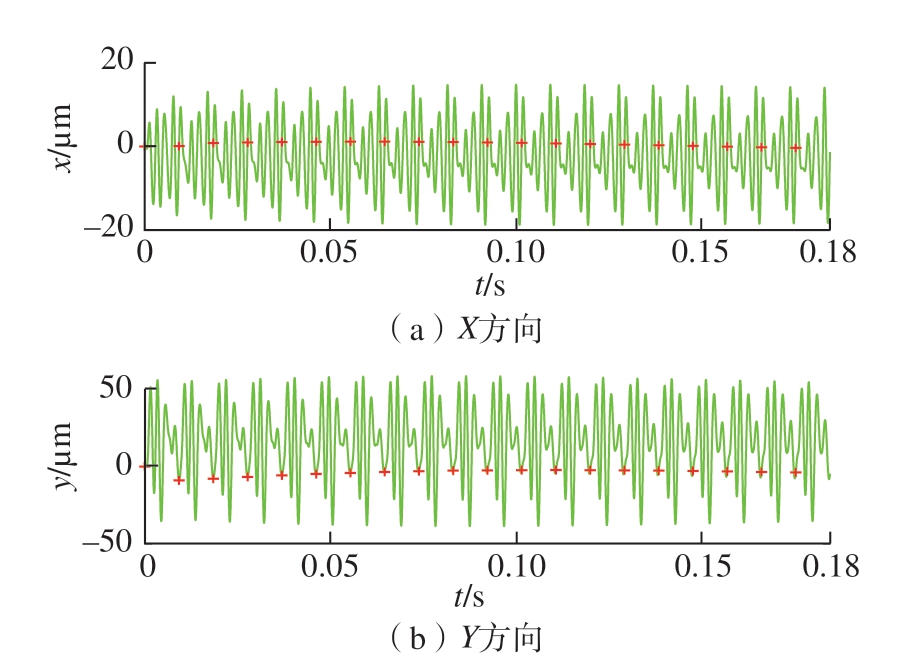
图5 图4中A点x方向（进给）和y方向的位移时程
Fig.5 Time history for the x direction (feed) and y direction displacements obtained from the point A in Fig.4
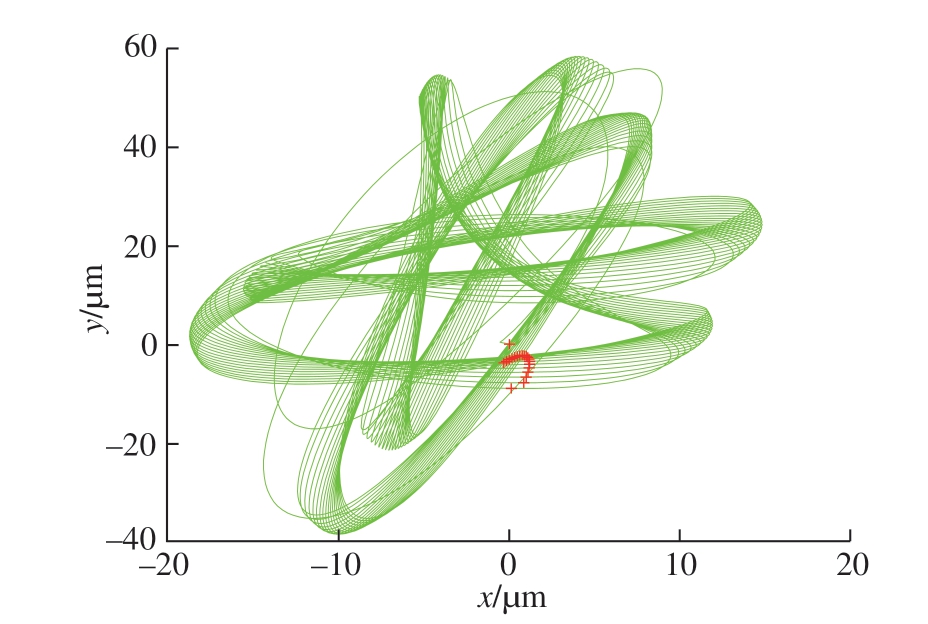
图6 A点x和y方向的位移图
Fig.6 Plot of x and y direction displacements obtained from the point A
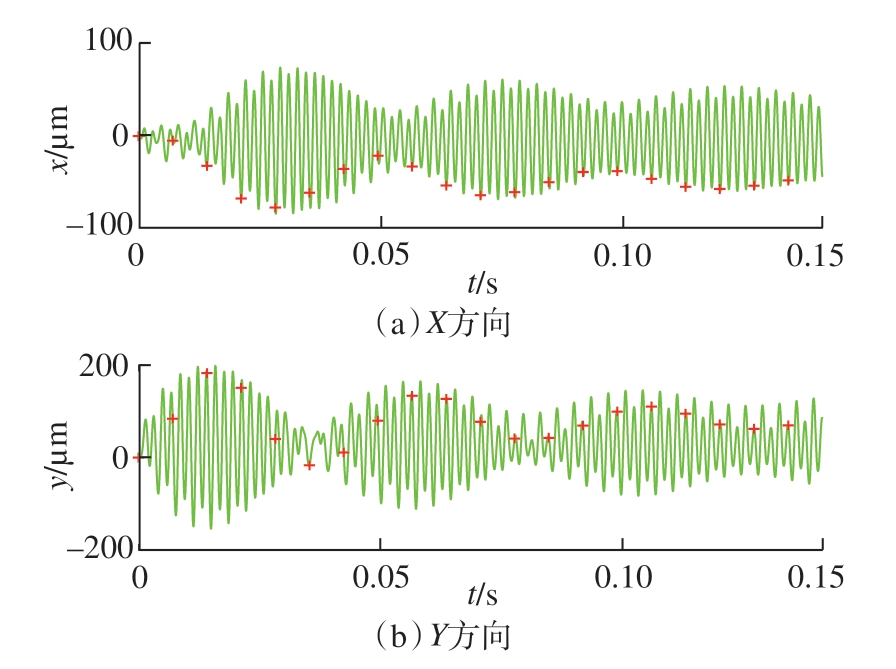
图7 图4中B点x方向（进给）和y方向的位移时程
Fig.7 Time history for the x direction (feed) and y direction displacements obtained from the point B in Fig.4
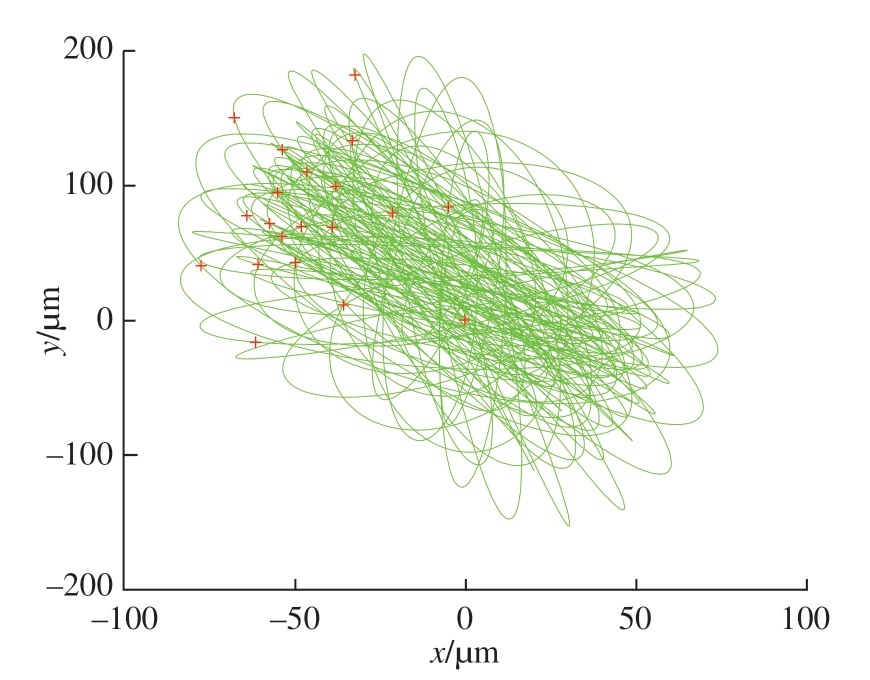
图8 B点x和y方向的位移图
Fig.8 Plot of the x and y direction displacements obtained from the point B
5 结论
针对变齿距铣削过程中变齿距引起的多时滞问题，提出了一种基于精细积分全离散法的变齿距铣削稳定性的预测方法。基于二自由度考虑螺旋角变齿距铣削模型，通过与改进半离散法对比及时域仿真，验证了本文方法的有效性。而且比较结果显示本文方法具有更高的计算效率和预测精度，在同等仿真条件下，本文方法计算效率可以提高约90%，拥有更高的使用价值。
[1]杨昀,张卫红,党建卫,等.航空薄壁件铣削加工动力学仿真技术[J].航空制造技术,2018,61(7): 42-47,69.
YANG Yun,ZHANG Weihong,DANG Jianwei,et al.Dynamic modelling technology on milling process of aerospace thin-walled workpiece[J].Aeronautical Manufacturing Technology,2018,61(7):42–47,69.
[2]李忠群,石晓芳,党剑涛,等.铣削加工过程动力学建模、仿真研究现状与展望[J].航空制造技术,2018,61(16): 16-22.
LI Zhongqun,SHI Xiaofang,DANG Jiantao,et al.Review and prospect on dynamic modeling and simulation for milling process[J].Aeronautical Manufacturing Technology,2018,61(16): 16-22.
[3]吴雅,师汉民,梅志坚,等.金属切削机床颤振理论与控制的新进展[J].中国科学基金,1993,7(2): 99-105.
WU Ya,SHI Hanmin,MEI Zhijian,et al.New developments of theory and cortrol for machine tool chatter[J].Bulletin of National Natural Science Foundation of China,1993,7(2): 99-105.
[4]李忠群,彭岳荣,夏磊,等.基于三阶龙格库塔法的铣削稳定性半解析法预测[J].航空制造技术,2016,59(3/4): 30-33.
LI Zhongqun,PENG Yuerong,XIA Lei,et al.Prediction of chatter stability for milling process using semi-analytical approach based on three-order runge-kutta method[J].Aeronautical Manufacturing Technology,2016,59(3/4): 30-33.
[5]ALTINTAŞ Y,BUDAK E.Analytical prediction of stability lobes in milling[J].CIRP Annals,1995,44(1): 357-362.
[6]MERDOL S D,ALTINTAS Y.Multi frequency solution of chatter stability for low immersion milling[J].Journal of Manufacturing Science and Engineering,2004,126(3): 459-466.
[7]INSPERGER T,STÉPÁN G.Updated semi-discretization method for periodic delay-differential equations with discrete delay[J].International Journal for Numerical Methods in Engineering,2004,61(1):117–141.
[8]DING Y,ZHU L M,ZHANG X J,et al.A full-discretization method for prediction of milling stability[J].International Journal of Machine Tools and Manufacture,2010,50(5): 502-509.
[9]张伟,张开飞,靳刚.基于变齿距铣刀的铣削稳定性试验[J].工具技术,2016,50(1): 33-35.
ZHANG Wei,ZHANG Kaifei,JIN Gang.Experimental investigation of milling stability based on variable pitch cutter[J].Tool Engineering,2016,50(1): 33-35.
[10]WAN M,ZHANG W H,DANG J W,et al.A unified stability prediction method for milling process with multiple delays[J].International Journal of Machine Tools and Manufacture,2010,50(1): 29-41.
[11]ZHANG X J,XIONG C H,DING Y,et al.Variable-step integration method for milling chatter stability prediction with multiple delays[J].Science China Technological Sciences,2011,54(12): 3137-3154.
[12]JIN G,ZHANG Q C,HAO S Y,et al.Stability prediction of milling process with variable pitch cutter[J].Mathematical Problems in Engineering,2013,2013: 932013.
[13]刘宽,孙剑飞.锥球头铣刀铣削力建模及变齿距减振优化设计[J].工具技术,2019,53(4): 54-57.
LIU Kuan,SUN Jianfei.Milling force modeling and optimization of variable reduction for cone ball end milling cutter[J].Tool Engineering,2019,53(4): 54-57.
[14]JIN G,QI H J,LI Z J,et al.Dynamic modeling and stability analysis for the combined milling system with variable pitch cutter and spindle speed variation[J].Communications in Nonlinear Science and Numerical Simulation,2018,63: 38-56.
[15]高强,谭述君,钟万勰.精细积分方法研究综述[J].中国科学: 技术科学,2016,46(12): 1207-1218.
GAO Qiang,TAN Shujun,ZHONG Wanxie.A survey of the precise integration method[J].Scientia Sinica (Technologica),2016,46(12):1207–1218.
[16]POWELL K B.Cutting performance and stability of helical endmills with variable pitch[D].Gainesville: University of Florida,2008.