我国航空事业不断发展，对零件上铆钉孔的制孔精度要求也越来越高，而飞机结构与系统中使用的大量零件包含铆钉孔特征[1]。通常对孔特征检测时，使用三坐标测量仪测出各个孔的坐标尺寸，但这种测量方式效率低，且不适合检测壁板等大型零件；使用专用孔检测工具 （如孔检测样板）对孔的尺寸和形位进行检测，但制造这种高精度检具耗时长且成本高[2]。随着非接触式数字化测量技术的提高，非接触式数字化测量设备也开始更多地应用在飞机零件铆钉孔检测上，这种检测方式具有精度高、效率高、柔性好等特点[3–4]。
目前，在非接触式圆孔测量方面已有了很多的研究与成果，主要有基于视觉图像的测量方法和基于三维点云的测量方法。基于视觉图像的测量方法主要是通过图像处理中的Canny 算子等边界识别算法提取照相测量图像中的边界特征进行圆孔参数拟合[5–6]，但该方法存在空间圆透视投影畸变的问题[7]，影响检测精度。基于三维点云的测量方法是使用三维激光扫描等测量设备获取零件点云，再提取点云中的孔边界特征进行圆孔参数拟合。针对点云中边界特征提取，Jenke 等[8]提出了一种将点云网格化再通过网格的拓扑结构识别边界特征的方法，这种方法可以有效提取点云孔洞边界特征，但需要网格化整个点云，数据量大时算法效率低。因此出现了直接对三维点云提取孔边界特征的方法，该方法通过建立点云空间拓扑关系，并设定某一特定判断机制用于识别边界特征点。Milroy[9]和Yang[10]等通过求解曲率极值提取点云边界，这种方法可以有效地提取比较光滑平坦的数据模型的边界点，不太适用于曲率变化大的数据模型。张杰等[11]提出了一种基于T–Scan测量的薄壁钣金件孔特征重构方法，通过扫描线点云结构中的孔截断线特征识别平面点和孔径点，拟合求解平面和空间圆，但该方法仅限于扫描线点云类型且提取精度受圆孔直径影响。刘增艺等[12]提出了一种曲面孔位视觉测量技术，使用手持式双目视觉线结构光测量曲面得到曲面点云，然后通过交互式方法提取散乱点云圆孔边缘点，进行圆孔拟合，由于该方法在圆孔识别过程中需要人工预先分割出圆孔所在区域，提取效率低且不能满足多孔自动提取需求。
基于以上分析，为解决目前面向铆钉孔检测领域的测量点云中的孔位与孔径参数提取方法限制多和人工交互较多的问题，本文提出了一种基于散乱点云的铆钉孔孔位与孔径提取方法，该方法可以自动识别散乱点云中的全部铆钉孔特征，并精确提取孔位和孔径参数。采用本文方法对试验件散乱点云进行数据处理，验证该方法的实用性与精度。
1 散乱点云预处理
各种数字化测量设备获得的点云根据其点的分布特征分为4 种类型：散乱点云、扫描线点云、网格化点云和多边形点云[13]。散乱点云相对于其他点云类型，其测量点无明显的几何分布特征，呈散乱无序状态，测量点是随机生成的。由于散乱点云无序和随机的分布特性，使用非接触式测量设备测量铆钉孔得到的点云分布情况如图1所示，大部分测量点分布在孔周围平面上，而孔边界测量点可能分布在孔内径或在孔周围平面上，有极少的点正好在孔边界上。
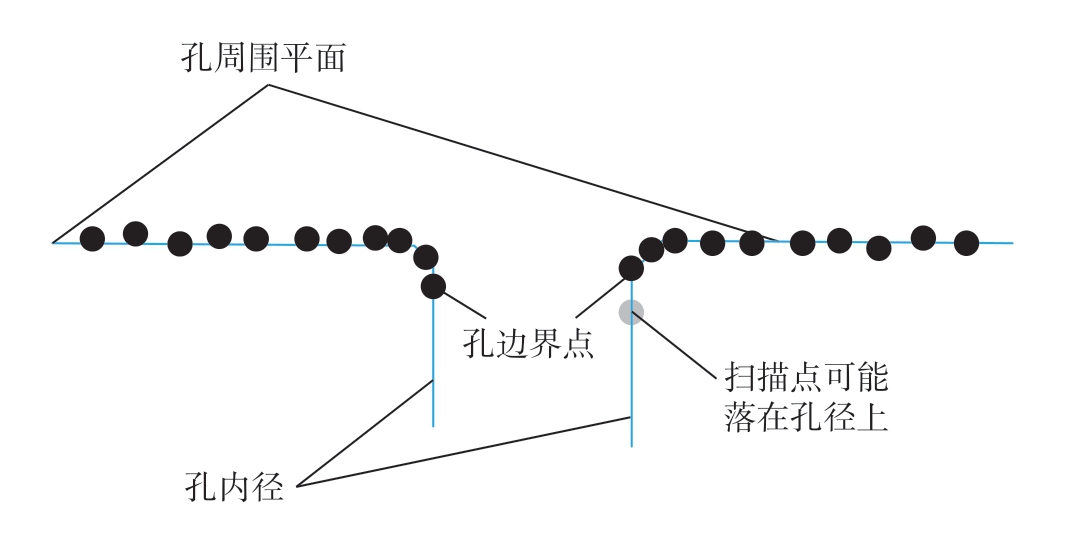
图1 铆钉孔边界测量点云分布
Fig.1 Distribution of measurement point cloud at rivet hole boundary
根据铆钉孔边界测量点云分布情况，本文通过点的k 邻域点几何分布来判断是否为边界点。若某一点为边界点，则其k 邻域点的分布将偏向于一侧 （图2（a））；若某一点不是边界点，则k 邻域点比较均匀地分布在该点周围 （图2（b））。因此，对于铆钉孔的散乱点云，需要进行边界点提取预处理。
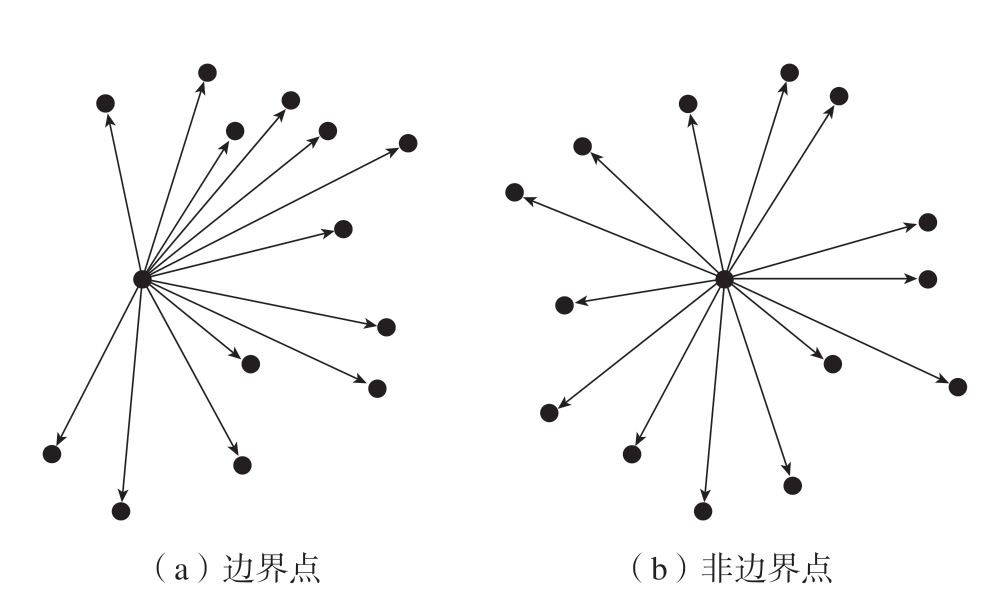
图2 基于k 邻域分布的边界点识别
Fig.2 Boundary point recognition based on k neighborhood distribution
由于散乱点云在数据存储结构中每个点是无规律排布的，在这样的数据结构中查找每个点的k 近邻必须循环每个点，效率低下，因此必须建立点云数据的空间拓扑结构。常见的k 近邻搜索算法有八叉树法、空间栅格法和kd 树法[14–16]。本文采用kd 树法建立散乱点云的kd 树结构，从而查询每个点Pi 的k 邻域点集Nj（j=0，1，2，…，k–1）。
以点Pi 和其k 邻域点Nj（j=0，1，2，…，k–1）构成的点集X 来最小二乘拟合得到Pi 点的局部切平面。在切平面上建立平面坐标系，如图3所示，以Pi 到切平面的投影点Pi′作为坐标原点，Pi′点和N0 点的投影点N0′构成的向量Pi′N0′作为坐标系x 轴，平面法向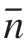
与向量Pi′N0′的叉乘
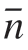×Pi′N0′作为坐标系y 轴。将点集X 中每个点的三维坐标都转换到该平面坐标系上，得到点集X的二维坐标点集合X′（u，V）。
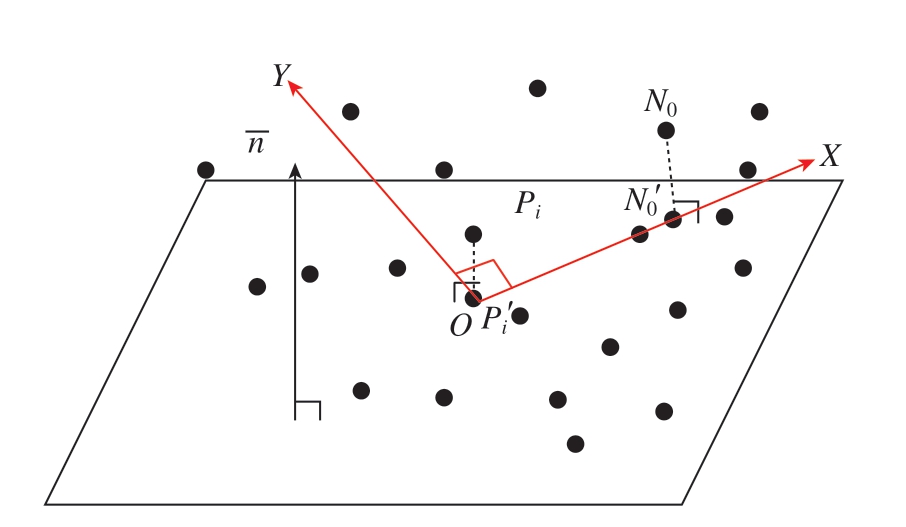
图3 建立局部平面坐标系
Fig.3 Establishing local plane coordinate system
以X′（u，V）中的Pi″点作为向量起点，Nj′点作为向量终点，得到平面向量集
计算
中每个向量到局部坐标系的x 轴的夹角αj和与y 轴的夹角βj。若βj＞π/2，则αj=αj+π。然后将αj以升序进行排列得到角度序列ηj，计算ηj 相邻角度之间的夹角θj=ηj–ηj–1，其中，j∈[1，k–1]，如图4所示。
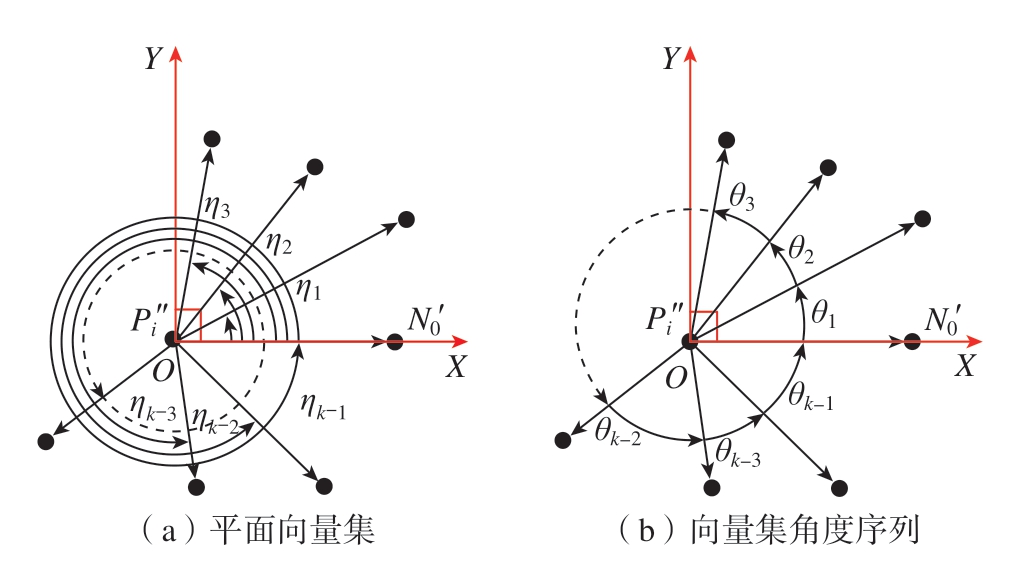
图4 计算相邻向量夹角
Fig.4 Calculating angle between adjacent vectors
当相邻角度序列θj 中的最大夹角θmax 超过最大夹角阈值εθ 时，则点Pi 为边界点，否则点Pi 为非边界点，如图5所示。阈值εθ 的大小要视点云分布情况而定，一般将阈值εθ 设置为π /2 可得到良好的识别结果。
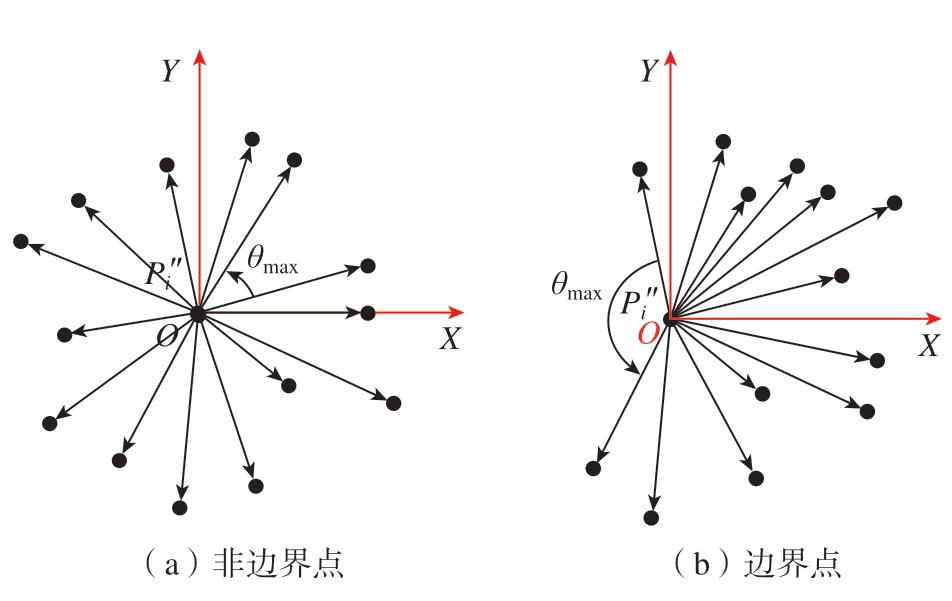
图5 边界点识别
Fig.5 Boundary point recognition
2 铆钉孔边界提取
点云预处理后得到的边界点中不仅包含有多个铆钉孔边界特征，还包含有点云外边界特征以及点云漏洞边界特征，如图6所示。边界点云在数据结构上仍为散乱点云，需要对边界点云建立点云拓扑结构，并对边界点云进行分割，得到属于不同边界特征的边界点云块，最后根据点云块的椭圆度和圆度提取其中的铆钉孔边界。
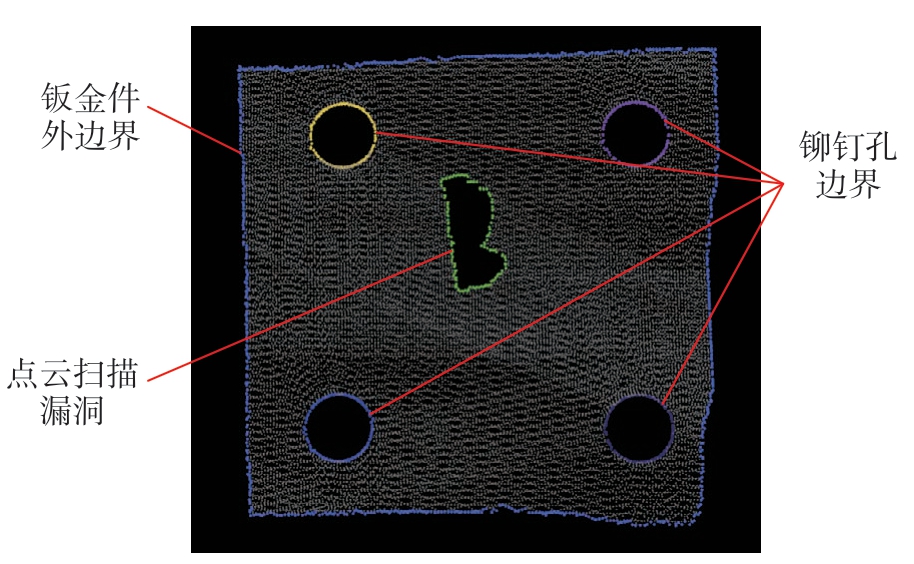
图6 点云中的边界特征
Fig.6 Boundary features in point clouds
2.1 边界点欧式聚类分割
边界点云中的不同边界特征具有同边界特征内相邻点距离连续的特点，即同边界特征内的相邻点距离间距较小，不同边界特征的最近点距离较大。基于此分布特点，本文采用欧式距离聚类分割算法[17]对边界点云中的边界特征进行分割。其边界点云聚类分割步骤如下。
步骤1。对边界点云X 建立kd 树点云结构，方便后续点邻域搜索。
步骤2。创建空的聚类集C 和点集Q。
步骤3。对任意点pi∈X，执行以下操作：（1）把pi加入Q 中 （2）对每个点pj ∈Q，通过边界点kd 树的k 近邻搜索算法找到pj 的k 邻域，放入点集Pjk；对每个pjk∈Pjk，若pjk 不在Q 中，且pjk 与pj 的欧式距离rj< dth（dth 为聚类分割阈值），则把pjk 加入Q 中并从X中移除。（3）当Q 找不到新点加入时，将Q 放入聚类集C 中，清空Q。
步骤4。当边界点云X 中每个点都执行过步骤3 后，就得到了聚类集C。
步骤5。删除聚类集C 中的点数量少于nmin（nmin为最小聚类点数量阈值）的点云块，得到最终聚类集C。
2.2 椭圆拟合结果提取铆钉孔
边界点云聚类分割后得到属于不同边界特征的点云块，对点云块分别拟合平面并把边界点投影到各自拟合平面上。由于铆钉孔边界点的拟合平面与理论铆钉孔所在圆柱相交成一椭圆形状，边界点在拟合平面上的投影点分布在该椭圆周围，如图7所示。因此本文对所有的边界点聚类分割点云块拟合平面椭圆，通过椭圆拟合结果判断是否为铆钉孔边界点。
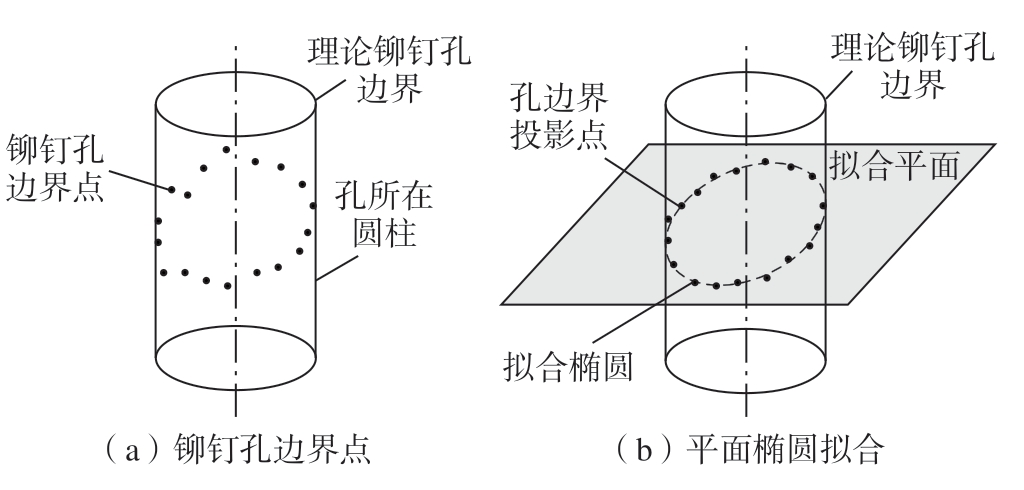
图7 铆钉孔边界点椭圆拟合
Fig.7 Ellipse fitting of rivet hole boundary points
首先对分割点云块ci∈C 最小二乘拟合平面，构建局部平面二维坐标系：以平面上的任一向量
⇀ 作为坐标系x 轴，平面的法向
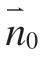⇀与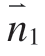
⇀ 的叉乘作为坐标系y轴，点云块ci 中的任一点p0 在平面上的投影点p0′作为坐标系原点。将点云块ci 中所有点的三维坐标转换到构建的局部平面二维坐标系下，得到二维坐标点集合ci′{ pj′（xj′，yj′），j=1，…，mj}。
然后对平面二维坐标点集合ci′最小二乘拟合平面椭圆。设椭圆方程为Ax2+Bxy+ Cy2+ Dx+ Ey+ F=0，并满足椭圆参数约束4AC–B2 > 0，拟合优化目标函数为
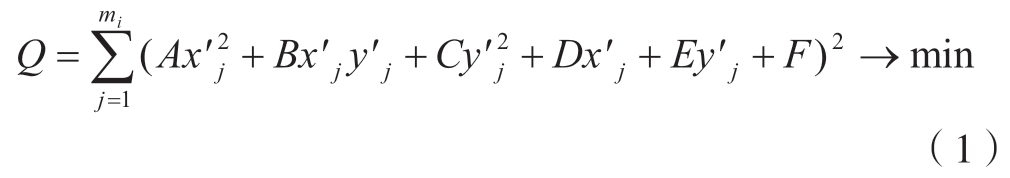
令W=[A，B，C，D，E，F]T
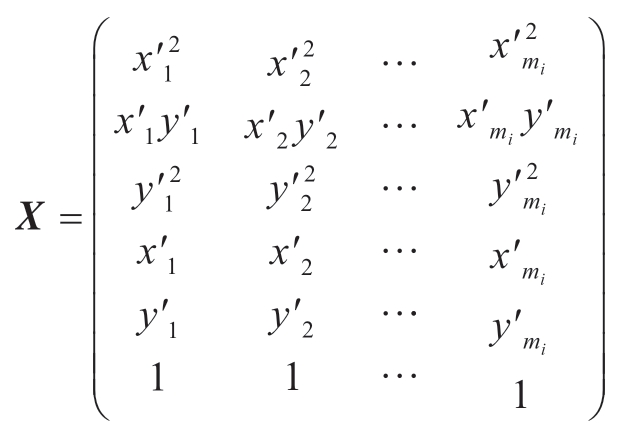
则优化目标为
式中，H=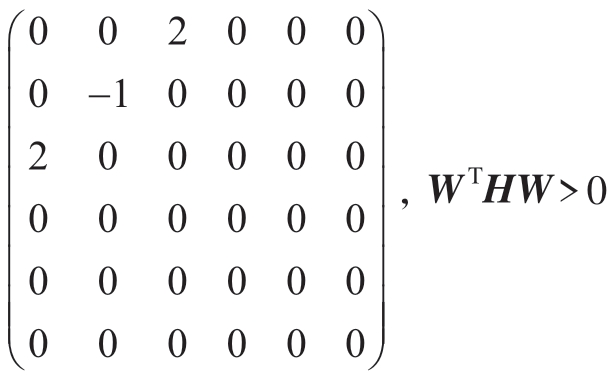
为椭圆参数约束。
由于||WTX||2 时，W 存在缩放因子使得所有W′=aW也满足优化目标，因此可令WTHW=1，于是优化目标就变为
构造拉格朗日函数，即
对式（4）求导，令
=0，可得
对式（4）进行求解。令S=XXT，则SW=λHW，通过求解广义逆矩阵得到6 个可能的解W。由于S 为正定矩阵，所以λ> 0，因此可以用WTHW=1 和λ> 0 这两个条件来筛选得到最终合格的解W=[A，B，C，D，E，F]T。
根据椭圆参数W=[A，B，C，D，E，F]T 计算椭圆圆心Oe（x0，y0）和长短轴半径ae、be：
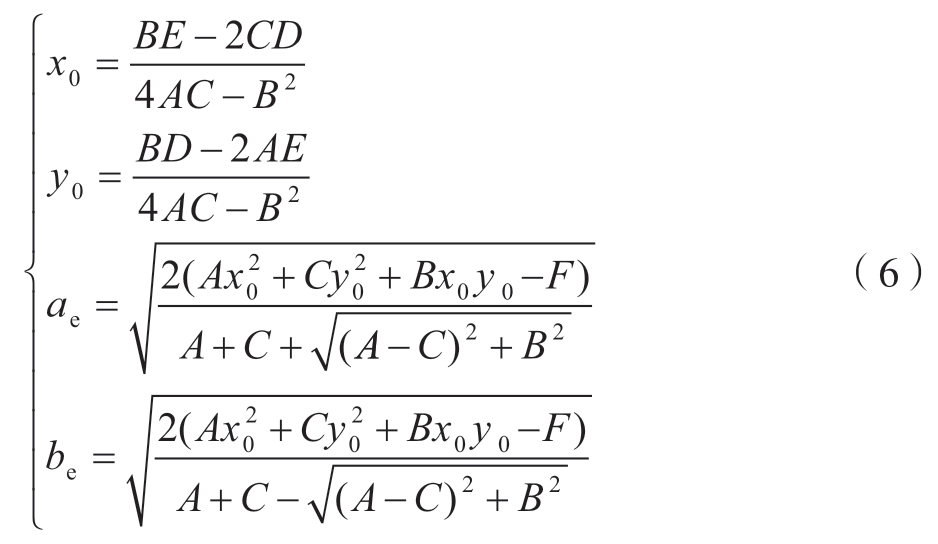
计算椭圆拟合误差Error 与长短轴之比Ratio：
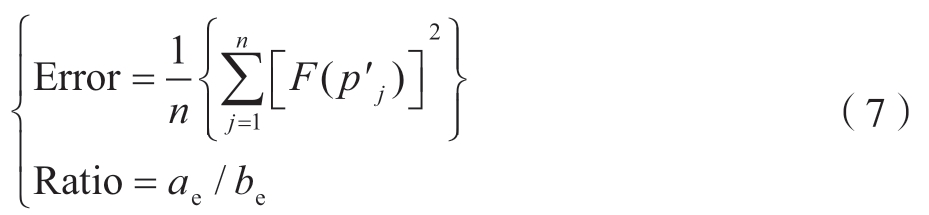
其中，F（p′j）=（Ax′j2+Bxj′yj′+Cy′j2+ Dxj′+Eyj′+F），n 为 点云块ci∈C 中点的数量。
若Error > εe（εe为拟合误差阈值），则为该分割点云块椭圆度低，为非椭圆，即非铆钉孔；若Error < εe，则比较长短轴之比。
若1–εr < Ratio < 1+εr（εr为长短轴比阈值），则该分割点云块圆度高，即为铆钉孔边界，否则为非铆钉孔边界。
若对铆钉孔半径大小有要求，可设置最大半径阈值rmax 和最小半径阈值rmin，将长短轴的均值与rmax 和rmin比较来提取满足半径要求的铆钉孔。
点云中可能有其他不是铆钉孔的圆孔，需要对其进行剔除。计算非铆钉孔理论圆心与该算法拟合椭圆圆心的空间距离dc，若dc 小于一定阈值εd，则剔除该提取孔。
3 铆钉孔参数提取
铆钉孔孔位孔径参数提取采用先投影孔边界点到孔定位面然后最小二乘拟合端面圆的方法。由于孔的边界点中部分点在孔内壁上，使用孔边界点直径求解孔定位面会降低参数提取精度，所以需要寻找孔周围一定范围内的点来拟合孔定位面。然后根据边界点拟合椭圆和孔定位面求得初始铆钉孔参数，根据边界点到初始铆钉孔参数的距离偏差剔除边界点中的噪声点，最后再将孔边界点投影到孔定位面上拟合圆孔。
3.1 孔定位面拟合
在铆钉孔边界提取过程中求得了所有边界点云块的椭圆拟合方程、椭圆圆心Oe 和长短轴ae、be，以拟合椭圆的圆心Oe 作为搜索中心，长短轴均值的ω 倍作为搜索半径Rs，通过建立的散乱点云kd 树结构进行半径邻域搜索找出铆钉孔周围Rs 范围内的点集Pr，如图8所示。
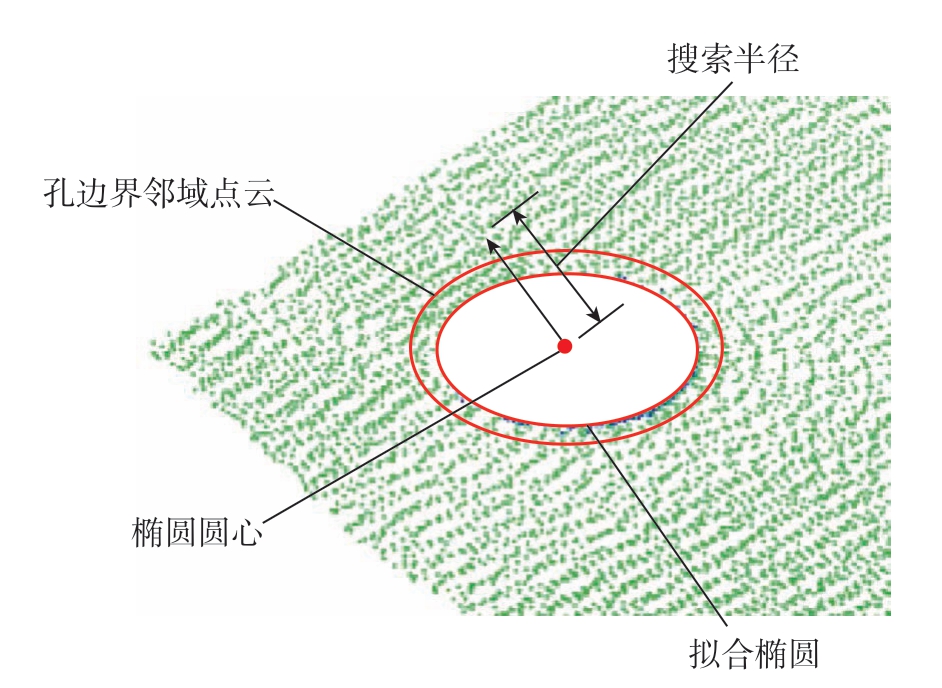
图8 铆钉孔邻域点云搜索
Fig.8 Point cloud search of rivet hole neighborhood
将点集Pr 精确拟合平面。设孔定位面方程为ax+by+cz+d=0，构建拟合目标函数：
用特征值法[18]求解式（8），得到平面参数a、b、c、d。然后计算点集中每个点pi∈Pr 到平面的距离di，当di > εd（εd 为平面拟合误差阈值）时，则认为该点是噪点并剔除，反之保留，最后使用保留的点重新拟合孔定位面。
3.2 端面圆孔拟合
在孔定位面上建立平面二维坐标系，将铆钉孔边界点的三维坐标转换成平面二维坐标点pj（xj，yj）。然后根据拟合椭圆和定位面计算初始铆钉孔参数，将椭圆圆心投影到孔定位面上，投影点即为铆钉孔圆心，椭圆短轴长度即为铆钉孔半径。
计算平面二维坐标点pj（xj，yj）到初始铆钉孔的距离δj，当δj> εc（εc 为圆孔拟合误差阈值）时，则认为该点为噪点并剔除，反之保留，最后使用保留的点重新拟合端面圆。
设端面圆孔方程为（x–A）2+（y–B）2=R2，令a=–2A，b=–2B，c= A2+ B2–R2，则方程变为x2+y2+ax+by+c=0，构建拟合目标函数：
式（9）中分别对a、b、c 求偏导，令偏导等于0，可得：
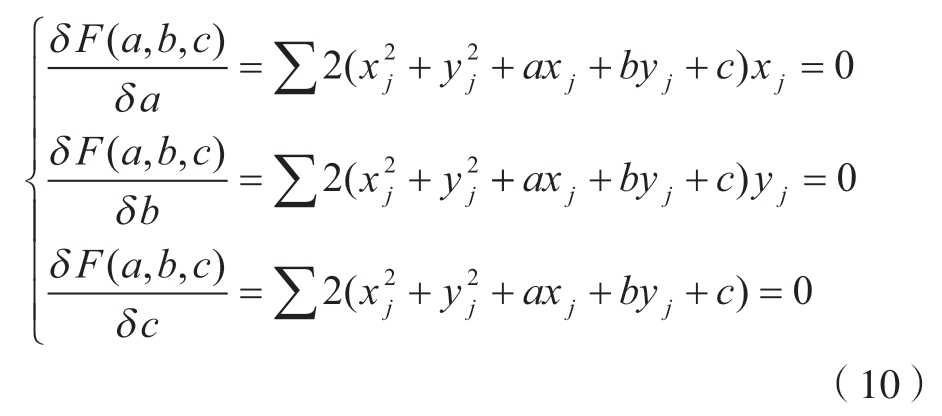
解式（10）可得端面圆参数a、b、c，则端面圆的二维圆心坐标为（x0，y0）=（a/–2，b/–2），半径
把二维圆心（x0，y0）坐标逆变换到三维空间中，得到三维空间圆心坐标（x′0，y′0，z′0），三维空间圆半径R等于平面圆半径r，孔法向（i，j，k）等于拟合平面的法向，铆钉孔参数提取完成。
4 试验验证
4.1 提取效果验证
应用本文方法对散乱点云中的铆钉孔特征进行提取，验证其提取效果，如图9所示。图9（a）为结构光扫描仪测得的某壁板零件的散乱点云数据，所含点数为90688；用本文边界点提取算法提取点云中的边界点，k=50、εθ=π/2 时如图9（b）所示，提取边界点数为3392；用本文边界点云欧氏距离聚类分割算法分割边界点，dth=2mm、nmin=10 时分割结果如图9（c）所示，共分割出14 个边界特征；依据椭圆拟合结果提取铆钉孔边界特征，εe=1、εr=0.05 时提取结果如图9（d）所示，14 个边界特征中的9 个铆钉孔特征全部提取成功。可以看出，本文方法可以有效提取散乱点云中的铆钉孔边界特征。
图9 铆钉孔特征提取效果
Fig.9 Results of rivet hole feature extraction
4.2 提取精度验证
为验证本文提出算法的铆钉孔参数提取精度，采用天远Robot-Scan 扫描仪对铆钉孔试验件进行测量和数据处理，Robot-Scan 相机像素为1000 万像素，平均单张点间距为0.16mm，单张测量精度为15μm。
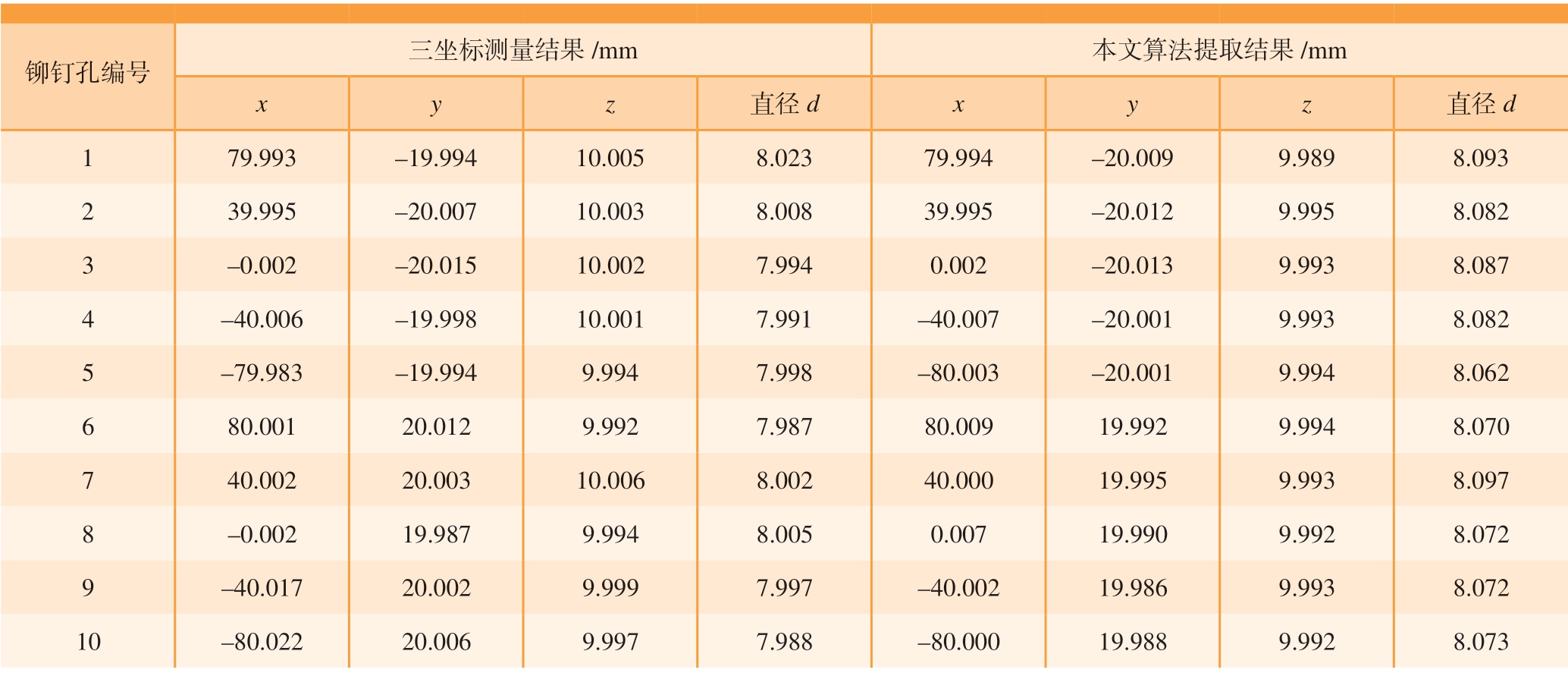
如图10所示，使用Robot-Scan 扫描仪对试验件上的10 个理论直径d=8mm 的铆钉孔进行测量得到试验件散乱点云数据。应用本文方法对数据进行处理，得到铆钉孔参数。然后将三坐标测量机测量试验件得到的参数作为真值，与本文方法提取结果进行比较得出本文方法铆钉孔参数提取偏差。三坐标测量机测量结果和本文参数提取结果如表1所示，铆钉提取偏差如图11所示。可以看出，本文提出方法对试验件上铆钉孔的孔位提取偏差均值为0.017mm，最大值为0.029mm；铆钉孔孔径提取偏差均值为0.0797mm，最大值为0.095mm。
图10 使用Robot–Scan 对铆钉孔试验件测量
Fig.10 Measurement of rivet hole test pieces with Robot–Scan
表1 铆钉孔参数提取试验结果
Table 1 Results of rivet hole parameter extraction experiment
铆钉孔编号 三坐标测量结果/mm 本文算法提取结果/mm直径d x y z 直径d 1 79.993–19.994 10.005 8.023 79.994–20.009 9.989 8.093 2 39.995–20.007 10.003 8.008 39.995–20.012 9.995 8.082 3–0.002–20.015 10.002 7.994 0.002–20.013 9.993 8.087 4–40.006–19.998 10.001 7.991–40.007–20.001 9.993 8.082 5–79.983–19.994 9.994 7.998–80.003–20.001 9.994 8.062 6 80.001 20.012 9.992 7.987 80.009 19.992 9.994 8.070 7 40.002 20.003 10.006 8.002 40.000 19.995 9.993 8.097 8–0.002 19.987 9.994 8.005 0.007 19.990 9.992 8.072 9–40.017 20.002 9.999 7.997–40.002 19.986 9.993 8.072 10–80.022 20.006 9.997 7.988–80.000 19.988 9.992 8.073 x y z
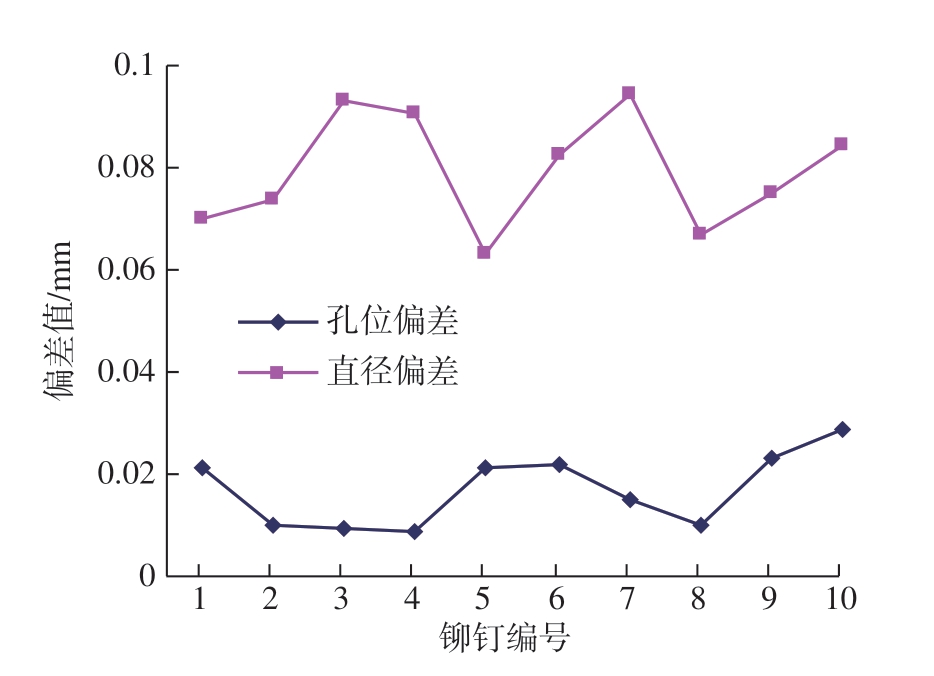
图11 铆钉孔提取偏差
Fig.11 Extraction deviation of rivet holes
从提取结果分析可以看出该方法孔位提取精度较高，可达0.029mm；铆钉孔孔径提取误差相比较孔位提取误差较大，这是由于测量设备测量得到的散乱点云具有一定的点间距，孔边界测量点不一定全部落在孔内径上，从而使得该方法对铆钉孔的直径提取精度相对于孔位提取精度较低。
5 结论
（1）本文提出了一种基于散乱点云的铆钉孔孔位参数提取方法。用该方法对试验件测量散乱点云数据进行了处理。试验表明，该方法能够精确提取散乱点云中的全部铆钉孔特征，且孔位提取精度高，提取精度可达0.029mm。
（2）使用本文方法需要注意，由于测量点不能够保证全部落在铆钉孔径上，导致了铆钉孔孔径提取误差相对较大。因此，为保证有较高的孔径提取精度，需要测量设备精度和点测量密度高，且尽量使测量点能够较多地落在孔内径上。
[1]喻龙,章易镰,王宇晗,等.飞机自动钻铆技术研究现状及其关键技术[J].航空制造技术,2017,60(9): 16–25.
YU Long,ZHANG Yilian,WANG Yuhan,et al.Research status of aircraft automatic drilling and riveting system and its key technology[J].Aeronautical Manufacturing Technology,2017,60(9): 16–25.
[2]徐超.基于视觉测量的沉头孔垂直度检测新技术研究[D].杭州: 浙江大学,2016.
XU Chao.A new method of perpendicularity detection of countersink based on machine vision[D].Hangzhou: Zhejiang University,2016.
[3]罗胜彬,宋春华,韦兴平,等.非接触测量技术发展研究综述[J].机床与液压,2013,41(23): 150–153.
LUO Shengbin,SONG Chunhua,WEI Xingping,et al.Review for the development and research of non-contact measurement technology[J].Machine Tool＆Hydraulics,2013,41(23): 150–153.
[4]杜颖,李真,张国雄.三维曲面的光学非接触测量技术[J].光学精密工程,1999,7(3): 1–6.
DU Ying,LI Zhen,ZHANG Guoxiong.Optical non contact measurement technology for 3D surface[J].Optics and Precision Engineering,1999,7(3): 1–6.
[5]TSUKADA T,WATANABE K,KOIDE M,et al.Development of 3–D position measurement method for a round hole[C]//2011 IEEE International Conference on Mechatronics and Automation.August 7–10,2011,Beijing,China.Piscataway,NJ: IEEE,2011: 624–629.
[6]刘建群,旷辉,李仕勇,等.基于机器视觉的硬盘驱动架尾孔尺寸检测系统[J].机械科学与技术,2007,26(4): 463–467.
LIU Jianqun,KUANG Hui,LI Shiyong,et al.Machine vision system for diameter inspection of tail-hole in a hard-disk driving shelf[J].Mechanical Science and Technology,2007,26(4): 463–467.
[7]徐博,习俊通,陈晓波.基于亚像素的圆孔几何参数立体视觉高精度测量[J].航空计算技术,2008,38(3): 94–96.
XU Bo,XI Juntong,CHEN Xiaobo.High accurate stereo vision metrology for geometric parameters of 3D-hole based on subpixel[J].Aeronautical Computing Technique,2008,38(3): 94–96.
[8]JENKE P,WAND M,BOKELOH M,et al.Bayesian point cloud reconstruction[J].Computer Graphics Forum,2006,25(3): 379–388.
[9]MILROY M,BRADLEY C,VICKERS G.Segmentation of a wrap-around model using an active contour[J].Computer-Aided Design,1997,29(4): 299–320.
[10]YANG M,LEE E.Segmentation of measured point data using a parametric quadric surface approximation[J].Computer-Aided Design,1999,31(7): 449–457.
[11]张杰,黄翔,李泷杲,等.基于T–scan 测量的薄壁钣金件孔特征重构[J].工程科学学报,2017,39(6): 917–923.
ZHANG Jie,HUANG Xiang,LI Shuanggao,et al.Hole feature reconstruction of thin-walled sheet metal parts based on T-scan measurement[J].Chinese Journal of Engineering,2017,39(6): 917–923.
[12]刘增艺,江开勇,林俊义.散乱点云特征边缘交互提取[J].计算机工程与应用,2016,52(6): 186–190.
LIU Zengyi,JIANG Kaiyong,LIN Junyi.Interactive extraction of boundary of specified target feature on scattered point cloud[J].Computer Engineering and Applications,2016,52(6): 186–190.
[13]蔡清华.散乱数据的NURBS 曲面建模与数控加工技术研究[D].沈阳: 沈阳工业大学,2004.
CAI Qinghua.Study on NURBS surface modeling and NC machining technique of scattered data[D].Shenyang: Shenyang University of Technology,2004.
[14]SU Y T,BETHEL J,HU S W.Octree-based segmentation for terrestrial LiDAR point cloud data in industrial applications[J].ISPRS Journal of Photogrammetry and Remote Sensing,2016,113: 59–74.
[15]刘晓东,刘国荣,王颖,等.散乱数据点的k 近邻搜索算法[J].微电子学与计算机,2006,23(4): 23–26,30.
LIU Xiaodong,LIU Guorong,WANG Ying,et al.K-neighbor searching of surface reconstruction from scattered points[J].Microelectronics＆Computer,2006,23(4): 23–26,30.
[16]安雁艳,杨秋翔,冯欣悦,等.点云数据的k 近邻快速建立改进算法[J].计算机工程与设计,2014,35(12): 4228–4232.
AN Yanyan,YANG Qiuxiang,FENG Xinyue,et al.Improved algorithm for finding k nearest neighbors of point cloud data[J].Computer Engineering and Design,2014,35(12): 4228–4232.
[17]LIU Y,ZHONG R F.Buildings and terrain of urban area point cloud segmentation based on PCL[J].IOP Conference Series: Earth and Environmental Science,2014,17: 012238.
[18]官云兰,程效军,施贵刚.一种稳健的点云数据平面拟合方法[J].同济大学学报(自然科学版),2008,36(7): 981–984.
GUAN Yunlan,CHENG Xiaojun,SHI Guigang.A robust method for fitting a plane to point clouds[J].Journal of Tongji University (Natural Science),2008,36(7): 981–984.