超声回波检测技术具有穿透能力好、检测灵敏度高、检测准确性好等优点[1],已广泛应用于航空制件检测领域,如航空发动机盘件径轴向裂纹检测[2]、航空发动机压气机叶片检测[3]等。由于受到环境噪声和超声回波采集装备自身结构噪声的影响,使得接收的超声回波信号被干扰,有用细节特征被掩盖,失去物理研究意义,考虑到超声回波信号是非线性、非平稳信号,传统的线性滤波方法并不适用。
常用的超声回波降噪方法有小波变换和经验模态分解 (Empirical mode decomposition,EMD)及其延伸算法。小波变换具有在时频域范围内分析信号的优势,但是在对信号降噪处理时,效果易受到小波基函数选取、分解层数、阈值处理方法的影响,且对于较低信噪比信号小波变换难以取得较好效果[4]。EMD 无须基函数,根据信号本身特性自适应分解成不同尺度的本征模态分量 (Intrinsic mode functions,IMFs),但是由于信号本身间歇性和外部噪声的影响,EMD 易产生模式混叠问题[5]。EEMD 是在EMD 的基础上,利用白噪声的零均值特性,对原始信号多次添加、抵消白噪声以减少噪声引起的模式混叠,但EEMD 预处理过程耗时过长,处理效率不高,且本征模态分量中有用信号的特征提取一直是国内外学者重点研究的问题[6]。刘忠等[7]基于HeurSure 阈值准则对EMD 处理后前一半IMF 阈值处理后的信号和后一半IMF 分量叠加重构实现对水轮机空化声发射信号的提取。张婷等[8]基于EEMD,对先后利用Savitzky–Golay(SG)滤波和阈值降噪对噪声主导分量进行处理,SG 是对数据在时域内基于局域多项式的最小二乘拟合,比较适合对降噪后信号的平滑修正。Gan 等[9]根据IMF 间功率谱密度关系确定噪声强度,采用硬阈值函数进行处理,但是无法克服硬阈值函数不连续的问题。Bai 等[10]提出了完全集合经验模态分解–排列熵–时域峰值检测的混合降噪方法,原始信号经完全集合经验模态分解,利用排列熵确定需要滤波的IMFs,最后采用时域峰值检测方法估计分析信号的瞬时频率,能够有效提取故障特征,但是时域峰值检测方法通用性不强,存在局限性。还有很多学者对EEMD和小波阈值降噪方法开展研究,并应用到局部放电[11]、爆破[12]、惯性导航[13]等多个领域,但小波阈值是估计值,在有噪声的先验知识前提下比较有效,并且对于噪声主导的IMFs,信噪比较低,小波阈值难以实现有用特征的精细提取。
降噪的目的是在剔除噪声干扰的同时尽量减少信号失真,为此,提出改进CEEMD–MRSVD 降噪方法,首先互补集合经验模态分解不需要过多的集合次数,且减少了重构误差,较EEMD 有更好的时效性和分解效果,然后根据信号和噪声相关性对IMFs 进行噪声主导和信号主导区分,针对两部分IMFs 有用细节特征提取,提出了优化多分辨率奇异值分解方法,更加精细、策略性地抑制噪声的同时,尽可能多保留有用信号特征。
1 改进CEEMD–MRSVD 降噪策略
1.1 CEEMD 降噪原理
作为时域分析方法,EMD 根据时域尺度上信号特征将信号分解为若干个IMFs,包含了信号的所有细节信息[14]。对于含噪信号,经EMD 处理后得到噪声主导和信号主导IMFs,但是EMD 存在模式混叠,即不同尺度上含有相同的信号特征,或是不同的信号特征分布在相同的尺度上。EEMD 是在EMD 基础上的改进算法,利用白噪声零均值特性,通过多次叠加平均减少异常事件的影响,一定程度上减少了模式混叠,然而,为充分消除异常事件的干扰,需要多次叠加白噪声,就导致处理效率不高。CEEMD 在此基础上做了进一步改进,其以正负对的形式叠加白噪声,相应减少了迭代次数,提高了计算效率。算法具体步骤如下。
(1)对原始信号s(t)叠加N 组正负对形式的白噪声n(t),得到两组模态分量:

式中,n(t)为白噪声;m1(t)、m2(t)为叠加白噪声后的信号。
(2)对叠加白噪声后的信号进行EMD 处理,得到本征模态分量,设定cij 为第i 个信号的第j 个IMF。
(3)经过平均计算和多组分量组合得到的分解结果为CCEMD 算法中一般取叠加白噪声的对数为100,白噪声幅值取0.01~0.10。
1.2 多分辨率奇异值分解
多分辨率奇异值分解是基于SVD 加入矩阵二分递推结构,将复杂信号分解为与原始信号相关性较少的细节信号,然后将与原始信号相关性较大的近似信号提取出来,根据噪声、信号和原始信号相关特性,细节信号中噪声占主导,近似信号中有用信号占主导,多分辨率奇异值分解的下一步思路是对近似信号构造行数为2 的矩阵进行继续分解,以此递推,得到多层细节信号和近似信号,详细分解过程如下[15]。
(1)对原始信号s(t)=(x1,x2,…,xN)构造行数为2 的如下矩阵:
(2)对H∈R(N–1)×2 进行奇异值分解:
式中,U∈R(N–1)×(N–1)、V∈R2×2为正交矩阵;Λ为对角矩阵;Λ=(diag(σ1,σ2),0)或其转置,秩为2。
(3)根据奇异值分解原理,较大奇异值对应信号为有用信号主导的近似信号Aj,较小的奇异值对应信号为噪声主导的细节信号Dj,再对近似信号进行继续分解,详细过程如图1所示。
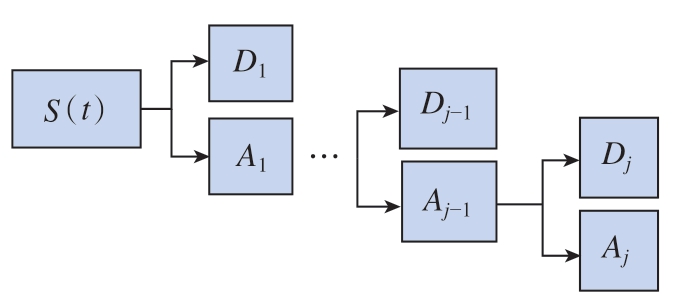
图1 MRSVD 分解过程
Fig.1 Decomposition process of MRSVD
(4)经过对信号多层次分解,可以将隐藏在复杂干扰下的信号特征提取出来,最后通过对提取信号进行逆运算重构实现降噪,MRSVD 无须确定有效奇异值的重构阶次,并且对于强噪声背景下有用细节特征提取较SVD 更加精细。
1.3 CEEMD–MRSVD 优化实施策略
原始信号经EMD 处理得到一系列IMFs,其中噪声主要分布在阶数较小的几个高频IMFs 中,信号主要分布在高阶IMFs 中。根据噪声和原始信号的互相关特征小于有用信号和原始信号的互相关特征,并且,噪声主导分量互相关系数变化缓慢,而信号主导分量互相关系数急剧增加,如图2所示[8]。
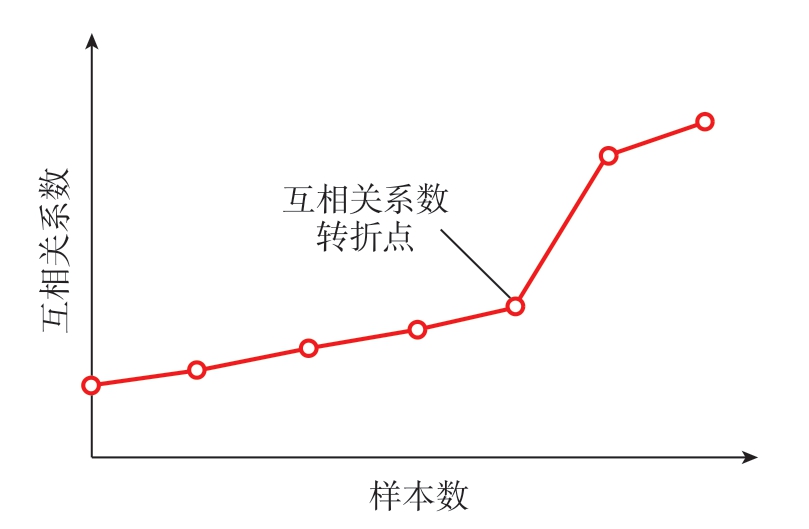
图2 互相关系数波形图[8]
Fig.2 Mutual relations waveform diagram[8]
CEEMD 处理后本征模态分量与原始信号的相关系数可以表示为

式中,IMFi 为第i 个IMF 分量;s(t)为原始信号。各IMFs和原始信号互相关系数曲率的最小值为高低频分量的临界点,曲率计算公式为[8]
式中,Ri 为第i 个IMF 和原始信号的相关系数。
在利用MRSVD 对IMFs 处理时,对于高频噪声主导IMFs,噪声主要分布在细节信号中,近似部分仍会含有部分噪声,对近似部分进行进一步分解,继续分离噪声细节,最后重构近似部分为有用信号提取,其分解过程可以参照图1;对于有用信号主导的IMFs,其中只含有少部分噪声,MRSVD 每次分量为2 个,则分解出的细节信号必定会含有部分有用信号,为了减少信号失真并剔除残余噪声,对细节信号进行下一步SVD 分解,其过程如图3所示。对IMFs 进行上述优化处理是根据不同IMF 中噪声强度不同,策略性选择细节信号或近似信号进行继续SVD 分解,目的是在分离噪声的同时,尽可能减少有用信号的流失。
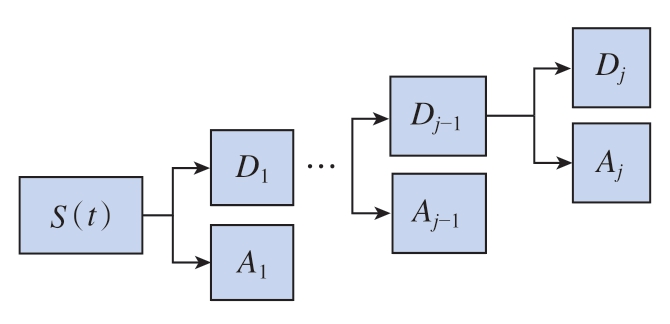
图3 信号主导IMFs 处理过程
Fig.3 Signal-dominated IMFs processing
考虑到原始信号中含有局部脉冲干扰的情况下,利用MRSVD 提取出的信号难免会存在毛刺、尖锐等问题,提取的信号不够平滑,因此本文利用SG 平滑滤波方法对MRSVD 提取的信号进行平滑修正处理。SG 平滑滤波方法是在时域内移动窗口条件下基于多项式最小二乘拟合的滤波方法[16],在平滑掉局部干扰的同时不会改变信号原有的宽度和形状。因此改进EEMD–MRSVD 的实施流程如图4所示。
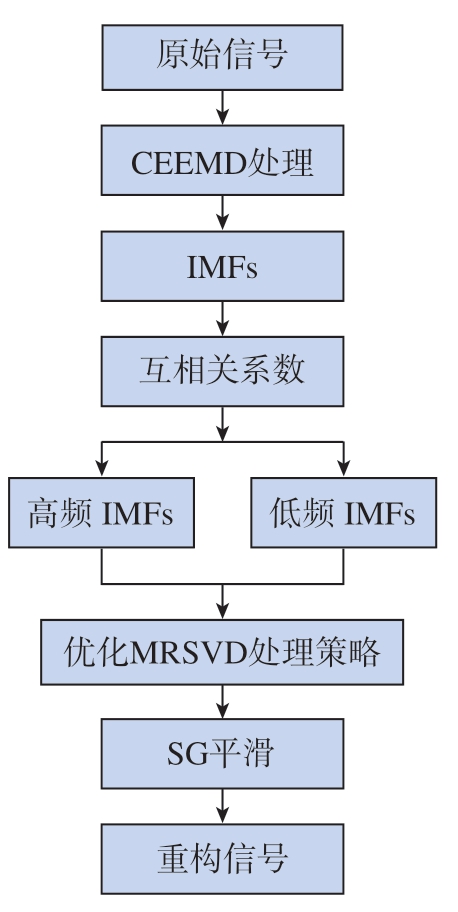
图4 改进EEMD–MRSVD 的实施流程
Fig.4 Process of improved EEMD–MRSVD
2 验证分析
2.1 仿真分析
为验证所提方法的有效性和优越性,以叠加5dB的“Doppler”时间序列为仿真对象,以信噪比 (Signal–to–Noise Ratio,SNR)和均方误差 (Mean square error,MSE)评价降噪效果,信噪比表征算法降噪能力大小,均方误差的物理意义是表示去噪后信号和原始信号的平均偏离程度,求解信噪比和均方误差的公式为

式中,x′(n)为去噪后的序列;x(n)为原始时间序列;var(·)为方差;x′(n)–x(n)为信号中的剩余噪声;N 为时间序列样本总数;n 为时间序列中第n 个样本。
对含有高斯白噪声的多普勒信号经CEEMD 分解结果如图5所示,可以看出,在干扰附近或信号起始位置的模式混叠基本被抑制,没有明显地在相同时间尺度上分布有噪声和信号两种特征的现象 (箭头所示位置),且低频IMF 中干扰得到很大程度削弱。图6为EEMD小波阈值降噪结果,其中,叠加平均白噪声次数为100,白噪声幅值为0.1,小波阈值采用软阈值函数,选用HeurSure 阈值准则进行处理,可以看出信号整体比较粗糙,局部干扰没有得到有效抑制。考虑到MRSVD 分解方式为2 的指数级分解,分解次数过多容易导致有用特征的流失[17],本文选取分解次数为3,图7(a)为CEEMD–MRSVD 尚未经过SG 平滑滤波处理的提取结果,其中箭头所示位置尚残留毛刺,信号整体不够平滑;图7(b)为经过SG 滤波方法平滑后的信号,局部毛刺尖锐被平滑掉,降噪后的序列图明显变得光滑、饱满,已无明显尖刺,证明了所提方法的优越性。
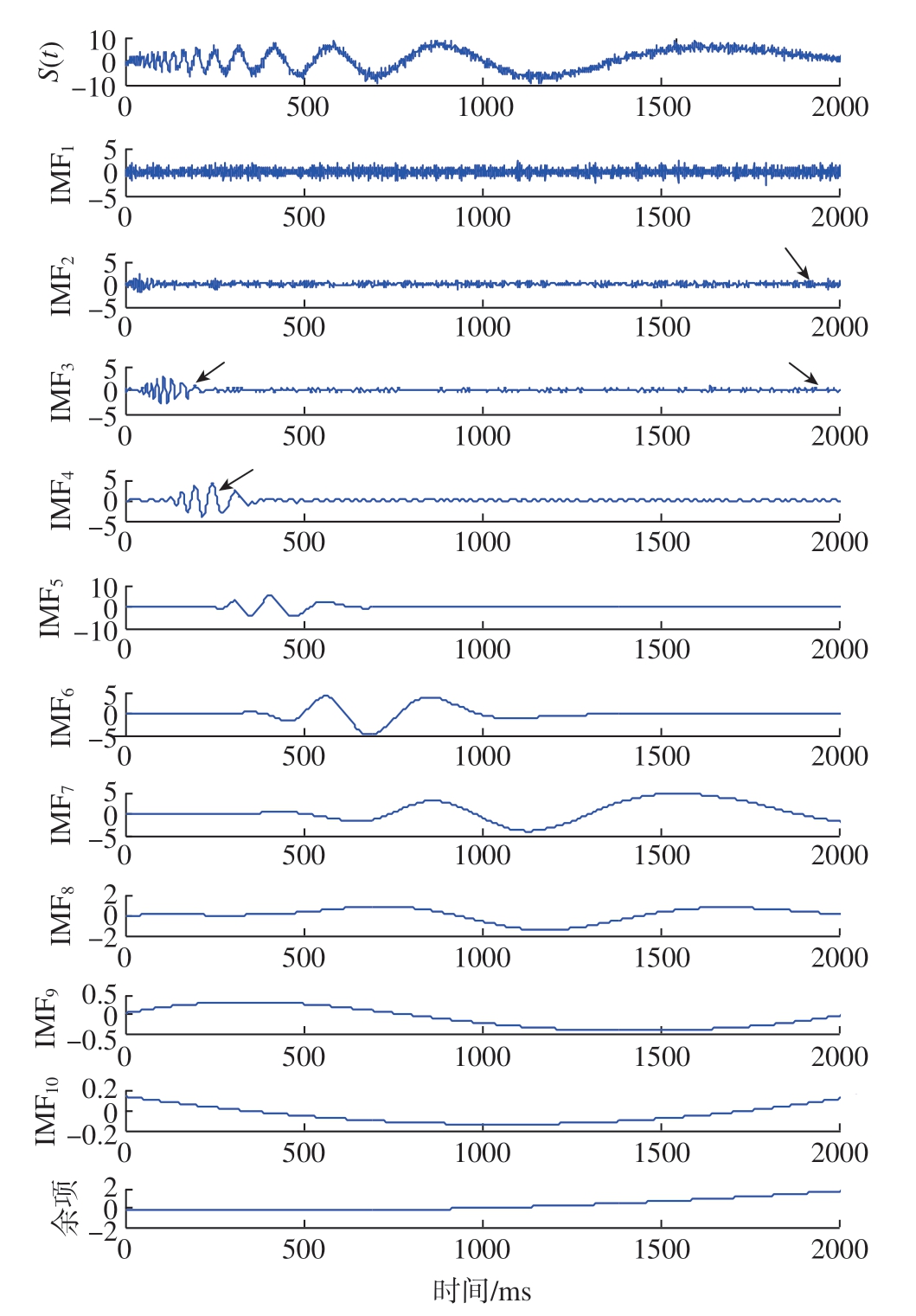
图5 多普勒信号EEMD 结果
Fig.5 EEMD results of Doppler signal
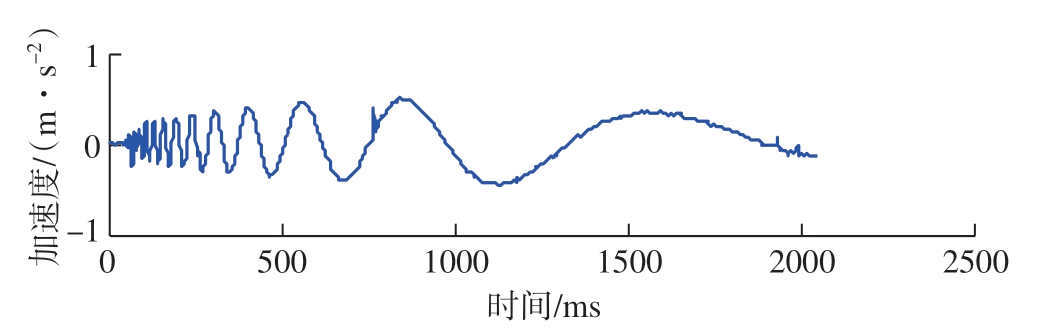
图6 EEMD 小波阈值降噪结果
Fig.6 EEMD-wavelet threshold denoising results
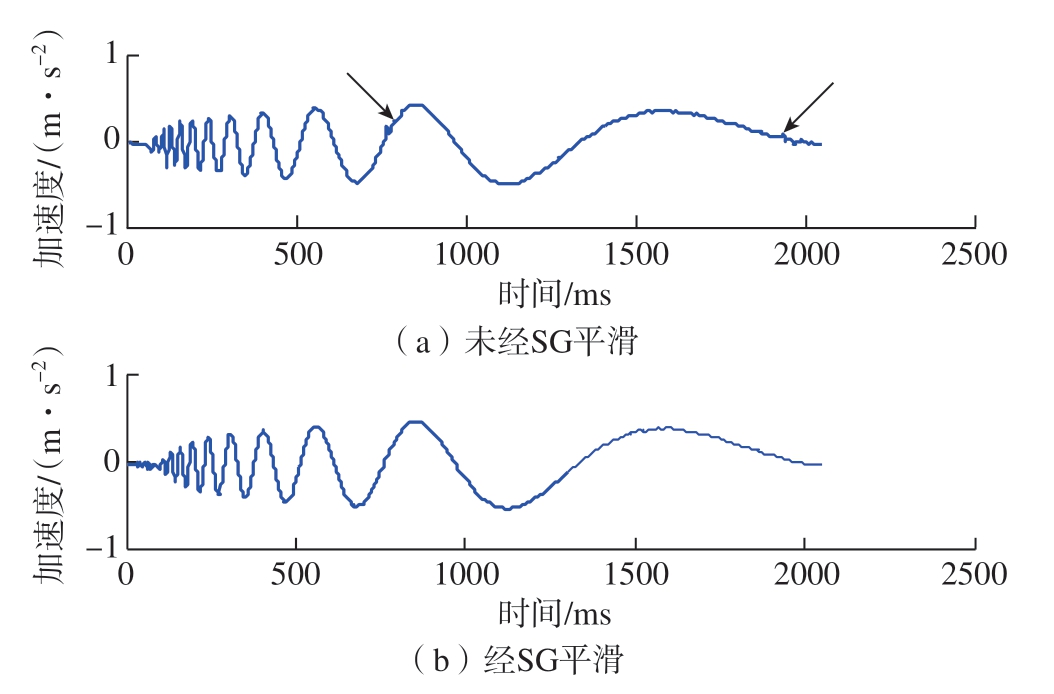
图7 改进CEEMD–MRSVD 降噪结果
Fig.7 Improved CEEMD–MRSVD denoising results
表1列出了EEMD 小波阈值和本文方法降噪后信号的SNR 和MSE,可以看出,本文方法将降噪后信号的信噪比较EEMD 小波阈值降噪方法在原始信号为5dB 的基础上提高了1.9dB。同时给出了不同信噪比原始信号降噪后的SNR 和MSE,可以看出,对于较高信噪比的原始信号,两种方法降噪效果相差较小,对于较低信噪比的原始信号,本文方法具有更好的降噪效果,证实了所提方法在较低信噪比条件下提取有用细节特征的优势。
表1 两种方法降噪结果比较
Table 1 Comparison of denoising results between two methods
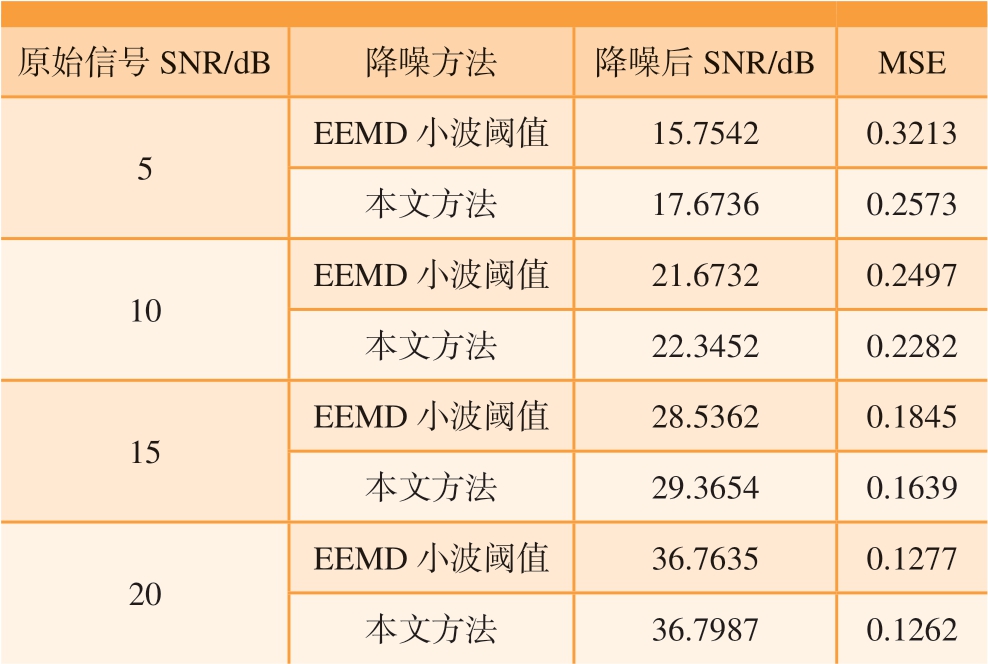
原始信号SNR/dB 降噪方法 降噪后SNR/dB MSE 5 EEMD 小波阈值 15.7542 0.3213本文方法 17.6736 0.2573 10 EEMD 小波阈值 21.6732 0.2497本文方法 22.3452 0.2282 15 EEMD 小波阈值 28.5362 0.1845本文方法 29.3654 0.1639 20 EEMD 小波阈值 36.7635 0.1277本文方法 36.7987 0.1262
2.2 试验分析
超声回波常见用于缺陷检验,通过超声波探头发射脉冲波到被试品内部,当被试品存在缺陷时,就会产生来自缺陷的回波信号,通过分析回波幅值、位置等信息评估缺陷位置和大小。超声检测试验系统如图8所示。参试设备包括超声波相控阵探伤仪、超声传感器、含缺陷的金属试件、计算机等,其中超声波相控阵探伤仪采集超声传感器检测到的超声回波信号,然后传输给计算机进行分析处理。
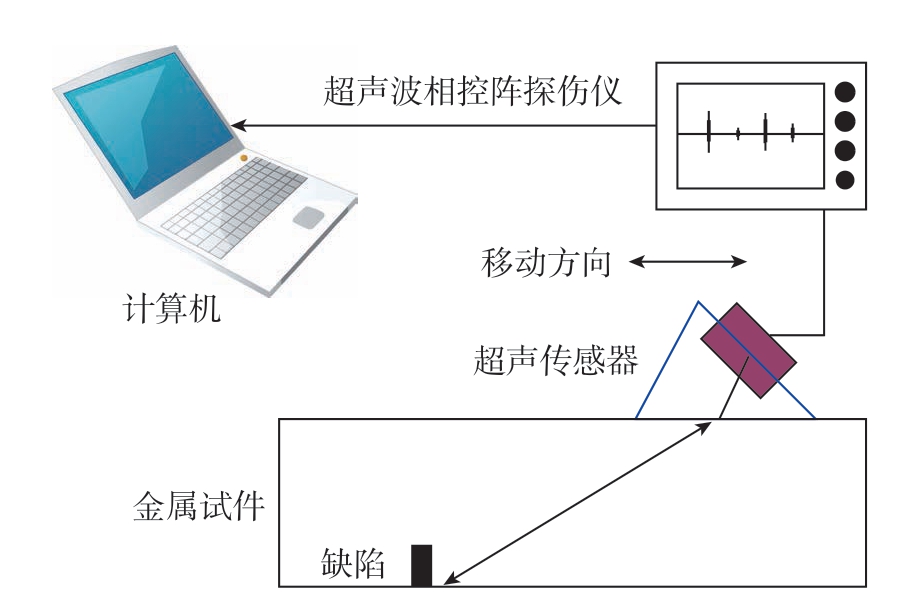
图8 超声检测试验系统
Fig.8 Ultrasound testing system
在超声回波检测过程中,单回波模型表示为
式中,α、τ、fc 分别表示带宽因子、回波抵达时间和中心频率;φ、β 表示信号本身相位和幅值。设置采样频率为100Hz,采样时间为20μs,单回波干净和染噪信号如图9(a)和(b)所示,可见信号被噪声淹没,很难直观发现回波特征,给后续缺陷特征提取带来很大困难。图9(c)和(d)分别为EEMD 小波阈值和本文所提方法降噪后的效果图。为了更加直观比较两种方法的降噪效果,图9(e)和(f)给出了两种方法降噪后信号和干净单回波信号的拟合误差结果,可以看出,在同一数量级条件下,本文方法降噪后信号和干净信号的拟合误差更小,说明本文方法降噪后信号更加接近干净信号,在剔除噪声的同时保留了有用细节特征,减少了信号失真。单回波信号表示单个缺陷的识别结果,由单回波模型延伸模拟多回波信号,可以模拟识别多个不同位置、大小的缺陷。多回波干净和染噪信号如图10(a)和(b)所示,分别用EEMD 小波阈值和本文所提方法对多回波染噪信号进行降噪处理,由图10(e)和(f)可以看出,结果和单回波一致,充分说明了所提方法的优越性。在Matlab R2014a 运行条件下,EEMD 小波阈值运行参数:白噪声总体平均次数选为100;白噪声幅值系数为0.1;小波阈值函数采用软阈值函数,阈值选用HeurSure 阈值准则,分解层数为3;本文方法运行参数为:白噪声对数为100,幅值取0.05,MRSVD 分解次数为3。两种方法的运行时间:EEMD 小波阈值为19.34s;本文方法为10.23s。可以看出,所提方法运行时间较EEMD 小波阈值节约了47.1%,证实了所提方法在时效性上的优势。
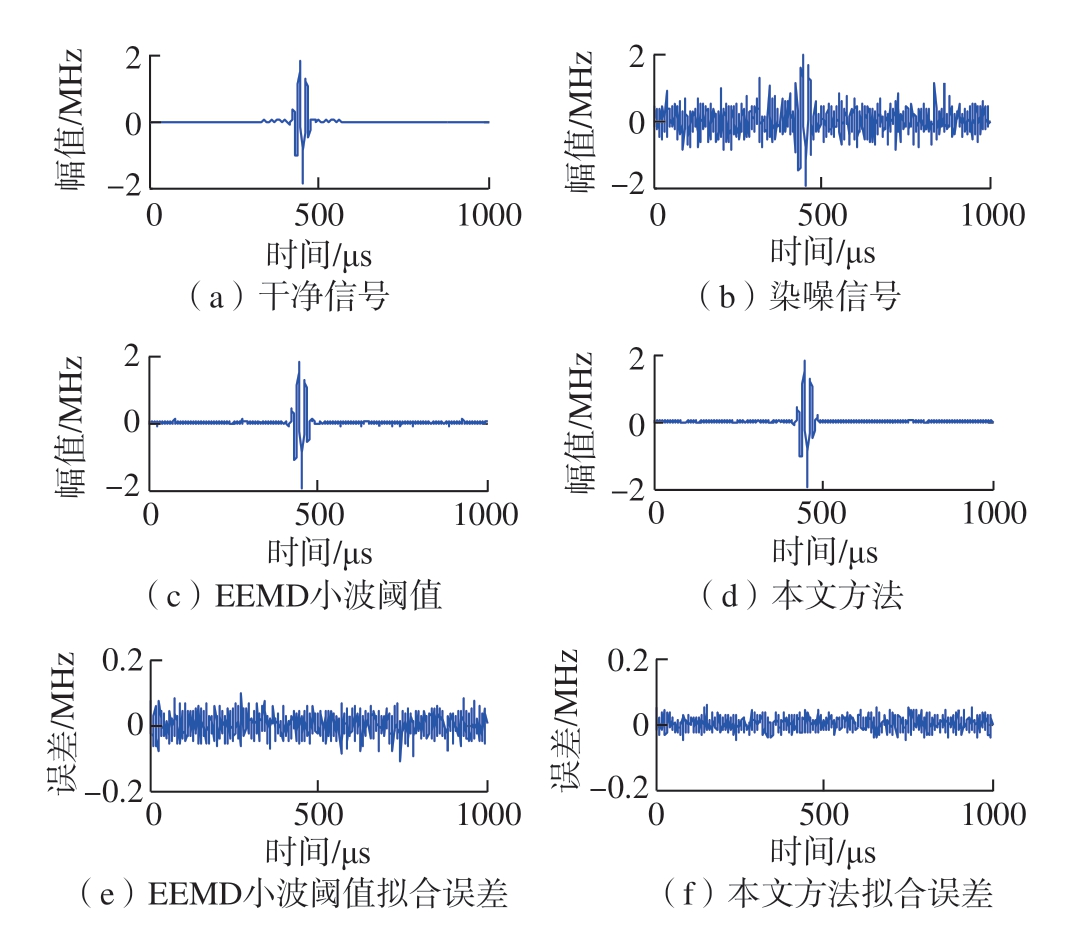
图9 单回波信号降噪结果
Fig.9 Denoising results of single echo signals
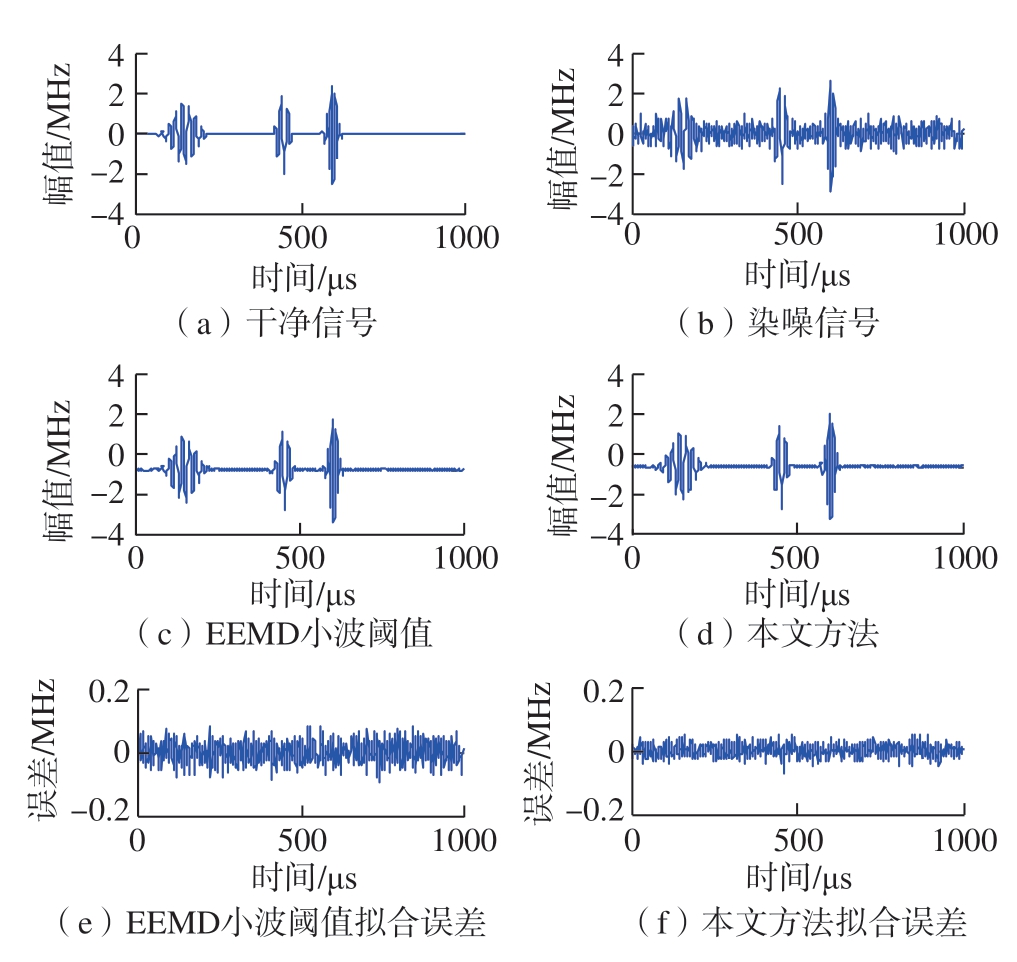
图10 多回波信号降噪结果
Fig.10 Denoising results of multiple echo signals
3 结论
提出了改进互补集合经验模态分解–多分辨率奇异值分解降噪方法。根据噪声强度不同,提出对噪声主导和信号主导的本征模态分量进行策略性优化的多分辨率奇异值处理方法,实现对有用信号的精细提取,经Savitzky–Golay 平滑滤波,进一步提升信号的完整性/平滑性。进行了仿真信号、单回波信号和多回波信号降噪处理,结果表明,本文所提方法不仅减少了EMD 模式混叠,提升了降噪效果,更加逼真还原了有用信号细节特征,而且较EEMD 小波阈值减少了运行时间,为工程实际应用提供了一种简便、有效的信号处理手段。
[1]袁梅,董韶鹏,鲍鹏宇.结构损伤在线监测回波信号处理方法研究[J].航空制造技术,2013,56(18): 78–83.
YUAN Mei,DONG Shaopeng,BAO Pengyu.Review on structural damage online monitoring based on ultrasonic echo wave signal processing[J].Aeronautical Manufacturing Technology,2013,56(18):78–83.
[2]杨平华,梁菁,王铮,等.航空发动机盘件径轴向裂纹底波监控超声检测方法研究[J].航空材料学报,2014,34(5): 88–92.
YANG Pinghua,LIANG Jing,WANG Zheng,et al.Research on ultrasonic back-wall echo monitoring method for radial-axial crack of aircraft engine disk[J].Journal of Aeronautical Materials,2014,34(5):88–92.
[3]杨雪娟,陈果,张震,等.航空发动机涡轮叶片热障涂层结构状态超声检测方法研究[J].南昌航空大学学报(自然科学版),2013,27(4): 59–64.
YANG Xuejuan,CHEN Guo,ZHANG Zhen,et al.Ultrasonic test for thermal barrier coatings of aeroengine turbine blade[J].Journal of Nanchang Hangkong University (Natural Sciences),2013,27(4): 59–64.
[4]YU X,DONG F,DING E J,et al.Rolling bearing fault diagnosis using modified LFDA and EMD with sensitive feature selection[J].IEEE Access,2018,6: 3715–3730.
[5]MOCTEZUMA L A,MOLINAS M.EEG-based subjects identification based on biometrics of imagined speech using EMD[J].Brain Informatics,2018,118: 201–208.
[6]李余兴,李亚安,陈晓.基于EEMD 的舰船辐射噪声特征提取方法研究[J].振动与冲击,2017,36(5): 114–119.
LI Yuxing,LI Yaan,CHEN Xiao.Ships’ radiated noise feature extraction based on EEMD[J].Journal of Vibration and Shock,2017,36(5): 114–119.
[7]刘忠,宋嘉城,邹淑云,等.基于EMD 的水轮机空化声发射信号阈值降噪方法[J].动力工程学报,2018,38(6): 501–507.
LIU Zhong,SONG Jiacheng,ZOU Shuyun,et al.Threshold denoising method for acoustic emission signals from hydraulic turbine cavitation based on EMD[J].Journal of Chinese Society of Power Engineering,2018,38(6): 501–507.
[8]张婷,李双田.改进的EEMD 算法在时域航空电磁信号降噪中的研究[J].信号处理,2016,32(7): 771–778.
ZHANG Ting,LI Shuangtian.Research of improved EEMD algorithm for time-domain airborne electromagnetic signal de-noising[J].Journal of Signal Processing,2016,32(7): 771–778.
[9]GAN Y,SUI L F,WU J F,et al.An EMD threshold de-noising method for inertial sensors[J].Measurement,2014,49: 34–41.
[10]BAI L L,HAN Z N,LI Y F,et al.A hybrid de-noising algorithm for the gear transmission system based on CEEMDAN–PE–TFPF[J].Entropy,2018,20(5): 361–376.
[11]王姣,李振春,王德营.基于CEEMD 的地震数据小波阈值去噪方法研究[J].石油物探,2014,53(2): 164–172.
WANG Jiao,LI Zhenchun,WANG Deying.A method for wavelet threshold denoising of seismic data based on CEEMD[J].Geophysical Prospecting for Petroleum,2014,53(2): 164–172.
[12]邓青林,赵国彦.基于EEMD 和小波的爆破振动信号去噪[J].爆破,2015,32(4): 33–38.
DENG Qinglin,ZHAO Guoyan.De-noising of blast vibration signal based on EEMD and wavelet[J].Blasting,2015,32(4): 33–38.
[13]刘韬,徐爱功,隋心.惯性导航EEMD 区间阈值降噪方法[J].测绘学报,2018,47(7): 907–915.
LIU Tao,XU Aigong,SUI Xin.EEMD interval threshold de-noising method for inertial navigation[J].Acta Geodaetica et Cartographica Sinica,2018,47(7): 907–915.
[14]李琳,张永祥,刘树勇.改进EMD–小波分析的转子振动信号去噪方法[J].噪声与振动控制,2015,35(2): 170–174.
LI Lin,ZHANG Yongxiang,LIU Shuyong.Denoising of rotor vibration signals based on improved EMD–wavelet analysis[J].Noise and Vibration Control,2015,35(2): 170–174.
[15]BHATNAGAR G,SAHA A,WU Q M J,et al.Analysis and extension of multiresolution singular value decomposition[J].Information Sciences,2014,277: 247–262.
[16]陈华舟,潘涛,陈洁梅.多元散射校正与Savitzky–Golay平滑模式的组合优选应用于土壤有机质的近红外光谱分析[J].计算机与应用化学,2011,28(5): 518–522.
CHEN Huazhou,PAN Tao,CHEN Jiemei.Combination optimization of multiple scatter correction and Savitzky–Golay smoothing modes applied to the near infrared spectroscopy analysis of soil organic matter[J].Computers and Applied Chemistry,2011,28(5): 518–522.
[17]ZHAO X Z.Theory of multi-resolution singular value decomposition and its application to signal processing and fault diagnosis[J].Journal of Mechanical Engineering,2010,46(20): 64–75.